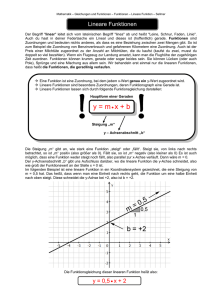
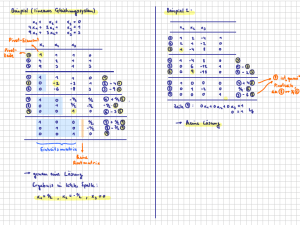
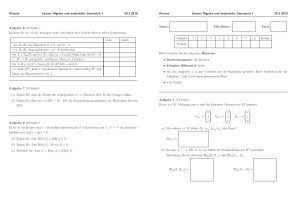
Wirtschaftsmathematik - für International

Wirtschaftsmathematik
für International Management (BA)
Wintersemester 2012/13
Stefan Etschberger
Hochschule Augsburg
Vorlesungsbegleitende Unterlagen
Arbeitsmaterial: Foliensatz, Aufgabenskript,
Mitschrift auf Wunsch
Bücher (unterstützend):
Luderer, Bernd (2003). Einstieg in die Wirtschaftsmathematik.
5. Aufl. Stuttgart, Leipzig, Wiesbaden: Teubner.
Opitz, O. (2004). Mathematik für Wirtschaftswissenschaftler.
9. Aufl. München: Oldenbourg.
Schäfer, Wolfgang, Kurt Georgi, Gisela Trippler und Christa Otto
(2009). Mathematik-Vorkurs: Übungs- und Arbeitsbuch für Studienanfänger. 6., durchges. Aufl., [1. Nachdr.] Studium. Wiesbaden: Teubner. ISBN: 9783835100367.
Sydsaeter, Knut und Peter Hammond (2008). Essential Mathematics for Economic Analysis. 3. Aufl. Prentice Hall. ISBN:
0273713248.
Opitz (2004) Luderer (2003) Sydsaeter und Hammond (2008) Schäfer u. a. (2009)
Studiengang
Vorkenntnisse,
zusätzliches Interesse,
Tempo
Vorlesung
(ab 10.10.2012)
Prüfung
International
Management
Betriebswirtschaft
normal
höher
normal
Mathe für IM
Mathe Plus
Mathe für BW
Mi ab 14.00
Raum B2.14
Klausur für IM
(90 Min., 6 Credits)
Mi ab 8.00
Di ab 11.30
jeweils Raum W1.05
Zusatzklausur
(30 Min., 2 Credits
als Wahlfach)
Mi ab 14.00
Raum W2.10
Klausur für BW
(90 Min., 6 Credits)
Prüfung
Klausur:
Klausur am Ende des Semesters
Bearbeitungszeit: 90 Minuten
Erreichbare Punktzahl: 50
Hilfsmittel:
Schreibzeug,
Taschenrechner, der nicht 70! berechnen kann,
ein Blatt (DIN-A4, vorne und hinten beschrieben) mit
handgeschriebenen Notizen (keine Kopien oder Ausdrucke),
Danach (optional): Für Teilnehmer der Mathe-Plus Vorlesung
noch eine 30-minütige Teilklausur über zusätzliche Inhalte
(2 Wahlfachcredits zusätzlich möglich)
Probleme, ...
...die Sie nach dem Kurs lösen können:
Sich widersprechende Politiker entlarven,
Bedarf an Einzelteilen in Produktionsprozessen bestimmen,
die Käuferfluktuation zwischen verschiedenen Produkten im
Zeitablauf analysieren,
die Nachfragereaktion von Kaffee auf Preisänderungen
bestimmen
Ihre Rente ausrechnen
Große Kisten in kleine Ecken quetschen
Möglichst viel Gewinn bei möglichst wenig
Ressourcenverbrauch machen
EduVote
Umfragen in Vorlesung mit EduVote:
System zur Abstimmung im Hörsaal
Herunterladen oder direkt benutzen unter eduvote.de
User-Id: [email protected]
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
Integration
1
Grundlegende Bausteine
Reelle Zahlen
Ganzzahlige Potenzen
Algebraische Umformungen
Brüche
Nichtganzzahlige Potenzen
Logarithmen
Zahlen
Mathematik
Stefan Etschberger
„Vernünftige“ Zahlen
Natürliche Zahlen: N
Ganze Zahlen; Z
1. Grundlegende
Bausteine
Rationale Zahlen: Q
1.1. Reelle Zahlen
Rationale Zahlen liegen unendlich dicht auf dem
Zahlenstrahl
1.3. Algebraische
Umformungen
1.2. Ganzzahlige Potenzen
Aber
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
Aber: Lösungen von Gleichungen wie
3. Lineare Algebra
x2 = 2
4. Lineare Programme
5. Folgen und Reihen
haben keine rationale Lösung
Folge: Es gibt auch irrationale Zahlen: Z.B.
6. Finanzmathematik
√
2
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
11
Dezimaldarstellung rationaler Zahlen
Mathematik
Stefan Etschberger
Zahldarstellung über Vielfache von 10
Die meisten Leute schreiben Zahlen heute im Dezimalsystem
Damit möglich: Schreiben jeder natürlichen Zahl mit
Kombinationen der Ziffern 0, 1, . . . , 9
3
2
1
0
z.B.: 2009 = 2 · 10 + 0 · 10 + 0 · 10 + 9 · 10
z.B.: 2,36 = 2 · 10 + 3 ·
1
101
+6·
z.B.: 10
3 = 3,333 . . . = 3 + 3 ·
(unendlicher Dezimalbruch)
1
101
1
102
(endlicher Dezimalbruch)
+3·
1
102
+3·
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
1.4. Brüche
Mit Dezimalkomma: Schreiben rationaler Zahlen möglich
0
1. Grundlegende
Bausteine
1
103
+ ...
Jede rationale Zahl kann man über einen periodischen
Dezimalbruch darstellen
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
12
Definition reeller Zahlen
Mathematik
Stefan Etschberger
Eine reelle Zahl hat die Form
x = m, a1 a2 a3 . . .
1. Grundlegende
Bausteine
Dabei: m: Ganze Zahl
und ai (mit i = 1, 2, . . .) ist unendliche Folge von Ziffern
von 0 bis 9
Damit: Nichtperiodische Dezimalbrüche heißen irrationale
Zahlen
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
Beispiele:
√
2,
√
− 17,
3. Lineare Algebra
π,
0,1121121112 . . .
4. Lineare Programme
5. Folgen und Reihen
Rechenoperationen +, −, ·, : mit reellen Zahlen ergeben
wieder reelle Zahlen
Einzige Ausnahme: p0 ist keine reelle Zahl
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
13
Ganzzahlige Potenzen
Mathematik
Stefan Etschberger
Abkürzung: 3 · 3 · 3 · 3 = 34 oder
Allgemein:
1
2
·
1
2
·
1
2
·
1
2
·
1
2
=
1 5
2
an = a · a · . . . a
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
Rechenregeln:
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
1.4. Brüche
1
a
= n
a
ar · as = ar+s
−n
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
3. Lineare Algebra
s
(ar ) = ar·s
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
Achtung: im allgemeinen
7. Reelle Funktionen
8. Differenzieren 1
(a + b)r 6= ar + br
9. Differenzieren 2
10. Integration
14
Anwendungsbeispiel für Potenzen
Mathematik
Stefan Etschberger
Zinseszinsen
Anlage von 1000 € auf Bankkonto
Verzinsung jeweils am Jahresende 2,5 %
Zinsen nach einem Jahr: 1000 · 2,5 % = 25
Kontostand am Jahresende:
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
1000 + 1000 · 2,5 % = 1000 · (1 + 0,025) = 1000 · 1,025
1.6. Logarithmen
(1000 · 1,025) + (1000 · 1,025) · 0,025
= 1000 · 1,025 · (1 + 0,025)
2
= 1000 · 1,025 · 1,025 = 1000 · 1,025
Allgemein: Kontostand ist bei Anfangskapital K und einem
Zinssatz von i nach n Jahren
n
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
Kontostand am Ende des zweiten Jahres:
Kn = K · (1 + i)
1.3. Algebraische
Umformungen
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
15
Wichtige Rechenregeln
Mathematik
Stefan Etschberger
Es gilt für beliebige Zahlen a, b, c:
(1) a + b = b + a
(2) (a + b) + c = a + (b + c)
1. Grundlegende
Bausteine
(3) a + 0 = a
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
(4) a + (−a) = 0
1.3. Algebraische
Umformungen
(5) ab = ba
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
(6) (ab)c = a(bc)
1.6. Logarithmen
(7) 1 · a = a
2. Grundlegende
Werkzeuge
(8) aa−1 = 1 (für a 6= 0)
3. Lineare Algebra
(9) (−a)b = a(−b) = −ab
(10) (−a)(−b) = ab
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
(11) a(b + c) = ab + ac
7. Reelle Funktionen
8. Differenzieren 1
(12) (a + b)c = ac + bc
9. Differenzieren 2
10. Integration
16
Einfache Algebra
Mathematik
Stefan Etschberger
Algebraische Ausdrücke
Beispiel für einen algebraischen Ausdruck:
4x2 y2 + 7y4 x − 9xy + 11xy4
2 2
Die einzelnen Summanden (4x y , −9xy, usw.) heißen
Terme des Ausdrucks
Faktoren vor den Buchstaben (4, 7, −9, 11): Koeffizienten
Terme, die sich maximal durch Koeffizienten unterscheiden,
genannt Koeffizienten von der gleichen Art, können
zusammengefasst werden:
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4
4
4
7y x + 11xy = 18xy
4. Lineare Programme
5. Folgen und Reihen
Binomische Formeln
2
2
(a + b) = a + 2ab + b
6. Finanzmathematik
2
(a − b)2 = a2 − 2ab + b2
(a + b)(a − b) = a2 − b2
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
17
Faktorisieren
Mathematik
Stefan Etschberger
Primfaktorzerlegung
Zahlen können multiplikativ in Primfaktoren zerlegt werden,
Beispiel
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
64 = 8 · 8 oder
1848 = 2 · 2 · 2 · 3 · 7 · 11
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
1.4. Brüche
Faktorisierung algebraischer Ausdrücke
1.5. Nichtganzzahlige
Potenzen
Analog bei algebraischen Ausdrücken:
Zerlegung in irreduzible Faktoren
1.6. Logarithmen
2. Grundlegende
Werkzeuge
Beispiele:
3. Lineare Algebra
4. Lineare Programme
5a2 b3 − 15ab2 = 5 · a · b2 · (ab − 3)
16a4 b2 − 9b4 = b2 · 4a2 − 3b · 4a2 + 3b
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
18
Brüche
Mathematik
Stefan Etschberger
Division zweier Zahlen (a, b ∈ R, b 6= 0) kann durch Bruch geschrieben
werden
a:b=
a
= a/b
b
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
Rechenregeln (a, b, c ∈ R):
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
a·c
a
=
b·c
b
−
(b, c 6= 0)
a
a
(−1)a
−a
= (−1) =
=
b
b
b
b
a
c
ad + cb
+ =
b
d
bd
a·
b
ab
=
c
c
a c
a d
ad
: = · =
b d
b c
bc
−a
(−a) · (−1)
a
=
=
−b
(−b) · (−1)
b
a
b
a+b
+ =
c
c
c
a+
b
ac + b
=
c
c
a c
ac
· =
b d
bd
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
19
Quadratwurzel
Mathematik
Stefan Etschberger
Potenz mit ax , wenn a ≥ 0 und x = 1/2: Quadratwurzel
Schreibweise:
1
a2 =
√
wenn a ≥ 0
a
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
Rechenregeln für a 6= 0 und b > 0:
√
√ √
ab = a b
r
√
a
a
= √
b
b
1.3. Algebraische
Umformungen
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Achtung: Im allgemeinen:
√
√
√
a + b 6= a + b
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
20
N-te Wurzeln
Mathematik
Stefan Etschberger
1
Problem: Was bedeutet z.B. 5 3 ?
1
Damit Rechenregeln gültig bleiben: 5 3 ist Lösung der
Gleichung x3 = 5
Also Allgemein (a ∈ R, n ∈ N):
1 n
an
= a1 = a
Schreibweise:
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
1
an =
√
n
a
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Allgemeine rationale Exponenten (a ∈ R, p ∈ Z, q ∈ N):
a
p
q
= a
1
q
p
√ p
= qa
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
21
Logarithmen
Mathematik
Stefan Etschberger
Wie löst man die Gleichung ax = b nach x auf?
(dabei soll gelten a, b > 0 und a 6= 1)
Neues Symbol: Der Logarithmus von b zur Basis a:
ax = b
⇔
x = loga b
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
1.3. Algebraische
Umformungen
Beobachtungen:
1.4. Brüche
loga a = 1
loga 1 = 0
loga (an ) = n
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
2. Grundlegende
Werkzeuge
Rechenregeln:
3. Lineare Algebra
4. Lineare Programme
loga (c · d) = loga c + loga d
c
loga = loga c − loga d
d
loga bn = n · loga b
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
22
Logarithmen
Mathematik
Stefan Etschberger
Spezielle Logarithmen:
log2 x = ld x
Logarithmus dualis
log10 x = log x
loge x = ln x
Dekadischer Logarithmus
Logarithmus naturalis
Umrechnung von Basen
1. Grundlegende
Bausteine
1.1. Reelle Zahlen
1.2. Ganzzahlige Potenzen
logc b
loga b =
logc a
1.3. Algebraische
Umformungen
1.4. Brüche
1.5. Nichtganzzahlige
Potenzen
1.6. Logarithmen
Beispiel
Nach wieviel Jahren verdoppelt sich ein Anfangskapital K mit einem
jährlichen Zins von 5%?
Lösung:
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
2K = K · (1 + 5%)n = K · 1,05n
6. Finanzmathematik
⇔
1,05n = 2
7. Reelle Funktionen
⇔
ln 2
n = log1,05 2 =
≈ 14,2
ln 1,05
8. Differenzieren 1
9. Differenzieren 2
10. Integration
23
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
2
Grundlegende Werkzeuge
Notation von Summen
Binomische Formel
Doppelsummen
Grundbegriffe der Logik
Grundlegendes über Mengen
Integration
Summenzeichen
Mathematik
Stefan Etschberger
Oft sinnvoll: Abkürzen
P von längeren Summen durch das
Summenzeichen
(Großes griechisches Sigma)
Beispiel: Summe von 6 durchnumerierten Zahlen:
N1 + N2 + N3 + N4 + N5 + N6 =
6
X
1. Grundlegende
Bausteine
Ni
i=1
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
Sprechweise: „Summe von i gleich 1 bis 6 über Ni “
Obere und untere Summationsgrenze kann variieren, z.B.
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
2.5. Grundlegendes über
Mengen
3. Lineare Algebra
q
X
4. Lineare Programme
ai = ap + ap+1 + . . . + aq
i=p
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Auch konkrete Berechnungsvorschriften sind möglich, z.B.
8. Differenzieren 1
9. Differenzieren 2
8
X
10. Integration
i2 = 32 + 42 + 52 + 62 + 72 + 82
i=3
25
Summenzeichen
Mathematik
Stefan Etschberger
Rechenregeln für das Summenzeichen
n
X
i=1
(ai + bi ) =
n
X
i=1
n
X
ai +
i=1
n
X
c · ai = c
n
X
Additivität
bi
i=1
Homogenität
ai
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
i=1
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
Damit leicht zu zeigen (Setze µx =
n
X
1
n
2.5. Grundlegendes über
Mengen
n
P
ai ):
i=1
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
(ai − µx ) = 0
i=1
n
X
2
(ai − µx ) =
i=1
7. Reelle Funktionen
n
X
i=1
a2i
!
8. Differenzieren 1
− n · µ2x
9. Differenzieren 2
10. Integration
26
Produktzeichen
Mathematik
Stefan Etschberger
Analog zum Summenzeichen:
Q
Das Produktzeichen
n
Y
i=1
ai = a1 · a2 · . . . · an ·
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
Zum Beispiel:
2.5. Grundlegendes über
Mengen
2
Y
x + (−1)
i=1
Spezielle Abkürzung:
i
3. Lineare Algebra
= (x − 1)(x + 1)
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
n
Y
i=1
9. Differenzieren 2
i = 1 · 2 · . . . · n = n!
„n Fakultät“
10. Integration
27
Binomialkoeffizient
Mathematik
Stefan Etschberger
Man definiert den Binomialkoeffizienten als:
m
Y
m
=
k
i
i=(m−k+1)
k
Y
j
m!
=
k! · (m − k)!
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
j=1
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
Wobei 0! = 1 gesetzt wird. Also:
Beispiel:
m
0
=1
5
5·4
=
= 10
2
1·2
Rechenregeln:
2.5. Grundlegendes über
Mengen
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
m
m
=
k
m−k
m+1
m
m
=
+
k+1
k
k+1
und
9. Differenzieren 2
10. Integration
28
Binomische Formel
Mathematik
Stefan Etschberger
Newtons binomische Formel
(a + b)m
m m
m m−1
=
a +
a
b + ···
0
1
m
m m
+
abm−1 +
b
m−1
m
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
2.5. Grundlegendes über
Mengen
Kurzform:
3. Lineare Algebra
(a + b)
m
m X
m m−k k
=
a
b
k
k=0
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
Zum Beispiel:
9. Differenzieren 2
10. Integration
(x + y)4 = x4 + 4x3 y + 6x2 y2 + 4xy3 + y4
29
Doppelsummen
Mathematik
Stefan Etschberger
Beispielsituation: Daten in Tabellenform in n Spalten und m
Zeilen
Einzelne Einträge: aij mit i ∈ 1, . . . , m und j ∈ 1, . . . , n
Summe über alle Zahlen mit Doppelsummen:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
m
X
i=1
ai1 +
m
X
ai2 + . . . +
i=1
m
X
ain =
i=1
n
X
j=1
m
X
i=1
aij
!
2.2. Binomische Formel
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
2.5. Grundlegendes über
Mengen
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Es gilt:
6. Finanzmathematik
m X
n
X
aij =
i=1 j=1
n X
m
X
7. Reelle Funktionen
aij
j=1 i=1
8. Differenzieren 1
9. Differenzieren 2
10. Integration
30
Sätze, Implikation und Äquivalenz
Mathematik
Stefan Etschberger
Satz: Aussage, die als wahr oder falsch nachgewiesen werden
kann
Implikation: Wenn Aussage A wahr ist muss Aussage B wahr
sein. Andernfalls ist Implikation falsch. Schreibweise:
A⇒B
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
2.5. Grundlegendes über
Mengen
Gilt A ⇒ B sagt man auch:
3. Lineare Algebra
A ist eine hinreichende Bedingung für B
B ist eine notwendige Bedingung für A
Äquivalenz: Gilt A ⇒ B und B ⇒ A gleichzeitig,
sind A und B äquivalent:
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
A⇔B
9. Differenzieren 2
10. Integration
31
Gleichungen und Äquivalenz
Mathematik
Stefan Etschberger
Warum Äquivalenzumformungen bei Gleichungen?
Gegeben: Kette von Äquivalenzumformungen
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
f(x) = 0
⇔
...
⇔
x = 1 ∨ x = 17
Ersetzen von „⇔“ durch „⇒“?
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
2.5. Grundlegendes über
Mengen
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Ersetzen von „⇔“ durch „⇐“?
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
32
Mengen und Elemente
Mathematik
Stefan Etschberger
Menge: Sammlung von Elementen
Aufzählung in geschweiften Klammern. Zum Beispiel
Menge E:
E = {Fisch, Nudeln, Huhn, Eis}
Zwei Mengen A und B sind gleich, wenn jedes Element von
A auch in B ist und andersherum, also:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
2.2. Binomische Formel
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
{a, 1, 4} = {4, 1, a}
2.5. Grundlegendes über
Mengen
3. Lineare Algebra
Darstellung von Mengen durch Beschreibung der Elemente,
z.B.
M = {x ∈ R : 0 ≤ x < 1}
Zugehörigkeit zu einer Menge:
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
x∈A
x ist ein Element der Menge A
10. Integration
33
Teilmengen und Verknüpfungen
Mathematik
Stefan Etschberger
Teilmengen
Ist Jedes Element einer Menge A auch Element der Menge B,
so heißt A Teilmenge von B
A⊂B
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2.1. Notation von Summen
Damit gilt:
2.2. Binomische Formel
2.3. Doppelsummen
2.4. Grundbegriffe der Logik
A=B
⇔
A ⊂ B und B ⊂ A
Mengenverknüpfungen
2.5. Grundlegendes über
Mengen
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Notation
Sprechweise
Die resultierende Menge besteht
aus den Elementen, die
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
A∪B
A∩B
A\B
Vereinigungsmenge von A
und B
mindestens zu A oder B gehören
Schnittmenge von A und B
sowohl in A als auch in B liegen
A ohne B
zu A, aber nicht zu B gehören
9. Differenzieren 2
10. Integration
34
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
Integration
3
Lineare Algebra
Matrizen und Vektoren
Matrixalgebra
Lineare Gleichungssysteme
Inverse Matrizen
Mathematik
Stefan Etschberger
Warum beschäftigen wir uns mit linearer Algebra?
Quantitative tabellarische Daten (Excel) sind aus betriebsund volkswirtschaftlichen Fragestellungen nicht
wegzudenken
Methoden der Matrizenrechnung erleichtern
beziehungsweise ermöglichen die Analyse solcher Daten
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
Wesentliche Lernziele
3.4. Inverse Matrizen
Kennenlernen der Eigenschaften von Matrizen
4. Lineare Programme
Beherrschen elementarer Matrixoperationen
5. Folgen und Reihen
Fähigkeit, lineare Gleichungssysteme aufzustellen, zu lösen
und diese Lösung darzustellen
6. Finanzmathematik
Beherrschen des Invertierens spezieller Matrizen
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
36
Einführung
Mathematik
Stefan Etschberger
Beispiel 1
Eine Unternehmung stellt mit Hilfe der Produktionsfaktoren F1 , F2 , F3 zwei Produkte
P1 , P2 her.
Zur Produktion für jede Mengeneinheit von Pj (j = 1,2) werden aij
Mengeneinheiten von Fi (i = 1,2,3) verbraucht.
Verbrauch
2. Grundlegende
Werkzeuge
für eine Einheit des Produkts
P1
P2
von Einheiten
der
Produktionsfaktoren
F1
F2
F3
a11
a21
a31
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
a12
a22
a32
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
Grafisch dargestellt:
5. Folgen und Reihen
6. Finanzmathematik
a12
F1
1. Grundlegende
Bausteine
a
a
21
F2
a 31
a
F3
22
8. Differenzieren 1
11
2
a3
P1
7. Reelle Funktionen
9. Differenzieren 2
10. Integration
P2
37
Einführung
Mathematik
Stefan Etschberger
Beispiel 2
Für fünf gleichartige Produkte P1 , . . . , P5 werden drei Merkmale erhoben,
und zwar der Preis, die Qualität und die Art des Kundenkreises, der das jeweilige
Produkt nachfragt.
Ergebnis:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Preis
Produkte
P1
P2
P3
P4
P5
20
18
20
16
18
Merkmale
Qualität
Kundenkreis
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
sehr gut
sehr gut
sehr gut
mäßig
ordentlich
A
B
A
C
B
Fragen:
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Ähnlichkeit von Produkten
8. Differenzieren 1
Finden von Kundensegmenten
9. Differenzieren 2
Zuordnen zu diesen Segmenten
10. Integration
−→ Marktforschung
38
Definitionen
Mathematik
Stefan Etschberger
Definition Matrix
Ein geordnetes, rechteckiges Schema von Zahlen oder Symbolen

a11
 a21

 ..
 .
A=
 ai1

 .
 ..
am1
a12
a22
..
.
ai2
..
.
am2
...
...
...
...
a1j
a2j
..
.
aij
..
.
amj
...
...
...
...

a1n
a2n 

.. 
. 
 = (aij )
m,n
ain 

.. 
. 
amn
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
mit m, n ∈ N heißt Matrix mit m Zeilen und n Spalten oder kurz
m × n-Matrix (Im Folgenden: aij ∈ R).
a11 , . . . , amn heißen Komponenten der Matrix.
Dabei gibt i die Zeile und j die Spalte an, in der aij steht.
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
i heißt Zeilenindex und j Spaltenindex von aij .
Sind alle Komponenten aij reelle Zahlen, so spricht man von einer
reellen Matrix.
39
Transponierte Matrix
Mathematik
Stefan Etschberger
Definition
Zu jeder m × n-Matrix

a11
 ..
A= .
...
am1
...
heißt die n × m-Matrix

a11

AT =  ...
...
a1n

a1n
.. 
. 
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
amn
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme

am1
.. 
. 
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
. . . amn
7. Reelle Funktionen
8. Differenzieren 1
die zu A transponierte Matrix
⇒ A
T T
9. Differenzieren 2
10. Integration
=A
40
Beispiel transponierte Matrix
a)
b)
A=
1 2
1 3

1

A = 1
2
T
3
5
4 5
2 4

2 3
3 4
5 0
Mathematik
Stefan Etschberger

1
2

⇒ AT = 
3
4
5
⇒
1. Grundlegende
Bausteine

1
3

5

2
4

1 1
T T

=A= 2 3
A
3 4
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme

2
5
0
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
41
Vektoren
Mathematik
Stefan Etschberger
Definition
1. Grundlegende
Bausteine
n × 1-Matrix heißt Spaltenvektor mit n Komponenten:


a1
 
a =  ... 
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
an
4. Lineare Programme
1 × n-Matrix heißt Zeilenvektor mit n Komponenten:
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
aT = (a1 , . . . , an )
8. Differenzieren 1
9. Differenzieren 2
10. Integration
42
Geometrische Veranschaulichung von Vektoren
•
−1
•
0
•
1
Mathematik
Stefan Etschberger
a1
•
2
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
a2
−1.8
0.6
•
a2
1
•
2
1•
•
1•
1
•
0
−1
1
•
a1
a3
 
0
2 
0
1
•
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
 
3
2 
2
 
3
0 
2
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
43
Relationen zwischen Matrizen
Definition
Seien A = (aij )m,n und B = (bij )m,n reelle Matrizen mit
übereinstimmender Zeilenzahl m und Spaltenzahl n.
Dann wird definiert:
A=B
⇔
aij = bij für alle i = 1, . . . , m , j = 1, . . . , n
A 6= B
⇔
aij 6= bij für mindestens ein Indexpaar (i, j)
A≤B
⇔
aij ≤ bij ∀(i, j)
A<B
⇔
aij < bij ∀(i, j)
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Entsprechend A ≥ B und A > B.
8. Differenzieren 1
9. Differenzieren 2
10. Integration
44
Spezielle Matrizen
Mathematik
Stefan Etschberger
Definition
a) A = (aij )n,n heißt quadratisch
b) A = (aij )n,n mit A = AT heißt symmetrisch
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
c) A = (aij )n,n heißt Dreiecksmatrix, wenn
aij = 0 für i < j (untere Dreiecksmatrix) oder
aij = 0 für i > j (obere Dreiecksmatrix)
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
d) A = (aij )n,n heißt Diagonalmatrix, wenn aij = 0 für alle
i 6= j
e) A = (aij )n,n heißt Einheitsmatrix, wenn aii = 1 für alle i
und aij = 0 für alle j 6= j
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
45
Addition und Subtraktion von Matrizen
Mathematik
Stefan Etschberger
Definition
Gegeben: A = (aij )m,n und B = (bij )m,n .
1. Grundlegende
Bausteine
Dann gilt:
2. Grundlegende
Werkzeuge
Addition: A + B = (aij )m,n + (bij )m,n = (aij + bij )m,n
3. Lineare Algebra
Subtraktion: A − B = (aij )m,n − (bij )m,n = (aij − bij )m,n
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
Damit:
5. Folgen und Reihen
A+B=B+A
6. Finanzmathematik
7. Reelle Funktionen
(A + B) + C = A + (B + C)
Addition/Subtraktion nicht definiert, wenn Zeilen- bzw.
Spaltenzahl nicht übereinstimmen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
46
Skalare Multiplikation
Mathematik
Stefan Etschberger
Definition
Gegeben: A = (aij )m,n und r ∈ R (Skalar).
Dann gilt:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
r · A = r · (aij )m,n = (r · aij )m,n = (aij · r)m,n = A · r
Beispiel:
1 2
5 10
5·
=
3 5
15 25
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
Außerdem gilt:
7. Reelle Funktionen
(rs)A
(r + s)A
r(A + B)
= r(sA)
= rA + sA
= rA + rB
(Assoziativgesetz)
(Distributivgesetz)
8. Differenzieren 1
9. Differenzieren 2
10. Integration
47
Matrixmultiplikation
Mathematik
Stefan Etschberger
Gegeben:
A = (aik )m,p und
B = bkj p,n .
B : p Zeilen q Spalten

b
12
Dann gilt:
22
×
22
a
.+
k=1
p,q
..
+
= (aik )n,p · bkj
!
p
X
=
aik bkj
b
a
+
21
×
A·B
2
p
a2
n,q
















Merke:
Zeile mal Spalte!
a11
a12
...
a1p
a21
a22
...
a2p
..
.
..
.
..
an1
an2
...
.
..
.
anp
×
bp
















b11
b12
...
b1q
b21
b22
...
b2q
..
.
..
.
..
..
.
bp1
bp2
...
.
bpq

















1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
































A : n Zeilen p Spalten
c11
c12
...
c1q
c21
c22
...
c2q
..
.
..
.
..
cn1
cn2
...
.
..
.
cnq
















5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
C = A × B : n Zeilen q Spalten
Quelle Grafik: Alain Matthes, altermundus.com
48
Spezialfälle und Rechenregeln
Mathematik
Stefan Etschberger
Spezialfälle der Matrixmultiplikation
A = (m × n)-Matrix, B = (n × m)-Matrix
⇒ es existiert
A·B
und
B·A
A quadratisch
⇒
1. Grundlegende
Bausteine
A · A = A2 existiert
A, B quadratisch ⇒ A · B existiert und B ·
Aber: Im Allgemeinen A · B 6= B · A
A1
existiert.
Ist E Einheitsmatrix, dann gilt:
A·E=E·A=A
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
Spezielle Rechenregeln
5. Folgen und Reihen
A = (m × p)-Matrix, B = (p × n)-Matrix. Damit gilt:
A·B
BT AT
AT A
AAT
und
= (A ·
B T · AT
existieren.
B)T
ist symmetrische (p × p)-Matrix und
ist symmetrische (m × m)-Matrix
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
49
Lineare Gleichungssysteme: Einführung
Mathematik
Stefan Etschberger
Beispiele linearer Gleichungssysteme
a)
2x1
x1
−
+
3x2
x2
=
=
−1
2
b)
x1
x1
+
+
x2
x2
=
=
4
2
c)
x1
−2x1
−
+
x2
2x2
=
=
1
−2
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
Probleme:
4. Lineare Programme
System lösbar oder nicht?
5. Folgen und Reihen
6. Finanzmathematik
Verfahren zum Auffinden von Lösungen
7. Reelle Funktionen
Darstellung von mehrdeutigen Lösungen
8. Differenzieren 1
9. Differenzieren 2
Dazu gibt es:
10. Integration
Den Gaußschen Algorithmus (erzeugt Dreiecksmatrix)
das Verfahren von Gauß-Jordan (modifizierte Gauß: erzeugt
Einheitsmatrix)
50
Allgemeines lineares Gleichungssystem
Mathematik
Stefan Etschberger
Ein System von Gleichungen
a11 x1
a21 x1
am1 x1
+
+
+
a12 x2
a22 x2
am2 x2
+
+
+
···
···
..
.
+ a1n xn
+ a2n xn
···
+ amn xn
=
=
b1
b2
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
=
bm
heißt lineares Gleichungssystem mit m Gleichungen und n
Unbekannten.
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
Die aij und bi heißen Koeffizienten des Gleichungssystems.
5. Folgen und Reihen
In Matrixform:
6. Finanzmathematik
7. Reelle Funktionen
Ax = b
Lösungsmenge:
8. Differenzieren 1
9. Differenzieren 2
10. Integration
L = {x :
Ax = b}
51
Lösungsdarstellung
Mathematik
Stefan Etschberger
Beispiel für Enddarstellung:
x1
+ x3
=4
x2 + 3x3 + 2x4 = 7
⇔
1
0
0
1
1
3
 
x1

0 x2 
4
· 
=

x3
2
7
x4
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Dabei bezeichnet:
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
E
xB
R
xN
=b
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
kann nach Basisvariablen aufgelöst werden:
x1 = 4 − x3 , x2 = 7 − 3x3 − 2x4 (allgemeine Lösung)
In diesem Fall immer lösbar, zum Beispiel mit
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
xN
x3
0
=
=
x4
0
⇒
x1
4
xB =
=
x2
7
Gesucht: Verfahren zur Überführung beliebiger Gleichungssysteme
in diese Form
Lösung von LGS
52
Mathematik
Stefan Etschberger
Elementare Umformungen
Das sind Umformungen der Koeffizientenmatrix, die die
Lösung nicht verändern. Erlaubt ist
Multiplikation einer Zeile mit beliebigen Zahlen c 6= 0
Addition einer Zeile zu einer anderen Zeile
Vertauschen von Zeilen oder Spalten
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
Lösungsalgorithmus
Lösung mit Verfahren von Gauß-Jordan:
Systematische Umformungen nach obigem
Prinzip, bis Darstellung der Koeffizientenmatrix in Einheits- und Restmatrix ensteht
Algorithmus und Lösungsvarianten
siehe Vorlesung
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
53
Invertierung von Matrizen
Mathematik
Stefan Etschberger
Definition
Gegeben: n × n-Matrix (quadratisch)
Existiert eine n × n-Matrix X mit AX = XA = E, so heißt X
die zu A inverse Matrix.
Schreibweise: X = A−1
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
⇒ AA−1 = A−1 A = E
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
Inverse Matrizen und Gleichungssysteme
4. Lineare Programme
Falls A−1 existiert, gilt:
5. Folgen und Reihen
6. Finanzmathematik
Ax = b
⇒
A−1 Ax = A−1 b
⇒
Ex = x = A−1 b
7. Reelle Funktionen
8. Differenzieren 1
Damit existiert genau eine Lösung und zwar:
9. Differenzieren 2
10. Integration
x = A−1 b
54
LGS und Orthogonalität
Mathematik
Stefan Etschberger
Berechnung inverser Matrizen durch den Gaußalgorithmus:
Ansatz:
Ax +
Ey = 0
−1
−1
⇒ A Ax + A Ey = 0
⇒
Ex + A−1 y = 0
Also: Gaußtableau mittels elementarer Umformungen
folgendermaßen umformen:
(A|E) −→
E|A−1
Orthogonale Matrizen
Eine n × n-Matrix A heißt orthogonal, wenn gilt:
AAT = AT A = E
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Bei orthogonalen Matrizen A gilt also: A−1 = AT .
Mit A ist damit auch AT orthogonal
55
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
Integration
4
Lineare Programme
Nebenbedingungen und
Zulässigkeitsbereich
Zielfunktion
Graphische Lösung
Lineare Programe: Beispiel
Mathematik
Stefan Etschberger
Ein holzverarbeitender Betrieb möchte ein Produktionsprogramm für
Spanplatten festlegen. Dabei sind folgende Restriktionen zu
berücksichtigen:
Es werden zwei Typen von Spanplatten hergestellt:
Typ A in der Quantität x1 für den Außenbereich und Typ B in der
Quantität x2 für den Innenbereich. Zur Herstellung der Spanplatten
werden zwei Arten von Furnierblättern F1 bzw. F2 unterschiedlicher
Qualität benutzt. Die Spanplatten werden mittels einer Presse, in
der die Furniere verleimt werden, hergestellt.
Zur Herstellung einer Platte vom Typ A wird ein Blatt von F1 und
zwei Blätter von F2 benötigt, während bei Typ B drei Blätter von F1
und ein Blatt von F2 benutzt werden.
Von F1 bzw. F2 stehen 1500 bzw. 1200 Stück zur Verfügung.
Die Presse steht insgesamt 700 Minuten zur Verfügung, wobei zur
Verleimung beider Plattentypen pro Stück jeweils eine Minute
benötigt wird.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
4.3. Graphische Lösung
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
57
Lineare Produktionsplanung: Beispiel
Mathematik
Stefan Etschberger
Tabellarische Darstellung der Problemdaten:
Produkt
Menge
Einheiten
von F1
Einheiten
von F2
Pressminuten
pro Stück
Typ A
Typ B
x1
x2
1
3
2
1
1
1
1500
1200
700
Kapazitäten
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Zusammenhang von Daten und Variablen durch System von linearen
Ungleichungen beschreibbar:
4. Lineare Programme
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
4.3. Graphische Lösung
Restriktionen:
5. Folgen und Reihen
(1)
(2)
(3)
x1
2x1
x1
(4)(5)
+
+
+
3x2
x2
x2
5
5
5
x1 , x2 = 0
1500
1200
700
(Vorrat F1 )
(Vorrat F2 )
(Kapazität Presse)
6. Finanzmathematik
7. Reelle Funktionen
(nicht-negative Mengen)
8. Differenzieren 1
9. Differenzieren 2
10. Integration
58
Lineare Produktionsplanung: Beispiel, Zulässigkeitsbereich
Mathematik
Stefan Etschberger
Begriffe und Beobachtungen
Jede (x1 , x2 )-Kombination, die alle Restriktionen (1) bis (5)
erfüllt, bezeichnet man als zulässige Lösung.
Die Menge
 x1


∈ R2+ : x1 + 3x2 5 1500;

x2
Z=
2x1 + x2 5 1200;



x1 + x2 5 700
1. Grundlegende
Bausteine







2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
4.3. Graphische Lösung
nennt man Zulässigkeitsbereich des Problems.
Wegen Restriktion x ∈ R2+ : Erster Quadrant des
Koordinatensystems genügt für graphische Darstellung des
Zulässigkeitsbereiches.
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
59
Beispiel: Graphische Darstellung Zulässigkeitsbereich
Mathematik
Stefan Etschberger
Ungleichung (1) mit x1 + 3x2 5 1500 entspricht dreieckigem
Bereich in R2+
Begrenzung durch die drei Geraden mit x1 + 3x2 = 1500, x1 = 0
und x2 = 0
Also: Grenzpunkte (0,500), (1500,0), (0,0)
1. Grundlegende
Bausteine
Analog für die übrigen Nebenbedingungen
2. Grundlegende
Werkzeuge
(1)
x1 + 3x2 5 1500
x1 , x2 = 0
(2)
x2
1200
6
2x1 + x2 5 1200
x1 , x2 = 0
(3)
x1 + x2 5 700
x1 , x2 = 0
3. Lineare Algebra
4. Lineare Programme
4.1. Nebenbedingungen und
Zulässigkeitsbereich
x2
x2 6
700
4.2. Zielfunktion
4.3. Graphische Lösung
6
5. Folgen und Reihen
500
6. Finanzmathematik
-x
1500 1
-x
600
1
700
-x
1
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Beispiel: Graphische Darstellung der Restriktionen
Beispiel: Graphische Darstellung Zulässigkeitsbereich
Die gesamte zulässige Lösungsmenge Z ergibt sich dann aus
dem Durchschnitt der angegebenen Bereiche.
Alle (x1 , x2 )-Kombinationen im mit Z gekennzeichneten
Bereich erfüllen damit die vorgegebenen Restriktionen.
60
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
4.3. Graphische Lösung
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
61
Mögliche Fälle für Z
Mathematik
Stefan Etschberger
1
Z = ∅, d.h., es existiert keine zulässige (x1 , x2 )-Kombination.
2
|Z| = 1, d.h., es existiert genau eine zulässige (x1 , x2 )-Kombination.
Dieser Fall tritt meist dann auf, wenn die Restriktionen in Form von
Gleichungen formuliert werden (Abschnitt 3.3).
3
|Z| > 1, d.h., es existieren mehrere zulässige Lösungen (Beispiel 1).
In den ersten beiden Fällen ist durch die Restriktionen das
Planungsergebnis festgelegt.
Im ersten Fall können nicht alle Restriktionen gleichzeitig erfüllt werden,
im zweiten Fall gibt es eine einzige Lösung, die alle Restriktionen erfüllt.
Im letzten Fall entsteht weiterer Planungsbedarf, da für die
Modellvariablen noch Spielraum besteht. Um diesen Spielraum
weiter einzuschränken, ist eine Zielsetzung zu formulieren, die die
zulässigen Lösungen bewertet. Kann diese Zielsetzung z als lineare
Funktion der Modellvariablen modelliert werden, so entsteht ein
lineares Optimierungsproblem mit der Zielfunktion z(x) und
Nebenbedingungen in Form von Gleichungen und/oder
Ungleichungen.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
4.3. Graphische Lösung
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
62
Lineare Produktionsplanung: Beispiel
Mathematik
Stefan Etschberger
Der holzverarbeitende Betrieb aus Beispiel 1 verfolgt die
Zielsetzung der Gewinnmaximierung. Die Spanplatten vom Typ A
bringen 4 €, die vom Typ B 5 € Gewinn pro Stück.
Zusammen mit den Restriktionen aus Beispiel 1 kann nun ein
mathematisches Modell in Form eines linearen
Optimierungsproblems formuliert werden.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Zielfunktion:
z(x1 , x2 ) = 4x1 + 5x2
Nebenbedingungen:
(1)
x1 + 3x2
(2)
2x1 +
x2
(3)
x1 +
x2
(4)(5)
x1 , x2
4. Lineare Programme
−→ max
(Gewinnmaximierung)
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
4.3. Graphische Lösung
5. Folgen und Reihen
5 1500
5 1200
5 700
=0
(Vorrat F1 )
(Vorrat F2 )
(Kapazität Presse)
(nicht-negative Mengen)
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
63
Beispiel: Graphische Lösung
Zur graphischen Lösung des Problems: Zusätzlich
Zielfunktion in Graphik
Zu diesem Zweck: Darstellung von Isogewinngeraden
Für Gewinn in Höhe von c:
c 4
z(x1 , x2 ) = 4x1 + 5x2 = c bzw. x2 = − x1 .
5 5
Graphische Darstellung der Optimallösung im Beispiel
Nur der Achsenabschnitt = c/5 hängt vom Wert c ab, die
Steigung = −4/5 jedoch nicht.
Im Beispiel maximaler c-Wert im Schnittpunkt der Geraden
für die Nebenbedingungen (1) und (3), d.h. in
(x1 , x2 ) = (300,400).
Ein höherer Zielfunktionswert als
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
4.3. Graphische Lösung
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
z(300,400) = 4 · 300 + 5 · 400 = 3200
9. Differenzieren 2
10. Integration
kann unter Einhaltung der Restriktionen nicht erreicht
werden. Man spricht von einer optimalen Lösung.
64
Beispiel, Bereich optimaler Lösungen
Mathematik
Stefan Etschberger
Variante: Gewinnbeiträge der Spanplatten aus Beispiel 1 jetzt für beide
Typen gleich 4.- € pro Stück, d.h. z(x1 , x2 ) = 4x1 + 4x2 ,
In diesem Fall: kein eindeutiges Optimum
Bereich Z∗ optimaler Lösungen; beschreibbar durch folgende Menge:
x1
∗
2
Z =
∈ R+ : 4x1 + 4x2 = 2800, x1 ∈ [300,500]
x2
1. Grundlegende
Bausteine
Z∗ entspricht der durch die Punkte C = (300,400) und D = (500,200) begrenzten
Strecke.
2. Grundlegende
Werkzeuge
Zusammenfassung für graphische Lösung linearer Optimierungsprobleme
(mit nicht-konstanter Zielfunktion):
4. Lineare Programme
3. Lineare Algebra
4.1. Nebenbedingungen und
Zulässigkeitsbereich
4.2. Zielfunktion
Optimale Lösungen liegen stets auf dem Rand des zulässigen Bereiches Z
beziehungsweise in „Ecken“ von Z.
Mindestens eine Ecke gehört zur optimalen Lösung.
Entspricht Menge der Optimallösungen genau einer Ecke von Z ⇐⇒ ist
Optimallösung eindeutig.
Gibt es zwei „optimale Ecken“ , so ist die Menge aller Punkte der durch diese
Ecken festgelegten Strecke optimal.
4.3. Graphische Lösung
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
65
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
5
Folgen und Reihen
Eigenschaften und Beispiele
Konvergenz und Grenzwert
Reihen
Integration
Folgen und Reihen
Mathematik
Stefan Etschberger
Warum beschäftigen wir uns mit Folgen und Reihen?
Analyse von Datensequenzen, insbesondere Modellierung
diskreter, zeitlicher Entwicklungen (z.B. von Aktienkursen,
Absatzmengen)
Grundlage der Finanzmathematik (z.B. Zinseszinsrechnung,
Tilgungsrechnung)
wesentlich zum Verständnis der Konzepte der Stetigkeit und
Differenzierbarkeit
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
5.1. Eigenschaften und
Beispiele
Wesentliche Lernziele:
Verständnis der Begriffe Folgen und Reihen
Fähigkeit Folgen und Reihen nach ihrer Art zu klassifizieren
Kennenlernen typischer, insbesondere der
Grenzwerteigenschaften von Folgen und Reihen
5.2. Konvergenz und
Grenzwert
5.3. Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Fähigkeit, diese Eigenschaften zu erkennen und
nachzuweisen
67
Definition und Eigenschaften
Mathematik
Stefan Etschberger
Definition
Eine Folge ist eine Abbildung a : N0 → R
Schreibweise für Folgenglieder: a(0), a(1), . . . oder
a0 , a 1 , . . .
Schreibweise für Folge: (an )n∈N0
oder
(an )
Leonardo von Pisa
(ca. 1180 - 1250)
Eigenschaften von Folgen: Eine Folge heißt
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
endlich (unendlich), falls Anzahl der Folgenglieder
endlich (unendlich) ist
4. Lineare Programme
5. Folgen und Reihen
gesetzmäßig gebildet, falls Folgenglieder einem
1
Bildungsgesetz folgen, zum Beispiel: an = n+1
5.1. Eigenschaften und
Beispiele
rekursiv definiert, falls zur Berechnung eines Folgengliedes frühere Werte
nötig sind
Beispiel: a0 = 0; a1 = 1 und an = an−1 + an−2 für n > 1
(Fibonacci-Folge)
5.3. Reihen
5.2. Konvergenz und
Grenzwert
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
Spezielle Folgen
Arithmetische Folge: (an ) : an+1 − an = d
Geometrische Folge: (an ) :
an+1
an
=q
∀n ∈ N0 mit d ∈ R
10. Integration
∀n ∈ N0 mit q ∈ R
68
Geometrische Folge: Beispiel Schachspiel
Mathematik
Stefan Etschberger
Sissa ibn Dahir, der Erfinder
des Schachspieles, darf sich
vom indischen König
Shihram eine Belohnung
wünschen.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Sein Wunsch: So viele
Weizenkörner, wie man auf
ein Schachbrett legen kann,
wenn
1 . Feld :
2 . Feld :
3 . Feld :
4 . Feld :
n. Feld
:
a0
a1
a2
a3
=1
=2
=4
=8
..
.
an−1 = 2 · an−2
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
5.1. Eigenschaften und
Beispiele
Korn
Körner
Körner
Körner
5.2. Konvergenz und
Grenzwert
5.3. Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Körner
69
Konvergenz und Grenzwert
Mathematik
Stefan Etschberger
Fragen: Bleiben Folgenglieder ab einem gewissen n in einen
kleinen Bereich um einen festen Wert?
Und: Kann man diesen Bereich beliebig verkleinern?
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Definition:
3. Lineare Algebra
a ∈ R heißt Grenzwert oder Limes von (an )
⇔
|an − a| < ∀ n > n()
∀ > 0 ∃ n() mit
Schreibweise für Grenzwert: lim an = a
n→∞
Existiert dieser Grenzwert, heißt die Folge konvergent
Ist der Grenzwert a = 0, heißt die Folge Nullfolge
Existiert kein Grenzwert, heißt die Folge divergent
4. Lineare Programme
5. Folgen und Reihen
5.1. Eigenschaften und
Beispiele
5.2. Konvergenz und
Grenzwert
5.3. Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
70
Beispiel zur Definition des Grenzwerts
Gegeben: an =
Mathematik
Stefan Etschberger
n
n+1
Vermutung: lim an = a = 1
n→∞
1. Grundlegende
Bausteine
Beweis: Wenn a = 1, dann folgt
⇔
⇔
⇔
n
|an − a| = n+1 − 1 < n−n−1 = 1 <
n+1
n+1
1
<n+1
1
−1<n
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
5.1. Eigenschaften und
Beispiele
5.2. Konvergenz und
Grenzwert
5.3. Reihen
6. Finanzmathematik
Also: Für jedes findet man ein n(), so dass die
Grenzwertbedingung stimmt
Zum Beispiel: Wähle
= 0,01 ⇒ n >
2. Grundlegende
Werkzeuge
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
1
−1=
1
0,01
− 1 = 100 − 1 = 99
71
Rechenregeln für Grenzwerte
Mathematik
Stefan Etschberger
Gegeben:
1. Grundlegende
Bausteine
und lim (bn ) = b
lim (an ) = a
n→∞
n→∞
kurz: (an ) → a
und
2. Grundlegende
Werkzeuge
(bn ) → b
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Dann gilt:
5.1. Eigenschaften und
Beispiele
(an + bn ) → a + b
(an − bn ) → a − b
(an · bn ) → a · b
an
bn
5.2. Konvergenz und
Grenzwert
5.3. Reihen
→
a
b
(b 6= 0)
(acn ) → ac
(an > 0, a > 0, c ∈ R)
(can ) → ca (c > 0)
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
72
Definition der Reihe
Mathematik
Stefan Etschberger
Gegeben: (an ) unendliche Folge in R
Dann heißt (sn ) mit
sn = a0 + a1 + . . . + an =
n
X
ai
n ∈ N0
i=0
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
eine unendliche Reihe.
3. Lineare Algebra
sn heißt n-te Partialsumme
4. Lineare Programme
Klar ist: Reihen sind spezielle Folgen
5. Folgen und Reihen
5.1. Eigenschaften und
Beispiele
5.2. Konvergenz und
Grenzwert
Beispiel:
(an ) geometrische Folge → (sn ) geometrische Reihe
sn =
n
X
5.3. Reihen
6. Finanzmathematik
ai ;
mit
i=0
an+1
=q
an
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
Offensichtlich gilt: an = an−1 q = an−2 q2 = . . . = a0 qn
10. Integration
⇒ sn =
n
X
i=0
a0 qi = a0 (1 + q + q2 + . . . + qn ) = a0
1 − qn+1
1−q
73
Geometrische Reihe: Beispiel Schachspiel
Mathematik
Stefan Etschberger
Summe aller Körner auf Schachbrett:
sn =
63
X
64
ai = a0
i=0
64
1−q
1−2
=1·
≈ 1,84467 · 1019
1−q
1−2
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Das bedeutet:
5. Folgen und Reihen
∧
−→ 1,8 · 1017 g
−→ 1,8 · 1014 kg
−→ 1,8 · 1011 t = 180 Mrd. t
100 Körner = 1 g Weizen
∧
5.1. Eigenschaften und
Beispiele
5.2. Konvergenz und
Grenzwert
5.3. Reihen
6. Finanzmathematik
7. Reelle Funktionen
1 Güterwagon = 50 t Weizen −→ 3,6 Mrd. Güterwagons
8. Differenzieren 1
−→ 36 Mrd. m langer Eisenbahnzug 9. Differenzieren 2
−→ 36 Mill. km
10. Integration
−→
100-fache Entfernung zwischen Erde und Mond
74
Konvergenzkriterien für Reihen
Gegeben: ai Folge,
sn =
n
X
Mathematik
Stefan Etschberger
ai
i=1
Divergenzkriterium
Ist sn konvergent
⇒
ai ist Nullfolge
1. Grundlegende
Bausteine
Also äquivalent dazu:
⇒
ai ist keine Nullfolge
2. Grundlegende
Werkzeuge
sn divergent
3. Lineare Algebra
Quotientenkriterium
4. Lineare Programme
ak+1 <1
lim
k→∞ ak ak+1 >1
lim
k→∞ ak 5. Folgen und Reihen
⇒
⇒
sn konvergent
5.1. Eigenschaften und
Beispiele
5.2. Konvergenz und
Grenzwert
sn divergent
5.3. Reihen
6. Finanzmathematik
7. Reelle Funktionen
a
Bemerkung: Für lim k+1
= 1 ist im Allgemeinen keine Aussage möglich
a
k→∞
k
Spezialfall geometrische Reihe:
ak+1
⇒
=q
ak
⇒
ak+1 =q
lim
k→∞ ak 8. Differenzieren 1
9. Differenzieren 2
10. Integration
⇒
q<1
q≥1
⇒
⇒
sn konvergent
sn divergent
75
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
6
Finanzmathematik
Zinsen
Renten
Tilgung
Kursrechnung
Integration
Zinsen
Zinsen sind der Preis,
den ein Schuldner für
die befristete
Überlassung von
Kapital bezahlen muss.
Der Betrag der Zinsen
(Z) wird aus der Höhe
des überlassenen
Kapitals K und der
Dauer der Überlassung
berechnet.
Mathematik
Stefan Etschberger
Verwendete Symbole:
Symbol
Bezeichnung
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
K0
Kn
n
f
x
Z
p
p
i = 100
q=1+i
v = q1
Anfangskapital
Endkapital
ganzzahlige Laufzeit
gebrochene Laufzeit
nicht–ganzzahlige Laufzeit
Zins
Prozentzinssatz
Zinssatz
Aufzinsungsfaktor
Abzinsungsfaktor
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
77
Einfache Verzinsung
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
Sparzinsen können zinseszinslich angelegt werden
Bei Kreditgeschäften zwischen Privatpersonen ist das illegal
(BGB, §248)
Deswegen: Einfache (lineare) Verzinsung gemäß
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Kn = K0 + Z
Zinseszinsen
Gemischte Verzinsung
= K0 + K0 · i · n
p · n
= K0 · 1 +
100
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
78
Unterjährige einfache Verzinsung
Mathematik
Stefan Etschberger
In Deutschland Einteilung des Zinsjahres in 12 Monate zu je
30 Tagen (360 Tage)
Dadurch Berechnung von Monats- bzw. Tageszinsen möglich
Laufzeit n ∈ N in Jahren wird dann zu Laufzeit f ∈ Q in
Jahren mit
t2 − t1
f=
360
(t1 entspricht Tag der Einzahlung, t2 Tag der Auszahlung)
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Daraus ergibt sich
Gemischte Verzinsung
Nominal- und Effektivzins
t
t
Kn = K0 + K0 · i ·
= K0 1 + i ·
360
360
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
Stellung eines Tages im Jahr:
9. Differenzieren 2
10. Integration
(Aktueller Monat − 1) · 30 + Tag im Monat
79
Barwert bei einfacher Verzinsung
Mathematik
Stefan Etschberger
K0 unbekannt: Abzinsung bzw. Diskontierung bzw.
Barwertberechnung
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Amtliche Diskontierung:
4. Lineare Programme
5. Folgen und Reihen
K0 =
Kn
1 + ni
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Kaufmännische Diskontierung (Nur erste Näherung):
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
K0 = Kn (1 − ni)
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
80
Die Zinseszinsformel
Mathematik
Stefan Etschberger
Während Laufzeit Zinszahlungen mit sofortiger Wiederanlage
und Verzinsung zum Zinssatz i
Entwicklung des Kapitals:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
K1 = K0 + K0 · i = K0 · (1 + i) = K0 · q
K2 = K1 · (1 + i) = (K0 · q) · q = K0 · q2
K3 = K2 · (1 + i) = K0 · q2 · q = K0 · q3
···
Damit folgt die Zinseszinsformel, mit n (zunächst)
ganzzahlig.
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
K n = K0 · q
n
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
qn heißt Aufzinsungfaktor
9. Differenzieren 2
10. Integration
81
Die Zinseszinsformel
Mathematik
Stefan Etschberger
Auflösung der Zinseszinsformel nach K0 , q und n:
K0 =
Kn
qn
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Abzinsungs- oder Diskontierungsformel
1
heißt Abzinsungsfaktor
qn
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
q=
r
n
Kn
K0
bzw.
i=
r
n
Gemischte Verzinsung
Nominal- und Effektivzins
Kn
−1
K0
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
ln Kn − ln K0
n=
ln q
8. Differenzieren 1
9. Differenzieren 2
10. Integration
82
Gemischte Verzinsung
Mathematik
Stefan Etschberger
Üblich: Einfache Verzinsung bei Restlaufzeiten kleiner einem
ganzzahliges Vielfachen der Zinsperiode
Genauer: Mit
∆t1 (Zinstage im ersten Jahr),
n (die weiteren, ganzen Zinsperioden) und
∆t2 (Zinstage im letzten Jahr),
gilt für das Endkapital Kx :
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
∆t1
Kx = K0 · 1 + i ·
360
∆t2
· (1 + i)n · 1 + i ·
360
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
Gemischte Zinsrechnung (unter Verwendung der
30/360−Methode), auch Sparbuchmethode.
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
83
Gemischte Verzinsung: Beispiel
Mathematik
Stefan Etschberger
Beispiel
Am 15 9 1996 wurden € 12 000 zu 3,75 % angelegt. Wie hoch
war der Endbetrag bei Kontoauflösung am 21 9 2003 (letzter
Zinstag 20 9 2003)?
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Lösung:
4. Lineare Programme
15 9. =
^ (9 − 1) · 30 + 15 = 255
⇒ ∆t1 = 360 − (255 − 1) = 106
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
20 9. =
^ (9 − 1) · 30 + 20 = 260
⇒ ∆t2 = 260
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
(n = 6):
6.3. Tilgung
0,0375 · 106
0,0375
·
260
Kx = 12 000 · 1 +
· 1,03756 · 1 +
360
360
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
= 15 541,20
84
Gemischte Verzinsung: Anmerkungen
Mathematik
Stefan Etschberger
Würde man – von t0 ausgehend – in ganze Jahre und einem
Rest aufteilen, so ergäbe sich:
0,0375
·
6
Kx = 12 000 · 1,03757 · 1 +
= 15 537,08
360
(7 Jahre von 15.9.96 bis 14.9.2003; dazu 6 Tage)
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Würde man die Zinseszinsformel mit nicht-ganzzahligem
Exponenten verwenden, so ergäbe sich Folgendes:
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
6
7+ 360
Kx = 12 000 · 1,0375
= 15 536,90
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
Gemischte Verzinsung ist also (zumindest für Kapitalanleger)
verbraucherfreundlich
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
85
Gemischte Verzinsung: Anmerkungen
Mathematik
Stefan Etschberger
Nachteil der gemischten Verzinsung
Die gemischte Verzinsung ist inkonsistent und vom Zeitpunkt
des Zinszuschlages (bzw. der Einzahlung) abhängig.
Im Beispiel: Wäre der Zeitraum um einen Monat verschoben
(vom 15.10.96 bis zur Auflösung am 21.10.2003), so ergäbe
sich . . .
0,0375
·
290
0,0375 · 76
· 1,03756 · 1 +
Kx = 12 000 · 1 +
360
360
= 15 540,31
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
Die Widersprüche verschwinden, wenn eine unterjährige
Verzinsung zum konformen Zinssatz vorgenommen wird.
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
86
Unterjährige Verzinsung
Mathematik
Stefan Etschberger
Zahlung von Zinsen nicht jährlich, sondern in kürzeren
Fristen
1. Grundlegende
Bausteine
Dazu: m gleich lange Zinsperioden pro Jahr
Typische Aufteilungen: m = 2, 4, 12 Zinsperioden
2. Grundlegende
Werkzeuge
Annahme: Laufzeit n in Jahren sei (aus
Vereinfachungsgründen) ein ganzzahliges Vielfaches von
(z.B. m = 2, n = 1,5 oder m = 12, n = 1,25).
3. Lineare Algebra
1
m
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Ist ein Jahreszins i gegeben, so heißt:
i∗ =
i
m
der relative Periodenzins.
i 0 der zu i konforme Periodenzins, wenn die periodische
Verzinsung mit i 0 zum selben Ergebnis führt wie die jährliche
Verzinsung mit i.
0 m
(1 + i )
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
= (1 + i)
9. Differenzieren 2
10. Integration
87
Unterjährige Verzinsung
Mathematik
Stefan Etschberger
Betrachte den relativen Periodenzinsen i∗ =
i
m,
so heißt:
i der nominelle Jahreszins
ieff der effektive Jahreszins, wenn jährliche Verzinsung mit ieff
zum selben Ergebnis führt wie die periodische Verzinsung
mit i∗ .
(Entsprechendes gilt für q∗ , q 0 , qeff ).
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
K1 = K0 · q m
∗ = K0 · qeff
⇒ qeff = qm
∗
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
i
mit q∗ = 1 + i∗ = 1 +
m
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
88
Unterjährige Verzinsung: Formel
Mathematik
Stefan Etschberger
Damit: Effektivzins qeff ist
qeff = (1 + i∗ )
m
m
i
= 1+
m
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Endkapital Kn ist:
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Kn = K0 · (1 + i∗ )
m·n
m·n
i
= K0 · 1 +
m
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
Anmerkung: m · n muss nach o.g. Bedingungen ganzzahlig
sein.
8. Differenzieren 1
9. Differenzieren 2
10. Integration
89
Beispiel zur unterjährigen Verzinsung
Mathematik
Stefan Etschberger
Beispiel
Ein Betrag von 10 000 € soll zu 5 % nominal bei monatlicher
Verzinsung angelegt werden. Welcher Betrag kann nach 16
Monaten entnommen werden? Wie hoch ist der Effektivzins?
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Lösung:
5. Folgen und Reihen
6. Finanzmathematik
Mit i = 5 %, m = 12 und m · n = 16 gilt:
Kn = K0 · 1 +
i
m
m·n
= 10 000 · 1 +
6.1. Zinsen
Einfache Verzinsung
0,05
12
16
Zinseszinsen
Gemischte Verzinsung
= 10 687,91 €
Stetige Verzinsung
Zeitwert
6.2. Renten
Effektiver Jahreszins:
ieff
Nominal- und Effektivzins
6.3. Tilgung
12
0,05
= 1+
− 1 = 5,12 %
12
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
90
Beispiel zur unterjährigen Verzinsung mit dem konformen Zinssatz
Widersprüche der gemischten Verzinsung aus Folie 85
verschwinden, wenn eine unterjährige Verzinsung mit dem
konformen Zinssatz gemäß den Richtlinien für den internationalen
Wertpapierhandel (ISMA – International Securities Market
Association) vorgenommen wird.
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Beispiel
4. Lineare Programme
Am 15 9 1996 (15 10 1996) wurden € 12 000 zu effektiv 3,75 %
angelegt. Wie hoch war der Endbetrag bei Kontoauflösung am 21 9 2003
(21 10 2003)?
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Lösung
Stetige Verzinsung
Wir verwenden den konformen Zins auf täglicher Basis,
√
1
also p 0 = 360 1,0375 = 1,0375 360
Kn = 12 000 · 1,0375
106
360
6
· 1,0375 · 1,0375
260
360
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
= 15 536,90
alternativ:
76
290
Kn = 12 000 · 1,0375 360 · 1,03756 · 1,0375 360 = 15 536,90
8. Differenzieren 1
9. Differenzieren 2
10. Integration
91
Stetige Verzinsung
Mathematik
Stefan Etschberger
Lässt man m → ∞ wachsen, so erhält man aus der obigen Formel
Kn = lim K0
m→∞
i
1+
m
m·n
= K0
lim
m→∞
i
1+
m
m n
n
= K0 ei
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
die Formel für die stetige Verzinsung:
4. Lineare Programme
5. Folgen und Reihen
Kn = K0 · ei·n
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Für den effektiven Jahreszinssatz gilt damit:
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
i
6.2. Renten
ieff = e − 1
6.3. Tilgung
6.4. Kursrechnung
Anwendung stetiger Wachstumsprozesse:
7. Reelle Funktionen
8. Differenzieren 1
Ökonomie (Bevölkerungswachstum),
Physik (radioaktiver Zerfall),
BWL (Portfolio- und Kapitalmarkttheorie)
9. Differenzieren 2
10. Integration
92
Beispiel zur stetigen Verzinsung
Mathematik
Stefan Etschberger
Beispiel
K0 = € 10 000, n = 5, nominaler Jahreszins p = 5 %. Wie hoch
ist Kn und peff bei stetiger Verzinsung?
1. Grundlegende
Bausteine
Lösung:
3. Lineare Algebra
Kn = K0 · ei·n = 10 000 · e0,05·5 = 12 840,25 €
2. Grundlegende
Werkzeuge
4. Lineare Programme
5. Folgen und Reihen
ieff = e0,05 − 1 = 5,127 %
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Anmerkung 1: Bei Variation von m ergeben sich:
Gemischte Verzinsung
Nominal- und Effektivzins
m
peff
1
5
2
5,063
4
5,095
12
5,116
∞
5,127
Anmerkung 2: Die stetige Verzinsung wird z.B. in der Portfoliotheorie
verwendet, da sie mathematisch einfacher zu handhaben
ist als die diskrete Verzinsung.
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
93
Äquivalenzprinzip der Finanzmathematik
Das Äquivalenzprinzip der Finanzmathematik für Vergleich
von Zahlungen, welche zu verschiedenen Zeitpunkten
anfallen.
Vereinfachende Annahmen:
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Zinseszinsliche Verzinsung
3. Lineare Algebra
Zahlungen stets am Anfang oder am Ende einer Zinsperiode
4. Lineare Programme
5. Folgen und Reihen
Prinzip
6. Finanzmathematik
Vergleich von 2 oder mehreren zu verschiedenen
Zeitpunkten anfallende Geldbeträge: Beziehen auf den
gleichen Zeitpunkt durch geeignetes Auf- oder Abzinsen.
Wahl des Zeitpunktes dabei unerheblich.
Meist: Zeitpunkt t = 0 oder t = n (Ende der Laufzeit)
t = 0 den Anfang des ersten Zinszeitraums („heute“).
t = 1 Ende des ersten Zinszeitraums (31.12. des ersten Jahres).
t = 2 Ende des zweiten Zinszeitraumes (31.12. des zweiten
Jahres).
t = n Ende des letzen Zinszeitraumes (31.12. des n-ten Jahres)
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
94
Äquivalenzprinzip: Herleitung
Mathematik
Stefan Etschberger
Zwei Zahlungen, A im Zeitpunkt tA und B im Zeitpunkt tB ,
sind dann gleichwertig (A ∼ B), wenn ihre Zeitwerte in
jedem Zeitpunkt t übereinstimmen.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Beispiel
Gegeben:
Gesucht:
4. Lineare Programme
A = 10 000, tA = 2, p = 7%
B mit tB = 5 so, dass A ∼ B.
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Lösung:
(5−2)
B = 10 000 · 1,07
Gemischte Verzinsung
= 12 250,43 €
Eine Zahlung von € 12 250,43 nach 5 Jahren ist also gleichwertig
zu einer Zahlung von € 10 000 nach 2 Jahren. Der Barwert („Wert
heute“) beider Zahlungen ist übrigens
10 000 · 1,07−2 = 12 250,43 · 1,07−5 = 8 734,39 [€].
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
95
Zahlungsströme, Barwert, Endwert
Mathematik
Stefan Etschberger
Ein Zahlungsstrom (A0 , . . . , An ) ist eine Folge von
Zahlungen mit Zahlungszeitpunkten t = 0, . . . , n.
Summe aller auf t = 0 abgezinsten Zahlungen (Kapitalwert):
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
K0 =
n
X
t=0
At
=
qt
n
X
t=0
At · q
−t
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Summe aller auf t = n abgezinsten Zahlungen (Endwert):
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Kn =
n
X
qn
t=0
At
=
qt
n
X
t=0
Zeitwert
6.2. Renten
At · qn−t
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
96
Gleichheit zweier Zahlungsströme
Mathematik
Stefan Etschberger
Zwei Zahlungsströme (At ), (Bt ), t = 0, . . . , n sind genau dann
äquivalent, wenn sie zu einem beliebigen Zeitpunkt T den
gleichen Zeitwert besitzen:
Pn
Pn
T −t
T −t
(At ) ∼ (Bt ) ⇔
A
·
q
=
t=0 t
t=0 Bt · q
Pn
Pn
⇔
qT t=0 At · q−t = qT t=0 Bt · q−t
Pn
−t
⇔
= 0
t=0 (At − Bt ) · q
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
(At ) ∼ (Bt ) ⇔
n
X
At − Bt
t=0
qt
Zeitwert
6.2. Renten
=0
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
97
Investitionsrechnung: Beispiel
Mathematik
Stefan Etschberger
Beispiel
p = 5 %, Welches Projekt ist zu bevorzugen?
Jahr t
At
Bt
1. Grundlegende
Bausteine
0
1
2
3
4
5
0
400
1.000
400
0
400
1.000
600
0
600
1.000
600
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
Lösung: Kapitalwert von (At ):
6.1. Zinsen
Einfache Verzinsung
Zinseszinsen
5
X
t=0
At
0
1 000
0
1 000
0
1 000
=
+
+
+
+
+
= 2 599,74
t
0
1
2
3
4
1,05
1,05
1,05
1,05
1,05
1,05
1,055
Gemischte Verzinsung
Nominal- und Effektivzins
Stetige Verzinsung
Zeitwert
Kapitalwert von (Bt ):
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
5
X
t=0
Bt
400
400
400
600
600
600
=
+
+
+
+
+
= 2 625,80
1,05t
1,050
1,051
1,052
1,053
1,054
1,055
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
Alternative B ist der Alternative A vorzuziehen.
10. Integration
98
Rentenrechnung
Definition
Rente: Zahlungsstrom mit Zahlungen in gleichen zeitlichen
Abständen und (meistens) in konstanter Höhe
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Unterscheidung zwischen Renten
mit Zahlung am Ende einer Rentenperiode (nachschüssig)
mit Zahlung zu Beginn einer Rentenperiode vorschüssig)
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
mit endlicher Laufzeit (endliche Renten)
mit unendlicher Laufzeit (ewige Renten)
8. Differenzieren 1
9. Differenzieren 2
10. Integration
99
Rentenrechnung: Symbole
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Symbol
Bezeichnungen
rt
n
m
p
R0
Rt
Rn
Rentenrate in Periode t
Laufzeit (t = 1, . . . , n)
Anzahl der Rentenzahlungen pro Zinsperiode
Prozentzinssatz
Barwert der Rente
Zeitwert der Rente
Endwert der Rente
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
100
Nachschüssige konstante (endliche) Renten
Mathematik
Stefan Etschberger
Rentenzahlung jeweils am Ende einer Zinsperiode, jeweils in
Höhe von
r1 = r2 = · · · = rn = const. = r
⇒ Rentenendwert Rn :
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Rn = r · qn−1 + r · qn−2 + . . . + r · q + r
= r · qn−1 + ·qn−2 + . . . + q + 1
=r·
n−1
X
t=0
n
qt
q −1
=r·
q−1
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
(geometrische Reihe)
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
101
Rentenendwert und Rentenbarwert
Mathematik
Stefan Etschberger
Endwert Rn der Rente:
n
Rn = r ·
q −1
= r · NREFp,n
q−1
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
NREF: Nachschüssiger Rentenendwertfaktor für endliche
konstante Rente.
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Barwert der Rente:
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
R0 = Rn · q−n
qn − 1
qn − 1
=r· n
= r · n+1
= r · NRBFp,n
q · (q − 1)
q
− qn
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
NRBF: Nachschüssiger Rentenbarwertfaktor
102
Beispiel Rentenendwert
Mathematik
Stefan Etschberger
Beispiel
Genau 10 Jahre lang wurde jeweils zum Jahresende ein Betrag
von 12.000 € zum Zinssatz von 4% angelegt. Wieviel kann zu
Beginn des 11. Jahres (entspricht dem Ende des 10. Jahres)
abgehoben werden?
1. Grundlegende
Bausteine
Lösung:
Mit n = 10, q = 1,04 und r = 12 000 gilt Folgendes:
5. Folgen und Reihen
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
10
R10
1,04 − 1
= 12 000 ·
1,04 − 1
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
= 12 000 · 12,006107
= 144 073,28
[€ ]
8. Differenzieren 1
9. Differenzieren 2
10. Integration
103
Beispiel Rentenbarwert
Mathematik
Stefan Etschberger
Beispiel
Aus welchem zum Zeitpunkt 0 eingezahlten Betrag kann 10 Jahre
lang bei 4% Zins eine konstante nachschüssige Rente von 12.000
€ bezahlt werden?
Lösung: Frage nach dem Barwert einer Rente. Mit n = 10,
q = 1,04 und r = 12 000 gilt:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
10
1,04 − 1
R0 = 12 000 ·
1,0411 − 1,0410
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
≈ 12 000 · 8,110896
≈ 97 330,75
8. Differenzieren 1
9. Differenzieren 2
[€ ]
10. Integration
104
Umformung der Rentenbar- und -endwertformel
Mathematik
Stefan Etschberger
Je nach Fragestellung: Laufzeit n, Rentenzahlung r,
Verzinsungsfaktor q .
Rentenzahlung r:
1. Grundlegende
Bausteine
R0
qn+1 − qn
Rn
q−1
r=
= R0 ·
=
=
R
·
n
NRBFp,n
qn − 1
NREFp,n
qn − 1
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Laufzeit n aus Rn :
ln 1 + Rnr ·i
n=
ln q
q aus R0 :
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
n+1
R0 q
!
n
− (R0 + r)q + r = 0 .
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
q aus Rn :
Laufzeit n aus R0 :
R0 ·i
− ln 1 − r
n=
ln q
Unterjährige Renten
8. Differenzieren 1
!
r · qn − Rn · q + Rn − r = 0 .
Berechnung von q im Allgemeinen
nur näherungsweise (iterativ)
möglich
9. Differenzieren 2
10. Integration
105
Beispiel nachschüssige Rente
Mathematik
Stefan Etschberger
Beispiel
Ein Steuerberater kauft die Kanzlei eines älteren Kollegen und
muss als Kaufpreis 10 Jahre lang jährlich–nachschüssig je 12.500
€ zahlen. Durch welchen Betrag könnte der Steuerberater diese
Zahlungsverpflichung sofort bei Vertragsabschluss ablösen, wenn
mit 8% Zinsen kalkuliert wird?
Lösung: Gesucht ist der Rentenbarwert mit r = 12 500, q = 1,08
und n = 10. Es gilt dann:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
10
R0 = 12 500 ·
1,08 − 1
1,0811 − 1,0810
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
= 12 500 · 6,710081
= 83 876,01
9. Differenzieren 2
10. Integration
[€ ]
106
Beispiel nachschüssige Rente
Mathematik
Stefan Etschberger
Beispiel
Der Barwert einer über 15 Jahre laufenden nachschüssigen
Jahresrente beträgt bei 5%-iger Verzinsung 10.380 €. Wie hoch
sind die jährlichen Rentenzahlungen?
Lösung: Gesucht sind die Rentenzahlungen r mit R0 = 10 380,
q = 1,05 und n = 15. Es gilt dann:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
1,0516 − 1,0515
r = 10 380 ·
1,0515 − 1
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
= 10 380 · 0,096342
= 1 000,03
[€ ]
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
107
Vorschüssige konstante Renten
Mathematik
Stefan Etschberger
Rentenbetrag wird jeweils zu Beginn der Zinsperiode in Höhe von
0 = r 0 bezahlt.
r10 = r20 = · · · = rn
Äquivalenzprinzip ⇒ Endwert der Rente:
vorschüssige Rentenzahlung
r ⇒ r = r 0q
r0
∼ nachschüssige Rentenzahlung
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Rn
=
r0 · q ·
qn
−1
= r 0 · VREFp,n
q−1
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
VREF: Vorschüssiger Rentenendwertfaktor
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
Barwert der Rente:
7. Reelle Funktionen
R0
=
Rn · q−n
=
r0
qn − 1
·q· n
q · (q − 1)
8. Differenzieren 1
=
r0
qn − 1
· n
= r 0 · VRBFp,n
n−1
q −q
9. Differenzieren 2
10. Integration
VRBF: Vorschüssiger Rentenbarwertfaktor
108
Unterjährige Raten und jährliche Verzinsung
Aufteilung der Zinsperiode in mehrere gleich lange
Rentenperioden, d.h. m Rentenzahlungen pro Zinsperiode (=
Jahr).
Dazu:
Rechnung mit einfacher Verzinsung innerhalb der
Zinsperiode
Rentenzahlungen nachschüssig (also am Ende jeder unterj.
Rentenperiode) oder vorschüssig möglich
Lösung: Errechnung von konformen (gleichwertigen) jährlich
nachschüssigen Ersatzzahlungen zu den m unterjährigen
Zahlungen.
Definition
re heißt konforme jährlich nachschüssige Ersatzrentenrate einer
nachschüssigen (oder vorschüssigen) unterjährigen Rentenrate r.
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
109
Konforme jährliche nachschüssige Ersatzrentenrate
Mathematik
Stefan Etschberger
Berechnung von re :
falls unterjährige Rente nachschüssig: falls unterjährige Rente vorschüssig:
1
1
re = r + r · 1 +
·i
re = r · 1 +
·i
m m
2
2
+r· 1+
·i
+r· 1+
·i
m
m
+ . . .
+ . . .
m m−1
·i
+r· 1+
+r· 1+
·i
m
m
=r·m
= r·m
1
1
(1 + 2 + . . . + m)
+i·r·
(1 + 2 + . . . + (m − 1))
+i·r·
m
m
m+1
m−1
re = r · m + i ·
re = r · m + i ·
2
2
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Aus Ersatzrentenrate re : Weiterrechnen mit Formeln für jährliche nachschüssige
Rente
110
Beispiel konforme Ersatzrentenraten
Mathematik
Stefan Etschberger
Beispiel
Ein Sparer legt monatliche nachschüssig 1.000 € auf ein Konto.
Wie hoch ist der Kontostand nach 10 Jahren bei einem Zinssatz
von 4%?
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Lösung: Gesucht ist der Rentenendwert auf Basis der konformen
Rentenraten. Mit n = 10, m = 12, q = 1,04 und r = 1 000 ergibt
sich Folgendes:
0,04 · 11 1,0410 − 1
R10 = 1 000 · 12 +
·
2
1,04 − 1
|
{z
}
12,22
= 12 220 · 12,006107 = 146 714,63
Beim Zinssatz von i = 4% kann eine monatlich nachschüssige
Rente von 1.000 € durch eine jährlich nachschüssige
Rentenzahlung von 12.220 € gleichwertig ersetzt werden. Der
Kontostand nach 10 Jahren beträgt 146 714,63 €.
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
111
Ewige Renten
Mathematik
Stefan Etschberger
Eine Rente heißt ewige Rente, wenn Anzahl n der
Ratenzahlungen nicht begrenzt, n also beliebig groß wird
(n → ∞).
Berechnung des Rentenendwertes dann nicht möglich
Rentenbarwert R0 existiert jedoch:
1 qn − 1
R0 = lim (r · NRBF) = r · lim n ·
n→∞
n→∞ q
q−1
!
1 − q1n
1
r
= r · lim
=r·
=
n→∞
q−1
q−1
i
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
7. Reelle Funktionen
Damit: Rentenbarwert einer nachschüssigen ewigen Rente:
8. Differenzieren 1
9. Differenzieren 2
r
R0 =
i
10. Integration
112
Ewige Renten: Beispiel
Mathematik
Stefan Etschberger
Beispiel
Wie groß ist der Barwert einer ewigen nachschüssigen Rente von
40.000 € pro Jahr, wenn der Zins bei 8% liegt?
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Lösung:
5. Folgen und Reihen
R0 =
40 000
= 500 000
0,08
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
Unterjährige Renten
Ewige Renten
6.3. Tilgung
6.4. Kursrechnung
Anmerkung: Geht man von einer vorschüssigen ewigen Rente
aus, so ergibt sich für den Rentenbarwert:
r0
0
R0 = r +
i
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
113
Tilgungsrechnung
Mathematik
Stefan Etschberger
Rückzahlung oder Tilgung größerer Darlehen oft in mehreren
Raten
Hier betrachtet: Tilgung in mehreren Teilbeträgen, in
konstanten Zeitabständen
Jede zu bezahlende Rate beinhaltet Zinsen und Tilgung
Verwendete Symbole:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Symbol
Bezeichnung
S
Rk
n
Zk
Tk
Ak
Darlehenssumme, Anfangsschuld
Restschuld zu Beginn des k-ten Jahres
Tilgungsdauer (∈ N)
Zinsquote am Ende des k-ten Jahres
Tilgungsquote am Ende des k-ten Jahres
Annuität am Ende des k-ten Jahres
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
6.3. Tilgung
Ratentilgung
Annuitätentilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Unterscheidung zwischen Ratentilgung und
Annuitätentilgung
114
Ratentilgung
Mathematik
Stefan Etschberger
Während Laufzeit sind Tilgungsquoten konstant. Daraus
folgt:
S
Tk = T =
n
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
und damit:
6.1. Zinsen
6.2. Renten
6.3. Tilgung
Ratentilgung
Rk = S − (k − 1) · T
Restschuld zu Beginn des k-ten Jahres
Zk = Rk · i
Zinsquote am Ende des k-ten Jahres
Ak = Zk + T
Annuität am Ende des k-ten Jahres
Annuitätentilgung
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
115
Annuitätentilgung
Mathematik
Stefan Etschberger
Problem der Ratentilgung: Belastung anfangs hoch, später
geringer
1. Grundlegende
Bausteine
Ausweg: Konstanthalten der Annuitäten über Rentenformel
2. Grundlegende
Werkzeuge
3. Lineare Algebra
qn (q − 1)
Ak = A = S ·
qn − 1
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
Daraus ergibt sich:
6.2. Renten
6.3. Tilgung
Ratentilgung
qn − qk−1
Rk = S ·
qn − 1
Zk = Rk · i = A · 1 − qk−n−1
Tk = A − Zk = A · qk−n−1
Annuitätentilgung
Restsch. zu Beg. des k-ten J.
Zinsen im k-ten Jahr
Tilgung im k-ten Jahr
6.4. Kursrechnung
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
116
Kursrechnung
Mathematik
Stefan Etschberger
Festverzinsliche Wertpapiere
Wertpapier: Investor erwirbt für bestimmten Preis ein Recht
auf Zahlungen
1. Grundlegende
Bausteine
Hier: Gesamtfällige festverzinsliche Wertpapiere
2. Grundlegende
Werkzeuge
Emission (Erstausgabe): Investor zahlt pro 100 € Nennwert
einen Preis C0 (Emissionskurs)
3. Lineare Algebra
Emittend: Zahlt während Laufzeit Zinsen (Kuponszahlung)
und (meist nach Ablauf ) Tilgung (Rücknahmekurs)
∗
Kuponzahlung: mittels nominellen Jahreszinses i (oder
Jahreszinsfuß p∗ ) auf den Nennwert an Investor, meist
jährlich nachschüssig
Falls i∗ = 0: Null-Kupon-Anleihen oder Zerobonds
Rücknahmekurs: Tilgung in einem Betrag am Ende der
Laufzeit Cn als Prozentsatz des Nennwertes
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
Emissionskurs
Duration
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Rendite: ieff Jährlicher Effektivzins, der Leistung des Investors
und des Emittenden gleichwertig macht
117
Kursrechnung
Mathematik
Stefan Etschberger
Äquivalenzgleichung für Emissionskurs
qn − 1 −n
C0 = p ·
· q + Cn · q−n
q−1
∗
Dabei:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
n : Laufzeit in Jahren
C0 : Emissionskurs
p∗ : Nominalzinsfuß, jährliche Zinszahlung pro 100 €
Nennwert
Cn : Rücknahmekurs am Ende der Laufzeut
q = 1 + ieff : Effektiver Jahreszins bzw. Rendite des festverz.
Wertpapiers
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
Emissionskurs
Duration
7. Reelle Funktionen
8. Differenzieren 1
Anmerkungen:
9. Differenzieren 2
Gleichung i.a. nicht elementar nach q auflösbar
Deswegen oft: Näherung durch Iteration (z.B. regula falsi)
Emissionskurs =
^ mit Rendite abgezinster Kapitalwert
sämtlicher zukünftiger Leistungen des Wertpapiers
10. Integration
118
Kursrechnung
Mathematik
Stefan Etschberger
Ganzzahlige Restlaufzeiten
Festverzinsliche Wertpapiere können meist jederzeit
gehandelt werden
Annahme zunächst: Handel nur unmittelbar nach
Kuponzahlung möglich
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Gesucht: Kurs Ct für eine Restlaufzeit von t Jahren
5. Folgen und Reihen
Lösung: Preis eines Wertpapiers ist zu jedem Zeitpunkt der
Kapitalwert aller in der Restlaufzeit noch ausstehenden
Leistungen
6. Finanzmathematik
Abgezinst wird dabei mit dem Marktzins (auch:
Umlaufrendite)
6.1. Zinsen
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
Emissionskurs
Duration
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
qt − 1 −t
Ct = p ·
· q + Cn · q−t
q−1
10. Integration
∗
119
Kursrechnung
Mathematik
Stefan Etschberger
Risikoanalyse – Duration
Änderung des Marktzinses:
Abhängig von Zeitpunkt
Auswirkung auf aktuellen
Wert des Papiers
Aktueller Wert
Fall 1 (Zins steigt): C0 ist
niedriger, aber Wiederanlage
der Kuponzahlungen
erbringen mehr Rendite
Fall 2 (Zins fällt): C0 ist höher,
aber Wiederanlage der
Kuponzahlungen erbringen
weniger Rendite
Vermutung: An einem
(Zeit-)Punkt heben sich diese
beiden Effekte auf
190
i=6%
i=4%
180
i=2%
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
170
5. Folgen und Reihen
6. Finanzmathematik
160
6.1. Zinsen
6.2. Renten
6.3. Tilgung
150
6.4. Kursrechnung
Emissionskurs
Duration
140
7. Reelle Funktionen
Zeit t
130
0
1
2
3
D
5
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Dieser Zeitpunkt heißt
Duration D.
120
Kursrechnung
Mathematik
Stefan Etschberger
Risikoanalyse – Duration
Der aktuelle Wert eines Papiers Ct (q) = qt · C0 (q) ändert
sich also nicht bzgl. Änderungen von q, wenn t = D
damit gilt für die Duration D
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
∂CD (q)
∂
∂C0 (q)
=
qD · C0 (q) = D·qD−1 C0 (q)+qD
=0
∂q
∂q
∂q
D−1
Da q
immer positiv ist muss also für D gelten
0 (q)
D · C0 (q) + q · ∂C∂q
= 0 und damit:
∂C0 (q)
q
C00 (q)
D=−
·
= −q ·
∂q
C0 (q)
C0 (q)
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
6.1. Zinsen
6.2. Renten
6.3. Tilgung
6.4. Kursrechnung
Emissionskurs
Duration
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Weitere mögliche Interpretation der Duration als
Bruttozinselastizität des Barwertes.
121
Kursrechnung
Mathematik
Stefan Etschberger
Partielle Ableitung des Kapitalwertes
Für die Berechnung von D ist C00 (q) zu bestimmen;
bei einem festverzinslichen Wertpapier ergibt sich so
C00 (q)
=−
n
qn+1
qn − 1
p∗ n · qn−1 (q − 1) − (qn − 1)
p∗·
+ Cn + n ·
q−1
q
(q − 1)2
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Varianten der Duration
6. Finanzmathematik
Elastizität (von i):
Modifizierte Duration:
6.1. Zinsen
6.2. Renten
6.3. Tilgung
C00 (q)
D
MD =
=−
q
C0 (q)
εC0 ,i
C00 (i)
i
=
· i = − · D = −MD · i
C0 (i)
q
Auswirkungen von Zinsänderungen
6.4. Kursrechnung
Emissionskurs
Duration
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
Bei bekanntem Emissionskurs: Auswirkungen kleiner
Zinsänderungen über Duration
10. Integration
C0 (i + ∆i) ≈ C0 (i) · (1 − MD · ∆i)
122
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
Integration
7
Reelle Funktionen
Grundbegriffe
Elementare Funktionen
Stetigkeit reeller Funktionen
Mathematik
Stefan Etschberger
Warum beschäftigen wir uns mit reellen Funktionen?
allgemein: kompakte und präzise Beschreibung von
Abhängigkeiten zwischen mehreren Faktoren
speziell: Modellierung technischer und ökonomischer
Systeme
Basis für Analyse und Optimierung von Systemen / Prozessen
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Wesentliche Lernziele
6. Finanzmathematik
Fähigkeit mit den wesentlichen Begriffen im Zusammenhang
mit Funktionen umzugehen
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
Kennenlernen der wichtigsten Klassen reeller Funktionen
8. Differenzieren 1
Beherrschen des Stetigkeitsbegriffs
9. Differenzieren 2
10. Integration
124
Beispiel
Mathematik
Stefan Etschberger
Kostenfunktion
Unternehmen ermittelt empirisch Kosten K für die
Herstellung von x Einheiten eines Produktes
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Dargestellt als Wertetabelle und als Grafik
3. Lineare Algebra
4. Lineare Programme
x
K
1
2
3
4
5
6
7
8
4,25
6,00
8,25
11,00
14,25
18,00
22,25
27,00
K(x)
5. Folgen und Reihen
30
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
20
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
10
9. Differenzieren 2
10. Integration
5
2
4
6
8
10
x
125
Beispiel
Mathematik
Stefan Etschberger
Kostenfunktion
Jetzt: Betrachte zusätzlich Funktion K(x) = 14 x2 + x + 3
für Definitionsbereich D = {1, . . . ,8}
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
K(x)
Darstellung durch
Funktion: kompakt,
eindeutig
30
Möglicher Ausgangspunkt
für Prognosen (Kosten für
9, 10, . . . Einheiten)
20
10
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
5
10. Integration
2
4
6
8
10
x
126
Begriff reelle Funktion
Mathematik
Stefan Etschberger
Definition
f : D → R heißt reellwertige Abbildung mit
Definitionsbereich D
Mit D ⊂ Rn heißt f reelle Funktion von n Variablen
Darstellung von Funktionen
Durch Funktionsgleichungen f(x1 , . . . , xn ) = y
x = (x1 , . . . , xn ): unabhängige (exogene) Variablen
y: abhängige (endogene) Variablen
Durch Wertetabellen
Durch Graphen
Für D ⊂ R: Darstellung im kartesischen Koordinatensystem
Für D ⊂ R2 : 3-dimensionale Darstellung oder Niveaulinien
f(x) = c mit c ∈ R
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
10. Integration
127
Beispiel
Mathematik
Stefan Etschberger
Cobb-Douglas-Funktion
neoklassische Produktionsfunktion der Form
a
a
f(x1 , . . . , xn ) = a0 · x1 1 · x2 2 · . . . xann
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Beispiel für zwei Produktionsfaktoren
√
1/2
1/2
f(x1 , x2 ) = 1 · x1 · x2 = x1 · x2
3. Lineare Algebra
4. Lineare Programme
Dreidimensionale Darstellung
Niveaulinien
5. Folgen und Reihen
für f(x1 , x2 ) = c mit c = 1/2, . . . , 3
6. Finanzmathematik
4
7. Reelle Funktionen
7.1. Grundbegriffe
3
4
2
8. Differenzieren 1
5
2
1,5
1,
2
1
0,5
0,5
2,5
1
9. Differenzieren 2
2
1
0
0,5
0
4
0
10. Integration
1,5
4
1
0,5
2
2
7.3. Stetigkeit
5
3
2
7.2. Elementare Funktionen
3
2,
0
0
1
0,5
2
3
4
128
Mathematik
Stefan Etschberger
Eigenschaften von Funktionen
Eine Funktion f : D → W mit D ⊂ Rn und W ⊂ R heißt:
surjektiv, wenn zu jedem y ∈ W ein x ∈ D mit f(x) = y
existiert,
injektiv, wenn für alle x, x̃ ∈ D gilt x 6= x̃ ⇒ f(x) 6= f(x̃),
bijektiv, wenn f surjektiv und injektiv ist.
Komposition von Funktionen
Voraussetzung: Funktionen f : Df → R und g : Dg → R mit
Df ⊂ Rn und f(Df ) ⊂ Dg ⊂ R
Zusammengesetzte Funktion: g ◦ f : Df → R: Zuordnung des
Werts (g ◦ f)(x) = g (f(x)) für alle x ∈ Df
Inverse Funktion / Umkehrfunktion
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
Voraussetzung: bijektive Funktion f : D → W mit D, W ⊂ R
10. Integration
Inverse Funktion: f−1 : W → D, y 7→ f−1 (y), wobei y für
alle x ∈ D mit y = f(x) zugeordnet wird
129
Invertierung: Beispiel
Mathematik
Stefan Etschberger
f : R → R,
Beispiel b)
f(x) = x3 + 1
→
1. Grundlegende
Bausteine
f(x)
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
5
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
1
9. Differenzieren 2
10. Integration
1
−1
2
x
130
Satz: Operationen zwischen Funktionen
Mathematik
Stefan Etschberger
Gegeben: f, g : D → R reelle Funktionen mit identischem
Definitionsbereich D ⊂ R.
Dann sind auch die folgenden Abbildungen relle Funktionen:
f+g:
f−g:
D→R
D→R
f·g:
D→R
f
:
g
D1 → R
mit
mit
mit
mit
x∈D
7→
(f + g)(x) = f(x) + g(x)
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
x∈D
7→
(f − g)(x) = f(x) − g(x)
x∈D
7→
x ∈ D1
7→
(f · g)(x) = f(x) · g(x)
f
f(x)
(x) =
g
g(x)
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
10. Integration
D1 = {x ∈ D : g(x) 6= 0}
131
Besondere Punkte bei Funktionen
Mathematik
Stefan Etschberger
Gegeben: Reelle Funktion f : D → R mit D ⊂ Rn
Definitionen
1. Grundlegende
Bausteine
c-Stelle von f: xc ∈ D mit f(xc ) = c
2. Grundlegende
Werkzeuge
Mit c = 0 heißt c-Stelle dann 0-Stelle von f
3. Lineare Algebra
Maximalstelle oder globales Maximum:
xmax ∈ D mit f(xmax ) ≥ f(x) für alle x ∈ D
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
Minimalstelle oder globales Minimum:
xmin ∈ D mit f(xmin ) ≤ f(x) für alle x ∈ D
≥
x∗ ∈ D mit f(x∗ )
f(x) für x ∈ [x∗ − a, x ∗ +a] ⊂ D
(≤)
heißt lokale Maximalstelle (Minimalstelle), f(x∗ ) lokales
Maximum
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Weitere Sprechweisen: Extremal-, Optimalstelle, Extremum,
Optimum
132
Beispiel: Maximal-, bzw. Minimalstellen
Wegen x1 , x2 ≥ 0 und
p1 , p2 ≥ 0 folgt
p1 ∈ [0,10] und p2 ∈ [0,12]
60 5
0
40
30
20
10
40
50
40
40
10
30
0
0
30
20
10
1. Grundlegende
Bausteine
30
50
20
Gegeben:
Preis-Absatz-Funktionen
x1 = 10 − p1 und
x2 = 12 − p2
50
Umsatzmaximierung für
zwei Produkte mit
Absatzquantitäten x1 , x2
und Preisen p1 , p2 :
Mathematik
Stefan Etschberger
3. Lineare Algebra
20
10
10
2
4
6
5
8
10 0
2. Grundlegende
Werkzeuge
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Gesamtumsatz?
7.1. Grundbegriffe
Maximalstelle?
7.3. Stetigkeit
Minimalstellen?
7.2. Elementare Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
133
Weitere Eigenschaften reeller Funktionen
Mathematik
Stefan Etschberger
f beschränkt ⇔ es gibt c0 , c1 ∈ R mit c0 ≤ f(x) ≤ c1
f monoton wachsend ⇔ (x1 < x2 ⇒ f(x1 ) ≤ f(x2 ))
f monoton fallend
⇔ (x1 < x2 ⇒ f(x1 ) ≥ f(x2 ))
bei strenger Monotonie entfällt „=“
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
f konvex ⇔ (x1 =
6 x2 ⇒ f(λx1 + (1 − λ)x2 ) ≤ λf(x1 ) + (1 − λ)f(x2 ))6. Finanzmathematik
f konkav ⇔ (x1 =
6 x2 ⇒ f(λx1 + (1 − λ)x2 ) ≥ λf(x1 ) + (1 − λ)f(x2 ))7. Reelle Funktionen
λ ∈ (0,1)
7.1. Grundbegriffe
7.2. Elementare Funktionen
bei strenger Konkavität entfällt „=“
f periodisch mit Periode p > 0
f gerade (ungerade)
⇔
⇔
7.3. Stetigkeit
f(x) = f(x ± p)
f(x) = f(−x) (−f(x) = f(−x))
8. Differenzieren 1
9. Differenzieren 2
10. Integration
134
Polynome
Mathematik
Stefan Etschberger
Definition
p : R → R mit
p(x) = a0 + a1 x + a2 x2 + . . . + an xn =
n
X
i=0
1. Grundlegende
Bausteine
ai xi
(mit an 6= 0)
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
heißt Polynom n-ten Grades
Schreibweise: grad(p) = n
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
Satz
7.3. Stetigkeit
Summen, Differenzen und Produkte von Polynomen sind
wieder Polynome.
p(x)
x−x1
p(x1 ) = 0 ⇒ u(x) =
grad(u) = grad(p) − 1
8. Differenzieren 1
9. Differenzieren 2
10. Integration
ist wieder Polynom mit
135
Rationale Funktionen
Mathematik
Stefan Etschberger
Definition
q : D → R mit
p1 (x)
q(x) =
p2 (x)
1. Grundlegende
Bausteine
(mit p1 , p2 (6= 0) sind Polynome)
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
heißt Rationale Funktion.
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
Satz
7.2. Elementare Funktionen
Jedes Polynom ist auch rationale Funktione (z.B. p2 (x) = c).
Summen, Differenzen, Produkte und Quotienten (falls
definiert) von rationalen Funktionen sind wieder rationale
Funktionen.
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
10. Integration
136
Weitere Funktionen
Mathematik
Stefan Etschberger
Potenzfunktion
f : R+ → R+ mit f(x) = xa , (a ∈ R) heißt Potenzfunktion.
f ist streng monoton wachsend für a > 0 und streng
monoton fallend für a < 0.
Für a 6= 0 existiert eine inverse Funktion f−1 zu f
Exponentialfunktion, Logarithmusfunktion
f : R → R+ mit f(x) = ax , (a > 0, a 6= 1) heißt
Exponentialfunktion zur Basis a.
g : R+ → R mit g(y) = loga (y), (a > 0, a 6= 1) heißt
Logarithmusfunktion zur Basis a mit g = f−1 .
Satz: f, g wachsen streng monoton für a > 1 und fallen
streng monoton für a < 1
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
10. Integration
137
Grenzwert einer Funktion
Mathematik
Stefan Etschberger
Ausgangssituation
Gegeben: Funktion f : D → R mit D ⊂ Rn
Grenzwert von f aufbauend auf Konvergenz von Zahlenfolgen
m T ∈ D mit Grenzwert
Dazu betrachte: Alle Folgen am = am
,
.
.
.
,
a
n
1
a ∈ Rn , also am → a für m → ∞
Untersuche Grenzwerte
lim f (am ) .
4. Lineare Programme
Definition des Grenzwerts einer Funktion
f heißt an der Stelle a ∈ R
konvergent gegen f̃ ∈ R,
2. Grundlegende
Werkzeuge
3. Lineare Algebra
am →a
n
1. Grundlegende
Bausteine
5. Folgen und Reihen
(die nicht notwendig zu D gehören muss)
6. Finanzmathematik
7. Reelle Funktionen
wenn
a) mindestens eine Folge (am ) mit am ∈ D, am 6= a und am → a existiert
( d.h. a ist kein „isolierter Punkt“)
b) für alle Folgen (am ) mit am ∈ D und am → a0 gilt f(am ) → f̃.
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
f̃ heißt dann Grenzwert von f(am ).
10. Integration
Schreibweise für alle gegen a konvergierende Folgen (am ):
lim
am →a
f a
m
= f̃
oder kurz
lim f(x) = f̃
x→a
138
Begriff der Stetigkeit
Mathematik
Stefan Etschberger
Gegeben
Funktion f : D → R mit D ⊂ Rn
Definition
1. Grundlegende
Bausteine
f heißt stetig in x0 ⇔ lim f(x) = f(x0 )
x→x0
f heißt stetig in T ⊂ D ⇔ f ist für alle x ∈ T stetig
Ist f für ein x̃ ∈ D nicht stetig, so heißt x̃ Unstetigkeitsstelle
oder Sprungstelle
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Satz
7.1. Grundbegriffe
7.2. Elementare Funktionen
Für stetige Funktionen f, g gilt:
f ± g, f · g, f/g (g(x) 6= 0) sind stetig
|f|, f ◦ g, sind stetig
Falls f auf einem Intervall definiert und invertierbar: f−1 stetig
7.3. Stetigkeit
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Alle elementaren Funktionen sind in ihrem
Definitionsbereich stetig
139
Zwischenwertsatz
Mathematik
Stefan Etschberger
Gegeben: f : [a, b] → R stetig
1. Grundlegende
Bausteine
Dann gilt:
⇒
f(a) < f(b)
2. Grundlegende
Werkzeuge
∀ y ∈ [f(a), f(b)] ∃ x ∈ [a, b]
mit f(x) = y
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
f(x)
6. Finanzmathematik
7. Reelle Funktionen
f(b)
7.1. Grundbegriffe
7.2. Elementare Funktionen
7.3. Stetigkeit
8. Differenzieren 1
a
b
x
9. Differenzieren 2
10. Integration
f(a)
140
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
Integration
8
Differenzieren 1
Differentialquotient und Ableitung
Änderungsrate und Elastizität
Kurvendiskussion
Warum Differentialrechnung?
Mathematik
Stefan Etschberger
Anwendungen
Analyse und ökonomische Interpretation
wirtschaftswissenschaftlicher Gesetzmäßigkeiten durch
Untersuchung der Charakteristika von Funktionen
Ermittlung von optimalen Lösungen betriebswirtschaftlicher
Entscheidungsprobleme wie zum Beispiel
Absatzmengenplanung, Loßgrößenplanung etc.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
Wesentliche Lernziele
Verständnis des Differentialquotienten
Fähigkeit, eine Funktion zu differenzieren
Bestimmung und Interpretation von Änderungsraten und
Elastizitäten
7. Reelle Funktionen
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
Durchführung und Interpretation von Kurvendiskussionen
142
Preisbestimmung beim Angebotsmonopol
Mathematik
Stefan Etschberger
Bekannt sind folgende Zusammenhänge:
p(x) = c1 − c2 x (Preis-Absatz-Funktion)
K(x) = c3 + c4 x (Kostenfunktion)
(mit c1 , c2 , c3 , c4 ∈ R+ Konstanten)
Damit ergibt sich:
Umsatzfunktion: U(x) = c1 x − c2 x2
Gewinnfunktion:
G(x) = U(x) − K(x) = c1 x − c2 x2 − (c3 + c4 x)
Fragen:
Welche Menge/Welcher Preis ist Umsatz-/Gewinnmaximal?
Welche Veränderung des Umsatzes ergibt sich bei einer
Veränderung der Absatzmenge?
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
143
Differenzenquotient: Idee
Mathematik
Stefan Etschberger
Tour de France: Anstieg nach L’Alpe d’Huez
Länge des Anstiegs: 13,9 km
1. Grundlegende
Bausteine
Auf einer Höhe von 740 m beginnen die 21 Kehren
2. Grundlegende
Werkzeuge
Zielankunft liegt auf 1850 m
Bestimmung von Steigungen:
3. Lineare Algebra
Höhendifferenz
Distanz
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
144
Differenzenquotient
Mathematik
Stefan Etschberger
Gegeben: Reelle Funktion f : D → R mit D ∈ R
Dann heißt der Ausdruck
f(x2 ) − f(x1 )
x2 − x1
1. Grundlegende
Bausteine
Differenzenquotient (Steigung) von f im Intervall [x1 , x2 ] ⊂ D
2. Grundlegende
Werkzeuge
Alternative Schreibweise, dabei Ersetzen von x2 durch x1 + ∆x1
3. Lineare Algebra
f (x1 + ∆x1 ) − f (x1 )
∆f (x1 )
=
∆x1
∆x1
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
f(x1 + ∆x1 ) •
f(x1 )
•
f(x)
B•
A•
|
•
x1
{z
∆x1
}
•
x1 + ∆x1







8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
∆f(x1 )
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
x
145
Differentialquotient
Mathematik
Stefan Etschberger
Eine reelle Funktion f : D → R mit D ⊂ R heißt an der
Stelle x1 ∈ D differenzierbar, wenn der Grenzwert
lim
∆x1 →0
∆f(x1 )
∆x1
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
existiert.
G. W. Leibniz
(1646-1716)
Ist f an der Stelle x1 differenzierbar, heißt
3. Lineare Algebra
4. Lineare Programme
lim
∆x1 →0
=
=
lim
∆x1 →0
5. Folgen und Reihen
∆f(x1 )
∆x1
f(x1 + ∆x1 ) − f(x1 )
∆x1
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
df
(x1 ) = f 0 (x1 )
dx1
8.2. Änderungsrate und
Elastizität
I. Newton
(1643-1727)
Differentialquotient oder erste Ableitung von f an der
Stelle x1 .
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
f heißt in D differenzierbar, wenn f für alle x ∈ D
differenzierbar ist.
146
Ableitungsregeln
Mathematik
Stefan Etschberger
Summen, Differenzen, Produkte und Quotienten (soweit definiert) von
differenzierbaren Funktionen sind differenzierbar.
Summenregel:
1. Grundlegende
Bausteine
0
0
0
(f ± g) (x) = f (x) ± g (x)
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Produktregel:
4. Lineare Programme
0
0
0
(f · g) (x) = f(x) · g(x) + f(x) · g (x)
5. Folgen und Reihen
6. Finanzmathematik
Daraus ergibt sich für eine Konstante c: (c · f) 0 (x) = c · f 0 (x)
7. Reelle Funktionen
Quotientenregel:
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
z
n
0
(x) =
z 0 (x) · n(x) − z(x) · n 0 (x)
(n(x))2
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
Kettenregel:
10. Integration
0
0
0
0
(g ◦ f) (x) = [g (f(x))] = g (f(x)) · f (x)
147
Ableitung elementarer Funktionen
Mathematik
Stefan Etschberger
Gegeben: f : D → R, mit D ⊂ R und a > 0, b ∈ R. Dann gilt:
f(x)
f 0 (x)
ln x
1
x
1
x ln a
x
loga x
ex
a ln a
b
b−1
a
x
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
e
x
7. Reelle Funktionen
x
bx
sin x
cos x
cos x
− sin x
1. Grundlegende
Bausteine
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
148
Ableitungen höherer Ordnung
Mathematik
Stefan Etschberger
Gegeben: f : D → R, mit D ⊂ R und a > 0, b ∈ R
Wenn der Differentialquotient f 0 : D → R in x ∈ D
differenzierbar ist, dann heißt
df 0 (x)
d2 f(x)
=
= f 00 (x)
2
dx
(dx)
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
zweite Ableitung oder Differentialquotient zweiter Ordnung
von f in x ∈ D.
Analog für n = 2,3, . . .:
d (n−1) d
f
(x) =
dx
dx
(n−1)
d
f(x)
(dx)(n−1)
!
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
= f(n) (x)
f(n) (x) bezeichnet dabei die n-te Ableitung von f in x ∈ D.
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
f heißt n-mal stetig differenzierbar in D, wenn f in D stetig
und in jedem Punkt x ∈ D n-mal differenzierbar ist
149
Definition Elastizität
Mathematik
Stefan Etschberger
Voraussetzung: D ⊂ R und f : D → R ist differenzierbar.
Dann heißt
0
ρf (x) =
f (x)
f(x)
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Änderungsrate von f
6. Finanzmathematik
7. Reelle Funktionen
und
8. Differenzieren 1
f (x) =
f 0 (x)
f(x)
x
f 0 (x) · x
=
= ρf (x) · x
f(x)
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
Elastizität von f.
10. Integration
150
Elastische versus unelastische Funktionen
Mathematik
Stefan Etschberger
Definition
Für |f (x)| > 1 reagiert die relative Änderung von f(x)
überproportional auf relative Änderungen von x, die
Funktion f heißt im Punkt x elastisch.
Für |f (x)| < 1 bezeichnen wir die Funktion f im Punkt x als
unelastisch.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Beispiel
6. Finanzmathematik
f(x) = aebx mit a, b 6= 0
0
ρf (x) =
7. Reelle Funktionen
⇒
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
bx
f (x)
abe
=
=b
f(x)
aebx
und f (x) = x · ρf (x) = bx
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
Die Änderungsrate der Exponentialfunktion ist also konstant
10. Integration
Die Elastizität wächst linear mit x.
151
Steigung und erste Ableitung
Mathematik
Stefan Etschberger
Gegeben:
f : [a, b] → R ist stetig und differenzierbar auf (a, b).
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Dann gilt:
4. Lineare Programme
f monoton wachsend in [a, b] ⇔ f 0 (x) ≥ 0 für alle x ∈ (a, b)
f monoton fallend in [a, b] ⇔ f 0 (x) ≤ 0 für alle x ∈ (a, b)
f konstant in [a, b] ⇔ f 0 (x) = 0 für alle x ∈ (a, b)
f (x) > 0 für alle x ∈ (a, b) ⇒ f streng monoton wachsend
in [a, b]
0
f 0 (x) < 0 für alle x ∈ (a, b) ⇒ f streng monoton fallend in
[a, b]
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
152
Krümmung und zweite Ableitung
Mathematik
Stefan Etschberger
Gegeben:
f : [a, b] → R ist stetig und zweimal differenzierbar auf
(a, b).
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Dann gilt:
5. Folgen und Reihen
f konvex in [a, b] ⇔ f 00 (x) ≥ 0 für alle x ∈ (a, b)
f konkav in [a, b] ⇔ f (x) ≤ 0 für alle x ∈ (a, b)
00
f beschreibt eine Gerade in [a, b] ⇔ f 00 (x) = 0 für alle
x ∈ (a, b)
f (x) > 0 für alle x ∈ (a, b) ⇒ f streng konvex in [a, b]
00
f 00 (x) < 0 für alle x ∈ (a, b) ⇒ f streng konkav in [a, b]
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
153
Beispiel
Mathematik
Stefan Etschberger
f : R → R mit f(x) = xe−x
f 0 (x) = e−x − xe−x = (1 − x)e−x
f(x)
Damit: f 0 (x) ≥ 0 für x ≤ 1 und
f 0 (x) ≤ 0 für x ≥ 1
e−1
⇒ f mon. wachsend für x ≤ 1
und f mon. fallend für x ≥ 1
2e−2
⇒ f global maximal bei x = 1
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
3e−3
6. Finanzmathematik
7. Reelle Funktionen
f 00 (x)
−e−x
=
(x − 2)e−x
− (1 −
x)e−x
=
⇒ f 00 (x) ≥ 0 für x ≥ 2 und
f 00 (x) ≤ 0 für x ≤ 2
8. Differenzieren 1
1
⇒ f konvex für x ≥ 2 und f
konkav für x ≤ 2
2
3
8.1. Differentialquotient und
Ableitung
x
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
154
Charakteristische Punkte
Mathematik
Stefan Etschberger
Definition Wendepunkt
f(x) hat in x0 ∈ (a, b) einen Wendepunkt
1. Grundlegende
Bausteine
wenn es ein r > 0 gibt mit
2. Grundlegende
Werkzeuge
f ist in [x0 − r, x0 ] streng konvex und
3. Lineare Algebra
f ist in [x0 , x0 + r] streng konkav und
(oder umgekehrt)
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Definition Terrassenpunkt
x0 ist Terrassenpunkt
wenn x0 Wendepunkt ist
und f 0 (x) = 0
8. Differenzieren 1
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
9. Differenzieren 2
10. Integration
155
Extremumsbedingung
Mathematik
Stefan Etschberger
Voraussetzung
f zweimal stetig differenzierbar in (a, b)
1. Grundlegende
Bausteine
und f 0 (x0 ) = 0 mit (x0 ∈ (a, b))
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Dann gilt
5. Folgen und Reihen
f 00 (x0 ) < 0
⇒
x0 ist lokales Maximum von f
6. Finanzmathematik
f 00 (x0 ) > 0
⇒
x0 ist lokales Minimum von f
7. Reelle Funktionen
8. Differenzieren 1
f 00 (x) < 0 für alle x ∈ (a, b)
von f
⇒
f 00 (x) > 0 für alle x ∈ (a, b)
von f
⇒
x0 ist globales Maximum
8.1. Differentialquotient und
Ableitung
8.2. Änderungsrate und
Elastizität
8.3. Kurvendiskussion
x0 ist globales Minimum
9. Differenzieren 2
10. Integration
157
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
Integration
9
Differenzieren 2
Partielle Ableitung
Kurvendiskussion
Optimierung mit Nebenbedingungen
Partielle Differenzierbarkeit
Mathematik
Stefan Etschberger
Betrachtet werden
Funktionen f : D → R,
D ∈ Rn
mit x = (x1 , . . . , xn ) 7→ f(x) = f(x1 , . . . , xn ) = z
außerdem: i-ter Einheitsvektor ei = (0, . . . ,0,1,0, . . . ,0)
und: x + h · ei ∈ D mit h > 0
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Definition
5. Folgen und Reihen
f heißt im Punkt x partiell differenzierbar bei Existenz des
Genzwerts:
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
f(x + h · ei ) − f(x)
lim
h→0
h
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
In diesem Fall heißt dieser Grenzwert fxi (x) die erste partielle
Ableitung von f nach xi im Punkt x. Schreibweisen:
fi (x) = fxi (x) =
10. Integration
∂f(x)
∂xi
159
Partielle Differenzierbarkeit
Mathematik
Stefan Etschberger
Differenzierbarkeit auf D1 ⊂ D
Die Funktion f : D ⊃ Rn → R
1. Grundlegende
Bausteine
heißt in D1 ⊂ D partiell differenzierbar
wenn f für alle x ∈ D1 partiell differenzierbar ist
Gradient
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Ist die Funktion f : D ⊃ Rn → R im Punkt x
nach allen Variablen x1 , . . . , xn differenzierbar, dann heißt
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
 ∂f(x) 

grad f(x) = ∇f(x) = 

∂x1
..
.
∂f(x)
∂xn



9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
10. Integration
Gradient von f im Punkt x ∈ D
160
Tangentialhyperebenen
Mathematik
Stefan Etschberger
Tangentialebene
Gegeben: f : D ⊃ R → R und ein Punkt x̃ = (x̃1 , x̃2 )
2
Gesucht: Ebene, die f in x̃ berührt
Tangentialebene:
T (x1 , x2 ) = f(x) +
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
∂f
x1 (x̃)
· (x1 − x̃1 ) +
∂f
x2 (x̃)
4. Lineare Programme
· (x2 − x̃2 )
Tangentialhyperebene
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
Gegeben: f : D ⊃ Rn → R und ein Punkt x̃
9. Differenzieren 2
Gesucht: Ebene, die f in x̃ berührt
9.1. Partielle Ableitung
Tangentialhyperebene:
9.3. Optimierung mit
Nebenbedingungen
9.2. Kurvendiskussion
10. Integration
T
H(x) = f(x̃) + (∇f(x̃)) · (x − x̃)
161
Beispiel Tangential(hyper)ebene
Mathematik
Stefan Etschberger
Gegeben: f : R2 → R mit f(x, y) = 4x3 y2 + 2y
Gesucht: Tangentialebene im Punkt (1, −2, f(1, −2))
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
1000
800
600
400
200
0
-200
-400
-600
-800
-1000
3
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
2
1
10. Integration
0
-1
-2
-3 3
2
1
0
-1
-2
-3
162
Richtungsableitungen
Mathematik
Stefan Etschberger
Voraussetzungen
f : Rn ⊃ D → R und ein Punkt
x∈D
1. Grundlegende
Bausteine
mit stetig partiellen Ableitungen in D
und
2. Grundlegende
Werkzeuge
f(x)
ein Punkt x ∈ D
3. Lineare Algebra
und ein Richtungsvektor r ∈ D mit
krk = 1.
4. Lineare Programme
5. Folgen und Reihen
f(x̂)
Außerdem: Es existiert sowohl ein
> 0 mit [x − r; x + r] ∈ D
f(x̂ + r)
6. Finanzmathematik
als auch der Grenzwert
7. Reelle Funktionen
r
8. Differenzieren 1
f(x + t · r) − f(x)
lim
t→0
t
9. Differenzieren 2
9.1. Partielle Ableitung
x̂ + r
9.2. Kurvendiskussion
x̂
x2
Richtungsableitung
x1
Dann heißt
9.3. Optimierung mit
Nebenbedingungen
10. Integration
T
(∇f(x)) · r
Richtungsableitung von f an der Stelle
x in Richtung r
163
Beispiel Tangential(hyper)ebene
Mathematik
Stefan Etschberger
Gegeben: f : R2 → R mit f(x, y) = x ey + cos(xy)
Gesucht: Ableitung im Punkt (2,0) in Richtung des Vektors
3
−4
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
6
5
4
3
2
1
0
-1
-2
-3
-4
-5
3
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
2
10. Integration
1
0
-1
-2
-3 0.5
0
-0.5
-1
-1.5
-2
-2.5
-3
-3.5
-4
164
Höhere partielle Ableitungen
Mathematik
Stefan Etschberger
Voraussetzungen
Funktion f : D → R, D ⊂ Rn
1. Grundlegende
Bausteine
in D nach allen Variablen x1 , . . . , xn partiell differenzierbar,
auch partiell differenzierbar: alle partiellen Ableitungen
fx1 , . . . , fxn .
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Dann heißt
6. Finanzmathematik
f zweimal partiell nach allen Variablen differenzierbar.
Partielle Ableitungen zweiter Ordnung für i, j = 1, . . . , n:
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
∂
f (x) = fxi xj (x) =
∂ xj
ij
∂
f(x)
∂ xi
9.2. Kurvendiskussion
∂2 f(x)
=
∂ xj ∂ xi
9.3. Optimierung mit
Nebenbedingungen
10. Integration
Achtung: Zuerst nach xi , dann nach xj differenzieren
165
Satz von Schwarz
Mathematik
Stefan Etschberger
Voraussetzungen
f : Rn ⊃ D → R ist zweimal stetig
partiell differenzierbar in D
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
2. partielle Ableitungen:
3. Lineare Algebra
4. Lineare Programme
2
∂ f(x)
∂xi ∂xj
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
mit i, j ∈ {1, . . . , n}
Dann gilt für alle x ∈ D
∂2 f(x)
∂2 f(x)
=
∂xi ∂xj
∂xj ∂xi
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
Hermann Schwarz (1843-1921)
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
10. Integration
166
Hessematrix
Mathematik
Stefan Etschberger
Gegeben
Zweimal stetig partiell differenzierbare
Funktion f : Rn ⊃ D → R
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Definition
4. Lineare Programme
5. Folgen und Reihen
Die symmetrische Matrix
6. Finanzmathematik
7. Reelle Funktionen

∂2 f
∂x1 ∂x1
∂2 f
∂x1 ∂x2
2 
 ∂2 f
∂ f

Hf (x) =
=  ∂x2.∂x1
 .
∂xi ∂xj
 .
∂2 f
∂x2 ∂x2
..
.
2
2
∂ f
∂xn ∂x1
∂ f
∂xn ∂x2
···
···
..
.
···
∂2 f
∂x1 ∂xn

8. Differenzieren 1
9. Differenzieren 2

∂2 f 
∂x2 ∂xn 

..

.

9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
10. Integration
2
∂ f
∂xn ∂xn
heißt Hessematrix
167
Lokale Extrema und der Gradient
Mathematik
Stefan Etschberger
Notwendige Bedingung für lokale Extrema
Gegeben: Funktion f : Rn ⊃ D → R stetig partiell nach allen
Variablen differenzierbar
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
f hat im Punkt x̃ ein lokales Minimum oder Maximum
3. Lineare Algebra
Dann gilt: ∇f(x̃) = 0
5. Folgen und Reihen
4. Lineare Programme
6. Finanzmathematik
7. Reelle Funktionen
Beispiel
f : R2 → R
f(x, y) = sin2 (x) · cos(4y)
8. Differenzieren 1
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
4
10. Integration
3.5
3
0
1
2.5
2
2
3
4
1.5
5 1
168
Definitheitseigenschaften der Hessematrix
Mathematik
Stefan Etschberger
1. Grundlegende
Bausteine
Am Punkt x̃ heißt die Hessematrix Hf (x̃)
positiv definit,
2. Grundlegende
Werkzeuge
3. Lineare Algebra
wenn xT Hf (x̃) x > 0,
4. Lineare Programme
T
positiv semidefinit, wenn x Hf (x̃) x ≥ 0,
negativ definit,
5. Folgen und Reihen
wenn xT Hf (x̃) x < 0,
6. Finanzmathematik
7. Reelle Funktionen
negativ semidefinit, wenn xT Hf (x̃) x ≤ 0
8. Differenzieren 1
9. Differenzieren 2
jeweils für alle x gilt.
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
Andernfalls heißt Hf (x̃) indefinit.
10. Integration
169
Einfache Kriterien zu Definitheitseigenschaften
Mathematik
Stefan Etschberger
Hauptunterdeterminanten
Gegeben: Symmetrische n × n-Matrix A
1. Grundlegende
Bausteine
Dann heißt
2. Grundlegende
Werkzeuge

a11
 .
det Hi = det  ..
ai1
···
···
a1i
.. 
. 
aii

3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
die i-te Hauptunterdeterminante (i = 1, . . . , n) von A.
8. Differenzieren 1
9. Differenzieren 2
Satz
9.1. Partielle Ableitung
9.2. Kurvendiskussion
Matrix A positiv definit ⇔ det Hi > 0
⇔ alle Eigenwerte von A sind positiv
9.3. Optimierung mit
Nebenbedingungen
10. Integration
Matrix A negativ definit ⇔ (−1)i det Hi > 0
⇔ alle Eigenwerte von A sind negativ
170
Hinreichende Bedingung für lokale Extrema
Mathematik
Stefan Etschberger
Voraussetzungen
D ⊂ Rn konvex und offen
Funktion f : D → R zweimal stetig partiell differenzierbar
Es gibt ein x̃, für das ∇f(x̃) = 0
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Satz
6. Finanzmathematik
Hf (x̃) ist negativ definit ⇒ x̃ ist lokale Maximalstelle von f
Hf (x̃) ist positiv definit ⇒ x̃ ist lokale Minimalstelle von f
Hf (x̃) ist indefinit ⇒ x̃ ist keine lokale Extremalstelle von f
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
Hf (x) ist positiv definit für alle x ∈ D
⇒ x̃ ist einziges globales Minimum von f
10. Integration
Hf (x) ist negativ definit für alle x ∈ D
⇒ x̃ ist globales Maximum von f
171
Konvexität und Konkavität
Mathematik
Stefan Etschberger
Voraussetzungen
D ⊂ Rn konvex und offen
Funktion f : D → R zweimal stetig partiell differenzierbar
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Satz
5. Folgen und Reihen
Hf (x) ist positiv definit für alle x ∈ D
⇒ f ist streng konvex in D
Hf (x) ist negativ definit für alle x ∈ D
⇒ f ist streng konkav in D
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
Hf (x) ist positiv semidefinit für alle x ∈ D
⇒ f ist konvex in D
9.3. Optimierung mit
Nebenbedingungen
10. Integration
Hf (x) ist negativ semidefinit für alle x ∈ D
⇒ f ist konkav in D
172
Beispiel
Mathematik
Stefan Etschberger
Problem
Betrachte f : R2 → R mit f(x, y) = x2 + 2y2
1. Grundlegende
Bausteine
Gesucht: Punkt in R2 mit kleinstem Wert von f
2. Grundlegende
Werkzeuge
auf der Geraden 2y + x − 3 = 0
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
10. Integration
173
Allgemeines Problem
Mathematik
Stefan Etschberger
Aufgabe
1. Grundlegende
Bausteine
Maximiere (oder minimiere) Funktion f : Rn → R
in Abhängigkeit von x = (x1 , . . . , xn ),
so dass die Nebenbedingungen gi (x) = 0 mit gi : Rn → R
und i = 1, . . . , m erfüllt sind
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
Kurz:
7. Reelle Funktionen
8. Differenzieren 1
f(x) → max
NB:
g1 (x) = 0
..
.
(min)
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
10. Integration
gm (x) = 0
174
Der Ansatz von Lagrange
Mathematik
Stefan Etschberger
Idee von Lagrange
Gut wäre: Transformation des Optimierungsproblems mit Nebenbedingungen in eines
ohne NB.
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Im Optimum: Gradient der zu optimierenden
Funktion und Gradient der NB sind parallel
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Lagrangefunktion
8. Differenzieren 1
Gegeben: Optimierungsproblem (O) mit f(x) → max(min)
unter den Nebenbedingungen gj (x) = 0 für j = 1, . . . , m
Dazu wird definiert: Lagrangefunktion L : Rn+m → R
L(x1 , . . . , xn , λ1 , . . . , λm ) = L(x, λ) = f(x) +
m
X
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
10. Integration
λj gj (x)
j=1
175
Satz von Lagrange
Mathematik
Stefan Etschberger
Voraussetzungen
f : Rn ⊃ D → R, zweimal stetig partiell differenzierbar
Optimierungsproblem (O) mit f(x) → max (min) unter den
Nebenbedingungen gj (x) = 0 für j = 1, . . . , m
Hessematrix der Lagrangefunktion:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
 ∂2 L(x,λ)
∂x1 ∂x1


^
HL (x, λ) = 

···
..
.
∂2 L(x,λ)
∂xn ∂x1
2

L(x,λ)
∂
∂x1 ∂xn
..
.
···
∂2 L(x,λ)
∂xn ∂xn




Eine Lösung (x̃, λ̃) des Systems ∇L(x, λ) = 0
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
Dann gilt:
10. Integration
^ L (x̃, λ̃) negativ definit ⇒ x̃ ist lokales Maximum von (O)
H
^ L (x̃, λ̃) positiv definit ⇒ x̃ ist lokales Minimum von (O)
H
^ L (x, λ̃) negativ definit für alle x ⇒ x̃ ist globales Maximum von (O)
H
^ L (x, λ̃) positiv definit für alle x
H
⇒
x̃ ist globales Minimum von (O)
176
Variable Lagrange Multiplikatoren
Mathematik
Stefan Etschberger
Voraussetzungen
f : Rn ⊃ D → R, zweimal stetig partiell differenzierbar
1. Grundlegende
Bausteine
Optimierungsproblem (O) mit f(x) → max (min) unter den
Nebenbedingungen gj (x) = 0 für j = 1, . . . , m
2. Grundlegende
Werkzeuge
Lagrangefunktion
4. Lineare Programme
^
L(x)
= f(x) +
m
X
3. Lineare Algebra
5. Folgen und Reihen
λ(x)gj (x)
j=1
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
9.1. Partielle Ableitung
9.2. Kurvendiskussion
9.3. Optimierung mit
Nebenbedingungen
Dann gilt:
10. Integration
^
Ist x̃ eine Maximalstelle bzw. Minimalstelle von L
mit gj (x̃) = 0 für alle j = 1, . . . , m
dann ist x̃ auch Maximalstelle bzw. Minimalstelle von (O)
177
Mathematik: Gliederung
1
Grundlegende Bausteine
2
Grundlegende Werkzeuge
3
Lineare Algebra
4
Lineare Programme
5
Folgen und Reihen
6
Finanzmathematik
7
Reelle Funktionen
8
Differenzieren 1
9
Differenzieren 2
10
Integration
10
Integration
Unbestimmte Integrale
Bestimmte Integrale
Uneigentliche Integrale
Mehrdimensionale Integrale
Einleitung
Mathematik
Stefan Etschberger
Umkehrung der Fragestellung der Differentialrechnung
Jetzt gesucht:
Funktion, deren Änderungsverhalten bekannt ist
Beispiel:
Bekannt:
Geschwindigkeit eines Körpers in Abhängigkeit der Zeit
Gesucht:
Ort in Abhängigkeit der Zeit
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Gliederung
8. Differenzieren 1
9. Differenzieren 2
1
Unbestimmte Integrale
2
Riemannsche Summen und bestimmte Integrale
1. Unbestimmte Integrale
3
Uneigentliche Integrale
3. Uneigentliche Integrale
4
Anmerkungen zu mehrdimensionalen Integralen
10. Integration
2. Bestimmte Integrale
4. Mehrdimensionale
Integrale
179
Stammfunktion
Mathematik
Stefan Etschberger
Eine differenzierbare Funktion F : D → R mit D ⊂ R heißt
Stammfunktion der Funktion f : D → R, wenn für alle x ∈ D
gilt
1. Grundlegende
Bausteine
F 0 (x) = f(x)
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Sind F, ^F beliebige Stammfunktionen von f,
gilt für alle x ∈ D:
^F(x) − F(x) = konstant
Also: Hat man eine Stammfunktion F gefunden, gilt für alle
anderen Stammfunktionen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
^F(x) = F(x) + c
4. Mehrdimensionale
Integrale
180
Unbestimmtes Integral
Mathematik
Stefan Etschberger
Ist F : D → R eine Stammfunktion von f : D → R,
so heißt
Z
1. Grundlegende
Bausteine
Z
f(x) dx = F 0 (x) dx = F(x) + c
für beliebiges c ∈ R
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
das unbestimmte Integral der Funktion f.
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Weitere Bezeichnungen:
8. Differenzieren 1
x : Integrationsvariable
f(x) : Integrand
c : Integrationskonstante
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
Unbestimmte Integration ist Umkehrung der Differentiation
4. Mehrdimensionale
Integrale
181
Einige unbestimmte Integrale
Mathematik
Stefan Etschberger
Sei f eine reelle Funktion und c ∈ R eine beliebige Konstante. Dann gilt:
Z
a)
f(x) = a (a ∈ R)
b)
xn
⇒
f(x) dx = ax + c
Z
f(x) =
(n ∈ N, x ∈ R)
f(x) = xm (m = −2, −3, . . . , x 6= 0)
f(x) = xr (r ∈ R, r 6= −1, x > 0)
c)
d)
f(x) = x−1 (x 6= 0)
f(x) = sin x (x ∈ R)
f(x) = cos x (x ∈ R)
e)
f(x) = ex (x ∈ R)
f(x) = ax (a > 0, a 6= 1, x ∈ R)
1
xn+1 + c
n+1
Z
1
⇒ f(x) dx =
xm+1 + c
m+1
Z
1
⇒ f(x) dx =
xr+1 + c
r+1
Z
⇒ f(x) dx = ln |x| + c
Z
⇒ f(x) dx = − cos x + c
Z
⇒ f(x) dx = sin x + c
Z
⇒ f(x) dx = ex + c
Z
1 x
⇒ f(x) dx =
a +c
ln a
⇒
f(x) dx =
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
182
Rechenregeln
Mathematik
Stefan Etschberger
Summen und konstante Faktoren
Für die reellen Funktionen f, g : D → R, D ⊂ R existiere das
unbestimmte Integral. Dann gilt:
Z
a)
Z
Z
(f(x) + g(x)) dx = f(x) dx + g(x) dx
Z
b)
Z
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
af(x) dx = a f(x) dx
für alle a ∈ R
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
Partielle Integration
9. Differenzieren 2
Für zwei stetig differenzierbare Funktionen f, g : D → R,
D ⊂ R gilt:
Z
Z
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
f(x)g 0 (x) dx = f(x)g(x) − f 0 (x)g(x) dx
183
Rechenregeln
Mathematik
Stefan Etschberger
Substitutionsregel
Die Funktion f : D → R, D ⊂ R besitze eine Stammfunktion
F und
g : D1 → R, D1 ⊂ R, g(D1 ) ⊂ D sei stetig differenzierbar.
Dann existiert die zusammengesetzte Funktion
f ◦ g : D1 → R mit z = f(y) = f(g(x)) = (f ◦ g) (x)
und es gilt mit y = g(x)
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
Z
Z
0
f(g(x))g (x) dx = f(y) dy
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
= F(y) + c = F(g(x)) + c
= (F ◦ g) (x) + c
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
mit c ∈ R beliebig.
184
Riemannsche Summen
Mathematik
Stefan Etschberger
Gegeben: Beschränkte und stetige Funktion f : [a, b] → R mit
a < b und f ≥ 0
Unterteilen von [a, b] in
[a, x1 ], [x1 , x2 ], . . . , [xi−1 , xi ], . . . , [xn−1 , b]
1. Grundlegende
Bausteine
mit a = x0 , b = xn
2. Grundlegende
Werkzeuge
In jedem Teilintervall: Wähle Maximum und Minimum:
3. Lineare Algebra
f(ui ) = min {f(x) : x ∈ [xi−1 , xi ]}
und
4. Lineare Programme
f(vi ) = max {f(x) : x ∈ [xi−1 , xi ]} .
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
f(x)
8. Differenzieren 1
f
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
f(vi )
2. Bestimmte Integrale
3. Uneigentliche Integrale
f(ui )
a = x0
x1
x2
x3
x4
4. Mehrdimensionale
Integrale
...
xi−1
xi
... b = xn
x
Riemannsche Summen
185
Mathematik
Stefan Etschberger
n
Untere und obere Grenze In
min 5 I 5 Imax für Flächeninhalt unter Kurve mit:
n
n
X
X
n
n
f(ui )(xi − xi−1 ), Imax =
f(vi )(xi − xi−1 )
Imin =
i=1
i=1
n
Jetzt: Verfeinerung der Unterteilung von [a, b] ⇒ Folgen (In
min ) und (Imax )
Existieren für n → ∞ die Grenzwerte der beiden Folgen und gilt für den
wahren Flächeninhalt I unter der Kurve
n
lim In
min = lim Imax = I
n→∞
n→∞
dann heißt f Riemann-integrierbar im Intervall [a, b]
Schreibweise:
Zb
I=
f(x) dx
a
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
Bezeichnungen:
I
x
f(x)
a, b
Bestimmtes Integral von f im Intervall [a, b]
Integrationsvariable
Integrand
Integrationsrenzen
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
186
Existenz von bestimmten Integralen
Mathematik
Stefan Etschberger
Gegeben: Reelle Funktion f : [a, b] → R. Dann gilt:
Zb
a) f stetig in [a, b]
⇒
f(x) dx existiert
a
b) f monoton in [a, b] ⇒
Zb
1. Grundlegende
Bausteine
f(x) dx existiert
2. Grundlegende
Werkzeuge
a
Beispiele: Gesucht:
R+1
−1 fi (x) dx
für
3. Lineare Algebra
4. Lineare Programme
2
f1 (x) =
1
für x < 0
für x = 0
5. Folgen und Reihen
und
6. Finanzmathematik
7. Reelle Funktionen
R
f2 (x) = |x|
8. Differenzieren 1
9. Differenzieren 2
f1 (x)
f2 (x)
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
2
3. Uneigentliche Integrale
1
−1
4. Mehrdimensionale
Integrale
1
x
1
−1
x
1
187
Sätze zu bestimmten Integralen
Mathematik
Stefan Etschberger
Gegeben: Integrierbare Funktionen f, g : [a, b] → R.
Dann gilt:
Zb
Zb
cf(x) dx = c
a)
a
1. Grundlegende
Bausteine
f(x) dx
für alle c ∈ R
b) f(x) 5 g(x)
für alle x ∈ [a, b] ⇒
Zb
Zb
f(x) dx 5
a
Zb
Zc
f(x) dx =
c)
2. Grundlegende
Werkzeuge
a
a
3. Lineare Algebra
g(x) dx
a
Zb
f(x) dx +
a
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
f(x) dx
für alle c ∈ (a, b)
c
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
Definiert wird außerdem:
Za
10. Integration
1. Unbestimmte Integrale
Za
f(x) dx = 0,
a
f(x) dx = −
b
2. Bestimmte Integrale
Zb
3. Uneigentliche Integrale
f(x) dx
4. Mehrdimensionale
Integrale
a
188
Zusammenhang bestimmtes und unbestimmtes Integral
Mathematik
Stefan Etschberger
Zusammenhang
Gegeben f : D → R, D ⊂ R eine in D stetige Funktion.
Dann existiert eine Stammfunktion F von f mit
F 0 (x) = f(x)
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
Z
sowie das unbestimmte Integral
3. Lineare Algebra
f(x)dx = F(x) + c
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
Zb
und das bestimmte Integral
7. Reelle Funktionen
f(x) dx = F(b) − F(a)
a
8. Differenzieren 1
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
Unterschiede
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
Bestimmtes Integral entspricht einer reellen Zahl
Unbestimmtes Integral entspricht Schar von Funktionen
189
Integrationsregeln
Mathematik
Stefan Etschberger
a) Für integrierbare Funktionen f, g : [a, b] → R gilt die
Additionsregel
Zb
Zb
(f(x) + g(x)) dx =
a
Zb
f(x) dx +
a
g(x) dx .
a
b) Für stetig differenzierbare Funktionen f, g : [a, b] → R gilt die
Regel der partiellen Integration
Zb
a
b Z b
f 0 (x)g(x) dx
f(x)g 0 (x) dx = f(x)g(x) −
a
a
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
c) Ist f : [α, β] → R integrierbar mit der Stammfunktion F und
g : [a, b] → R mit g[a, b] ⊂ [α, β] stetig differenzierbar, so gilt die
Substitutionsregel
Zb
a
b
Z g(b)
f(g(x)) g (x) dx = F(g(x)) = F(g(b)) − F(g(a)) =
f(y) dy .
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
0
a
g(a)
190
Grenzen bei ±∞
Mathematik
Stefan Etschberger
Die reelle Funktion f sei für alle x ∈ R definiert und integrierbar.
Zb
f(x) dx, falls er existiert, das konvergente
Dann heißt der Grenzwert lim
b→∞ a
uneigentliche Integral von f im Intervall [a, ∞), und man schreibt
Zb
lim
b→∞ a
f(x) dx =
Z∞
f(x) dx .
a
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
Andernfalls spricht man von einem divergenten uneigentlichen Integral.
Entsprechend definiert man das konvergente uneigentliche Integral von f
im Intervall (−∞, b], falls folgender Grenzwert existiert:
Zb
lim
a→−∞ a
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Zb
8. Differenzieren 1
f(x) dx =
f(x) dx
−∞
9. Differenzieren 2
10. Integration
Za
Sind beide Integrale
f(x) dx und
−∞
auch
Z∞
Z∞
1. Unbestimmte Integrale
f(x) dx konvergent, so existiert
a
f(x) dx =
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
Za
−∞
2. Bestimmte Integrale
f(x) dx +
Z∞
−∞
f(x) dx .
a
191
Beliebige Grenzen
Mathematik
Stefan Etschberger
Geg.: Reelle Funktion f : [a, b) → R, die für alle x ∈ [a, b − ] mit
Rb−
∈ (0, b − a) integrierbar. Dann heißt Grenzwert lim a
f(x) dx (falls er
→0
existiert)
konvergentes uneigentliches Integral von f im Intervall [a, b]. Schreibweise:
Z b−
lim
→0 a
1. Grundlegende
Bausteine
Zb
f(x) dx =
f(x) dx .
a
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
Andernfalls: Divergentes uneigentliches Integral
Analog für alle x ∈ [a + , b] mit ∈ (0, b − a), konvergentes
uneigentliches Integral von f in [a, b], mit
Zb
lim
→0 a+
Zb
f(x) dx =
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
f(x) dx .
a
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
Ist f in (a, b) definiert und sind für c ∈ (a, b) die uneigentlichen Integrale
Rc
Rb
f(x)
dx
und
a
c f(x) dx konvergent, dann ist auch folgendes Integral
konvergent:
Zb
Zc
Zb
f(x) dx =
f(x) dx +
f(x) dx
a
a
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
c
192
Parameterintegral: Satz
Mathematik
Stefan Etschberger
f(x1 , x2 )
)
,x2
1. Grundlegende
Bausteine
b1
f(x
f(
1,b
2)
2. Grundlegende
Werkzeuge
3. Lineare Algebra
0
x2
F1 (b2 )
b2
F2 (b1 )
x1
b1
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
Ist die Funktion f : [a1 , b1 ] × [a2 , b2 ] → R stetig, so ist auch
F1 : [a2 , b2 ] → R mit F1 (x2 ) =
Z b1
9. Differenzieren 2
10. Integration
f(x1 , x2 ) dx1 und
1. Unbestimmte Integrale
a1
F2 : [a1 , b1 ] → R mit F2 (x1 ) =
Z b2
8. Differenzieren 1
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
f(x1 , x2 ) dx2 stetig.
a2
193
Vertauschung: Intergration und Differentiation
Mathematik
Stefan Etschberger
Gegeben: stetige Funktion f : [a1 , b1 ] × [a2 , b2 ] → R und f ist
nach beiden Variablen stetig partiell differenzierbar.
Dann sind die Funktionen F1 , F2 mit
Z b1
F1 (x2 ) =
f(x1 , x2 ) dx1
1. Grundlegende
Bausteine
und F2 (x1 ) =
a1
Z b2
2. Grundlegende
Werkzeuge
f(x1 , x2 ) dx2
a2
stetig differenzierbar, und es gilt:
3. Lineare Algebra
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
dF1
dx2
dF2
dx1
d
=
dx2
d
=
dx1
Z b1
f(x1 , x2 ) dx1
Z b1
a2
f(x1 , x2 ) dx2
7. Reelle Funktionen
a1
10. Integration
a2
∂f(x1 , x2 )
dx2
∂x1
=
a1
Z b2
∂f(x1 , x2 )
dx1
∂x2
Z b2
=
8. Differenzieren 1
9. Differenzieren 2
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
Also: Differentiation und Integration können vertauscht werden.
194
Satz von Fubini
Mathematik
Stefan Etschberger
Die stetige Funktion f : [a1 , b1 ] × [a2 , b2 ] → R sei nach
beiden Variablen stetig partiell differenzierbar.
Dann gilt:
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
b
Z2 bZ1
5. Folgen und Reihen
b
Z1 bZ2
f(x1 , x2 ) dx1 dx2 =
a2 a1
6. Finanzmathematik
f(x1 , x2 ) dx2 dx1
7. Reelle Funktionen
8. Differenzieren 1
a1 a2
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
195
Interpretation über Riemannsche Summen
Mathematik
Stefan Etschberger
Existieren die Grenzwerte der unteren und oberen Schranke
von I analog dem eindimensionalen Fall für n → ∞ und sind
sie identisch, so heißt die Funktion
f : [a1 , b1 ] × [a2 , b2 ] → R in ihrem Definitionsbereich
integrierbar.
Ist f stetig und stetig partiell differenzierbar, so gilt
b
Z2 bZ1
b
Z1 bZ2
f(x1 , x2 ) dx1 dx2 =
I=
a2 a1
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
4. Lineare Programme
f(x1 , x2 ) dx2 dx1 .
a1 a2
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
Man bezeichnet das Doppelintegral I als das bestimmte
Integral von f im Bereich [a1 , b1 ] × [a2 , b2 ], ferner
x1 , x2 als Integrationsvariable,
f(x1 , x2 ) als Integrand und
9. Differenzieren 2
10. Integration
1. Unbestimmte Integrale
2. Bestimmte Integrale
3. Uneigentliche Integrale
4. Mehrdimensionale
Integrale
a1 , b1 , a2 , b2 als Integrationsgrenzen
196