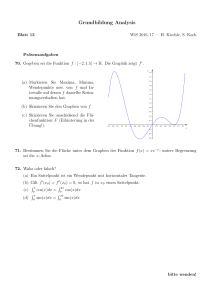
Mathematik für Molekulare Biologen
Werbung

Skriptum zur Vorlesung Mathematik für Molekulare Biologen Christian Schmeiser1 Contents 1 Einleitung 1 2 Zahlensysteme, Grundrechnungsarten 2 3 Komplexe Zahlen, Polynome 5 4 Die Polardarstellung, Winkelfunktionen 9 5 Reelle Funktionen, Grenzwerte 12 6 Differentialrechnung, die Exponentialfunktion 17 7 Integration 24 8 Kleinste Fehlerquadrate 33 9 Differentialgleichungen – Reaktionskinetik 40 1 Einleitung Es ist das Ziel dieser Vorlesung, mit einigen mathematischen Methoden Bekanntschaft zu machen, die bei quantitativen Zugängen zur Molekularbiologie eingesetzt werden. Dazu sind als Vorbereitung einige mathematische Grundlagen notwendig, deren Behandlung den größeren Teil der Vorlesung (bis einschließlich Kapitel 7) in Anspruch nimmt. Prinzipiell sind keinerlei mathematische Vorkenntnisse notwendig (nicht einmal solche aus der Schule). Allerdings werden HörerInnen, bei denen das wirklich der Fall ist, das Tempo wahrscheinlich als sehr hoch empfinden. Mathematische Theorien bestehen im Wesentlichen aus Axiomen, Definitionen und Sätzen. Axiome sind Annahmen über die Natur mathematischer Objekte, die vorausgesetzt werden und daher nicht weiter diskutiert werden müssen, wenn man sich diesbezüglich geeinigt hat. Definitionen führen (aufbauend auf Bekanntem) neue Begriffe ein. Sätze sind aus Axiomen, Definitionen und schon bewiesenen Sätzen beweisbare Aussagen. In diesem Skriptum wird der Stoff nicht streng nach diesen Gesichtspunkten präsentiert. Allerdings erscheinen bei Farbdruck Teile des Textes in Blau bzw. Rot, was auf ihren logischen Rang als Definitionen bzw. Sätze hinweist. 1 Institut für Mathematik, [email protected] Universität Wien, Nordbergstraße 1 15, 1090 Wien, Austria. chris- Die Standardschreibweise der Mengentheorie wird verwendet wie das aufzählende Verfahren zur Angabe von Mengen, z.B. A = {mein Schlüsselbund, meine Geldbörse, mein Handy, mein Laptop} , sowie das beschreibende Verfahren, z.B. B = {x : x ist in meinem Rucksack} . Die Aussage x gehört zur Menge A bzw. x ist Element der Menge A schreibt man als x ∈ A, ihre Verneinung als x ∈ / A. Die leere Menge {} ist die Menge ohne Elemente. Teilmengen: A⊂B gilt genau dann, wenn jedes Element von A auch Element von B ist. Vereinigungs- und Durchschnittsmengen: A ∪ B = {x : x ∈ A oder x ∈ B} , A ∩ B = {x : x ∈ A und x ∈ B} , wobei das oder in der Definition der Vereinigungsmenge ein inklusives oder ist. Differenzmenge: A \ B = {x : x ∈ A und x ∈ / B} . 2 Zahlensysteme, Grundrechnungsarten Die Menge der natürlichen Zahlen IIN = {1, 2, 3, . . .} ist abgeschlossen bezüglich der Addition, d.h. die Summe zweier beliebiger natürlicher Zahlen ist wieder eine natürliche Zahl. Für die Umkehroperation zur Addition, die Subtraktion, gilt das nicht: 3 − 5 ist keine natürliche Zahl. Um diesem Ausdruck Sinn zu geben, erweitert man auf die Menge der ganzen Zahlen ZZ = {. . . , −2, −1, 0, 1, 2, . . .} , die auch bezüglich der Subtraktion abgeschlossen ist. Die Menge der natürlichen Zahlen ist auch bezüglich der Multiplikation abgeschlossen. Diese lässt sich auch auf die ganzen Zahlen erweitern (und zwar so, dass die wichtigsten Rechenregeln gültig bleiben). Wieder besteht das Problem, dass die Umkehroperation zur Multiplikation, die Division p/q nicht für beliebige p, q ∈ ZZ wieder eine ganze Zahl ergibt. Als Konsequenz führt eine weitere Erweiterung auf die Menge der rationalen Zahlen Q = {p/q : p ∈ ZZ, q ∈ IIN} . Man beachte, dass damit die Abgeschlossenheit nur fast vollständig hergestellt ist: Division durch Null ist auch in Q nicht erlaubt. Die rationalen Zahlen sind den Menschen schon seit langer Zeit bekannt, so bildeten sie z.B. das Zahlensystem der Pythagoräer. So wie man durch fortgesetztes Addieren mit demselben Summanden auf das Multiplizieren kommen kann, führt das fortgesetzte Multiplizieren mit demselben Faktor auf das Potenzieren: xn = xxn−1 für n ≥ 2 , 2 x1 = x . Figure 1: Graphischer Beweis des Pythagoräischen Lehrsatzes Bemerkung 1 Das ist eine sogenannte rekursive Definition. Man beachte, dass auf diese Art xn für alle n ∈ IN I definiert ist. Der Grund ist das, was die natürlichen Zahlen im Kern ausmacht: Sie beginnen bei 1 und man erreicht jede von ihnen, indem man bei 1 zu Zählen beginnt. Hat man das Potenzieren definiert, ist man natürlich wieder an der Umkehroperation, dem Wurzelziehen interessiert. Als Beispiel betrachten√wir die Quadratwurzel: Die Tatsachen, dass √ 2 2 1 = 1 und 2 = 4√gilt, schreibt man auch als 1 = 1 und 2 = 4. Da 2 zwischen 1 und 4 liegt, erwarten wir, dass 2 zwischen 1 und 2 liegt. Mit Hilfe des Pythagoräischen Lehrsatzes (graphischer Beweis siehe Fig. 1, vorpythagoräischer Beweis siehe Fig. √ 2) können wir sogar ein geometrisches Konstruktionsverfahren für eine Strecke mit der Länge 2 (z.B. cm) angeben: Es ist die Länge der Diagonale eines Quadrates mit der Kantenlänge 1. Nach der Logik der pythagoräischen Mathematik muss es also eine rationale Zahl √ p/q = 2 geben. Um p, q ∈ IIN eindeutig festzulegen, nehmen wir an, dass die Darstellung gekürzt ist, d.h. dass p und q keine gemeinsamen Teiler haben. Aus der obigen Gleichung folgt (durch Quadrieren und Multiplizieren mit q 2 ) p2 = 2q 2 . Daraus folgt aber, dass p2 eine gerade Zahl ist, was weiter impliziert, dass p eine gerade Zahl ist. Wir können p daher darstellen als p = 2r mit r ∈ IIN. Setzen wir das in die obige Gleichung ein und dividieren diese durch 2, so ergibt sich 2r2 = q 2 . Daraus folgt aber analog zu oben, dass q 2 und daher auch q eine gerade Zahl ist. Dass p und q beides gerade Zahlen sind, widerspricht aber unserer Annahme, dass die Darstellung p/q gekürzt ist. Dieses Argument zeigt, dass es keine rationale Zahl gibt, deren Quadrat 2 ist. 3 Figure 2: Beweis des ’Satzes von Pythagoras’ aus Zhou Bi Suan Jing (Zhou-Dynastie, 1046–256 B.C., bzw. Han-Dynastie, 256 B.C. – 220 A.D.) Diese katastrophale Erkenntnis des Mitglieds Hippasus der Pythagoräer wird das Dilemma der griechischen Mathematik genannt. Geometrisch gesehen zeigt es, dass das Einzeichnen aller Punkte, die den rationalen Zahlen entsprechen, auf einer Zahlengeraden Lücken hinterlässt. Heute bezeichnen wir diese Lücken als irrationale Zahlen, die wir zusätzlich in unser Zahlensystem aufnehmen, wodurch die Menge IR der reellen Zahlen entsteht. Eine wesentliche Aussage über irrationale Zahlen ist, dass jede irrationale Zahl beliebig gut durch rationale Zahlen approximiert werden kann. Genauer heißt das, dass man eine beliebige irrationale Zahl und einen beliebig kleinen Fehler vorgeben kann, und dann immer eine rationale Zahl findet, deren Abstand zu der gegebenen irrationalen Zahl kleiner als der vorgegebene Fehler √ ist. Am Beispiel der irrationalen Zahl 2 werden wir dieses Resultat demonstrieren. Wir wissen schon, dass √ 1< 2<2 √ gilt, d.h. beide rationalen Zahlen 1 und 2 haben höchstens den Abstand 1 von 2. Wir werden das sogenannte Bisektionsverfahren oder Halbierungsverfahren verwenden, um genauere Approximationen zu finden. In der Mitte zwischen 1 und 2 liegt 3/2, und es gilt (3/2)2 = 9/4 > 8/4 = 2. Daraus folgern wir 2 √ 3 < 2< , 2 2 √ woraus folgt, dass wir 2 schon bis auf einen Fehler 1/2 approximiert haben. In der Mitte zwischen 2/2 und 3/2 liegt (2/2 + 3/2)/2 = 5/4, und es gilt (5/4)2 = 25/16 < 32/16 = 2 und daher 5 √ 6 < 2< . 4 4 4 Einen Schritt machen wir noch: (5/4 + 6/4)/2 = 11/8, (11/8)2 = 121/64 < 128/64 = 2, woraus folgt 11 √ 12 < 2< . 8 8 Damit haben wir gezeigt, dass sowohl 11/8 als auch 12/8 = 3/2 höchstens den Abstand 1/8 von √ 2 haben. Da der Abstand in jedem Schritt halbiert wird, kann er beliebig klein gemacht werden. Die wichtigsten Teilmengen von IR sind Intervalle, die an ihren Enden offen oder abgeschlossen sein können: (a, b) := {x ∈ IR : a < x < b} , [a, b] := {x ∈ IR : a ≤ x ≤ b} , [a, b) := {x ∈ IR : a ≤ x < b} , (a, b] := {x ∈ IR : a < x ≤ b} . Intervalle können auch unbeschränkt sein: (a, ∞) := {x ∈ IR : x > a} , [a, ∞) := {x ∈ IR : x ≥ a} , (−∞, a) := {x ∈ IR : x < a} , (−∞, a] := {x ∈ IR : x ≤ a} . Übungsaufgaben 2.1. Man berechne den Flächeninhalt des gleichschenkeligen Dreiecks mit den Kantenlängen 4, 3, 3. √ 2.2. Man zeige, dass 3 keine rationale Zahl ist. √ 2.3. Man approximiere 5 mithilfe des Bisektionsverfahrens bis auf einen Fehler von maximal 1/8. 2.4. Man approximiere eine positive und eine negative Lösung von x2 + x = 5 jeweils bis auf einen Fehler von maximal 1/4. 3 Komplexe Zahlen, Polynome Leider haben wir mit der Einführung der reellen Zahlen das Problem des Quadratwurzelziehens noch nicht vollständig gelöst, weil das Quadrat einer reellen Zahl nicht negativ sein kann. Es gibt daher keine reelle Zahl x, für die x2 = −1 gilt. Um diesem Problem Herr zu werden, ist eine kühne (aber simple) Idee notwendig: Man postuliert einfach, dass es eine solche Zahl gibt und gibt ihr einen Namen. Der Name i bezeichnet ab nun eine Zahl, für die i2 = −1 (1) gilt. Diese Zahl wird als imaginäre Einheit bezeichnet. Damit diese Erweiterung des Zahlenraumes in unserem Sinne brauchbar wird, ist aber die Abgeschlossenheit bezüglich aller Grundrechnungsarten notwendig. Es müssen also auch Ausdrücke wie 1 + i oder 5i definiert sein. Das führt auf die Definition der Menge der komplexen Zahlen C = {a + ib : a, b ∈ IR} . 5 Für eine komplexe Zahl z = a+ib bezeichnen wir die beiden reellen Zahlen Re(z) = a und Im(z) = b als Realteil und Imaginärteil. Jede relle Zahl z kann auch komplexe Zahl mit Im(z) = 0 angesehen werden. Die Menge aller rein imaginären Zahlen mit Re(z) = 0 liefert √ Quadratwurzeln für alle negativen reellen Zahlen. Sei nämlich x ∈ I R, x < 0. Dann existiert −x ∈ IR und für die rein √ imaginäre Zahl z = i −x gilt √ 2 √ 2 −x = (−1) · (−x) = x . z 2 = i −x = i2 Wie oben erwähnt, können die reellen Zahlen als Punkte auf einer Zahlengeraden geometrisch interpretiert werden. Ähnlich gibt es für die komplexen Zahlen eine geometrische Interpretation als Punkte in einer Ebene, die in diesem Zusammenhang als Gaußsche Zahlenebene bezeichnet wird. Dabei verwendet man ein kartesisches (d.h. rechtwinkeliges) Koordinatensystem und identifiziert die komplexe Zahl z = a+ib mit dem Punkt mit den Koordinaten (a, b). Die a-Achse wird als reelle Achse und die b-Achse als imaginäre Achse bezeichnet. Die reelle Achse repräsentiert die Menge der reellen Zahlen als Teilmenge von C und die imaginäre Achse die Menge der rein imaginären Zahlen. Als Erweiterung für den Begriff des Betrages einer reellen Zahl definieren wir den Betrag einer komplexen Zahl geometrisch als ihren Abstand vom Ursprung in der Gaußschen Zahlenebene, den wir mit Hilfe des Pythagoräischen Lehrsatzes aus Realteil und Imaginärteil berechnen können: |a + ib| = p a2 + b2 ≥ 0 . Beim Rechnen praktisch ist oft die konjugiert komplexe Zahl z zu einer komplexen Zahl z = a + ib, die geometrisch durch Spiegelung an der reellen Achse definiert wird: z := a − ib . Als Beispiel für ihre Verwendung sei die Identität |z|2 = zz angeführt. Wie erhofft, ist die Menge der komplexen Zahlen abgeschlossen bezüglich der Grundrechnungsarten (abgesehen von der Division durch Null, die in den reellen Zahlen auch schon verboten war), wobei diese erst zu definieren sind. Dazu sind aber nur die üblichen Rechengesetze und die Beziehung (1) notwendig: Addition: (a + ib) + (c + id) = (a + c) + i(b + d) , d.h. bei der Addition zweier komplexer Zahlen sind einfach die Realteile und die Imaginärteile zu addieren. Analog: Subtraktion: (a + ib) − (c + id) = (a − c) + i(b − d) . Etwas komplizierter wird es bei der Multiplikation: (a + ib)(c + id) = ac + i2 bd + ibc + iad = (ac − bd) + i(ad + bc) , und noch etwas komplizierter bei der Division, bei der wir mit der konjugiert Komplexen des Nenners erweitern, um diesen reell zu machen: a + ib (a + ib)(c − id) ac + bd + i(bc − ad) ac + bd bc − ad = = = 2 +i 2 . 2 2 2 c + id (c + id)(c − id) c +d c +d c + d2 6 Das funktioniert natürlich nur, wenn zumindest eine der beiden reellen Zahlen c und d verschieden von Null ist, d.h. c + id 6= 0. Offensichtlich sind i und −i zwei verschiedene Lösungen der quadratischen Gleichung z 2 +1 = 0. Für allgemeinere quadratische Gleichungen der Form az 2 + bz + c = 0 (2) mit reellen Koeffizienten a 6= 0, b, c verwendet man zunächst quadratische Ergänzung: b b b2 az + bz + c = a z + z + c = a z 2 + z + 2 a a 4a 2 2 b = a z+ 2a 2 + 4ac − b2 . 4a = b2 − 4ac 4a2 ! +c− b2 4a Die Gleichung (2) kann daher in der Form z+ b 2a 2 geschrieben werden. Wurzelziehen liefert die Lösungsformel √ −b ± b2 − 4ac , z1,2 = 2a und daher zwei reelle Lösungen, wenn b2 − 4ac > 0 gilt. Lassen wir auch komplexe Lösungen zu, dann gibt es auch im Fall b2 − 4ac < 0 zwei Lösungen, nämlich √ −b ± i 4ac − b2 z1,2 = . 2a Man rechnet leicht nach, dass sich in beiden Fällen die linke Seite der Gleichung (2) faktorisieren (d.h. als Produkt schreiben) lässt als az 2 + bz + c = a(z − z1 )(z − z2 ) . Das gilt auch im Grenzfall b2 − 4ac = 0 mit z1 = z2 = −b/(2a). In diesem Fall nennt man −b/(2a) eine doppelte Lösung. Wenn man diese auch doppelt zählt, ergibt sich das Resultat, dass eine quadratische Gleichung mit reellen Koeffizienten immer 2 komplexe Lösungen hat. Das lässt sich in zwei Richtungen verallgemeinern: Auf Gleichungen mit komplexen Koeffizienten und auf Gleichungen höherer Ordnung. Dazu definieren wir zunächst den Begriff des Polynoms: Ein Polynom n-ten Grades mit komplexen Koeffizienten ist ein Ausdruck der Form p(z) = n X ak z k = an z n + an−1 z n−1 + · · · + a1 z + a0 , k=0 mit a0 , . . . , an ∈ C, an 6= 0. Eine Lösung z der Gleichung p(z) = 0 nennt man eine Nullstelle des Polynoms. Das wesentliche Grundresultat (das nicht so leicht zu beweisen ist) ist 7 Satz 1 Jedes Polynom mit komplexen Koeffizienten und mindestens ersten Grades besitzt mindestens eine komplexe Nullstelle. Für das Weitere benötigen wir die (leicht nachzurechnende) Identität z k − z1k = (z − z1 )(z k−1 + z k−2 z1 + · · · + zz1k−2 + z1k−1 ) . Sei nun z1 eine Nullstelle des Polynoms p, d.h. p(z1 ) = 0. Dann gilt wegen der obigen Gleichung p(z) = p(z) − p(z1 ) = n X ak (z k − z1k ) = (z − z1 )q(z) , k=0 wobei q ein Polynom (n − 1)-sten Grades ist. Diese Rechnung und Satz 1 ermöglichen für jedes Polynom p mit Grad n ≥ 1 die folgende Vorgangsweise: Der Satz 1 garantiert, dass p eine Nullstelle z1 ∈ C besitzt. Dasselbe gilt für q(z) = p(z)/(z − z1 ), wenn n ≥ 2 gilt. Nach n Schritten ist ein Polynom mit Grad Null, d.h. eine Konstante, und zwar an , übrig. Diese Ergebnisse kann man zusammenfassen im Fundamentalsatz der Algebra: Satz 2 Jedes Polynom n-ten Grades mit komplexen Koeffizienten besitzt n Nullstellen z1 , . . . , zn (Mehrfachnennungen möglich) und kann in der Form p(z) = an (z − z1 )(z − z2 ) · · · (z − zn ) geschrieben werden. Bei Polynomen zweiten Grades mit reellen Koeffizienten haben wir gesehen, dass im Fall komplexer Nullstellen diese als konjugiert komplexes Paar auftreten. Auch diese Eigenschaft kann verallgemeinert werden. Satz 3 Polynome mit reellen Koeffizienten haben eine gerade Anzahl komplexer (genauer: nicht reeller) Nullstellen, die nur als konjugiert komplexe Paare auftreten. Übungsaufgaben 3.1. Für folgende komplexe Zahlen gebe man Realteil und Imaginärteil an: a) c) (2 + i)(4 − 3i) b) (8 + 3i)(8 − 3i) 3 3 − 2i 2+i d) + 4 − 3i i 4 + 6i 3.2. Man zeichne die komplexen Zahlen 3+5i, −2/3+5i/2 und ein. 3+5i −3+i 3.3. Man berechne den √ Betrag folgender komplexer Zahlen: 2−i i(3 + 2i), 2 − i 5, 3i, 2 + 5i, 5 − 2i, 2+5i , i+ in der Gaußsche Zahlenebene 1+i 7−3i . 3.4. Wo liegen die Punkte z in der Gaußschen Zahlenebene, für die gilt a) |z| = 2, b) Re(z) = −1 (Re bezeichnet den Realteil von z) 8 3.5. Sei z = a + bi eine komplexe Zahl, und z die konjugiert komplexe Zahl zu z. Man bestimme Real- und Imaginärteil von: a) i|z| , b) z , z c) 1 , z d) z z + . z z 3.6. Man bestimme alle Lösungen der Gleichung 2z 2 − 4z + 20 = 0 . 3.7. Man bestimme alle Nullstellen des Polynoms z 2 − 6z + 10 und gebe die entsprechende Faktorisierung an. 3.8. 2i ist eine Lösung der Gleichung 4. Ordnung z 4 + 5z 3 + 11z 2 + 20z + 28 = 0 . Man berechne die restlichen Lösungen. 4 Die Polardarstellung, Winkelfunktionen Das Ziel dieses Abschnittes ist es, manche Rechnungen mit komplexen Zahlen zu erleichtern. Zunächst stellen wir fest, dass ein Punkt in der Gaußschen Zahlenebene auch beschrieben werden kann, indem man einerseits den Abstand r des Punkes vom Ursprung und andererseits den Winkel ϕ zwischen der reellen Achse und der Geraden durch den Punkt und den Ursprung angibt. Man nennt das die Polardarstellung einer komplexen Zahl und das Paar (r, ϕ) die Polarkoordinaten. Dabei verwenden wir als Maß für den Winkel die Bogenlänge auf dem Einheitskreis. Um einen Zusammenhang zu der Darstellung mit Real- und Imaginärteil herzustellen, brauchen wir Winkelfunktionen: Für Punkte mit Abstand r = 1 vom Ursprung (d.h. Punkte auf dem Einheitskreis) und mit Winkel ϕ nennt man den Realteil den Cosinus von ϕ bzw. cos ϕ, und den Imaginärteil den Sinus von ϕ bzw. sin ϕ. Aus dem Pythagoräischen Lehrsatz folgt daher sin2 ϕ + cos2 ϕ = 1 . (3) Weitere Eigenschaften von Sinus und Cosinus, die sich aus der Definition ergeben: Sinus ist ungerade und Cosinus gerade: sin(−ϕ) = − sin ϕ , cos(−ϕ) = cos ϕ . Sinus und Cosinus sind periodisch mit Periode 2π (Umfang des Einheitskreises): sin(ϕ + 2π) = sin ϕ , cos(ϕ + 2π) = cos ϕ . Sinus und Cosinus gehen auseinander durch Verschiebung hervor: sin(ϕ + π/2) = cos ϕ . Spezielle Werte: 9 ϕ 0 π/4 π/2 3π/4 π sin ϕ 0√ 1/ 2 1√ 1/ 2 0 cos ϕ 1√ 1/ 2 0√ −1/ 2 −1 Für die Zahl z mit den Polarkoordinaten (r, ϕ) gilt z = r(cos ϕ + i sin ϕ) bzw. Re(z) = r cos ϕ , Im(z) = r sin ϕ . Kann man umgekehrt auch die Polarkoordinaten aus Real- und Imaginärteil berechnen? Sei z = a + bi. Dann gilt p b sin ϕ r = a2 + b2 und = =: tan ϕ , a cos ϕ wobei die rechte Seite der Tangens von ϕ ist. Bei der Verwendung der zweiten Gleichung ist allerdings Vorsicht geboten. Sie definiert den korrekten Winkel nicht eindeutig. Für die beiden Zahlen z = a + bi und −z = −a − bi ergibt sich derselbe Wert für tan ϕ. Die auf den meisten Taschenrechnern vorhandene Funkton Arcustangens liefert für arctan(b/a) immer Werte zwischen −π/2 und π/2, d.h. im 1. oder 4. Quadranten. Liegt z im 2. (a < 0, b > 0) oder 3. (a, b < 0) Quadranten, dann ist der korrekte Winkel gegeben durch ϕ = arctan b +π. a Beispiel: z = −1 + i im 2. Quadranten, a = −1, b = 1. Es gilt r = ϕ = arctan(−1) + π = − √ 2, tan ϕ = −1 und daher π 3π +π = . 4 4 Wichtige Rechenregeln für die Winkelfunktionen sind die Summensätze: Satz 4 Für alle α, β ∈ IR gilt sin(α + β) = sin α cos β + sin β cos α , (4) cos(α + β) = cos α cos β − sin α sin β . (5) Verwendet man die Summensätze, dann zeigt sich, dass die Polardarstellung die Multiplikation komplexer Zahlen einfach macht: Für z1 = r(cos ϕ + i sin ϕ), z2 = %(cos ψ + i sin ψ) gilt z1 z2 = r%(cos ϕ cos ψ − sin ϕ sin ψ + i(sin ϕ cos ψ + sin ψ cos ϕ)) = r%(cos(ϕ + ψ) + i sin(ϕ + ψ)) . Um 2 komplexe Zahlen zu multiplizieren, muss man also die Beträge multiplizieren und die Winkel addieren. Als Konsequenz ergibt sich für Potenzen von z = r(cos ϕ + i sin ϕ): z n = rn (cos(nϕ) + i sin(nϕ)) . Als Abschluss dieses Kapitels berechnen wir die Nullstellen spezieller Polynome der Form p(z) = z n − w, wobei w 6= 0 eine beliebige gegebene komplexe Zahl ist. Die Nullstellen nennen wir die 10 Figure 3: Graphischer Beweis der trigonometrischen Summensätze für 0 ≤ α, β, α + β ≤ π/2. n-ten Wurzeln von w. Wenn z bzw. w die Polarkoordinaten (r, ϕ) bzw. (%, ψ) besitzen, dann muss also rn (cos(nϕ) + i sin(nϕ)) = %(cos ψ + i sin ψ) √ gelten. Offensichtlich lässt sich diese Gleichung durch die Wahl r = n % und ϕ = ψ/n erfüllen. Der Fundamentalsatz der Algebra sagt allerdings die Existenz von n n-ten Wurzeln voraus. Weitere Wurzeln kann man finden, indem man sich die Periodizität der Winkelfunktionen zunutze macht. Da rn (cos(nϕ) + i sin(nϕ)) = rn (cos(nϕ + 2kπ) + i sin(nϕ + 2kπ)) , für alle k ∈ ZZ, gilt, ergibt jede Wahl √ n ψ + 2kπ n mit k ∈ ZZ eine n-te Wurzel von w. Unter den entsprechenden komplexen Zahlen gibt es allerdings nur n verschiedene, nämlich r= zk = √ n % cos ψ + 2kπ n Diese bilden ein dem Kreis mit Radius %, ϕk = + i sin √ n ψ + 2kπ n , k = 0, . . . , n − 1. % eingeschriebenes regelmäßiges n-Eck. Übungsaufgaben 4.1. Für die folgenden komplexen Zahlen gebe man Real-, Imaginärteil und Polarkoordinaten an, und man skizziere ihre Lage in der Gaußschen Zahlenebene. √ √ a)2i, b) − 2 − 2i, c)1 − i, 1 d) − 5, e) − 3 + 5i f) . i 11 4.2. Man gebe die kartesische Form folgender komplexer Zahlen an: √ b) − 3[cos(−π/2) + i sin(−π/2)] , a) 3[cos(π/6) + i sin(π/6)] , √ c) 2[cos(π/4) − i sin(π/4)] , d) cos(π) + i sin(π) . 4.3 Man berechne (1+i)4 (1−i)8 auf zwei Arten. 4.4. Man bestimme alle Lösungen der Gleichung z 5 = 64(1 + √ 3i) . 4.5. Man berechne alle Lösungen der Gleichung z 4 + i(1 + i) = 0 . 4.6. Man zeige, dass die folgende Gleichung für alle ϕ ∈ IR gilt: cos(3ϕ) = −3 cos(ϕ) + 4 cos3 (ϕ) . 5 Reelle Funktionen, Grenzwerte Eine Funktion f : A → B ist eine Vorschrift, die jedem Element x der Definitionsmenge A eindeutig ein Element y der Wertemenge B zuordnet. Man verwendet die Schreibweise y = f (x). Für relle Funktionen gilt A, B ⊂ IR. Zumeist geht man von der Abbildungsvorschrift aus, also z.B. f (x) = x2 . In diesem Fall kann man A = IR, B = [0, ∞) wählen, wobei die maximale Definitionsmenge und dann die minimale Wertemenge gewählt wurde. Beispiele: 1. f (x) = x1 , A = B = IR \ {0} = (−∞, 0) ∪ (0, ∞). 2. f (x) = tan x, A = IR \ {kπ + π/2 : k ∈ ZZ}, B = IR. Der Graph einer reellen Funktion f : A → B ist die Menge {(x, y) : x ∈ A, y = f (x)} , d.h. eine Menge von Punkten in der (x, y)-Ebene, für die der y-Wert jeweils das Bild des entsprechenden x-Wertes ist. Eine Skizze des Graphen ist zumeist eine gute Illustration der wesentlichen Eigenschaften einer Funktion. Beispiele für Funktionseigenschaften: • Eine Funktion f heißt (streng) monoton wachsend, wenn aus x1 < x2 folgt, dass f (x1 ) ≤ f (x2 ) (f (x1 ) < f (x2 )) gilt. Sie heißt (streng) monoton fallend, wenn aus x1 < x2 folgt, dass f (x1 ) ≥ f (x2 ) (f (x1 ) > f (x2 )) gilt. Bei einer monoton wachsenden Funktion geht der Graph von links nach rechts bergauf, bei einer fallenden bergab. 12 • Eine Funktion f : A → B heißt beschränkt, wenn die (minimale Werte) Menge {y = f (x) : x ∈ A} beschränkt ist. Das ist der Fall, wenn der ganze Graph zwischen zwei waagrechten Geraden liegt. • Eine Funktion f : A → B heißt gerade (bzw. ungerade), wenn für jedes x ∈ A auch −x ∈ A und f (x) = f (−x) (bzw. f (x) = −f (−x)) gilt. Der Graph einer geraden Funktion ist symmetrisch bezüglich der y-Achse, der einer ungeraden Funktion bezüglich des Ursprungs. • Eine Funktion f : IR → B heißt periodisch mit Periode p > 0, wenn f (x + p) = f (x) für alle x ∈ IR. Der Graph einer periodischen Funktion geht in sich selbst über, wenn er um die Periode nach rechts (oder links) verschoben wird. • Eine Funktion f : A → B heißt injektiv, wenn jeder y-Wert höchstens einmal als Bild vorkommt; genauer: Aus f (x1 ) = f (x2 ) folgt x1 = x2 . Das gilt, wenn der Graph von jeder waagrechten Linie höchstens einmal geschnitten wird. Ist B der minimale Wertebereich, d.h. B = {f (x) : x ∈ A}, dann existiert die Umkehrfunktion f −1 : B → A, die definiert wird durch f −1 (y) = x genau dann, wenn f (x) = y. Den Graphen von f −1 erhält man, indem man den Graphen von f an der ersten Mediane (45-Grad-Diagonale im ersten und dritten Quadranten) spiegelt. Beispiel zur Berechnung der Umkehrfunktion: y = f (x) = ⇔ x−1 x+2 ⇔ (x + 2)y = x − 1 x(y − 1) = −1 − 2y A = IR \ {−2} , ⇔ x = f −1 (y) = 1 + 2y , 1−y B = IR \ {1} . Wenn ich um 10 Uhr in Wien abfahre und um 13 Uhr im 300 km entfernten Salzburg ankomme, dann ist meine Durchschnittsgeschwindigkeit auf dieser Fahrt 300km 3h = 100 km/h. Genauere Informationen über den Fortgang meiner Fahrt könnte man dadurch angeben, dass man Durchschnittsgeschwindigkeiten für Teilzeiten berechnet. Bezeichnen wir mit s(t) die Strecke (in km), die ich nach der Zeit t (in Stunden) zurückgelegt habe (mit den Eigenschaften s(0) = 0 und s(3) = 300), dann ergibt sich für die mittlere Geschwindigkeit im Zeitraum von t bis t + h die Formel s(t + h) − s(t) . h (6) Unser Ziel ist es, zum Begriff der Momentangeschwindigkeit zum Zeitpunkt t zu gelangen, indem wir die Länge des Zeitraumes h immer kleiner wählen. Bevor wir dieses Ziel im nächsten Abschnitt realisieren, stellen wir als Vorbereitung zunächst einige mathematische Werkzeuge bereit. Der wichtigste Begriff in diesem Zusammenhang ist der des Grenzwertes: Wir sagen, dass f0 der Grenzwert (bzw. Limes) der Funktion f (x) für x gegen x0 ist, als Formel lim f (x) = f0 , x→x0 (7) wenn die Werte f (x) beliebig nahe bei f0 sind für alle x, die genügend nahe bei x0 sind. Genauer gesagt bedeutet das, dass ich bei folgendem Spiel immer gewinne: Zuerst gibt mein Gegenspieler einen (beliebig kleinen) Abstand ε von f0 vor. Dann gewinne ich das Spiel, wenn ich einen (genügend kleinen) Abstand δ von x0 angeben kann, sodass für alle x, die höchstens den Abstand δ zu x0 haben, 13 die Werte f (x) höchstens den Abstand ε von f0 haben. Noch genauer: Für jedes > 0 gibt es ein δ > 0, sodass |f (x) − f0 | ≤ ε für alle x mit |x − x0 | ≤ δ. Wenn (7) gilt und außerdem x0 ∈ A, dann liegt es nahe, f0 mit f (x0 ) zu vergleichen. Man nennt die Funktion f stetig and der Stelle x0 , wenn lim f (x) = f (x0 ) . x→x0 Zur Berechnung von Grenzwerten gibt es einige nützliche Rechenregeln. Satz 5 Sei α ∈ IR und gelte lim f (x) = f0 , lim g(x) = g0 , x→x0 x→x0 dann gilt auch lim (f (x) ± g(x)) = f0 ± g0 , lim (αf (x)) = αf0 , x→x0 x→x0 lim (f (x)g(x)) = f0 g0 , lim x→x0 x→x0 f0 f (x) = , g(x) g0 wobei man für die Gültigkeit der letzten Regel natürlich die zusätzliche Annahme g0 6= 0 braucht. Beispiele: • 32 − 2 7 x2 − 2 = = , x→3 x + 5 3+5 8 lim Insbesondere ist die Funktion f (x) = x2 −2 x+5 stetig an der Stelle x = 3. • Ohne Beweis: Für a > 0 ist durch f (x) = ax eine auf IR stetige Funktion, die Exponentialfunktion mit Basis a gegeben. Für diese gelten die Rechenregeln ax+y = ax ay und axy = (ax )y . Satz 6 Sei f (x) ≤ g(x) ≤ h(x) und limx→x0 f (x) = limx→x0 h(x) = f0 . Dann gilt auch limx→x0 g(x) = f0 . Man kann in der Definition des Grenzwertes x0 und/oder f0 durch ∞ (bzw. −∞) ersetzen, indem man beliebig (genügend) nahe bei ∞ durch beliebig (genügend) groß ersetzt. Als Beispiel: Es gilt lim f (x) = f0 , x→∞ wenn es für alle (beliebig kleinen) ε > 0 ein (genügend großes) M ∈ IR gibt, sodass |f (x) − f0 | ≤ ε für alle x ≥ M . Die obigen Rechenregeln gelten dann auch, wobei man für α > 0 folgende Regeln verwendet: α ± ∞ = ±∞ , α∞ = ∞, α = 0, ∞ 14 α = ∞, 0 ∞ + ∞ = ∞. Figure 4: Vergleich zwischen Dreiecks- und Kreissegmentflächen Beispiele: 1) 2) 3) 1 = 0 , lim xn = ∞ für alle n ∈ IIN , x→∞ xn 2 x + 2x + 3 1 + 2/x + 3/x2 1 lim = lim = , x→∞ 2x2 − x + 5 x→∞ 2 − 1/x + 5/x2 2 2 3 x + 1/x x +1 = lim = ∞. lim x→∞ 1 + 1/x x→∞ x2 + x lim x→∞ Schwierigkeiten entstehen, wenn die Anwendung der Rechenregeln auf unbestimmte Ausdrücke führt wie z.B. 0 , 0 ∞ , ∞ 0∞, ∞ − ∞, denen kein sinnvoller Wert zugewiesen werden kann, weil verschiedene Beispiele verschiedene Grenzwerte erzeugen. Eine Möglichkeit, mit unbestimmten Ausdrücken umzugehen, wurde in den obigen Beispielen 2) und 3) verwendet, die auch zeigen, dass ∞/∞ keinen eindeutigen Wert haben kann. Noch drei Beispiele für den Umgang mit unbestimmten Ausdrücken (in diesem Fall 0/0): • lim √ x→ x4 − 4 (x2 − 2)(x2 + 2) 2 = lim = lim √ √ (x + 2) = 4 . 2 x2 − 2 2x −2 x→ 2 x→ 2 • Wir wollen den Grenzwert limx→0 sinx x berechnen. Dazu vergleichen wir zunächst in Fig. 4 die Flächeninhalte A1 des rechtwinkeligen Dreiecks mit den Kathetenlängen sin x und cos x, A2 des Kreissegments mit Öffnungswinkel x und A3 des großen rechtwinkeligen Dreieecks mit Kathetenlängen 1 und tan x. Offensichtlich gilt A1 < A2 < A3 , A1 = 15 sin x cos x , 2 A3 = tan x . 2 Um A2 zu berechnen, verwenden wir, dass der Flächeninhalt des Einheitskreises gleich π ist (was wir allerdings nicht bewiesen haben) und dass das Verhältnis von A2 zum Flächeninhalt des Einheitskreises dasselbe ist wie das Verhältnis des Winkels x zu 2π: A2 /π = x/(2π) und daher A2 = x/2. Verwendet man das in den obigen Ungleichungen und formt sie etwas um, dann erhält man sin x 1 cos x < < . x cos x Aus cos 0 = 1 und Satz 6 folgt schließlich sin x lim = 1. (8) x→0 x • Für |x| ≤ π/2 gilt cos x ≥ 0 und daher 1 − cos x (1 − cos x)(1 + cos x) 1 − cos2 x sin x ≤ = = sin x . x x x x Aus dem obigen Resultat, sin 0 = 0 und wieder Satz 6 folgt cos x − 1 = 0. lim x→0 x 0≤ (9) Übungsaufgaben 5.1. Für folgende Funktionen gebe man den maximalen Definitionsbereich (in IR) an und klassifiziere sie bezüglich Beschränktheit und der Begriffe ’gerade’ und ’ungerade’. √ x−2 a) f (x) = , b) f (x) = x3 − 5x , x+1 1 , d) f (x) = x2 + x − 6 . c) f (x) = 2 (x + 7)3 5.2. Man bestimme, welche der folgenden Funktionen periodisch sind, und man gebe gegebenenfalls die kleinste Periode an. 1+x 3 a) , b) . 2 cos(x) − 5 sin (x) − 1 5.3. Man ermittle den maximalen Definitionsbereich folgender Funktionen. Man bestimme weiters, welche dieser Funktionen eine Umkehrfunktion besitzen und man gebe sie gegebenenfalls an. s a) 3−x , x−5 b) exp(−x + 2) , c) 3 . cos(x) − 5 5.4. Man berechne x+9 , x→3 x2 − 9 a) lim x−5 , x→5 x2 − 3x − 10 b) lim x2 + 3x − 4 . x→∞ 5x2 + 32x + 2 c) lim 5.5. Wo sind folgende Funktionen stetig? Wo sind Lücken im Definitionsbereich? a) f (x) = x2 + ( √ c) f (x) = x−1 , x+1 x−2 x−4 1/4 16 b) f (x) = x2 − 9 , x(x − 3) für x 6= 4 , x ≥ 0 , für x = 4 . 6 Differentialrechnung, die Exponentialfunktion Um zu unserer Motivation zurückzukehren: Unser Ziel ist es, in (6) den Limes für h → 0 zu berechnen. Leider führt auch das, wenn s and der Stelle t stetig ist, auf einen unbestimmten Ausdruck, nämlich 0/0, und wir können im Allgemeinen nicht garantieren, dass es den Grenzwert gibt. Definition 1 Sei f : (a, b) → IR und x ∈ (a, b). Man sagt, f ist differenzierbar an x, wenn der Grenzwert f (x + h) − f (x) f 0 (x) = lim h→0 h existiert. Er heißt Ableitung von f and der Stelle x, und es wird auch die Schreibweise f 0 (x) = df dx (x) verwendet. Dementsprechend spricht man auch von einem Differentialquotienten (im Verf (x+h)−f (x) gleich mit dem Differenzenquotienten ∆f ∆x = (x+h)−x ). Wir haben die Ableitung mit der Idee der Momentangeschwindigkeit motiviert. Sie hat aber auch eine geometrische Bedeutung als Tangentenanstieg: Definition 2 Sei f an x0 differenzierbar. Dann nennen wir die Gerade in der x-y-Ebene mit der Gleichung y = f (x0 ) + f 0 (x0 )(x − x0 ) die Tangente and den Graphen von f im Punkt (x0 , f (x0 )). Beispiele: • f (x) = x2 : f (x + h) − f (x) (x + h)2 − x2 x2 + 2xh + h2 − x2 = = = 2x + h . h h h Daher gilt f 0 (x) = 2x. Die Tangente an x0 = 1 hat die Gleichung y = 1 + 2(x − 1) = 2x − 1. √ • f (x) = x: √ √ √ √ √ √ x+h− x ( x + h − x)( x + h + x) 1 √ = =√ √ √ . h h( x + h + x) x+h+ x Daher gilt f 0 (x) = 1 √ . 2 x • f (x) = 1/x: 1 h 1 1 − x+h x = −1 . x(x + h) Daher gilt f 0 (x) = −1/x2 . • f (x) = sin x: Wir verwenden die Summensätze (Satz 4): sin(x + h) − sin x cos h − 1 sin h = sin x + cos x . h h h Aus unseren früheren Resultaten (8) und (9) folgt (sin x)0 = cos x. Analog zeigt man (cos x)0 = − sin x. 17 Satz 7 Seien f und g differenzierbar an der Stelle x. Dann gilt (f (x) ±g(x))0 = f 0 (x) ± g 0 (x), die Produktregel (f (x)g(x))0 = f 0 (x)g(x)+f (x)g 0 (x) und die Quotientenregel wobei für letztere natürlich g(x) 6= 0 verlangt werden muss. f (x) 0 g(x) = f 0 (x)g(x)−f (x)g 0 (x) , g(x)2 Beweis: a) (f (x + h) ± g(x + h)) − (f (x) ± g(x)) f (x + h) − f (x) g(x + h) − g(x) = ± . h h h b) Produktregel: f (x + h)g(x + h) − f (x)g(x) f (x + h) − f (x) g(x + h) − g(x) = g(x + h) + f (x) . h h h c) Quotientenregel: f (x + h) f (x) f (x + h)g(x) − f (x)g(x + h) − = g(x + h) g(x) hg(x)g(x + h) 1 f (x + h) − f (x) g(x + h) − g(x) = g(x) − f (x) . g(x)g(x + h) h h 1 h Beispiele: • Sei fn (x) = xn . Behauptung: fn0 (x) = nxn−1 für alle n ∈ IIN. Beweis: Vollständige Induktion: n = 1: (x+h)−x = 1 = 1x0 . h 0 n−1 Nehmen wir nun an, es stimmt, dass fn (x) = nx für ein bestimmtes n. Dann gilt fn+1 (x) = xfn (x) und daher wegen der Produktregel 0 fn+1 (x) = fn (x) + xfn0 (x) = xn + x nxn−1 = (n + 1)xn . • (tan x)0 = sin x cos x 0 = cos x cos x − sin x(− sin x) 1 = . cos2 x cos2 x Satz 8 (Kettenregel) Sei g differenzierbar an x und f differenzierbar an g(x), dann gilt f (g(x))0 = f 0 (g(x))g 0 (x). Beweis: f (g(x + h)) − f (g(x)) f (g(x) + k) − f (g(x)) g(x + h) − g(x) = . h k h mit g(x + h) − g(x) = k. Die Beobachtung, dass für h → 0 auch k → 0, vervollständigt den Beweis. Beispiel: f (x) = x−n = (1/x)n . Daher f 0 (x) = n n−1 1 x −1 = −nx−n−1 . x2 Geometrische Überlegungen legen nahe, dass Funktionsgraphen zu Sekanten parallele Tangenten besitzen: 18 Satz 9 (Mittelwertsatz der Differentialrechnung, ohne Beweis) Sei f : [a, b] → IR stetig und auf (a, b) stetig differenzierbar, d.h differenzierbar für alle x ∈ (a, b) und f 0 (x) ist eine in (a, b) stetige Funktion. Dann gibt es ein x0 ∈ (a, b), sodass f 0 (x0 ) = f (a) − f (b) . a−b Das Vorzeichen der Ableitung sagt etwas über Monotonie aus: Satz 10 Sei f : (a, b) → IR stetig differenzierbar, und es gelte f 0 (x) > 0 (bzw. f 0 (x) < 0) für alle x ∈ (a, b). Dann ist f streng monoton wachsend (bzw. fallend) und daher injektiv. Ersetzt man > (bzw. <) durch ≥ (bzw. ≤), dann ist f immer noch monoton, aber im allgemeinen nicht streng monoton und daher auch nicht unbedingt injektiv. Beweis: Sei f 0 > 0 und a < c < d < b. Dann gilt wegen des Mittelwertsatzes f (d) = f (c) + f 0 (x0 )(d − c) > f (c). Andere Fälle analog. Dieses Resultat hat eine einfache Konsequenz: Satz 11 Sei f : (a, b) → IR stetig differenzierbar, und es gelte f 0 (x) = 0 für alle x ∈ (a, b). Dann ist f konstant, d.h. es existiert f0 ∈ IR, sodass f (x) = f0 für alle x ∈ (a, b). Satz 12 (Ableitung der Umkehrfunktion) Sei f : (a, b) → IR stetig differenzierbar, und es gelte f 0 (x) 6= 0, x ∈ (a, b). Dann ist f −1 differenzierbar, und es gilt f −1 (y)0 = 1 für alle y = f (x), x ∈ (a, b) . f 0 (f −1 (y)) Beweis: Differenziert man f (f −1 (y)) = y nach y (Kettenregel), dann erhält man das Resultat. Beispiele: • f (x) = xn , f −1 (y) = y 1/n , für x, y > 0, n ∈ IIN. f −1 (y)0 = 1 n(y 1/n )n−1 = 1 1/n−1 y . n • f (x) = xp/q = (xp )1/q , x > 0, p ∈ ZZ, q ∈ IIN. 1 p f 0 (x) = (xp )1/q−1 pxp−1 = xp/q−1 . q q • Ohne Beweis: Es gilt auch (xα )0 = αxα−1 für x > 0, α ∈ IR. • (arctan x)0 = cos2 (arctan x) = cos2 (arctan x) 1 = . 2 1 + x2 sin (arctan x) + cos2 (arctan x) 19 Nun beschäftigen wir uns mit der Exponentialfunktion f (x) = ax , a > 0. Es gilt ax+h − ax ah − 1 x = a . h h Da (ohne Beweis) der Grenzwert ca = limh→0 (ah − 1)/h existiert, ist ax an jeder Stelle x ∈ IR differenzierbar, und die Ableitung ist gegeben durch (ax )0 = ca ax . Für a ≤ b gilt (ah − 1)/h ≤ (bh − 1)/h und daher ca ≤ cb . Unter Berücksichtigung dieser Tatsache legen Experimente mit dem Taschenrechner nahe, dass es eine Zahl e ∈ (2, 3) gibt, sodass ce = 1. Das ist auch wirklich der Fall, und diese (irrationale) Zahl wird Eulersche Zahl genannt. Die Exponentialfunktion mit Basis e (oder einfach die Exponentialfunktion) ist ihre eigene Ableitung: (ex )0 = ex . Sie wird oft auch als exp(x) := ex geschrieben. Für kleine reelle Zahlen h erwarten wir eh − 1 ≈1 h ⇐⇒ e ≈ (1 + h)1/h , und tatsächlich gilt e = lim (1 + h)1/h . h→0 (ex )0 ex Da = > 0, existiert eine Umkehrfunktion der Exponentialfunktion, genannt der (natürliche) Logarithmus ln x, x > 0, d.h. exp(ln x) = x (ln steht für logarithmus naturalis). Differenzieren gibt exp(ln x)(ln x)0 = 1 und daher 1 (ln x)0 = , x > 0. x Mit Hilfe des Logarithmus können wir die Ableitung der Exponentialfunktion mit Basis a > 0 bestimmen: Mit λ = ln a folgt ax = eλx und daher mit der Kettenregel (ax )0 = (eλx )0 = λeλx = (ln a)ax , also ca = ln a . Aus den Rechenregeln für die Exponentialfunktion folgt für den Logarithmus (x, y > 0) ln(xy) = ln x + ln y , ln(xy ) = y ln x . Noch ein kleiner Ausflug zurück zu den komplexen Zahlen und Polarkoordinaten: Für den Ausdruck f (ϕ) = cos ϕ + i sin ϕ gilt f 0 (ϕ) = − sin ϕ + i cos ϕ = if (ϕ) , weswegen sich die Schreibweise eiϕ := cos ϕ + i sin ϕ anbietet. Damit kann die Exponentialfunktion auch auf komplexe Zahlen angewendet werden: ex+iy = ex (cos y + i sin y), und die Polardarstellung einer komplexen Zahl erhält die Form z = reiϕ (Man merke das einfache Multiplizieren: (reiϕ )(%eiψ ) = r% ei(ϕ+ψ) ). Damit können wir auch eine Lieblingsgleichung vieler MathematikerInnen angeben: eiπ + 1 = 0 20 die die wichtigsten Konstanten der Mathematik (0, 1, e, π und i) enthält. Ein weiterer Ausflug zurück zu unbestimmten Ausdrücken: Angenommen, f, g sind differenzierbar an x0 , f (x0 ) = g(x0 ) = 0 und g 0 (x0 ) 6= 0. Dann gilt lim x→x0 f (x) (f (x) − f (x0 )/(x − x0 ) f 0 (x0 ) = lim . = 0 g(x) x→x0 (g(x) − g(x0 )/(x − x0 ) g (x0 ) Allgemeiner gilt: Satz 13 (Regel von de l’Hopital, ohne Beweis) Seien f und g differenzierbar an x0 , f (x0 ) = g(x0 ) = 0 und es existiere der Grenzwert limx→x0 f 0 (x)/g 0 (x). Dann gilt lim x→x0 f (x) f 0 (x) = lim 0 . g(x) x→x0 g (x) Beispiele: 1. lim √ x→ 2. lim x→0 x4 − 4 4x3 2 = lim = lim √ √ 2x = 4 . 2 2x −2 x→ 2 2x x→ 2 sin x = lim cos x = 1 , x→0 x lim x→0 cos x − 1 = lim (− sin x) = 0 . x→0 x 3. In manchen Fällen muss man die Regel mehrmals anwenden: 3x2 − 4x + 1 6x − 4 x3 − 2x2 + x = lim = lim = 1. 2 x→1 x→1 x→1 x − 2x + 1 2x − 2 2 lim Ist eine Funktion f auf einem Intervall (a, b) differenzierbar, dann ist f 0 ebenfalls eine auf (a, b) definierte Funktion, und man kann die Frage nach deren Differenzierbarkeit stellen. Definition 3 Sei f : (a, b) → IR. Dann sind höhere Ableitungen von f rekursiv definiert durch f (0) (x) := f (x) , f (n+1) (x) := (f (n) (x))0 , n ≥ 0, solange die rechte Seite existiert. Existiert die n-te Ableitung f (n) (x) für alle x ∈ (a, b), dann sagt man, f ist in (a, b) n-mal differenzierbar. Ist f (n) stetig in (a, b), dann sagt man, f ist in (a, b) n n-mal stetig differenzierbar. Es werden auch die Schreibweisen f (n) = ddxnf , f (2) = f 00 , f (3) = f 000 verwendet. So wie die erste Ableitung etwas über geometrische Eigenschaften des Funktionsgraphen aussagt (Anstieg der Tangente), ist das auch für höhere Ableitungen der Fall. Ist zum Beispiel die zweite Ableitung in einem Intervall größer Null, dann wird der Tangentenanstieg von links nach rechts größer. Definition 4 Sei f in (a, b) zweimal stetig differenzierbar und f 00 ≥ 0 (bzw. f 00 > 0, f 00 ≤ 0, f 00 < 0) in (a, b), dann nennt man f konvex (bzw. streng konvex, konkav, streng konkav) in (a, b). 21 Diese Bezeichnungen sollten verständlich sein, wenn man den Graphen ’von unten’, d.h. in die positive y-Richtung, anschaut. Will man den Graphen skizzieren, dann ist es hilfreich, Punkte zu kennen, an denen das Vorzeichen von f , die Monotonie, oder die Konvexität wechselt. Kandidaten dafür sind Stellen, an denen f , f 0 , bzw. f 00 Null wird. Das muss aber nicht der Fall sein, wie die folgenden Beispiele zeigen: • Für f (x) = x2 gilt f (0) = 0. Trotzdem ändert f an der Stelle Null nicht das Vorzeichen. • Für f (x) = x3 gilt f 0 (0) = 0. Trotzdem ändert f an der Stelle Null nicht die Monotonie. • Für f (x) = x4 gilt f 00 (0) = 0. Trotzdem ändert f an der Stelle Null nicht die Konvexität. Man beachte, dass in allen 3 Fällen die ’nächste’ Ableitung nach der untersuchten an der Stelle x = 0 auch Null ist. Satz 14 (ohne Beweis) Sei f stetig differenzierbar in (a, b), f (0) = 0 und f 0 (0) > 0 (bzw. f 0 (0) < 0). Dann ist f nahe bei x = 0 für x < 0 negativ (bzw. positiv) und für x > 0 positiv (bzw. negativ). Definition 5 Sei f : (a, b) → IR stetig. a) Eine Stelle x0 ∈ (a, b) mit f (x0 ) = 0 nennt man eine Nullstelle von f . b) Eine Stelle x0 ∈ (a, b), für die es ein offenes Intervall I ⊂ (a, b) gibt mit x0 ∈ I, sodass f (x) ≤ f (x0 ) für alle x ∈ I, nennt man ein relatives Maximum von f . c) Eine Stelle x0 ∈ (a, b), für die es ein offenes Intervall I ⊂ (a, b) gibt mit x0 ∈ I, sodass f (x) ≥ f (x0 ) für alle x ∈ I, nennt man ein relatives Minimum von f . d) Eine Stelle x0 ∈ (a, b), die entweder ein relatives Maximum oder ein relatives Minimum ist, nennt man ein relatives Extremum. e) Eine Stelle x0 ∈ (a, b), an der das Verhalten von f von streng konvex auf streng konkav (oder umgekehrt) wechselt, nennt man einen Wendepunkt von f . Das folgende Resultat ist eine Konsequenz aus Satz 14. Satz 15 Sei f in (a, b) dreimal stetig differenzierbar. Dann gilt a) An einer Nullstelle von f , an der die erste Ableitung nicht Null ist, ändert f das Vorzeichen. b) Eine Stelle x0 ∈ (a, b), für die f 0 (x0 ) = 0 und f 00 (x0 ) < 0 (bzw. f 00 (x0 ) > 0) gilt, ist ein relatives Maximum (bzw. Minimum) von f . c) Eine Stelle x0 ∈ (a, b), für die f 00 (x0 ) = 0 und f 000 (x0 ) 6= 0 gilt, ist ein Wendepunkt von f . Die Aufgabe, mit Hilfe der oben definierten speziellen Punkte den Graphen einer Funktion zu skizzieren, nennt man Kurvendiskussion. Beispiel: f (x) = x3 − 3x2 + 2x = x(x − 1)(x − 2). Wir berechnen zunächst √ √ f 0 (x) = 3x2 − 6x + 2 = 3(x − 1 − 1/ 3)(x − 1 + 1/ 3) , f 00 (x) = 6x − 6 = 6(x − 1) . Offensichtlich gibt es 3 Nullstellen, x = 0, 1, 2, von denen x = 1 gleichzeitig der einzige Wendepunkt ist, an dem das Verhalten von konkav (x < 1) auf konvex (x > 1) wechselt. Der Anstieg der Wendetangente (d.h. der Tangente am Wendepunkt) ist f 0 (1) = −1. Es gibt 2 relative Extrema 22 √ √ an x = 1 − 1/ 3 und an x = 1 + 1/ 3, von denen wegen des Konvexitätsverhaltens das erste ein Maximum und das zweite ein Minimum ist. Zusätzliche Information: limx→∞ f (x) = ∞, limx→−∞ f (x) = −∞. Jetzt kann der Graph leicht skizziert werden. Übungsaufgaben 6.1. Man überprüfe, ob die folgenden Funktionen stetig an x = 2 sind. Sind sie differenzierbar? ( a) f (x) = ( x2 für x ≥ 2 , 2x für x < 2 . b) f (x) = x2 für x ≥ 2 , 4(x − 1) für x < 2 . 6.2. Sei y(t) = a sin(ωt) die vertikale Auslenkung eines an einem Federpendel hängenden Massenpunktes. Man bestimme die Geschwindigkeit des Massenpunktes zu jeder Zeit t. Zu welcher Zeit steht der Massenpunkt still? 6.3. Man vereinfache folgende Ausdrücke: 2 2 a) 2 ln x − ln 4 − ln x + ln e , 3 5 c) ln + ln 10 9 b) ln x e ·5 e2 . 6.4. Man berechne die Ableitung von a) x2 + 9 , x+3 b) cos(x) , x2 c) x2 + 3x − 4 . ex 6.5. Man berechne die Ableitung von a) ax 2 +4x , b) e4x 2 −√x x2 , c) e 3x+1 . 6.6. Man berechne die Ableitung von a) tan(x2 + 2x) , b) sin2 (3x) , c) sin(2) . cos(2x) 6.7. Man berechne die Grenzwerte a) lim x→∞ ln(x) , x b) lim x→∞ exp(−x) . ln(1 + x1 ) 6.8. Man berechne die Grenzwerte a) lim x→∞ exp(x) , x2 + 3x b) lim x→0 23 sin(x) . exp(x) − 1 − ln 5 , 6.9. Sei f (x) = x2 . Man finde alle ξ, für die f (3) − f (−1) = f 0 (ξ) 4 gilt, und fertige eine Skizze an. 6.10. Man bestimme die lineare Approximation der Funktion f (x) = exp(x) in der Nähe von x = 0. 6.11. Sei f (x) = x2 sin(x). Man berechne die vierte Ableitung f (4) (x). 6.12. Mit Hilfe von Nullstellen, Extrempunkten und Wendepunkten skizziere man den Graphen von f (x) = xx−1 2 +1 . 7 Integration Motivation – Umfang und Flächeninhalt des Kreises Als Einstimmung berechnen wir den Umfang und den Flächeninhalt des Kreises. Genau genommen werden wir aber erst definieren, was diese beiden Dinge überhaupt sind. Die Idee besteht darin, die Begriffe Länge bzw. Flächeninhalt von der Strecke bzw. vom Rechteck auf gekrümmte Objekte zu übertragen. Wir beginnen damit, einem Kreis mit Radius r ein gleichseitiges N -Eck einzuschreiben, indem wir, ausgehend von einem beliebigen Radius, N Radien einzeichnen, die paarweise jeweils den Winkel 2π/N miteinander einschließen. Wenn man N groß wählt, kann man das N -Eck als eine Approximation für den Kreis sehen und daher auch seinen Umfang UN und seinen Flächeninhalt FN als Approximation für das, was wir uns unter Umfang und Flächeninhalt des Kreises vorstellen. Das motiviert die Definitionen: Wenn der Grenzwert limN →∞ UN existiert, dann nennen wir ihn den Umfang des Kreises. Wenn der Grenzwert limN →∞ FN existiert, dann nennen wir ihn den Flächeninhalt des Kreises. Aus der Definition der Winkelfunktionen folgt, dass eine Seite des N -Ecks die Länge 2r sin(π/N ) besitzt. Daraus folgt UN = 2rN sin(π/N ) = 2rπ sin(π/N ) → 2rπ π/N für π/N → 0 . Damit haben wir gezeigt, dass der Kreis gemäß unserer Definition einen Umfang besitzt und dass dieser gleich 2rπ ist. Wieder mit Hilfe der Definition der Winkelfunktionen und mit dem Summensatz für den Sinus kann man zeigen, dass der Flächeninhalt eines der N Dreiecke, die das N -Eck bilden, gleich 2 r sin(π/N )r cos(π/N ) = r2 sin(2π/N ) ist. Daher FN = r2 N sin(2π/N ) sin(2π/N ) = r2 π → r2 π 2 2π/N für 2π/N → 0 . Der Kreis besitzt also auch einen Flächeninhalt, und der ist gleich r2 π. 24 Figure 5: Riemannsumme: Flächen unterhalb der x-Achse werden negativ gerechnet. Das Riemann-Integral – grundlegende Eigenschaften Stellen wir uns nun die verwandte Aufgabe zu definieren, was der Flächeninhalt einer Fläche ist, die vom Graphen einer Funktion f (x), der x-Achse und von den vertikalen Geraden x = a und x = b eingeschlossen wird. Eine mögliche Vorgangsweise besteht darin, das Intervall [a, b] in N gleich lange Teilintervalle der Länge ∆x = b−a N zu teilen, indem man die Teilungspunkte x0 = a, x1 = a + ∆x, x2 = a + 2∆x, . . . , xN = a + N ∆x = b einführt und den gesuchten Flächeninhalt durch die Summe der Flächeninhalte von N Rechtecken approximiert, wobei das i-te Rechteck eine Seite ∆x besitzt und die andere gleich f (ti ) mit xi−1 ≤ ti ≤ xi ist. Das ergibt für den Flächeninhalt die Approximation (Fig. 5) FN = N X f (ti )∆x . i=1 Definition 6 Wenn in der oben beschriebenen Situation der Grenzwert limN →∞ FN existiert und unabhängig von der Auswahl der Punkte ti ist, dann heißt er das (Riemann)Integral der Funktion f über das Intervall [a, b] und wird bezeichnet mit Z b f (x)dx . a Man sagt dann: f ist (Riemann-)integrierbar über [a, b]. Bemerkung 2 1) Die Approximation FN wird eine Riemannsumme genannt. Die Einführung des Integrals als Grenzwert von Riemannsummen ist nur eine von mehreren Möglichkeiten; deswegen R die genauere Bezeichnung Riemann-Integral. Das Integralzeichen ist ein stilisiertes ’S’, das an die Definition mit Hilfe einer Summe erinnern soll. Das Symbol dx erinnert dabei an die x-Differenz 25 Figure 6: Mittelwertsatz der Integralrechnung ∆x = xi − xi−1 . 2) Die Funktion f kann auch negative Werte annehmen. Das Integral ist dann so zu verstehen, dass Flächen zwischen dem Graphen und der x-Achse, die unter der x-Achse liegen, als negativer Beitrag gerechnet werden. Das Integral hat Eigenschaften, die man erwarten kann: Kann man den Graphen zwischen zwei horizontalen Linien einschließen, dann liegt der Wert des Integrals zwischen den Flächeninhalten der entsprechenden Rechtecke; durch eine vertikale Gerade kann die Fläche in zwei Teile geteilt werden. Satz 16 Sei f integrierbar über [a, b]. 1) Aus m ≤ f (x) ≤ M für alle x ∈ [a, b] folgt m(b − a) ≤ Z b f (x)dx ≤ M (b − a) . a 2) Für c ∈ (a, b) gilt Z b Z c f (x)dx + f (x)dx = a Z b a f (x)dx . c Das Integral ist gleich dem Flächeninhalt eines geeignet gewählten Rechtecks. Das entsprechende Resultat heißt Mittelwertsatz der Integralrechnung (siehe Fig. 6): Satz 17 Sei f stetig auf [a, b]. Dann ist f integrierbar über [a, b], und es existiert ein ξ ∈ [a, b], sodass Z b f (x)dx = f (ξ)(b − a) . a 26 Der Hauptsatz der Differential- und Integralrechnung Erinnern wir uns an die Fahrt von Wien nach Salzburg, wo wir die nach der Zeit t zurückgelegte Strecke mit s(t) bezeichnet haben. Bezeichnen wir den Zeitpunkt der Ankunft mit T und unterteilen wir das Zeitintervall [0, T ] in N gleiche Teile, d.h. ti = i∆t, i = 0, . . . , N , mit ∆t = T /N , dann gilt s(T ) − s(0) = N X (s(ti ) − s(ti−1 )) , i=1 womit wir die Gesamtstrecke in Teilstücke zerlegt haben. Mit der Momentangeschwindigkeit v(t) = s0 (t) folgt aus dem Mittelwertsatz der Differentialrechnung s(T ) − s(0) = N X v t̃i ∆t , i=1 mit geeignet gewählten t̃i ∈ [ti−1 , ti ]. Der Ausdruck auf der rechten Seite ist eine Riemannsumme. Mit N → ∞ folgt daher Z T s(T ) − s(0) = v(t)dt . 0 Wir können also aus der Momentangeschwindigkeit die zurückgelegte Strecke berechnen. Wir haben gerade (im wesentlichen) den Hauptsatz der Differential- und Integralrechnung bewiesen: Satz 18 Sei F stetig differenzierbar auf dem Intervall [a, b]. Dann gilt Z b b F 0 (x)dx . F (x) := F (b) − F (a) = a a Beispiele: 1. Z π 0 2. Z 2π 0 3. Z 1 −2 |x|dx = π sin x dx = − cos x = 2 , 0 2π sin x dx = − cos x Z 0 Z 1 (−x)dx + −2 0 0 = 0. x2 0 x2 1 5 x dx = − + = . 2 −2 2 0 2 Ersetzen wir den festen Wert b durch ein variables x ∈ [a, b], dann sieht man, dass die Funktion F aus einem Anfangswert F (a) und aus ihrer Ableitung berechnet werden kann: Z x F (x) = F (a) + F 0 (y)dy . a Man kann daher die Integration als Umkehroperation zur Differentiation sehen. Die Reihenfolge kann dabei auch umgedreht werden: Sei f stetig in [a, b]. Definiert man Z x F (x) := f (y)dy , a 27 dann gilt für h > 0 F (x + h) − F (x) 1 = h h Z x+h f (y)dy = f (ξh ) , x wobei die erste Gleichung aus Satz 16, 2) folgt und die zweite (mit x ≤ ξh ≤ x + h) aus dem Mittelwertsatz der Integralrechnung. Für h → 0 gilt ξh → x und daher wegen der Stetigkeit von f auch f (ξh ) → f (x), woraus F 0 (x) = f (x) folgt, d.h. d dx Z x f (y)dy = f (x) . a Stammfunktionen – Integrationsmethoden Definition 7 Seien f, F : (a, b) → IR und F 0 (x) = f (x) für alle x ∈ (a, b). Dann heißt F eine Stammfunktion von f . Die obigen Resultate zeigen, dass man mit Hilfe von Stammfunktionen Integrale berechnen kann. Es stellt sich die Frage, wie die Menge der Stammfunktionen einer Funktion aussieht. Satz 19 Seien F und G Stammfunktionen von f . Dann existiert eine Konstante c ∈ IR, sodass F (x) = G(x) + c in (a, b). Mit anderen Worten: Kennt man eine Stammfunktion, dann erhält man alle anderen Stammfunktionen durch Addition von Konstanten. Beweis: Für die Funktion H(x) := F (x) − G(x) gilt H 0 (x) = F 0 (x) − G0 (x) = f (x) − f (x) = 0 und daher ist H wegen Satz 11 konstant. R Man schreibt manchmal f (x)dx als Abkürzung für die Gesamtheit aller Stammfunktionen von R f , und nennt diesen Ausdruck das unbestimmte Integral (also z.B. 2x dx = x2 + c) im Gegensatz Rb zum bestimmten Integral a f (x)dx. Aufgrund der im vorigen Kapitel berechneten Ableitungen lassen sich für manche Funktionen leicht Stammfunktionen bestimmen. Beispiele: f (x) xα 1/x sin x cos x ax (1 + x2 )−1 F (x) xα+1 α+1 ln(x) − cos x sin x x a / ln a arctan x für x > 0, α 6= −1 für x > 0 für a > 0, a 6= 1 Das Finden von Stammfunktionen, soweit diese überhaupt mit Hilfe von Standardfunktionen angeschrieben werden können, ist eine zwar trickreiche, aber trotzdem automatisierbare Aufgabe (siehe z.B. http://integrals.wolfram.com/index.jsp). Drei der dabei verwendeten Tricks sollen hier vorgestellt werden. Der erste heißt partielle Integration und beruht darauf, die Produktregel für Ableitungen zu verwenden: Aus (f g)0 = f 0 g + f g 0 folgt Z f 0 (x)g(x)dx = f (x)g(x) − 28 Z f (x)g 0 (x)dx , bzw. für bestimmte Integrale Z b a b Z b a a f 0 (x)g(x)dx = f (x)g(x) − f (x)g 0 (x)dx . Das ist dann brauchbar, wenn das Integral auf der rechten Seite leichter zu berechnen ist, als das auf der linken. Beispiele: 1. Z 2. 3. xex dx = f 0 (x) = ex , g(x) = x = xex − Z Z ln(x)dx = f 0 (x) = 1, g(x) = ln x = x ln x − Z ex sin x dx = ex sin x − Z =⇒ Z ex dx = ex (x − 1) + c . x dx = x(ln x − 1) + c . x Z ex cos x dx = ex sin x − ex cos x − ex sin x dx = Z ex sin x dx ex (sin x − cos x) + c . 2 Der zweite Trick heißt Substitution und beruht auf der Kettenregel, aus der offensichtlich Z f 0 (g(x))g 0 (x)dx = f (g(x)) + c folgt. Beispiele: 1. 1 2 Z 1 sin(2x)(2x)0 dx = − cos(2x) + c , 2 x cos(x2 )dx = 1 2 Z Z sin(2x)dx = mit f (y) = − cos y, g(x) = 2x. 2. Z cos(x2 )(x2 )0 dx = 1 sin(x2 ) + c , 2 mit f (y) = sin y, g(x) = x2 . 3. sin2 x + c, 2 mit f (y) = y 2 /2, g(x) = sin x. Hier funktioniert allerdings auch g(x) = cos x mit dem Resultat Z Z cos2 x + c. sin x cos x dx = − cos x(cos x)0 dx = − 2 Besteht zwischen den beiden Resultaten ein Widerspruch? Z Z sin x cos x dx = sin x(sin x)0 dx = Satz 20 (Substitution für bestimmte Integrale) Sei f integrierbar über [a, b] und g : [c, d] → [a, b] stetig differenzierbar und invertierbar (d.h. streng monoton). Dann gilt y = g(x) f (y)dy = dy = g 0 (x)dx a Z b Z −1 g (b) f (g(x))g 0 (x)dx . = g −1 (a) 29 Dabei gilt g −1 (a) = c und g −1 (b) = d, wenn g streng monoton wachsend ist, und g −1 (a) = d und g −1 (b) = c, wenn g streng monoton fallend ist. Im zweiten Fall gilt die Konvention Z c f (g(x))g 0 (x)dx = − Z d f (g(x))g 0 (x)dx . c d Beispiele: 1. y = sin x sin x cos x dx = dy = cos x dx Z π/2 0 Z 1 y2 y dy = = 2 0 1 1 = . 2 0 2. y =3−x (3 − x) dx = dy = −dx 0 Z 3 2 Z 3 Z 0 y3 y 2 dy = y 2 dy = =− 3 0 3 Kontrolle: Z 3 2 (3 − x) dx = Z 3 0 2 (9 − 6x + x )dx = 0 3 = 9. 0 ! x3 3 9x − 3x + = 9. 3 0 2 3. Stammfunktion von 1/x für x < 0: Z dx x = −y = dx = −dy x Z dy = ln(y) + c = ln(−x) + c . = y Die Resultate für positive und negative x zusammengefasst: Z dx = ln |x| + c , x x 6= 0 . 4. Für x 6= 0: Z y = ex − 1 dx = ex − 1 dy = ex dx = (y + 1)dx Z dy . = y(y + 1) Um hier weiterzukommen, brauchen wir den dritten Trick, genannt Partialbruchzerlegung, der im Prinzip bei beliebigen rationalen Funktionen, d.h. Brüchen mit Polynomen in Zähler und Nenner, funktioniert. Im allgemeinen kann seine Anwendung sehr aufwendig sein, und wir zeigen ihn nur an diesem Beispiel. Der Integrand kann in einfachere Ausdrücke zerlegt werden: 1 1+y−y 1+y y 1 1 = = − = − . y(y + 1) y(y + 1) y(y + 1) y(y + 1) y y+1 Daher gilt Z und daher dy = y(y + 1) Z Z y 1 1 + c, − dy = ln |y| − ln |y + 1| + c = ln y y+1 y + 1 ex − 1 dx −x = ln ex + c = ln |1 − e | + c , ex − 1 30 x 6= 0 . Uneigentliche Integrale Die Berechnung von Integralen als Grenzwert von Riemannsummen beruht auf den Annahmen, dass der Integrand eine beschränkte Funktion ist und dass das Integrationsintervall beschränkt ist. Beide Annahmen kann man loswerden: Definition 8 1) Sei a ∈ IR und f für jedes b > a über [a, b] integrierbar. Dann heißt der Grenzwert Z ∞ Z b f (x)dx := lim b→∞ a a f (x)dx , wenn er existiert, ein uneigentliches Integral mit unbeschränktem Integrationsintervall. Analog für (−∞, a]. 2) Sei a < b ∈ IR und für jedes c ∈ (a, b) sei f integrierbar über [a, c]. Weiters sei limc→b |f (x)| = ∞. Dann heißt der Grenzwert Z b Z c f (x)dx := lim c→b a a f (x)dx , wenn er existiert, ein uneigentliches Integral mit unbeschränktem Integranden. Analog für Unbeschränktheit bei x = a. Bei Unbeschränktheit im Inneren des Integrationsintervalles muss dieses an der Unendlichkeitsstelle geteilt werden und die beiden Teilintegrale unabhängig berechnet werden. Beispiele: 1. Z ∞ dx 2 2. x3 Z b = lim b→∞ 2 Z 1 dx √ = lim x a→0 0 3. Sei 0 < a < 1. x−3 dx = lim b→∞ Z 1 1 b 1 1 = lim − 2x2 2 b→∞ 8 2b2 − Z 1 dx a = 1 . 8 √ 1 √ x−1/2 dx = lim 2 x = lim 2(1 − a) = 2 . a a→0 a x3/2 a→0 2 1 2 = − √ = √ − 2 . x a a Der Grenzwert für a → 0 existiert offensichtlich nicht und daher auch nicht das uneigentliche R Integral 01 x−3/2 dx. 4. Wenn man genügend Erfahrung hat (so wie wir nach diesen ersten Beispielen), kann man sich die Limes-Schreibweise oft ersparen: sin x = y √ dx = cos x dx = dy sin x Z π/2 cos x 0 5. Beim uneigentlichen Integral Z ∞ 0 x2 Z 1 dy √ 1 = √ = 2 y = 2. 0 y 0 dx √ + x gibt es Schwierigkeiten sowohl bei x = 0 als auch bei x = ∞. Eine Stammfunktion ist nicht so leicht zu finden. Trotzdem kann man versuchen festzustellen, ob das Integral konvergiert. √ Für x nahe bei Null kann man wohl x2 im Vergleich zu x vernachlässigen. Der einfachere 31 √ Integrand 1/ x kann aber von x = 0 weg integriert werden, wie die vorigen Beispiele zeigen. √ Für große x dominiert x2 im Vergleich zu x. Die Stammfunktion −1/x von 1/x2 besitzt einen Limes für x → ∞. Deswegen kann man erwarten, dass das obige uneigentliche Integral existiert. Diese Argumentation kann zu einem Beweis verschärft werden. Übungsaufgaben 7.1. Man berechne Z 1 a) 3 2 (x + 8x − 1)dx , b) −1 Z 4 4x + 5 1 x dx . 7.2. Man berechne mittels partieller Integration Z a) Z cos2 (x)dx , x2 sin(x)dx . b) 7.3. Man berechne folgendes Integral mittels Partialbruchzerlegung: Z dx . x2 − 3x + 2 Hinweis: Man bestimme A und B so, dass x2 1 1 A B = = + . − 3x + 2 (x − 1)(x − 2) x−1 x−2 7.4. Man berechne mit Hilfe der Substitutionsmethode Z 2 a) p 3 (4x + 2) 2x2 + 2x − 1dx , 1 du (Hinweis: ln x = −u). 1 + eu Z b) 1 7.5. Man finde die Stammfunktionen: Z a) e 3x+4 Z dx , b) x(ln(x))2 dx . 7.6. Man berechne die Fläche zwischen dem Graphen der Funktion f (x) = x2 −2x und der x-Achse zwischen den Nullstellen. 7.7 Man berechne Z ∞ 1 x2 dx − 2x + 2 (Hinweis: x − 1 = y) . 32 8 Kleinste Fehlerquadrate Ein bisschen Wahrscheinlichkeitsrechnung Ein Nachweis von naturwissenschaftlichen Hypothesen besteht meist darin, dass diese oft genug in einem wiederholbaren Experiment beobachtet werden. Abgesehen von der Frage, was ’oft genug’ bedeutet, ist eines der praktischen Hauptprobleme die exakte Wiederholbarkeit, die (oft aus prinzipiellen Gründen) normalerweise nicht möglich ist. Insbesondere treten Abweichungen bei quantitativen Hypothesen immer aufgrund von Messfehlern auf. Könnte man die Abweichungen exakt vorhersagen, dann könnte man sie auch eliminieren. Trotzdem lassen sich bei oft mit denselben Geräten durchgeführten Experimenten systematische Beobachtungen über die Abweichungen machen. Das einfachste, wohl allen bekannte Beispiel ist der Wurf einer Münze. Ist sie fair, d.h. symmetrisch bezüglich der Kopf- und der Zahlseite, dann ist es zwar einerseits unmöglich, den Ausgang eines einzelnen Münzwurfes vorherzusagen, andererseits wird aber nach vielen Würfen ungefähr die Hälfte ’Kopf’ und die andere Hälfte ’Zahl’ ergeben. Eine idealisierte Annahme, die diese Beobachtung beschreibt, ist das Gesetz der großen Zahlen lim n→∞ kn 1 = , n 2 wobei kn die Anzahl der Ausgänge ’Kopf’ nach n Münzwürfen bezeichnet. Dabei ist es wichtig festzuhalten, dass kn keinen festen Wert hat, sondern dass bei jedem Experiment, das aus n Münzwürfen besteht, der Wert anders sein kann. Sicher ist nur kn ∈ {0, . . . , n}. Daher ist die obige Grenzwertaussage auch mit gewisser mathematischer Vorsicht zu genießen. Ein Grundprinzip der Wahrscheinlichkeitsrechnung besteht nun darin, die obige Beobachtung als Aussage über den Ausgang eines einzelnen Münzwurfes zu formulieren: Bei einem Münzwurf ist die Wahrscheinlichkeit von ’Kopf ’ gleich 1/2. Definition 9 Ein Wahrscheinlichkeitsraum besteht aus einer Menge M (von Elementarereignissen) und einer Funktion W , die jeder Teilmenge A von M (jedem Ereignis) ihre (seine) Wahrscheinlichkeit W (A) ∈ [0, 1] zuordnet. Dabei muss die Wahrscheinlichkeit 2 Eigenschaften haben. Zum einen muss W (M ) = 1 gelten (’irgendetwas passiert sicher’), zum anderen W (A ∪ B) = W (A) + W (B), wenn A ∩ B = { }. Beispiele: 1) Den Münzwurf kann man als Wahrscheinlichkeitsraum beschreiben durch M = {k, z} mit W ({k}) = W ({z}) = 1/2. Das ist ein Beispiel für einen endlichen Wahrscheinlichkeitsraum, d.h. dass M eine Menge mit endlich vielen Elementen ist. Ein solcher kann immer durch Angabe der Wahrscheinlichkeiten der Elementarereignisse bestimmt werden. 2) Der Wurf eines fairen Würfels kann beschrieben werden durch M = {1, 2, 3, 4, 5, 6} und W ({j}) = 1/6, j = 1, . . . , 6. Die Wahrscheinlichkeit, eine gerade Zahl zu würfeln, ist dann W ({2, 4, 6}) = W ({2}) + W ({4}) + W ({6}) = 1 1 1 1 + + = . 6 6 6 2 3) Ein einfaches Beispiel für einen unendlichen Wahrscheinlichkeitsraum ist die Gleichverteilung auf einem Intervall M = [a, b], definiert durch W ([c, d]) = d−c = b−a Z d c dt , b−a 33 für a ≤ c ≤ d ≤ b . 4) Eines der wichtigsten Beispiele ist die Gaußverteilung (mit Mittel 0 und Varianz 1, was weiter unten erklärt wird) mit M = IR und 1 W ([c, d]) = √ 2π Z d 2 /2 e−t dt . c 2 Die Funktion f (t) = (2π)−1/2 e−t /2 (Gaußsche Glockenkurve) nennt man die Dichtefunktion. Die Konstante (2π)−1/2 ist so gewählt, dass Z ∞ f (t)dt = 1 W (IR) = −∞ gilt (was nicht so leicht nachzurechnen ist). Vergleich mit dem letzten Beispiel zeigt, dass die Dichtefunktion für die Gleichverteilung durch die konstante Funktion f (t) = (b − a)−1 gegeben ist (wobei sich der konstante Wert wieder aus der Forderung W (M ) = 1 ergibt). Während bei der Gleichverteilung die Wahrscheinlichkeit eines Intervalles nur von seiner Länge abhängt, ist bei der Gaußverteilung ein Intervall wahrscheinlicher als ein gleichlanges, dessen Mittelpunkt weiter von t = 0 entfernt liegt. Angenommen, ich spiele ein Würfelspiel mit folgenden Regeln: Für einmal Würfeln muss ich 1 Euro bezahlen. Würfle ich 5, dann bekomme ich 2 Euro Gewinn ausgezahlt, würfle ich 6, sind es 5 Euro Gewinn. Bei 1–4 Augen gibt es keinen Gewinn. Es stellt sich die Frage, was passiert, wenn ich dieses Spiel oft spiele. Werde ich eher verlieren oder gewinnen, und wieviel? Wenn der Würfel fair ist, kann ich den Wahrscheinlichkeitsraum aus obigem Beispiel 2) verwenden. Außerdem definieren wir die Nettogewinnfunktion x : {1, 2, 3, 4, 5, 6} → IR durch x(1) = x(2) = x(3) = x(4) = −1, x(5) = −1 + 2 = 1, x(6) = −1 + 5 = 4. Definition 10 Sei (M, W ) ein Wahrscheinlichkeitsraum. Dann nennt man eine Funktion x : M → IR eine Zufallsvariable. Spiele ich das Spiel n-mal mit einem großen n, dann erwarte ich, dass ich jede Augenzahl ungefähr n6 -mal würfle. Ich erwarte also den Nettogewinn 6 X n n n n n 1 n n (−1) + (−1) + (−1) + (−1) + + 4 = n x(j) = , 6 6 6 6 6 6 6 6 j=1 was man so interpretieren kann, dass ich pro Spiel im Durchschnitt 1 6 Euro gewinne. Definition 11 1) Sei (M, W ) ein endlicher Wahrscheinlichkeitsraum (mit M = {m1 , . . . , mk }) und x eine Zufallsvariable. Dann ist der Erwartungswert (oder Mittelwert) von x definiert durch E(x) := k X x(mj )W ({mj }) . j=1 2) Sei M = [a, b] mit −∞ ≤ a < b ≤ ∞, W ([c, d]) = cd f (t)dt (mit der Dichte f (t) ≥ 0, a f (t)dt = 1) und x eine Zufallsvariable. Dann ist der Erwartungswert von x definiert durch R Rb Z b E(x) := x(t)f (t)dt . a 34 Beispiel: Fährt die U-Bahn mit einem Intervall von T = 4 Minuten und ich komme zu einem zufälligen Zeitpunkt an der Haltestelle an, wie lange muss ich dann im Durchschnitt auf den nächsten Zug warten? Modellieren wir meinen Ankunftszeitpunkt als gleichverteilt im Zeitintervall [0, T ] zwischen zwei Zugsabfahrten (d.h. f (t) = 1/T ), dann ist meine Wartezeit gegeben durch x(t) = T − t. Der Erwartungswert ist also Z T 0 1 1 (T − t) dt = T T !T t2 Tt − 2 0 1 = T T2 T − 2 2 ! = T . 2 Die erwartete Wartezeit von 2 Minuten ist nicht sehr überraschend (aber beruhigend, dass es stimmt). Kehren wir zum Würfelspiel zurück, dann wäre eine alternative Variante, einen festen Nettogewinn von 16 Euro unabhängig von der gewürfelten Augenzahl festzulegen. Das ergibt natürlich auch den Erwartungswert 16 Euro für den Nettogewinn, also denselben wie im ursprünglichen Spiel. Trotzdem gibt es zwischen den beiden Spielen natürlich wesentliche Unterschiede, was das involvierte Risiko anlangt. Dieses Risiko kann bewertet werden, indem man fragt, wie weit der Nettogewinn durchschnittlich vom Erwartungswert entfernt ist. Definition 12 Sei x eine Zufallsvariable. Dann ist die Varianz von x definiert durch V (x) = E([x − E(x)]2 ) . Sie gibt die durchschnittliche pquadratische Abweichung vom Erwartungswert an. Die Standardabweichung ist gegeben durch V (x). In unserem Würfelspiel ergibt sich die Varianz −1 − 1 6 2 4 1 + 1− 6 6 2 1 1 + 4− 6 6 2 1 ≈ 3, 47 . 6 Die Standardabweichung ≈ 1, 86 Euro ist also recht hoch im Vergleich zum erwarteten Gewinn. Die Spielvariante mit fixem Gewinn hat natürlich die Varianz Null. Noch einmal zur Gaußverteilung mit Mittel Null und Varianz Eins. Das sagt man, weil E(t) = Z ∞ −t2 /2 e t √ −∞ 2π dt = 0 , (da der Integrand eine ungerade Funktion ist,) und −t2 /2 2 e−t /2 V (t) = E(t ) = t √ dt = − t √ 2π 2π −∞ −∞ 2 Z ∞ 2e Z ∞ !0 dt = Z ∞ −t2 /2 e √ −∞ 2π dt = 1 , was aus partieller Integration folgt. Schätzung von Erwartungswert und Varianz: Oft kennt man die Wahrscheinlichkeitsverteilung nicht und ist nur mit einer Anzahl von Werten x1 , . . . , xn einer Zufallsvariablen x konfrontiert. Aus dem Gesetz der großen Zahlen ergibt sich, dass die Mittelwerte En = x = n 1X xj n j=1 und Vn = (x − x)2 = n 1X (xj − En )2 n j=1 brauchbare (und bei großem n sogar gute) Schätzwerte für E(x) und V (x) sind. 35 Bestimmung der Monomerzahl in einem Aktinfilament: Aus dem Protein Aktin aufgebaute Polymerfilamente bilden einen wesentlichen Bestandteil des Zytoskeletts. Jedes Monomer trägt d = 2,7nm zur Länge eines Filamentes bei. Angenommen, mit Hilfe eines Elektronenmikroskops könnte die Gesamtlänge eines Filamentes bestimmt werden, wobei ein maximaler Messfehler von 2d zu erwarten ist. Die gemessene Länge wird auf ganzzahlige Vielfache von d gerundet, um die Anzahl der Monomere im Filament zu bestimmen. Wie verlässlich sind die Resultate? Zunächst brauchen wir ein Wahrscheinlichkeitsmodell (auch stochastisches Modell genannt) für den Messfehler. Wenn wir annehmen, dass kleinere Fehler wahrscheinlicher sind als größere, dann käme z.B. das Modell 2d − |t| M = [−2d, 2d] , f (t) = , 4d2 in Frage. Liegt der Fehler in [−d/2, d/2], dann wird nach Rundung die korrekte Monomerzahl bestimmt. Liegt er in [d/2, 3d/2], dann ist die gemessene Anzahl um 1 zu groß. Liegt der Messfehler in [3d/2, 2d], dann ist sie um 2 zu groß. Analoges gilt für negative Messfehler. Die Wahrscheinlichkeit, die korrekte Monomerzahl zu bestimmen, beträgt also Z d/2 f (t)dt = W ([−d/2, d/2]) = −d/2 Z d/2 2 4d2 (2d − t)dt = 0 7 . 16 Um 1 zu groß (bzw. zu klein) wird die Anzahl mit der Wahrscheinlichkeit Z 3d/2 W ([d/2, 3d/2]) = d/2 1 f (t)dt = 2 4d Z 3d/2 (2d − t)dt = d/2 1 4 bestimmt. Um 2 zu groß (bzw. zu klein) wird die Anzahl mit der Wahrscheinlichkeit Z 2d f (t)dt = W ([3d/2, 2d]) = 3d/2 1 4d2 Z 2d (2d − t)dt = 3d/2 1 32 sein. Sieht man den Fehler in der ermittelten Monomerzahl als Zufallsvariable, dann hat diese den Erwartungswert 7 1 1 1 1 0 + 1 + (−1) + 2 + (−2) = 0 , 16 4 4 32 32 was man bei Messfehlern üblicherweise annimmt, weil man es durch geeignete Kalibrierung des Messgerätes normalerweise erreichen kann. Interessanter ist die Varianz 7 1 1 1 1 5 0+ 1+ 1+ 4+ 4= , 16 4 4 32 32 8 die eine (in diesem Fall sehr brauchbare) Standardabweichung von p 5/8 ≈ 0, 8 ergibt. Lineare Regression Angenommen, bei einem Experiment kann die Größe x eingestellt und dann die Größe y gemessen werden. So werden n Messpunkte (x1 , y1 ), . . . , (xn , yn ) bestimmt. Nimmt man weiter an, dass theoretische Überlegungen einen linearen Zusammenhang der Form y = a + bx 36 nahelegen, dann stellt sich die Frage, wie man aus den Messdaten geeignete Schätzwerte für die Parameter a und b bestimmt, wenn man mehr als zwei Messpunkte hat, d.h. n > 2. In diesem Fall ist obiger Zusammenhang für alle Messpunkte im Allgemeinen nicht exakt zu erreichen. Als Grund dafür kann man nicht beeinflussbare Schwankungen im Aufbau des Experimentes oder auch Messfehler bei der Bestimmung von y sehen. Das führt auf das modifizierte stochastische Modell y = a + bx + ε , in dem ε als Zufallsvariable interpretiert wird, die die Systemschwankungen bei verschiedenen Experimenten und/oder die Messfehler beschreibt. Die Bestimmung geeigneter Werte für a und b orientiert sich an der Idee, die beobachteten Schwankungen εi := yi − (a + bxi ), i = 1, . . . , n, möglichst klein zu machen. Die gängigste Methode, die Methode der kleinsten Fehlerquadrate, besteht darin, dass die Summe der Quadrate der Schwankungen, F (a, b) = n X (yi − (a + bxi ))2 , i=1 minimiert wird. Wie findet man nun die optimalen Werte a und b? Angenommen, man würde b schon kennen, dann würde man Kandidaten für ein Minimum von F als Funktion von a finden, indem man die Ableitung nach a gleich Null setzt. Ebenso für b bei bekanntem a. Die Ableitungen nach a bei festem b und umgekehrt nennt man partielle Ableitungen von F und bezeichnet sie mit ∂F ∂F ∂a und ∂b . Notwendige Bedingungen dafür, dass F an der Stelle (a, b) minimal wird, sind n X ∂F (a, b) = −2 (yi − (a + bxi )) = 0 , ∂a i=1 n X ∂F (a, b) = −2 [(yi − (a + bxi ))xi ] = 0 . ∂b i=1 Dividiert man die beiden Gleichungen durch −2n, dann nehmen sie die Form a + bx = y , ax + bx2 = xy an. Ausrechnen von a aus der ersten Gleichung und Einsetzen in die zweite ergibt x2 − (x)2 b = xy − x y (10) Die Nebenrechnung n n 1X 1X (xi − x)2 = x2i − 2xi x + (x)2 = x2 − 2(x)2 + (x)2 = x2 − (x)2 n i=1 n i=1 zeigt, dass der Koeffizient von b in (10) nur dann Null sein kann, wenn alle xi gleich sind, was bedeuten würde, dass alle Datenpunkte auf einer vertikalen Gerade liegen, die natürlich nicht in der Form y = a + bx geschrieben werden kann. Schließen wir diesen Sonderfall aus, dann sind a und b eindeutig bestimmt: b= xy − x y , x2 − (x)2 a = y − bx . 37 Aus einer weiteren Nebenrechnung ähnlich der obigen ergibt sich die alternative Darstellung Pn b= i=1 (xi − x)(yi − Pn 2 i=1 (xi − x) y) Diese Werte für a und b liefern tatsächlich den minimalen Wert von F (um das zu zeigen würden wir mehr Wissen über Funktionen in mehreren Variablen brauchen, was über den Stoff dieser Vorlesung hinausgeht). In Abhängigkeit der Schwankungen ε1 , . . . , εn kann man die Resultate auch so interpretieren, dass a und b so gewählt sind, dass der geschätzte Erwartungswert der Schwankung verschwindet, d.h. ε = 0, und dass die geschätzte Varianz F = (ε − ε)2 minimal wird. Beispiel: Haben wir folgende Werte: i x i yi 1 1 2 2 2 3 3 3 4.5 F (a, b) = (2 − (a + b))2 + (3 − (a + 2b))2 + (4.5 − (a + 3b))2 Die notwendigen Bedingungen für das Extremum: 9 ∂ F (a, b) = (−2)[(2 − a − b)) + (3 − a − 2b)) + ( − a − 3b))] = 0 ∂a 2 ∂ 9 F (a, b) = (−2)[(2 − a − b)) + 2(3 − a − 2b)) + 3( − a − 3b))] = 0 ∂b 2 Die zwei Gleichungen: 19 − 3a − 6b = 0 2 43 − 6a − 14b = 0 2 liefern die Lösung a = 23 und b = 45 für die Ausgleichsgerade y = 23 + 54 x. Wir können a und b auch direkt ausrechnen. Zuerst berechnen wir die arithmetischen Mittel x = 1+2+3 = 2 und y = 2+3+4.5 = 19 3 3 6 , also haben wir für b und a: b = a = − 2) + (3 − 19 6 )(2 − 2) + (4.5 − 2 (−1) + 02 + 12 2 19 5 − ·2= 6 4 3 (2 − 19 6 )(1 19 6 )(3 − 2) = 5 4 Nichtlineare Ansätze Quadratisches Polynom: Grades voraus, d.h. Sagt unsere Theorie einen Zusammenhang durch ein Polynom zweiten y = a + bx + cx2 , 38 dann versuchen wir die drei Parameter a, b und c so zu ermitteln, dass die mittlere quadratische Abweichung minimal wird. Wir führen wiederum die Funktion F ein: F (a, b, c) = n X (yi − (a + bxi + cx2i ))2 i=1 Die notwendigen Bedingungen für ein Extremum sind: n X ∂ F (a, b, c) = (−2) (yi − (a + bxi + cx2i )) = 0 ∂a i=1 n X ∂ F (a, b, c) = (−2) [(yi − (a + bxi ) + cx2i )xi ] = 0 ∂b i=1 n X ∂ F (a, b, c) = (−2) [(yi − (a + bxi + cx2i ))x2i ] = 0 ∂c i=1 Exponentialfunktion: Ist die Modellvorhersage y = Aebx , dann ist jetzt das Problem, dass der unbekannte Parameter b nichtlinear eingeht. Wir führen statt y die Größe u = ln y ein, die linear von x abhängt: u = ln A + bx . Mit a = ln A ist es nun plausibel, die Ausgleichsgerade für (xi , ui ) zu bestimmen. Beispiel: i xi yi ui = ln yi 1 1 1 0 2 2 0.5 − ln 2 3 3 0.2 − ln 5 4 4 0.05 − ln 20 Die Funktion F ist dann F (a, b) = [−(a + b)]2 + [− ln 2 − (a + 2b)]2 + [− ln 5 − (a + 3b)]2 + [− ln 20 − (a + 4b)]2 . Die Bedingungen für einen Extrempunkt sind: ∂ F (a, b) = (2)[(a + b) + ln 2 + (a + 2b) + ln 5 + (a + 3b) + ln 20 + (a + 4b)] = 0 ∂a ∂ F (a, b) = (2)[(a + b) + (ln 2 + (a + 2b))2 + (ln 5 + (a + 3b))3 + (ln 20 + (a + 4b))4] = 0 ∂b d.h. 4a + 10b + ln 200 = 0 10a + 30b + ln(8 · 107 ) = 0 √ √ 1 a = ln( 10), also A = 10 ≈ 3.16 und b = − 10 ln(20000) ≈ −0.99 39 Übungsaufgaben 8.1. Man bestimme die Ausgleichsgerade für die Punkte (1, 6), (2, 7), (3, 9), (4, 10). 8.2. Zu den Zeitpunkten t1 = 1, t2 = 2 und t3 = 3 werden die Konzentrationen c1 = 1, 5, c2 = 2, 1 bzw. c3 = 3, 7 (ohne Einheit) gemessen. Eine Theorie sagt den zeitlichen Konzentrationsverlauf c(t) = aebt voraus. Man schätze a und b mit der Methode der kleinsten Fehlerquadrate sowie die Konzentration zum Zeitpunkt t = 9. 9 Differentialgleichungen – Reaktionskinetik Mathematische Modelle chemischer Reaktionen: Setzen wir einen gut gemischten chemischen Reaktor voraus, d.h. ein Gefäß, in dem die chemischen Substanzen X1 , . . . , Xn gleichmäßig verteilt sind mit den Konzentrationen c1 (t), . . . , cn (t) zum Zeitpunkt t. Die zeitliche Veränderung wird bewirkt durch m chemische Reaktionen mit den Reaktionsraten r1 (t), . . . , rm (t) und den stöchiometrischen Koeffizienten νij ∈ ZZ, i = 1, . . . , n, j = 1, . . . , m. Die Reaktionsraten geben an, wie oft die Reaktionen pro Zeiteinheit stattfinden. Die stöchiometrischen Koeffizienten haben folgende Bedeutung: Ist νij > 0, dann werden bei jedem Stattfinden der j-ten Reaktion νij Moleküle der Substanz Xi erzeugt. Ist νij < 0, dann werden bei jedem Stattfinden der j-ten Reaktion −νij Moleküle der Substanz Xi verbraucht. Ist νij = 0, dann ist die Substanz Xi an der j-ten Reaktion unbeteiligt. Das rechteckige Schema ν11 · · · ν1m .. .. N = . . νn1 · · · νnm nennt man die stöchiometrische Matrix. Für die zeitliche Veränderung der Konzentrationen müssen die Differentialgleichungen m X dci = νij rj , i = 1, . . . , n, dt j=1 gelten. Das einfachste Modell für die Reaktionsraten (für einfache Reaktionen) ergibt sich aus dem Massenwirkungsgesetz: Y −νij rj = kj ci , j = 1, . . . , m , i: νij <0 mit den Reaktionskonstanten kj > 0. Das Produkt enthält für jedes Molekül der Substanz Xi , das bei der Reaktion verbraucht wird, einen Faktor ci . Die Gesamtzahl der bei einer Reaktion verbrauchten Moleküle nennt man die Ordnung der Reaktion. Nennt man den Zeitpunkt des Beginns eines Experimentes t = 0 und die Konzentrationen zu diesem Zeitpunkt c10 , . . . , cn0 , dann gelten die Anfangsbedingungen ci (0) = ci0 , i = 1, . . . , n . 40 Ein Beispiel – qualitative Analyse: Als Beispiel betrachten wir eine Reaktion X1 + X2 → X3 und ihre Umkehrreaktion. Die stöchiometrische Matrix ist −1 1 N = −1 1 . 1 −1 Die Vorwärtsreaktion hat daher die Rate r+ = k+ c1 c2 (und ist daher zweiter Ordnung) und die Umkehrreaktion r− = k− c3 (erster Ordnung), woraus die Differentialgleichungen dc1 = k− c3 − k+ c1 c2 , dt dc2 = k− c3 − k+ c1 c2 , dt dc3 = k+ c1 c2 − k− c3 , dt folgen. Die Anfangsbedingungen sind c1 (0) = c10 , c2 (0) = c20 , c3 (0) = c30 , mit gegebenen Anfangskonzentrationen ci0 ≥ 0. Solche Systeme nichtlinearer Differentialgleichungen kann man im Allgemeinen nicht explizit lösen. Obwohl es in diesem Fall möglich wäre, werden wir es nicht tun, sondern uns auf andere Art Informationen über die Lösung beschaffen. Zunächst gilt offensichtlich dc1 dc3 dc1 dc2 − = 0 und + = 0, dt dt dt dt was auf die angesichts der Reaktionsgleichung wenig überraschenden Aussagen führt, dass sich die Differenz der Konzentrationen von X1 und X2 mit der Zeit nicht ändert, genauso wie die Summe der Konzentrationen von X1 und X3 . Das liefert c2 (t) = c1 (t) − c10 + c20 , c3 (t) = −c1 (t) + c10 + c30 . Einsetzen in die Differentialgleichung für c1 liefert dc1 = f (c1 ) , dt mit f (c1 ) = k− (c10 + c30 ) − c1 (k− + k+ c20 − k+ c10 ) − k+ c21 . Wir konnten also ein System von drei Differentialgleichungen durch eine einzelne Gleichung ersetzen, was eine wesentliche Vereinfachung darstellt. Ein einfache Kurvendiskussion zeigt, dass f genau eine positive Nullstelle c1 besitzt (die man natürlich als Lösung einer quadratischen Gleichung auch explizit berechnen kann). Offensichtlich wäre die Konstante c1 (t) = c1 die Lösung unseres Problems, wenn c10 = c1 gälte, was wir im Allgemeinen nicht erwarten können. Man nennt c1 einen stationären Punkt der Differentialgleichung. Es gilt f (c1 ) > 0 für 0 ≤ c1 < c1 und f (c1 ) < 0 für c1 > c1 . Daher wird c1 (t) mit der Zeit größer, solange es kleiner als c1 ist und umgekehrt. Es ist daher zu erwarten, dass lim c1 (t) = c1 t→∞ gilt. Man nennt den stationären Punkt c1 asymptotisch stabil. Natürlich folgt daraus, dass auch c2 (t) und c3 (t) für t → ∞ konvergieren und sich daher der ganze Reaktor mit der Zeit einem Gleichgewichtszustand nähert, in dem k+ c1 c2 = k− c3 gilt. 41 Einfacher Zerfall: In der einfachsten Situation mit n = m = 1 gibt es nur eine Spezies mit Konzentration c(t) und eine Zerfallsreaktion erster Ordnung mit Reaktionsrate kc mit der Reaktionskonstanten k > 0. Für die Konzentration ergibt sich dann das Anfangswertproblem dc = −kc , dt c(0) = c0 , das explizit gelöst werden kann. Die Idee ist, die Differentialgleichung durch c zu dividieren, dc/dt(t) = −k , c(t) und festzustellen, dass das geschrieben werden kann als d (ln(c(t)) + kt) = 0 . dt Der Ausdruck in der Klammer ist daher konstant und damit gleich seinem Wert an der Stelle t = 0: ln(c(t)) + kt = ln(c0 ) . Aus dieser Gleichung kann man c(t) berechnen: c(t) = e−kt c0 . Klarerweise nimmt die Konzentration ab (und zwar exponentiell). Herleitung einer Reaktion nullter Ordnung (Skalierung, Störungsrechnung): Eine kleine Erweiterung des letzten Beispiels besteht darin, die Reaktion X1 → X2 und ihre Umkehrung zu betrachten. Das ergibt das Anfangswertproblem dc1 = k− c2 − k+ c1 , dt dc2 = k+ c1 − k− c2 , dt c1 (0) = c10 , c2 (0) = c20 . Angenommen, die Reaktionskonstante der Umkehrreaktion ist viel kleiner als die der Vorwährtsreaktion, als Formel: k− k+ . Die beiden Reaktionsraten können nur dann von gleicher Größenordnung sein, wenn c1 viel kleiner als c2 ist, was wir für die Anfangskonzentrationen annehmen: c10 c20 . Um herauszufinden, wie sich diese Annahmen auf die Dynamik auswirken, führen wir eine Skalierung durch. Das bedeutet, dass wir für alle auftretenden Größen Einheiten wählen, und zwar so, dass die Maßzahlen möglichst von moderater Größe sind. Das kann man üblicherweise erreichen, indem man als Einheiten sogennante intrinsische Referenzgrößen verwendet, die aus den Parametern des Problems gebildet werden. In unserem Problem brauchen wir Einheiten für die Konzentrationen und für die Zeit. Für die Konzentrationen bieten sich ihre Anfangswerte an. Für die Zeit könnten wir entweder 1/k+ oder 1/k− verwenden und entscheiden uns für den kleineren Wert 1/k+ . Die dimensionslosen Maßzahlen von c1 , c2 und t nennen wir u1 , u2 bzw. τ . Genauer bedeutet das die Transformationen u1 (τ ) = c1 (τ /k+ ) , c10 u2 (τ ) = 42 c2 (τ /k+ ) c20 Das ergibt die Differentialgleichungen u01 (τ ) = u02 (τ ) = k− c20 u2 (τ ) − k+ c10 u1 (τ ) k− c20 c01 (τ /k+ ) = = u2 (τ ) − u1 (τ ) , c10 k+ c10 k+ k+ c10 c10 k− c20 u1 (τ ) − u2 (τ ) . c20 k+ c10 Entsprechend unserer obigen Annahmen schreiben wir k− = ε, k+ c10 = εa , c20 wobei ε sehr klein und a von moderater Größe ist. Das gibt u01 = u2 − u1 , a u02 = ε(au1 − u2 ) , u1 (0) = u2 (0) = 1 . Eine Approximation ergibt sich mit ε → 0: u2 (τ ) = 1 für τ ≥ 0 und damit u01 = 1 − u1 , a u1 (0) = 1 . Die Rate der Umkehrreaktion wird also durch die Konstante 1/a approximiert. Man spricht daher von einer Reaktion nullter Ordnung. Die Substanz stellt also ein großes Hintergrundreservoir dar, das sich durch die Reaktionen nur unwesentlich ändert. Das Näherungsproblem für u1 kann explizit gelöst werden. Zunächst beobachten wir, dass die Differentialgleichung den stationären Punkt u1 = 1/a besitzt. Die Abweichung v(τ ) = u1 (τ ) − 1/a erfüllt das Anfangswertproblem v 0 = −v , v(0) = 1 − 1/a , das analog zu oben explizit gelöst werden kann: v(τ ) = e−τ (1 − 1/a). Daraus folgt u1 (τ ) = 1/a + e−τ (1 − 1/a) und daraus für die unskalierte Konzentration von X1 : k− c20 k− c20 + e−k+ t c10 − k+ k+ c1 (t) = . Für t → ∞ konvergiert c1 (t) also exponentiell gegen die stationäre Lösung. Michaelis-Menten-Kinetik: Wir betrachten eine von einem Enzym E gesteuerte Reaktion, bei der das Substrat S in das Produkt P umgewandelt wird. Das passiert durch zwei Teilreaktionen, wobei zuerst das Enzym mit dem Substrat den Komplex ES bildet, der dann in das Produkt und das unverändert aus dem Prozess hervorgehende Enzym zerfällt, also E + S → ES → P + E. Wir nehmen an, dass zu Beginn nur Enzym und Substrat vorhanden sind mit einer viel kleineren Enzymkonzentration. Das ergibt das Anfangswertproblem c0S = −k1 cE cS , c0E c0ES c0P cS (0) = cS0 , = k2 cES − k1 cE cS , cE (0) = cE0 , = k1 cE cS − k2 cES , cES (0) = 0 , = k2 cES , cP (0) = 0 . 43 Wieder führen wir eine Skalierung durch, wobei wir für cS und cP die Einheit cS0 verwenden, für cE und cES die Einheit cE0 , sowie die Zeiteinheit 1/(k1 cE0 ). Für die neuen Variablen uS , uP , uE und uES , die von τ = k1 cE0 t abhängen, ergibt sich das Problem u0S = −uE uS , ε u0E ε u0ES u0P uS (0) = 1 , = a uES − uE uS , uE (0) = 1 , = uE uS − a uES , uES (0) = 0 , = a uES , uP (0) = 0 , mit den dimensionslosen Parametern ε= cE0 , cS0 a= k2 . k1 cS0 Wie oben erwähnt, nehmen wir an, dass ε sehr klein ist. Außerdem nehmen wir an, dass die Raten der beiden Reaktionen von derselben Größenordnung sind, was bedeutet, dass a moderate Werte annimmt. Addieren der zweiten und der dritten Differentialgleichung ergibt die plausible Tatsache, dass die Summe der Konzentrationen von Enzym und Komplex konstant ist: uE (τ ) + uES (τ ) = 1 , wobei die Konstante auf der rechten Seite aus den Anfangsbedingungen folgt. Verwendet man das in der zweiten Differentialgleichung und führt den Grenzwert ε → 0 durch, dann ergibt sich 0 = a(1 − uE ) − uE uS , woraus uE berechnet werden kann: uE = a . a + uS Das führt dazu, dass wir nun eine direkte Reaktionsrate für S → P angeben können: u0P = −u0S = a uS a + uS In den ursprünglichen unskalierten Variablen ergibt sich c0P = −c0S = k1 k2 cE0 cS k2 + k1 cS Dieses Resultat wird Michaelis-Menten-Kinetik genannt. Man kann es als Interpolation zwischen einer Reaktion erster Ordnung (Rate ≈ k1 cE0 cS ) für sehr kleine Werte von cS und einer Reaktion nullter Ordnung (Rate ≈ k2 cE0 ) für sehr große Werte von cS ansehen. 44