Grundbildung Analysis

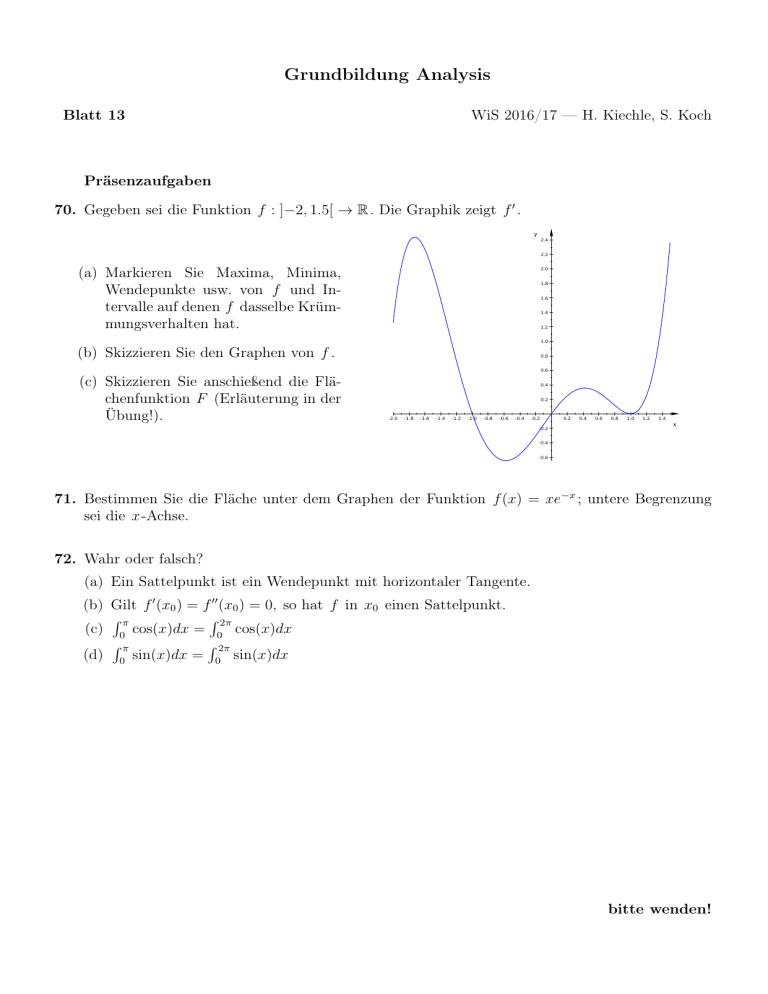
Grundbildung Analysis
Blatt 13
WiS 2016/17 — H. Kiechle, S. Koch
Präsenzaufgaben
70. Gegeben sei die Funktion f : ]−2, 1.5[ → R. Die Graphik zeigt f 0 .
y
2.4
2.2
2.0
(a) Markieren Sie Maxima, Minima,
Wendepunkte usw. von f und Intervalle auf denen f dasselbe Krümmungsverhalten hat.
1.8
1.6
1.4
1.2
1.0
(b) Skizzieren Sie den Graphen von f .
0.8
0.6
(c) Skizzieren Sie anschießend die Flächenfunktion F (Erläuterung in der
Übung!).
0.4
0.2
-2.0
-1.8
-1.6
-1.4
-1.2
-1.0
-0.8
-0.6
-0.4
-0.2
-0.2
0.2
0.4
0.6
0.8
1.0
1.2
1.4
x
-0.4
-0.6
71. Bestimmen Sie die Fläche unter dem Graphen der Funktion f (x) = xe−x ; untere Begrenzung
sei die x-Achse.
72. Wahr oder falsch?
(a) Ein Sattelpunkt ist ein Wendepunkt mit horizontaler Tangente.
(b) Gilt f 0 (x0 ) = f 00 (x0 ) = 0, so hat f in x0 einen Sattelpunkt.
Rπ
R 2π
(c) 0 cos(x)dx = 0 cos(x)dx
Rπ
R 2π
(d) 0 sin(x)dx = 0 sin(x)dx
bitte wenden!
Hausaufgaben (freiwillig, keine Abgabe)
73. Gedämpfter harmonischer Oszillator
Beim harmonischen Oszillator, wie er in der Vorlesung behandelt wurde, blieb die Reibung unberücksichtigt. Bei schwacher Reibung und kleinen Geschwindigkeiten, kann man die Reibungskraft
proportional zur Geschwindigkeit annehmen. Mit den Bezeichnungen aus der Vorlesung und der
Proportionalitätskonstante δ > 0 für die Reibungskraft ergibt sich die Differentialgleichung
ms00 (t) + δs0 (t) + ks(t) = 0
Verifizieren Sie, dass die Funktion
s(t) = e−αt (A1 sin(ωt) + A2 cos(ωt)) ,
im Fall
k
m
mit α =
δ
2m
und ω 2 =
k
− α2
m
> α2 („schwache Dämpfung“) für je zwei reelle Zahlen A1 , A2 eine Lösung ist.
74. Bestimmen Sie mit partieller Integration
R
(a) x sin x dx
R
(b) ln x dx
Tipp: ln x = 1 · ln x
R x
(c) e cos x dx
75. Bestimmen Sie durch eine geeignete Substitution
R
(a) x sin(x2 ) dx
R
(b) tan x dx
R2
2
(c) 0 xe−x dx