funktion(seminar

Unterrichtsplanung
Funktionen
für die 5. Klasse der AHS-Oberstufe
Yu Hui
01/2013
Yu Hui / 15.05.2016
75882528
1
Inhalt
Lernbezüge
1, Reelle Funktion
1,1 Der Begriff der
Reellen Funktion
1,2 Zeichnen und
Interpretieren von
Funktionsgraphen?
Yu Hui / 15.05.2016
UE
• Begriff der reellen Funktion:
Eindeutigkeit, Abhängigkeit
• Wichtige Eigenschaften einer Funktion:
G=
Definitionsmenge Df
(Argument) und Funktionswert Wf
• Darstellung der Funktion:
Funktionstabelle, Funktionsgraphen,
Funktionsgleichung.
• Interpretieren von Funktionsgraphen
Ablesen der Eigenschaften der Funktionen
75882528
2
4
2, Lineare Funktion
• Begriff der homogenen linearen Funktion
und der direkten Proportionalitäts (f(x)= kx,
2,1 Die homogene
mit k≠0, k€ R)
lineare Funktion
• Begriff der inhomogenen linearen Funktion
(f(x)= kx+ d mit k, d € R)
2,2 Direkte
• Grafische Darstellung als Gerade (Monotonie:
Proportionalität
steigend oder fallend)
• Wichtige Eigenschaften der linearen
2,3 Die inhomogene
Funktion (Steigung der Gerade k, Nullstelle,
lineare Funktion
y-Achsenabschnitt d, Steigungsdreieck,
Steigungswinkel)
2,4 Rekursive
Darstellung der linearen • Die parallele oder identische Gerade
• Anwendung linearer Funktionen (Zeit-WegFunktion
Funktionen, Kosten-und Gebührenfunktionen,
2,5 Anwendung linearer rekursive Darstellung mit der
Rekursionsgleichung)
Funktionen
Yu Hui / 15.05.2016
75882528
3
8
3, Einige nichtlineare
Funktionen
3,1 Indirekte
Proportionalität
3,2 Weitere nichtlineare
Funktionen
3,3 Veränderungen von
Funktionsgraphen
Yu Hui / 15.05.2016
• Begriffe der indirekten
Proportionalitätsfunktion (indirekte
Proportionalität) (f(x)=k/x mit k 0)
• Wichtige Eigenschaften der indirekten
Proportionalitätsfunktion (drei Sätze, grafische
Darstellung als Hyperbel)
• Wichtige Typen der nichtlinearen Funktionen
(z.B, a/x. a/x², abschnittweise definierte
Funktion, Sprungfunktion)
• Die Auswirkung der Veränderung des
Funktionsterms auf den Graphen der Funktion
(die Verschiebung einer Parabel durch eine
Streckung oder eine Stauchung)
75882528
4
4
4, Quadratische
Funktion
Yu Hui / 15.05.2016
• Begriff der quadratischen Funktion
(f(x)=ax²+ bx+ c mit a 0 )
• Wichtige Eigenschaften der quadratischen
Funktion
• Grafische Darstellung als Parabel
(Normalparabel und Verschobene Parabel,
die Orientierung nach oben oder nach unten,
schmaler oder steiler, Nullstelle,
Scheitelpunkt)
• Die quadratische Funktionsgleichung
(Hauptform, Scheitelpunktform)
75882528
5
5
Lehrplan
 Beschreiben von Abhängigkeiten der Funktionen, die durch reelle Funktionen in
einer Variablen erfassbar sind (mittels Termen, Tabellen und Graphen).
 Reflektion über den Modellcharakter von Funktionen.
 Arbeiten mit Funktionen in anwendungsorientierten Bereichen.
 Beschreiben und Untersuchen von linearen (f(x)= k x+ d) und einfachen
nichtlinearen Funktionen (z.B.: a/x, a/x², ax²+bx+c, abschnittweise definierte
Funktionen).
 Untersuchen von Formeln im Hinblick auf funktionale Aspekte, Beschreiben von
direkten und indirekten Proportionalitäten mit Hilfe von Funktionen.
Yu Hui / 15.05.2016
75882528
6
Mathematische Grundkompetenzen
 Für gegebene Zusammenhänge entscheiden können, ob man sie als Funktionen
betrachten kann.
 Formeln als Darstellung von Funktionen interpretieren und den Funktionstyp
zuordnen können.
 Zwischen tabellarischen und grafischen Darstellungen funktionaler Zusammenhänge wechseln können.
 Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln
und im Kontext deuten können.
 Eigenschaften von Funktionen erkennen, benennen, im Kontext deuten und zum
Erstellen von Funktionsgraphen einsetzen können: Monotonie,
Monotoniewechsel (lokale Extrema), Achsensymmetrie, asymptotisches
Verhalten, Schnittpunkte mit den Achsen.
 Funktionen als mathematische Modelle verstehen um damit verständig arbeiten
zu können.
 Durch Gleichungen (Formeln) gegebene Funktionen mit mehreren
Veränderlichen im Kontext deuten können, Funktionswerte ermitteln können.
Yu Hui / 15.05.2016
75882528
7
Didaktische Überlegungen
 Der Unterricht sollte zum Leistungsniveau und Alter der Schüler passen. Die
Präsentation sollte für die Schüler anschaulich und deutlich sein.
 Die Arbeitsblätter sollten übersichtlich aufgebaut, klar formuliert und die
Abbildungen müssen zur besseren Anschaulichkeit farbig dargestellt werden. Die
Inhalte der Rechenaufgaben sollten dem Erfahrungsbereich der Schüler
entsprechen.
 Der Schwerpunkt besteht nicht darin, Zusammenhänge selbst herzustellen und
mathematische Beweise zu führen, sondern er liegt darin, mathematische
Zusammenhänge und Sachverhalte zu erkennen und nachzuvollziehen. Das
Lernziel beinhaltet die Einübung von mathematischen Formeln und ihrer
sicheren und sinnvollen Anwendung auf unterschiedliche mathematische
Sachverhalte.
 Die Aufgaben in anwendungsorientierten Bereichen sollten so gewählt werden,
dass die Notwendigkeit der Anwendung mathematischer Kenntnisse im Alltag
gezeigt wird.
 Durch Überprüfungen des Lernfortschritts sollten Lehrer die Reaktionen der
Schüler auf Probleme beobachten und eigens gestellte Verständnisfragen
diagnostizieren , um rechtzeitig Verständnislücken aufdecken zu können und
Yu Hui / 15.05.2016
75882528
8
sodann Anhaltspunkte für gezielte Hilfen und Maßnahmen geben zu können.
Yu Hui / 15.05.2016
75882528
9
1, Reelle Funktion
1,1 Der Begriff der Reellen Funktion
1,2 Zeichnen und Interpretieren von Funktionsgraphen
Ziel
Die SchülerInnen sollen am Ende des Unterrichts in der Lage sein, funktionale
Zusammenhänge innerhalb und außerhalb der Mathematik zu identifizieren und
diese Zusammenhänge, wo es sinnvoll ist, mathematisch, mithilfe von Funktionen in
unterschiedlicher Form darstellen können (Tabelle, Graph, Term,
Funktionsgleichung), um in der Folge entsprechende Berechnungen anstellen zu
können. Gleichzeitig sollen sie befähigt werden, grafische Darstellungen richtig zu
interpretieren.
Verlauf des Unterrichts
Einführung der Definition der reellen Funktion
Yu Hui / 15.05.2016
75882528
10
1, Begriff der Zuordnung und der Zuordnungsvorschrift
Beispiel(a): Ein Auto fährt mit einer konstanten Geschwindigkeit v=120 km/h auf
einer Autobahn. Wo befindet sich das Auto nach 1, 2, 3, t Stunden?
Lösung:
t(h)
s(km)
1
120
2
240
3
360
t
120t
Der zurückgelegte Weg s hängt von der verstrichenen Zeit t ab. D.h., t und s stehen
im Zusammenhang f. Dann sagen wir, dass der Zusammenhang f jeder Zeit t den
Weg s zuordnet: Zeit t Weg s.
f heißt eine Zuordnung. S= 120t ist die Zuordnungsvorschrift.
Oben ist die Darstellung der Zuordnungstabelle (Tabelle)
Wir können die Zuordnung auch durch ein Pfeildiagramm darstellen.
Yu Hui / 15.05.2016
75882528
11
1
120
2
240
3
360
t
s=120t
s
Bei graphischer Darstellung werden in einem Koordinatensystem möglichst viele
Zuordnungspunkte P(x|y) eingezeichnet, um eine bessere Übersicht (ein Schaubild)
zu erhalten.
S(km)
360
240
120
Yu Hui / 15.05.2016
75882528
12
0
1
2
3
t(h)
2, Definition der reellen Funktion
A sei eine Menge von reellen Zahlen. Wird jeder
Zahl x A genau eine Zahl y R zugeordnet, so heißt
diese Zuordnung (reelle) Funktion.
X
y
Ordnet eine Funktion f der Zahl x die Zahl y zu, so schreibt man: y=f(x)
von x].
Was ist typisch für alle Funktionen?
Lies: y ist f
(a) Eindeutigkeit
Sieht eine
Zuordnungsvorschrift so aus,
dass einem x nur ein Element y
zugeordnet wird (dabei können
mehrere x-Werte zu einem y-
Yu Hui / 15.05.2016
75882528
13
Wert gehören), so liegt eine eindeutige Zuordnung vor.
Eine Zuordnung ist nicht eindeutig, wenn einem
Element x mehrere Elemente y zugeordnet sind. In
einer Zeichnung sieht das so aus.
(b)Abhängigkeit der Funktion
Yu Hui / 15.05.2016
75882528
14
Bei einer Funktion ist eine Größe y von der anderen x anhängig. Die „unabhängige
Größe x“ zieht zwangweise die „abhängige Größe y“ nach sich.
Beispiel
Welche der folgenden Zuordnungen ist eine Funktion?
e) Jeder Mutter wird ihre Kinder
zugeordnet.
Lösung:
Die Zuordnungen
von a, b, c sind
Funktionen. Aber d,
e nicht.
3, Die Eigenschaft der Funktion
X
Stelle oder Argument
Y=f(x)
Funktionswert (Wert) der Funktion f an der Stelle x
A=Df
Definitionsmenge der Funktion f
Wf
Wertmenge von f für x A
Yu Hui / 15.05.2016
75882528
15
Df ={ a1, a2, a3 }
Wf ={ b1, b3, } (ohne b2)
Im Bespiel A ist jeder Zeit t ein bestimmter Weg s zugeordnet, damit ist der Weg s
eine Funktion der Zeit t. Ihre Definitionsmenge ist Df={x|x>0 x€R}, ihre Wertmenge
ist Wf=={y|y>0 y€R}
Funktionen kann man in unterschiedlicher Form darstellen (Tabelle( Wertetabelle),
Graph, Term, Funktionsgleichung). Die Form der Funktionsgleichung ist y=f(x).Im
Bespiel (a) wird eine Tabelle (Zuordnungstabelle) dargestellt. Diese
Funktionsgleichung ist y=120x, 120x ist die Term.
Schularbeit
1. Aufgabe
Gib die Funktionsgleichung zu folgenden Zuordnungen an:
a) Einer Zahl wird die Summe der vierfachen Zahl und der Zahl 5 zugeordnet.
Lösung: f(x)=4x+5
b) Einer Zahl wird die um 3 größere Gegenzahl zugeordnet.
Lösung: f(x)=-x+3
c) Einer Zahl wird das Vierfache ihres Quadrats zugeordnet.
Yu Hui / 15.05.2016
75882528
16
d) Einer Zahl wird die um 2 kleinere Gegenzahl zugeordnet.
2, Aufgabe
Welche der
folgenden
Pfeildiagramme
stellen Funktionen
an? Gib die
Definitionsmenge
und den
Wertebereich der
Funktion in
aufzählender Form
an.
3, Aufgabe
Ergänze das Diagramm so, dass du eine Funktion erhältst-
Yu Hui / 15.05.2016
75882528
17
Stelle die Funktion in einer Tabelle dar.
4,
Aufgabe
Zeichne zu folgenden Zuordnungen Pfeildiagramme und prüfe, ob eine Funktion vorliegt.
5, Aufgabe
Gib an, ob eine Funktion vorliegt, Wenn nicht, begründe warum.
Yu Hui / 15.05.2016
75882528
18
6, Aufgabe Welche Aussage ist richtig?
(a) Der Umfang u eines Kreises ist von seinem Radiums r abhängig ( u ist eine Funktion von r).
(b)Der Radius r eines Kreises ist von seinem Umfang u abhängig ( r ist eine Funktion von u).
4, Interpretieren von Funktionsgraphen
 Aus einem Funktionsgraphen kann man vieles herauslesen. Wichtig ist, die
Eigenschaft der Funktion zu erkennen:
 Welcher Funktionswert gehört zu einem bestimmten Argument?
 Wie ändert sich der Funktionswert, wenn die Argumente in bestimmter Weise
verändert werden?
 In welchen Bereichen steigt (wächst) oder fällt (abnimmt) es, wo nimmt sie ihren
größten oder kleinsten Werte an.
Yu Hui / 15.05.2016
75882528
19
 Wo nimmt eine Funktion den Wert 0 an? (Nullstellen)

Beispiel:
Die Eigenschaft der Funktion f:
1, Definitionsmenge: X ]-5, 5]
2, Wertemenge: Y ]-1,5, 2]
Yu Hui / 15.05.2016
75882528
20
3, Nullstellen: X0 {-4, 3}
4, Der Schnittpunkt mit der y-Achse: (0, 0,5)
5, Die Funktion ist im Intervall ]-5, -2,5[ streng monoton steigend(wachsend)].
6, Die Funktion ist im Intervall ]-2,5, -0,5[ und ]2. 5[ streng monoton fallend.
7, Die Funktion ist im Intervall ]-0,5, 2[ konstant.
8, Wenn X
, nimmt die Funktion positive Werte ( y>0 )
9, Wenn X
3, 5[ , nimmt die Funktion negative Werte ( y<0 )
10, Der größte Wert der Funktion ist Ymax= 2.
11, Die Funktion hat keinen kleinen Wert.
Yu Hui / 15.05.2016
75882528
21
Beschreibung von Eigenschaften einer Funktion:
 Definitionsmenge Df
 Wertemenge Wf
 Nullstelle (der Schnittpunkt mit der x-Achse)
 Der Schnittpunkt mit der y-Achse.
 Eine Funktion kann positive oder negative Werte annehmen.
 Eine Funktion kann streng monoton steigend oder streng monoton
fallend sein.
 Eine Funktion kann konstant sein.
 Eine Funktion kann einen kleinsten (Ymin) oder einen größten (Ymax)
Wert haben.
Aufgabe 1 Ergänze die Tabelle
1, Eine Funktion ist…..
a) die Argumente wachsen und die Wert
wachsen.
2, Die Nullstelle ist………
b) Graph, Pfeildiagramm, Tabelle, Funktionsgleichung darstellen.
3, Die Funktionswerte sind negative, wenn…
c) f(x)>0
Yu Hui / 15.05.2016
75882528
22
4, Die Funktionswerte sind positiv, wenn…
d) die Argument wachsen und die Wert
fallen.
5, Eine Funktion kann man als…..
e) f(x)<0
6, Eine Funktion ist streng monoton fallend,
wenn…..
f) die Stelle, wo der Graph der Funktion
die x-Achse schneidet-
7, Eine Funktion ist streng monoton steigend,
wenn…
g) eine Zuordnung, bei der jedem Element einer Menge genau ein Wert zugeordnet wird.
Aufgabe 2
Wie sind die Eigenschaften der Funktion.
Yu Hui / 15.05.2016
75882528
23
Yu Hui / 15.05.2016
75882528
24
Aufgabe 3
Aufgabe 4
Yu Hui / 15.05.2016
75882528
25
Bestimme die Definitionsmenge
Lösung für (d) als Beispiel
3x+5≥ 0
X+7 ≠ 0
x≥
x≠ 7
Df={x| x ≥
x≠ 7, x€R}
Aufgabe 5
Berechne für die Funktion f die Werte für die Argumente -1, 0,
, 3, 1, -
.
2. Lineare Funktion
Yu Hui / 15.05.2016
75882528
26
2,1 Die homogene lineare Funktion
2,2 Direkte Proportionalität
2,3 Die inhomogene linearen Funktion
2,4 Rekursive Darstellungen der linearen Funktion
2,5 Anwendung linearer Funktionen
Verlauf des Unterrichts
1,Einführung des Begriffs der direkten Proportionalität
Beispiel1.1: Drei Radfahrer fahren mit verschiedenen Geschwindigkeiten von 1)
150 m/min, 2) 300 m/min, 3) 450 m/min. Mit der Hilfe einer Tabelle zeichne das so
genannte “Zeit-Weg-Diagramm“ in ein gemeinsames Koordinatensystem.
Yu Hui / 15.05.2016
75882528
27
In unserem Fall gilt:
1) S= 150t
2) S= 300t
3) S= 450t
K=S: t = 150
K=S: t = 300
K=S: t = 450
Wir können sehen, je länger (kürzer) die Zeit ist,
desto länger (kürzer) ist der zurückgelegte Weg. Ihr
Quotient S:t ist für jeden Fahrer konstant (ihre
eigene Geschwindigkeit). Wir sagen: der
zurückgelegte Weg und die Zeit stehen in einem
“direkten Verhältnis“
Yu Hui / 15.05.2016
75882528
28
2) Die Definition der direkten Proportionalität
Zwei veränderliche Größen x und y sind zueinander direkt
proportional, wenn ihr Quotient y : x einen festen Wert k hat: y : x = k
K ist der Proportionalitätsfaktor.
Dem 2-, 3-, 4-,…. N-fachen der einen Größe x entspricht das 2-, 3-, 4-,…. Nfache der anderen Größe x. vˑy = k(vˑx )
Weitere Beispiele für direkte Proportionalität.
Je größer die Warenmenge ist, desto größer ist der zu zahlende Preis.
Fahrstrecke und Fahrpreis (gleiches Transportmittel): Je länger (kürzer) die
Fahrstrecke ist, desto höher (geringer ) ist der Fahrpreis.
Drehzahl des Motors (bei einem bestimmten Gang) und Geschwindigkeit: Je
größer (kleiner) die Drehzahl ist, desto höher (geringer) ist die Geschwindigkeit.
Yu Hui / 15.05.2016
75882528
29
3, Der Begriff der homogenen linearen Funktion
Die homogene lineare Funktion
Funktionen mit der Funktionsgleichung y = kˑx ( k€ R, k ≠ 0 ) heißen
homogene lineare Funktionen. Ihr Graph ist eine Gerade durch den
Ursprung des Koordinatensystems.
k nennt man die Steigung der Geraden.
4, Die Steigung der Geraden
Yu Hui / 15.05.2016
75882528
30
Yu Hui / 15.05.2016
75882528
31
Die Steigung der Geraden K
Steigende Gerade ( von links nach rechs): Fallende Gerade ( von links nach
K > 0 ⟹ 00 <  < 900
rechts) k < 0 ⟹ -900<  <00
Die Steigung k= Δy /Δ x (konstant)
Das Dreieck OPQ heißt Steigungsdreieck, der Winkel  heißt
Steigungswinkel.
Aufgaben
Aufgabe 1 Gegeben sind vier homogene lineare Funktionen.
f1: y = 3,8 x f2: y = -6x f3: y = x f4: y =3,9x
a) Welche der Funktionen besitzt den am “steilsten“ ansteigenden Graphen?
Zeichne ihn im Intervall -2,5 ≤ x ≤ 2,5!
b) Welche dieser Funktionen besitzt als Graph eine fallende Gerade?
Zeichne diesen Graphen im Intervall -3 ≤ x ≤ 3 (Einheit auf der y-Achse: 5 mm)!
Yu Hui / 15.05.2016
75882528
32
Aufgabe 2,
Yu Hui / 15.05.2016
75882528
33
5, Die Einführung des Begriffs
der Inhomogenen linearen
Funktion
Welche gegenseitige Lage haben
die Graphen der gegeben
Funktionen zueinander?
f1: y = 0,8x
f2: y = 0,8x + 1,5
f3: y = 0,8x – 1,5
Yu Hui / 15.05.2016
75882528
34
Wir können auf dem Graphen erkennen:
Der Graph der Funktion f2: y = 0,8x + 1,5 entsteht
aus dem Graphen der homogenen linearen
Funktion f1: y = 0,8x, in dem wir jeden Punkt um
den Wert +1,5 nach „ Oben“ verschieben. Ihre
Steigung k = 0,8.
Der Graph der Funktion f3: y = 0,8x - 1,5 entsteht aus dem Graphen der
homogenen linearen Funktion f1: y = 0,8x, in dem wir jeden Punkt um den Wert
+1,5 nach „ unten“ verschieben. Ihre Steigung k = 0,8.
Setzt man in den Funktionen f2 und f3 für x= 0 ein, erhält man die Schnittpunkte S2
und S3 der Funktionen mit der y-Achse. Den Abstand des Schnittpunkte des
Funktionsgraphen mit der y-Achse vom Ursprung bezeichnet man mit d
(Abschnitt auf der y-Achse)
Yu Hui / 15.05.2016
75882528
35
6, Die Definition der inhomogenen linearen Funktion
Die inhomogene lineare Funktion
Eine Funktion mit der Funktionsgleichung y = kx + d ( d, k € R, d ≠ 0. k≠ 0 )
heißt inhomogene lineare Funktion.
Der Graph einer inhomogenen lineare Funktion ist eine Gerade.
K heißt die Steigung der Gerade.
Wenn k > 0 ist, steigt( von links nach rechts) die Gerade.
Wenn k < 0 ist, fällt( von links nach rechts) die Gerade.
Die Funktion y = kx ist die zugehörige homogene Funktion.
Wenn x = 0, y = d (Abschnitt auf der y-Achse)
7, Zusammenfassung
Yu Hui / 15.05.2016
75882528
36
Wenn k=0, y=d, ist der
Funktionsgraph
konstant( Die Gerade verläuft
parallel zur x-Achse)
Yu Hui / 15.05.2016
75882528
37
Beispiel:
Zeichne den Graphen der Funktion y=- x+ 1! Gib jeweils 1) die Steigung k, 2) den
Steigungswinkel  (durch Ablesen), 3)den Abschnitt d des Graphen auf der y-Achse an!
Lösung
Berechne die Koordinaten zweier
Punkte(P, Q) des Graphen!
x
0
4
y
1
-1
X=0⟹y=- ˑ0 +1=1 ⟹ P(0|1)
X=4⟹y=- ˑ4 +1=-1 ⟹ Q(4|-1)
Die beiden Punkte P und Q legen die
Gerade fest.
Zeichne den Graphen der zugehörigen homogenen Funktionen linearen Funktion f1:
y= - x, Verschiebe diese Gerade um Wert d=+1 parallel „ oben“!
1) Steigung k=-1/2
2)Steigungswinkel -270
Yu Hui / 15.05.2016
75882528
3)Abschnitt d auf der y-Achse: d=1
38
Aufgaben
Aufgabe 1
1) Die Gleichung einer Geraden ist durch y = k x + d festgelegt! Beantworte folgende Fragen (3
Punkte): Welche Bedeutung hat k ? Durch welche Punkt gehen alle Funktionen der Form
y(x) = k x + d mit d konstant (z.B.d = -1) und k variabel? ............................
Eine Gerade mit y(x) = k x + d steigt, wenn .......................................
Eine Gerade mit y(x) = k x + d fällt, wenn .........................................
Ist k = 0, so erhält man als Graph .................................................
Aufgabe 2
2) Zeichne aufgrund der gegebenen Angaben die Geraden sauber in ein Koordinatensystem.
Bestimme die Steigung und den y-Achsenabschnitt und gib jeweils die zugehörige
Funktionsgleichung an.
a) Gegeben sind 2 Punkte A (1 / 5), B(4/-1)
b) Gegeben ist der Punkt C (-2 / -1) und die Steigung m = 0,5
Aufgabe 3
3) Gegeben ist die lineare Funktion f(x)=
x–1
a) Zeichne die Funktion in einem Koordinatensystem.
b) Berechne die Funktionswerte f(-1), f(0), f(1).
Yu Hui / 15.05.2016
75882528
39
c) An welcher Stelle schneidet der Graph die x-Achse?
d) An welcher Stelle schneidet der Graph die y-Achse?
e) Bestimme x so, dass der Punkt A (x|4) auf dem Schaubild liegt.
Aufgabe 4
Wählen die richtigen
Antworten mit der
Hilfe des Schaubildes
aus.
Yu Hui / 15.05.2016
75882528
40
Aufgabe 5
8, Rekursive Darstellungen der linearen Funktion
Yu Hui / 15.05.2016
75882528
41
Beispiel 8,1 1 kg Apfel kosten 0.80€. Wie viel kosten 2 kg, 3 kg,…, n kg Äpfel?
Lösung:
Der Preis P einer Ware ist eine lineare Funktion der Warenmenge n
Wir können in zwei Arten den Preis(in €) von n kg Äpfel mit P(n) für n=1,2,3….bezeichnen.
Yu Hui / 15.05.2016
75882528
42
Die zweite Darstellungsart bezeichnet man als rekursive Darstellung.
Mit Hilfe der Rekursionsgleichung P(n+1)=P(n)+0,80 kann man jeweils aus P(n)
(Termdarstellung der Funktion)den nächsten Wert P(n+1) berechnen, wobei man
von der Anfangsbedingung P(0)=0 ausgeht.
Aufgaben
Aufgabe1
Leite aus der folgenden Termdarstellung eine rekursive Darstellung her.
a)f(n)=7.n b) f(n)=5n+9 c) f(n)=80n+ 120 d) f(n)=10n – 5
Lösung von b)
f(n+1)=5(n+1)+9 =5n +5 + 9= (5n+9) +5= f(n)+ 5
Aufgabe2
Ida bekommt ab jetzt jede Woche 4€ Taschengeld, das sie nicht ausgibt. Es sei T die Funktion, die
jedem Zeitpunkt n (in Wochen) den Taschengeldbetrag T(n) zuordnet. Gib eine Termdarstellung
und eine rekursive Darstellung der Funktion T an und zeichne ihren Graphen.
Yu Hui / 15.05.2016
75882528
43
Aufgabe3
Mit einem Lastwagen, der 16 m3 fasst, wird Sand auf eine Baustelle Transportiert. Nach jeder
Stunde kommt der Lastwagen mit einer vollen Ladung Sand an. S(n) sei die Menge Sand, die nach n
Stunden auf der Baustelle zur Verfügung steht.
a)Zeichne den Graphen der Funktion S, die jedem n den Wert S(n) zuordnet.
b)Gib eine rekursive Darstellung und eine Termdarstellung von S
9, Anwendung linearer Funktionen
Die Zeit-Weg-Funktion für eine gleichförmige Bewegung ist vom Typ „Zeit(t)→
Weg(s)“, wobei S(t)=Vˑt + S0, S0 ist die Strecke für t=0 (Beispiel 1.1)
Die Kosten-und Gebührenfunktion ist eine lineare Funktionen
Ihre Funktionsgleichung ist in der Form: k(x)=kˑx + d
k ist die Kosten pro Produkt.
d ist die fixen Kosten.
Yu Hui / 15.05.2016
75882528
44
Beispiel 9.1
In einem Betrieb werden Rohre erzeugt. Die fixen Kosten für diese Produktion
betragen 10000 €, die variablen Kosten betragen 5 € pro Meter erzeugen Rohres.
1) Berechne die Produktionskosten (in Euro) für Produktion von 0, 1000, 2000,
3000 bzw. x m Rohr. Lege eine Tabelle an.
2) Es sei die Funktion, die jeder Rohrlänge x die gesamten Produktionskosten k(x)
zugeordnet (x in m, k(x) in €). Gib eine Termdarstellung dieser Funktion an und
zeichne ihren Graphen.
Lösung:
Yu Hui / 15.05.2016
75882528
45
3) k: R+→R mit k(x)=10000 + 5x
Aufgaben
Aufgaben1
a) Geben sein die Zeit-Weg-Funktion s mit s(t)= 4,2t + 10. Was bedeuten die Zahlen 4,2 und 10?
b) Geben sei die Kostenfunktion k mit k(x)=4,2x + 10. Was bedeuten die Zahlen 4,2 und 10?
c) Gib eine weitere Funktion f mit f(x)=4,2x + 10 an und erläutere, Was die Zahlen 4,2 und 10
Aufgaben2
Nebenstehende Abbildung zeigt das Zeit-Weg-Diagramm
eines Autos, das auf einer wenig befahrenen Autobahn mit
annähernd konstanter Geschwindigkeit fährt( t in h, s(t) in
km).
a) Wie groß ist s(0)? Was bedeutet s(0)?
b) Wie lange dauert die Fahrt und welchen Weg legt das
Auto dabei zurück?
c) Wie groß ist die Geschwindigkeit des Autos? Wie kann
diese aus dem Graphen abgelesen werden?
Yu Hui / 15.05.2016
75882528
46
Aufgaben3
In einer Großstadt gilt folgende Regel für Taxifahrten. Unabhängig von der Fahrstecke zahlt man
eine Grundgebühr von 1€, für jeden Kilometer zahlt man zusätzlich 0,8€.
a) Zeichne ein Punktdiagramm.
b) Wie groß ist die Steigung der
Graden, auf der die Punkte liegen?
c) Wenn man weiter fährt als geplant,
in welchem Verhältnis steht dann
die Erhöhung des
Rechnungsbetrages zur Erhöhung
der Kilometeranzahl?
d) Wenn man das Taxi telefonisch bestellt, zahlt man zusätzlich zur Grundgebühr noch eine
Anfahrgebühr von 1€. Wie sieht jetzt das Punktdiagramm aus? Zeichne die neuen Punkte in
das a) angefertigte Diagramm ein.
Yu Hui / 15.05.2016
75882528
47
Einige nichtlineare Funktionen
1,1 Die quadratische Funktionen
1, Der Begriff der quadratischen Funktionen
 Quadratische Funktionen haben eine
Funktionsgleichung, die sich zu y= ax2 + bx+ c mit
a≠ 0 umformen lässt.
 Der zugehörige Graph ist eine Parabel, die bei
a> 0 nach oben und bei a< 0 nach unten geöffnet
Ist.
 Der höchste bzw. niedrigste Punkt heißt
Scheitelpunkt.
Yu Hui / 15.05.2016
75882528
48
2, Normalparabel und verschobene Normalparabel
Der Graph der Funktion mit der Gleichung y =x2 heißt Normalparabel.
Eine Funktion mit der Gleichung
Yu Hui / 15.05.2016
75882528
49
 y= x2 + b hat als Graphen eine um b Einheiten längs der y-Achse verschobene
Normalparabel mit dem Scheitelpunkt S( 0| b).
 y= (x+ a)2 hat als Graphen eine um -a Einheiten längs der x-Achse
verschobene Normalparabel mit dem Scheitelpunkt S( -a| 0).
 y= (x+ a)2 + b hat als Graphen eine verschobene Normalparabel mit dem
Scheitelpunkt S( -a| b)
 Die Form y= (x+ a)2 + b einer Funktionsgleichung heißt deshalb
Scheitelpunktform.
3, Getauchte und gestreckte Parabeln
Yu Hui / 15.05.2016
75882528
50
Aufgaben
Aufgabe 1
Yu Hui / 15.05.2016
75882528
51
Aufgabe 2
Aufgabe 3
Gegeben ist die quadratische Funktion f mit f(x) = x² + x + 3.
a) Berechne den Funktionswert an der Stelle 5.
b) Für welche x gilt f(x) = 9?
c) Gib f(–2) an.
Yu Hui / 15.05.2016
75882528
52
Aufgabe 4
Yu Hui / 15.05.2016
75882528
53
Die Sammlung der Schularbeit
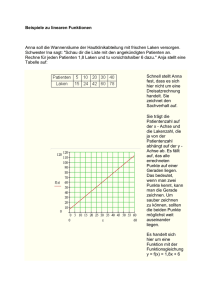
1 direkte Proportionalität und indirekte Proportionalität
1)Ein Pkw verbraucht auf 100 km 9,6 Liter Benzin.
Welche Strecke kann er mit einer Tankfüllung von 60 Litern zurücklegen?
(625 km, direkte Proportionalität)
2)Im Baumarkt kosten 40 Linsenkopf - Stahlstifte 0,68 €.
Wie viel € würden 250 Stahlstifte gleichen Typs kosten?
(4,25 €., direkte Proportionalität)
3)Eine Straße steigt auf 2,4 km Länge um 8,4 m.
Wie viel m würde sie bei gleichbleibender Steigung auf 5 km steigen?
17,5 m, direkte Proportionalität)
4)Zur Herstellung einer Garageneinfahrt benötigen drei Pflasterer 7,5 Stunden.
Wie lange würde die Arbeit dauern, wenn 5 Pflasterer eingesetzt werden können?
(4,5 Stunden, indirekte Proportionalität)
5)Um 1800 m3 Wasser 12 m hoch zu fördern, wird eine Pumpe von 4 kW benötigt.
Welche Wassermenge könnte von einer 8 kW Pumpe 16 m hoch gefördert werden?
(2700 m3, direkte und indirekte Proportionalität)
Yu Hui / 15.05.2016
75882528
54
2, Quadratische Funktion
3, Der Begriff der Funktion und Lineare Funktion
Yu Hui / 15.05.2016
75882528
55
Yu Hui / 15.05.2016
75882528
56
Yu Hui / 15.05.2016
75882528
57
Yu Hui / 15.05.2016
75882528
58
Yu Hui / 15.05.2016
75882528
59
Yu Hui / 15.05.2016
75882528
60
Verwendete Literatur
1, Math. Verstehen 5 Lb. (Ma) Schulbuchnummer 115925
2,Math.1 für HTL und Fachschulen( computerunterstüzt). Schulbuch-Nr: 0899
3, Math.-Lehrbuch 5(Gö). Schulbuch, SB-Nr. 115848
4,Math. für die 5. Klasse AHS Schulbuch-Nr: 115002
5, Das ist Mathematik 4. Lehrbuch und Aufgabensammlung.
Schulbuch-Nr:105288
Yu Hui / 15.05.2016
75882528
61