Teil5

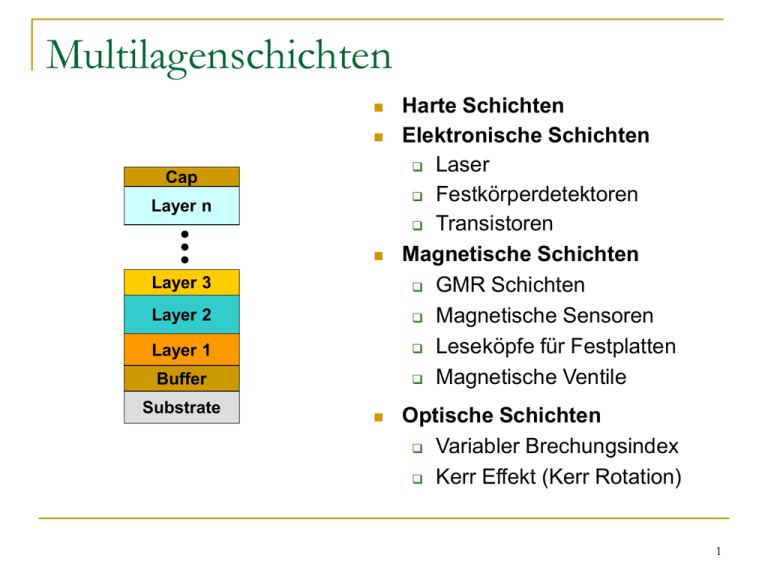
Multilagenschichten


Cap
Layer n

Layer 3
Layer 2
Layer 1
Buffer
Substrate

Harte Schichten
Elektronische Schichten
 Laser
 Festkörperdetektoren
 Transistoren
Magnetische Schichten
 GMR Schichten
 Magnetische Sensoren
 Leseköpfe für Festplatten
 Magnetische Ventile
Optische Schichten
 Variabler Brechungsindex
 Kerr Effekt (Kerr Rotation)
1
Obligatorische Untersuchungsmethoden
Transmissionselektronenmikroskopie (TEM)



Bild: magnetische
Multilagenschicht (Fe/Au)

Information über die Dicke
einzelner Schichten und über die
Morphologie der Grenzflächen in
ausgewählten Regionen im
direkten Raum
Komplizierte Probenpräparation
Destruktive Methode
Bei einer kleinen Dicke der
einzelnen (magnetischen)
Schichten ist die HRTEM
notwendig
2
Obligatorische Untersuchungsmethoden
Mikroskopie atomarer Kräfte (AFM)


Information über die
Morphologie der Oberfläche
Nicht destruktive Methode
Bild: selbst organisierte GaAs/GaInAs
Strukturen
3
Obligatorische Untersuchungsmethoden
Röntgenbeugung und Röntgenstreuung (XRD, XRR)
d-spacing (Å)
Intensity (a.u.)
100
10
8
10
6
10
4
10
2
10
0
50
30
10
20


0
1
2
3
4
5
6
7
8
9
10

o
Scattering angle ( 2  )
d-spacing (Å)
Intensity (a.u.)
4.5 4
10
3
10
2
3.5
3
2.5
2
1.5

10
1
20
25
30
35
40
45
50
55
Nicht destruktive
Untersuchungsmethode
Keine spezielle
Probenpräparation ist
erforderlich
Information über die Dicke,
Elektronendichte und atomare
Anordnung einzelner Schichten
und über die Morphologie der
Grenzflächen
Beobachtungen im reziproken
Raum (komplizierte Auswertung)
60
o
Diffraction angle ( 2  )
4
Modell einer Multilagenschicht
Cap
Layer n
Beugungskontrast
(Unterschied in atomaren
Streufaktoren)
Kristallinität der einzelnen
Schichten,
Vorzugsorientierung der
Kristallite und Kristallitgröße
Layer 3
Layer 2
Layer 1
Buffer
Substrate
Makroskopische Periodizität
Mittlerer Netzebenenabstand
und Netzebenenanzahl und
ihre Verteilung
Atomare Anordnung
5
Weitwinkelbeugung – experimentelle
Anordnung
 Koplanare Beugungsgeometrie
 Symmetrischer Modus
 Divergenter Primärstrahl
 Einfache Scans im reziproken Raum (der
Beugungsvektor ist senkrecht zur
Probenoberfläche)
 Diffraktierende Beugungsebenen sind
parallel zur Probenoberfläche
qz
cos o  cos i 
q z  2 sin  o  sin  i 
qx 
2

q x  0, q y  0, q z  1  10Å -1
qx
6
Weitwinkelbeugung – Interpretation des
Beugungsbildes
Lagen der Beugungsmaxima
Fe/Au (3.24nm/1.41nm)  12
Fe: 16  0.20268 nm, Au: 6  0.2355 nm
35

-2
-3
30
-1
-4
20

1
n

d 
Makroskopische Periodizität
(des wiederholten Motivs)
 d
0
25
Intensity (a.u.)
2 sin  n
  N Ad A  N B d B
+1
15
Mittlerer Netzebenenabstand
10
+2
5
0
30
32
34
36
38
d 
dB
dA
40
42
44
46
48
N Ad A  N B d B


N A  NB
N A  NB
50
o
Diffraction angle ( 2  )
7
Strukturmodell für Weitwinkelbeugung
d-spacing, dB
Intralayer
disorder, d
tB=NB.dB
 = tA+tB
Interlayer
disorder, c
d-spacing, dA
Interlayer distance, a
tA=NA.dA
8
Berechnung der diffraktierten Intensität
Kinematische Beugungstheorie
I  FSL F
*
SL
, FSL   Fn exp iqx n 
n
xn+1
Fn+1
xn
Fn
M
FSL  Fbuff   exp iqx L FAL  exp iq t AL  a AL FBL  exp iq t AL  a AL  t BL  aBL FCL 
L 1
M
  exp iqx L exp iq t AL  a AL  t BL  aBL  tCL  aCL FDL  exp( iqxtop ) Ftop
L 1
Gaußförmige Verteilung der Abstände
zwischen den nächsten Schichten
 aL  a 2 
1
P(aL ) 
exp 

2c 2 
2 c 
E.E. Fullerton, I.K. Schuller, H. Vanderstraeten, and Y. Bruynserade, Phys. Rev. B 45(16) (1992) 9292.
9
Strukturfaktor einzelner Schichten in der
Multilagenschicht
Amplitude der Streustrahlung (kinematisch)
 
FL   f L exp iq  r 
NL
Ideal georderte Struktur:
NL
exp iqN L d L   1

r  0,0, nd L   FL   f n exp iqnd L   f n
exp iqd L   1
n 1
Zufällige atomare Verschiebung:
NL
FL  
n 1

r  0,0, nd L  d 
 d 2 
 q 2d 2 
exp iqN L d L   1

f n exp iqnd L   P0 exp iq d  exp 
d d   f n
 exp  
2 


d
exp
iqd

1
4


L




10
Strukturfaktor einzelner Schichten in der
Multilagenschicht


r  0,0, nd L  n d
Korrelierte Atompositionen:
NL
FL  
n 1
NL

n 1

 d 2 
f n exp iqnd L   P0 exp iq n d exp 
d d  
2 
d



 
q 2d 2 
exp N L   1
q 2d 2
  f n
f n exp n iqd L 
;   iqd L 


4
exp


1
4

 



d … Breite der Gaußschen Verteilung für atomare Verschiebungen
(charakterisiert die Kristallinität der Schichten)
dL … mittlerer Netzebenenabstand innerhalb der Schicht L
11
Atomarer Streufaktor und die
Elektronendichte

 

f 0 q     * exp iq  r dr


  
 r    *  f 0    r  exp iq  r dr
   2  
s  s 0 
q  k  k0 
… q ist der Beugungsvektor (k und k0
sind die Wellenvektoren)

f  f 0  f   if 
4

sin 2 

f q    a j exp   b j

j 1

…  ist die gesamte Wellenfunktion des
Atoms
…  ist die Elektronendichte

  c  f   if 

… f’ und f” sind Korrektionsfaktoren
für anomale Dispersion und anomale
Absorption
… Approximation des atomaren
Streufaktors durch eine 9-ParameterAnnäherung
J.A. Ibers and W.C. Hamilton (ed.): International Tables for X-ray Crystallography, Vol. IV, The Kynoch
Press, Birmingham, 1974.
12
Simulation der Beugungsbilder im Weitwinkelbereich
Continuous interface roughness
Intralayer disorder (degree of crystallinity)
40
40
c = 0.3
35
d =0
35
30
c=0
25
20
15
10
5
0
30
32
34
36
38
40
42
44
46
48
Sqrt of intensity (a.u.)
Sqrt of intensity (a.u.)
c = 0.1
d =0.2
25
20
15
10
5
0
30
50
d =0.1
30
32
34
o
Diffraction angle ( 2  )
 (Fe)=0,
50
 (Fe)=1,
 (Fe)=0,
 (Au)=1
 (Fe)=1,
30
 (Au)=1
20
10
38
40
42
44
o
Diffraction angle ( 2  )
46
48
50
Sqrt of intensity (a.u.)
Sqrt of intensity (a.u.)
40
36
42
44
46
48
50
45
Continuous roughness
40
Intralayer disorder
Discrete roughness
 (Au)=0
34
40
o
 (Au)=0
32
38
Diffraction angle ( 2  )
Discrete interface roughness
0
30
36
35
30
25
20
15
10
5
0
30
32
34
36
38
40
42
44
46
48
50
o
Diffraction angle ( 2  )
13
Simulation der Beugungsbilder im Weitwinkelbereich
Number of atomic planes
Change in the interplanar spacing
16xFe, 6xAu
35
14xFe, 8xAu
d(Au)=2.0268Å
10xFe,11xAu
50
Sqrt of Intensity (a.u.)
Sqrt of Intensity (a.u.)
40
30
20
10
0
32
34
36
38
40
42
44
o
Diffraction angle ( 2  )
46
48
d(Au)=2.0568Å
30
6xFe 15xAu
25
20
15
10
5
0
30
32
34
36
38
40
42
44
46
48
50
o
Diffraction angle ( 2  )
Das Beugungsbild einer Multilagenschicht im Weitwinkelbereich ist sehr
empfindlich:
(1) zur Dicke einzelner Schichten
(2) zum Netzebenenabstand
14
Röntgenbeugung an realen Multilagenschichten
Sqrt of intensity (a.u.)
Eine gut kristalline Multilagenschicht: Fe/Au (14Å/23Å)12
35
Atom d[nm]
t[nm]
[nm]
30
Au
Fe
2.292
1.396
0.28
0.17
25
20
d0(Au, 111) = 0.2355 nm
d0(Fe, 110) = 0.2027 nm
15
10
5
0
25
0.2355
0.2027
30
35
40
45
o
Diffraction angle ( 2  )
50
55
a = 0.2156 nm
(dave = 0.2191 nm)
c = 0.0033 nm
d = 0.0108 nm
15
Röntgenbeugung an realen Multilagenschichten
Sqrt of intensity (a.u.)
Eine mäßig kristalline Multilagenschicht: Fe/Au (25Å/23Å)10
35
Atom d[nm]
t[nm]
[nm]
30
Au
Fe
2.326
2.518
0.24
0.20
25
20
0.2355
0.2027
d0(Au, 111) = 0.2355 nm
d0(Fe, 110) = 0.2027 nm
15
10
5
0
30
35
40
o
45
Diffraction angle ( 2  )
50
a = 0.2175 nm
(dave = 0.2191 nm)
c = 0.0217 nm
d = 0.0117 nm
16
Röntgenbeugung an realen Multilagenschichten
Sqrt of intensity (a.u.)
Eine schlecht kristalline Multilagenschicht: Fe/Gd (21Å/30Å)8
35
Atom d[nm]
t[nm]
[nm]
30
Gd
Fe
2.975
2.136
0.11
0.39
25
20
d0(h-Gd, 100) = 0.3100 nm
d0(h-Fe, 002) = 0.1970 nm
15
10
5
0
25
0.3074
0.1967
30
35
40
45
o
Diffraction angle ( 2  )
50
55
a = 0.2380 nm
(dave = 0.2520 nm)
c = 0.0010 nm
d = 0.0215 nm
17