Thermische Eigenschaften von Werkstoffen

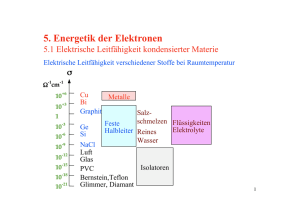
Thermische Eigenschaften von
Werkstoffen
 Wärmeleitfähigkeit (Elektronen, Phononen)
 Wärmekapazität (spezifische Wärme) beim
konstanten Volumen
 Wärmekapazität (spezifische Wärme) beim
konstanten Druck
 Wärmeausdehnung
1
Wärmeleitfähigkeit (Übersicht)
Beiträge zur Wärmeleitfähigkeit:
 Phononen (Schwingungen des Kristallgitters)  schlechte
Wärmeleitfähigleit
 Elektronen (mit der elektrischen Leitfähigkeit verbunden)  gute
Wärmeleitfähigkeit
2
Spezifische Wärme
(Wärmekapazität)
Einstein und Debye Modell
– quantenmechanische
Beschreibung der
Transportphänomene
3
Definition der physikalischen
Größen
E  W  Q
… Änderung der Energie eines thermodynamischen
Systems (W ist die Arbeit, Q die Wärme)
Es wird angenommen, dass
W=0
E = Q
4
Wärmekapazität
Energie (Wärme), die zum Aufheizen des Werkstoffs um 1K (1°C)
notwendig ist
 E 
CV  

 T V
… Wärmekapazität beim konstanten Volumen
 H 
C p  
 ; H  U  pV
 T  p
… Wärmekapazität beim konstanten Druck (H
ist die Enthalpie)
 2TV
CV  C p 

 … Volumenausdehnungskoeffizient
1 V

V T
1 V
 
V p
T … (absolute) Temperatur
V … Volumen des Materials
 … Kompressibilität
5
Spezifische Wärme
… pro Masseneinheit:
C
m
1  E 
cV  

m  T V
c
… pro Mol:
CV  cV  M
E  Q  mcV T
Temperaturabhängig
6
Temperaturabhängigkeit der
spezifischen Wärme
CV = 25 J mol-1 K-1 = 5.98 cal mol-1 K-1
Experimentelle Ergebnisse:
1. Spezifische Wärme der
Werkstoffe mit einem Atom in
der Elementarzelle liegt bei
der Raumtemperatur bei 25 J
mol-1 K-1.
2. Bei niedrigen Temperaturen
nimmt die spezifische Wärme
ab. Cv  T in Metallen, Cv  T3
in Isolatoren.
3. In magnetischen Werkstoffen
steigt die spezifische Wärme,
wenn sich der Werkstoff
magnetisch ordnet.
7
Spezifische Wärme bei
Phasenübergängen
Spezifische
Wärmekapazität von
KH2PO4, das bei 120 K
einen Phasenübergang
erster Ordnung besitzt.
Der Werkstoff benötigt
zusätzliche Energie
(Wärme) für die
Phasenumwandlung
8
Strukturübergang in KH2PO4:
paraelektrisch  ferroelektrisch
c
c
o
b
a
o
b
a
…K
Paraelektrisch
…P
RG: I -42d (tetragonal)
…O
a = 7.444Å, c = 6.967Å
…H
Ferroelektrisch
RG: Fdd2 (orthorhombisch)
a = 10.467Å,
b = 10.467Å,
c = 6.967Å
9
Magnetischer Phasenübergang in
CePtSn
2.0
1.6
-1
-2
7.438
7.437
4.614
3
6
9
12
15
18
21
b (Å)
4.613
7.998
1.2
0.8
0.4
0.0
4.612
3
6
9
12
15
18
21
T (K)
4.611
3
6
9
12
15
18
21
Antiferromagnetisch mit
TN = 7.5 K
7.997
c (Å)
C/T (mJ.mol K )
a (Å)
7.439
7.996
7.995
3
6
9
12
T (K)
15
18
21
Änderung in der Anordnung
der magnetischen Momente
10
Ideales Gas
pV  NkBT  nN a k BT  nRT
Na = 6.022 x 1023 mol-1
R = kB Na = 8.314 J mol-1 K-1 = 1.986 cal mol-1 K-1
Kinetische Energie des idealen Gases
Ekin 
1 mv 2
2
F 1 d mv

 p
A A dt
1 N
p   z  2mv   mv 2
3 V
Nk BT 1 N
p
  mv2
V
3 V
1
2
k BT   mv2  Ekin
3
3
p
dV  Adx  Avdt
1 N
1 N
z   dV   Avdt
6 V
6 V
z
1 N
z
  v
Adt 6 V
p … Druck
p* … Impuls
A … Fläche
N … Anzahl der
Atome
T … Temperatur
Ekin  12 mv2  32 k BT
11
Klassische Theorie der
Wärmekapazität (ideales Gas)
Ekin 
3k T
2 B
E  E pot  Ekin
 E 
CV     3N a k B  3R
 T V
CV = 25 J mol-1 K-1 = 5.98 cal mol-1 K-1
E pot  Ekin
E  3k BT
Emol  3N a k BT
Emol … Energie/Mol
Gute Übereinstimmung mit
dem Experiment bei hohen
Temperaturen
12
Quantentheorie
1903: Einstein postulierte das Quantenverhalten der Gitterschwingungen
analog zum Quantenverhalten der Elektronen.
Die Quanten der Gitterschwingungen werden als Phononen bezeichnet.
p


… der Impuls (de Broglie)
Longitudinale Schwingungen
En  n … die Energie
Transversale Schwingungen
13
Dispersionszweige
Analogie zum Energiebänder
(Bänderschema) bei den Photonen
Frequenz
Optische Phononen
Akustische
Phononen
Wellenvektor
Optische Phononen … höhere Energie
(Frequenz)
Akustische Phononen … niedrigere
Energie (Frequenz)
14
Beispiele
15
Akustischer und optischer
Dispersionszweig für eine lineare
Atomkette
16
Energie eines (quantenmechanischen)
Oszillators
En  n
N phonons 
… Energiequanten
1
  
  1
exp 
 k BT 


1
 F E  

 E  EF
exp 

 k BT




 
  1
 
… Bose-Einstein
Verteilung
… Fermi-Funktion
(Verteilung) für
Elektronen
17
Wärmekapazität – Das Einstein Modell
E n  n
E = 0.01 eV
nQM 
KP
QM
1
  
  1
exp 
 k BT 
E KP  3k BT  nKP 
nKP 
k BT

18
Wärmekapazität – Das Einstein Modell
Eosc 

  
  1
exp 
k
T
 B 
Klassische
Annäherung

E  3N a
  
  1
exp 
k
T
 B 
CV = 3R
 E 
CV  
 
 T V
  

exp 
 k BT 
2
  

 3 N a k B 
2
 k B T      
  1
exp 
k
T
  B  
CV  exp(/kBT)
Extremfälle:
CV  3N a k B  x
2
ex
;x
2
e 1
x

k BT
T  0  x  0  CV  3N a k B  3R
T  0  x    CV  3N a k B  x 2e  x  3N a k B  e  x
19
Vergleich der theoretischen Ergebnisse
mit Experiment
Experimentelle Ergebnisse:
1. Spezifische Wärme der Werkstoffe
mit einem Atom in der
Elementarzelle liegt bei der
Raumtemperatur bei 25 J mol-1 K-1.
2. Bei niedrigen Temperaturen nimmt
die spezifische Wärme ab. Cv  T in
Metallen, Cv  T3 in Isolatoren.
Theorie (Einstein-Modell):
1. Spezifische Wärme liegt bei hohen
Temperaturen bei 25 J mol-1 K-1.
Im Einstein-Modell werden nur Phononen
mit einer bestimmten Frequenz
berücksichtigt.
2. Bei niedrigen Temperaturen nimmt
die spezifische Wärme als
exp(-/kBT) ab.
20
Wärmekapazität – das Debye Modell
Phononen mit unterschiedlichen Energien
N phon
4 3
V  
 3


K

 
3 3
2 v 
2  s 
2 
D  
V
dN phon
d

3
… Anzahl der (akustischen) Phononen
vs … Schallgeschwindigkeit
3V  2
2
2
… Verteilung (Dichte) der Schwingungsfrequenzen
[Zustandsdichte der Elektronen]
vs3
E   Eosc D d
E
D
3V

2 2vs3 0

d
  
  1
exp 
k
T
 B 
1
3
 2 N phon 
 2 2 N elem


D 
vs  



3V
V



N phon  3 N elem
2
3V
2
 E 
CV  

 
2
3
 T V 2 vs k BT 2
3
D

0
  

 k BT 
 4 exp 
    
  1
exp 
  k BT  
2
1
3

 vs


21
d
Wärmekapazität – das Debye Modell
CV 
3V
2 2vs3

  

k
T
 B 
 4 exp 
D
2

2
    
  1
exp 
  k BT  

k T

x
 d  B dx ;  D 
k BT

kB
CV 
 D3
3V
2 2vs3

k BT
d
0
k B4T 3

2
D T
3
x 4 exp  x 
 exp x   12 dx
0
3  2 2vs3
9Na
3V
3
Na 

3
3V
2 2vs3  D
3 D T
 T 
 
CV  9 N a k B 
 D 
x 4 exp  x 
 exp x   12 dx
0
22
Debye-Temperaturen
23
Wärmekapazität bei hohen und niedrigen
Temperaturen (nach dem Debye-Modell)
3 D T
 T 
 
T  0 : CV  9 N a k B 
 D 
T  0   D
D T

0
D T
x 4 1  x 
D T
x 4 1  x 
 1  x  12 dx
0
3
2
3
1  D   1  D 
dx

x
dx

x
dx



3 T 
4 T 
2




1  x  1
0
0
3
4
3
 T  1  D 
  3 
CV  9 N a k B 
  3R
 T 
 D 
 T   x 4 exp  x 
3
  
T   : CV  9 N a k B 
dx

T
2
  D  0 exp  x   1
3
T  0  D
Cv  T3: Bessere Übereinstimmung mit Experiment bei tiefen Temperaturen
!!! Für Isolatoren !!!
24
Gesamte Wärmekapazität
Phononen (Debye Modell)
Elektronen
T < QD
CV  T
CV 
3
 2 N a k B2
2
EF
T  T
CV/T
 … Phononenbeitrag
CVtot  CVel  CVph  T  T 3
CVtot
   T 2
T
 … Elektronenbeitrag
T2
25
Experimentelle Methoden
für Untersuchung von Temperaturschwingungen
Röntgenbeugung
Neutronenbeugung
Änderung der Form der
Elektronendichte (Temperaturschwingungen der Elektronen)
Wechselwirkung der
niederenergetischen (langsamen)
Neutronen mit Phononen
Einfluss auf die Intensitäten der
Beugungslinien
26
Wärmeleitung
Wärmeleitfähigkeit: K

J   K grad T
T
 div J
t
T
 div K grad T 
t
T
x
J

x
  T 
 K

x  x 
J  K
Partielle Differentialgleichung:
Lösung bei bestimmten Anfangund Randbedingungen
T
t
T
t
Temperaturänderung – ähnlich wie die Konzentrationsänderung bei Diffusionsprozessen
1.0
1
.
0
T = konst.
0
.
6
Concetrai
0
.
4
0
.
2
0
.
0
0
5
0
1
0
0
1
5
0
D
i
s
t
a
n
c
e
J=0
0.8
T = konst.
Concentration
0
.
8
2
0
0
J=0
0.6
0.4
0.2
0.0
0.0
0.2
0.4
0.6
Relative distance
0.8
1.0
27
Wärmeleitfähigkeit

 T  
E1  z  32 k B  T0   
  
 x  

nv
T 

 v  32 k B  T0  

6
x 

nv
T 

E2  v  32 k B  T0  

6
x 

nv
T
J Q  E1  E2   v  k B 
2
x
nv
T
JQ  K
; K  v  kB
x
2
n … Anzahl der Elektronen
l … freier Weg zwischen zwei Kollisionen
(Elektron-Gitterschwingung)
v … Geschwindigkeit der Elektronen
E  nv  32 k BT

 dE 
CVel  
  nv  32 k B 

 dT V
1 el
  K  3 CV v
n vk 

K v B

2
28
Wärmeleitfähigkeit
Metalle
Wärmeleitfähigkeit, W/cm/K
Dielektrika
Temperatur, K
Wiedemann-Franz Gesetz:
Werkstoffe mit guter elektrischer Leitfähigkeit
besitzen auch eine gute Temperaturleitfähigkeit
K
 2k B2
8 J
L

2
,
443

10
T
3e 2
K 2s
Material
K [W/cm/K]
SiO2
NaCl
Al2O3
Cu
Ga
0,13 – 0,50 (bei 273K bzw. 80K)
0,07 – 0,27 (bei 273K bzw. 80K)
200 bei 30K
50 bei 20K
845 bei 1,8 K
29
Wärmeausdehnung

Atomare Bindungskräfte
W  U x  cx  gx  fx
2
3
x 
4
 U  x 
xe
dx



 U  x 
e
dx



e

 U  x 
dx 



 U  x 
 xe
dx 


e
 cx 2
x  gx
 cx
 xe


dx  0 ;  fx  e
5
dx 

4

 fx5 dx 

2
e
 cx 2
 cx 2

c
3  g
3 2

4 c5 2
dx  0

Harmonische Schwingungen:
x 0
Anharmonische Schwingungen:
x 
3g
4c
2
k BT
Wärmeausdehnung
30
Wärmeausdehnung
Änderung des mittleren Atomabstandes
mit der Temperatur:
da
3g
 x  2 k BT
dT
4c
T
Argon (kfz)
Dichte [g/cm³]
Gitterparameter [Å]
Temperaturabhängigkeit des Gitterparameters:
Temperatur [K]
a
3g
2
4
c
0
k BT dT   T 2
Gitterparameter wächst ungefähr
quadratisch mit der Temperatur
Bei T = 0K ist die
Wärmeausdehnung gleich Null
31
Wärmeausdehnung in GdNiAl
32