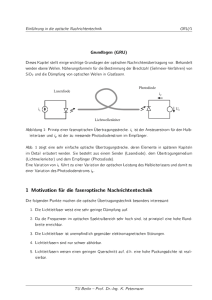
FWHM

Einführung in die optische Nachrichtentechnik
ÜB/1
Beschreibung des optischen Übertragungskanals (ÜB)
1 Begrenzende Faktoren
Die maximal mögliche Übertragungsrate in faseroptischen Übertragungssystemen wird neben dem
Rauschen (siehe Abschnitt EDFA) im wesentlichen durch folgende Eekte begrenzt:
1. Chromatische Dispersion, womit die wellenlängenabhängige Gruppenlaufzeit in der Faser bezeichnet wird. Sie wird bestimmt durch die Materialdispersion (vgl. Abschnitt GRU) sowie durch
die Wellenleiterdispersion (vgl. STU 11/12).
2. Unterschiedliche Laufzeiten der einzelnen Eigenwellen in Multimode-Fasern, auch bezeichnet als
Laufzeitstreuung oder (Inter-) Modendispersion (vgl. Abschnitt GRA).
3. Nichtlineare Eekte im Lichtwellenleiter bei höheren optischen Leistungen.
2 Vorüberlegungen
2.1 Impulsverbreitung
Sowohl die chromatische Dispersion als auch die unterschiedlichen Laufzeiten in Multimode-Fasern
führen zu einer Impulsverbreiterung, die sich in erster Nährung quadratisch überlagern lassen:
(t )2 = (tc )2 + (ts )2
(1)
wobei tc die Impulsverbreiterung aufgrund der chromatischen Dispersion und ts die Impulsverbreiterung aufgrund der Laufzeitstreuung in Multimode-Fasern bezeichnen (ts = 0 für einwellige Fasern).
Für einen ersten Eindruck des Übertragungsverhaltens ist es zweckmäÿig, eine Impulsantwort h(t )
bezüglich der optischen Leistung am Ende einer Faserstrecke für einen sehr schmalen Eingangspuls zu
denieren. Wenn man eine Gauÿ'sche Impulsantwort mit
h(t ) =
+R1
1
h(t )dt = 1 annimmt, läÿt sich schreiben.
exp( (t=t )2 )
pt
(2)
Die Fouriertransformierte von h(t ) entspricht der Übertragungsfunktion
H (j! ) mit
h(t )
H (j! ) = exp( ln2(f =fg )2 )
(3)
(4)
mit ! = 2f . Die Übertragungsfunktion hat damit ein Tiefpaÿverhalten mit der Grenzfrequenz fg mit
j H(j! = j 2fg ) j= 12 . Abb. 1 zeigt schematisch h(t ), wobei häug auch die Puls-Halbwertsbreite
TU Berlin Prof. Dr.-Ing. K. Petermann
Einführung in die optische Nachrichtentechnik
ÜB/2
p D t h (t)
D t
F W H M
1
1 /2
1 /e
D t
Abb. 1: Gauÿ'sche Impulsantwort h(t)
tF W HM (FWHM - full width half maximum) verwendet wird, die sich für einen Gauÿ'schen Puls nach
Abb. 1 ergibt zu
p
tF W HM = 2 ln2 t
(5)
Die Grenzfrequenz fg ergibt sich dann zu
fg =
p
1
0:44
ln2 1
2ln2
=
=
t
tF W HM tF W HM
(6)
Die weitere Betrachtung beschränkt sich auf einwellige Fasern, bei denen eine Impulsverbreitung nur
aufgrund der chromatischen Dispersion zu berücksichtigen ist. Bei einer spektralen Breite der Lichtquelle (full width half maximum) ergibt sich dann
tF W HM = L j d=d j
(7)
mit der Faserlänge L und der chromatischen Dispersion d=d.
Beispiel: LED mit = 80nm; = 1:55m und einer chromatischen Dispersion d=d = 17ps=(km nm). Dann ergibt sich ein tF W HM = 1:36ns=km bzw. eine Grenzfrequenz fg = 320 MHz (km/L).
Nach (6) hätte es den Anschein, daÿ sich für ! 0 ein t ! 0 und damit eine unendlich hohe
Bandbreite realisieren lieÿe. Tatsächlich bewirkt eine schnelle Modulation aber auch eine spektrale
Verbreitung, wodurch die erreichbare Übertragungsrate begrenzt wird.
2.2 Intuitive Abschätzung der maximalen Übertragungsrate
Wir gehen von einer binären Puls-Code-Modulation (PCM) mit der Bitrate B aus, wobei dann die
spektrale Breite der modulierten Lichtquelle auch ungefähr durch B und damit
= 2 =c = B 2 =c
TU Berlin Prof. Dr.-Ing. K. Petermann
(8)
Einführung in die optische Nachrichtentechnik
ÜB/3
gegeben ist. Die Grenzfrequenz fg ergibt sich dann mit (6), (7) zu
fg = 0:44 c=(B 2 L j d=d j)
(9)
Zur Übertragung der binären Bitfolge muÿ die Grenzfrequenz
fg > B=2
sein, woraus mit (9) folgt:
p
B L<
s
2
(10)
0:88 c
j d=d j
p
(11)
Man erhält also als Begrenzung durch die chromatische Dispersion ein maximales Bitr aten Lange -P r odukt .
Wenn man eine Standardfaser mit j d=d j= 17ps=(km nm) und = 1:55m zugrunde legt, ergibt
sich als Zahlenwert
p
p
(12)
B L < 80Gbit=s km
was beispielsweise bei einer Bitrate von B = 10 Gbit/s noch eine Übertragungslänge von L = 64 km
ermöglicht.
3 Signalübertragung unter Berücksichtigung der chromatischen
Dispersion
3.1 Grundlagen
Bei der obigen Beschreibung handelt es sich noch um eine recht grobe Betrachtung, so daÿ hier
genauer die Ausbreitung des modulierten elektrischen Feldes entlang einer dispersiven Faser analysiert
werden soll. Wir verwenden dazu das komplexe orts- und zeitabhängige elektrische Feld
E (z; t ) = A(z; t )exp( j0 z + j!0 t )
(13)
A(z; t ) bezeichnet dabei eine im Vergleich zur optischen Frequenz langsam variierende komplexe Amplitudenfunktion für ein monochromatisches optisches Feld mit der optischen Frequenz !0 und der
dazugehörigen Phasenkonstanten 0 . Das reale elektrische Feld in der Faser (z.B. Ex für die LP01 Welle) entspricht dabei dem Realteil von (13). Die Signalausbreitung entlang der Faser läÿt sich sehr
einfach im Frequenzbereich mit der Fouriertransformierten von E (z; t ) beschreiben:
E (z; t ) E (z; j!)
(14)
gemäÿ
E (z; j!) = E (z = 0; j! ) exp( j (!)z )
(15)
Die Phasenkonstante (! ) wird um ! = !0 in eine Taylor-Reihe entwickelt:
(!) = 0 + (!
1
!0 ) + 2 (!
2
1
!0 )2 + 3 (!
6
TU Berlin Prof. Dr.-Ing. K. Petermann
!0 )3 + :::
(16)
Einführung in die optische Nachrichtentechnik
ÜB/4
mit 0 = (!0 ) wie bereits in (13), der Gruppenlaufzeit pro Länge
= d=d! ;
der chromatischen Dispersion
2 =
d 2
d
=
=
2
d!
d!
(17)
d 2
(
)
d 2c
(18)
und der Änderung der chromatischen Dispersion (englisch: dispersion slope)
3 =
d 3
d d
=
( )
3
d!
d! d!
(19)
Gl. (15) führt mit (16) auf:
E (z; j!) = E (z = 0; j! ) exp( j0 z )exp( jz (!
1
exp( j 3 z (!
6
1
!0 ))exp( j 2 z (!
2
!0 )3 )
!0 )2 ) (20)
Mit Gl. (20) ist die Signalausbreitung prinzipiell vollständig beschrieben. Uns interessiert jedoch die
Signalausbreitung bezüglich der Amplitudenfunktion A(z; t ), wobei es zweckmäÿig ist, eine retardierte
Zeitachse (t 0 = t z ) einzuführen, da die Gruppenlaufzeit des Signals im wesentlichen durch
z gegeben ist. Für die Amplitudenfunktion wird nun eine Fouriertransformierte mit t = t 0 + z
eingeführt:
A(z; j )
(21)
A(z; t 0 + z ) wobei die Frequenz der Dierenz zwischen ! des Feldes in Gl.(14)-(16) und !0 , d.h. = ! !0 ,
entspricht. Es ist nun das Ziel, die Signalübertragung bezüglich A(z; t ) bzw. A(z; j ) zu beschreiben.
Die Fouriertransformation in (21) bedeutet
A(z; j ) =
und damit mit t 0 = t
+
Z1
1
A(z; t 0 + z )exp( j t 0 )dt 0
(22)
z und dt 0 = dt :
A(z; j ) = exp(j z )
+
Z1
1
A(z; t )exp( j t )dt
(23)
Wenn man Gl. (13) nach A(z; t ) auöst:
A(z; t ) = E (z; t )exp(j0 z )exp( j!0 t )
(24)
und in Gl. (23) einsetzt, ergibt sich
A(z; j ) = exp(j z )exp(j0 z )
+
Z1
1
E (z; t )exp( j (
+ !0 )t )dt
TU Berlin Prof. Dr.-Ing. K. Petermann
(25)
Einführung in die optische Nachrichtentechnik
ÜB/5
und damit
A(z; j ) = exp(j z )exp(j0 z )E (z; j! )
(26)
Mit E (z; j! ) aus Gl(20) ergibt sich schlieÿlich
1
A(z; j ) = E (z = 0; j! )exp( j 2 z (!
2
und damit
1
!0 )2 )exp( j 3 z (!
6
1
1
A(z; j ) = A(z = 0; j )exp( j 2 z 2 )exp( j 3 z 3 )
2
6
!0 )3 )
(27)
(28)
Gl.(28) läÿt sich als Dierentialgleichung schreiben,
@A(z; j )
1
= A(z; j )( j 2 2
@z
2
Mit der retardierten Zeitachse t
mieren:
t
1
j 3 3 )
6
(29)
z und @=@t = j läÿt sich (29) in den Zeitbereich transfor-
@A(z; t )
@ 2 A(z; t ) 3 @ 3 A(z; t )
=j 2
+
(30)
@z
2
@t 2
6
@t 3
Die Kenntnis der Signalform A(z; t ) an der Stelle z ermöglicht damit die Berechnung der Signalform
an der Stelle (z + z ).
3.2 Übertragung eines Gauÿ'schen Pulses
Gl.(30) entspricht bei Vernachlässigung von 3 genau der Ausbreitungsgleichung für Strahlwellen
(STR, Gl. (3)) mit den Entsprechungen t x; y und 2 k10 n . Insofern ist es naheliegend, ähnlich wie
bei der Gauÿ'schen Strahlwelle die Ausbreitung eines Gauÿförmigen Pulses entlang einer dispersiven
Faser zu analysieren. Die komplexe Amplitude A(z; t ) sei so normiert, daÿ für die optische Leistung
P in der Faser
P (z; t ) =j A(z; t ) j2
(31)
gilt. Für z=0 sei
P (z = 0; t ) = P0 exp( [t=t0 ]2 )
(32)
und damit für die komplexe Amplitude
A(z = 0; t ) =
p
P0 exp(
1
(t=to )2 )exp(j(t ))
2
(33)
mit einer eventuellen zusätzlichen Phasenmodulation (t ). Beispielsweise führt die Modulation eines
Halbleiterlasers (aber auch von sonstigen externen Modulatoren) nicht nur zu einer Leistungsmodulation, sondern auch zu einer Modulation der optischen Frequenz (chirp). Dies liegt daran, daÿ sich
bei einer Modulation der optischen Verstärkung auch die Brechzahl innerhalb des Halbleiterlasers und
damit die optische Emissionsfrequenz ändert. Dies läÿt sich durch einen Parameter
ch =
n 0
n00
TU Berlin Prof. Dr.-Ing. K. Petermann
(34)
Einführung in die optische Nachrichtentechnik
ÜB/6
beschreiben, der die Kopplung zwischen einer Variation des Imaginärteils und des Realteils der Brechzahl beschreibt. Für eine Lasermodulation gilt (siehe z.B. K. Petermann, 'Laser diode modulation and
noise', Kluwer Academic 1991):
d
= 2( (t )
dt
0 ) =
ch 1 dP
(
)
2 P dt
(35)
woraus für den Gauÿförmigen Puls von Gl.(32) folgt:
d
= (ch =t02 )t
dt
bzw.
(t ) =
ch
(t=t0 )2
2
(36)
(37)
so daÿ sich die komplexe Amplitude gemäÿ Gl.(33) ergibt zu
A(z = 0; t ) =
p
P0 exp(
1
(t=t0 )2 (1 + jch ))
2
(38)
A(z; t ) ergibt sich dann gemäÿ Gl.(29),(30).
Für 3 = 0 bleibt die Gauÿ'sche Pulsform bei Ausbreitung entlang der Faser erhalten, wie beim
Gauÿ'schen Strahl
P (z; t ) exp( (t=t1 (z ))2 )
mit
s
t1 (z ) = t0 (1
ch
2 z 2
z
) + ( 22 )2
t02
t0
(39)
(40)
Abb. 2 zeigt den Verlauf der Pulsbreite für 2 < 0 (wie bei einer Standardfaser mit = 1; 55m, dort
ist 2 20ps 2 =km). LD bezeichnet dabei die sogenannte Dispersionslänge
LD = t02 = j 2 j
(41)
Ohne 'chirp' (ch = 0) ergibt sich eine monotone Pulsverbreiterung, während sich für ch 2 > 0
auch eine Pulsverschmälerung ergeben kann. Aufgrund der Pulsverbreiterung eines Gauÿ-Pulses läÿt
sich die maximal mögliche Übertragungsrate abschätzen.
3.3 Maximale Übertragungsrate ohne chirp (ch = 0)
Ohne chirp (ch = 0) ergibt sich die minimale Impulsbreite am Ausgang (z = L) für t02 =j 2 L j zu
t12 = 2 j 2 L j
(42)
was ungefähr eine maximale Bitrate B < 1=(2t1 ) ermöglicht und damit
p
q
B L < 1= 8 j 2 j =
s
(2=8) c
j d=d j 2
in guter Übereinstimmung mit Gl.(11).
TU Berlin Prof. Dr.-Ing. K. Petermann
(43)
Einführung in die optische Nachrichtentechnik
ÜB/7
4.0
b2<0
3.5
3.0
ach=2
ach=-2
t 1/t 0
2.5
2.0
1.5
ach=0
1.0
0.5
0.0
0.0
0.5
1.0
z/LD
1.5
2.0
Abb. 2: Pulsbreite als Funktion der Faserlänge
3.4 Maximale Übertragungsrate mit Vorchirp
Mit einem geeignet gewählten 'chirp'-Parameter ch < 0 (für 2 < 0) läÿt sich gemäÿ Abb. 2
eine Pulsverschmälerung und damit eine Erhöhung der Übertragungsrate erreichen. Leider ist bei der
direkten Modulation von Halbleiterlasern normalerweise ch > 0 (typisch ch 3::::6), aber mit
speziellen Modulatoren ist auch ch < 0 möglich.
Mit genügend groÿem negativen ch lassen sich prinzipiell beliebig kleine Pulsbreiten erreichen. Für
die Abschätzung der maximalen Übertragungsrate ist jedoch bestenfalls eine Anfangsimpulsbreite
t1 (z = L) = t0
(44)
sinnvoll.
Die Forderung (44) für minimales t0 = t1 (z = L) führt mit (40) auf ch =
t12 (z = L) = t02 =j 2 L j
In Analogie zu (42), (43) ergibt sich ein maximales Bitr aten p
q
pLange -P r odukt von
B L < 1= 4 j 2 j
d.h. daÿ sich mit Vorchirp (ch =
verdoppeln läÿt.
1( fur 2 < 0) und
(45)
(46)
1) die Übertragungslänge bei gleicher Bitrate gegenüber (43)
TU Berlin Prof. Dr.-Ing. K. Petermann
Einführung in die optische Nachrichtentechnik
ÜB/8
4 Übertragungsverhalten von Lichtwellenleitern unter
Berücksichtigung der Nichtlinearitäten
4.1 Grundsätzliche Eekte
Bezüglich des nichtlinearen Verhaltens von Lichtwellenleitern unterscheiden wir einmal nichtlineare
Streuprozesse sowie die Veränderung der Brechzahl bei hohen Leistungen (Kerr-Eekt).
4.1.1 Nichtlineare Streuprozesse
Bei den nichtlinearen Streuprozessen ndet eine Wechselwirkung statt mit Phononen, wodurch die optische Signalwelle in Wellen kleinerer Photonenenergie umgesetzt wird, was auch zu einer nichtlinearen
Dämpfung der Signalwelle führt. Man unterscheidet im wesentlichen zwischen der Brillouin- und der
Raman-Streuung.
Bei der Brillouin-Streuung wird die Signalwelle an einer akustischen Welle längs des Lichtwellenleiters
reektiert, wobei sich aufgrund des Doppler-Eekts eine reektierte Welle ergibt, die eine um ca. 10
GHz reduzierte optische Frequenz aufweist. Die für die Brillouin-Streuung relevante Bandbreite ist
mit 100 MHz relativ gering. Die Brillouin-Streuung führt zu erheblichen Störungen der Signalübertragung, sobald die optische Leistung innerhalb eines Bandbreitenintervalls von 100 MHz einige mW
überschreitet. Um trotzdem möglichst hohe Signalleistungen in der Faser zulassen zu können, ist es
zweckmäÿig, Modulationsverfahren zu verwenden, die die optische Signalleistung möglichst gleichmäÿig auf eine groÿe Spektralbreite verteilen.
Bei der Raman-Streuung handelt es sich um die Wechselwirkung mit optischen Phononen, die auch zu
einer Dämpfung der Signalwelle führen kann. Die Raman-Streuung ist sehr viel breitbandiger, wobei
aber eine nennenswerte Dämpfung der Signalwelle erst bei Leistungen 500 mW auftritt.
4.1.2 Intensitätsabhängige Brechzahl
Aufgrund des Kerr-Eekts ergibt sich eine intensitätsabhängige Brechzahl, die sich am besten be~ ergibt
schreiben läÿt mit der elektrischen Polarisation P~ , aus der sich die dielektrische Verschiebung D
mit
wobei
~ = 0 E
~ + P~
D
(47)
P~ = P~L + P~NL
(48)
~
P~L = 0 1 E
(49)
den linearen Anteil der elektrischen Polarisation beschreibt. Wenn man zunächst nur den linearen Anteil
~ = 0 (1 + 1 )E
~ , so daÿ sich 1 mit
der Polarisation P~ in (47) berücksichtigt, ergäbe sich D
r = 1 + 1
TU Berlin Prof. Dr.-Ing. K. Petermann
(50)
Einführung in die optische Nachrichtentechnik
ÜB/9
der relativen Dielektrizitätskonstante zuordnen läÿt. Die nichtlineare Polarisation P~NL aufgrund des
Kerr-Eekts ist im wesentlichen ein Eekt 3. Ordnung gemäÿ
~ E
~ )E
~
P~NL = 0 3 (E
(51)
Um den Einuÿ der nichtlinearen Polarisation besser zu verstehen, betrachten wir ein (skalar angenommenes) elektrisches Feld, das sich aus 2 harmonischen Komponenten zusammensetzt:
E = Re E 1 exp(j!1 t ) + Re E 2 exp(j!2 t ) =
1
E 1 exp(j!1 t ) + E 2 exp(j!2 t ) + c:c:
2
(52)
Wenn man (52) in (51) einsetzt, ergeben sich für die nichtlineare Polarisation Frequenzkomponenten
insbesondere bei !1 ; !2 ; (2!1 +!2 ); (2!2 +!1 ). Für die Frequenzkomponente !1 ergibt sich beispielsweise
3
PNL (!1 ) = 0 3 (jE 1 j2 +2 j E 2 j2 )Re (E 1 exp(j!1 t )
(53)
4
wodurch sich dann bei der Frequenz !1 in Erweiterung zu 50 ein eektives r einführen läÿt gemäÿ
3 r (!1 ) = 1 + 1 + 3 j E 1 j2 +2 j E 2 j2
4
woraus sich dann auch für die Brechzahl n =
p
r
(54)
ein linearer und nichtlinearer Anteil ergibt
n j!1 = n1 + n2 (I1 + 2I2 )
(55)
mit I1;2 der Intensität (= Leistungsdichte) bei der Frequenz !1 bzw. !2 . Da die Phasenkonstante
proportional zur Brechzahl ist, führt gemäÿ Gl. (55) die Variation der Intensität zu einer Phasenmodulation des Signals, wobei die eigene Intensität (!1 ) die Phase halb so stark beeinuÿt - man
spricht von Selbstphasenmodulation - wie die Intensität I2 des Signals bei der anderen Frequenz (bzw.
Wellenlänge) - man spricht dann von Kreuzphasenmodulation.
4.2 Nichtlineare Schrödingergleichung
Solange die Brillouin- und die Raman-Streuung noch keine Rolle spielt, genügt es, nur die nichtlineare
Phasenverschiebung entsprechend 4.1.2 für die Signalausbreitung in der Faser mit zu berücksichtigen.
Gl. (30) wird dazu erweitert einmal um einen Term, der die Dämpfung in der Faser beschreibt
sowie die nichtlineare Phasenverschiebung in Anlehnung an Gl. 55. Es ergibt sich dann die sogenannte
nichtlineare Schrödingergleichung:
@ 2 A(z; t ) 3 @ 3 A(z; t )
@A(z; t )
=j 2
+
@z
2
@t 2
6
@t 3
A(z; t )
j j A j2 A(z; t )
(56)
wobei die nichtlineare Phasenverschiebung durch den Parameter beschrieben wird, der bei einer
Quarzglasfaser den Wert
=
1:31 80 m2
W km Aef f
TU Berlin Prof. Dr.-Ing. K. Petermann
(57)
Einführung in die optische Nachrichtentechnik
ÜB/10
annimmt. Aef f bezeichnet die eektive wirksame Fläche der LP01 -Grundwelle, die bei einer Standardfaser typischerweise den Wert Aef f = 80m2 aufweist. Die nichtlineare Phasenverschiebung kann
für
Z
P (z )dz << 1
(58)
vernachlässigt werden, wobei das Integral in Gl. (58) über die gesamte Faserstrecke (einschlieÿlich der
optischen Verstärker) zu erstrecken ist. So spielt die nichtlineare Phasenverschiebung für P (z ) 1mW
und eine Streckenlänge L =100 km beispielsweise noch keine Rolle, für L =1000 km jedoch muÿ sie
mit berücksichtigt werden. Die nichtlineare Phasenverschiebung in Gl. (56) führt insbesondere zu
folgenden Eekten:
1. Selbstphasenmodulation
Aufgrund der intensitätsabhängigen Phasenverschiebung wird die Phase des Signals selbst moduliert (siehe Gl. 55), was unter Umständen zu einer erheblichen spektralen Verbreiterung führen
kann.
2. Kreuzphasenmodulation
Bei einem Wellenlängenmultiplexsystem wird die Phase eines Kanals auch durch die Intensitätsschwankungen der Nachbarkanäle moduliert (siehe Gl. 55). Dies führt zu einem Übersprechen
zwischen den verschiedenen Kanälen.
3. Vierwellenmischung
Bei 3 vorhandenen Signalen der optischen Frequenzen !i , !j , !k ergibt sich z.B. ein viertes Signal
bei der Frequenz !i (!j !k ). Auch dies führt zu einem Übersprechen zwischen verschiedenen
Kanälen.
Eine Analyse der Signalausbreitung mit den obigen Eekten ist im allgemeinen nur durch numerische
Auswertung von Gl. (56) möglich. Wichtig ist dabei auch die Gröÿe der chromatischen Dispersion. Im
allgemeinen ist es vorteilhaft, wenn die lokale Dispersion j 2 (z ) j möglichst groÿ ist.
4.3 Solitonen
Die nichtlineare Phasenverschiebung läÿt sich positiv ausnutzen, wenn die nichtlineare Phasenverschiebung j A j2 A gerade die Dispersion (2 =2) d 2 A=dt 2 kompensiert (Annahme: 3 = 0 und
dämpfungsfreies System mit = 0). Bei geeignet gewählten Leistungspegeln ergeben sich kurze
Pulse (sogenannte Solitonen), die entweder unabhängig von z sind oder zumindest eine Periodizität
entlang z mit der Solitonenperiode Lper aufweisen.
Solitonen existieren nur für 2 < 0. Sie werden charakterisiert durch ihre Solitonenordnung Nsol .
2 =
Nsol
Pp Tp2
j 2 j
TU Berlin Prof. Dr.-Ing. K. Petermann
(59)
Einführung in die optische Nachrichtentechnik
ÜB/11
und die Solitonenperiode
Tp2
(60)
2 j 2 j
mit der Pulsspitzenleistung Pp und der halben Pulsbreite Tp . Abb. 3 zeigt Beispiele für Solitonen mit
Nsol =1...3.
Lper =
Z e itb e r e ic h
N
s o l
F r e q u e n z b e r e ic h
= 1
z
w
t
N
s o l
z
= 2
N
t
z
w
t
s o l
= 3
z
w
z
z
Abb. 3: Solitonen der Ordnung Nsol = 1; 2; 3 im Zeit- und Frequenzbereich
Beispiel:
Es wird ein 10 Gbit/s-System betrachtet. Damit sich die Solitonenpulse nicht beeinussen, muÿ die
Pulsbreite deutlich kleiner als die Bitperiode sein, also z.B. Tp = 10ps. Für eine Standardfaser bei
1; 55m mit 2 = 20ps2 =km ergibt sich dann eine Solitonenperiode Lper = 8km.
Hier ist zu beachten, daÿ Solitonen streng genommen nur für ein verlustfreies System mit = 0 existieren können. Diese Bedingung kann so verallgemeinert werden, daÿ innerhalb einer Solitonenperiode
die Verluste ausgeglichen werden müssen, d.h. Loa < Lper (Loa - Verstärkerabstand). Da Verstärkerabstände Loa > 50km angestrebt werden, ist die im obigen Beispiel abgeschätzte Solitonenperiode
viel zu kurz für ein praktisches System. Dies bedeutet, daÿ ein 10 Gbit/s-Solitonen-System nur mit
Fasern erheblich geringerer Dispersion realisierbar ist.
TU Berlin Prof. Dr.-Ing. K. Petermann
Einführung in die optische Nachrichtentechnik
ÜB/12
Weiterführende Literatur: G.P. Agrawal, 'Fiber-optic Communication Systems', John Wiley, 2nd Ed.,
1997
5 Ausblick
Zur Beurteilung konkreter Übertragungssysteme ist im allgemeinen eine numerische Systemanalyse
erforderlich. Weiterhin unterscheidet man zwischen RZ- und NRZ-Systemen (RZ- return to zero, NRZnon return to zero). Verbreiteter sind NRZ-Systeme, bei denen die Pulsbreite gerade der Bitperiode
entspricht und somit die optische Leistung bei aufeinanderfolgenden '1'-Signalen nicht auf 0 zurückgeht
(siehe Abb. 4). Bei kürzeren Pulsen erhält man dann ein RZ-Signal, wobei das Verhältnis zwischen
Pulsbreite und Bitintervall als Tastverhältnis bezeichnet wird.
0
1
1
0
0
1
0
1
1
1
0
Power
1
NRZ
t=Dt/TB=1
RZ
t=Dt/TB=0.5
Power
t/TB
Dt
TB
t/TB
Abb. 4: Vergleich zwischen RZ- und NRZ-Modulation
Bei Solitonensystemen handelt es sich beispielsweise um ein RZ-System, wobei zur Vermeidung der
Wechselwirkung zwischen den einzelnen Solitonen 0:25 gelten muÿ. Ein Beispiel für die Analyse
eines NRZ-Systems (reine Intensitätsmodulation ohne 'chirp') im Rahmen der linearen Näherung (Gl.
30) zeigt Abb. 5. Die dargestellte 'power penalty' gibt die Reduktion der Önung im Augendiagramm
an. Für eine 'penalty' von 1 dB und 10 Gbit/s ergibt sich eine Streckenlänge von 63 km (bei 40 Gbit/s
jedoch nur 4 km) in guter Übereinstimmung mit Gl. (11)(12),(43).
Um gröÿere Streckenlängen zu erreichen, besteht die naheliegendste Möglichkeit darin, in die Faserstrecke dispersionskompensierende Fasern einzufügen. Prinzipiell ist eine perfekte Kompensation der
chromatischen Dispersion möglich, es verbleiben jedoch die Begrenzungen aufgrund der Nichtlinaritäten.
TU Berlin Prof. Dr.-Ing. K. Petermann
Einführung in die optische Nachrichtentechnik
ÜB/13
power penalty (dB)
3.5
3.0
back-to-back
2.5
2.0
1.5
1.0
0.5
length (km)
0
0
20
40
60
80
100
0
1.25
2.5
3.75
5
6.25
10 Gbit/s
40 Gbit/s
Abb. 5: Reduzierung der Augenönung (in dB) bei einem 10- bzw. 40 Gbit/s-System im Rahmen der
linearen Näherung (Standardfaser)
TU Berlin Prof. Dr.-Ing. K. Petermann