Lösungen Π0 - Leuphana Universität Lüneburg

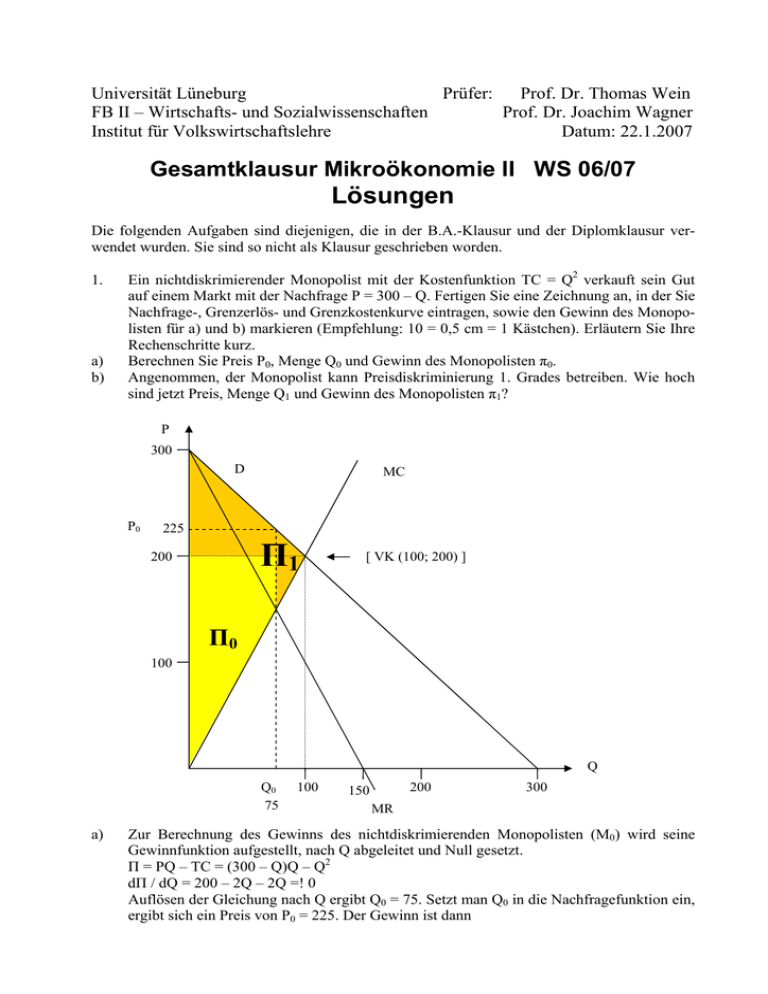
Universität Lüneburg
Prüfer:
Prof. Dr. Thomas Wein
FB II – Wirtschafts- und Sozialwissenschaften
Prof. Dr. Joachim Wagner
Institut für Volkswirtschaftslehre
Datum: 22.1.2007
Gesamtklausur Mikroökonomie II WS 06/07
Lösungen
Die folgenden Aufgaben sind diejenigen, die in der B.A.-Klausur und der Diplomklausur verwendet wurden. Sie sind so nicht als Klausur geschrieben worden.
1.
a)
b)
Ein nichtdiskrimierender Monopolist mit der Kostenfunktion TC = Q2 verkauft sein Gut
auf einem Markt mit der Nachfrage P = 300 – Q. Fertigen Sie eine Zeichnung an, in der Sie
Nachfrage-, Grenzerlös- und Grenzkostenkurve eintragen, sowie den Gewinn des Monopolisten für a) und b) markieren (Empfehlung: 10 = 0,5 cm = 1 Kästchen). Erläutern Sie Ihre
Rechenschritte kurz.
Berechnen Sie Preis P0, Menge Q0 und Gewinn des Monopolisten π0.
Angenommen, der Monopolist kann Preisdiskriminierung 1. Grades betreiben. Wie hoch
sind jetzt Preis, Menge Q1 und Gewinn des Monopolisten π1?
P
300
D
P0
MC
225
Π1
200
[ VK (100; 200) ]
Π0
100
Q
Q0
75
a)
100
200
150
300
MR
Zur Berechnung des Gewinns des nichtdiskrimierenden Monopolisten (M0) wird seine
Gewinnfunktion aufgestellt, nach Q abgeleitet und Null gesetzt.
Π = PQ – TC = (300 – Q)Q – Q2
dΠ / dQ = 200 – 2Q – 2Q =! 0
Auflösen der Gleichung nach Q ergibt Q0 = 75. Setzt man Q0 in die Nachfragefunktion ein,
ergibt sich ein Preis von P0 = 225. Der Gewinn ist dann
b)
2.
Π0 = 75*225 – 752 = 3*752 – 752 = 2*752 = 2*5.625 = 11.250.
Der Gewinn Π0 ist die gelb (in schwarz-weiß: hell) markierte Fläche.
Bei Preisdiskriminierung 1. Grades gibt es gerade keinen einheitlichen Preis, sondern der
Monopolist M1 nimmt von jedem Nachfrager dessen persönlichen Maximalpreis und
schöpft so die gesamte Konsumentenrente ab. Dies tut er so lange, bis für ihn MR = MC
gilt. Wichtig dabei ist zu beachten, daß der Grenzerlös MR hier mit der Nachfragekurve
identisch ist, da er seinen Preis für eine vorher verkaufte Einheit nicht senken muß, wenn
er eine weitere Einheit verkauft. Es ergeben sich so die Menge, die auch bei vollkommener
Konkurrenz verkauft wird, Q1 = 100. Diese Menge verkauft er zu Preisen zwischen 300
und 200.
Der Gewinn ist die gelbe plus die orangene (schwarz-weiß: dunklere) Fläche zusammen.
Er läßt sich am einfachsten ausrechnen, in dem man die Inhalte der beiden Dreiecke ausrechnet, die die Konsumentenrente und die Produzentenrente (hier nicht eingezeichnet, da
nur bei vollkommener Konkurrenz gültig) darstellen:
(300 – 200)*100 / 2 = 5.000
200*100/2 = 10.000
Gesamtgewinn Π1 = 15.000.
Das Modell monopolistischen Wettbewerbs unterscheidet sich in welcher Annahme von
dem Modell vollkommenen Wettbewerbs?
a)
b)
c)
d)
Freier Marktein- und austritt.
Produkthomogenität.
Große Anzahl an Firmen.
Perfekte Information.
Antwort b.
3.
Auf der Nachfragekurve unten sind vier Punkte, A–D, eingezeichnet, die vier mögliche Oligopolmarktergebnisse in Menge und Preis darstellen. Welche der folgenden Antworten
stellt die Ergebnisse in der richtigen Reihenfolge dar?
Preis P
A
B
C
D
Menge Q
a)
b)
c)
d)
A = Bertrand, B = Cournot, C = Stackelberg, D = Kollusion.
A = Cournot, B = Bertrand, C = Stackelberg, D = Kollusion.
A = Kollusion, B = Cournot, C = Stackelberg, D = Bertrand.
A = Kollusion, B = Cournot, C = Bertrand, D = Stackelberg.
Kollusion bedeutet, daß die Unternehmen faktisch wie ein Monopol agieren, hier sind die Preise
am höchsten, die Mengen am niedrigsten: A. Im Cournot-Wettbewerb konkurrieren die Unternehmen über die Menge und somit nicht sehr stark gegeneinander: B. Im Stackelberg-Wettbe-
werb agiert das eine Unternehmen (Führer) und bezieht die Reaktion des anderen (Folger) mit
ein, der Wettbewerb wird dadurch schärfer: C. Im Bertrand-Wettbewerb konkurrieren die Unternehmen über die Preise, unterbieten sich gegenseitig und landen so bei P = MC, dies ist der
schärfste Wettbewerb mit den niedrigsten Preisen und der größten verkauften Menge. Antwort c.
4.
Wenn zwei Tit-for-Tat-Spieler über eine lange Zeit immer wieder aufeinandertreffen, dann
ist das Ergebnis
a)
b)
c)
d)
Kooperation.
Defektion.
Grenzkostenpreissetzung.
Es wird sich ein Führer herausbilden, wie beim Stackelberg-Modell.
Ein Tit-for-Tat-Spieler wird nie als erstes von der Kooperationsstrategie abweichen (= defektieren). Wenn zwei Tit-for-Tat-Spieler aufeinandertreffen, dann wird niemand defektieren und es
bildet sich ein stabile und dauerhafte Kooperation.
Antwort a.
5.
Welche der folgenden Aussagen über Nash-Gleichgewichte und Gleichgewichte in dominanten Strategien ist wahr?
a)
b)
c)
d)
Jedes Nash-Gleichgewicht ist auch ein Gleichgewicht in dominanten Strategien, aber
nicht umgekehrt.
Jedes Gleichgewicht in dominanten Strategien ist auch ein Nash-Gleichgewicht, aber
nicht umgekehrt.
Ein Gleichgewicht in dominanten Strategien und ein Nash-Gleichgewicht schließen
sich gegenseitig aus; d.h. ein Gleichgewicht kann nur das eine oder das andere sein.
Keine der obigen Aussagen ist wahr.
In einem Gleichgewicht in dominanten Strategien ziehen beide immer ihre dominante Strategie,
unabhängig davon, was der andere macht. Diese Strategie ist gleichzeitig ihre beste Strategie,
gegeben das, was der andere macht (nämlich immer seine dominante Strategie ziehen) – also ist
ein Gleichgewicht in dominanten Strategien immer auch ein Nash-Gleichgewicht (Damit sind
die Antworten c. und d. falsch). Umgekehrt gilt das nicht: Ein Nash-Gleichgewicht ist allgemein
davon abhängig, was der der andere zieht, damit ist nicht jedes Nash-Gleichgewicht ein Gleichgewicht in dominanten Strategien – Antwort a. ist falsch.
Antwort b.
6.
Für einen Monopolisten auf dem Gütermarkt verläuft die kurzfristige Nachfragekurve nach
Arbeit sinkend. Der Grund dafür ist, daß
a)
b)
c)
d)
seine Skalenerträge steigen.
seine Grenzproduktkurve der Arbeit sinkt.
seine Grenzerlöskurve steigt.
keine der obigen Antworten ist richtig.
Skalenerträge sind ein langfristiges Konzept, sie sind auf kurzfristige Situationen nicht anwendbar (a. ist falsch). Die kurzfristig Gewinnmaximierungsbedingung für den Monopolisten lautet
w = MPL*MR. Mit zunehmender Arbeitsmenge sinkt das Grenzprodukt der Arbeit MPL, da alle
anderen Faktoren konstant gehalten werden.
Antwort b.
Gleichzeitig sinkt aber auch der Grenzerlös, da er Monopolist auf dem Gütermarkt ist, c. ist also
falsch.
7.
Gegeben sei eine Situation, in der nur ein Produktionsfaktor variabel ist. Im Vergleich dazu ist die Nachfrage nach diesem Faktor, wenn mehrere Produktionsfaktoren variabel sind,
a)
b)
c)
d)
weniger elastisch.
unverändert.
elastischer.
waagerecht.
Je mehr Produktionsfaktoren variabel sind, desto eher können bei einer Preisänderung des untersuchten Faktors andere Faktoren eingesetzt werden. Die Nachfrage nach diesem Faktor wird also
elastischer. Antwort c.
8.
Eine Maschine bewirkt eine Zahlung von €200 am Ende des ersten Jahres und von €200
am Ende des zweiten Jahres und zerfällt danach zu Staub. Der Gegenwartswert des Zahlungsstroms ist ungefähr
a)
b)
c)
d)
€462, wenn der Zins 10% ist.
€347, wenn der Zins 10% ist.
€330, wenn der Zins 10% ist.
€400, unabhängig von der Höhe des Zinses.
Für die Berechnung des Gegenwartswertes ist die Zahlung von €200 abzuzinsen. 200 / (1+0,1) +
200/ (1+0,1)2 = 347,10.
Antwort b.
9.
Gemäß dem zweiten Wohlfahrtstheorem / zweiten Lehrsatz der Wohlfahrtsökonomie
a)
b)
c)
d)
sind Gerechtigkeit und Effizienz eng miteinander verbunden.
sind Gerechtigkeit und Effizienz voneinander separabel.
ist Gerechtigkeit für Ökonomen unwichtig.
ist Gerechtigkeit nur in einer effizient produzierenden Gesellschaft möglich.
Das zweite Wohlfahrtstheorem besagt, daß unter der Bedingung, daß alle Marktteilnehmer konvexe Präferenzen haben, jede pareto-effiziente Allokation ein Tausch-Gleichgewicht ist. Die
wichtigste Implikation des zweiten Wohlfahrtstheorems ist, daß Verteilung und Effizienz getrennt werden können: Da jede Allokation die (pareto-)effizient ist, das Ergebnis einer bestimmten Anfangsallokation ist, kann diese Anfangsallokation z.B. durch Umverteilung erreicht werden. Nach der anfänglichen Umverteilung braucht nicht mehr in den Marktmechanismus eingegriffen werden (a. ist falsch).
Antwort b.
10.
Eine Transaktion, die eine Pareto-Verbesserung darstellt, ist eine,
a)
b)
c)
in der die Verlierer weniger verlieren als die Gewinner gewinnen.
in der alle Beteiligten gewinnen.
in der niemand verliert und mindestens einer gewinnt.
d)
durch die alle Beteiligten auf der Kontraktkurve landen.
Das Pareto-Kriterium beinhaltet, daß sich niemand verschlechtert, Antwort a. ist somit falsch.
Allerdings müssen bei der Transaktion nicht alle gewinnen (b. ist falsch), es reicht, wenn einer
gewinnt und niemand verliert.
Antwort c.
Hier ist nur nach einer Pareto-Verbesserung gefragt, d. wäre die Antwort auf die Frage, welche
Transaktion ein Pareto-Optimum herbeiführt (d. ist falsch).
11.
John ist ein 55-jähriger starker Raucher mit 30kg Übergewicht, einem Herzinfarkt hinter
sich, der mehrfach im Monat Alkohol im Übermaß zu sich nimmt. Angenommen, es liegt
adverse Selektion bei Risikolebensversicherungen vor (Risikolebensversicherungen zahlen
nur im Todesfall des Versicherungsnehmers während des Versicherungszeitraumes). Dann
a)
b)
c)
d)
ist die Wahrscheinlichkeit, daß John eine Risikolebensversicherung abschließt, geringer als für eine durchschnittliche Person, weil seine Prämie auf seinem persönlichen Risiko basiert und nicht auf dem durchschnittlichen Risiko.
ist die Wahrscheinlichkeit, daß John eine Risikolebensversicherung abschließt, höher
als für eine durchschnittliche Person, weil seine Prämie auf dem durchschnittlichen
Risiko basiert und nicht auf seinem persönlichem Risiko.
gibt John nach Abschluß einer Risikolebensversicherung noch weniger auf seine Gesundheit acht als vorher.
gibt John nach Abschluß einer Risikolebensversicherung stärker auf seine Gesundheit acht als vorher.
Adverse Selektion bei einer Versicherung basiert darauf, daß die Versicherung die unterschiedlichen Wahrscheinlichkeiten, daß ein Versicherungsfall eintritt, aufgrund ihres Informationsdefizites nicht den Versicherungsnehmern zuordnen und somit auch keine angepaßten Prämien nehmen kann. Sie muß somit eine durchschnittliche Prämie nehmen. Da John eine überdurchschnittliche Wahrscheinlichkeit hat zu sterben, ist eine Risikolebensversicherung für ihn bzw. die Begünstigten sehr lukrativ und er wird sie mit erhöhter Wahrscheinlichkeit abschließen.
Antwort b.
Die Antworten c. und d. beziehen sich auf eine Verhaltensänderung nach Vertragsabschluß, die
durch den Inhalt des Vertrages (Schutz bei Schadensfall) ausgelöst wird, sie beschreiben Moral
Hazard (c. und d. sind falsch).
12.
Die folgende Tabelle gibt das Einkommen eines Handelsvertreters in Abhängigkeit von
seiner Anstrengung e (effort) und seinem Glück wieder.
Pech
Glück
Niedrige Anstrengung (e = 0) € 5.000 € 7.000
Hohe Anstrengung (e = 1)
€ 7.000 € 13.000
Kosten der Anstrengung:
c = € 5.000e
Wahrscheinlichkeiten:
Pech = 0,75;
Glück = 0,25.
Wenn der Handelsvertreter sich wenig anstrengt (e = 0), dann ist sein erwartetes Einkommen
a)
b)
c)
€ 5.000.
€ 5.500.
€ 6.000
d)
€ 7.000
Wenn der Handelsvertreter sich wenig anstrengt, ist sein Einkommen entweder 5.000 oder 7.000
Euro. Zur Berechnung des erwarteten Einkommens müssen diese mit den Wahrscheinlichkeiten
malgenommen werden, mit denen die jeweiligen Situationen auftreten:
5.000*0,75 + 7.000*0,25 = 5.500.
Antwort b.
13.
Jane kann mit oder ohne Filter auf ihrem Schornstein produzieren. Janes Gewinne und
Helgas Schäden durch den Rauch sind in der folgenden Tabelle aufgestellt.
Janes Gewinn
Helgas Schaden
Mit Filter
€ 100
€0
Ohne Filter
€ 120
€ 25
Wenn Jane für den Schaden aus ihrem Rauch nicht verantwortlich ist und Verhandlungen
kostenlos sind, dann
a)
b)
c)
d)
wird Jane auf ihre Kosten einen Filter installieren.
wird Jane keine Filter installieren.
wird Helga Jane dafür bezahlen, einen Filter zu installieren.
keine der obigen Antworten ist richtig.
Wenn die Verhandlungen kostenlos sind, wird das gesellschaftlich effiziente Ergebnis erzielt
werden. Dies ist die Installation eines Filters, weil die gesellschaftlichen Gewinne dann € 100
und damit höher als ohne Filter (120 – 25 = 95) sind. Da Jane nicht verantwortlich ist, wird Helga sie für die Installation eines Filters bezahlen.
Antwort c.
14.
Aufgrund der Art der Externalitäten, die durch Forschung & Entwicklung verursacht werden, wird der Preis für Forschungs- & Entwicklungsressourcen ________ und die Menge
__________ dem gesellschaftlich optimalen Niveau liegen.
a)
b)
c)
d)
über,
unter,
über,
unter,
unter
über
über
unter
Forschung & Entwicklung bewirken positive externe Effekte: Einmal erreichte Forschungsergebnisse stehen nicht nur den Forschern, sondern grundsätzlich allen zur Verfügung (u.a.m.).
Ohne Einflußnahme gehen diese Effekte jedoch nicht in den Marktpreis ein, so daß der Preis unter dem gesellschaftlich effizienten Niveau liegt und Forschung zu wenig nachgefragt wird.
Antwort d.