Kapitel 10 Elemente der Infinitesimalrechnung

Kapitel 10
Elemente der
Infinitesimalrechnung
Gegenstand sind die infiniten Prozesse im Bereich der reellen Zahlen. Grob gesagt
wird “das Unendliche” (ob unendlich klein oder unendlich groß) mit in die Betrachtungen einbezogen. Anfangsgründe der Infinitesimalrechnung wurden von I. Newton
und – etwa zeitgleich – von G.W. Leibniz formuliert. Ausformulierung erfolgte durch
A.L. Cauchy und Zeitgenossen.
10.1
Zahlenfolgen, Konvergenz und Grenzwert
Sie erinnern sich: Eine Zahlenfolge ist eine auf N definierte Funktion mit Werten in
R, sofern es sich um eine reelle Folge handelt, und Werten in C, sofern es sich um
eine komplexe Folge handelt. Statt a(n) für den Wert der Folge an der Stelle n, wie
c
!Martin
Wilkens
115
7. März 2012
116
Elemente der Infinitesimalrechnung
es für Funktionen üblich ist, notiert man an , genannt das n-te Glied der Folge. Die
Folge selber schreibt man dann auch (an ) oder einfach a1 , a2 , . . ..
Definiton “konvergent”: Eine Folge (an ) heißt konvergent, wenn es eine Zahl a
gibt, die die Eigenschaft aufweist, dass zu jedem ε > 0 ein Nε ∈ N existiert,
so dass
|an − a| < ε für alle n > Nε
(10.1)
Die Zahl a heißt Grenzwert oder Limes der Folge, notiert
lim an = a bzw. an → a für n → ∞
n→∞
(10.2)
Der Ausdruck n → ∞ ist dabei nicht zu lesen “wenn n den Wert ‘unendlich’ erreicht” (eine Zahl mit einem solchen Wert gibt es nicht), sondern “n wächst über
alle Grenzen” (es lässt sich kein N ∈ N angeben, so dass für alle n gilt n ≤ N ).
Geometrisch kann die Konvergenzbedinung für komplexe Folgen formuliert werden,
dass alle Folgenglieder an mit n > Nε in einer Kreisscheibe
Uε (a) := {z ∈ C| |z − a| < ε}
(10.3)
der sog. ε-Umgebung von a liegen. Für reelle Folgen ist die ε-Umgebung das Intervall
Iε (a) := {x ∈ R| |x − a| < ε}.
Eine Folge mit Grenzwert 0 heißt auch Nullfolge. Die Folge ( n1 ) beispielsweise ist
eine Nullfolge: für vorgegebenes ε > 0 setze Nε := 1/ε. Für alle n > Nε ist dann
1/n < 1/Nε = ε, wie für eine Nullfolge gefordert.
Hat man eine konvergente Folge an mit Grenzwert a, also an → a, so ist (an −
a) offensichtlich eine Nullfolge. Eine Folge, die keinen Grenzwert aufweist, heißt
7. März 2012
116
c
!Martin
Wilkens
10.1 Zahlenfolgen, Konvergenz und Grenzwert
117
divergent. Die Folge (2n ), beispielsweise, ist divergent. Aber auch die Folge ((−1)n )
konvergiert nicht, gilt daher als divergent.
Der Grenzwert einer konvergenten Folge ist eindeutig bestimmt. Seien nämlich a,
b Grenzwerte der Folge xn und ε > 0 beliebig. Da die Folge nach Voraussetzung
konvergiert gibt es ein n > N mit |xn − a| < ε, |xn − b| < ε, woraus
|a − b| = |(xn − b) − (xn − a)| ≤ |xn − b| + |xn − a| < 2ε
(10.4)
folgt. Und da ε beliebig, insbesondere beliebig klein (und positiv), ist a − b = 0 bzw.
a = b.
qed
Summe, Differenz, Produkt und Quotient zweier – allgemein: endlich vieler – konvergenter Folgen sind gliedweise erklärt. Die resultierende Folge konvergiert dann
gegen einen Grenzwert, der gleich der Summe, Differenz, Produkt oder Quotient der
ursprünglichen Folgen ist (eine Ausnahmen ist die Division durch 0). Beispiele:
"
!
1
1
= lim 1 + lim = 1 + 0 = 1
(10.5)
lim 1 +
n→∞
n→∞ n
n→∞
n
#
$
!
"
limn→∞ 1 + n1
n+1
1
#
$=
lim
=
(10.6)
3
2n + 3
2
limn→∞ 2 + n
Das ist typisch Mathe: ausgehend von einem “Basisobjekt” (hier : Zahl) führt man
zunächst ein “Metaobjekt” ein (hier: Zahlenfolge), vereinbart “Metametaobjekte”
(hier: Grenzwert von Zahlenfolge), und sucht dann die Verknüpfungen, die auf der
Ebene der Basisobjekte bereits eingeführt sind (hier: die Arithmetischen Operationen Addition, Subtraktion, Multiplikation und Division), auf die Ebene der Metaobjekte zu erweitern (hier: die “Addition” zweier Folgen wird über die bereits
etablierte Addition von Folgengliedern= Zahlen definiert), so dass sich die Erweiterung auf die Ebene der Metametaobjekte fortsetzen lässt (hier: Limes einer Summe
zweier Folgen ist die Summe der Limiten der beiden einzelnen Folgen).
c
!Martin
Wilkens
117
7. März 2012
118
Elemente der Infinitesimalrechnung
Eine Folge (an ) heißt
• beschränkt, wenn es eine reelle Zahl K ≥ 0 gibt, so dass für alle Folgenglieder
|an | ≤ K,
• monoton wachsend, wenn für alle n gilt an+1 ≥ an ,
• monoton fallend, wenn für alle n gilt an+1 ≤ an .
Jede konvergente Zahlenfolge (an ) ist beschränkt – aber Beschränktheit ist lediglich
notwendige Bedingung für Konvergenz, nicht hinreichend. Die Folge (−1)n , beispielsweise ist beschränkt, aber keineswegs konvergent. Notwendig und hinreichend
ist Beschränktheit allerdings für solche Folgen, die monoton wachsen oder fallen.
Folgen eignen sich auch, um Zahlenmengen zu charakterisieren. Etwa so: Eine Teilmenge M von R oder C heißt
abgeschlossen, wenn jede konvergente Folge von Elementen an ∈ M einen
Grenzwert a in M hat.
beschränkt, wenn es eine Zahl R gibt, so dass |x| ≤ R für alle x ∈ M
kompakt, wenn M abgeschlossen und beschränkt ist.
Die mit Abstand nettesten Mengen sind die kompakten Mengen – in ihnen bleibt
immer allles schön endlich und man stößt in ihnen nicht auf Überraschungen.1 . So
ist beispielsweise jedes abgeschlossene Intervall [a, b] ⊂ R abgeschlossen (gut so –
Eine Überraschung bietet beispielsweise die Folge (1 + n−1 )n . Das ist nämlich eine Folge in
der Menge der rationalen Zahlen zwischen 1 und 3, und die Überraschung ist, dass der Grenzwert
– die Eulerzahl e – keine rationale Zahl ist. Oops . . .
1
7. März 2012
118
c
!Martin
Wilkens
10.1 Zahlenfolgen, Konvergenz und Grenzwert
119
abgeschlossene Intervalle sind abgeschlossen), und – da beschränkt – auch kompakt.
Hingegen ist das rechtsseitig offene Intervall [a, b[ zwar beschränkt, aber nicht abgeschlossen – der Grenzwert der Folge a + (b − a)/2n ist b, und liegt somit nicht in
[a, b[ – und somit auch nicht kompakt.
Eine reelle oder komplexe Zahl h heißt Häufungswert der Folge (an ), wenn jede
Umgebung Uε (h) von h unendlich viele Folgenglieder an enthält, wenn also gilt
|h − an | < ε für unendlich viele n. Eine konvergente Folge hat demnach genau
ihren Grenzwert als Häufungspunkt, die nicht-konvergente Folge ((−1)n ) hat die
Häufungspunkte 1 und −1, . . . und eine surjektive Folge N → Q hat jede(!) reelle
Zahl als Häufungswert (da jedes Intervall unendlich viele rationale Zahlen enthält).
Das ist ziemlich cool – kann man doch die reellen Zahlen als die Menge aller
Häufungswerte solcher Folgen rationaler Zahlen einführen!
Satz (Bolzano-Weierstrass): Jede beschränkte Folge komplexer Zahlen besitzt
mindestens einen Häufungswert. Äquivalent: Jede beschränkte Folge komplexer Zahlen besitzt mindestens eine konvergente Teilfolge.
Definition “Cauchy-Folge”: Eine Folge (an ) ist eine Cauchy-Folge, auch genannt
Fundamentalfolge, wenn es zu jeder positiven Zahl ε eine natürliche Zahl Nε
gibt, so dass
|am − an | < ε für alle m, n ≤ Nε .
(10.7)
Bei einer Cauchy-Folge ziehen sich die Folgenglieder mit wachsendem n immer mehr
zusammen. Von einem Grenzwert ist dabei nicht die Rede. Es gilt aber der wichtige
Satz: Eine Folge konvergiert genau dann in R (oder C) , wenn sie eine CauchyFolge ist (Ohne Beweis). Das ist eine wertvolle Einsicht, kann man doch über die
Konvergenz (oder nicht-Konvergenz) einer Folge entscheiden ohne den Grenzwert
angeben zu müssen.
c
!Martin
Wilkens
119
7. März 2012
120
Elemente der Infinitesimalrechnung
Cantor hat seinerzeit die rellen Zahlen als Äquivalenzklassen von Fundamentalfolgen
in den rationalen Zahlen konstruiert. Beispiel: en := (1 + n1 )n ist eine Cauchy-Folge
in den rationalen Zahlen. Der Grenzwert limn→∞ en := e (Eulers e = 2, 71 . . .) ist
allerdings nicht rational – er gestattet keine endliche Bruchdarstellung – ist aber
Elemet der reellen Zahlen.
10.2
Reihen
Hat man eine beliebige Folge (an ), kann
% man daraus eine neue Folge (SN ) bilden,
die Folge der Partialsummen SN = N
n=1 an . Hat die Folge (SN ) einen Grenzwert,
notiert man
S := lim SN =
N →∞
und nennt
7. März 2012
%
n
∞
&
an .
(10.8)
n=1
an eine konvergente Reihe. Andernfalls heißt die Reihe divergent.
120
c
!Martin
Wilkens
10.2 Reihen
121
Beispiel für eine konvergente Reihe (mit Hilfe von Partialbruchzerlegung)
∞
&
n=1
"
&!1
1
1
=
−
n(n + 1)
n n+1
(10.9)
∞
∞
&
1 & 1
=
−
n n=1 n + 1
n=1
(10.10)
∞
∞
&
1 & 1
= 1+
−
n n=1 n + 1
n=2
= 1+
= 1.
∞
&
(10.11)
∞
& 1
1
−
m + 1 n=1 n + 1
m=1
(10.12)
(10.13)
Beispiel für eine divergente Reihe ist die sog. harmonische Reihe
∞
&
1
1 1
= 1 + + + . . . = ∞.
n
2 3
n=1
(10.14)
%1
wobei ∞ bedeutet “es gibt keine natürliche Zahl N so dass
< N ”.
n
%∞
Reihen der Form n=0 an z n , worin z eine beliebige komplexe (oder reelle) Zahl,
heißen Potenzreihe. Eine gegebene Potenzreihe wird i.A. nicht für alle z konvergieren,
sondern nur für solche z deren Betrag kleiner ist als der Konvergenzradius der Reihe.
Die geometrische Reihe beispielsweise
∞
&
n=0
c
!Martin
Wilkens
zn =
1
,
1−z
|z| < 1
(10.15)
121
7. März 2012
122
Elemente der Infinitesimalrechnung
konvergiert nur für |z| < 1. Es gilt nämlich (1 − z)(1 + z + z 2 + · · · + z N −1 ) = 1 − z N ,
N
daher 1 + z + z 2 + · · · + z N −1 = 1−z
, im Limes N → ∞ folgt die Behauptung sofern
1−z
nur |z| < 1.
Um zu entscheiden, ob eine gegebene Reihe konvergiert oder nicht greift man gerne
auf einfach zu entscheidende Kriterien zurück,
das Majorantenkriterium%beispiels%
weise: Existiert für eine gegebene Reihe
an eine %
konvergente Reihe
bn = B
und ist |an | ≤ bn für fast alle n,'%
so konvergiert
auch
a
.
Beweis
via
Abschätzung
n
'
%
%∞
'≤ ∞
des Reihenrestes: |S − SN | = ' ∞
a
|a
n
n| ≤
n=N +1
n=N +1
n=N +1 bn → 0 für
N → ∞.
%
Von praktischer Bedeutung das Quotientenkriterium: Eine Reihe
an bei der der
Quotient zweier aufeinanderfolgender Glieder die Ungleichung |an+1 /an | ≤ δ < 1 fast
immer (d.h. bis auf endlich viele Ausnahmen) erfüllt, ist konvergent.
|an+1 /an | ≤
% Aus
n−1
δ < 1 folgt nämlich |an%
| ≤ δ n−1 |a1 |. Die geometrische Reihe ∞
δ
|a1 | ist aln=1
so eine Majorante von
an . Sofern δ < 1 konvergiert die Majorante, nach
% dem
Majorantenkriterium also auch die durch die Majorante majorisierte Reihe
an .
10.3
Exponentialfunktion
%
zn
Betrachte die Reihe ∞
n=0 n! worin z irgendeine komplexe Zahl. Bildet man hier
n+1
|z|
den Quotienten zweier aufeinanderfolgender Summanden, |z| |z|n/(n+1)!
= n+1
erkennt
/n!
man, dass es für jedes z ein N gibt (etwa N = INT(|z|), worin INT(x) die Aufrundung
|z|
von x auf die nächst-größere ganze Zahl), so dass n+1
< 1 für alle n > N , und also
die fragliche Reihe für jedes z konvergiert! Sie ist damit eine Funktion,
exp(z) :=
∞
&
zn
n=0
7. März 2012
122
n!
(10.16)
c
!Martin
Wilkens
10.3 Exponentialfunktion
123
genannt die Exponentialfunktion.
Für z, w zwei komplexe Zahlen berechnet sich das Produkt exp(z) exp(w) wie folgt,
( ∞
) (∞
)
∞ &
∞
& zm
& wn
&
z m wn
·
=
(10.17)
m!
n!
m!
n!
m=0
n=0
m=0 n=0
( k
)
∞
&
& z m wk−m
=
(10.18)
m! (k − m)!
m=0
k=0
∞
k ! "
&
1 & k m k−m
=
z w
(10.19)
k! m=0 m
k=0
& 1
=
(z + w)k
(10.20)
k!
k=0
kurz
exp(z) · exp(w) = exp(z + w) .
(10.21)
Aus Gl. (10.21) folgt unmittelbar exp(z) exp(−z) = 1, und das übersetzt sich mittels
() in die Identität
1
exp(−z) =
(10.22)
exp(z)
Die Funktionalgleichung (10.21) erinnert an die Identität ap aq = ap+q , und man
schreibt daher
exp(z) ≡ ez
(10.23)
worin e die Eulerzahl,
e := exp(1) = 2, 7182818 + R ,
c
!Martin
Wilkens
|R| < 2 · 10−7
123
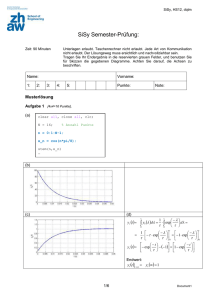
Abb 10.1 Die Exponentialfunktion für
reelle Argumente nebst ihrer Umkehrfunktion ln(x) (deren Graph man durch “Spiegelung an der Diagonalen” erhält).
(10.24)
7. März 2012
124
Elemente der Infinitesimalrechnung
Angesichts (10.23) nennt man die Exponentialfunktion auch die e-Funktion.
Zur Berechnung von ex mit x reell bestimmt man zunächst eine ganze Zahl g und
nicht-negative reelle Zahl ξ so dass x = g + ξ, bzw. ex = eg eξ . Zur näherungsweisen Bestimmung von e und eξ kann ein endlicher Abschnitt der Exponentialreihe
verwendet werden. Die Abschätzung des Fehlers ergibt sich dabei wie folgt. Sei
zunächst
& xk
(10.25)
ex =
n + Rn+1 (x)
k!
k=0
dann gilt für |x| ≤ 1
∞
&
|x|k
|Rn+1 (x)| ≤
k!
k=n+1
"
|x|
|x|2
1+
+
+ . . .(10.26)
n + 2 (n + 2)(n + 3)
!
"
|x|n+1
1
1
≤
1 + + 2 + ...
(10.27)
(n + 1)!
2 2
|x|n+1
≤ 2
,
(10.28)
(n + 1)!
|x|n+1
=
(n + 1)!
!
lies: für |x| ≤ 1 ist der Fehlerbetrag höchstens so groß wie der doppelte Betrag des
ersten weggelassenen Summanden. Verwendet man also zur Berechnung von e den
2
Abschnitt 1 + 1!1 + 2!1 + . . . + n!1 , so ist der Fehler 0 < Rn+1 (1) < (n+1)!
. Dank der
Fakultät im Nenner, konvergiert die Exponentialriehe für e sehr schnell. Für n = 10
beispielsweise ist R11 (1) < 6 · 10−8 , bzw. e wie in Gl. (10.24) unter Berücksichtigung
der Rundungsfehler angegeben.
Aus der Reihendarstellung (10.16) folgt [exp(z)]∗ = exp(z ∗ ) bzw. für z = x + iy mit
x, y reell,
[exp(x + iy)]∗ = exp(x − iy)
(10.29)
7. März 2012
124
c
!Martin
Wilkens
10.3 Exponentialfunktion
125
Insbesondere wenn z rein imaginär, z = iϕ, ergibt sich
[exp(iϕ)]∗ = exp(−iϕ)
(10.30)
und also | exp(iϕ)| = 1. Da jede komplexe unimodulare Zahl dargestellt werden kann
cos ϕ + i sin ϕ liefert der Vergleich von Real- und Imaginärteil von exp(iϕ) mit der
Darstellung exp(iϕ) = cos ϕ + i sin ϕ die Reihendarstellung der trigonometrischen
Funktionen für reellwertig Argumente
cos ϕ =
∞
&
n=0
∞
&
(−1)n
ϕ2n
ϕ2 ϕ4 ϕ6
=1−
+
−
+ ...
(2n)!
2!
4!
6!
ϕ2n+1
ϕ3 ϕ5 ϕ7
sin ϕ =
(−1)
=ϕ−
+
−
+ ...
(2n + 1)!
3!
5!
7!
n=0
n
(10.31)
(10.32)
Der Cosinus hat im Intervall [0, 2] genau eine Nullstelle, bezeichnet π/2, also cos π2 =
0, angesichts cos2 + sin2 = 1 auch sin π2 = 1. Die Euler’sche Formel liefert dann
iπ/2
= cos π2 + i sin π2 = i, quadriert
eiπ = −1
(10.33)
eine der schönsten Formeln der modernen Mathematik, vereinigt sie doch Eulers e,
Euklids π Gauss’ i und die negative Einheit −1.
Es spricht nichts dagegen, für die trigonometrischen Funktionen auch komplexe Argumente zuzulassen. Man erweitere einfach die Definitionen, und setze für beliebiges
z∈C
eiz + e−iz
eiz − e−iz
cos z :=
,
sin z :=
.
(10.34)
2
2i
Die Reihendarstellung ist dann wie in (10.31,10.32) nur mit ϕ ersetzt durch z.
c
!Martin
Wilkens
125
7. März 2012
126
Elemente der Infinitesimalrechnung
Nach wie vor gilt hier die Euler’sche Formel
eiz = cos z + i sin z ,
(10.35)
cos2 z + sin2 z = 1 ,
(10.36)
cos(z + w) = cos z cos w − sin z sin w ,
sin(z + w) = sin z cos w + cos z sin w .
(10.37)
(10.38)
der Satz des Pythagoras
und die Additionstheoreme
Ebenso wie die trig-Funktionen könne auch die Hyperbelfunktionen für komplexe
Argumente definiert werden,
ez + e−z
ez − e−z
,
sinh z :=
.
(10.39)
2
2
Offensichtlich sind die Hyperbelfunktionen und die Trigonometrischen Funktionen
verknüpft
cosh z = cos(iz) ,
sinh z = −i sin(iz) ,
(10.40)
cosh z :=
woraus sich mit Hilfe (10.38) Additionstheoreme angeben lassen,
cosh(z + w) = cosh z cosh w + sinh z sinh w
sinh(z + w) = sinh z cosh w + cosh z sinh w ,
(10.41)
(10.42)
und es gilt der hyperbolische Pythagoras,
cosh2 z − sinh2 z = 1 .
(10.43)
Die Reihendarstellung entnimmt man (10.39) und Berücksichtigung von (10.16),
∞
&
z 2n
cosh z =
,
(2n)!
n=0
7. März 2012
126
sinh z =
∞
&
n=0
z 2n+1
.
(2n + 1)!
(10.44)
c
!Martin
Wilkens
10.4 Aufgaben
10.4
127
Aufgaben
& Aufgabe 10-1
Zeigen Sie
lim
n→∞
!
n+1
2n + 3
"
=
1
.
2
(10.45)
& Aufgabe 10-2
Zeigen Sie
1
= 0 für jedes positives s ∈ Q.
n→∞ ns
√
lim n a = 1 für jedes reelle a > 0.
n→∞
√
lim n n = 1 .
lim
(10.46)
(10.47)
(10.48)
n→∞
& Aufgabe 10-3
Zeigen Sie
∞
&
n=1
1
1
=
.
4n2 − 1
2
(10.49)
Hinweis: Eine Partialbruchzerlegung des Summanden könnte sich als nützlich erweisen . . .
& Aufgabe 10-4
√
Falls Sie sich jemals gefragt haben, wie man Wurzeln zieht (vulgo “ 2 ausrechnet”)
– hier ist die Antwort: mit Hilfe der Rekursion
!
"
1
a
xn+1 =
(10.51)
xn +
2
xn
c
!Martin
Wilkens
127
7. März 2012
128
Elemente der Infinitesimalrechnung
worin a eine vorgegebene reelle Zahl größer Null (deren Wurzel man berechnen
möchte).
(a) Berechnen Sie für den Fall a = 2 und Startwert x0 = 1 die drei ersten Glieder
der Folge (). Lassen Sie sich anschließend die Wurzel aus 2 von Ihrem Taschenrechner anzeigen und vergleichen Sie x3 mit der Anzeige Ihres Taschenrechners.
√
(b) Zeigen Sie: Bei beliebig gewähltem Startwert x0 > 0√gilt xn ≥ a und die
Folge () konvergiert ab n = 1 monoton fallend gegen a.
√
(c) Zeigen Sie, dass der Fehler fn := xn − a abgeschätzt wird |fn+1 | ≤ 2√1 a fn2 .
√
−4
Schließen Sie, dass für x3 im obigen Beispiel |x3 − 2| < 2−4 ·10
√ . Auf wieviele
Stellen (hinter dem Komma) approximiert also x3 die Zahl 2?
& Aufgabe 10-5
1
Man skizzieren der Funktionsgraphen der Funktion 1+z
2 (für reelle z = x) und
beweise
∞
&
1
=
(−1)n z 2n ,
|z| < 1 .
(10.55)
2
1+z
n=0
Warum ist hier die Einschränkung |z| < 1 vorzunehmen? Was passiert für z → ±i
auf der linken Seite und auf der rechten Seite der Identit—ät (10.55)?
& Aufgabe 10-6 (Pythagoräische Weihnachen)
Zeichnen Sie ein regelmäßiges Fünfeck (Pentagon), tragen die Diagonalen ein, erhalten so ein Pentagramm, und überzeugen sich davon, dass hier gilt
Diagonale : Seite = Seite : (Diagonale − Seite)
7. März 2012
128
(10.56)
c
!Martin
Wilkens
10.4 Aufgaben
129
Hinweis: Die Diagonalen bilden in der Mitte wiederum ein Pentagon – hilft das
weiter?
Benennen Sie
g := Diagonale : Seite
(10.57)
und zeigen dass g nicht rational.
Die Zahl g nennt man den goldenen Schnitt. Betrachten Sie zum Startwert x0 = 1
die Folge
1
(10.58)
xn+1 = 1 +
xn
und zeigen Sie limn→∞ xn = g mit
√ +
1*
g=
1+ 5 .
(10.59)
2
Gehen Sie auf Wikipedia, und lesen dort unter dem Stichwort “Pythagoräer” und
“Goldener Schnitt” nach, was es mit den beiden auf sich hat.
c
!Martin
Wilkens
129
7. März 2012
130
7. März 2012
Elemente der Infinitesimalrechnung
130
c
!Martin
Wilkens