Kapitel 6

T6
T6.1
Elektrodynamik in Materie
Die phänomenologischen Maxwell Gleichungen
Wir wollen hier den Einfluss von Materie auf makroskopische elektromagnetische Phänomene beschreiben. Wir betrachten zunächst ein einfaches Beispiel.
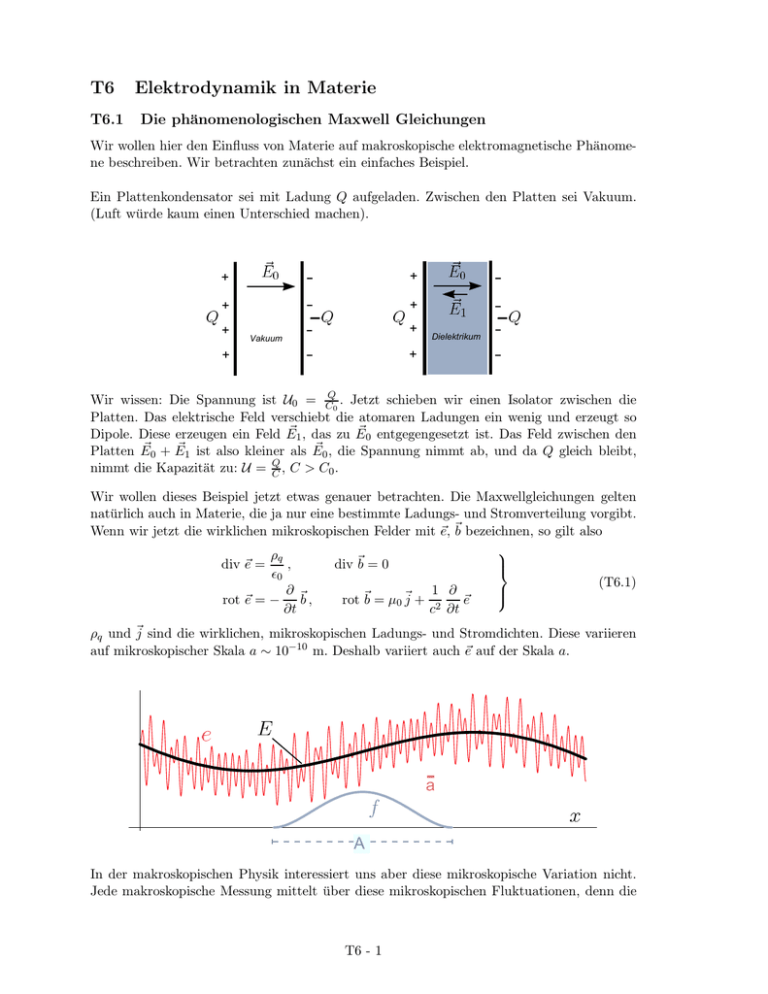
Ein Plattenkondensator sei mit Ladung Q aufgeladen. Zwischen den Platten sei Vakuum.
(Luft würde kaum einen Unterschied machen).
+
-
+
-
+
-
+
-
-
+
-
+
+
+
Vakuum
Dielektrikum
-
Wir wissen: Die Spannung ist U0 = CQ0 . Jetzt schieben wir einen Isolator zwischen die
Platten. Das elektrische Feld verschiebt die atomaren Ladungen ein wenig und erzeugt so
~ 1 , das zu E
~ 0 entgegengesetzt ist. Das Feld zwischen den
Dipole. Diese erzeugen ein Feld E
~0 + E
~ 1 ist also kleiner als E
~ 0 , die Spannung nimmt ab, und da Q gleich bleibt,
Platten E
Q
nimmt die Kapazität zu: U = C , C > C0 .
Wir wollen dieses Beispiel jetzt etwas genauer betrachten. Die Maxwellgleichungen gelten
natürlich auch in Materie, die ja nur eine bestimmte Ladungs- und Stromverteilung vorgibt.
Wenn wir jetzt die wirklichen mikroskopischen Felder mit ~e, ~b bezeichnen, so gilt also

ρq

div ~e =
,
div ~b = 0

ǫ0
(T6.1)
1 ∂
∂ ~


~
~
~e
rot b = µ0 j + 2
rot ~e = − b ,
∂t
c ∂t
ρq und ~j sind die wirklichen, mikroskopischen Ladungs- und Stromdichten. Diese variieren
auf mikroskopischer Skala a ∼ 10−10 m. Deshalb variiert auch ~e auf der Skala a.
a
A
In der makroskopischen Physik interessiert uns aber diese mikroskopische Variation nicht.
Jede makroskopische Messung mittelt über diese mikroskopischen Fluktuationen, denn die
T6 - 1
Ausdehnung des Messgeräts ist viel größer als a. Wir müssen also gemittelte ’makroskopische
Felder’ definieren. Wir definieren eine Gewichtsfunktion f (~r) mit folgenden Eigenschaften:

f (~r) ≥ 0 , f (~r) = 0 für | ~r | > A




−10
−3
10 m ∼ a ≪ A ≪ 10 m
(T6.2)
Z


3


a | ∇ f (~r) | ≪ 1 ,
d r f (~r) = 1 .
Die gemittelten makroskopischen Felder sind
Z
~
E(~r, t) = d3 r ′ f (~r − ~r ′ ) ~e(~r ′ , t)
Z
~
B(~r, t) = d3 r ′ f (~r − ~r ′ ) ~b(~r ′ , t) .
Diese Mittelung1 beseitigt die mikroskopischen Fluktuationen.




(T6.3)



In der obigen Abbildung wurde als ’mikroskopische’ Funktion e(x) = 1.5 − 0.3 x + sin x + 13 sin (15 π x) +
15
1
2
2 2
5 cos (16 π x) + cos (13 π x) gewählt. Die Gewichtsfunktion ist f (x) = 16 (1 − x ) , | x | ≤ A = 1. Die
Mittelung beseitigt im wesentlichen die rasch oszillierenden Terme ∼ sin(15 π x), cos (16 π x), und ersetzt
cos2 (13 π x) durch den Mittelwert 12 .
Jetzt mitteln wir die Maxwell Gleichungen, z.B.
div ~b = 0
0=
Z
d3 r ′ f (~r − ~r ′ )
3
X
∂
bα (~r ′ , t) .
′
∂
r
α
α=1
Nun gilt
Z
∂
bα (~r ′ , t)
d3 r ′ f (~r − ~r ′ )
∂ r ′α
Z
∂
= − d3 r ′
f (~r − ~r ′ ) bα (~r ′ , t)
∂r ′α
Z
∂
f (~r − ~r ′ ) bα (~r ′ , t)
=
d3 r ′
∂rα
(Die Randterme verschwinden wegen f = 0 für | ~
r | > A)
Es folgt
0=
oder
Z
d3 r ′ f (~r − ~r ′ ) ∇r ′ · ~b(~r ′ , t) = ∇r ·
Z
d3 r ′ f (~r − ~r ′ ) ~b(~r ′ , t) .
~ = 0.
div B
~ ist das Feld E
~0 + E
~ 1 in der oben durchgeführten einfachen Betrachtung des
Das gemittelte Feld E
Plattenkondensators.
1
T6 - 2
Genauso geht es für alle anderen Terme, die ~e oder ~b enthalten. Definieren wir noch die
gemittelten Ladungs- und Stromdichten:
Z


3 ′
′
′

ρ̂q (~r, t) = d r f (~r − ~r ) ρq (~r , t)

Z
(T6.4)


~ˆj(~r, t) = d3 r ′ f (~r − ~r ′ ) ~j(~r ′ , t) .

So erhalten die gemittelten Maxwell Gleichungen die Form
~ = ρ̂q ,
div E
ǫ0
~ =− ∂B
~,
rot E
∂t
~ =0
div B
~ = µ0 ~ˆj + 1 ∂ E
~.
rot B
c2 ∂t



(T6.5)


Um einen Ausdruck für ρ̂q zu gewinnen, teilen wir die mikroskopische Ladungsdichte auf:
ρq = ρ(int)
+ ρ(ext)
.
q
q
(ext)
ρq
sind die uns explizit bekannten, von außen eingebrachten Ladungen. Die Mittelung
verschmiert diese Ladungen über ein Volumen mit Durchmesser ∼ A, aber da A klein gegen
(ext)
(ext)
die makroskopischen Abstände ist, können wir auch nach der Mittelung ρ̂q
≈ ρq
als
die explizit eingebrachte äußere Ladungsdichte betrachten.
(int)
ist die interne Ladungsdichte der Materie, die auf der Skala a variiert. Um zu sehen,
ρq
was die Mittelung ergibt, wollen wir ein schematisches Beispiel betrachten.
Wir betrachten ein einzelnes ’Molekül’, bestehend aus
Ladungen ± q im Abstand a -, also einen Dipol.
Mikroskopische Ladungsdichte
a a ρ(Mol)
(~r ′ ) = q δ ~r ′ − ~e − δ ~r ′ + ~e .
q
2
2
Mittelung ergibt
Z
a a d3 r ′ f (~r − ~r ′ ) ρq(M ol) (~r ′ ) = q f ~r − ~e − f ~r + ~e
2
2
a
a
= q f (~r) − ~e · ∇r f (~r) − f (~r) − ~e · ∇r f (~r) + O(a3 ) , (Taylorentwicklung),
2
2
= − q a ~e · ∇r f (~r) + O (a3 )
~ Dipolmoment des Moleküls.
q a ~e = d:
T6 - 3
Da d~ von ~r unabhängig ist, können wir weiter schreiben
− d~ · ∇r f (~r) = −∇r · f (~r) d~ .
Dies ist der führende Beitrag unseres Moleküls zur gemittelten Ladungsdichte. Unser Molekül
war am Ort ~r = 0 lokalisiert. Um dies deutlich zu machen, schreiben wir das Ergebnis als
Z
− ∇r · d3 r ′ f (~r − ~r ′ ) d~ δ(~r ′ ) .
Ein Dielektrikum besteht aus vielen molekularen Dipolen. Molekül Nummer j befinde sich
am Ort ~rj und habe die Dipolstärke d~j . Sein Beitrag zur gemittelten Ladungsdichte ist also
Z
− ∇r d3 r ′ f (~r − ~r ′ ) d~j δ(~r ′ − ~rj ) .
Falls das von außen angelegte Feld zeitabhängig ist, wird auch die durch dieses erzeugte Dipolstärke zeitabängig sein: d~j = d~j (t). Wir definieren nun die Polarisation des Dielektrikums
als
Z
X
d~j δ(~r ′ − ~rj ) .
(T6.6)
P~ (~r, t) = d3 r ′ f (~r − ~r ′ )
j
Sie ist also die gemittelte lokale Dipolstärke. Damit erhalten wir für die gemittelte Ladungsdichte
ρ̂q (~r, t) = − div P~ (~r, t) + ρ(ext)
(~r, t) .
q
(T6.7)
Eine analoge - allerdings kompliziertere - Betrachtung liefert
~ (~r, t) + ∂ P~ (~r, t) + ~j (ext) (~r, t) .
~ˆj(~r, t) = rot M
∂t
(T6.8)
~ (~r, t) ist die ’Magnetisierung’. Im Rahmen der klassischen Physik beschreibt sie den geM
mittelten Effekt von in den Molekülen fließenden ’Ringströmen’. Wirklich zu verstehen ist
sie erst in der Quantenmechanik, denn solche ’Ringströme’ gibt es eigentlich nicht. Der Term
∂ ~
∂t P beschreibt die Ströme, die zur Änderung des Dipolmoments führen. Er sorgt dafür, dass
die Kontinuitätsgleichung erfüllt ist.
Betrachten wir nun die Gleichung
~ = ρ̂q = 1 − div P~ + ρ(ext)
div E
,
q
ǫ0
ǫ0
~ und 1 div P~ zusammen fassen können. Dies definiert ein neues
so sehen wir, dass wir div E
ǫ0
~
Feld D, das als ’dielektrische Verschiebung’ bezeichnet wird.
Ebenso definiert man
~ =E
~ + 1 P~ .
D
ǫ0
(T6.9)
~ =B
~ − µ0 M
~ .
H
(T6.10)
T6 - 4
~ wird allgemein als ’Magnetfeld’ bezeichnet, B
~ heißt ’magnetische Induktion’. Mit (T6.8)H
~ = µ0 ~ˆj + 12 ∂ E
~
(T6.10) erhält man aus rot B
c
∂t
~.
~ = µ0 ~j (ext) + µ0 ∂ P~ + 1 ∂ E
rot H
2 ∂t
∂t
c
|
{z
}
1 ∂ ~
D
c2 ∂t
Damit erhalten die makroskopischen Maxwell Gleichungen die Form
~ = 1 ρ(ext) ,
div D
ǫ0 q
~,
~ =− ∂B
rot E
∂t
~ =0
div B
~ = µ0 ~j (ext) + 1 ∂ D
~.
rot H
c2 ∂t
Dies sind die Gleichungen, die die gemittelten Felder erfüllen.



(T6.11)


Um mit diesen Gleichungen etwas anzufangen, müssen wir noch den Zusammenhang zwi~ (bzw. P~ ) und E
~ und zwischen H
~ (bzw. M
~ ) und B
~ kennen. Dieser hängt vom
schen D
~
Material ab. Es gibt Substanzen, für die auch ohne äußeres B-Feld die Magnetisierung von
Null verschieden ist:
~ = 0,
B
~ =M
~ 0 6= 0 .
M
Dies sind Ferromagneten - die bekannten Permanentmagneten. Ebenso gibt es Ferroelektrika:
~ = 0,
E
P~ = P~0 6= 0 .
~ 0 = 0 , P~0 =
Solche Substanzen wollen wir hier nicht betrachten. Wir beschränken uns auf M
~
0. Dann wird die Polarisation nur durch das äußere E-Feld erzeugt, das die Ladungen in den
Molekülen verschiebt. In einfachster Näherung schreiben wir
~ r , t) .
P~ (~r, t) = χe E(~
(T6.12)
Die Konstante χe ist die elektrische Suszeptibilität, und (T6.12) ist der erste Term einer
~ Höhere Terme braucht man im allgemeinen nicht zu betrachten Taylorentwicklung nach E.
~
außer man hat es mit extremen E-Feldern
zu tun wie sie bei höchst intensiven Lasern auftreten. (Solche Effekte der ’nichtlinearen Optik’ sind heute ein sehr aktuelles Forschungsgebiet).
Damit erhalten wir aus Gleichungen (T6.9), (T6.12)
~ r , t) = ǫ E(~
~ r , t) .
D(~
ǫ =1−
χe
ǫ0
(T6.13)
(T6.14)
ist die Dialektrizitätskonstante des Materials. Ebenso schreiben wir
~ r , t) = 1 B(~
~ r , t) ,
H(~
µ
T6 - 5
(T6.15)
mit der Permeabilität µ. Empirisch stellt sich heraus, dass Gl.(T6.13) die meisten Substanzen
sehr gut beschreibt. Allerdings muss man sie für Kristalle je nach Struktur etwas verallgemeinern. Die Polarisierbarkeit kann von der Richtung im Kristall abhängen. Dies wird durch
den Dialektrizitätstensor ǫαβ beschrieben, und (T6.13) erhält die Term
Dα (~r, t) =
3
X
ǫαβ Eβ (~r, t) ,
α = 1, 2, 3 .
β=1
Dies ist die Ursache des Phänomens der ’Doppelbrechung’. Wir werden uns hier auf isotrope
Substanzen beschränken, in denen Gl. (T6.13) gilt.
Gleichung (T6.15) ist weniger nützlich. Es stellt sich heraus, dass für unmagnetische Mate~ und H
~ eigentlich
rialen µ sehr nah bei µ = 1 ist, so dass die Unterscheidung zwischen B
überflüssig ist, wenn man nicht penibel nach speziellen Effekten sucht. Hingegen bricht für
~
magnetische Materialen (z.B. Eisen) die lineare Näherung (T6.15) schon für sehr kleine B~
~
~
Felder zusammen und man muss die volle nichtlineare Funktion M = M (B) diskutieren.
Mit all diesen Komplikationen können wir uns hier nicht befassen. Wir werden im Weiteren die Gleichungen (T6.11), (T6.13), (T6.15) zu Grunde legen, die viele Dielektrika (Glas,
Kunststoffe) sehr gut beschreiben.
T6.2
Wellen in Dielektrika
Wir betrachten hier die homogenen makroskopischen Maxwell Gleichungen:
ρ(ext)
= 0 , ~j (ext) = 0 .
q
~ und H
~ in linearer Näherung (T6.13), (T6.15), so erhalten wir aus (T6.11)
Eliminieren wir D
~ = 0,
div E
~ =0
div B
~ =− ∂B
~ , rot B
~ = µǫ ∂ E
~.
rot E
∂t
c2 ∂t


(T6.16)

Dies sind aber die selben Gleichungen wie im Vakuum. Nur die Phasengeschwindigkeit c ist
√
durch c/ µ ǫ ersetzt. Man definiert den Brechungsindex
n=
√
µǫ.
(T6.17)
Dass n wirklich der Brechungsindex ist, werden wir in § 6.3 sehen.
Wir halten fest:
Im (isotropen) Dielektrikum haben elektromagnetische Wellen denselben Charakter wie im
T6 - 6
Vakuum. Es sind transversal polarisierte Wellen. Nur die Phasengeschwindigkeit ist geändert:
c(n) =
c
.
n
(T6.18)
Dies bedeutet auch, dass die Dispersionsrelation der ebenen Wellen abgeändert ist:
c
c
ω = √ | ~k | = | ~k | ,
µǫ
n
(T6.19)
oder, mit | ~k | = 2π/λ
ω=
2π c
.
nλ
(T6.20)
Es ist klar, dass wir hier die Materie auf rein phänomenologischem Niveau behandeln. Vergleicht man mit dem Experiment, so sieht man, dass man die Beschreibung modifizieren
muss. Die Dielektrizitätskonstante ǫ - und damit der Brechungsindex - hängt im Allgemeinen
von der Wellenlänge λ ab. Dies führt auf das Phänomen der Dispersion: Wellen verschiedener Wellenlänge, d.h. mit verschiedenen | ~k |, werden unterschiedlich stark gebrochen. Die
’Dielektrizitätskonstante’ wird also zu einer Funktion ǫ = ǫ(k), und damit wird die Frequenz
eine nichtlineare Funktion von k = | ~k |
ω(k) = p
ck
µ ǫ (k)
.
(T6.21)
Die Ursache dieser Komplikation ist leicht zu verstehen. Die Dielektrizitätskonstante bechreibt den gemittel~ erzeugt werden. Oszilliert das
ten Effekt der molekularen oder atomaren Dipole, die durch das äußere Feld E
Feld mit Frequenz ω, so werden auch die Dipole mit Frequenz ω oszillieren. Die Amplitude dieser Schwingungen und damit das Dipolmoment wird von ω abhängen: Wenn wir dicht bei einer Eigenfrequenz des
mikroskopischen Systems sind, wird sie besonders groß, wie wir im ersten Semester gelernt haben.
Wir wollen die Konsequenzen für die Ausbreitung eines Wellenpakets an einem einfachen
~ = E(x,
~
Beispiel illustrieren. E
t) habe die Form
~e2
~
E(x,
t) = √ E0
2π
+∞
Z
2
d k e− (k−k0 ) /2Γk ei(k x−ω(k)t) .
(T6.22)
−∞
Dies ist ein Gauß-Paket der Breite 2 Γk im k-Raum. Das Maximum liegt bei k0 . Im Bereich,
2
in dem e−(k−k0 ) /2Γ wesentlich von Null verschieden ist, möge ω(| ~k |) nur wenig variieren, so
dass wir um k0 entwickeln dürfen
ω(k) = ω(k0 ) + (k − k0 )
d ω(k0 )
+ O (k − k0 )2 .
d k0
2
(T6.23)
Bemerkung: Diese Definition von Γk unterscheidet sich von der in §4.3, Beispiel B4.1 verwendeten von
~ 2 betrachtet haben, hier aber E
~ selbst diskutieren.
einem Faktor 2. Der Grund ist, dass wir dort E
T6 - 7
Einsetzen in (T6.22) ergibt
+∞
~0 Z
E
(k − k0 )2
d ω(k0 )
~
E(x, t) = ~e2 √
d k exp −
+ i k x − i t ω(k0 ) + (k − k0 )
2 Γk
d k0
2π
−∞
E0 i (k0 x−ω(k0 )t)
e
= ~e2 √
2π
+∞
Z
k ′2
d ω(k0 )
′
′
d k exp −
·
+ ik x −
t
.
2 Γk
d k0
−∞
(Substitution k − k0 = k ′ ).
Mit der Notation
Γx =
ergibt das Integral3
r

2π

exp −
Γx
1
.
Γk
x−
dω(k0 )
d k0
2 Γx
~ (phys) = Re E
~
Damit folgt für das physikalische Feld E
(T6.24)
2 

.
1
~ (phys) (x, t) = ~e2 E0 cos (k0 x − ω(k0 )t) · √1 e− 2 Γx
E
Γx
“
”2
d ω(k )
x− d k 0 t
0
(T6.25)
Dies ist eine oszillierende Funktion, deren Amplitude mit einer Gauß-Funktion der Breite
Γx moduliert ist. Die Flächen konstanter Phase k0 x − ω(k0 )t = const bewegen sich mit der
Phasengeschwindigkeit
cph =
c
c
ω(k0 )
=
.
=p
k0
n(k0 )
µ ǫ(k0 )
(T6.26)
Das Maximum der Amplitude liegt bei
d ω(k0 )
t,
d k0
es bewegt sich also mit der Gruppengeschwindigkeit
x=
cgr =
d ω(k0 )
.
d k0
(T6.27)
Geht man in der Taylorentwicklung (T6.23) zu höheren Ordnungen, so sieht man, dass sich
auch die Form des Wellenpaketes mit der Zeit ändert.
Phasengeschwindigkeit und Gruppengeschwindigkeit stimmen nur überein, wenn der Brechungsindex von der Wellenlänge λ = 2 π/k unabhängig ist:
n(k) = n0 = const .
3
So ein Integral tauchte auch schon in Beispiel B4.1 auf.
T6 - 8
Dann gilt ω =
c
n0 k
und es folgt
cgr =
dω
c
=
= cph .
dk
n0
(T6.28)
cgr 6= cph .
(T6.29)
Im Allgemeinen gilt
und für die Physik ist die Gruppengeschwindigkeit die wichtigere Größe. Für ein allgemeines
Wellenpaket, dessen Schwerpunkt im Fourierraum bei ~ks liegt, ist sie durch
~cgr = ∇k ω (| ~k |) ~k=~ks
(T6.30)
~ des Wellenpadefiniert. Sie gibt an, wie sich der Bereich verschiebt, in dem die Amplitude E
~ 2 , ist ~cgr die
kets wesentlich von Null verschieden ist. Da für die Energiedichte w gilt w ∼ E
Geschwindigkeit mit der die Energie wandert. Es ist auch die Geschwindigkeit, mit der wir
Information übertragen können. Wir erhalten die in einem Wellenpaket irgendwie kodierte
Information (Radio, Fernsehen) erst, wenn das Wellenpaket bei uns angekommen ist.
Zum Abschluss betrachten wir noch die Energiedichte einer Welle im Dielektrikum. Das ist
sehr einfach. Wir setzen in den Maxwellgleichungen (T6.16) c2 = ǫ01µ0 :
~
div E
~
div B
= 0,
= 0,
~ = ǫ0 ǫ µ 0 µ ∂ E
~,
rot B
∂t
~
~ =− ∂B
rot E
∂t ,
und wir vergleichen mit den Maxwellgleichungen im Vakuum (T4.7):
~
div E
~
div B
= 0,
= 0,
~ = ǫ0 µ 0 ∂ E
~,
rot B
∂t
~ =− ∂B
~
rot E
∂t ,
Offensichtlich müssen wir in den Ergebnissen aus § T4.6, die im Vakuum gelten, nur ǫ0
durch ǫ0 ǫ und µ0 durch µ0 µ ersetzen. Aus (T4.73) erhalten wir für die Energiedichte im
Dielektrikum
w(~r, t) =
ǫ0 ǫ ~ 2
1 ~2
E (~r, t) +
B (~r, t) .
2
2 µ0 µ
(T6.31)
(T4.74) ergibt für die Energiestromdichte
~σ (~r, t) =
1
µ0 µ
~ r , t) × B(~
~ r , t) .
E(~
(T6.32)
Nach wie vor gilt die Kontinuitätsgleichung
∂
w(~r, t) + div ~σ (~r, t) = 0 .
∂t
T6 - 9
(T6.33)
Die gemittelte Energiedichte w̄ und die gemittelte Energiestromdichte einer ebenen Welle
ergeben sich aus (T4.77), (T4.78):
¯=
~σ
T6.3





1
ǫ0 ǫ E02
2
w̄ =
~k
~k

1
c

= w̄
. 
w̄

√
~
ǫ0 ǫ µ0 µ | ~k |
n
|k|
(T6.34)
Randbedingungen an den Oberflächen von Dielektrika, Reflektion,
Brechung
Wenn Licht auf eine Glasfläche trifft, so wird es teilweise reflektiert, und der in das Glas
eindringende Teil wird gebrochen. Im ersten Semester haben wir Reflektionsgesetz und Brechungsgesetz schon aus Newton’s Korpuskel-Modell des Lichtes hergeleitet. Wesentlich war
dabei die Erhaltung der Energie und der Impulskomponente parallel zur Oberfläche. Allerdings war nicht zu verstehen, wieso ein und derselbe Lichtstrahl sowohl reflektiert als
auch gebrochen wird. Jetzt wollen wir diese Phänomene im Rahmen der Elektrodynamik
behandeln. Hierzu müssen wir zunächst überlegen, welche Bedingungen die Felder an der
Grenzfläche erfüllen, die zwei Dielektrika trennt. Da wir am Ende der Betrachtung zu differenziell kleinen Flächenstücken übergehen werden, können wir die Grenzfläche als eben
betrachten, und so orientieren, dass die Flächenormale in Richtung ~e1 zeigt.
Wir betrachten einen kleinen Quader der von
der Grenzfläche geschnitten wird.4 Die Fläche
δ f~1 = − δ F ~e1 liegt im Dielektrikum 1,
Normalenvektor − ~e1 , δ F~2 = δ f ~e1 liegt im
Dielektrikum 2, Normalenvektor +~e1 . Die
Dicke in ~e1 -Dichtung ist a. Wir integrieren
~ = 0 über diesen
die Maxwell Gleichung div B
Quader und verwenden den Gauß’schen Satz
0=
Z
~ =
d3 r div B
Z
~ ·B
~.
df
F
Ω
Wir können a beliebig klein wählen. Daher fällt der Beitrag der Flächen der Breite a weg
und wir erhalten
Z
Z
~ = 0.
~−
df ~e1 · B
df ~e1 · B
δ f2
δ f1
~ über die Flächen als konstant anDa wir δ f beliebig klein machen können, dürfen wir B
(1)
~
~
~
~ (2) . Es folgt
nehmen. In Medium 1 sei B = B , in Medium 2 sei B = B
~ (1) − ~e1 · B
~ (2) = 0
δ f ~e1 · B
4
Die Diskussion folgt genau den Schritten der Bestimmung der Oberflächenladung in § T2.3.
T6 - 10
oder
~ (1) = ~e1 · B
~ (2) .
~e1 · B
(T6.35)
~ ist auf der Grenzfläche stetig.
Die Normalkomponente von B
~ = 1 ρ(ext)
an und finden
Wir wenden dasselbe Argument auf die Gleichung div D
ǫ0 q
Z
~ (1) − ~e1 · D
~ (2) = 1 lim d3 r ρ(ext) (~r, t) .
δ f ~e1 · D
q
ǫ0 a→0
Ω
Rechts steht jetzt die auf der Oberfläche sitzende Ladung. Für δ f → 0 erhalten wir
~ (1) (~r, t) − ~e2 · D
~ (2) (~r, t) = 1 σ(~r, t) ,
~e1 · D
ǫ0
(T6.36)
wobei σ(~r, t) die (Flächen-)Dichte der Oberflächenladungen ist.
~
Falls die Flächenladungsdichte von Null verschieden ist, ist die Normalkomponente von D
auf der Grenzfläche unstetig.
Eine Flächenladungsdichte kann nur bei leitfähigen Dielektrika auftreten. In Isolatoren kann
~ ist stetig.
keine Ladung zur Oberfläche transportiert werden, σ ist Null und ~e1 · D
Weitere Randbedingungen folgen aus den Maxwell Gleichungen, die die Rotation enthalten.
Wir betrachten jetzt ein kleines Rechteck, das von der
Grenzfläche geteilt wird. Die Kanten der Länge b sind
parallel zu ~e1 . Die Kanten ~s1 , ~s2 sind parallel zur Grenzfläche:
~s1 = − δ ℓ ~e,
~s2 = δ ℓ ~e,
~e · ~e1 = 0 .
~ =− ∂ B
~ über die Fläche des Rechtecks und verwenden
Wir integrieren die Gleichung rot E
∂t
den Stokes’schen Satz
Z
Z
Z
~ · ∂ B
~ · rot E
~.
~ = df
~ = d~r · E
df
∂t
F
C
F
~
∂B
∂t
ist sicher endlich. Deshalb verschwindet für b → 0 die rechte Seite, ebenso wie der Beitrag
der entsprechenden Kanten zum Kurvenintegral. Machen wir nun noch δ ℓ so klein, dass wir
~ auf den Kanten ~s1 , ~s2 vernachlässigken können, so folgt
die Variation von E
~ (2) − ~e · E
~ (1) = 0 ,
δ ℓ ~e · E
also
~ (2) = ~e · E
~ (1) .
~e · E
T6 - 11
Da ~e ein beliebiger Einheitsvektor parallel zur Oberfläche ist, folgt:
~ ist auf der Grenzfläche stetig.
Die Parallelkomponente von E
~ (2) .
~ (1) = E
E
||
||
(T6.37)
~
Führen wir dasselbe Argument für die rot H-Gleichung
durch, so erhalten wir zunächst
Z
~ · ~j .
~ (2) − ~e · H
~ (2) = µ0 lim df
(T6.38)
δ ℓ ~e · H
b→0
F
~ d ist senkrecht zu ~e. Rechts steht also
F schneidet die Oberfläche, und die Richtung von df
die Komponente senkrecht zu ~e eines Stromes, der in der Oberfläche fließt. In Isolatoren ist
~j ≡ 0, und wir erhalten:
~ stetig.
Auf der Grenzfläche zwischen zwei Isolatoren ist die Parallelkomponente von H
~ || unstetig. Dies ist aber nur eine grobe
Ist mindestens einer der Körper leitend, so ist H
Näherung, anwendbar für Substanzen
mit sehr guter Leitfähigkeit. Damit im Limes b → 0
R
~
ein endlicher Betrag des Integrals df · ~j übrig bleibt, muss die Stromdichte unendlich werF
den. Bei endlicher Leitfähigkeit ist dies nicht möglich. Die Oberflächenströme fließen immer
~ || ist stetig. Wir werden dies in § T6.4 noch genauer
in einer Schicht endlicher Dicke und H
betrachten. Übrigens spricht dieser Einwand nicht gegen die Existenz einer Oberflächenladung. Wir können Elektronen in einer auf makroskopischer Skala beliebig dünnen Schicht
anhäufen.
Jetzt können wir uns Reflektion und Brechung zuwenden. Wir betrachten folgende Situation.
Der linke Halbraum (x < 0) sei mit Dielektrikum 1 gefüllt, der rechte (x > 0) mit Dielektrikum 2. Von links falle eine ebene Welle, Wellenvektor ~kI ein. ~kI und der Normalenvektor
~e1 auf der Grenzfläche x = 0 spannen die Einfallsebene auf, die wir mit der ~e3 − ~e1 Ebene
(y = 0) identifizieren.
Es wird eine reflektierte Welle, Wellenvektor ~kR und eine transmittierte Welle, Wellenvektor
~kT entstehen. Der Winkel zwischen − ~e1 und ~kI sei ϑ1 , der zwischen ~kT und ~e1 sei ϑ2 , der
zwischen − ~e1 und ~kR sei ϑR .
T6 - 12
√
~
Das (komplexe) E-Feld
einer ebenen Welle im Dielektrikum mit Brechungsindex n = ǫµ
hat die Form
~ r , t) = E
~ 0 exp i ~k · ~r − ωt
E(~
,
mit
ω=
c
k
n
,
k = | ~k | .
~
Das zugehörige B-Feld
ist
mit
~ r , t) = B
~ 0 exp i ~k · ~r − ωt
B(~
,
~ 0 = 1 ~k × E
~0 .
B
(T6.39)
ω
Die Frequenzen aller drei Teilwellen unseres Problems müssen gleich sein; sonst können die
~ (1) = ~e1 · B
~ (2) - nicht für alle Zeiten erfüllt sein. Die Wellen
Randbedingungen - etwa ~e1 · B
haben also die Form
einlaufend:
reflektiert:
transmittiert:
~I = E
~ (I) exp i ~kI · ~r − ωt ,
E
0
kI =
~R = E
~ (R) exp i ~kR · ~r − ωt ,
E
0
kR =
n1 ω
c
(T6.41)
kT =
n2 ω
.
c
(T6.42)
~T = E
~ (T ) exp i ~kT · ~r − ωt ,
E
0
n1 ω
c
(T6.40)
~
Die zugehörigen B-Felder
folgen aus dem Obigen.
Wir nehmen weiter an, dass beide Dielektrika Isolatoren sind, so dass weder Oberflächenladungen noch Oberflächenströme auftreten.
Die Bestimmung von ~kR und ~kT ist sehr einfach. Wir werten zunächst die Randbedingung
~ ist stetig
(T6.35) aus: Die Normalkomponente von B
~ I (~r, t) + B
~ R (~r, t) = ~e1 · B
~ T (~r, t) ,
~e1 · B
oder
~ (T ) ei ~kT ·~rF .
~ (I) ei ~kI ·~rF + B
~ (R) ei ~kR ·~rF = ~e1 · B
~e1 · B
0
0
0
(T6.43)
Hier ist ~rF = y ~e2 + z ~e3 ein beliebiger Vektor in der Grenzfläche. Damit diese Gleichung
erfüllt werden kann, müssen alle Exponenten die gleiche ~rF -Abhängigkeit aufweisen. Also
müssen die zur Trennfläche parallelen Komponenten aller ~k-Vektoren gleich sein.

~kI = ~k|| + ~kI,1 ~e1



~kR = ~k|| + ~kR,1 ~e1
(T6.44)



~kT = ~k|| + ~kT,1 ~e1 .
Alle ~k-Vektoren liegen in der Einfallsebene.
T6 - 13
Außerdem gilt
2 2
~k2 = n1 ω = ~k2 .
R
I
c2
Mit (T6.44) folgt
2
2
kR,1
= kI,1
.
Da die Welle reflektiert wird, ist nur die Lösung
kR,1 = −kI,1
(T6.45)
möglich. Es folgt sofort das Reflektionsgesetz
ϑR = ϑ1 .
Weiter gilt
(T6.46)
2 2
~k2 = ~k2 sin2 ϑ1 = n1 ω sin2 ϑ1 ,
I
||
c2
aber auch
2 2
~k2 = ~k2 sin2 ϑ2 = n2 ω sin2 ϑ2 .
I
||
c2
Es folgt das Brechungsgesetz
sin ϑ1
n2
=
.
sin ϑ2
n1
(T6.47)
Wenn Sie diese Rechnung mit der Argumentation im Korpuskelmodel vergleichen, so stellen
Sie fest, dass beide Herleitungen sehr ähnlich sind. Was damals der Impuls war, ist jetzt der
Vektor ~k, und statt der Energieerhaltung verwenden wir die Erhaltung der Frequenz ω.
Aber die Wellentheorie beschreibt sogar bei der einfachen Reflektion Effekte, die es nach der
Korpuskelvorstellung gar nicht geben darf. Wir wissen, dass für n1 > n2 das Phänomen der
Totalreflektion auftritt: Gl. (T6.47) kann geschrieben werden als
sin ϑ2 =
n1
sin ϑ1 .
n2
Da sin ϑ2 ≤ 1, kann diese Gleichung für sin ϑ1 > nn12 nicht erfüllt werden und es gibt keine
transmittierte Welle. In der Korpuskelvorstellung bedeutet dies, dass die Lichtteilchen auf
eine Potentialbarriere stoßen, die zu hoch ist als dass sie sie überwinden könnten. Die Dicke
der Barriere ist hierbei völlig belanglos.
Betrachten wir nun diese Situation in der Wellenbeschreibung. Wir wissen
2 2
~k2 = ~k2 + k2 = n2 ω .
T
T,1
||
c2
Andererseits gilt
2
2 2
2 2 n
1
~k2 = n1 ω sin2 ϑ1 = n2 ω
sin
ϑ
> kT2 .
1
||
c2
c2
n2
| {z }
>1
T6 - 14
Dies erzwingt
"
2 #
n1
n22 ω 2
sin ϑ1
1−
< 0.
=
c2
n2
2
kT,1
Also ist kT,1 imaginär.
kT,1 =
δ
n2 ω
=
c
−1
s
i
δ
n1
sin ϑ1
n2
2
− 1 > 0.
Damit hat die Ortsabhängigkeit der transmittierten Welle die Form
~
ET ∼ ei·k|| ·~r−x/δ ∼ BT .
Auch bei Totalreflektion dringt die Welle in das reflektierende Medium ein, wird allerdings
in dem Medium exponentiell gedämpft.
Newton
Stellen wir uns jetzt vor, dass das Medium 2 nur aus
einer Schicht der Dicke D . δ besteht, so wird auch
auf der der einfallenden Welle abgewandten Seite
der Schicht noch ein nicht zu vernachlässigendes
Wellenfeld existieren, das sich weiter ausbreitet. Die
Welle kann also eine Barriere durchdringen. Dies
ist ein reiner Welleneffekt, den man auch durchaus
experimentell nachweisen und nutzen kann. In der
Quantenphysik wird Ihnen dies als ’Tunneleffekt’
wieder begegnen.
Maxwell
..
Totalreflektion an einer dunnen Barriere
Bei streifendem Einfall |ϑ1 → π2 | erhalten wir
c 1
δ=
ω n2
Setzen wir n2 = 1 (Vakuum),
ω
c
=
2π
λvak ,
δ=
n1
n2
2
!− 1
2
−1
.
so folgt
λvak
2π
−2
n21 − 1
.
Für eine Luftschicht zwischen zwei Glasschichten (n1 ≈ 1.5) folgt δ ≈ λvak
7 , also für Licht
4
−7
−9
(λvak ≈ 400 10 m) : δ ≈ 7 10 m. Einen Luftspalt dieser Breite kann Licht also ’durchtunneln’. Ist n1 kleiner, so ist δ größer.
T6 - 15
Anders als im Korpuskelmodell können wir in der Elektrodynamik die Feldamplituden und
damit die Intensität der reflektierten und transmittierten Wellen bestimmen. Z.B. haben wir
Gl. (T6.43) noch gar nicht voll ausgenutzt. Mit Gl. (T6.44) können wir die Exponentialfunktionen heraus kürzen und erhalten
~ (I) + B (R) = ~e1 · B
~ (T ) .
~e1 · B
(T6.48)
0
0
0
Auch aus den anderen Randbedingungen fallen die Exponentialfunktionen heraus, da sie ja
immer auf der Trennfläche x = 0 gelten. Wir erhalten folgende Gleichungen
~ = ǫ ~e1 · E
~
Stetigkeit von ~e1 · D
~ ||
Stetigkeit von E
~ || =
Stetigkeit von H
1
µ
~ (I) + E
~ (R) = ǫ2~e1 · E
~ (T ) .
ǫ1~e1 E
0
0
0
(T6.49)
~ (T ) .
~ (k) = E
~ (I) + E
E
0,||
0,||
0,||
(T6.50)
1 ~ (I) ~ (P ) 1 ~ (I)
.
B0,|| + B0,|| = 2 B
µ1
µ 0,||
(T6.51)
~ || .
B
~ 0 und E
~ 0 (T6.39), bilden (T6.48)–(T6.51) ein
Zusammen mit der Beziehung zwischen B
lineares Gleichungssystem zur Berechnung der reflektierten und der transmittierten Welle
bei gegebener einlaufender Welle.
Die Lösung dieses Gleichungssystems ist nicht schwer, aber länglich. Das Ergebnis sind die
~
Fresnel’schen Formeln. Wir spalten alle E-Vektoren
auf gemäß
~ =E
~ (S) + E
~ (P ) .
E
(T6.52)
~ (S) steht senkrecht auf der Einfallsebene, E
~ (P ) liegt in der Einfallsebene.
E
Fresnel’sche Formeln
=
n1
µ1
n1
µ1
cos ϑ1 −
n2
µ2
n2
µ2
cos ϑ2
=
n2
µ2
n2
µ2
cos ϑ1 −
n1
µ1
n1
µ1
cos ϑ2
(R,S)
E0
(I,S)
E0
(R,P )
E0
(I,P )
E0
cos ϑ1 +
cos ϑ1 +
(T,S)
E0
(I,S)
E0
= 1+
(I,P )
E0
2 nµ11 cos ϑ1
=
=
n1
µ1
cos ϑ1 +
2 nµ11 cos ϑ2
(T,P )
E0
(I,S)
E0
n2
µ2
cos ϑ1 +
(T6.54)
cos ϑ2
(R,S)
E0
(T6.53)
cos ϑ2
n1
µ1
cos ϑ2
n2
µ2
cos ϑ2
.
Damit haben wir Reflektion und Brechung für Isolatoren vollständig beschrieben.
T6 - 16
(T6.55)
(T6.56)
Diese Gleichungen braucht man sich nicht zu merken, aber eine Konsequenz sollte man sich
klar machen. Auch wenn der einfallende Strahl unpolarisiert ist, z.B. aus vielen Wellen besteht, deren Polarisationsrichtungen in der Ebene senkrecht zu ~kI gleich verteilt sind, so ist
im Allgemeinen sowohl die reflektierte als auch die durchgehende Welle teilweise polarisiert.
Die Polarisationsrichtungen sind nicht mehr gleich verteilt. So hat Molus 1808 zufällig die
Polarisation des Lichts entdeckt, indem er das Spiegelbild der Sonne in einem Fenster durch
einen Kalkspatkristall betrachtete, der als Polarisationsfilter wirkt. Für einen speziellen Einfallswinkel ist der reflektierte Strahl sogar vollständig senkrecht zur Einfallsebene polarisiert.
Dies wollen wir jetzt noch diskutieren.
(R,P )
Wir suchen einen Einfallswinkel ϑ1 , den ’Brewsterwinkel’, so dass E0
= 0 ist. Setzen wir,
wie für unmagnetische Materialien angemessen, µ1 = µ2 = 1, so erhalten wir aus (T6.54)
die Bedingung
cos ϑ1 =
n1
cos ϑ2 ,
n2
oder
1 − sin2 ϑ1 =
n21 n21
−
sin2 ϑ2
n22 n22
Brechungsgesetz:
sin2 ϑ2 =
n21
sin2 ϑ1 .
n22
Also erhalten wir
n21
n41
2
−
1
sin
ϑ
=
− 1,
1
n42
n22
oder
sin2 ϑ1 =
1
n21
n22
+1
=
n22
< 1.
n21 + n22
(T6.57)
Also gibt es einen solchen Winkel.
Der Brechungsindex von Luft ist n1 ≈ 1, der von normalem Glas ist n2 ≈ 1.5. Dies ergibt
ˆ 560 . Für diesen Einfallswinkel ist also das an der Grenzfläche
sin ϑ1 ≈ .83, oder ϑ1 ≈ .98 ≈
Luft-Glas reflektierte Licht vollständig senkrecht zur Einfallsebene polarisiert. Der BrewsterWinkel hat noch eine andere Besonderheit. Bei diesem Einfallswinkel stehen der reflektierte
und der durchgehende Strahl senkrecht aufeinander.
Wir wollen uns noch mit der Intensität der reflektierten bzw. transmittierten Welle befassen.
Ein Maß für die Intensität ist die zeitgemittelte Energiestromdichte. Für eine ebene Welle
gilt nach Gl. (T6.34)
~σ =
~
c
~ 02 k .
ǫ0 ǫ E
2n
|~k|
Das Verhältnis der Intensität der reflektierten Welle zur Intensität der einlaufenden Welle
definiert den Reflektionskoeffizienten R. Genauer gesagt, wir müssen den auf die Trennfläche,
T6 - 17
Normalenrichtung ~nF , einfallenden Strom ~σI · ~nF mit dem reflektierten Strom ~σR · ~nF ver(S)
(P )
gleichen. Da nach Konstruktion die Feldkomponenten E0 und E0 senkrecht aufeinander
stehen, folgt
Der Faktor
c
2 n ǫ0 ǫ
(R,S) 2
(R,P ) 2
E0
+ E0
R= .
(I,S) 2
(I,P ) 2
E0
+ E0
(T6.58)
fällt heraus, da beide Wellen im gleichen Medium laufen. Das gleiche gilt
wegen Einfallswinkel = Reflektionswinkel für die Skalarprodukte
onskoeffizient T ist entsprechend das Verhältnis
~σ · ~n T F
T =
.
~σI · ~nF
~k
|~k|
· ~nF . Der Transmissi-
(T6.59)
Ein Blick auf die Fresnel’schen Formeln zeigt, dass R und T recht kompliziert vom Einfallswinkel abhängen werden. Immer aber muss gelten
R + T = 1.
(T6.60)
Dies ist Energieerhaltung: Der einlaufende Energiestrom teilt sich in den reflektierten und
den transmittierten Strom auf.
Wir wollen den Spezialfall senkrechten Einfalls betrachten: ϑ1 → 0, ϑ2 → 0. Wir setzen
wieder µ2 = µ1 = 1. Aus (T6.53), (T6.54) folgt
(R,P )
E0
(I,P )
E0
=
n2 − n1
.
n2 + n1
=
n1 − n2
.
n1 + n2
(R,S)
E0
(I,S)
E0
Setzen wir dies in (T6.58) ein, so folgt
R=
n2 − n1
n2 + n1
2
.
(T6.61)
Um so größer der Unterschied zwischen den Brechungsindizes ist, um so stärker reflektiert
die Grenzfläche. R hängt nicht davon ab, ob die einfallende Welle aus dem optisch dünneren
oder aus dem optisch dichteren Medium kommt. Für eine Fensterscheibe (n2 ≈ 1.5, n1 ≈ 1)
1
= 0.04. Damit wird T für eine Grenzfläche T = 0.96, und für die Scheibe
erhält man R = 25
2
0.96 ≈ 0.92. Sie lässt (bei senkrechtem Einfall) also ungefähr 92 % des Lichts durch.5
5
Beachten Sie, dass n2 =
p
ǫ(k)µ von der Wellenlänge abhängt. n2 ≈ 1.5 gilt für normales Tageslicht.
T6 - 18
T6.4
Metallische Oberflächen
An den Oberflächen leitfähiger Körper können Oberflächenladungen und Oberflächenströme
auftreten. Um dies genauer zu studieren, betrachten wir ein Metall, das von Außen mit einer
elektromagnetischen Welle bestrahlt wird. Wir nehmen zunächst an, dass die Leitfähigkeit σ
des Metalls unendlich ist. Dann kann das elektrische Feld nicht eindringen. Es würde einen
unendlichen Strom erzeugen. Statt dessen verschiebt es momentan die Ladungen so, dass im
Inneren gilt
~ = 0.
E
~
Ebenso wenig kann ein oszillierendes B-Feld
eindringen. Es würde sofort Ströme anwerfen,
die es nach der Lenz’schen Regel kompensieren. Also gilt im Inneren auch
~ = 0.
B
Damit folgt aus den Randbedingungen (T6.37) und (T6.35): Auf der Oberfläche eines idea~ und die Normalkomponente eines
len Leiters verschwinden die Tangentialkonponente von E
~
zeitlich variierenden Feldes B.
Hier sollten wir stutzen. Wir wissen, dass ein zeitunabhängiges Magnetfeld ohne weiteres
durch ein (unmagnetisches) Metall hindurchgeht. Wieso soll dann ein auch nur langsam oszillierendes Feld vollständig abgeschirmt werden? Um dies genauer zu verstehen wollen wir
das Problem in sehr einfacher Geometrie, aber ohne die Idealisierung σ = ∞, behandeln.
Im Halbraum x < 0 sei Vakuum (ǫ = 1 = µ), der Halbraum x > 0 sei mit einer leitfähigen Substanz (ǫ > 1, µ = 1, σ > 0) gefüllt. Aus dem Vakuum falle eine ebene Welle in
~e1 -Richtung ein.

~ (I) (x, t) = ~e2 E (I) ei (kx+ωt) ,

E

0
(I)
x<0
(T6.62)

~ (I) (x, t) = ~e3 E0 ei (kx+ωt) ,

B
c
ω = ck
~ einen Strom gemäß
Im Metall erzeugt E
~.
~j = σ E
(T6.63)
Damit lauten die Maxwell Gleichungen im Metall (x > 0) in allgemeiner Form (µ = 1)
~
div E
=
~ =
rot E
1
ǫ0 ǫ
∂
∂t
(ext)
ρq
~,
B
,
~
div B
=0
ǫ ∂
~
~.
rot B = µ0 σ + 2
E
c ∂t
~ die RichFür unsere Geometrie vereinfachen sie sich aber erheblich. Auch im Metall wird E
tung ~e2 haben und nur von x und t abhängen. Die Frequenz kann sich nicht ändern. Ent~ Also machen wir den Ansatz
sprechendes gilt für B.

~ (T ) (x, t) = ~e2 E (T ) (x) e−i ωt

E
x>0
(T6.64)

~ (T ) (x, t) = ~e3 B (T ) (x) e−i ωt
B
T6 - 19
Es folgt
~ (T ) = ∂ E (T ) (x) e−i ωt = 0 .
div E
∂y
+
+
+
+
+
+
+
+
-
Elektronen,beweglich
..
Ionenrumpfe,ortsfest
(ext)
Also muss ρq
= 0 gelten. Was bedeutet das? Mit unserem Ansatz gilt ~j = ~e2 j(x), also
div ~j = 0. Die Elektronen werden nur in ~e2 -Richtung hin- und hergeschoben, ohne das lokal
(ext)
~ parallel zur
eine Netto-Ladung ρq
erzeugt wird. Influenzladungen treten nicht auf, da E
Oberfläche ist.
~ = 0, div B
~ = 0 erfüllt. Aus rot E
~ =
Mit unserem Ansatz sind damit die Gleichungen div E
∂ ~
− ∂t B ergibt sich
∂ × ~e2 E (T ) (x) = i ω ~e3 B (T ) (x) ,
∇ × ~e2 E (T ) (x) = ~e1
∂x
also
∂ (T )
E (x) = i ω B (T ) (x) .
∂x
(T6.65)
Die letzte Gleichung ergibt
∂
ǫ
× ~e3 B (T ) (x) = µ0 σ − i ω 2 ~e2 E (T ) (x) .
~e1
∂x
c
{z
}
|
∂ (T )
− ~e2
B (x)
∂x
Wir schreiben das als
ω
∂ (T )
B (x) = i 2 ǫ(ω)E (T ) (x) ,
∂x
c
(T6.66)
mit
ǫ(ω) = ǫ + i
µ0 c2 σ
σ
=ǫ+ i
.
ω
ǫ0 ω
(T6.67)
ǫ(ω) ist die komplexe Dielektrizitätskonstante des Metalls. Ihr Realteil ist die übliche reelle
Dielektrizitätskonstante ǫ, ihr Imaginärteil beschreibt die endliche Leitfähigkeit.
T6 - 20
Die Gleichungen (T6.65), (T6.66) sind leicht zu lösen. Wir differenzieren (T6.66) nach x,
verwenden (T6.65), und erhalten eine Gleichung für B (T ) .
∂ 2 (T )
ω
∂ (T )
ω2
B
(x)
=
i
ǫ(ω)
E
(x)
=
−
ǫ(ω) B (T ) (x) .
∂x2
c2
∂x
c2
(T6.68)
Die allgemeine Lösung ist
B (T ) (x) = a ei
ω
c
√
ǫ (ω)x
+ b e−i
ω
c
√
ǫ (ω)x
.
Nun gilt Re ω(ǫ) = ǫ > 0, Im ǫ(ω) = ǫ0σω > 0, d.h. ǫ(ω) liegt im ersten Quadranten der
p
p
komplexen Ebene. Damit liegt auch ǫ (ω) im ersten Quadranten, also
Im
ǫ (ω) > 0.
√
√
ω
ω ǫ (ω)x
exponentiell
Damit fällt ei c ǫ (ω)x mit wachsendem x exponentiell, während e− i c
wächst. Die physikalisch sinnvolle Randbedingung ist
lim B (T ) (x) = 0 .
x→∞
Wir erhalten also
B (T ) (x) = a ei
ω
c
√
ǫ(|ω)x
.
(T6.69)
E (T ) (x) folgt aus Gl. (T6.66):
∂
c2 1
B (T ) (x)
ω ǫ (ω) ∂x
√
ω
c
p
a ei c ǫ (ω)x .
ǫ (ω)
E (T ) (x) = −i
=
(T6.70)
Damit haben wir das Verhalten der Felder im Metall.
B (T ) (x) ∼ ei k
(T ) x−x/δ
∼ E (T ) (x) ,
(T6.71)
mit
p
p
1
ω
ω
Re
=
Im ǫ (ω) .
ǫ (ω),
c
δ
c
Dies sind gedämpfte Wellen. δ ist die Eindringtiefe.
k(T ) =
(T6.72)
Zur vollständigen Lösung des Problems müssen wir noch die Amplitude a aus den Randbedingungen an der Oberfläche bestimmen. Im Halbraum x < 0 gibt es außer der einfallenden
Welle (T6.62) noch die reflektierte Welle

(R)
~ (R) (x, t) =

E
~e2 E0 e−i(kx+ωt)






1
(R)
(R)
−i(kx+ωt)
~
B (x, t) =
(−~e1 ) × ~e2 E0 e
(T6.73)
c




(R)

E


=
− ~e3 0 e−i(kx+ωt)
c
T6 - 21
~ stetig. Also gilt
Auf der Grenzfläche x = 0 ist ~e2 · E
(I)
(R)
E0 + E0
=ap
c
.
ǫ (ω)
(T6.74)
~ =
Da σ endlich ist, gibt es keine Oberflächenströme. Also ist auch die Komponente von H
1 ~
~ stetig ist.
e3 · B
µ B parallel zur Oberfläche stetig, und wegen µ = 1 folgt, dass ~
(R)
(I)
E0
c
−
E0
c
= a.
(T6.75)
Es folgt sofort
(I)
2 E0
= ac
oder
(R)
E0
1
1+ p
ǫ (ω)
!
,
p
ǫ (ω)
2
(I)
p
a=
E0
c 1 + ǫ (ω)
(I)
= − E0 +
1+
2
p
(I)
ǫ (ω)
E0 .
(T6.76)
(T6.77)
Wir diskutieren jetzt dieses Ergebnis unter der Annahme
σ
≫ 1.
ǫ ǫ0 ω
Für Kupfer und andere gut leitende Metalle ist ǫσǫ0 von der Größenordnung 1017 Herz. Also
gilt diese Annahme bis zu sehr hohen Frequenzen, (Licht ∼ 1015 Herz).6 Damit können wir
unsere Ergebnisse vereinfachen
r
r
p
√
σ
ǫ ǫ0 ω
ǫ (ω) =
i
1−i
ǫ0 ω
σ
r
√
σ
i
≈
ǫ0 ω
r
1
σ
.
(T6.78)
= √ (1 + i)
ǫ
2
0ω
Aus (T6.73) folgt
1 ω
1
=√
δ
2 c
r
1
σ
=√
ǫ0 ω
2c
r
σω
= kT .
ǫ0
6
Lichtwellenlänge ∼ 400 10−9 m. Für wesentlich höhere Frequenzen, Wellenlängen ∼ 10−9 m bricht die
makroskopische Theorie zusammen, da die Wellenlänge in die Größenordnung der atomaren Abstände kommt.
T6 - 22
(T6.77) ergibt
2
a=
c
1
1+ p
ǫ (ω)
Weiter folgt
(R)
E0
≈
!−1
(I)
−E0
(I)
E0 ≈
2 (I)
E .
c 0
2
(I)
E0
+p
ǫ (ω)
(I)
2E
p 0 ei x/δ−x/δ
ǫ (ω)
E (T ) (x) ≈
2 (I) i x/δ−x/δ
E e
.
c 0
B (T ) (x) ≈











(T6.79)










Betrachten wir zunächst den Fall eines idealen Leiters: σ → ∞. Für ω 6= 0 gilt dann
√
2c
lim δ = lim q
=0
σ→∞
σ→∞
lim
σ→∞
p
σω
ǫ0
ǫ (ω) = ∞ .
Also dringen die Felder nicht in das Metall ein:
lim E (T ) (x) = 0 = lim B (T ) (x) .
σ→∞
σ→∞
Dies bestätigt unsere Überlegungen zu den idealisierten Randbedingungen vom Beginn dieses
Abschnitts. Weiter folgt
(R)
E0
(I)
= −E0 .
Die Grenzfläche ist ein idealer Spiegel, Reflektionskoeffizient R = 1.
Wie ändern sich diese Ergebnisse im realen Fall σ < ∞? Jetzt hängt das Verhalten sehr
stark von der Frequenz ab. Betrachten wir zunächst den Limes ω → 0. Dann gilt
1
→ 0,
δ
| ǫ (ω) | → ∞ .
Mit (T6.79) ergibt dies
(R)
E0
(I)
+ E0
= 0
E (T ) (x) = 0
B (T ) (x) =
2 I
E = const .
c 0
Auf der Oberfläche und im Leiter verschwindet das elektrische Feld und das Magnetfeld geht
glatt durch. Wir haben das Verhalten der Felder gemäß Elektrostatik und Magnetostatik
wiedergefunden.
T6 - 23
Jetzt betrachten wir einen Zwischenbereich von Frequenzen, für den gilt
r
p
σ
ǫ (ω) ≈
≫ 1,
endlich,
ǫ0 ω
r
σ
1 ω
δ=√
sehr viel kleiner als makroskopische Abmessungen .
ǫ0 ω
2 c
Dann dringen die Felder in das Metall ein und werden dort exponentiell gedämpft. Die
Amplitude von E (T ) (x) ist sehr viel kleiner als die von c B (T ) (x).
2
1.5
1
0.5
0
1
2
3
4
Bild = Platzhalter
In diesem Fall können wir wieder näherungsweise einfache Randbedingungen annehmen: Da
~ auf der Oberfläche
E (T ) praktisch verschwindet, können wir die Tangentialkomponente von E
gleich Null setzen. Da die Strom führende Schicht ∼ δ sehr dünn ist, können wir sagen,
~ = B
~ springt, um einen Betrag, der durch einen
dass die Tangentialkomponente von H
Oberflächenstrom gegeben ist.
Schließlich sehen wir auch, dass die reflektierte Welle eine etwas kleinere Amplitude hat als
die einfallende Welle. Der Reflektionskoeffizient ist
(I)
(R) 2
Re E0
R=
≈
2
E0I
2
1 − Re p
ǫ (ω)
!2
≈1−4
√
2
r
ǫ0 ω
,
σ
(E0 ǫ R angenommen). Also hängt der Reflektionskoeffizient eines Metalls direkt mit seiner
Leitfähigkeit zusammen. Weil Silber eine hohe Leitfähigkeit hat, versilbert man Spiegel.
Die Differenz zwischen der einfallenden Intensität und der reflektierten Intensität wird im
Metall absorbiert, d.h. durch den Ohm’schen Widerstand der in der Oberflächenschicht
∼ δ fließenden Ströme in Wärme verwandelt. Zum Schluss sei noch erwähnt, dass der hier
diskutierte Effekt den Namen ’Skin Effekt’ trägt: Die Ströme fließen in einer dünnen ’Haut’
des Metalls. δ ist die ’Skin-Dicke’.
T6 - 24