2.2. Skalarprodukt
Werbung

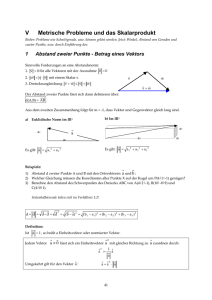
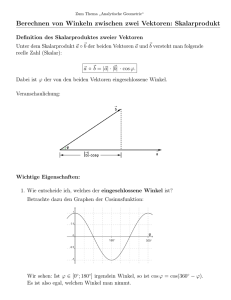
2.2. Skalarprodukt Kraftvektoren treten bei vielen physikalisch-technischen Problemen auf; sie greifen an einem Punkt in verschiedenen Richtungen an. Die bekannte Formel Arbeit = Kraft mal Weg muß man dann vektoriell interpretieren. Aber wie multipliziert man zwei Vektoren? Und ist das Ergebnis eine Zahl oder ein Vektor? Wir befassen uns zunächst mit der zweiten Alternative, die auf das Skalarprodukt führt. Beispiel 1: Spinnfäden sind im Vergleich zu ihrer Dicke erheblich stabiler als in der Technik hergestellten Kabel! Sie müssen auch enormen Kräften standhalten, und zwar um so mehr, je waagerechter sie gespannt sind. Geschwindigkeitsvektoren ergeben sich bei allen Bewegungen. Sie zeigen jeweils in Richtung der Bahnkurve. Beispiel 2: Mathe auf dem Snowboard Wir zeichnen die auftretenden Kraft- bzw. Geschindigkeitsvektoren: Je flacher die Bahn, desto kleiner die Geschwindigkeit! Ist die Rutschbahn nicht eben, so muß man, um die jeweilige Steigung variabel gestalten zu können, die Ableitung der Funktion berechnen, welche die Bahnkurve beschreibt. 1 f := x → sin x 2 Betrachten wir nun die einzelnen Vektoren genauer! Projektionen Der Gewichtsvektor a wird zerlegt in eine beschleunigende Kraftkomponente a[b] in Richtung b der Bahn und eine dazu senkrechte Kraftkomponente a-a[b], die einen Druck auf die Bahn, aber natürlich keine Bewegung bewirkt (allenfalls eine Bremsung). Umgekehrt kann man auch den Bahnvektor b in eine vertikale Komponente b[a] und eine horizontale Komponente b-b[a] zerlegen. Man nennt a[b] die Projektion und a-a[b] das Lot von a auf b, und entsprechend b[a] die Projektion und b-b[a] das Lot von b auf a. Also ist der Ausgangsvektor die Summe von Projektion und Lot auf einen beliebigen (von 0 verschiedenen) Vektor. Dies ist die sogenannte Orthogonalzerlegung. Wird der Schlitten nach oben gezogen, ist der Winkel zwischen Zug- und Gewichtsvektor stumpf. Die Projektionen zeigen dann in die umgekehrte Richtung wie die Vektoren, auf die sie projeziert wurden! Das Skalarprodukt Wir bezeichnen den (gegen den Uhrzeigersinn orientierten!) Winkel zwischen a und b mit (a|b) und nennen die Zahl ab = |a||b|cos(a|b) das Skalarprodukt von a und b. Wie die definierenden Gleichungen zeigen, ist es kommutativ, d.h. es gilt ab = ba. Das Skalarprodukt hängt mit den Projektionen eng zusammen, und zwar über die Gleichungen |ab| = |a||b[a]| = |ba| = |b||a[b]|. Diese Gleichungen kann man mit Hilfe des Sehnensatzes bestätigen, indem man den Thaleskreis über der Strecke zwischen a und b einträgt: Bei stumpfen Winkeln wird das Skalarprodukt negativ. Also: Skalarprodukt positiv <==> spitzer Winkel (kleiner als Skalarprodukt negativ <==> stumpfer Winkel (größer als Skalarprodukt gleich 0 <==> rechter Winkel (gleich π 2 ) π 2 π 2 ) ) Die Hubleistung ist das Produkt |a||b[a]| von Gewicht und Hubgeschwindigkeit, also die aufzuwendende Leistung, wenn wir den Schlitten nach oben ziehen, statt ihn nach unten gleiten zu lassen. Die Zugleistung in Bahnrichtung ist das Produkt |b||a[b]| von Bahngeschwindigkeit und Zugkraft. Die Kommutativität des Skalarprodukts besagt, daß diese beiden physikalischen Größen gleich sind. Rechenregeln für das Skalarprodukt Wir kennen schon das Kommutativgesetz ab = |a||b|cos(a|b) = |b||a|cos(b|a) = ba . Neben den ebenfalls bekannten vektoriellen Assoziativgesetzen (rs)b = r(sb) = s(rb) in denen sowohl r als auch s eine Zahl, der ganze Ausdruck aber ein Vektor ist, ergeben sich unmittelbar aus der Definition des Skalarprodukts die sehr ähnlich aussehenden skalaren Assoziativgesetze (ra)b = r(ab) = a(rb) bei denen jedoch a und b Vektoren sind und r ebenso wie der Gesamtausdruck eine reelle Zahl ist! Dagegen ist das "Assoziativgesetz" a(bc) = (ab)c ?? für Vektoren gründlich falsch, denn der Vektor auf der linken Seite zeigt in Richtung von a, der auf der rechten jedoch in Richtung von c (und die ist meist eine ganz andere). Zum Beispiel finden wir für einen auf a senkrechten Vektor b = c der Länge 1: a(bc) = a , aber (ab)c= 0. Das Distributivgesetz (a+b)c = ac+bc ergibt sich durch Multiplikation mit |c| bzw. -|c| aus der entsprechenden Gleichung für die Projektionen: |(a+b)[c]| = |a[c]+b[c]|. Im zweidimensionalen Fall ist diese unmittelbar aus der folgenden Zeichnung abzulesen: Die Situation ist nicht ganz so offensichtlich, wenn a,b und c nicht in einer Ebene liegen. Im Raum bilden wir die Projektionen auf die Koordinatenachsen, bzw. auf die kanonischen Einheitsvektoren der Länge 1 in Richtung der Koordinatenachsen i = e1 , j = e2 , k = e3 und erhalten die Koordinaten als Skalarprodukte ai = a1 , aj = a2 , ak = a3 . Man unterscheidet meist nicht zwischen einem Vektor a und seiner Koordinatendarstellung ( a1 , a2 , a3 ) (bzw. (a1, a2) in der Ebene). Wir zerlegen den Vektor ( a1 , a2 , a3 ) = ( 1, 1, 1 ) und jetzt den Vektor ( a1, a2, a3 ) = ( 1, 0, 0.8 ) Um das Distributivgesetz auch in der räumlichen Konstellation zu begründen, legt man das Koordinatensystem so, daß c (ähnlich wie in obiger Skizze für die Ebene) auf eine Koordinatenachse fällt, z.B. die zu e1 gehörige. Dann ist immer noch a[c] = a1 , b[c] = b1 und (a+b)[c] = a1 + b1 . Mit Hilfe des Distributivgesetzes gelangt man nun sofort zur koordinatenweisen Berechnung des Skalarprodukts Es gilt für beliebige Vektoren a = (a1, a2) , b = (b1, b2) der Ebene: ab = a1 b1 + a2 b2 und entsprechend für Vektoren a = (a1, a2, a3) , b = (b1, b2, b3) des Raumes: ab = a1 b1 + a2 b2 + a3 b3 . Die Länge eines Vektors kann man darstellen als Wurzel aus seinem Skalarprodukt mit sich selbst: aa = |a||a|. Wie wir zuvor sahen, gilt im Raum ab = a1 b1 + a2 b2 + a3 b3 . Insbesondere lautet die dreidimensionale Version des Satzes von Pythagoras 2 2 2 aa = a1 + a2 + a3 und daraus ergibt sich als Länge von a : |a| = 2 2 2 a1 + a2 + a3 . Flächendiagonale 2 d2 = a1 + a2 2 Raumdiagonale 2 2 2 r 2 = d2 + a3 = a1 + a2 + a3 2 3D-Pythagoras Die Fläche des schräg senkrecht stehenden großen Quadrates ist gleich der Flächensumme der beiden liegenden und des senkrechten hinteren Quadrates Orthogonalität Ob zwei Vektoren aufeinender senkrecht stehen, lässt sich rein rechnerisch prüfen, indem man ihr Skalarprodukt bestimmt und feststellt, ob es gleich 0 ist: a | b <==> ab = 0 . Der Cosinus eines beliebigen Winkels zwischen zwei Vektoren lässt sich nun ebenfalls berechnen: a1 b1 + a2 b2 + a3 b3 cos(a|b) = ab/|a||b| = 2 2 2 2 2 2 ( a1 + a2 + a3 ) ( b1 + b2 + b3 ) Richtungscosinus Ein von 0 verschiedener Vektor a = (a1, a2, a3) im Raum bildet mit den Koordinaten-Einheitsvektoren i, j und k drei Winkel α = α1, β = α2, γ = α3 , für die der jeweilige Cosinus sich berechnet nach der Formel cos( α1 ) = a1 / |a| , cos( α2 ) = a2 / |a| , cos( α3 ) = a3 / |a| . 2 2 2 a1 + a2 + a3 folgt daraus Wegen |a| = 2 2 2 cos( α1 ) + cos( α2 ) + cos( α3 ) = cos( α )2 + cos( β )2 + cos( γ )2 = 1. Wir zeichnen die drei Winkel α, β, γ als Kreisbögen mit Hilfe von Kugelkoordinaten. Das ist schon recht trickreich und wird später noch genauer erklärt! sin( t ) a2 sin( t ) a3 α = cos( t ), , 2 2 2 2 a2 + a3 a2 + a3 , t = 0 .. arccos sin( t ) a1 sin( t ) a3 β = , cos( t ), 2 2 a 2+a 2 a1 + a3 1 3 , t = 0 .. arccos sin( t ) a1 sin( t ) a2 γ = , , cos( t ) , t = 0 .. arccos 2 2 a 2+a 2 a1 + a2 1 2 a1 2 2 a1 + a2 + a3 2 a2 2 2 a1 + a2 + a3 2 a3 2 2 a1 + a2 + a3 2 Eine besonders schöne Konsequenz der Kommutativität des Skalarproduktes ist der "schiefwinklige Kathetensatz" In diesem Bild entsprechen nun die beiden oberen Rechtecksflächen den Skalarprodukten ab und ba die beiden rechten Rechtecksflächen den Skalarprodukten ac und ca die beiden linken Rechtecksflächen den Skalarprodukten bc und cb. Daß die beiden zugehörigen Flächeninhalte jeweils gleich sind, besagt schlicht die Kommutativität des Skalarprodukts! Statt des Satzes von Pythagoras gilt im schiefwinkligen Dreieck mit den Seitenlängen a = |a|, b = |b|, c = |b-a| der Cosinussatz für den zwischen a und b liegenden Winkel γ : c2 = a2 − 2 a b cos( γ ) + b2. Denn es ist ja aufgrund des Distributiv- und Kommutativgesetzes ( a − b )2 = (a-b)(a-b) = aa - 2ab + bb = a2 − 2 a b cos( γ ) + b2. Auch diesen Satz kann man aus der obigen Figur ablesen: Je eines der beiden oberen Rechtecke hat den Flächeninhalt ab = a b cos( γ ). Zieht man diese Flächen von der Summe der beiden Quadrate ab, so bleibt je ein linkes und ein rechtes Rechteck, und deren Flächen entsprechen in ihrer Summe dem unteren Quadrat. Aufgrund des Cosinussatzes kann man z.B. bei gegebenen Seitenlängen a,b,c den Cosinus eines Eckwinkels mit der folgenden Formel berechnen: cos( γ ) = a2 + b2 − c2 2ab .