Skript zur Vorlesung Statistik - Fachbereich Mathematik und

Skript zur Vorlesung Statistik
Dietrich Baumgarten
«
21. Mai 2012
Inhaltsverzeichnis
1 Grundlagen
1
1.1
Übersicht und Lernziele
. . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.2
Zum Begri Statistik . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.3
Wahrscheinlichkeitstheorie, beschreibende und schlieÿende Statistik
. . .
2
. . . . . . . . . . . . . . . .
2
. . . . . . . . . . . . . . .
3
. . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.4
Gliederung einer statistischen Untersuchung
1.4.1
Beispiele statistischer Untersuchungen
1.5
Statistische Grundbegrie
1.6
Bestands- und Bewegungsmassen
. . . . . . . . . . . . . . . . . . . . . .
4
1.7
Einteilung von Merkmalen . . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.8
Messen und Skalenniveaus
6
1.9
Fragebögen
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.10 Die Datenmatrix
1.11 Aufgaben
. . . . . . . . . . . . . . . . . . . . . . . . . .
7
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2 Darstellung univariater Daten
11
2.1
Übersicht und Lernziele
. . . . . . . . . . . . . . . . . . . . . . . . . . .
11
2.2
Die vier Grundformen von Datensätzen . . . . . . . . . . . . . . . . . . .
11
2.3
Absolute und relative Häugkeiten
12
2.4
Kumulierte absolute und relative Häugkeiten
2.5
Häugkeitstabellen
2.6
Stab- Säulen- und Balkendiagramme
2.7
Empirische Verteilungsfunktion
2.8
Der Sonderfall nominaler Merkmale . . . . . . . . . . . . . . . . . . . . .
17
2.9
Aufgaben
18
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
13
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
. . . . . . . . . . . . . . . . . . . .
14
. . . . . . . . . . . . . . . . . . . . . . .
15
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 Maÿzahlen einer Verteilung
19
3.1
Übersicht und Lernziele
. . . . . . . . . . . . . . . . . . . . . . . . . . .
19
3.2
Denition und Einteilung . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
3.3
Modus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
3.4
Median . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
3.4.1
Eigenschaften des Medians . . . . . . . . . . . . . . . . . . . . . .
21
3.5
Quantile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
3.6
Median und Quantile aus einer Häugkeitstabelle
. . . . . . . . . . . . .
23
3.7
Boxplots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
3.7.1
Spannweite und Interquartilsabstand
3.7.2
Prinzip der Boxplots
. . . . . . . . . . . . . . . .
25
. . . . . . . . . . . . . . . . . . . . . . . . .
25
iii
Inhaltsverzeichnis
3.7.3
3.8
3.9
Eine Variante des Boxplots . . . . . . . . . . . . . . . . . . . . . .
Das arithmetische Mittel . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
3.8.1
28
Eigenschaften des arithmetischen Mittels . . . . . . . . . . . . . .
Streuungsmaÿe mit Bezug auf den Mittelwert
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
3.9.1
Die Varianz
3.9.2
Stichprobenvarianz
. . . . . . . . . . . . . . . . . . . . . . . . . .
30
3.9.3
Die Standardabweichung . . . . . . . . . . . . . . . . . . . . . . .
31
28
3.9.4
Der Variationskoezient . . . . . . . . . . . . . . . . . . . . . . .
31
3.10 Arbeitstabelle zur Berechnung . . . . . . . . . . . . . . . . . . . . . . . .
32
3.11 Transformationseigenschaften der Maÿzahlen . . . . . . . . . . . . . . . .
33
3.12 Mittlere absolute Abstände . . . . . . . . . . . . . . . . . . . . . . . . . .
34
3.13 Anforderungen an Maÿzahlen metrischer Merkmale
34
. . . . . . . . . . . .
3.14 Abschlieÿendes Beispiel . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
3.15 Excel-Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
3.16 Aufgaben
37
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 Klassenbildung
41
4.1
Übersicht und Lernziele
4.2
Klassen
4.3
Häugkeitstabelle klassierter Daten . . . . . . . . . . . . . . . . . . . . .
44
4.4
Histogramme
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
4.5
Approximierende empirische Verteilungsfunktion . . . . . . . . . . . . . .
45
4.6
Maÿzahlen bei klassierten Daten . . . . . . . . . . . . . . . . . . . . . . .
46
4.6.1
Der Modus
46
4.6.2
Median und Quantile
4.6.3
Arithmetisches Mittel und Varianz
4.7
Aufgaben
. . . . . . . . . . . . . . . . . . . . . . . . . . .
41
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
48
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
5.1
Übersicht und Lernziele
5.2
Absolute und relative Konzentration
5.3
5.4
46
. . . . . . . . . . . . . . . . .
5 Darstellung und Kennzahlen von Konzentration
iv
26
51
. . . . . . . . . . . . . . . . . . . . . . . . . . .
51
. . . . . . . . . . . . . . . . . . . .
51
Relative Konzentration . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
5.3.1
Die Merkmalssumme und ihre Verteilung . . . . . . . . . . . . . .
52
5.3.2
Die Lorenzkurve
54
5.3.3
Der Gini-Koezient
. . . . . . . . . . . . . . . . . . . . . . . . .
54
5.3.4
Der normierte Gini-Koezient . . . . . . . . . . . . . . . . . . . .
56
5.3.5
Relative Daten
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
5.3.6
Klassierte Daten
. . . . . . . . . . . . . . . . . . . . . . . . . . .
56
5.3.7
Vorgehensweise mit Excel
Absolute Konzentration
. . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
58
. . . . . . . . . . . . . . . . . . . . . . . . . . .
59
5.4.1
Konzentrationskurve und Rosenbluth-Index
. . . . . . . . . . . .
59
5.4.2
Rosenbluth-Index . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
5.4.3
Herndahl-Index
. . . . . . . . . . . . . . . . . . . . . . . . . . .
60
5.4.4
Relative Daten
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
Inhaltsverzeichnis
5.5
Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
5.6
Aufgaben
63
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6 Einführung in die Wahrscheinlichkeitsrechnung
67
6.1
Übersicht und Lernziele
. . . . . . . . . . . . . . . . . . . . . . . . . . .
67
6.2
Diskrete Verteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
6.3
Laplace-Experimente . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
69
6.4
Allgemeine Zufalls-Experimente . . . . . . . . . . . . . . . . . . . . . . .
69
6.5
Wahrscheinlichkeit von Ereignissen
71
6.6
Rechenregeln für Ereignisse
6.7
Abhängige mehrstuge Zufallsexperimente
. . . . . . . . . . . . . . . . .
74
6.8
Unabhängige mehrstuge Zufallsexperimente . . . . . . . . . . . . . . . .
76
6.9
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
72
Bedingte Wahrscheinlichkeit und stochastische Unabhängigkeit . . . . . .
79
6.10 Der Satz von Bayes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
82
6.11 Aufgaben
85
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7 Diskrete Zufallsvariable
87
7.1
Lernziele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2
Einführung und Denition . . . . . . . . . . . . . . . . . . . . . . . . . .
87
7.3
Die Verteilung einer diskreten Zufallsvariablen . . . . . . . . . . . . . . .
88
7.4
Die Wahrscheinlichkeitsfunktion einer diskreten Zufallsvariablen
. . . . .
89
7.5
Verteilungsfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
7.6
Erwartungswert und Varianz . . . . . . . . . . . . . . . . . . . . . . . . .
91
7.7
Bernoulli-Verteilung
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
7.8
Unabhängige Zufallsvariable . . . . . . . . . . . . . . . . . . . . . . . . .
95
7.9
Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
96
7.10 Aufgaben
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8 Ausgewählte Lösungen
87
98
99
8.1
Zu Kapitel 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99
8.2
Zu Kapitel 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99
8.3
Zu Kapitel 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
8.4
Zu Kapitel 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
8.5
Zu Kapitel 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
8.6
Zu Kapitel 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
v
Abbildungsverzeichnis
2.1
Stabdiagramme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.2
Empirische Verteilungsfunktion
. . . . . . . . . . . . . . . . . . . . . . .
16
2.3
Häugkeitstabelle und Säulendiagramm . . . . . . . . . . . . . . . . . . .
18
3.1
Einfacher Boxplot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
3.2
Eine weitere Form des Boxplots
. . . . . . . . . . . . . . . . . . . . . . .
26
3.3
Arbeitstabelle für einige Maÿzahlen . . . . . . . . . . . . . . . . . . . . .
33
4.1
Diskrete Auswertung
41
4.2
Histogramm und approximierende empirische Verteilungsfunktion
5.1
5.2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . .
45
Arbeitstabelle zum Beispiel 5.1
. . . . . . . . . . . . . . . . . . . . . . .
53
Arbeitstabelle zum Beispiel 5.2
. . . . . . . . . . . . . . . . . . . . . . .
53
5.3
Zusammenhang zwischen Lorenzkurve und Gini-Koezient . . . . . . . .
55
5.4
Arbeitsblatt für Lorenzkurve mit klassierten Daten
. . . . . . . . . . . .
57
5.5
Arbeitsblatt für Lorenzkurve mit klassierten Daten
. . . . . . . . . . . .
57
5.6
Arbeitsblatt für Konzentrationskurve, Rosenbluth- und Herndahl-Index
59
5.7
Arbeitsblatt für absolute Konzentration bei relativen Daten . . . . . . . .
62
6.1
Zufallsgeräte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
70
6.2
Baumdiagramm zum Beispiel 6.4
. . . . . . . . . . . . . . . . . . . . . .
75
6.3
Baumdiagramm von Beispiel 6.5 . . . . . . . . . . . . . . . . . . . . . . .
76
6.4
Baumdiagramm zum Beispiel 6.4
. . . . . . . . . . . . . . . . . . . . . .
77
6.5
Baumdiagramm zum Beispiel 6.7
. . . . . . . . . . . . . . . . . . . . . .
78
6.6
Der Satz von der totalen Wahrscheinlichkeit
. . . . . . . . . . . . . . . .
82
6.7
Arbeitstabelle zum Beispiel 6.15 . . . . . . . . . . . . . . . . . . . . . . .
83
6.8
Arbeitstabelle für das Beispiel 6.16
. . . . . . . . . . . . . . . . . . . . .
85
7.1
Diskrete Zufallsvariable . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
7.2
Diskrete Zufallsvariable . . . . . . . . . . . . . . . . . . . . . . . . . . . .
97
8.1
Häugkeitstabelle und Säulendiagramm.
99
8.2
Maÿzahlen der Aufgabe . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
8.3
Häugkeitstabelle, Diagramme und Maÿzahlen der Verteilung.
8.4
Häugkeitstabelle und Diagramme
8.5
Boxplot zu den Daten des Beispiels 2.1 . . . . . . . . . . . . . . . . . . . 102
8.6
Häugkeitstabelle, Diagramme und Maÿzahlen.
8.7
Einfacher Boxplot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
. . . . . . . . . . . . . . . . . .
. . . . . . 101
. . . . . . . . . . . . . . . . . . . . . 102
. . . . . . . . . . . . . . 103
vii
Abbildungsverzeichnis
8.8
Variante des Boxplots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
8.9
Lösung zur Aufgabe
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
8.10 Klassierte Häugkeitstabelle und Diagramme . . . . . . . . . . . . . . . . 105
8.11 Häugkeitstabelle und Lorenzkurve
. . . . . . . . . . . . . . . . . . . . . 106
8.12 Konzentrationskurve und Rosenbluth- sowie Herndahl-Index
. . . . . . 106
8.13 Konzentrationskurve und Rosenbluth- sowie Herndahl-Index
. . . . . . 107
8.14 Häugkeitstabelle und Diagramme.
. . . . . . . . . . . . . . . . . . . . . 108
8.15 Häugkeitstabelle und Lorenzkurve
. . . . . . . . . . . . . . . . . . . . . 108
8.16 Häugkeitstabelle und Lorenzkurve
. . . . . . . . . . . . . . . . . . . . . 109
8.17 Häugkeitstabelle, Histogramm und Verteilungsfunktion.
8.18 Baumdiagramme
. . . . . . . . . 110
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
8.19 Baumdiagramm und Verteilung
. . . . . . . . . . . . . . . . . . . . . . . 112
8.20 Arbeitstabelle für die Aufgabe 10
. . . . . . . . . . . . . . . . . . . . . . 115
8.21 Arbeitstabelle für den Satz von Bayes . . . . . . . . . . . . . . . . . . . . 116
8.22 Verteilung von Chuck-a-luck . . . . . . . . . . . . . . . . . . . . . . . . . 118
viii
Tabellenverzeichnis
1.1
Eine Datenmatrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1
Aufbau einer Häugkeitstabelle
2.2
Liste der Weltmeister im Fuÿball
8
. . . . . . . . . . . . . . . . . . . . . . .
14
. . . . . . . . . . . . . . . . . . . . . .
17
3.1
Notenverteilung Herren . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
3.2
Anzahl von Cocktails . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
3.3
Benötigte Werte für den Boxplot
. . . . . . . . . . . . . . . . . . . . . .
26
3.4
Notenverteilung der Teilnehmer
. . . . . . . . . . . . . . . . . . . . . . .
38
4.1
Häugkeitstabelle eines stetigen Merkmals
. . . . . . . . . . . . . . . . .
4.2
Häugkeitstabelle eines stetigen Merkmals
. . . . . . . . . . . . . . . . .
47
4.3
Brumm, Brumm
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
5.1
Gröÿe von Haushalten, BRD 1970 . . . . . . . . . . . . . . . . . . . . . .
63
5.2
Fiktive Einkommen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
6.1
Diskrete Wahrscheinlichkeitsverteilung
69
6.2
Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.4
. . . . . . . . . .
75
6.3
Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.5
. . . . . . . . . .
76
6.4
Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.6
. . . . . . . . . .
77
6.5
Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.7
. . . . . . . . . .
77
7.1
Bernoulliverteilung
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
8.1
Notenverteilung der Teilnehmer
8.2
Brumm, Brumm
8.3
Gröÿe von Haushalten, BRD 1970 . . . . . . . . . . . . . . . . . . . . . . 107
8.4
Fiktive Einkommen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
. . . . . . . . . . . . . . . . . . .
44
. . . . . . . . . . . . . . . . . . . . . . . 100
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
ix
1 Grundlagen
1.1 Übersicht und Lernziele
Wenn Sie dieses Kapitel durchgearbeitet haben, sollten Sie
- den Unterschied zwischen schlieÿender und beschreibender Statistik kennen;
- wissen, welche Rolle die Wahrscheinlichkeitstheorie spielt;
- die wichtigsten Grundbegrie der Statistik wie Grundgesamtheit, Stichprobe und
Merkmalsträger verstehen;
- die vier Arten von Merkmalen unterscheiden können;
- wissen, wie die Ergebnisse einer Befragung in einer Datenmatrix festgehalten werden.
1.2 Zum Begri Statistik
Statistik
geht auf das neulateinische Wort status zurück, dessen Bedeutungen Staat
und Zustand sind. Statistik betraf ursprünglich alle Daten, die der Verwaltung bei der
Entscheidungsndung behilich sein konnten, etwa Daten über die Bevölkerung (Geburten, Eheschlieÿungen und Todesfälle), Handel und Gewerbe sowie Ein- und Ausgaben
des Staates. Datensammlungen dieser Art werden heute als amtliche Statistik bezeichnet, wofür staatliche Organisationseinheiten wie etwa das Statistische Bundesamt zuständig sind. Inzwischen sammeln aber auch Unternehmen und andere Organisationen
Daten über Kunden, Mitarbeiter oder Geschäftspartner. Die erste Bedeutung des Begris Statistik ist also die Zusammenstellung von Zahlen und Daten über bestimmte
Gesamtheiten.
Weiterhin versteht man unter Statistik alle Methoden zur Analyse von variierenden
Eigenschaften von Objekten einer fest umrissenen Gesamtheit. Die Unterschiede bei
den Ausprägungen der Eigenschaften müssen dabei zumindest teilweise zufälliger Natur
sein. Dabei muss zunächst eine präzise Frage gestellt und in ein Modell verwandelt
werden. Danach erfolgt die Erhebung von Daten und deren Auswertung bezüglich der
Fragestellung.
Halten wir fest: Der Begri Statistik bezeichnet sowohl Datenbestände und deren
Erhebung wie Bevölkerungsstatistik als auch Methoden zur Untersuchung von Massenphänomenen, die unter Einuss des Zufalls entstanden sind, durch die Auswertung
bestehender oder extra zu diesem Zweck erhobener Daten.
1
1 Grundlagen
1.3 Wahrscheinlichkeitstheorie, beschreibende und
schlieÿende Statistik
In der Statistik, geht es um das Problem, Beobachtungen, die unter Einuss des Zufalls
entstanden sind, zu analysieren.
Die
beschreibende oder deskriptive Statistik
erfasst und bereitet Daten auf und verdich-
tet sie in Form von Tabellen, graphischen Darstellungen und Kennzahlen wie Mittelwert
und Varianz. Die beschreibende Statistik beschäftigt sich nur mit den vorliegenden Daten, daher beziehen sich alle Aussagen auch nur auf diese Daten.
Die
schlieÿende oder induktive Statistik
stellt Methoden zur Verfügung, die einen
Schluss von Teilerhebungen auf Grundgesamtheiten erlauben. Meinungsforschungsinstitute benötigen die schlieÿende Statistik, um die Ergebnisse von Umfragen auf die
Gesamtheit zu übertragen. Da statistische Schlüsse auf den Daten einer Stichprobe genannten Auswahl beruhen, sind Schlussfolgerungen auf die Gesamtheit möglicherweise
fehlerhaft. Zu einem Verfahren der schlieÿenden Statistik gehören Abschätzungen der
Fehler. Diese liefert die
Wahrscheinlichkeitstheorie ,
ein Spezialgebiet der Mathematik
zur Beschreibung zufallsabhängiger Vorgänge. Die Wahrscheinlichkeitsrechnung entstand
aus Untersuchungen von Glücksspielen und basierte zunächst auf rein kombinatorischen
Methoden. Die moderne Wahrscheinlichkeitstheorie beruht auf einem für Nichtmathematiker kaum verständlichen axiomatischen Regelwerk des russischen Mathematikers
Kolmogorov.
1.4 Gliederung einer statistischen Untersuchung
Eine statistische Untersuchung besteht aus mehreren Schritten.
(1)
Festlegung der Fragestellung und der Grundgesamtheit
Statistische Untersuchungen sollen Vermutungen bestätigen oder widerlegen, daher
müssen zunächst die Objekte der Untersuchung genau festgelegt werden. Diese Objekte, z.B. die Wahlberechtigten zur Bundestagswahl 2009, bilden die so genannte
Grundgesamtheit .
(2)
Voll- oder Teilerhebung
Vollerhebung werden alle Objekte der Grundgesamtheit untersucht, bei einer Teilerhebung dagegen nur ein Teil der Grundgesamtheit, eine so genannte Stichprobe . Vollerhebungen sind bei groÿen Grundgesamtheiten oft aus Kostengründen
Bei einer
nicht sinnvoll, manchmal sogar prinzipiell unmöglich. Bei einer Teilerhebung hat
die richtige Auswahl der Stichprobe eine groÿe Bedeutung für die Übertragung der
gewonnenen Ergebnisse auf die Grundgesamtheit, im Beispiel der Bundestagswahl
muss eine Teilerhebung alle gesellschaftlichen Strömungen der wahlberechtigten Bevölkerung widerspiegeln. Man kann daher die Stichprobe bewusst nach bestimmten
Kriterien aussuchen, oder aber die Auswahl dem Zufall überlassen. Eine hinreichend
groÿe Zufallsstichprobe wird in der Regel durchaus repräsentativ für die Grundgesamtheit sein.
2
1.5 Statistische Grundbegrie
(3)
Datenerhebung
Hat man Grundgesamtheit und Stichprobe gewählt, stellt sich das Problem der Datenerhebung. Man kann Daten durch
Beobachtung
und durch
Befragung
gewinnen.
Daten können durch schriftliche oder mündliche Befragung erhoben werden, wobei
die mündliche Befragung persönlich oder über Telefon erfolgen kann. Die Auswahl
sollte sich danach richten, was am besten für das Ziel der Untersuchung geeignet ist.
(4)
Die Datenaufbereitung und Datendarstellung
Zunächst werden fehlerhafte Daten bereinigt und dann in einer Datenbank erfasst
und von geeigneten Programmen wie SAS oder SPSS ausgewertet und dargestellt,
etwa in Form von Tabellen, Diagrammen und Kennzahlen, also mit Verfahren der
beschreibenden Statistik.
(5)
Datenanalyse
Bei der Auswertung werden Methoden der schlieÿenden Statistik eingesetzt. Die
schlieÿende Statistik ist stark mathematisch orientiert und beschäftigt sich damit,
welche Schlüsse von einer Stichprobe auf die Grundgesamtheit möglich sind. Im
Beispiel der Bundestagswahl geht es dabei um die Frage, wie gut die Stimmanteile
der einzelnen Parteien durch die Stichprobe geschätzt werden. Die Angabe erfolgt
meist in der Form von so genannten Kondenzintervallen in der Form: mit eine
Wahrscheinlichkeit von 99 % wird die CDU einen Stimmanteil zwischen 33 % und
36 % haben.
1.4.1 Beispiele statistischer Untersuchungen
Ich gebe zur Verdeutlichung einige typische Fragen an, die mit statistischen Untersuchungen beantwortet werden können.
•
Berechnung der Anteils von derzeitigen Wählern der FDP.
Die Grundgesamtheit sind hier alle Wahlberechtigten in Deutschland. Da nur amtliche Stellen diese Grundgesamtheit kennen, ist diese Frage nur über eine Stichprobe zu beantworten, die Auswertung muss mir Methoden der schlieÿenden Statistik
erfolgen und wird somit fehlerhaft sein.
•
Wohnungszählung in Deutschland im Rahmen der Volkszählung 2011.
Die Grundgesamtheit sind hier alle Gebäude in Deutschland. Da alle Eigentümer
befragt werden und auskunftspichtig sind, liegt eine Vollerhebung vor.
•
Bestimmung des Anteils fehlerhafter Glühbirnen an einem Produktionsstandort.
Auch hier kann man nur eine Teilerhebung durchführen, es sei denn, die Glühbirnen
werden innerhalb der Produktion sofort getestet.
1.5 Statistische Grundbegrie
Zur Beschreibung statistischer Untersuchungen werden folgende Begrie benutzt:
3
1 Grundlagen
•
Statistische Einheit oder Merkmalsträger
Dieser Begri beinhaltet Personen oder Gegenstände, aber auch Ereignisse wie
Geburten oder Sterbefälle.
•
Grundgesamtheit
So wird die Menge der statistischen Einheiten genannt.
•
Bestandsmasse
Besitzen die statistischen Einheiten der Grundgesamtheit einen längeren Bestand,
so spricht man von einer Bestandsmasse. Die Erfassung erfolgt zu einem bestimmten Zeitpunkt. Der Wohnungsbestand und die Einwohner einer Stadt sind typische
Bestandsmassen, eine Befragung erfasst den Zustand in einem bestimmten Augenblick.
•
Bewegungsmasse oder Ereignismasse
Die statistischen Einheiten einer Ereignismasse sind Ereignisse von kurzer Lebensdauer wie Geburten, Todesfälle oder Störfälle in einem Kraftwerk. Wegen der kurzen Lebenszeit eines Ereignisses, werden die statistischen Einheiten einer Ereignismasse über einen längeren Zeitraum hinweg erfasst.
•
Merkmale
Die bei einer statistischen Einheit erhobenen Eigenschaften wie Geschlecht, Alter
oder Haarfarbe bei Personen, werden Merkmale genannt.
•
Merkmalsausprägungen
Die verschiedenen Werte, die ein Merkmal annehmen kann, werden Merkmalsausprägungen genannt. Beim Merkmal Haarfarbe beispielsweise gibt es die klassischen Ausprägungen wie blond, rot bzw. schwarzhaarig, das Geschlecht hat die
beiden Ausprägungen weiblich und männlich und die Ausprägungen des Merkmals
Alter einer Person sind die natürlichen Zahlen.
1.6 Bestands- und Bewegungsmassen
Bei den Gesamtheiten wird zwischen Bestandsmassen und Bewegungsmassen unterschieden. Bestandsmassen werden an einem
einer
Zeitspanne
Zeitpunkt, Bewegungsmassen dagegen innerhalb
erfasst. Oft korrespondieren die beiden Gesamtheiten miteinander. Die
Einwohner Heidelbergs werden am 1.1.2010 und dann wieder am 1.1.2011 gezählt, also
jeweils an einem festen Zeitpunkt, daher handelt es sich um Bestandsmassen. Die Stadtverwaltung erfasst auch alle in einem Jahr erfolgten An- und Abmeldungen, sowie alle
Geburten und Todesfälle. Das sind vier Bewegungsmassen, die den Unterschied zwischen
den beiden Bestandsmassen erklären:
Einw. 2011
4
= Einw.
2010
+ Geburten − Todesfälle + Abmeldungen − Anmeldungen
1.7 Einteilung von Merkmalen
1.7 Einteilung von Merkmalen
Je nach Fragestellung können Personen, Unternehmen oder ganze Länder statistische
Einheiten bilden. Wichtig ist eine räumlich, zeitlich und sachlich klar umrissene Fragestellung mit geeigneten Merkmalen. Merkmale spielen eine so bedeutende Rolle, dass die
statistischen Einheiten oft auch als
Merkmalsträger
bezeichnet werden. Weitere Beispiele
für Merkmale sind die Konfession mit den Ausprägungen wie RK (römisch katholisch),
EKD (evangelische Kirche Deutschlands) oder andere. Bei einer Wohnung gibt es
Merkmale wie Anzahl der Zimmer, Gröÿe im qm, Balkon usw. mit Ausprägungen wie
4, 80 qm und keiner.
Merkmale werden mit groÿen lateinischen Buchstaben wie etwa
X
bezeichnet, die
zugehörigen Merkmalsausprägungen mit kleinen, wobei zur Unterscheidung ein Index
verwendet wird, also
x 1 , x2 , x3 , . . . , x n .
Merkmale lassen sich je nach Typ der Werte ihrer Ausprägung in vier Klassen einteilen.
(1)
Nominale Merkmale
Nominal stammt vom lateinischen Wort nomen für Namen ab, weil die möglichen
Werte der Ausprägungen nur benannt können werden, es gibt keine Maÿeinheit. Dies
trit auf Merkmale wie Geschlecht mit den Ausprägungen w und m und auf
Konfession mit den erwähnten Ausprägungen RK, EKD und andere zu. Bei
der Erfassung werden nominale Merkmalsausprägungen meistens durch Zahlwerte
kodiert, etwa 0 für w und 1 für m, das ändert aber nichts an der prinzipiell
zahlenfernen Natur dieser Merkmale. Da man die Ausprägungen nur in Kategorien
einteilen kann, werden nominale Merkmale auch
kategoriell
genannt. Wenn es für
die Ausprägung eines nominalen Merkmals nur zwei mögliche Werte gibt, spricht
man von einem
dichotomen ,
sonst von einem
polytomen
Merkmal. Das Merkmal
Geschlecht ist somit dichotom, während das Merkmal Nationaltät polytom ist.
(2)
Ordinale Merkmale
Hier lassen sich die Ausprägungen in eine Rangfolge bringen, aber man kann für
die Werte und deren Abstände untereinander kein Maÿ angeben. Das trit z.B. auf
Schulnoten zu, sehr gut ist besser als gut, gut besser als befriedigend, aber man
kann nicht sagen, dass die Noten sehr gut und gut denselben Abstand wie die Noten
gut und befriedigend haben. Auch die Werte ordinal skalierter Merkmale werden zur
besseren Auswertung mit Zahlen codiert.
(3)
Metrische Merkmale
Sind bei einem Merkmal die Ausprägungen Zahlen mit sinnvollen Einheiten, so
spricht man von einem metrischen Merkmal. Hier können die Abstände zwischen
den Werten sinnvoll bestimmt werden. Beispiele sind die Merkmale Gröÿe, Gewicht
und Alter einer Person. Metrische Merkmale werden auch
kardinal
genannt. Metri-
sche Merkmale werden noch weiter unterteilt, und zwar in diskret und stetig. Das
Gewicht einer Person ist ein stetiges metrisches Merkmal, da die Werte stetig über
ein ganzes Intervall verteilt sind. Dagegen hat das Merkmal Anzahl der Kinder nur
endlich viele Werte, was man als diskret bezeichnet.
5
1 Grundlagen
Die vier Merkmalsklassen sind also nominal, ordinal, metrisch diskret und metrisch stetig, wobei statt nominal auch kategoriell und statt metrisch auch kardinal verwendet
qualitatativ
zusammengefasst, die beiden metrischen Merkmale werden dagegen quantitativ genannt.
werden. Nominale und ordinale Merkmale werden unter dem Oberbegri als
Fassen wir zusammen:
Sie müssen Merkmale also zunächst in qualitativ oder quantitativ einteilen und danach
entscheiden, ob sich ein als qualitativ erkanntes Merkmal ordnen lässt, dann wird es ordinal und sonst nominal genannt. Bei einem quantitativen Merkmal ist zu untersuchen
ob nur endlich oder abzählbar unendlich viele Werte auftreten, dann spricht man von
einem diskreten metrischen Merkmal. Liegen die Werte stetig in einem ganzen Intervall
verteilt, spricht man von einem stetigen metrischen Merkmal. Metrische Merkmale werden oft auch kardinale Merkmale genannt und nominale Merkmale werden manchmal
als kategoriell bezeichnet.
Entscheidend ist, die wesentlichen Qualitätsunterschiede der Merkmalskategorien und
deren Konsequenzen zu kennen: Bei metrischen Merkmalen können Abstände quantiziert werden, was bei ordinalen und nominalen Merkmalen nicht der Fall ist, während bei
ordinalen Merkmalen immerhin noch eine natürliche Rangfolge unter den Merkmalswerten existiert. Diese Unterschiede haben Konsequenzen u.a. hinsichtlich der Möglichkeit
der Berechnung von Mittelwerten, aber auch anderer statistischer Maÿzahlen und Verfahren. Mittelwerte sowie andere statistische Maÿzahlen und deren Anwendbarkeit bei
den drei Merkmalskategorien werden noch ausführlich behandelt.
Abschlieÿend noch einige Beispiele. Geschlecht, Haarfarbe und Nationalität sind alles nominale Merkmale. Schulnoten, die Vergabe von Sternen, etwa 1 bis 5, an Hotels
oder die Einteilung der Sympathie zu Politikern in die Ränge Mag ich, Na ja und
Eher nicht sind ordinale Merkmale. Die folgenden Merkmale sind diskret und metrisch: Zahl der Eheschlieÿungen, Einwohnerzahl von Darmstadt, Anzahl von Studenten
der Hochschule Darmstadt. Körpergröÿe und Gewicht einer Person sind stetige metrische
Merkmale, deren mögliche Werte z.B. 1,80 m und 78,44 kg sein können.
1.8 Messen und Skalenniveaus
Dieser Abschnitt ist zunächst nur für den hartgesottenen Leser.
Den Ausprägungen eines Merkmals müssen bestimmte Werte zugeordnet werden. Die
Wahl muss dabei so getroen werden, dass die Werte strukturtreu sind, sodass die Werte
die realen Unterschiede auch korrekt wiedergeben. Das sei am Beispiel des Merkmals
Religionszugehörigkeit verdeutlicht. Im Jahr 1950 waren in Deutschland die drei Werte
evangelisch, römisch katholisch und andere oder keine ausreichend, während diese
Einteilung heute sicher nicht mehr strukturtreu ist, es sei denn, dass es nur um die
Abführung der Kirchensteuer geht.
Die Ausprägungen eines Merkmals müssen messbar sein und einem so genannten
lenniveau
Ska-
zugeordnet werden können. Obwohl es unzählige Merkmale gibt, werden nur
vier Skalenniveaus benötigt und diese decken sich auch noch weitgehend mit der Einteilung der Merkmale. Jedem Skalenniveau entsprechen bestimmte Relationen, in der je
6
1.9 Fragebögen
zwei Messwerte zueinander stehen.
Ich gebe jetzt die vier Skalenniveaus und ihre denierende Relation an.
(1)
Nominalskala
Die Beziehung besteht in der Feststellung, ob zwei Messwerte gleich sind oder nicht,
weitere Unterscheidungen sind nicht möglich. Die Nominalskala passt daher genau
zu den nominalen Merkmalen wie Geschlecht oder Familienstand.
(2)
Ordinalskala
Bei einer Ordinalskala lassen sich ebenfalls je zwei Messwerte auf Gleichheit untersuchen, aber zusätzlich ist ein Gröÿenvergleich möglich, die Messwerte lassen sich
anordnen, aber man kann keine Abstände zwischen den Messwerten angeben. Die
Merkmale mit einer Ordinalskala sind also genau die ordinalen Merkmale.
(3)
Intervallskala
Bei einer Intervallskala ist der Abstand zwischen je zwei Messwerten deniert. Streng
genommen ist das keine Relation, aber eine eindeutige Festlegung des Begris Intervallskala. Ein Abstand von 0 bedeutet Gleichheit, ein positiver Abstand entspricht
der Beziehung Gröÿer, eine Intervallskala ist somit immer auch eine Ordinalskala.
Intervallskalen gelten für metrische Merkmale, wofür Abstände zwischen den Ausprägungen aber nicht notwendig Verhältnisse gebildet werden können. Beispiel von
Merkmalen mit einer Intervallskala sind die Temperatur, die Uhrzeit, das Datum sowie Längen- und Breitengrade von Orten auf der Erde. In jedem Fall ist der Abstand
zwischen zwei Messwerten genau deniert, aber es können keine Verhältnisse gebildet werden. Mittag ist genau zwei Stunden vor 10:00, aber nicht um 20 % später, so
wenig wie Rom 12 % südlicher als München liegt.
(4)
Verhaltnisskala (Ratioskala)
Bei dieser Skala können zusätzlich zu den Abständen auch die Verhältnisse von Messwerten gebildet werden. Diese Messwerte besitzen einen natürlichen Nullpunkt. Beispiele von Merkmalen mit Verhältnisskala sind das Gewicht und die Gröÿe oder das
Vermögen. Man kann hier Aussagen treen wie, Am Nachmittag kommen doppelt
so viel Studenten in die Vorlesung wie am Morgen oder Mein Elefant nimmt pro
Jahr 5 % zu.
Die vier Skalenniveaus sind also geordnet, d.h. jede höhere Skala schlieÿt die niedrigeren Skalen ein. Verhältnisskala und Intervallskala werden auch als metrische Skalen
bezeichnet; eine Vielzahl von statistischen Berechnungen benötigen metrisch skalierte
Merkmale, um sie sinnvoll anwenden zu können.
1.9 Fragebögen
Die Erhebung basiert in der Regel auf Fragen, die dem Untersuchungsziel angepasst
sind. Die einzelnen Fragen werden zu einem
Fragebogen
zusammengefasst. Ein Dozent
befragt beispielsweise die Teilnehmer seines Kurses nach Geschlecht, Alter, Hobbies und
7
1 Grundlagen
Schulabschluss. Die Hobbies werden auf Sport und Reisen begrenzt und bilden eine so
genannte
Mehrfachfrage . In diesem Fall wird jedem Hobby ein eigenes Merkmal zugeord-
net, mit den zulässigen Antworten ja und nein. Abschlieÿend soll jeder Teilnehmer
mit eigenen Worten die Mensa bewerten.
Man unterscheidet oene und geschlossene Fragen. Bei
geschlossenen Fragen
muss
eine Antwort aus einer Liste oder einem Zahlenbereich ausgewählt werden, das trit auf
die Fragen nach Geschlecht, Alter, Schulabschluss und den Hobbies zu. Die Bewertung
der Mensa ist eine
oene Frage , die sicherlich zu sehr unterschiedlichen Antworten führt
und deshalb statistisch schwierig auszuwerten ist.
1.10 Die Datenmatrix
Die ausgefüllten Fragebögen werden in Form einer Tabelle zusammengefasst, der so
genannten
Datenmatrix .
Die Tabelle 1.1 zeigt die zu den erwähnten Fragen erstellte
Datenmatrix.
Tabelle 1.1: Eine Datenmatrix
ID
X (Sex)
V (Alter) Y1 (Sport) Y2 (Reisen) Z (Schulabschluss)
1
1 männlich
27
1 Ja
1 Ja
3 Mittlere Reife
2
0 weiblich
54
1
1
3
3
1
34
1
0 Nein
4 Abitur
4
0
16
0 Nein
1
2 Hauptschule
5
0
15
0
1
1 nichts
In einer Zeile stehen die Antworten eines Befragten, also einer statistischen Einheit
bzw. eines Merkmalsträgers, der durch eine eindeutige ID zu identizieren ist, In jeder Spalte sind die Werte der Merkmale zu nden. Jedem Merkmal wird eine Variable
zugeordnet, hier das nominale Merkmal
Z
X
für das Geschlecht, das ordinale Merkmal
für den Schulabschluss und das metrische Merkmal
Merkmale
Y1
und
Y2
V
für das Alter. Die nominalen
sind Teile einer , hier nach dem Hobby, worauf der gemeinsame
Buchstabe Y hinweist. Die Werte der Variablen
Y1
und
Y2
sind ja oder nein, also
handelt es sich um dichotome Merkmale. Die Rohdaten einer Befragung werden meist
auch für qualitative Merkmale durch Zahlen codiert, hier etwa 0 für weiblich und 1 für
männlich. Oft zeigt man diese Codierung beim ersten Auftreten in der Datenmatrix
an. Trotz der zahlenmäÿigen Erfassung sollte klar sein, dass das arithmetische Mittel
des Geschlechts der Merkmalsträger nicht 0,4 ist.
8
1.11 Aufgaben
1.11 Aufgaben
1.) Eine Firma der Metallverarbeitung fasst die wichtigsten Daten über alle Mitarbeiter
in einer Datenmatrix zusammen, deren Felder das Geschlecht, die Abteilung, das
Geburtsjahr sowie Tarifgruppe und Gehalt sind.
a) Was sind hier die statistische Gesamtheit und die statistische Einheiten?
b) Welcher Art ist die Erhebung?
c) Welcher Art sind die oben erwähnten Merkmale und welche möglichen Ausprägungen haben diese?
d) Geben Sie die Datenmatrix mit den Werten von zwei ktiven Merkmalsträgern
an.
2.) Eine Hochschule befragt 100 zufällig ausgewählte Studenten nach Geschlecht, Nationalität, Alter, Schulbildung und Fachbereich.
a) Was sind hier die statistische Gesamtheit und die statistische Einheiten?
b) Welcher Art ist die Erhebung?
c) Welcher Art sind die oben erwähnten Merkmale und welche möglichen Ausprägungen haben diese?
d) Geben Sie die Datenmatrix mit den Werten von zwei ktiven Merkmalsträgern
an.
3.) Zeigen Sie am Beispiel der in Deutschland zugelassenen PKW den Zusammenhang
zwischen Bestands- und Bewegungsmassen.
9
2 Darstellung univariater Daten
2.1 Übersicht und Lernziele
Wenn Sie dieses Kapitel durchgearbeitet haben, sollten Sie
- wissen wie man die Werte eines Merkmals durch eine Häugkeitstabelle darstellt;
- wissen wie man die Häugkeitsverteilung durch ein Stabdiagramm veranschaulicht;
- wissen wie die empirische Verteilungsfunktion deniert ist;
2.2 Die vier Grundformen von Datensätzen
Bei der univariaten Datenanalyse verwendet man vier verschiedene, aber eng verwandte
Listen von Daten.
(1)
Urliste
Die Daten einer Erhebung werden in einer Datenmatrix festgehalten, bei der eine
Zeile den vollständigen Datensatz einer statistischen Einheit, also eines Merkmalsträgers, beschreibt. In den Spalten stehen die Werte der einzelnen Merkmale. Bei
der univariaten Datenauswertung wird nur ein Merkmal allein ausgewertet. Bei einer
Grundgesamtheit mit
n
Merkmalsträgern besteht eine Spalte somit aus einer Folge
x1 , x2 , . . . , xn ,
wobei
als
(2)
xi die Merkmalsausprägung des i-ten Merkmalsträgers ist. Diese Werte werden
Urliste
bezeichnet und stehen am Anfang jedes Verfahrens.
aufsteigend geordnete Urliste
Die Urliste ist unübersichtlich und wird deshalb der Gröÿe nach geordnet, um etwas
Licht ins Dunkel zu bringen, und zwar in der Regel in aufsteigender Ordnung
x(1) ≤ x(2) ≤ . . . ≤ x(n) .
Die seltsame Bezeichnung
x(j)
ist in der beschreibenden Statistik für die Elemente
der aufsteigend geordneten Urliste üblich.
(3)
absteigend geordnete Urliste
Manchmal fängt die Ordnung auch beim gröÿten Einzelwert an und verläuft dann
11
2 Darstellung univariater Daten
absteigend. Auch hierfür haben sich die Statistiker eine seltsame Bezeichnung einfallen lassen
x(1) ≥ x(2) . . . ≥ x(n) .
Die Elemente der absteigend geordneten Liste werden mit
(4)
x(j)
bezeichnet,
Ausprägungen
Innerhalb einer Urliste treten in der Regel manche Werte mehrfach auf. Es gibt dann
nur
k
wirklich verschiedene Werte, die ich wie Handl mit
ai
bezeichne, der Gröÿe
nach anordne
a1 < a2 < a3 . . . < ak−1 < ak
und als
Ausprägungen
bezeichne.
Ich bezeichne mit n immer die Anzahl der Daten und mit k die Anzahl der Ausprägungen.
Nur wenn alle Werte verschieden sind, ist k = n, sonst ist k < n.
Beispiel 2.1.
9
Hier sind
6
7
Die folgende Liste zeigt die Studiendauer einer Gruppe von Studenten
10
n = 10
7
5
7
9
x4 = 10,
und
6
denn der vierte Wert der Urliste ist 10. Die nach
zunehmenden Werten geordnete Liste
5
6
6
6
7
7
7
6.
9
9
x(j)
ist
10.
Aus dieser ergibt sich durch Weglassen der Wiederholungen die Liste
aj
der Ausprägun-
gen
5
6
Somit sind
7
9
x(4) = 6
10
und
a4 = 9 ,
denn in der zunehmend geordneten Liste ist das vierte
Element 6 und in der Liste der Ausprägungen ist das vierte Element 9. Da es nur fünf
Ausprägungen gibt, ist
k = 5.
2.3 Absolute und relative Häugkeiten
Bei der Datenanalyse wird gezählt, wie viele Merkmalsträger
Man nennt diese Zahl die
absolute Häugkeit
ni
ai
hat.
der Ausprägung. Die absolute Häugkeit
allein ist wenig aussagekräftig, dazu ist der Bezug zur Anzahl
nötig, also die
die Ausprägung
relative Häugkeit
n
der Merkmalsträger
fi = ni /n.
In manchen Fällen liegt die Urliste der Daten nicht vor, weil bei der Datenerfassung bereits die möglichen Ausprägungen bekannt sind und nur noch die absoluten Häugkeiten
ausgezählt werden müssen. Die Paare
Da die absoluten Häugkeiten
ergeben, liegen die Werte der
12
fi
ni
(ai , ni )
werden als
zwischen
1
und
n
Häugkeitsliste
bezeichnet.
liegen und zusammengezählt
n
zwischen 0 und 1 und ihre Summe ist genau 1. Relative
2.4 Kumulierte absolute und relative Häugkeiten
Häugkeiten werden oft auch in Prozent angegeben, dafür müssen die Werte mit 100
multipliziert werden und die Summe ergibt 100.
Die Merkmale mit gleichem Wert bilden eine Gruppe, man spricht auch von
gruppier-
ten Daten . Die Anzahl von Gruppen werde ich immer mit k bezeichnen. Wenn alle Werte
k = n und x(j) = aj . Im Beispiel 2.1 gibt es k = 5
Gruppen mit den absoluten Häugkeiten n1 = 1, n2 = 3, n3 = 3, n3 = 2 sowie n5 = 1
und den relativen Häugkeiten f1 = 0, 1, f2 = 0, 3, f3 = 0, 3, f4 = 0, 2 und f5 = 0, 1. Die
absoluten Häugkeiten ni summieren sich zu n und die relativen Häugkeiten zu 1.
der Urliste verschieden sind, folgen
k
X
i=1
k
X
ni = n1 + n2 + · · · + nk = n
(2.1)
fi = f1 + f2 + · · · + fk = 1
(2.2)
i=1
2.4 Kumulierte absolute und relative Häugkeiten
Bei mindestens ordinalen Merkmalen sind die Ausprägungen
a1 , a2 , . . . , ak
der Gröÿe
nach geordnet. Deshalb ist eine stufenweise Ansammlung (Kumulation) bereits erreichter
Anteile möglich, um etwa bei den Ergebnissen einer Klassenarbeit, den Prozentsatz
von Schülern anzugeben, die mindestens eine vier erreicht haben. Sind
n1 , n2 , . . . , nk
die absoluten Häugkeiten der geordneten Merkmalsausprägungen, so werden die i-te
kumulierte absolute bzw. relative Häugkeit durch
Ni =
k
X
nj = n1 + n2 + · · · + ni
(2.3)
fj = f1 + f2 + · · · + fi
(2.4)
j=1
Fi =
k
X
j=1
berechnet.
Bei den Daten des Beispiels 2.1 ergeben sich folgende Werte für die kumulierten abso-
N1 = 1, N2 = 4, N3 = 7, N4 = 9 und N5 = 10 und entsprechend nach
Division dieser Werte durch n = 10 die kumulierten relativen Häugkeiten F1 = 0, 1,
F2 = 0, 4, F3 = 0, 7, F5 = 0, 9 und F5 = 1.
luten Häugkeiten
2.5 Häugkeitstabellen
Die Ausprägungen und deren absoluten und relativen Häugkeiten sowie die entsprechenden kumulierten Werte werden in einer Tabelle zusammengefasst, die man
keitstabelle
Häug-
nennt. Im Beispiel der Studiendauer ergibt sich die Häugkeitstabelle wie in
der Tabelle 2.1 dargestellt. Nach diesem Muster wird die Häugkeitstabelle eines jeden
mindestens ordinalen Merkmals aufgebaut.
13
2 Darstellung univariater Daten
Tabelle 2.1: Aufbau einer Häugkeitstabelle
i
ai
ni
Ni
fi
Fi
1
5
1
1
0,1
0,1
2
6
3
4
0,3
0,4
3
7
3
7
0,3
0,7
4
9
2
9
0,2
0,9
5
10
1
10
0,1
1
In der ersten Spalte steht der Index
Ausprägungen
ai ,
i
der jeweiligen Zeile, in der zweiten stehen die
in der dritten die absoluten Häugkeiten, in der vierten die kumu-
lierten absoluten Häugkeiten, in der fünften die relativen Häugkeiten, in der letzten
die kumulierten relativen Häugkeiten. Den kumulierten relativen Häugkeiten können
wir unter anderem entnehmen, dass die Studiendauer bei 90 Prozent der untersuchten
Studenten höchstens 9 Semester lang war.
2.6 Stab- Säulen- und Balkendiagramme
.
Absolute und relative Häugkeiten lassen sich durch Diagramme veranschaulichen. Bei
Stab- und Säulendiagrammen werden die Werte der Häugkeiten
ni
bzw.
fi
in Längen
von Stäben oder Höhen von Säulen umgerechnet und über den Werten von
ai
abge-
tragen. Deshalb kann man die Werte der Häugkeiten sehr gut vergleichen und sogar
ablesen. Die Stabdiagramme der absoluten und relativen Häugkeiten der Verteilung
der Häugkeitstabelle 2.1 zeigt die folgende Abbildung.
1
2
3
4
5
6
7
8
9
10
A B
i ai
1
2
3
4
5
5
6
7
9
10
C
ni
1
3
3
2
1
5 5
0 0,1
0 1
D
Ni
E
fi
F
Fi
1
4
7
9
10
0,1
0,3
0,3
0,2
0,1
0,1
0,4
0,7
0,9
1
G
H
I
J
K
L
M
N
fi
6
6
0 0,3
0
3
Q
R
S
ni
ai
4 5 6 7 8 9 10 11
7 7
0 0,3
0 3
P
Abs. Stabdiagramm
Rel. Stabdiagramm
0,3
0,2
0,1
0
O
3
2
1
0
9 9
0 0,2
0 2
ai
4 5 6 7 8 9 10 11
10 10
0 0,1
0
1
Abbildung 2.1: Stabdiagramme
Für eine Stabverteilung wird über jeder Ausprägung
Länge der relativen Häugkeit
14
fi
ai eine senkrechte Strecke mit der
(ai , 0)(ai , fi ).
nach oben abgetragen, also die Strecken
2.7 Empirische Verteilungsfunktion
Die Anfangs- und Endpunkte dieser
k
Strecken benden sich im Bereich B8:O9 des
abgebildeten Arbeitsblatts. Jeder Stab ist eine Punkt-Grak für sich, der erste Stab
wird durch den Bereich B8:C9 erzeugt, dann kommen die leeren Zellen D8:C9 und dann
folgen die Koordinaten des zweiten Stabs, usw. bis zu den Koordinaten des letzten Stabs.
Die Zeile 10 enthält die y-Werte für das Stabdiagramm der absoluten Häugkeiten.
Bei einem Balkendiagramm werden die Werte
Werte der
fi
ai
auf der y-Achse eingetragen und die
nach rechts, also waagrecht wie ein Balken.
2.7 Empirische Verteilungsfunktion
Bis jetzt wurden nur die Häugkeiten grasch dargestellt. Es gibt aber auch eine grasche Darstellung der kumulierten relativen Häugkeiten als Graph einer Funktion, der
sogenannten empirischen Verteilungsfunktion.
Diese ist nur für die Merkmalsausprägungen mindestens ordinaler Merkmale deniert.
Die
empirische Verteilungsfunktion F : R → [0, 1]
einer Urliste von
...,
xn
für jede reelle Zahl
leitet sich aus der Forderung ab, dass
F (x)
Anteil der Werte angibt, welche kleiner oder höchstens gleich
x
n
Werten
x
x1 , x2 ,
den relativen
sind; die Funktion ist
also für alle reellen Zahlen deniert und nicht nur für die eigentlichen Messwerte. Die
formale Denition der empirischen Verteilungsfunktion lautet
F (x) =
Anzahl der Daten
xi ≤ x
n
.
Die empirische Verteilungsfunktion gibt die Summe der relativen Häugkeiten aller Daten an, die kleiner oder gleich
x
sind, daher ist sie zwischen zwei benachbarten Daten
x1 ,
xn . Die Gröÿe des Sprunges am Wert xi ist die relative Häugkeit von xi .
Liegen n verschiedene Einzelbeobachtungen mit der aufsteigend geordneten Urliste
x(1) , x(2) , . . . , x(n) vor, so hat jeder Sprung die Höhe 1/n und die empirische Verteilungsfunktion zwischen x(i) und x(i+1) den Wert i/n.
konstant, hat also die Form einer Treppe. Die Sprungstellen sind gerade die Daten
x2 ,
...,
Wenn nicht alle Beobachtungen verschieden sind, wird die empirische Verteilungsfunktion über die Ausprägungen bestimmt. Da diese eine der Gröÿe nach geordnete Reihe
a1 < a2 < a3 . . . < ak−1 < ak
bilden, ist die empirische Verteilungsfunktion in jedem Intervall
und zwar mit dem Wert
tive Häugkeit
fi
Treppenfunktion
Fi−1
ai−1 ≤ x < ai konstant,
ai um die rela-
und springt an der nächsten Ausprägung
nach oben auf den neuen Wert
Fi .
Funktionen dieser Art werden als
bezeichnet. Damit ergibt sich für die empirische Verteilungsfunktion:


0,
F (x) = Fi ,


1,
wenn
wenn
wenn
x < a1 ;
ai ≤ x < ai+1 ,
x ≥ ak .
1 ≤ i ≤ k − 1;
Die empirische Verteilungsfunktion beginnt ihren langen Weg von
Ausprägung
a1
beim Wert 0, macht dann an jedem der
k
−∞
bis zur kleinsten
Messwerte einen Sprung nach
15
2 Darstellung univariater Daten
oben und erreicht am gröÿten Messwert
bis
ak
den Endwert 1, und verharrt auf diesem Wert
∞. Gezeichnet wird die empirische Verteilungsfunktion deshalb von einem Wert etwas
links vom kleinsten bis zu einem Wert etwas rechts von der gröÿten Ausprägung.
Die empirische Verteilungsfunktion des Merkmals
X
Anzahl der benötigten Semes-
ter ergibt sich aus der Häugkeitstabelle der Abbildung 2.1.


0,



0, 1,



0, 4,
F (x) =

0, 7,





0, 9,



1,
wenn
wenn
wenn
wenn
wenn
wenn
x < 5;
5 ≤ x < 6;
6 ≤ x < 7;
7 ≤ x < 9;
9 ≤ x < 10;
x ≥ 10.
Mit der empirischen Verteilungsfunktion kann man den Anteil
malsträger, deren Merkmalsausprägung im Intervall
(a, b]
f (a < X ≤ b)
der Merk-
liegt, bestimmen:
f (a < X ≤ b) = F (b) − F (a)
Der Anteil an Studenten, die länger als 6 und höchstens 9 Semester bis zum Abschluss
benötigten, ist also
F (9) − F (6) = 0, 9 − 0, 4 = 0, 5.
Den Graph der empirischen Verteilungsfunktion habe ich ebenfalls mit Excel erstellt.
A B
1 i ai
2 1 5
3 2 6
4 3 7
5 4 9
6 5 10
7
8
9 4 5
10 0 0
C
D
E
F
ni Ni fi Fi
1 1 0,1 0,1
3 4 0,3 0,4
3 7 0,3 0,7
2 9 0,2 0,9
1 10 0,1 1
G
H
I
6
0,1 0,1
K
L
M
N
O
P
Empirische Verteilungsfunktion
1
0,8
0,6
0,4
0,2
0
Fi
Q
R
5
6
7
9
10
0,1
0,4
0,7
0,9
1
ai
4
5
J
5
6 7
0,4 0,4
6
7
8
7 9
0,7 0,7
9
10
11
9 10
0,9 0,9
10 11
1 1
Abbildung 2.2: Empirische Verteilungsfunktion
In der Abbildung 2.2 ist der Graph dieser Funktion zu sehen. Die empirische Verteilungsfunktion ist rechtsstetig, d.h. die Treppenfunktion beginnt nach jedem Sprung
gleich am Anfang, also an der Stelle
ai
mit dem neuen Wert
Fi . Man deutet dies grasch
mit einer Klammer oder wie in der Abbildung mit einer Markierung am Anfang der
Treppenstufen an. Formal bedeutet die Rechtsstetigkeit für
1≤i≤k
F (ai ) = lim F (ai + ε),
ε→0+
wobei hier nur
ε > 0 erlaubt ist, da die Annäherung von rechts erfolgt. An allen anderen
Punkten ist die Funktion ohnehin stetig.
16
2.8 Der Sonderfall nominaler Merkmale
Für die empirische Verteilungsfunktion
rechte Strecken
F (x)
müssen also für
1 ≤ i ≤ k
die waag-
(ai , Fi )(ai+1 , Fi ) eingezeichnet werden. Vor dem kleinsten Wert a1 ist
0, nach dem gröÿten Wert ak konstant 1. Ich habe die Koordina-
die Funktion konstant
ten der jeweiligen Anfangs- und Endpunkte der Treppenstufen im Bereich A9:Q10 des
Excel-Arbeitsblatts von Abbildung 2.2 aufgeführt. Auch hier ist jede Stufe der Treppenfunktion eine Punktgrak. Die Markierungen am Anfang der Treppen werden ebenfalls
als Punktgrak erzeugt, die zugehörigen Koordinaten stehen im Bereich R1:S5.
Bemerkung 2.1. Der Begri empirisch bezieht sich immer auf Erfahrungen, Messungen
oder Beobachtungen und wird oft im Gegensatz zum Begri theoretisch verwendet. Empirische Verteilungsfunktionen basieren auf beobachteten Daten, während theoretische
Verteilungsfunktionen von einem Modell abgeleitet sind. Für weitere Auskünfte über
den Unterschied zwischen theoretischen und empirischen Verteilungsfunktionen wenden
Sie sich an den Hütchenspieler ihres Vertrauens oder lesen dessen Allgemeine Geschäftsbedingungen.
2.8 Der Sonderfall nominaler Merkmale
Nominale Merkmale haben keine natürliche Rangordnung, man verwendet für die Anordnung die vorgenommene Kodierung oder eine Anordnung nach dem Alphabet, trotzdem
ist keine Anhäufung möglich, daher entfallen in der Häugkeitstabelle die beiden Spalten
für
Ni
und
Fi .
Beispiel 2.2.
Seit 1930 werden alle vier Jahre mit Ausnahme von 1942 und 1946 Fuÿ-
ballweltmeisterschaften in wechselnden Ländern ausgetragen. Bisher gab es nur 9 Weltmeister und zwar in alphabetischer Reihenfolge Argentinien, Brasilien, Deutschland,
England, Frankreich, Italien, Spanien und Uruguay. Die folgende Tabelle zeigt die Anfangsbuchstaben der Weltmeisternationen und die verkürzte Jahreszahl ihres Triumphs.
Diese Datensammlung ist die Urliste, die in einer Datenmatrix eine Spalte wäre, hier
Tabelle 2.2: Liste der Weltmeister im Fuÿball
30
34
38
50
54
58
62
66
70
74
78
82
86
90
94
98
02
06
10
U
I
I
U
D
B
B
E
B
D
A
I
A
D
B
F
B
I
S
aber aus Platzgründen in einer Zeile steht. Ich fasse die einmaligen Weltmeister England,
Frankreich und Spanien zum Rest zusammen.
Die ungeordnete und die in alphabetischer Reihenfolge der Anfangsbuchstaben geordnete Urliste sowie die Ausprägungen sind dann
U I I U D B B R B D A I A D B F B I R
A A B B B B B D D D I I I I R R R U U
A B D I R U
17
2 Darstellung univariater Daten
Somit sind
x3 = I , x(3) = B und a3 = D, denn der Wert des dritten Merkmals der Urliste
ist I, der dritte Wert der geordneten Urliste ist B und die dritte Ausprägung ist
D. Weiterhin sind
und
n6 = 2.
n = 19, k = 6
sowie
n1 = 2, n2 = 5, n3 = 3, n4 = 4, n5 = 3
Die Ausprägungen und ihre Häugkeiten ergeben sich aus der geordneten
Urliste. Die zugehörige Häugkeitstabelle ist in Abbildung 2.3 zu sehen, wobei ich die
Ländernamen durch drei Buchstaben kodiert habe.
1
2
3
4
5
6
7
A
B
C
i
1
2
3
4
5
6
ai
Arg
Bra
Deu
Ita
Uru
Rst
ni
2
5
3
4
2
3
D
E
fi
6
10,53% # 5
4
26,32% W 3
15,79% M 2
1
21,05%
0
10,53%
15,79%
F
G
Arg Bra Deu Ita
Land
Uru Rst
Abbildung 2.3: Häugkeitstabelle und Säulendiagramm
Hier sind
a2 = Bra, n2 = 5
und
f2 = 5/19 = 26, 32 %.
Das Säulendiagramm der Ver-
teilung der Weltmeister ist in der Abbildung 2.3 zu sehen, wobei ich hier absolute Zahlen
verwendet habe. Die Ergebnisse einer Wahl zum Bundestag werden dagegen besser mit
relativen Häugkeiten dargeboten. Bei nominalen Merkmalen sind Säulen- und Balkendiagramme meist die richtige Wahl. Die Presse verwendet sehr gerne
Kreisdiagramme ,
dafür müssen die Anteile in Flächeninhalte von Kreissektoren umgerechnet werden, oder
man überlässt das Excel.
2.9 Aufgaben
1.) An einem Kochkurs nahmen neun Männer und elf Frauen teil. Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher
Art ist das beschriebene Merkmal und welche möglichen Ausprägungen gibt es? Berechnen Sie die Häugkeitstabelle und stellen dann die Daten als Säulendiagramm
dar. Warum gibt es hier keine kumulierten Häugkeiten und somit auch keine Verteilungsfunktion?
18
3 Maÿzahlen einer Verteilung
3.1 Übersicht und Lernziele
Wenn Sie dieses Kapitel durchgearbeitet haben, sollten Sie
- die Einteilung der Maÿzahlen in
Lagemaÿe, Streuungsmaÿe
und
Schiefemaÿe
ken-
nen;
- die Lagemaÿe Mittelwert, Modus und Median verstehen und berechnen können;
- die Streuungsmaÿe Varianz und Standardabweichung verstehen und berechnen
können;
- wissen, wie man Quantile deniert und berechnet;
- wissen, was ein Boxplot ist.
3.2 Denition und Einteilung
Die Verteilungen von Merkmalen lassen sich durch Tabellen und Diagramme ohne Informationsverlust darstellen. Durch einige treende Maÿzahlen will man die Information
bewusst verdichten, um spezische Eigenschaften zu betonen. Dies erleichtert die Vergleichbarkeit von Verteilungen. Man unterscheidet dabei zwischen
ungsmaÿen
und
Lagemaÿen , Streu-
Schiefemaÿen . Lagemaÿe geben an, wo sich die Zentren der Verteilung
benden, Streuungsmaÿe sind Indikatoren dafür, wie gedrängt oder verstreut sich die
Beobachtungen um die Lagemaÿe verteilen. Schiefemaÿe zeigen Abweichungen von der
Symmetrie und der so genannten Normalverteilung an. Diese werden hier nicht behandelt.
3.3 Modus
Die Merkmalsausprägung, die am häugsten vorkommt, wird
Modus
genannt, und kann
für jedes Messniveau bestimmt werden. Der Modus ist nicht immer eindeutig, da zwei
oder mehr Beobachtungen gleich oft auftreten können. Wenn sogar alle Werte verschieden sind, ist jeder davon auch ein Modus. Eine andere Bezeichnung für den Modus ist
Modalwert .
19
3 Maÿzahlen einer Verteilung
Betrachten wir die Noten einer Klausur, aufgeteilt nach Geschlecht und beginnen mit
(xi )
der Urliste
der Noten der sieben teilnehmenden Damen:
gut, ausreichend, befriedigend, gut, befriedigend, ausreichend, gut
(3.1)
Das Merkmal Note ist ordinal, der häugste Wert ist hier gut.
Besonders einfach wird die Bestimmung des Modus, wenn für die Verteilung bereits
eine Häugkeitstabelle vorliegt, der Modus ist dann in der Zeile mit dem gröÿten
ni
zu nden. Die Häugkeitstabelle 2.1 auf Seite 14 zeigt die Verteilung der Studiendauer
einer Gruppe von Studenten. Hier sind
a2 = 6
als auch
a3 = 7
n2 = n3 = 3
Modi. Bei der Häugkeitstabelle 2.2 auf Seite 17 mit den
Fuÿballweltmeistern ist der Modus eindeutig, da
somit ist
a2 = Bra(silien)
die gröÿten Werte, also sind sowohl
n2 = 5
ni
ist,
X,
den
gröÿer als alle anderen
der Modus.
3.4 Median
Der
Median
ist derjenige Merkmalswert eines mindestens ordinalen Merkmals
mindestens 50 Prozent aller Merkmalswerte einer Stichprobe vom Umfang
n unterschrei-
ten oder höchstens erreichen und den mindestens 50 Prozent aller Merkmalswerte überschreiten oder zumindest erreichen. Der Median wird mit dem Symbol
Der Median wird manchmal auch Zentralwert genannt und mit
Z
x0,5
bezeichnet.
bezeichnet.
Ordinale Daten lassen sich der Gröÿe nach ordnen, bei den Noten der Studentinnen
ergibt sich dann die geordnete Urliste
(x(i) )
gut, gut, gut, befriedigend, befriedigend, ausreichend, ausreichend
Ist die Anzahl
x0,5 .
n
der Beobachtungen ungerade, so ist der Wert
x((n+1)/2)
(3.2)
der Median
Bei den sieben Noten der Studentinnen mit der Urliste von 3.1 ist somit der vierte
Wert
x(4)
Schwieriger wird der Fall,
nissen
x0,5 = befriedigend.
wenn n gerade ist, wie
der Median, also ist
(x(i) )
bei den bereits geordneten Ergeb-
der Studenten:
sehr gut, sehr gut, sehr gut, gut, befriedigend, ausreichend.
(3.3)
Hier ist der Median nicht mehr eindeutig, denn sowohl die dritte als auch die vierte Note
erfüllen die an den Median gestellten Bedingungen, denn drei und damit genau 50 %
aller Werte sind kleiner oder höchstens gleich
oder gleich
x(3) .
x(3) = sehr
gut und vier Werte sind gröÿer
Dagegen sind vier Werte kleiner oder gleich
sind gröÿer oder gleich
x(4) =
gut und drei Werte
x(4) .
Halten wir als Ergebnis fest, dass bei mindestens ordinalen Merkmalen die Werte
zunächst geordnet werden. Der Median wird aus der geordneten Urliste
(x(i) )
wie folgt
gefunden:
x0,5
20
(
x((n+1)/2) ,
=
x(n/2) und x(1+n/2)
für
für
n
n
ungerade,
gerade.
(3.4)
3.4 Median
Ist die Anzahl
n
der Daten eine gerade Zahl, so ist der Median also nicht eindeutig.
Ist das Merkmal metrisch, wird für gerade Werte von
durch Mittelung von
x(n/2)
und
x0,5 =
x(1+n/2)
n die Eindeutigkeit des Medians
erzwungen. Es ergibt sich dann:
(
x((n+1)/2) ,
für
x(n/2) +x(1+n/2)
,
2
für
n
n
ungerade;
(3.5)
gerade
3.4.1 Eigenschaften des Medians
Der Median teilt die Merkmalsträger der Untersuchung in zwei gleich groÿe Gruppen, die
bezogen auf das untersuchte Merkmal besser und schlechter abschneiden. Der Median
einer Einkommens- oder Vermögensverteilung trennt die Merkmalsträger in zwei Hälften,
deren Einkommen bzw. Vermögen oberhalb oder unterhalb des Medians liegt.
Der Median hat eine Reihe von bemerkenswerten Eigenschaften, u.a. ist der Median
der Wert, der die Summe der Beträge der Abstände zu den Messwerten (x1 , x2 , . . . , xn )
minimiert, d.h. der Median erfüllt die Bedingung
x0,5 = min g(x) = min
x∈R
n
X
x∈R
|x − xi |
(3.6)
i=1
Hier werden natürlich metrische Merkmale vorausgesetzt. Diese Eigenschaft ist nicht
durch Dierentiation zu lösen, da die zu minimierende Funktion
g(x)
wegen der Be-
tragsstriche nicht dierenzierbar ist.
Beispiel 3.1.
Die Post hat neun Kunden in einer Straÿe, die täglich einmal Briefe
abgeben wollen. Die Standorte der Kunden liegen vom Anfang der Straÿe aus gemessen
200, 350, 140, 600, 800, 100, 260, 320, 1000
Meter entfernt. Die Straÿe liegt in einer Fuÿgängerzone, der mit der Einsammlung der
Briefe betraute Mitarbeiter darf sein Fahrzeug aber an jedem Ort abstellen, wohin die
Kunden gegen 16:00 die Briefe abliefern. An welchem Ort sollte dies geschehen, damit
die Summe der Wege der Kunden minimal wird?
Die geordnete Urliste lautet
100, 140, 200, 260, 320, 350, 600, 800, 1000
Der Median ist der fünfte Wert der geordneten Liste, also sollte der Fahrer sein Fahrzeug 320 m vom Anfang der Straÿe aus abstellen.
Eine weitere Eigenschaft des Medians ist seine Robustheit gegen extreme Werte, so
genannte
Ausreiÿer . Einige vereinzelte Langzeitstudenten ändern nichts am Median der
Studiendauer, können aber das arithmetische Mittel empndlich nach oben drücken.
21
3 Maÿzahlen einer Verteilung
3.5 Quantile
Der Median
x0,5
teilt die Beobachtungen in zwei gleich groÿe Teile. Man kann die ge-
ordnete Urliste nach demselben Prinzip für jede beliebige Zahl
0<p<1
durch einen
Quantil genannten und mit xp bezeichneten Wert aufteilen. Dabei sollen mindestens
100p Prozent der Beobachtungen kleiner oder gleich dem Quantil xp und mindestens
100(1 − p) Prozent der Beobachtungen gröÿer oder gleich dem Quantil xp sein. Da n
Werte vorliegen, ist x(np) der natürliche Kandidat für xp . Ist np ganzzahlig, so sind x(np)
und x(1+np) gleichwertig, daher wird in diesem Fall bei metrischen Merkmalen wieder
der Mittelwert von beiden genommen. Ist np nicht ganzzahlig, so nimmt man x(C(np))
für xp , wobei C(np) diejenige ganze Zahl bezeichnet, die aus Aufrunden nach oben aus
np entsteht. Es gilt also z.B. C(7, 2) = 8, C(9, 1) = 10, aber C(7) = 7. Das C steht
dabei für ceil, dem englischen Wort für Decke.
Das ergibt folgende Formel für metrische Merkmale:
(
x(C(np)) ,
xp =
0, 5 x(np) + x(1+np) ,
für
für
np
np
nicht ganzzahlig;
(3.7)
ganzzahlig;
Bei ordinalen Merkmalen ist eine Mittelung verboten. Somit deniert man hier
(
x(C(np)) ,
xp =
x(np) und x(1+np)
Der Median ist das zu
p = 0, 5
für
für
np nicht ganzzahlig;
n gerade.
(3.8)
gehörende Quantil und wird genauso berechnet wie
alle anderen Quantile und daher nicht mehr gesondert betrachtet.
Die Quantile
und
Q3
x0,25
und
x0,75
heiÿen
unteres
bzw.
oberes Quartil
und werden mit
Q1
bezeichnet. Der Median ist das mittlere Quartil und wird daher in diesem Zu-
sammenhang mit
Q2
bezeichnet. Durch die drei Quartile werden die Werte der Gröÿe
nach in vier gleich groÿe Abschnitte geteilt, die jeweils ein Viertel der Werte umfassen.
Durch Terzile werden die Werte der Gröÿe nach in drei gleich groÿe Abschnitte geteilt:
unteres, mittleres und oberes Drittel. Man benötigt dafür die Terzile
T1 = x1/3
und
T2 = x2/3 .
Beispiel 3.2. Betrachten wir die bei einem Wettkampf erbrachten Weiten von 15 Sportstudenten im Kugelstoÿen mit der in [m] angegebenen Messreihe:
6,1
6,6
6,9
7,1
7,2
7,3
7,4
7,7
7,9
8,2
8,4
nicht ganzzahlig.
geordneten Urliste. Die drei Quartile sind somit:
Q1 = x0,25 = x(4) = 7, 1
Q2 = x0,5 = x(8) = x4 = 7, 7
Q3 = x0,75 = x(12) = x12 = 9, 1
22
10,3
10,5
11,4
Q1 , Q2 und Q3 sowie das erste Terzile T1 .
3, 25 = 15 · 0, 25 als auch 7, 5 = 15 · 0, 5 sowie 11, 25 = 15 · 0, 75
Deshalb ist Q1 der vierte, Q2 der achte und Q3 der zwölfte Wert der
Zu berechnen seien die drei Quartile
Hier sind sowohl
9,1
3.6 Median und Quantile aus einer Häugkeitstabelle
T1 = x1/3
Für das erste Terzil
wird zunächst
np = 15/3 = 5
berechnet. Diese Zahl ist
ganzzahlig, somit ist
T1 = 0, 5(x(5) + x(6) ) = 0, 5(7, 2 + 7, 3) = 7, 25.
Tatsächlich sind nun fünf Daten kleiner oder höchstens gleich
mindestens
x1/3
Beispiel 3.3.
1
4
x1/3
und zehn Daten
oder gröÿer.
Ein Barkeeper zählt die Anzahl von Cocktails seiner Gäste:
3
6
3
2
2
2
Zu berechnen seien die Quantile
1
4
Q1 , Q2
und
Q3
sowie
T1 .
Die zugehörige geordnete Urliste lautet
1
Für
1
2
2
Q1 = x0,25
2
3
3
4
muss zunächst
4
6
np = 10 · 0, 25 = 2, 5
bestimmt werden. Diese Zahl ist
nicht ganzzahlig, also muss sie nach oben aufgerundet werden, was 3 ergibt. Deshalb ist
Q1
der dritte Wert der geordneten Urliste.
Für
Q3 = x0,75
muss zunächst
np = 10 · 0, 75 = 7, 5
bestimmt werden. Diese Zahl ist
nicht ganzzahlig, also muss sie nach oben aufgerundet werden, was 8 ergibt. Deshalb ist
Q3
der achte Wert der geordneten Urliste.
Dagegen ist
5 = 10·0, 5 ganzzahlig, also ist der Median der Mittelwert aus dem fünften
und sechsten Wert. Die drei Quartile sind somit:
Q1 = x0,25 = x(3) = 2
Q2 = x0,5 = 0, 5(x(5) + x(6) ) = 0, 5(2 + 3) = 2, 5
Q3 = x0,75 = x(8) = 4
Für
T1 = x1/3
muss zunächst
np = 10 · 1/3 = 3, 3333
bestimmt werden. Diese Zahl ist
nicht ganzzahlig, also muss sie nach oben aufgerundet werden, was 4 ergibt. Deshalb ist
T1
der vierte Wert der geordneten Urliste, also
T1 = 2.
3.6 Median und Quantile aus einer Häugkeitstabelle
Oft wurde für die Daten bereits eine Häugkeitstabelle erstellt. Das Quantil
xp
wird
dann wie folgt bestimmt.
i mit Fi > p sowie Fi−1 < p, so ist die zugehörige Ausprägung ai das
xp . Gibt es dagegen eine Zeile i mit Fi > p sowie Fi−1 = p, so sind bei ordinalen
Merkmalen sowohl ai als auch ai−1 das Quantil xp . Bei metrischen Merkmalen wird der
Mittelwert von ai und ai−1 verwendet.
Gibt es eine Zeile
Quantil
Beispiel 3.4.
Die in 3.3 auf Seite 20 aufgelisteten Noten der Studenten ergeben die
Häugkeitstabelle
23
3 Maÿzahlen einer Verteilung
Tabelle 3.1: Notenverteilung Herren
i
ai (Note)
1
ni
fi
Fi
sehr gut
3
3/6
3/6
2
gut
1
1/6
4/6
3
befriedigend
1
1/6
5/6
4
ausreichend
1
1/6
1
p = 0, 5 und in der Häugkeitstabelle 3.1 gilt für i = 2 zum ersten Mal Fi > 0, 5, aber es ist Fi−1 = 0, 5, also sind
bei diesem ordinalen Merkmal sowohl die Ausprägung a2 =sehr gut als auch a1 =gut
Der Median ist nicht eindeutig, denn für den Median ist
der Median.
Q1 und Q2 . Das untere
x0,25 . Die erste Ausprägung mit Fi > p = 0, 25 bendet sich in
der ersten Zeile mit F1 = 1/2 und es ist F0 = 0 < 0, 25, also ist Q1 = a1 = sehr gut. Das
obere Quartil ist das Quantil x0,75 . Die erste Ausprägung mit Fi > p = 0, 75 ist in der
dritten Zeile mit F3 = 5/6 , und es ist F2 = 2/3 < 0, 75, also ist Q3 = a3 = befriedigend.
Eindeutig sind dagegen das untere und das obere Quartil
Quartil ist das Quantil
Beispiel 3.5.
Die Werte des Beispiels 3.3 auf Seite 23 stammen von einem metrischen
Merkmal und führen zu folgender Häugkeitstabelle:
Tabelle 3.2: Anzahl von Cocktails
i
ai
ni
fi
Fi
1
1
2
0,2
0,2
2
2
3
0,3
0,5
3
3
2
0,2
0,7
4
4
2
0,2
0,9
5
6
1
0,1
1
Hier berechnen sich die drei Quartile wie folgt
Q1 = x0,25 = a1 = 2
Q2 = x0,5 = 0, 5(a2 + a3 ) = 2, 5
Q3 = x0,75 = a4 = 4,
i = 2 ist das erste Mal Fi > 0, 25 und es
ist gleichzeitig F1 < 0, 25. Für den Median ist p = 0, 55 und für i = 3 gilt zum ersten Mal
Fi > p, aber gleichzeitig ist F2 = p = 0, 5, also muss für den Median der Mittelwert von
a2 und a3 gebildet werden. Die Begründung für das dritte Quartil überlasse ich Ihnen.
denn für das erste Quartil ist
24
p = 0, 25
und für
3.7 Boxplots
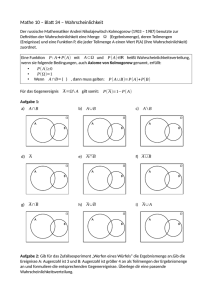
3.7 Boxplots
3.7.1 Spannweite und Interquartilsabstand
p = r/s, r = 1, 2, . . . , s − 1 in
s gleich groÿe Teile zerlegt werden. Besonders häug werden die Daten in s = 4 Teile zerlegt, die benötigten Quantile werden Quartile genannt und mit Q1 , Q2 und Q3
bezeichnet. Das Quartil Q2 ist der Median x0,5 , das so genannte untere Quartil Q1 entspricht dem Quantil x0,25 , das so genannte obere Quartil Q3 entspricht dem Quantil x0,75 .
Die Dierenz zwischen Q3 und Q1 wird Interquartilsabstand IQR (von der englischen
Bezeichnung interquartile range abgeleitet) genannt. Innerhalb des Intervalls [Q1 , Q3 ]
liegen 50 % der Daten. Die Dierenz zwischen dem gröÿten Wert x(n) und dem kleinsten
Wert x(1) wird Spannweite R genannt (von englisch range).
Bezeichnet man den kleinsten Wert x(1) mit Q0 und den gröÿten Wert x(n) mit Q4 , so
Jede angeordnete Datenreihe kann durch Quantile mit
ergibt sich
R = Q4 − Q0
IQR = Q3 − Q1
(3.9)
(3.10)
3.7.2 Prinzip der Boxplots
Ein
Boxplot
ist eine komprimierte graphische Darstellung eines Datensatzes, die von
Tukey (1977) eingeführt worden ist. Ein Boxplot besteht aus der eigentlichen Box und
zwei so genannten Zäunen (auch Antennen genannt), die an die Box anschlieÿen. Die Box
ist immer ein Rechteck, das durch das erste und dritte Quartil begrenzt und durch den
Median unterteilt wird, wobei der Median aber normalerweise nicht in der Mitte der Box
liegt. Die Box vermittelt einen Überblick über die mittleren 50 % der Beobachtungen
eines Datensatzes, während die Zäune (whiskers, adjacent values) das erste und letzte
Viertel der Verteilung veranschaulichen. Bei der einfachsten Form reichen die Zäune
gerade bis an den kleinsten bzw. gröÿten Wert heran.
Der Boxplot zum Beispiel 3.3 sieht dann so aus:
Abbildung 3.1: Einfacher Boxplot
Q0 = 1, der gröÿte Q4 = 6
Q1 = 2, Q2 = 2, 5 und Q3 = 4 berechnet.
Der kleinste Wert ist nämlich
3.5 bereits
und es wurden im Beispiel
Boxplots veranschaulichen also vier Bereiche mit je einem Viertel der Werte. Die Box
selber umfasst die mittlere Hälfte der Daten, bestimmt durch den Interquartilsabstand.
Die Box wird durch den Median in zwei in der Regel ungleich groÿe Teile geteilt. Die
Lage des Medians gibt Aufschluss über die Symmetrie. Liegt der Median ungefähr in
25
3 Maÿzahlen einer Verteilung
der Mitte der Box, so deutet dies auf eine symmetrische Verteilung hin. Bei einer rechtsschiefen Verteilung liegt der Median näher am unteren Quartil und bei einer linksschiefen
Verteilung näher am oberen Quartil.
3.7.3 Eine Variante des Boxplots
Bei der folgenden weit verbreiteten Variante des Boxplots werden nur die Zäune verändert, und zwar sind die Zäune durch diejenigen Beobachtungen festgelegt, die gerade
[Q1 −1, 5IQR, Q3 +1, 5IQR] liegen. Der untere Zaun beginnt
also beim kleinsten Z0 genannten Wert, der gröÿer oder gleich Q1 − 1, 5IQR ist und der
obere Zaun endet beim gröÿten Z4 genannten Wert, der kleiner oder gleich Q3 + 1, 5IQR
noch innerhalb des Bereichs
ist. Darüber hinaus liegende Beobachtungen gelten als mögliche Ausreiÿer und werden
einzeln durch ein bestimmtes Symbol wie ein Kreis oder ein Sternchen gekennzeichnet.
Beispiel 3.6.
Die in Meter gemessenen Weiten
X
im Speerwurf einer Gruppe von
Sportstudenten waren wie folgt:
35, 45, 50, 50, 51, 51, 51, 53, 54, 54, 55, 56, 56, 56, 57
57, 57, 58, 58, 60, 61, 61, 61, 62, 62, 62, 62, 65, 70, 75
Die Beobachtungen sind bereits geordnet, der Boxplot wird nach den Werten der folgenden Tabelle gezeichnet.
Tabelle 3.3: Benötigte Werte für den Boxplot
Q1
Q2
Q3
IQR
Q1 − 1, 5IQR
Q3 + 1, 5IQR
Z0
Z4
53
57
61
8
41
73
45
70
Überzeugen Sie sich selbst: Der Median
Q2
ist der Mittelwert des 15. und 16. Wertes,
also 57. Das untere Quartil ist der achte Wert, denn
30·0, 25 = 7, 5 und das obere Quartil
ist der 23. Wert, also 61. Somit ist der Interquartilsabstand 8 und das 1,5-fache davon
41 = Q1 − 1, 5IQR, also
gleich 73 = Q3 + 1, 5IQR,
12. Der untere Zaun beginnt beim kleinsten Wert gröÿer gleich
bei 45. Der obere Zaun endet beim gröÿten Wert kleiner
also bei 70. Verdächtig als Ausreiÿer sind lediglich die Werte 35 und 75. Der zugehörige
Boxplot sieht daher wie folgt aus:
Abbildung 3.2: Eine weitere Form des Boxplots
Die Box wird wie beim einfachen Boxplot durch
Q1 , Q2
und
Q3
festgelegt, aber die
Zäune nicht mehr durch den kleinsten und den gröÿten Wert, sondern durch
26
Z0
und
Z4 .
3.8 Das arithmetische Mittel
3.8 Das arithmetische Mittel
Das
arithmetische Mittel , auch als Mittelwert
bezeichnet, mittelt über alle Beobachtun-
gen. Daher muss das Merkmal metrisch sein. Es gilt dann
n
1X
x1 + x2 + · · · + xn
=
xi .
x̄ =
n
n i=1
Kennt man bereits die Ausprägungen
ai
(3.11)
mit ihren absoluten Häugkeiten
ni ,
so gilt
k
n1 a1 + n2 a2 + · · · + nk ak
1X
x̄ =
=
n i ai .
n
n i=1
Wegen
fi = ni /n
(3.12)
gilt auch
x̄ = f1 a1 + f2 a2 + · · · + fk ak =
k
X
f i ai .
(3.13)
i=1
Beispiel 3.7.
Die IT-Abteilung eines Unternehmens besteht aus zwei Teams. Das erste
hat vier Mitarbeiter mit den Gehältern von 2.000, 2.600, 3.000 und 4.000 Euro. Im
zweiten verdienen je zwei Mitarbeiter 2.000 bzw. 3.000 und die Leiterin 6.000 Euro im
Monat.
Im ersten Team sind alle
n=4
Werte verschieden, daher wird der Mittelwert nach
der Formel (3.11) berechnet
x̄ = (2.000 + 2.600 + 3.000 + 4.000)/4 = 11.600/4 = 2.900.
n = 5 Werte verschieden, sondern es sind a1 = 2.000
n2 = 2 sowie a3 = 6.000 und n3 = 1, daher wird der
In der zweiten Gruppe sind nicht alle
und
n1 = 2, a2 = 3.000
und
Mittelwert nach der Formel (3.12) berechnet
x̄ = (2 · 2.000 + 2 · 3.000 + 1 · 6.000)/5 = 16.000/5 = 3.200.
Beispiel 3.8.
Betrachten wir eine Altersverteilung einer Gruppe von
n = 13
junger
Menschen mit den bereits geordneten Werten
18, 18, 18, 19, 19, 19, 20, 21, 21, 21, 22, 22, 22
so gelten
18 + 18 + 18 + 19 + 19 + 19 + 20 + 21 + 21 + 21 + 22 + 22 + 22
260
=
= 20
13
13
3 · 18 + 3 · 19 + 20 + 3 · 21 + 3 · 22
260
x̄ =
=
= 20
13
13
3
3
1
3
3
260
x̄ =
· 18 +
· 19 +
· 20 +
· 21 +
· 22 =
= 20
13
13
13
13
13
13
x̄ =
27
3 Maÿzahlen einer Verteilung
3.8.1 Eigenschaften des arithmetischen Mittels
Da das arithmetische Mittel über alle Einzelwerte mittelt, ist die Summe der Abweichungen gleich 0, also
n
X
(xi − x̄) = 0
(3.14)
i=1
Gibt es umgekehrt eine Zahl
z,
die diese Bedingung erfüllt, so ist
z = x̄.
Man kann an
der Datenreihe der Altersverteilung damit sofort raten, dass 20 das arithmetische Mittel
ist, denn zu jeder Abweichung nach oben gibt es eine genau so groÿe Abweichung nach
unten.
Auch das arithmetisches Mittel erfüllt eine Minimumeigenschaft, es minimiert nämlich
die quadrierten Abstände zu den Beobachtungen, genauer es gilt
x̄ = min f (x) = min
x∈R
x∈R
n
X
(x − xi )2 .
(3.15)
i=1
Diese Eigenschaft ist sehr einfach mit Mitteln der Dierentialrechnung zu beweisen, denn
die zu minimierende Funktion
f (x)
ist dierenzierbar.
3.9 Streuungsmaÿe mit Bezug auf den Mittelwert
Lagemaÿe charakterisieren die Mitte einer Verteilung, Streuungsmaÿe sollen widerspiegeln, wie stark die Werte um das Zentrum verstreut sind. Bei geringer Streuung liegen
die einzelnen Werte überwiegend in der Nähe von Median und Mittelwert, bei groÿer
Streuung sind die durchschnittlichen Abweichungen vom Zentrum entsprechend groÿ.
Streuungsmaÿe nehmen also in der Regel Bezug auf ein Lagemaÿ. Zunächst wird als
Lagemaÿ das arithmetische Mittel verwendet. Als einfaches Streungsmaÿ bietet sich an,
die absoluten Abstände vom arithmetischen Mittel zu mitteln
dx̄ =
n
X
|xi − x̄|
(3.16)
i=1
Es gibt aber geeignetere Streuungsmaÿe.
3.9.1 Die Varianz
Ausdrücke mit Betragsstrichen sind nicht dierenzierbar, daher verwendet man für die
Messung von Variabilität lieber quadratische Abweichungen vom Mittelwert. Zunächst
führe ich folgende Bezeichnung ein:
QS(c) =
n
X
i=1
28
(xi − c)2 .
(3.17)
3.9 Streuungsmaÿe mit Bezug auf den Mittelwert
Die Bezeichnung QS steht für Quadratsumme. Der Wert von
Verschiebungssatz von Steiner
Es gilt folgende Beziehung, die
QS(c) =
n
X
(xi − c)2 =
i=1
n
X
c
ist zunächst beliebig.
genannt wird.
(xi − x̄)2 + n (x̄ − c)2 .
(3.18)
i=1
Daraus folgt, dass die Funktion
QS(c)
für
c = x̄
minimal wird.
Der Beweis dieser wichtigen Beziehung sei nun skizziert.
QS(c) =
=
n
X
2
(xi − c) =
i=1
n
X
n
X
([xi − x̄] + [x̄ − c])2
i=1
(xi − x̄)2 + 2(xi − x̄)(x̄ − c) + (x̄ − c)2
i=1
=
n
X
(xi − x̄)2 + n (x̄ − c)2 .
i=1
Dabei wurde die Beziehung
n
X
(xi − x̄) = 0
i=1
verwendet. Die mittlere quadratische Abweichung vom Mittelwert ist somit ein geeigne2
tes Streuungsmaÿ, das
genannt und mit σ bezeichnet wird.
Varianz
n
1X
(xi − x̄)2
σ = QS(x̄) =
n i=1
2
(3.19)
Die Varianz hat nur dann den Wert 0, wenn jede einzelne quadratische Dierenz verschwindet, also alle Datenwerte mit dem Mittelwert übereinstimmen und folglich konstant sind. Bei nicht konstanten Daten ist die Varianz immer positiv.
Setzt man im Verschiebungssatz von Steiner c
2
für die Varianz σ :
n
1X 2
2
x
σ =
n i=1 i
= 0, kommt man auf eine zweite Formel
− x̄2 .
(3.20)
Diese Formel ist bei Rechnungen mit der Hand oder einem Taschenrechner meist einfacher als die Formel (3.19).
Beispiel 3.9.
Seien noch einmal die Einkünfte des ersten IT-Teams betrachtet mit den
Werten von 2.000, 2.600, 3.000 und 4.000 Euro. Das arithmetische Mittel
11.600/4 = 2.900.
x̄ hat den Wert
Somit gilt:
(2.000 − 2.900)2 + (2.600 − 2.900)2 + (3.000 − 2.900)2 + (4.000 − 2.900)2
4
= 530.000
2.0002 + 2.6002 + 3.0002 + 4.0002
σ2 =
− 2.9002 = 530.000
4
σ2 =
29
3 Maÿzahlen einer Verteilung
(a1 , a2 , . . . , ak ), k < n mit
Häugkeiten fi auf, so gelten:
Kennt man bereits die Ausprägungen
gkeiten
ni
bzw. mit den relativen
den absoluten Häu-
k
1X
σ =
ni (ai − x̄)2 ,
n i=1
2
k
X
2
σ =
fi (ai − x̄)2 ,
(3.21)
(3.22)
i=1
k
1X
ni a2i − x̄2 .
n i=1
σ2 =
Beispiel 3.10.
(3.23)
Betrachten wir dazu jetzt die Monatseinkünfte des zweiten Teams von
zweimal 2.000 und zweimal 3.000 sowie einmal 6.000 Euro:
2 · (2.000 − 3.200)2 + 2 · (3.000 − 3.200)2 + (6.000 − 3.200)2
= 2.160.000,
5
1
σ2 =
2 · 2.0002 + 2 · 3.0002 + 6.0002 − 3.2002 = 2.160.000.
5
σ2 =
3.9.2 Stichprobenvarianz
Die Varianz wird verwendet, wenn das Merkmal einer Grundgesamtheit untersucht wird,
was in der beschreibenden Statistik sehr oft der Fall ist, da die Daten aus amtlichen
oder betrieblichen Vollerhebungen stammen. In der schlieÿenden Statistik stammen die
Daten in der Regel von einer Stichprobe. In diesem Fall dividiert man die Summe der
n, sondern durch n−1 und spricht
empirischen Varianz s2 . Somit besteht zwischen
quadrierten Abweichungen vom Mittelwert nicht durch
von der
Stichprobenvarianz
oder der
der Varianz und der Stichprobenvarianz der einfache Zusammenhang
s2 =
n
σ2.
n−1
(3.24)
Daraus ergeben sich folgende Formeln
n
1 X
s =
(xi − x̄)2
n − 1 i=1
2
(3.25)
n
1 X 2
n
s =
xi −
x̄2
n − 1 i=1
n−1
2
(3.26)
bzw. bei Kenntnis der Häugkeitsliste
k
s2 =
1 X
ni (ai − x̄)2
n − 1 i=1
(3.27)
k
1 X
n
s =
ni a2i −
x̄2 .
n − 1 i=1
n−1
2
30
(3.28)
3.9 Streuungsmaÿe mit Bezug auf den Mittelwert
Beim Team mit den Monatseinkünften von 2.000, 2.600, 3.000 und 4.000 Euro erhält
man also
4
4
s2 = σ 2 = · 530.000 = 706.666, 67
3
3
1
s2 =
(2.000 − 2.900)2 + (2.600 − 2.900)2 + (3.000 − 2.900)2 + (4.000 − 2.900)2
3
= 706.666, 67
4
1
s2 =
2.0002 + 2.6002 + 3.0002 + 4.0002 − 2.9002 = 706.666, 67.
3
3
Beim anderen Team mit den Monatseinkünften von zweimal 2.000 und zweimal 3.000
sowie einmal 6.000 Euro, so kann die empirische Varianz wie folgt berechnet werden
5
5
s2 = σ 2 = · 2.160.000 = 2.700.000
4
4
1
s2 =
2 · (2.000 − 3.200)2 + 2 · (3.000 − 3.200)2 + (6.000 − 3.200)2 = 2.700.000
4
5
1
s2 =
2 · 2.0002 + 2 · 3.0002 + 6.0002 − 3.2002 = 2.700.000.
4
4
3.9.3 Die Standardabweichung
Varianz und empirische Varianz haben nicht die Maÿeinheiten der Beobachtungen selbst.
Daher wird die Quadratwurzel aus der Varianz bzw. der empirische Varianz gezogen. Die
somit erhaltenen Werte werden
chung s genannt.
Standardabweichung σ
Im Beispiel des ersten Teams ergibt sich
σ =
bzw.
empirische Standardabwei-
√
530.000 = 728, 01
Euro. Für die
empirische Standardabweichung muss die Wurzel aus der empirischen Varianz gezogen
√
s= √
706.666, 67 = 840, 63 Euro.
2.160.000 = 1.469, 69 Euro.
sich σ =
werden, also erhält man beim erstem Team
Im Beispiel des zweiten Teams ergibt
Für die
empirische Standardabweichung muss die Wurzel aus der empirischen Varianz gezogen
werden, also erhält man
s=
√
2.700.000 = 1.643, 17
Euro.
3.9.4 Der Variationskoezient
Die Standardabweichung ist ebenso wie die Spannweite und die mittleren absoluten
Abweichungen vom arithmetischen Mittel oder vom Median, ein Maÿ für die absolute
Streuung. Diese sind im Allgemeinen dimensionsbehaftete Maÿe, die von der Einheit
abhängen, in der ein Merkmal gemessen wird. Relative Streuungsmaÿe sind dagegen
dimensionslos. Ein Beispiel eines solchen relativen Maÿes ist der so genannte
koezient .
abweichung
Für ein metrisches Merkmal
σ
X
ist der Variationskoezient
mit arithmetischem Mittel
v
v=
x̄
Variations-
und Standard-
deniert durch
σ
.
x̄
(3.29)
31
3 Maÿzahlen einer Verteilung
Der Variationskoezient ist ein relatives Streuungsmaÿ, denn das absolute Streuungsmaÿ
σ
wird ins Verhältnis gesetzt zum arithmetische Mittel des Merkmals. Der Varia-
tionskoezient hat keine Einheit, da er der Quotient zweier Gröÿen gleicher Dimension
ist.
Beim ersten Team ergibt sich
v = σ/x̄ = 728, 01/2.900 = 0, 2510.
Bei dem Team mit den Monatseinkünften von zweimal 2.000 und zweimal 3.000 sowie
einmal 6.000 ergibt sich
v = σ/x̄ = 1.469, 69/3.200 = 0, 4593.
Betrachten wir die bei einem Wettkampf erbrachten Weiten von 15 Sportstudenten
im Kugelstoÿen mit der in [m] angegebenen Messreihe:
6, 1 6, 6 6, 9 7, 1 7, 2 7, 2 7, 4 7, 7 7, 9 8, 2 8, 4 9, 1 10, 3 10, 5 11, 4
Man erhält:
1
(6, 1 + 6, 6 + · · · + 11, 4) = 8, 13
15
1
σ 2 = (6, 12 + 6, 62 + · · · + 11, 42 ) − 8, 132 = 2, 24
15
p
σ = 2, 24 = 1, 496662955
σ
v = = 0, 184091384
x̄
2
s = (15/14)σ 2 = 2, 4
p
s = 2, 4 = 1, 549193338
x̄ =
3.10 Arbeitstabelle zur Berechnung
Der Mittelwert und die Varianz sowie die davon abgeleiteten Gröÿen lassen sich mit
Arbeitstabellen berechnen. Ich zeige dies ein letztes Mal an den Daten der Einkünfte der
beien IT-Teams. Im linken Tabellenteil werden die Daten des ersten Teams verwendet.
In den Zellen B2 bis B5 stehen die Daten, darunter deren Summe, die durch die Anzahl
n=4
der Daten geteilt wird und den Mittelwert
x̄
in der Zelle A8 ergibt. In der Spalte
C sehen Sie direkt die Quadrate der Daten, in der Zelle C6 dann deren Summe. Die
Varianz ergibt sich in der Zelle B8 durch Division dieser Summe durch
2
das Quadrat des Mittelwerts, also x̄ , abgezogen wird.
Für das zweite Team müssen die Ausprägungen
ai
n,
wovon dann
und deren Häugkeiten
ni
berück-
sichtigt werden, die entsprechenden Werte stehen im Bereich F2:G4. In den Zellen H2
2
bis H4 stehen die Produkte ni · ai und in den Zellen I2 bis I4 die Produkte ni · ai . Die
jeweiligen Summen benden sich in den Zellen H6 bzw. I6. Der Mittelwert x̄ steht in
der Zelle G8 und ergibt sich durch Division des Wertes der Zelle H6 durch
32
n = 5.
Die
3.11 Transformationseigenschaften der Maÿzahlen
A
1
2
3
4
5
6
7
8
9
10
B
i
1
2
3
4
xi
2.000
2.600
3.000
4.000
11.600
σ2
530.000
xquer
2900
2
s
s
706.666,6667 840,6347
C
D E
2
i
xi
4.000.000
6.760.000
9.000.000
16.000.000
35.760.000
F
ai
1 2000
2 3000
3 6000
σ
728,0110
v
0,2510
G
H
ni
2
2
1
5
xquer
3.200
s2
2.700.000
I
ni*ai
4.000
6.000
6.000
16.000
ni*ai2
8.000.000
18.000.000
36.000.000
62.000.000
σ2
2.160.000
σ
1.469,6938
s
1643,1677
v
0,4593
Abbildung 3.3: Arbeitstabelle für einige Maÿzahlen
Varianz steht in der Zelle H8 und ergibt sich durch Division des Wertes der Zelle G6
2
durch n = 5, wovon dann wieder x̄ abgezogen wird.
Schneller und sicherer kommen Sie mit den Excel-Funktionen zum Ziel, die ich später
vorstellen werde. Das gezeigte Schema ist für Rechnungen mit der Hand geeignet.
3.11 Transformationseigenschaften der Maÿzahlen
Oft werden die ursprünglichen Daten
(x1 , x2 , . . . , xn )
einer linearen Transformation un-
terworfen, d.h.
yi = a xi + b.
Durch diese Transformation ändern sich auch die Maÿzahlen und zwar gelten folgende
Beziehungen:
ȳ = a x̄ + b
y0.5 = a x0.5 + b
σy2 = a2 σx2
σy = |a| σx
(3.30)
(3.31)
(3.32)
(3.33)
Nehmen wir wieder das Team mit den Ausgangswerten von je zweimal 2.000 Euro bzw.
3.000 EURO und einmal 6.000 Euro als Beispiel. Der dankbare Chef erhöhe die Gehälter
um den Sockelbetrag von 200 Euro und um zusätzliche 5 Prozent. Dann gilt also:
yi = 1, 05 xi + 200.
33
3 Maÿzahlen einer Verteilung
Ohne Berechnung der Einzelwerte können wir somit folgende neue Lagemaÿe angeben:
ȳ = a x̄ + b = 1, 05 · 3.200 + 200 = 3.560
y0.5 = a x0.5 + b = 1, 05 · 3.000 + 200 = 3.350
σy2 = a2 σx2 = 1, 052 · 2.160.000 = 2.381.400
σy = a σx2 = 1, 05 · 1.469, 690 = 1.543, 18
3.12 Mittlere absolute Abstände
Die Streungsmaÿe Varianz und Standardabweichung beziehen sich auf das arithmetische
Mittel. Es gibt aber auch Streungsmaÿe, die als Lagemaÿ den Median verwende, und
zwar die gemittelten absoluten Abstände vom Median. Es ergibt sich dann
n
dx0,5
1X
=
|xi − x0,5 |
n i=1
(a1 , a2 , . . . , ak ), k < n
Häugkeit fi auf, so gelten
Kennt man bereits die Ausprägungen
gkeiten
ni
bzw. mit der relativen
(3.34)
mit den absoluten Häu-
k
dx0,5
1X
ni |ai − x0,5 | ,
=
n i=1
dx0,5 =
k
X
(3.35)
fi |ai − x0,5 | .
(3.36)
i=1
Beispiel 3.11.
Die IT-Abteilung eines Unternehmens besteht aus zwei Teams. Das
erste hat vier Mitarbeiter mit den Gehältern von 2.000, 2.600, 3.000 und 4.000 Euro. Im
zweiten verdienen je zwei Mitarbeiter 2.000 bzw. 3.000 und die Leiterin 6.000 Euro im
Monat.
Hier ist im ersten Team der Median der Mittelwert zwischen dem zweiten und drittem
Wert, also 2.800 Euro. Im zweiten Team ist der Median der dritte Wert, also 3.000 Euro.
Somit folgen die Werte
|2.000 − 2.800| + |2.600 − 2.800| + · |3.000 − 2.800| + · |4.000 − 2.800|
= 600;
4
2 · |2.000 − 3.000| + 2 · |3.000 − 3.000| + |6.000 − 3.000|
= 1.000
=
5
dx0,5 =
dx0,5
Die Werte der zweiten Gruppe sind stärker verstreut als in der ersten Gruppe.
3.13 Anforderungen an Maÿzahlen metrischer
Merkmale
Abschlieÿend sei kurz gestreift, welche allgemeinen Anforderungen an Maÿzahlen metrischer Merkmale gestellt werden. Der Ausgangspunkt ist der Datensatz
34
(x1 , . . . , xn ).
Bei
3.14 Abschlieÿendes Beispiel
metrischen Merkmalen wird eine Maÿzahl
m durch eine Abbildung ϕ : Rn → R wie folgt
festgelegt
m = ϕ(x1 , . . . , xn )
Bei Lagemaÿen sollte die Funktion
ϕ
(3.37)
die beiden Eigenschaften
ϕ(x1 + t, x2 + t, . . . , xn + t) = ϕ(x1 , x2 , . . . , xn ) + t,
ϕ(ax1 , ax2 , . . . , axn ) = aϕ(x1 , x2 , . . . , xn )
(3.38)
(3.39)
erfüllen. Wenn alle Daten um einen konstanten Wert verändert werden, soll auch das
Lagemaÿ sich entsprechend anpassen. Werden dagegen alle Daten mit einem Faktor
multipliziert, soll sich das auch auf das Lagemaÿ so auswirken.
Bei Streuungsmaÿen werden dagegen
ϕ(x1 , x2 , . . . , xn ) ≥ 0
ϕ(x1 + t, x2 + t, . . . , xn + t) = ϕ(x1 , x2 , . . . , xn ),
ϕ(ax1 , ax2 , . . . , axn ) = |a|p ϕ(x1 , x2 , . . . , xn ), p > 0
(3.40)
(3.41)
(3.42)
gefordert. Streuungsmaÿe müssen nichtnegativ und für nicht konstante Daten sogar positiv sein und dürfen sich bei einer Verschiebung der Daten nicht ändern, während die
Multiplikation mit einem Faktor das Streuungsmaÿ um eine Potenz
p des Betrags dieses
ϕ ste-
Faktors vergröÿert. Auÿerdem sollte bei allen Maÿzahlen die zugehörige Funktion
tig sein, damit kleine Änderungen bei den Daten auch nur kleine Änderungen bei den
Maÿzahlen nach sich ziehen.
3.14 Abschlieÿendes Beispiel
Beispiel 3.12.
Die folgende Urliste stammt von Frondel und gibt Auskunft über die
Körpergröÿen von 20 Teilnehmern eines Kurses in Statistik.
1,56, 2,05, 1,76, 1,68, 1,86, 1,71, 1,62, 1,83, 1,76, 1,83
1,75, 1,69, 1,91, 1,89, 1,83, 1,93, 1,71, 1,78, 1,71, 1,83
Es sollen nun die wichtigsten Kennzahlen berechnet werden. Für die Bestimmung der
Quantile wird die aufsteigend geordnete Urliste benötigt, sie lautet
1,56, 1,62, 1,68, 1,69, 1,71, 1,71, 1,71, 1,75, 1,76, 1,76
1,78, 1,83, 1,83, 1,83, 1,83, 1,86, 1,89, 1,91, 1,93,
Hier sind sowohl
10 = 20 · 0, 5
als auch
5 = 20 · 0, 25
2,05
sowie
15 = 20 · 0, 75
ganzzahlig.
Deshalb ergibt sich für die Quartile:
x0,25 = Q1 = 0, 5(x(5) + x(6) ) = 0, 5(1, 71 + 1, 71) = 1, 71
x0,5 = Q2 = 0, 5(x(10) + x(11) ) = 0, 5(1, 76 + 1, 78) = 1, 77
x0,75 = Q3 = 0, 5(x(15) + x(16) ) = 0, 5(1, 83 + 1, 86) = 1, 845
35
3 Maÿzahlen einer Verteilung
Für das obere Terzil
T2 = x2/3
ergibt sich wegen
13, 3333 = 20 · 2/3
T2 = x2/3 = x(14) = 1, 83.
Weitere Kennzahlen werden wie folgt berechnet
1
(1, 56 + 2, 05 + · · · + 1, 83) = 1, 7845
20
1
σ 2 = (1, 562 + 2, 052 + · · · + 1, 832 ) − 1, 78452 = 0, 01244
20
p
σ = 0, 01244 = 0, 11156
σ
0, 11156
v= =
= 0, 062516
x̄
1, 7845
s2 = (20/19)σ 2 = 0, 013099737
p
s = 0, 013094737 = 0, 114454082
x̄ =
3.15 Excel-Funktionen
Für die hier vorgestellten Maÿzahlen gibt es Funktionen in Excel. Vorausgesetzt wird
immer, dass die Daten in einem zusammenhängenden Bereich stehen, z.B. folgende acht
Zahlen im Bereich A1:A8
1
3
4
6
9
10
11
12
Der Mittelwert wird durch =MITTELWERT(A1:A8) berechnet.
2
Für die Varianz muss man unterscheiden zwischen der Varianz σ für eine Gesamt2
heit, englisch Population, und der Stichprobenvarianz s . Die Funktion VARIANZEN
berechnet die Varianz der Werte im markierten Bereich anhand der Grundgesamtheit
aller Werte. Die Funktion VARIANZ berechnet die empirische Varianz der Werte, also
als Stichprobe. Im neueren Excel sollen diese Funktionen nicht mehr verwendet werden,
sondern die einsichtigeren VAR.P und VAR.S, wobei sich P immer auf die Grundgesamtheit und S auf eine Stichprobe bezieht. Bei den obigen Zahlen ergibt sich somit
sowohl für =VARIANZEN(A1:A8) als auch für =VAR.P(A1:A8) der Wert 14,5 und
für =VARIANZ(A1:A8) als auch für =VAR.S(A1:A8) der Wert 16,57142857, also
das 8/7-fache von 14,5.
Für die Standardabweichung einer Grundgesamtheit gibt es die beiden Funktionen
STABWN und STABW.N. Warum hier ein N statt dem P steht, weiÿ niemand.
Bei den obigen Zahlen ergibt sich somit sowohl für =STABWN(A1:A8) als auch für
=STABW.N(A1:A8) der Wert 3,807886553, also die Quadratwurzel von 14,5.
Für die Standardabweichung einer Stichprobe gibt es die beiden Funktionen STABW
und STABW.S. Daher haben =STABW(A1:A8) und =STABW.S(A1:A8) den Wert
4,070801957, also die Quadratwurzel von 16,57142857. Das ist sehr verwirrend, lesen Sie
immer die eingeblendete Beschreibung der verwendeten Funktionen durch.
36
3.16 Aufgaben
Die Quantile berechnet Excel anders als von mir beschrieben. Es gibt ab Excel 2010
zwei Funktionen, und zwar QUANTIL.INKL und QUANTIL.EXKL. Die erste entspricht
der alten Funktion QUANTIL. Sie müssen als erstes Argument einen Bereich eingeben,
hier also A1:A8 und als zweiten den Wert von
p
als Zahl zwischen 0 und 1. Das erste
Quartil sollte somit durch =QUANTIL.INKL(A1:A8;0,25) bestimmt werden. Excel
liefert 3,75, während nach meiner Denition der Mittelwert von 3 und 4 zu bilden ist,
also 3,5.
Excel rechnet dabei wie folgt
r = (n − 1) · p, wobei n die Anzahl der bereits aufsteiist. Zerlege r in den ganzzahligen Teil i und den Rest
1. Bestimme zunächst die Zahl
gend angeordneten Werte
nach dem Komma
2. Das Quantil
xp
d.
ist dann
xp = (1 − d)x(i) + dx(i+1) .
p = 0, 25 und es ist n = 8.
i = 2 und d = 0, 75 und deshalb
Im obigen Beispiel sind für das erste Quartil
r = (8 − 1)/4 = 2, 75,
und somit sind
Also ist
xp = (1 − d)x(i) + dx(i+1) = 0, 25 · 3 + 0, 75 · 4 = 3, 75.
Bitte beachten Sie, dass diese Berechnungsmethode zwar einleuchtend ist, aber von der
in der Statistik üblichen abweicht!
3.16 Aufgaben
1.) Im Sportunterricht kam eine Gruppe von Mädchen beim Kugelstoÿen auf folgende
Weiten
X
3,23
in [m]
2,35
5,37
3,49
6,90
2,93
1,81
4,26
4,44
2,73.
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen
Ausprägungen gibt es?
b) Berechnen Sie das untere Quartil, den Median, das obere Quartil, das arithmetische Mittel, die Varianz und die Standardabweichung sowie die empirische
Varianz und die empirische Standardabweichung und dann noch den Variationskoezienten des Merkmals
X.
2.) In der Tabelle 3.4 sind die Noten der Teilnehmer eines Kurses aufgeführt. Welcher
Art ist das beschriebene Merkmal und welche möglichen Ausprägungen gibt es?
Berechnen Sie die Häugkeitstabelle und zeichnen dann die Stabverteilung sowie
die empirische Verteilungsfunktion. Geben Sie abschlieÿend den Modus, das untere
Quartil, den Median und das obere Quartil sowie das 95 % Quantil an. Warum ist
es hier nicht sinnvoll Mittelwert und Varianz zu berechnen?
37
3 Maÿzahlen einer Verteilung
Tabelle 3.4: Notenverteilung der Teilnehmer
Note
sehr gut
gut
befriedigend
ausreichend
mangelhaft
6
5
5
3
1
ni
3.) Ein Gastwirt zählt die Anzahl
X
der Gäste an seinen Tischen und kommt auf fol-
gende Werte:
3
6
5
8
6
4
4
4
3
6.
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
b) Berechnen Sie die Häugkeitstabelle und zeichnen Sie dann die Stabverteilung
für die relativen Häugkeiten sowie die empirische Verteilungsfunktion.
c) Berechnen Sie den Modus, das untere Quartil, den Median, das obere Quartil, die
Quantile
x0,2
sowie
x0,9 ,
das arithmetische Mittel, die Varianz und die Standard-
abweichung sowie die empirische Varianz und die empirische Standardabweichung
und dann noch den Variationskoezienten des Merkmals
X.
4.) Erstellen Sie den einfachen Boxplot zu den Daten des Beispiels 2.1 auf Seite 12.
5.) In der folgenden Urliste ist das Lebensalter
X
von Studenten eines Kurses aufgeführt.
19, 21, 26, 20, 22, 19, 20, 19, 23, 21, 52, 22, 19, 21, 20, 23, 22, 21, 21, 20, 20
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung?
b) Welcher Art ist das beschriebene Merkmal und welche möglichen Werte gibt es?
c) Berechnen Sie die Häugkeitstabelle und zeichnen Sie dann die Stabverteilung
für die relativen Häugkeiten sowie die empirische Verteilungsfunktion.
d) Berechnen Sie den Modus, das untere Quartil, den Median, das obere Quartil, die
Quantile
x0,4
sowie
x0,9 ,
das arithmetische Mittel, die Varianz und die Standard-
abweichung sowie die empirische Varianz und die empirische Standardabweichung
und dann noch den Variationskoezienten des Merkmals
X.
e) Der Wert 52 ist ein Zahlendreher und wäre korrekt 25. Wie ändern sich die
Ergebnisse von d) dadurch?
f ) Ein anderer Auswerter dieser Daten unterdrückt den Ausreiÿer von 52 ganz, geht
also nur noch von 20 statt 21 Werten aus. Wie ändern sich dadurch die Ergebnisse
von d)?
6.) In einem Projekt zur Betriebsinformatik wurden die Studierenden unter anderem
nach dem Alter ihres Vaters gefragt. Hier ist die geordnete Stichprobe:
38
3.16 Aufgaben
44 46 49 50 50 51 51 51 51 51 52 52 53 53 53 54 55 56 57 58 60
Man erstelle beide Varianten des Boxplots. Die Daten stammen von Heindl, Seite
117.
39
4 Klassenbildung
4.1 Übersicht und Lernziele
Wenn Sie dieses Kapitel durchgearbeitet haben, sollten Sie wissen
- wie man für stetige metrische Merkmale Klassen bildet;
- wie die Verteilungsdichte- und die empirische Verteilungsfunktion von klassierten
Daten gebildet werden.
- wie man näherungsweise bei klassierten Daten Median und Quantile berechnet;
- wie man näherungsweise bei klassierten Daten Mittelwert und Varianz berechnet;
4.2 Klassen
Werte
1,56
1,62
1,68
1,69
1,71
1,75
1,76
1,78
1,83
1,86
1,89
1,91
1,93
2,05
ni Ni
1
1
1
1
3
1
2
1
4
1
1
1
1
1
1
2
3
4
7
8
10
11
15
16
17
18
19
20
fi
Fi
0,05
0,05
0,05
0,05
0,15
0,05
0,1
0,05
0,2
0,05
0,05
0,05
0,05
0,05
0,05
0,1
0,15
0,2
0,35
0,4
0,5
0,55
0,75
0,8
0,85
0,9
0,95
1
0,2
0,1
0
1,5
1,6
1,7
1,8
1,9
2
2,1
1,5
1,6
1,7
1,8
1,9
2
2,1
1
0,5
0
Abbildung 4.1: Diskrete Auswertung
Im abgebildeten Excel-Arbeitsblatt ist die Häugkeitstabelle sowie das Stabdiagramm
und die Verteilungsfunktion der Daten des Beispiels 3.12 von Seite 35 zu sehen. Die Werte der Daten sind fast alle verschieden, daher ist im Stabdiagramm wenig über das Wesen
41
4 Klassenbildung
der Verteilung zu erkennen. Das liegt daran, dass die Körpergröÿe ein stetiges Merkmal
ist, das beliebig genau gemessen werden kann, weswegen nur selten Werte mehrfach vorliegen. Ähnliches trit auf andere stetige Merkmale wie Gewicht, Zeitmessungen eines
Volksmarathons oder die Brenndauer von Glühbirnen zu, aber auch bei ökonomischen
Daten, die wie das Einkommen oder Vermögen in einer Währung angegeben werden. In
der Praxis behandelt man oft auch diskrete metrische Merkmale wie das Alter oder die
erreichte Punktzahl in einer Klausur als stetig, wenn sie sehr viele Merkmalsausprägungen besitzen.
Man gewinnt an Übersichtlichkeit durch die Bildung von
Klassen
genannten Interval-
len, wobei jeweils die Obergrenze einer Klasse die Untergrenze der benachbarten rechten
Klasse ist. Die Klassenbildung erfordert also die Wahl einer Folge von aufsteigenden
Werten
x∗0 < x∗1 < x∗2 < . . . < x∗k−1 < x∗k ,
∗
∗
wobei die Werte der Urliste alle zwischen x0 und xk liegen sollten. Die erste Klasse ist
∗
∗
∗
∗
∗
∗
∗
∗
dann [x0 , x1 ], die zweite (x1 , x2 ], gefolgt von (x2 , x3 ] bis zu (xk−1 , xk ]. Die erste Klasse
ist ein abgeschlossenes Intervall, da beide Grenzen zur Klasse gehören. Danach folgen
links oene und rechts abgeschlossene Klassen, d.h. die Obergrenze gehört zur Klasse,
die Untergrenze hingegen nicht.
Ich habe die Klassengrenzen x∗i zur Unterscheidung von den Daten mit einem *
gekennzeichnet.
Vor der Klassenbildung wird die aufsteigend geordnete Urliste gebildet, sie lautet hier
1,56, 1,62, 1,68, 1,69, 1,71, 1,71, 1,71, 1,75, 1,76, 1,76
1,78, 1,83, 1,83, 1,83, 1,83, 1,86, 1,89, 1,91, 1,93,
2,05
Es muss also der Bereich zwischen 1,56 und 2,05 abgedeckt werden. Klassengrenzen
∗
sollten mit den Ziern 0 oder 5 enden, es bietet sich an bei x0 = 1, 50 anzufangen und
∗
bei x5 = 2, 10 aufzuhören. Für die mittleren Klassengrenzen seien die Werte 1,65, 1,75,
1,85 und 1,95 gewählt. Damit ergeben sich die Klassen
[1, 50, 1, 65], (1, 65, 1, 75], (1, 75, 1, 85], (1, 85, 1, 95], (1, 95, 2, 10].
Wie erwähnt ist die erste Klasse abgeschlossen, die folgenden sind links oen und rechts
abgeschlossen. Der 1,75 m groÿe Teilnehmer gehört also zur Klasse
(1, 65, 1, 75].
Bei der Klassenbildung werden folgende Begrie verwendet.
(1)
Klassenanzahl
Ich werde die Anzahl aller Daten der Urliste immer mit
Klassen mit
k
n
und die Anzahl aller
bezeichnen. In Beispiel der Körpergröÿen sind somit
n = 20
und
k = 5.
(2)
Klassenbreite
Die Dierenz aus oberer und unterer Klassengrenze wird als
net, also hat man
k
Klassenbreiten
∆i = x∗i − x∗i−1 ,
42
i = 1, . . . , k.
Klassenbreite
bezeich-
4.2 Klassen
Meistens werden Klassen gleicher Breite gewählt, aber es sind auch Klassen unterschiedlicher Breiten möglich.
(3)
Absolute und relative (kumulierte) Häugkeit
Für
i = 1, 2, . . . , k
bezeichnet die absolute Häugkeit
Urliste, die in der i-ten Klasse liegen und
(4)
fi = ni /n
ni
die relative Häugkeit.
Absolute und relative kumulierte Häugkeit
Die kumulierten absoluten und relativen Häugkeiten
solute bzw. relative Anzahl aller Daten der Urliste mit
(5)
die Anzahl aller Daten der
Ni und Fi
xj ≤ x∗i .
stehen für die ab-
Absolute und relative Häugkeitsdichte
Die Klassenbildung erfordert noch zwei weitere Gröÿen, die so genannte absolute
und relative
Häugkeitsdichte .
Damit werden die Verhältnisse der absoluten (ni )
bzw. der relativen Häugkeit (fi ) der i-ten Klasse zur entsprechenden Klassenbreite
∆i
bezeichnet. Die Häugkeitsdichte misst also für jede Klasse den Anteil der Daten
pro Einheit. Damit erst werden Vergleiche zwischen Klassen unterschiedlicher Breite
möglich. Die beiden Häugkeitsdichten berechnen sich für
1≤i≤k
ni
∆i
∗
n
fi
fi∗ = i =
n
∆i
n∗i =
(6)
wie folgt
(4.1)
(4.2)
Klassenmitte
Die Mitte einer Klasse wird wenig überraschend
Klassenmitte
genannt. Sie dient
bei manchen Rechnungen als gemeinsamer Wert aller Daten der Urliste, die in einer
Klasse liegen. Die Klassenmitte ist das arithmetische Mittel aus unterer und oberer
Klassengrenze, also
(7)
x∗i + x∗i−1
,
mi =
2
i = 1, . . . , k
Klassenmittelwert
Der
Klassenmittelwert x̄i
der Klasse
i
ist das arithmetische Mittel aller Werte
der Urliste, die innerhalb der betrachteten Klasse
i
xk
liegen. Das Klassenmittel kann
nur bei Kenntnis der Urliste berechnet werden, sonst muss man die Klassenmitte
nehmen.
Der Unterschied zwischen der Klassenmitte und dem Klassenmittelwert sei an der vierten Klasse
(1, 85, 1, 95]
erläutert. Die Klassenmitte ist die Mitte zwischen den Grenzen,
also deren arithmetisches Mittel, in diesem Fall somit
m4 = 1, 90. Der Klassenmittelwert
ist das arithmetische Mittel aller Werte, die in der Klasse liegen, das sind hier die vier
Werte 1,86, 1,89, 1,91 und 1,93. Deren Mittelwert ist
x̄4 = (1, 86 + 1, 89 + 1, 91 + 1, 93)/4 = 1, 8975,
und somit verschieden von
m4 = 1, 90.
43
4 Klassenbildung
4.3 Häugkeitstabelle klassierter Daten
Die Häugkeitstabelle klassierter Daten zeigt die erwähnten Gröÿen übersichtlich angeordnet. Der allgemeine Aufbau einer solchen Häugkeitstabelle ist beispielhaft in Tabelle
4.1 zu nden.
Tabelle 4.1: Häugkeitstabelle eines stetigen Merkmals
Klasse
x∗i−1
x∗i
∆i
ni
n∗i
Ni
fi
fi∗
Fi
1
1,50
1,65
0,15
2
13,33
2
0,10
0,67
0,10
2
1,65
1,75
0,10
6
60
8
0,30
3,00
0,40
3
1,75
1,85
0,10
7
70
15
0,35
3,50
0,75
4
1,85
1,95
0,10
4
40
19
0,20
2,00
0,95
5
1,95
2,10
0,15
1
6,67
20
0,05
0,34
1,00
Man kann der Häugkeitstabelle entnehmen, dass 95 Prozent aller Teilnehmer höchstens 1,95 m groÿ waren und die Häugkeitsdichte in der Klasse
(1, 75, 1, 85]
am gröÿten
und in der letzten Klasse am kleinsten ist.
4.4 Histogramme
Graphisch werden Klassen mit einem
Histogramm
dargestellt. Dabei zeichnet man in
einem rechtwinkligen Koordinatensystem auf der horizontalen Achse, der Abszisse, die
Klassengrenzen ein und trägt über jeder Klasse ein Rechteck ab, dessen Fläche gleich
der relativen Häugkeit fi der Klasse ist. Die Höhe des Rechtecks ist daher der Wert
∗
der Häugkeitsdichte fi = fi /∆i , also der Bruch aus relativer Häugkeit fi und Klassenbreite ∆i . Die Summe aller Flächeninhalte der Rechtecke ist die Summe der relativen
Häugkeiten
fi ,
also 1.
Ein Histogramm ist also die Darstellung der Verteilungsdichte klassierter Daten durch
∗
eine Reihe von Rechtecken. Man kann einem Histogramm eine Funktion
zuordnen, die man
empirische Dichtefunktion
(
fi∗ ,
f ∗ (x) =
0,
für
f : R → R
nennt. Sie ist wie folgt deniert
x∗i−1 < x ≤ x∗i
1≤i≤k
sonst.
Im Beispiel der Körpergröÿen lese ich die Klassengrenzen aus der zweiten und dritten
Spalte ab, die Werte der Häugkeitsdichten übertrage ich aus der vorletzten Spalte. Die
44
4.5 Approximierende empirische Verteilungsfunktion
empirische Dichtefunktion lautet somit:

0, 67,





3, 0,



3, 5,
f ∗ (x) =

2, 0,




0, 34,



0,
für
für
für
für
für
1, 50 < x ≤ 1, 65
1, 65 < x ≤ 1, 75
1, 75 < x ≤ 1, 85
1, 85 < x ≤ 1, 95
1, 95 < x ≤ 2, 10
sonst.
Die Abbildung 4.2 zeigt das zugehörige Histogramm und die noch zu besprechende empirische Verteilungsfunktion. Um ganz genau zu sein: Das Histogramm besteht aus Recht-
F*
f*
F*
f*
3
1,00
0,75
2
0,50
1
0,25
0
0,00
1,40
1,50
1,60
1,70
1,80
1,90
2,00
2,10
Größe in [m]
Abbildung 4.2: Histogramm und approximierende empirische Verteilungsfunktion
ecken, der Graph der empirischen Dichtefunktion
f ∗ (x)
nur aus deren oberen Seiten,
also ohne die senkrechten Seiten der Rechtecke.
4.5 Approximierende empirische Verteilungsfunktion
In der Abbildung 4.2 bendet sich noch eine zweite Funktion, und zwar die zugehörige Verteilungsfunktion, deren Werte sich auf die rechte Ordinate beziehen. Durch die
Klassenbildung gehen aber alle Informationen über die einzelnen Werte innerhalb einer Klasse verloren, daher kennt man die empirische Verteilungsfunktion nur noch an
den Klassengrenzen. Anstelle der eigentlichen empirischen Verteilungsfunktion wird eine
∗
Funktion F (x) konstruiert, für die an den Klassengrenzen
F ∗ (x∗i ) = Fi ,
i = 1, . . . , k.
gilt. Diese Werte sind in der Abbildung 4.2 markiert. Für die Werte dazwischen verwendet man lineare Interpolation und erhält eine stetige Funktion aus zusammenhängenden
45
4 Klassenbildung
Geradenstücken, einem so genannten Polygonzug. Somit gilt


0,
∗
F (x) = Fi−1 +


1,
für
x ≤ x∗0 .
x∗i−1 < x ≤ x∗i , i = 1, 2, . . . , k
für
x ≥ x∗k .
für
Fi −Fi−1
x∗i −x∗i−1
x − x∗i−1 ,
Da diese Funktion nicht exakt die empirische Verteilungsfunktion ist, nennen manche
Autoren sie
approximierende empirische Verteilungsfunktion
(vgl. Handl). Dem werde
ich mich anschlieÿen.
Wegen
Intervall
fi = Fi − Fi−1 hat die approximierende empirische Verteilungsfunktion im
(x∗i−1 , x∗i ) die Steigung fi∗ , also die Höhe des Rechtecks im Histogramm. Daher
gilt auÿer an den Klassengrenzen
F ∗0 (x) = f ∗ (x).
Diese Beziehung zwischen Dichte-und Verteilungsfunktion ist typisch für stetige Merkmale.
4.6 Maÿzahlen bei klassierten Daten
Die Klassenbildung dient der Übersichtlichkeit, führt aber zu einem Informationsverlust.
Liegen die Daten eines stetigen Merkmals noch als geordnete Urliste vor, so sollten
die Maÿzahlen wie beschrieben ermittelt werden. Wenn aber nur noch die klassierte
Häugkeitstabelle vorliegt, können die Maÿzahlen nur näherungsweise berechnet werden.
4.6.1 Der Modus
Liegen die Daten nur in Form einer klassierten Häugkeitstabelle vor, so ist der Modus
∗
eine ganze Klasse, nämlich wieder diejenige mit dem gröÿten Wert von fi . Betrachten
Sie dazu bitte die Tabelle 4.1 der Körpergröÿen. Hier ist der Modus die ganze Klasse
mit den Grenzen
(1, 75, 1, 85].
Möchte man einen eindeutigen Wert, muss man sich für
die Klassenmitte entscheiden, hier also für 1,80.
4.6.2 Median und Quantile
Steht nur noch die Häugkeitstabelle der klassierten Daten zur Verfügung, so ergibt
sich der Median wie in der Abbildung 4.1 auf Seite 41 zu sehen näherungsweise über
den Schnitt der Geraden y = 0, 5 mit dem Graphen der approximierenden empirischen
∗
Verteilungsfunktion F , d.h. der Median ist die Lösung der Gleichung
0, 5 = F ∗ (x0,5 )
(4.3)
Nach demselben Schema wird auch das allgemeine p-Quantil bei klassierten Daten
berechnet, d.h. das p-Quantil ist näherungsweise die Lösung der Gleichung
p = F ∗ (xp ).
46
(4.4)
4.6 Maÿzahlen bei klassierten Daten
(x∗i−1 , x∗i ] mit Fi = p,
Fi > p gilt. Wegen
so ist
Gibt es eine Klasse
zum ersten Mal
F ∗ (x) = Fi−1 +
xp = x∗i .
Sonst wählt man die Klasse, wo
Fi − Fi−1
∗
x
−
x
i−1
x∗i − x∗i−1
folgt aus der Bedingung (4.4) die Grundformel zu Berechnung des p-Quantils:
(p − Fi−1 ) x∗i − x∗i−1
xp ≈ x∗i−1 +
Fi − Fi−1
(4.5)
Betrachten wir dazu noch einmal die Tabelle der Körpergröÿen mit klassierten Daten
Tabelle 4.2: Häugkeitstabelle eines stetigen Merkmals
Klasse
x∗i−1
x∗i
∆i
ni
fi
fi∗
Fi
1
1,50
1,65
0,15
2
0,10
0,67
0,10
2
1,65
1,75
0,10
6
0,30
3,00
0,40
3
1,75
1,85
0,10
7
0,35
3,50
0,75
4
1,85
1,95
0,10
4
0,20
2,00
0,95
5
1,95
2,10
0,15
1
0,05
0,34
1,00
Wir verwenden die Grundformel (4.5) jetzt zur näherungsweisen Bestimmung einiger
Quantile.
x0,05
Zur Bestimmung des Quantils
F1 = 0, 10
sowie
F1−1 = F0 =
muss die erste Klasse betrachtet werden. Hier ist
0. Weiter sind x∗1 = 1, 65 und x∗0 = 1, 50 und damit folgt
x0,05 ≈ 1, 50 +
(0, 05 − 0, 00) (1, 65 − 1, 50)
= 1, 575
0, 10 − 0, 00
Das stimmt sehr gut mit dem exakten Wert von 1,59 überein.
Zur Bestimmung des unteren Quartils
Hier ist
F2 = 0, 40
sowie
F2−1 =
x0,25
muss die zweite Klasse betrachtet werden.
0, 10. Weiter sind x∗2 = 1, 75 und x∗1 = 1, 65 und damit
folgt
(0, 25 − 0, 10) (1, 75 − 1, 65)
= 1, 70
0, 40 − 0, 10
Für den Median ist p = 0, 5, also i = 3, F3 = 0, 75 sowie F2 = 0, 40.
x∗3 = 1, 85 und x∗2 = 1, 75 und damit folgt
x0,25 ≈ 1, 65 +
(0, 5 − 0, 4) (1, 85 − 1, 75)
= 1, 78
0, 75 − 0, 4
Quartils x0,75 muss die dritte Klasse
Weiter sind
x0,5 ≈ 1, 75 +
Zur Bestimmung des dritten
Hier ist
F3 = 0, 75
betrachtet werden.
und somit gilt
x0,75 ≈ x3 = 1, 85
Die Näherungswerte stimmen sehr gut mit dem exakten Wert von 1,71, 1,77 und 1,845
überein, siehe Beispiel 3.12 auf Seite 35.
47
4 Klassenbildung
4.6.3 Arithmetisches Mittel und Varianz
Bei klassiertem Datenmaterial fehlen die Einzelwerte, manchmal sind aber die Klassenmittelwerte
x̄i
der Werte, die in einer Klasse liegen, bekannt. Dann ergeben sich das
arithmetische Mittel und die Varianz durch die Formeln
Pk
ni x̄i
n1 x̄1 + n2 x̄2 + · · · + nk x̄k
= i=1
,
x̄ =
n
n
Pk
ni x̄2i
n1 x̄21 + n2 x̄22 + · · · + nk x̄2k
2
2
σ ≈
− x̄ = i=1
− x̄2
n
n
Hier sind
ni
(4.6)
(4.7)
die absoluten Häugkeiten der Klassen.
Sind die Klassenmittelwerte unbekannt, werden näherungsweise die Klassenmitten
mi
verwendet. Das arithmetische Mittel und die Varianz werden dann durch
Pk
ni mi
n1 m1 + n2 m2 + · · · + nk mk
= i=1
,
x̄ ≈
n
n
P
k
ni m2i
n1 m21 + n2 m22 + · · · + nk m2k
2
2
σ ≈
− x̄ = i=1
− x̄2
n
n
(4.8)
(4.9)
angenähert.
Betrachten wir die Daten der Tabelle 4.2. Die Klassenmittelwerte sind nicht vorhanden, daher muss der Mittelwert näherungsweise über die Klassenmitten
mi
berechnet
werden. Damit erhalten wir folgende Näherungen
x̄ ≈ (2 · 1, 575 + 6 · 1, 70 + 7 · 1, 80 + 4 · 1, 90 + 1 · 2, 025) /20 = 1, 78
σ 2 ≈ 2 · 1, 5752 + 6 · 1, 702 + 7 · 1, 802 + 4 · 1, 902 + 1 · 2, 0252 /20 − 1, 782 = 0, 0077.
Die Näherung für das arithmetische Mittel kommt sehr nah an den exakten Wert von
1,7845 heran. Die näherungsweise berechnete Varianz weicht dagegen deutlich vom exakten Wert 0,012106 ab. Das liegt daran, dass bei der Näherung für die Varianz die
Streuung innerhalb der Klassen nicht berücksichtigt wird. Es gibt deshalb Korrekturformeln, auf die ich aber nicht eingehen möchte. Näheres dazu siehe von der Lippe.
4.7 Aufgaben
1.) (Wikipedia, 19.2.2009) Es liegen für 32 europäische Länder als Indikator für den
Wohlstand die Zahlen der PKWs pro 1000 Einwohner vor. Die Werte werden in
Klassen eingeteilt wie folgt. In 9 Ländern kommen z.B. auf je 1.000 Einwohner mehr
Tabelle 4.3: Brumm, Brumm
48
[0, 200]
(200, 300]
(300, 400]
(400, 500]
(500, 700]
5
6
6
9
6
4.7 Aufgaben
als 400 und bis zu 500 PKW. Erstellen Sie die klassierte Häugkeitstabelle, das Histogramm sowie die approximierende Verteilungsfunktion. Berechnen Sie dann näherungsweise die Quartile
Q1 , Q2
und
Q3
sowie den Mittelwert und die Varianz.
2.) Die Daten seien wieder die Körpergröÿen der Abbildung 4.1, aber die Klassengrenzen
seien 1,50, 1,70, 1,80, 1,90 und 2,10. Erstellen Sie die klassierte Häugkeitstabelle,
das Histogramm sowie die approximierende Verteilungsfunktion. Berechnen Sie dann
näherungsweise die Quartile
Q1 , Q2
und
Q3
sowie den Mittelwert und die Varianz.
49
5 Darstellung und Kennzahlen von
Konzentration
5.1 Übersicht und Lernziele
Wenn Sie dieses Kapitel durchgearbeitet haben, sollten Sie
- den Unterschied zwischen absoluter und relativer Konzentration kennen;
- wissen, wie man relative Konzentration durch die Lorenzkurve veranschaulicht;
- den Gini-Koezient berechnen und deuten können;
- wissen, wie man absolute Konzentration durch die Konzentrationskurve veranschaulicht;
- den Rosenbluth- und den Herndahl-Index berechnen und deuten können.
5.2 Absolute und relative Konzentration
Konzentration ist das Gegenteil von Ausgeglichenheit, in der Wirtschaftstheorie meint
man damit eine marktbeherrschende Stellung von wenigen Anbietern. Das kann daran liegen, dass es überhaupt nur eine kleine
kleiner
Anteil
Anzahl
von Anbietern gibt oder dass ein
von Anbietern einen groÿen Teil der Nachfrage abdeckt. Im ersten Fall
spricht man von
absoluter,
im zweiten von
Konzentration wird auch als
Disparität
relativer Konzentration.
Eine hohe relative
bezeichnet. Laut Duden leitet sich Disparität
vom spätlateinischen disparitas ab und bedeutet Ungleichheit, hier bezogen auf die
relativen Marktanteile.
Ein schönes Beispiel über den Unterschied zwischen absoluter und relativer Konzentration ist die Verteilung des Grundbesitzes in Schottland, wovon 80 Prozent auf 1200
Personen, also weniger als einem Prozent der Einwohnerschaft fallen. Quelle: Newsweek
(20.1.2003), zitiert nach Uebe. Hier liegt relative aber keine absolute Konzentration vor.
Oft überdecken sich beide Begrie auch. Es gibt kaum mehr als fünf Anbieter von Suchmaschinen, wobei davon aber noch einmal 90 Prozent aller Suchanfragen auf nur einen
Anbieter fallen. Hier ist die Anzahl der Anbieter gering, also liegt absoluter Konzentration vor, aber selbst innerhalb dieser kleinen Gruppe sind die relativen Anteile sehr
ungleichmäÿig verteilt, das Kennzeichen von relativer Konzentration oder Disparität.
51
5 Darstellung und Kennzahlen von Konzentration
Weit stärker als die marktbeherrschende Stellung von Google missfällt vielen Mitbürgern die ungleiche Verteilung von Einkommen, Vermögen oder Grundbesitz, sei es innerhalb eines Landes wie Deutschland oder global zwischen Erdteilen. Auch der Verbrauch
von Energie und Rohstoen ist weltweit stark auf einen kleinen Anteil der Weltbevölkerung konzentriert. Hier geht es immer um Disparität, also relative Konzentration.
Konzentration beschreibt einen Zustand, ist aber oft das Ergebnis länger anhaltender Prozesse der Marktbereinigung. Der Zustand der absoluten Konzentration ist das
Ergebnis von Übernahmen oder Ausscheiden von Konkurrenten, während bei relativer
Konzentration einige Wettbewerber ihren Marktanteil überproportional ausweiten konnten oder bereits von Anfang an marktbeherrschend waren.
5.3 Relative Konzentration
5.3.1 Die Merkmalssumme und ihre Verteilung
Zunächst müssen die verwendeten Begrie geklärt werden. Betrachtet wird ein verhältnisskaliertes Merkmal mit nichtnegativen Ausprägungen, da von den Ausprägungen nicht
nur Summen und Teilsummen sondern auch Verhältnisse gebildet werden sollen. Bisher wurde die durch das Merkmal erzeugte Verteilung der Merkmalsträger untersucht,
jetzt geht es zusätzlich um die Verteilung der Merkmalssumme auf die Merkmalsträger.
Die Merkmalssumme ist bildlich gesprochen der ganze zu verteilende Kuchen, etwa der
Gesamtlohn eines Unternehmens, das Volkseinkommen oder der gesamte Umsatz einer
Branche.
Die Werte der Urliste werden zunächst nach
zunehmenden Merkmalsbeträgen geordnet
x(1) ≤ x(2) ≤ . . . ≤ x(n) .
Die seltsame Bezeichnung
x(j)
ist in der beschreibenden Statistik für die Elemente der
i Merkmalsträger mit kleinstem Anteil haben
Fi = i/n. Die Merkmalssumme, sowie die relativen
aufsteigend geordneten Urliste üblich. Die
die kumulierte relative Häugkeit
und die kumuliert relativen Anteile an ihr ergeben sich aus
S=
n
X
xj ,
qj = x(j) /S
j=1
Da die
x(j)
Qi =
i
X
qj
j=1
der Gröÿe nach geordnet sind, folgt
0 ≤ Qi ≤ Fi ≤ 1.
Die Punkte
(Fi , Qi )
liegen somit alle unterhalb oder höchstens auf der Winkelhalbierenden des Einheitsquadrats des ersten Quadranten.
Beispiel 5.1.
Eine Kleinstadt hat fünf Bäcker, die sich unterschiedlicher Beliebtheit
erfreuen. Die Jahresgewinne sind 60, 40, 150, 20 und 90 in 1.000 Euro. Hier ist also
n = 5
und somit
fi = 1/5
sowie
Fi = i/5
für
1 ≤ i ≤ 5.
Die aufsteigend geordnete
Urliste ist 20, 40, 60, 90 und 150, die Gesamtsumme des Gewinns ist 360 und somit etwa
q3 = 60/360
und
Q3 = 120/360.
von Excel erledigt.
52
Die lästige Rechnerei habe ich in einem Arbeitsblatt
5.3 Relative Konzentration
1
2
3
4
5
6
7
8
A B
C
D
E
F
G
H
I
xi
x(i)
fi
qi
0,056
0,111
0,167
0,250
0,417
1,000
Qi
0,000
0,056
0,167
0,333
0,583
1,000
0,000
Gi
0,2
0,2
0,2
0,2
0,2
1,0
Fi
0,0
0,2
0,4
0,6
0,8
1,0
0,0
1,0
0,8
0,6
0,4
0,2
0,0
i
1 60 20
2 40 40
3 150 60
4 20 90
5 90 150
360 360
0,011
0,044
0,100
0,183
0,317
0,344
J
0,0 0,2 0,4 0,6 0,8 1,0
Abbildung 5.1: Arbeitstabelle zum Beispiel 5.1
Manchmal sind die Merkmale gruppiert, d.h. die Daten der Urliste kann man zu
k < n
aufsteigend geordneten Ausprägungen
umordnen. Die kumulierten Häugkeiten
Fi ,
ai ,
die mit der Häugkeit
Merkmalssumme
S,
ni
auftreten,
sowie die relativen
und die kumuliert relativen Anteile an ihr ergeben sich aus
fj = nj /n,
Fi =
i
X
fj ,
S=
k
X
j=1
nj aj
qj =
,
S
n j aj ,
j=1
Qi =
i
X
qj .
j=1
Beispiel 5.2. Betrachten wir ein Unternehmen, das nach vier Tarifen bezahlt. Die Tarife
berücksichtigen nur die Qualikation des Mitarbeiters, nicht aber Alter oder Familienstand. Die Jahreslöhne in 1.000 Euro betragen 20, 45, 72 und 108. Von den 20 Mitarbeitern gehören 6 der untersten Tarifgruppe, 4 der nächst höheren und jeweils 5 den beiden
höchsten an. Zur besseren Übersicht zeige ich diese Werte in einer Häugkeitstabelle, die
um drei Spalten erweitert ist, um die Merkmalssumme zu berechnen sowie deren relative
und die kumulierte relative Aufteilung auf die Mitarbeiter der vier Tarifgruppen.
A B
1
2
3
4
5
6
7
i
ai
1 20
2 45
3 72
4 108
C
D
ni ni*ai
6 120
4 180
5 360
5 540
20 1200
E
F
G
H
I
fi
qi
Fi
Qi
Gi
0,1
0,15
0,3
0,45
1
0
0,3
0,5
0,75
1,000
0
0
0,100
0,250
0,550
1,000
0
0,030
0,070
0,200
0,388
0,313
0,3
0,2
0,25
0,25
1
J
K
1
0,8
0,6
0,4
0,2
0
0 0,2 0,4 0,6 0,8 1
Abbildung 5.2: Arbeitstabelle zum Beispiel 5.2
ni Mitarbeiter der i-ten Tarifgruppe tragen den Wert si = ni ai zur Merkmalssumme S = 1.200 bei. Der entsprechende relative Anteil qi = si /S steht neben dem relativen
Anteil der fi . Der Tabelle kann entnommen werden, dass die 5 Mitarbeiter der höchsten
Die
Tarifgruppe 25 Prozent der Belegschaft ausmachen, aber 45 Prozent der Lohnsumme auf
53
5 Darstellung und Kennzahlen von Konzentration
sich vereinigen. Die kumulierten Häugkeiten
Fi
und die kumulierten Anteile
Qi
sind
ebenfalls benachbart. Alle Mitarbeiter der drei ersten Tarifgruppen bilden 75 Prozent
der Belegschaft und haben einen Anteil von 55 Prozent an der Merkmalssumme.
5.3.2 Die Lorenzkurve
Die um die kumulierten relativen Anteile an der Merkmalssumme erweiterten Häugkeitstabellen werden durch die so genannte
Lorenzkurve
veranschaulicht. Werden wie im
Fi und die kumulierten
Qi bezeichnet, so ergibt sich die Lorenzkurve als
Punkte (0, 0), (F1 , Q1 ), . . . , (Fn−1 , Qn−1 ), (1, 1). Zur Ver-
vorigen Abschnitt die kumulierten Anteile des Merkmals mit
Anteile an der Merkmalssumme mit
streckenweise Verbindung der
anschaulichung der Konzentration wird auch immer noch die Winkelhalbierende, also
die Verbindung der Punkte
(1, 1)
Für das Beispiel 5.1 werden die
(0, 8, 0, 583)
und
(1, 1)
(0, 0), eingezeichnet.
Punkte (0, 0), (0, 2, 0, 056), (0, 4, 0, 167), (0, 6, 0, 333),
und
durch Strecken verbunden, wodurch die Lorenzkurve entsteht,
und dann wird vom letzten Punkt der Lorenzkurve, also von
zurück nach
(0, 0)
(1, 1)
noch die Strecke
erzeugt. Die Koordinaten dieser Punkte stehen im Bereich F2:E8 des
Arbeitsblatts. Die ebenfalls abgebildete Lorenzkurve entsteht in Excel durch Darstellung
dieses Bereichs durch ein so genanntes Punktdiagramm, wobei ich als Typ Punkte mit
geraden Linien und Datenpunkten wählte.
Für das Beispiel 5.2 werden die Punkte
(1, 1)
und
(0, 0)
(0, 0), (0, 3, 0, 1), (0, 5, 0, 25), (0, 75, 0, 55),
durch Strecken zu verbinden. Die Koordinaten dieser Punkte stehen im
Bereich G2:H7.
5.3.3 Der Gini-Koezient
Je ungleicher die Merkmalssumme auf die Grundgesamtheit verteilt ist, desto stärker
hängt die Lorenzkurve nach rechts unten durch, während bei gleichen Anteilen Lorenzkurve und Winkelhalbierende zusammenfallen. Die Winkelhalbierende teilt das Einheitsquadrat in zwei Dreiecke mit Flächeninhalt von 1/2. Die Fläche zwischen der Winkelhalbierenden und der Lorenzkurve ist ein Maÿ für die Abweichung von der Gleichheit.
Der
Gini-Koezient
ist das Verhältnis des Inhalts dieser Fläche zum Inhalt der Ge-
samtäche des Dreiecks. Damit ist der Gini-Koezient ein Wert zwischen 0 und 1, wobei
der Wert 0 gleiche Anteile und der Wert 1 vollständige Konzentration anzeigt.
In der Abbildung 5.3 ist links noch einmal die Lorenzkurve des Beispiels 5.2 zu sehen,
n Einheiten
n−1 leer ausgehen und das gesamte Einkommen auf die letzte Einheit fällt. Die
rechts daneben bendet sich der Extremfall der Ungleichverteilung, wo von
die ersten
Fläche zwischen der Winkelhalbierenden und der Lorenzkurve ist jeweils grau ausgefüllt.
Da die Gesamtäche
I
des Dreiecks den Inhalt 1/2 hat, beträgt der Flächeninhalt der
Fläche zwischen der Lorenzkurve und der Winkelhalbierenden
I = 1/2 −
X
Inhalt der Trapeze,
da die Lorenzkurve sich aus lauter Trapezen zusammensetzt. Betrachten wir in der Abbildung 5.3 in der linken Lorenzkurve das Trapez mit den Eckpunkten
54
(F2 , 0), (F2 , Q2 ),
5.3 Relative Konzentration
Abbildung 5.3: Zusammenhang zwischen Lorenzkurve und Gini-Koezient
(F3 , Q3 ) sowie (0, Q3 ). Die
0, 5 (Q2 + Q3 ) und daher ist
Breite ist
f3 = F 3 − F 2
und die durchschnittliche Höhe
f3 · 0, 5 (Q2 + Q3 ).
der Inhalt dieses Trapezes
Somit hat die
Fläche zwischen Lorenzkurve und Winkelhalbierender den Inhalt
I = 1/2 −
k
X
fi · 0, 5 (Qi−1 + Qi ) ,
i=1
mit
Q0 = 0.
Teilt man diesen Wert jetzt noch durch 1/2, ergibt sich die Formel für den
Gini-Koezient
G=1−
k
X
fi (Qi−1 + Qi ) ,
mit
Q0 = 0
(5.1)
i=1
f1 = 0, 3, f2 = 0, 2, f3 = 0, 25, f4 = 0, 25 sowie Q0 = 0, Q1 = 0, 1,
Q2 = 0, 25, Q3 = 0, 55, Q4 = 1. Also ergibt sich für den Gini-Koezient:
Im Beispiel 5.2 sind
G = 1 − 0, 3 (0, 1 + 0) + 0, 2 (0, 25 + 0, 1) + 0, 25 (0, 55 + 0, 25) + 0, 25 (1 + 0, 55) = 0, 3125
Für den Gini-Koezient habe ich die letzte Spalte des Arbeitsblatts von Abbildung
5.2 eingerichtet. Es werden die Produkte
fi (Qi + Qi−1 ) benötigt. Somit steht in Zelle I3
zunächst die Formel
= E3 ∗ (H2 + H3)
Diese Formel ziehe ich am Ausfüllkästchen bis zur Zelle I6 nach unten. In der Zelle I7
trage ich dann noch die Formel
= 1 − Summe(I3 : I6)
ein und erhalte damit den Gini-Koezient.
55
5 Darstellung und Kennzahlen von Konzentration
5.3.4 Der normierte Gini-Koezient
In der Abbildung 5.3 ist rechts der Extremfall vollständiger Konzentration der Merkmalssumme auf eine einzige von insgesamt
n statistische Einheiten zu sehen. Selbst dann
hat der Gini-Koezient nicht den Wert 1 werden, denn die Lorenzkurve verläuft dann
von 0 bis
1/(n − 1)
auf der Abszisse und steigt dann als Strecke zum Punkt
(1, 1).
Die
Fläche zwischen Lorenzkurve und Winkelhalbierender ist ein Dreieck mit Grundseite
(n − 1)/n
und Höhe 1, also mit einem Flächeninhalt von
Wert durch
1/2
Gmax =
Man deniert daher bei
Koezient
(n − 1)/(2n).
Teilt man diesen
ergibt sich für den Gini-Koezient der Maximalwert von
n
n−1
n
statistischen Einheiten den so genannten
wie folgt:
Gnorm =
n
G.
n−1
normierten Gini(5.2)
Im Beispiel 5.1 sind 5 statistische Einheiten vorhanden, der normierte Gini-Koezient
ist somit
Gnorm =
Im Beispiel 5.2 sind
n = 20
5
0, 344 = 0, 431
4
statistische Einheiten auf
k = 4
Gruppen verteilt, der
normierte Gini-Koezient ist somit
Gnorm =
20
0, 3125 = 0, 328947368
19
5.3.5 Relative Daten
Lorenzkurve und die beiden Gini-Koezienten hängen nur von relativen Werten der
Ausprägungen und der Verteilungen der Merkmalssumme ab. Deshalb werden manchmal
auch nur relative Werte angegeben. Betrachten wir ein ktives Land, wo die ärmsten
30 Prozent der Bevölkerung über 10 Prozent des Gesamteinkommens verfügen und die
nächsten 20 Prozent der Bevölkerung auf weitere 15 Prozent des Gesamteinkommens
kommen. Die nächsten 25 Prozent der Bevölkerung haben am Gesamteinkommen einen
Anteil von 30 Prozent und die letzten 25 Prozent teilen sich die restlichen 45 Prozent.
Die Gesamtzahl der Bevölkerung und deren Gesamteinkommen sind hier nicht bekannt. Die Arbeitstabelle in der Art von Abbildung 5.2 beginnt somit erst ab der Spalte
mit den relativen Anteilen
fi ,
gefolgt von der Spalte mit den relativen Anteilen an der
Merkmalssumme, gefolgt von den restlichen Spalten. Wenn Sie die Daten von hier genauer untersuchen, werden sie feststellen, dass sie mit den Daten der Abbildung 5.2
übereinstimmen, Lorenzkurve und die beiden Gini-Koezienten sind deshalb gleich.
5.3.6 Klassierte Daten
Lorenzkurven und Gini-Koezient werden sehr häug auf bereits klassierte Daten angewandt. Beachtet werden muss, ob für die Klassen aus der Urliste ein Klassenmittelwert
56
5.3 Relative Konzentration
vorhanden ist oder nicht. Im letzteren Fall wird anstelle des Klassenmittelwerts die Klassenmitte als Näherung genommen. Ich zeige die Vorgehensweise an zwei Beispielen.
Beispiel 5.3.
Die monatlichen Einkommen (in Asturios) in Costa Asturia sind so wie
im abgebildeten Arbeitsblatt über die 15 Millionen Einwohner verteilt. Ein freundlicher
Statistiker hat hier vor der Klassenbildung noch die Klassenmittelwerte
x̄i
ausgerechnet
und in die Spalte E eingetragen. Die zweite Klasse umfasst alle Einkommen über 1.000
bis höchstens 2.000 Asturios mit
n2 = 6
Mio. und
x̄2 = 1.600.
Diese Klasse trägt zur
gesamten Merkmalssumme von 52.800 Millionen Asturios den Beitrag 9.600 Millionen
Asturios bei. Der Beitrag der i-ten Klasse zur Merkmalssumme ist entsprechend
si =
x̄i ni .
1
2
3
4
5
6
7
8
A
B
i
xi*
C
1
2
3
4
5
0
1000
2000
3500
über
D
E
F
G
H
I
J
K
L
M
x(i)* ni
KMWi si
fi
qi
Fi
Qi
Gi
1
(Mio)
0
0
1000
2
600 1200 0,133 0,023 0,133 0,023 0,003
2000
6 1600 9600 0,400 0,182 0,533 0,205 0,091 0,5
3500
3 2800 8400 0,200 0,159 0,733 0,364 0,114
6000
2 4800 9600 0,133 0,182 0,867 0,545 0,121
0
6000
2 12000 24000 0,133 0,455 1,000 1,000 0,206
0 0,2 0,4 0,6 0,8 1
15
52800
1
1
0
0 0,465
Abbildung 5.4: Arbeitsblatt für Lorenzkurve mit klassierten Daten
x∗i
und die Häugkeiten ni angegeben, dann muss der
mi = 0, 5(x∗i−1 + x∗i ) ersetzt werden. Der
Beitrag der i-ten Klasse zur Merkmalssumme ist entsprechend si = mi ni .
Oft sind nur die Klassengrenzen
Klassenmittelwert
Beispiel 5.4.
x̄i
durch die Klassenmitte
In einem Betrieb wurden die im Bereich A3:D6 der Abbildung 5.5 stehen-
den Daten über die monatlichen Einkommen in 100 Euro der 25 Mitarbeiter erhoben.
[5, 12] mit 5 Mitarbeitern, die letzte
(30, 50] mit ebenfalls 5 Mitarbeitern. Hier sind die Klassenmittelwerte unbekannt und
Hier wurden also vier Klassen gebildet, die erste ist
ist
wurden durch die Klassenmitten angenähert.
A B
1
2
3
4
5
6
7
8
C
D
E
i xi* x(i)* ni mi
1 5
2 10
3 18
4 30
10
18
30
50
5 7,50
8 14,00
7 24,00
5 40,00
25
F
si
G
fi
37,5
112
168
200
517,5
0,200
0,320
0,280
0,200
1
H
qi
0,072
0,216
0,325
0,386
1
I
Fi
0
0,200
0,520
0,800
1,000
0
J
Qi
0
0,072
0,289
0,614
1,000
0
K
Gi
0,0145
0,1156
0,2527
0,3227
0,2945
0,3068
L
M
1
0,5
0
0 0,25 0,5 0,75 1
Abbildung 5.5: Arbeitsblatt für Lorenzkurve mit klassierten Daten
57
5 Darstellung und Kennzahlen von Konzentration
5.3.7 Vorgehensweise mit Excel
Die Berechnungen seien am Arbeitsblatt des Beispiels 5.4 ausführlich erläutert. Ausgangspunkt sind die Klassen und die entsprechenden Häugkeiten, also die vier ersten
Spalten. In der Spalte E stehen entweder die Klassenmittelwerte oder die Klassenmitten.
Der Klassenmittelwert der ersten Klasse steht in der Zelle E3 und ergibt sich aus der
Formel
= 0, 5 ∗ (B3 + C3)
Diese Formel lässt sich am Ausfüllkästchen bequem nach unten bis zur Zelle E6 ziehen.
In der Spalte F stehen die Teilbeiträge zur Merkmalssumme, in Zelle F3 kommt zunächst
die Formel
= D3 ∗ E3
Auch diese Formel lässt sich am Ausfüllkästchen bequem nach unten bis zur Zelle F6
ziehen. Danach werden die Summen der Spalten D und F berechnet. In den Zellen D8
und F8 stehen die Formeln
= Summe(D3 : D6)
Für die
fi
= Summe(F 3 : F 6)
müssen die in der dritten Spalte stehenden Häugkeiten durch die Spalten-
summe dieser Spalte geteilt werden. Dazu trägt man in der Zelle G3 die Formel
= D3/D$7
Das Dollarzeichen vor der 7 verhindert, dass sich beim Ziehen am Ziehpunkt die Zelle D7
mit nach unten zieht. Das ganze müssen Sie für die Spalte H wiederholen, also zunächst
in H3 die Formel
= F 3/F $7
eintragen und dann ziehen. Die kumulierten Werte der
Population sind in Spalte I. Sie müssen zunächst in der Zelle I3 die Formel
= I2 + G3
eintragen, da die Formel
Fi = Fi−1 + fi
gilt mit
F0 = 0 Dies ist der Grund für die beiden
Nullen in der zweiten Zeile. Diese Formel können Sie am Ausfüllkästchen nach unten
ziehen.
Das führen Sie dann sinngemäÿ für die nächste Spalte durch, also zunächst in Zelle J3
= J2 + H3
eintragen und dann nach unten ziehen.
Für den Gini-Koezient habe ich die letzte Spalte eingerichtet. Es werden die Produkte
fi (Qi + Qi−1 )
benötigt. Somit steht in Zelle K3 zunächst die Formel
= G3 ∗ (J2 + J3).
Das wird nach unten gezogen. In der Zelle K7 trage ich dann noch die Formel
= 1 − Summe(K3 : K6)
ein und erhalte damit den Gini-Koezient. Da die Anzahl
n = 25
der statistischen
Einheiten noch nicht übermäÿig groÿ ist, lohnt es sich den normierten Gini-Koezient
auszurechnen, der in der Zelle K8 steht und über die Formel
dem Gini-Koezient zusammenhängt.
58
= K7 ∗ D7/(D7 − 1)
mit
5.4 Absolute Konzentration
5.4 Absolute Konzentration
5.4.1 Konzentrationskurve und Rosenbluth-Index
Absolute Konzentration liegt vor, wenn eine geringe Anzahl von Merkmalsträgern einen
groÿen Anteil an der Merkmalssumme auf sich vereinigt, d.h. es kommt auf die kumulierten Anteile der gröÿten Marktteilnehmer an. Die Werte der Urliste werden hier deshalb
nach
abnehmenden
Merkmalsbeträgen geordnet
x(1) ≥ x(2) . . . ≥ x(n) .
Die Elemente der absteigend geordneten Liste werden mit
x(j)
bezeichnet, daraus wird
zunächst die Merkmalssumme berechnet, danach die relativen Anteile davon und abschlieÿend die kumulierten relativen Anteile:
S=
n
X
(j)
x ,
(j)
cj = x /S,
Ci =
j=1
Die Gröÿen
Ci heiÿen Konzentrationsraten
i
X
cj .
j=1
und beschreiben den kumulierten Anteil der
i
gröÿten Merkmalsträger. Soweit deckt sich alles mit der Vorgehensweise bei der relativen
Konzentration, nur erfolgt die Kumulation von oben nach unten und nicht von unten
nach oben. Zeichnet man die geordneten Paare
(i, Ci )
in ein kartesisches Koordinaten-
system ein und verbindet man die Punkte mit den Koordinaten
so heiÿt der daraus resultierende Polygonzug
(0, 0), (1, C1 ), . . . , (n, 1),
Konzentrationskurve .
Die maximale Kon-
zentration ist erreicht, wenn der gröÿte Merkmalsträger die gesamte Merkmalssumme
auf sich vereinigt. Dann gelten
x(1) = S, x(2) = x(3) = · · · = x(n) = 0,
C1 = C2 = · · · = Cn = 1
In der folgenden Abbildung ist die Konzentrationskurve der Bäcker von Beispiel 5.1
zu sehen.
Abbildung 5.6: Arbeitsblatt für Konzentrationskurve, Rosenbluth- und Herndahl-Index
In der ersten Spalte stehen die jährlichen Gewinne der fünf Bäcker, in der zweiten
folgen die Gewinnzahlen abnehmend geordnet. Dann werden die relativen Anteile berechnet, die zugehörigen Konzentrationsraten
Ci
stehen in der übernächsten Spalte. Da-
zwischen, also in der Spalte D habe ich die Laufzahlen
i
der Bäcker eingetragen. Die
59
5 Darstellung und Kennzahlen von Konzentration
Konzentrationskurve ist dann wieder der Polygonzug, der zum Bereich D2:E8 gehört.
Die Spalten F und G dienen der Berechnung von zwei weiteren Kennzahlen, die ich jetzt
nacheinander vorstelle.
5.4.2 Rosenbluth-Index
So wie der Gini-Koezient aus der Lorenzkurve abgeleitet wird, stammt der
Index
Rosenbluth-
aus der Konzentrationskurve. Anders als der Gini-Koezient wird aber nicht die
Fläche zwischen der Diagonalen und dem Graph der Konzentrationskurve herangezogen,
y = 1, wobei die y-Achse die
n Trapezen, wobei das erste zu
sondern die Fläche oberhalb dieses Graphen bis zur Geraden
natürliche linke Begrenzung ist. Diese Fläche besteht aus
einem Dreieck verkümmert ist. Ich habe die Trapeze in der Abbildung 5.6 abwechselnd
grau und weiÿ ausgefüllt. Die Breite de Trapeze sind die
ist
i − 0, 5.
F =
n
X
ci (i − 0, 5) =
i=1
da die
ci
ci ,
die durchschnittliche Höhe
Damit hat die besagte Fläche den Inhalt
n
X
ci i − 0, 5
n
X
i=1
ci =
i=1
n
X
ci i − 0, 5,
i=1
F liegt zwischen 1/2 und n/2, denn
somit F = 1/2, während bei gleichmäÿiger
aufsummiert 1 ergeben. Der Wert von
bei maximaler Konzentration ist
c1 = 1
und
Verteilung der Graph der Konzentrationskurve mit der Diagonalen des Rechtecks mit
den Seitenlängen 1 und
gröÿer ist
F,
n
deshalb wäre
Wert zwischen
2/n
zusammenfällt. Je geringer also die Konzentration ist, umso
1/F
ein gutes Konzentrationsmaÿ. Allerdings verliefe dessen
und 2, weswegen der Rosenbluth-Index,
festgelegt wird und zwischen
KR =
1/n
2
KR
genannt, durch
und 1 liegt. Ich halte das in einer Formel fest
1
,
i=1 ci i − 1
Pn
1/n ≤ KR ≤ 1.
In der Spalte F des abgebildeten Arbeitsblatts stehen die Produkte
wird der Rosenbluth-Index,
KR
1/(2F )
(5.3)
ci i .
In der Zelle F8
durch die Excel-Formel
= 1/(2 ∗ SU M M E(F 3 : F 7) − 1)
berechnet.
5.4.3 Herndahl-Index
Der
Herndahl-Index KH
ist bekannteste Maÿ der absoluten Konzentration. Er berech-
net sich aus der Summe der Quadrate der relativen Anteile an der Merkmalssumme,
also
KH =
n
X
i=1
60
c2i
Pn
x2
= Pni=1 i 2 .
( i=1 xi )
(5.4)
5.4 Absolute Konzentration
Man muss zur Berechnung dieses Index noch nicht einmal die Urliste ordnen. Ich habe
die Spalte G für den Herndahl-Index eingerichtet. Hier benden sich im Bereich G3:G7
die Quadrate der
ci
und in der Zelle G8 die Formel
= SU M M E(G3 : G7)
Der Herndahl-Index ist eng mit dem Variationskoezient
KH =
vX
verwandt. Es gilt
2
vX
+1
.
n
(5.5)
n Werte xj gleich sind.
1/n. Damit ergibt sich die Untergrenze des Herndahl-Index
Der Herndahl-Index nimmt seinen kleinsten Wert an, wenn alle
Dann haben alle ci den Wert
aus
min
KH
n
X
=
(1/n)2 = n/n2 = 1/n.
i=1
Bei vollständiger Konzentration ergibt sich sofort
max
KH
= 1.
Der Herndahl-Index wird in den USA auch als Herndahl-Hirschman Index bezeichnet. Er wird auch zuweilen mit Zinsfüÿen berechnet, statt etwa 0,75 wird dann mit 75
gerechnet. Der Wertebereich ist dann
100/n ≤ KH ≤ 100.
Der Herndahl-Index wird
eingesetzt, um die Wettbewerbssituation in Märkten zu beurteilen. Geringer Wettbewerb
wird in der Wirtschaftstheorie für schädlich gehalten, da Monopolbildungen, Absprachen
und mangelnde Ezienz die Folge sind. Der Herndahl-Index wird herangezogen, wenn
in problematischen Märkten Zusammenschlüsse oder Übernahmen beantragt werden.
Das amerikanische Wikipedia schreibt dazu am 13.8.2011:
If the Herndahl index is above a certain threshold then economists consider
the market to have a high concentration. The Antitrust Division of the Department of Justice considers Herndahl indices between 0.1000 and 0.1800
to be moderately concentrated and indices above 0.2500 to be concentrated, while the EU prefers to focus on the level of change, for instance that
concern is raised if there is a 0.025 change when the index already shows a
concentration of 0.1.
In den USA gelten Werte des Herndahl-Index unter 0,1 für unbedenklich, bei Werten
zwischen 0,1 und 0,18 sieht man Anhaltspunkte für Konzentration und deutet Werte
über 0,25 als klares Zeichen von hoher Konzentration. Die EU, also die Europäische
Union, möchte es erst gar nicht zu hoher Konzentration kommen lassen, und schaut
bei möglichen Zusammenschlüssen auf die Veränderung des Herndahl-Index und sieht
Zuwächse von mehr als 0,025 kritisch, wenn der Herndahl-Index vorher bereits über 0,1
war.
Beispiel 5.5.
Das US-Wikipedia liefert auch gleich ein Beispiel eines Marktes für was
auch immer mit 26 Firmen, zufällig genauso viel wie das Alphabet Buchstaben hat. Die
61
5 Darstellung und Kennzahlen von Konzentration
Gesellschaften heiÿen nach Buchstaben und haben folgende Marktanteile: A: 0,3, B bis
F jeweils 0,1 und G bis Z jeweils 0,01. Der Herndahl-Index ist somit
KH = 0, 32 + 5 · 0, 12 + 20 · 0, 012 = 0, 142.
Wenn jetzt C beantragt B und D zu übernehmen, verändert sich der Herndahl-Index
wie folgt
KH = 0, 32 + 0, 32 + 2 · 0, 12 + 20 · 0, 012 = 0, 202.
Nach amerikanischer Auslegung ist das kein Problem, denn der Herndahl-Index bleibt
auch nach dem Zusammenschluss unter 0,25, mit europäischen Augen gesehen, steigt
der Herndahl-Index aber von einem Wert über 0,1 um mehr als 0,025.
5.4.4 Relative Daten
Die Konzentrationskurve sowie der Rosenbluth- und der Herndahl-Index werden aus
den relativen Anteilen der Merkmalsträger an der Merkmalssumme berechnet. Deshalb
werden manchmal auch nur relative Werte angegeben, wie im folgenden Beispiel, das
Konzentration als einen zeitabhängigen Vorgang darstellt.
Beispiel 5.6.
In Costa Asturia wird der Energiemarkt durch fünf Unternehmen abge-
deckt, deren Marktanteile für das Jahr 2000 in der Spalte A der Abbildung 5.7 zu nden
sind. Die Konzentrationskurve sowie der Rosenbluth-Index
KH
KR und der Herndahl-Index
werden allein aus den relativen Daten erzeugt. Im Jahr 2010 war der vormals kleins-
te Anbieter durch Übernahme vom Markt verschwunden und zusätzlich haben sich die
Marktanteile zugunsten des ersten Anbieters drastisch verschoben, siehe Spalte J. Dies
wirkt sich auch auf die Konzentrationskurve aus und verändert die beiden Indizes eindrucksvoll.
A
B
C
D
E
1
ci
K_H
0,40
0,25
0,20
0,10
0,05
1,00
Ci
0,00
0,40
0,65
0,85
0,95
1,00
0,00
KR
2
3
4
5
6
7
8
i
0
1
2
3
4
5
0
0,400
0,500
0,600
0,400
0,250
0,303
0,160
0,063
0,040
0,010
0,003
0,275
F
G
H I
1,0
0,8
0,6
0,4
0,2
0,0
0
1
2
3
4
5
J
K
L
M
N
ci
i
0
1
2
3
4
0
Ci
0,0
0,6
0,8
0,9
1,0
0,0
KR
K_H
0,600
0,400
0,300
0,400
0,417
0,36
0,04
0,01
0,01
0,42
0,6
0,2
0,1
0,1
1,0
O
P
Q
1,0
0,8
0,6
0,4
0,2
0,0
0
1
2
3
4
Abbildung 5.7: Arbeitsblatt für absolute Konzentration bei relativen Daten
5.5 Zusammenfassung
Man unterscheidet absolute und relative Konzentration. Relative Konzentration untersucht anteilsmäÿige Ungleichverteilung an der Merkmalssumme. Das Ausmaÿ an relativer Konzentration wird durch die Lorenzkurve veranschaulicht. Der Gini-Koezient
62
5.6 Aufgaben
verdichtet die Informationen der Lorenzkurve zu einer Kennzahl, nämlich dem Zweifachen des Inhalts der Fläche zwischen der Lorenzkurve und der Winkelhalbierenden. Bei
einer geringen Zahl
n
von Merkmalsträgern wird der Gini-Koezient mit dem Faktor
n/(n − 1) multipliziert, was den normierten Gini-Koezienten ergibt. Hat der normierte
Gini-Koezient den Wert 0, ist die Merkmalssumme gleichmäÿig auf die Merkmalsträger verteilt, bei einem Wert von 1 ist die Merkmalssumme auf eine einzige statistische
Einheit konzentriert.
5.6 Aufgaben
1.) In der Kleinstadt des Beispiels 5.1 auf Seite 52 hat der erfolgreichste der fünf Bäcker
sein Geschäft auf seine zwei Söhne verteilt, die Jahresgewinne von 60 und 90 Tausend
Euro erwirtschaften. Die Jahresgewinne der anderen Bäckereien veränderten sich
nicht. Somit sind die Jahresgewinne der nun sechs Bäcker 60, 40, 60, 90, 20 und 90
in Tausend Euro.
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
b) Erstellen Sie die Häugkeitstabelle und berechnen Sie die beiden Gini-Koezienten
und zeichnen Sie die Lorenzkurve.
c) Zeichnen Sie die Konzentrationskurve und berechnen sie den Rosenbluth- und
den Herndahl-Index.
2.) Auf Drängen der EU-Kommission wurde der Energiemarkt in Costa Asturia neu
geordnet, das bisher gröÿte Unternehmen wurde in drei Anbieter mit je 20 Prozent
Marktanteil aufgeteilt. Das bisher zweitgröÿte Unternehmen konnte seinen Marktanteil um fünf Prozent auf Kosten des kleinsten Unternehmens steigern, sodass die nun
sechs Anbieter Marktanteile von 25, dreimal 20, 10 und 5 Prozent haben. Zeichnen
Sie die Konzentrationskurve und berechnen sie den Rosenbluth- und den HerndahlIndex.
3.) (Anderson et al.). In der Tabelle 5.1 ist die Zahl der Personen in Privathaushalten
in der BRD 1970 aufgeführt.
Tabelle 5.1: Gröÿe von Haushalten, BRD 1970
Haushaltsgröÿe
Zahl der Haushalte in 1000
1
2
3
4
5527
5959
4314
3351
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
63
5 Darstellung und Kennzahlen von Konzentration
b) Erstellen Sie die Häugkeitstabelle und berechnen Sie den Gini-Koezienten und
zeichnen Sie die Lorenzkurve.
4.) Diese Aufgabe stammt von von der Lippe, ich habe nur andere Zahlen verwendet:
200 Angehörige eines primitiven Volksstammes, sogenannte Urmenschen, gehen
auf die Jagd nach Federvieh. Ihre Beute beträgt 1.000 Wildgänse. Durch das an sich
nur bei primitiven Völkern bekannte Gerangel um Geld, Gut und Prestige entstand
trotz Eingreifens des Häuptlings eine etwas ungleiche Verteilung der Beute. Es bekamen 78 Jäger drei, 58 fünf, 41 sechs und 23 sogar zehn Gänse. Erstellen Sie die
Lorenzkurve und berechnen Sie die beiden Gini-Koezienten.
5.) (Anderson et al.) In der folgenden Tabelle steht die Verteilung der Beschäftigten auf
Arbeitsstätten im Produzierenden Gewerbe in Westdeutschland im Jahr 1970.
Arbeitsstätten
Anzahl in 100
Beschäftigte in 1000
1 - 4
3493
735
5 - 9
1231
800
10 - 19
636
854
20 - 49
442
1350
50 - 99
176
1226
100 - 199
98
1353
200 - 499
62
1884
500 und mehr
32
4658
6170
12860
Summen
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
b) Erstellen Sie die Häugkeitstabelle und berechnen Sie die beiden Gini-Koezienten
und zeichnen Sie die Lorenzkurve.
6.) (Uebe) In einem Betrieb wurden folgende Daten über die monatlichen Einkommen
(in 100
e)
der beschäftigten Frauen erhoben:
Tabelle 5.2: Fiktive Einkommen
Einkommen
Anzahl der Frauen
(6, 12]
(12, 16]
(16, 20]
(20, 24]
(24, 30]
10
15
10
5
4
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
64
5.6 Aufgaben
b) Stellen Sie die durch die Tabelle 5.2 gegebene Einkommensverteilung als Häugkeitstabelle und als Histogramm dar und erstellen Sie dann den Graphen der
approximierenden Verteilungsfunktion.
c) Erstellen Sie die Lorenzkurve und berechnen Sie die beiden Gini-Koezienten.
d) Berechnen Sie für die Einkommen der Frauen näherungsweise Modus, unteres
Quartil, Median, oberes Quartil, die Quantile
x0,1
sowie
x0,9 ,
Mittelwert sowie
Varianz und empirische Varianz und Standardabweichung und empirische Standardabweichung und den Variationskoezient.
7.) Man beweise die Beziehung (5.5) auf Seite 61.
65
6 Einführung in die
Wahrscheinlichkeitsrechnung
6.1 Übersicht und Lernziele
Es werden einführende Themen und Begrie der Wahrscheinlichkeit vorgestellt wie
- Zufallsgeräte und Zufallsexperimente;
- Ergebnis und Ergebnismenge sowie Ereignis bei einem Zufallsexperiment;
- Laplace-Experimente;
- Mehrstuge Zuzfallsexperimente und ihre Modellierung durch Baumdiagramme;
- Produktwahrscheinlichkeitsraum
- Stochastische Unabhängigkeit und bedingte Wahrscheinlichkeit
- Der Satz von Bayes
6.2 Diskrete Verteilungen
Es gibt Experimente, deren Ausgang bis auf Messungenauigkeiten vorhersehbar ist, etwa
das Fallen eines Balles, was durch bekannte physikalische Gesetze beschrieben werden
kann. Solche Experimente und Ereignisse heiÿen deterministisch. Es gibt aber auch Experimente, deren Ausgang ungewiss ist, etwa die Bundestagswahl 2013 oder die FussballEuropameisterschaft 2012. Obwohl man hier den exakten Ausgang nicht kennt, gibt es
aber doch gewisse Gesetzmäÿigkeiten, die zur ungefähren Vorhersage des Ausgangs dienen. Im Beispiel der Bundestagswahl kann man damit rechnen, dass CDU und CSU
wieder die stärkste Fraktion bilden und wahrscheinlich auf einen Stimmenanteil zwischen 30 und 40 Prozent kommen. Im Falle der Europameisterschaft weiÿ man, dass nur
eine der 16 qualizierten Nationen gewinnen kann, somit steht schon mal eine Menge
Ω
möglicher Ausgänge fest. Das trit auch auf die Ausgänge typischer Glücksspiele zu,
beim Roulette bleibt die Kugel auf einer der Zahlen von 0 bis 36 liegen, ein Würfel
fällt auf einer der Zahlen von 1 bis 6 und eine Münze musss sich für Wappen oder Zahl
entscheiden.
67
6 Einführung in die Wahrscheinlichkeitsrechnung
Denition 6.1. Bei einem Zufallsexperiment gibt es eine meist mit Ω bezeichnete Menge
möglicher Ergebnisse. Diese Menge wird
Ergebnismenge des Zufallsexperiments genannt.
Die Elemente dieser Menge sind die möglichen Ausgänge des Zufallsexperiments und
werden als
Ergebnis oder Ausfall bezeichnet. Die Teilmengen von Ω werden als Ereignisse
bezeichnet. Wenn der Ausgang des Zufallsexperiments in einer Teilmenge
man: Das Ereignis
A
liegt, sagt
A ist eingetreten. Ereignisse, die nur aus einem Element, also einem
Ergebnis bestehen, werden
Elementarereignis
genannt.
Ich werde zunächst nur endliche oder abzählbar unendliche Ergebnismengen betrachten. Solche Mengen können durchgezählt werden, d.h.
Ω = { ω1 , ω2 , . . . , ωn , . . . } = { ωi : i ∈ I }.
i werden zu einer Indexmenge I zusammengefasst,
I = { 1, 2, 3, . . . , n } und bei unendlichen Mengen in der
Die Indizes genannten ganzen Zahlen
wobei bei endlichen Mengen
Regel
I=N
ist.
Die Ergebnisse beim Werfen eines Würfels sind die ganzen Zahlen von 1 bis 6, die
Ω = { 1, 2, 3, 4, 5, 6 } bilden. Möglich Ereignisse
A = { 1, 3, 5 } oder { 2, 4, 6 }. Das Ereignis A tritt also genau
zusammen die Ergebnismenge
sind etwa
die Teilmengen
dann ein,
wenn eine gerade Zahl gewürfelt wird. Für das Zufallsexperiment Werfen einer Münze
erhält man die Ergebnismenge
Ω = { Wappen, Zahl }.
Die meisten Zufallsexperimente können zumindest theoretisch beliebig oft wiederholt
ω1 , ω2 , . . . ,
ωn gibt. Bei N -maliger Wiederholung des Zufallsexperiments tritt jedes Ergebnis ωi mit
einer absoluten Häugkeit ni und einer relativen Häugkeit fi = ni /N ein. Für sehr groÿe
Werte von N werden sich in vielen Fällen die relativen Häugkeiten stabilisieren und
gegen einen Grenzwert pi konvergieren. Dieser Wert wird als die Wahrscheinlichkeit des
Eintreens des Ergebnisses ωi bezeichnet. Aus der Beschreibenden Statistik ist bekannt,
werden. Sei zunächst angenommen, dass es nur endlich viele Ergebnisse
dass die Summe der relativen Häugkeiten 1 ist, deshalb trit dies auch auf die Summe
der
n
Wahrscheinlichkeiten
pi
zu.
Diese anschaulichen Überlegungen werden nun in eine strenge mathematische Form
gebracht.
Denition 6.2.
Es sei
Ω = {ω1 , ω2 , . . . , ωn , . . .}
(6.1)
p : Ω → R heiÿt
diskrete Verteilung auf Ω, wenn
eine endliche oder abzählbar unendliche Ergebnismenge. Eine Funktion
diskrete Wahrscheinlichkeitsverteilung
oder nur kurz
folgende beide Bedingungen erfüllt sind:
p(ω1 ) + p(ω2 ) + · · · + p(ωn ) + · · · = 1
p(ωi ) ≥ 0.
Dabei wird die Zahl
gedeutet. Statt
p(ωi )
p(ωi )
(6.2)
(6.3)
als Wahrscheinlichkeit für das Eintreten des Ergebnisses
schreibt man meist nur
ωi
pi .
Eine diskreten Wahrscheinlichkeitsverteilung kann also durch eine Tabelle beschrieben
werden, in deren beiden Zeilen die Ergebnismenge
68
Ω
und die Verteilung
p
stehen:
6.3 Laplace-Experimente
Tabelle 6.1: Diskrete Wahrscheinlichkeitsverteilung
Ω ω1
ω2
...
ωn
p
p2
...
pn
p1
6.3 Laplace-Experimente
Bei manchen Zufallsexperimeneten lassen sich die exakten Wahrscheinlichkeiten angeben. Bei einem sehr gut gearbeiteten Würfel sollte jede der sechs Seiten mit gleicher
Wahrscheinlichkeit oben erscheinen, bei einer Münze sollten beide Seiten mit gleicher
Wahrscheinlichkeit fallen und aus einem gut durchgemischten Kartenstapel sollte jede
Karte mit derselben Wahrscheinlichkeit gezogen werden können. Zufallsexperimente dieser Art werden
n
Laplace-Experimente
genannt. Bei einem Laplace-Experiment gibt es nur
Ergebnisse, die alle mit derselben Wahrscheinlichkeit
1/n
auftreten. Zufallsgeräte wie
Münzen und Würfel, die Laplace-Experimente erzeugen, werden meist fair, ideal oder
Laplace genannt. Obwohl es fast unmöglich ist, Würfel oder Münzen mit perfekter
Symmetrie zu bauen, wird man in viel Modellen von einem Laplace-Experiment ausgehen. Beim Lotto mit 49 Zahlen scheint die Durchmischung so gut zu gelingen, dass
jede Zahl eine Wahrscheinlichkeit von
1/49
hat. Ein Casino muss im eigenen Interesse
Sorge dafür tragen, dass alle Zahlen von 0 bis 36 mit derselben Wahrscheinlichkeit
1/37
auftreten, da sonst Verluste drohen.
Halten wir das Gesagte in einer Denition fest.
Denition 6.3.
Ein Zufallsexperiment auf einer
endlichen
Menge
Ω = { ω1 , ω2 , . . . , ωn }
heiÿt eine Laplace-Experiment, wenn alle Wahrscheinlichkeiten
Solche Verteilungen werden
Gleichverteilungen
(6.4)
pi
den Wert
1/n
haben.
genannt.
Betrachten wir einige Laplace-Experimente und die zugehörigen Ergebnismengen.
Ω = {Wappen, Zahl } beschreibt das Werfen einer fairen MünVerteilung ist pi = 1/2, i = 1, 2.
1. Die Ergebnismenge
ze. Die zugehörige
2. Beim Werfen eines fairen Würfels, auch als Laplace-Würfel oder L-Würfel bezeichnet, erhält man die Ergebnismenge
ist
Ω = { 1, 2, 3, 4, 5, 6 }. Die zugehörige Verteilung
pi = 1/6, i = 1, . . . , 6.
3. Beim Roulette erhält man die Ergebnismenge
rige Verteilung ist
Ω = { 0, , 1, 2, . . . , 36 }.
Die zugehö-
pi = 1/37, i = 0, . . . , 36.
6.4 Allgemeine Zufalls-Experimente
Zufallsexperimente basieren oft auf Geräten, die so konstruiert sind, dass der Ausgang nicht vorhersehbar ist, eben zufällig, aber nicht beliebig. Beim Lotto wird eine
69
6 Einführung in die Wahrscheinlichkeitsrechnung
Trommel mit 49 Kugeln sehr lange und sehr raniert durchmischt, sodass jede Kugel dieselbe Wahrscheinlichkeit zu fallen hat. Ich werde in Anlehnung an Engel Geräte mit zufälligem Ausgang Zufallsgeräte nennen. Die bisher beschriebenen LaplaceZufallsexperimente sind das Ergebnis der Zufallsgeräte Münze, Würfel und Roulettekessel. In der Abbildung 6.1 sind Zufallsgeräte zu sehen, die nicht zu Gleichverteilungen
führen.
G
R
R
G
G
B
RG-Rad
ANANAS
RGB-Rad
KSW-Urne
ANS-Urne
1
2 3 3
3
3
B-Würfel
Abbildung 6.1: Zufallsgeräte
Links sehen Sie zwei Glücksräder. Ein Glücksrad ist ein Zufallsgerät, wenn der Zeiger
mit groÿer Geschwindigkeit angestoÿen wird und dann zufällig in einer beliebigen Winkelposition zur Ruhe kommt. Die Wahrscheinlichkeit, dass der Zeiger dann in einem der
Sektoren steht, ist proportional zum Winkel des Sektors. Das berühmteste Glücksrad ist
der Roulettekessel mit 37 gleich groÿen Sektoren. Bei Urnen erfolgt die zufällige Auswahl durch einem blinden, des Lesens unkundigen Aen, dem zur Sicherheit die Augen
verbunden werden. Ganz rechts ist die Abwicklung eines Würfels zu sehen, bei dem nur
die Zahlen von 1 bis 3 vorkommen. Die Grundmengen und die zugehörigen Verteilunge
sind dann wie folgt.
1. Beim linken Glücksrad sei der kleinere Sektor rot (R), der gröÿere grün (G). Damit
erhält man die Ergebnismenge
1/4
und
pG = 3/4,
Ω = {R, G }
mit den Wahrscheinlichkeiten
pR =
da der grüne Sektor dreimal so groÿ wie der rote ist. Dieses
Zufallsgerät werde ich RG-Rad nennen.
2. Beim rechten Glücksrad sei der kleinste Sektor rot (R), der nächst gröÿere grün
Ω = {R, G, B }
pB = 1/2, da der zweite
(G) und der gröÿte blau (B). Damit erhält man die Ergebnismenge
mit den Wahrscheinlichkeiten
pR = 1/6, pG = 1/3
und
Sektor doppelt so groÿ wie der erste ist und der dritte genauso groÿ wie die beiden
anderen zusammen. Dieses Zufallsgerät werde ich RGB-Rad nennen.
3. Die linke Urne enthält vier schwarze (S), acht weiÿe (W) und 10 karierte (K)
Ω = {S, W, K }. Die zugehörigen
= 4/11 und pK = 5/11. Dieses Zufalls-
Kugeln. Damit erhält man die Ergebnismenge
Wahrscheinlichkeiten sind
pS = 2/11, pW
gerät werde ich KSW-Urne nennen.
4. Die rechte Urne enthält drei A, zwei N und ein S. Damit erhält man die Ergebnismenge
pN = 1/3
70
Ω = {A, N, S }. Die zugehörigen Wahrscheinlichkeiten sind pA = 1/2,
pS = 1/6. Dieses Zufallsgerät werde ich ANS-Urne nennen.
und
6.5 Wahrscheinlichkeit von Ereignissen
5. Der Würfel enthält je eine Seite mit den Zahlen 1 und 2 und vier Seiten mit der
Ω = { 1, 2, 3 } mit der Wahrscheinp3 = 2/3. Dieses Zufallsgerät werde ich
Zahl 3. Damit erhält man die Ergebnismenge
lichkeitsverteilung
p1 = p2 = 1/6
sowie
B-Würfel nennen.
6.5 Wahrscheinlichkeit von Ereignissen
Bei Zufallsexperimenten sind nicht nur die Wahrscheinlichkeiten der Ergebnisse wichtig,
sondern auch die Wahrscheinlichkeit von Ereignissen
nismenge
Ω
A,
die als Teilmengen der Ergeb-
betrachtet werden. Beim Monopoly möchte man gern den Besuch teurer
Grundstücke vermeiden und ermittelt die Wahrscheinlichkeit für bestimmte den Ruin
bedeutende Augenzahlen wie etwa 6, 7 oder 9. Beim Roulette kann man auf die ungeraden Zahlen setzen mit der Ereignismenge
U = { 1, 3, . . . , 35 }.
Bei bekannter Verteilung
kann man jeder Teilmenge
A = { ωr , ωs , . . . , ωt }
(6.5)
auf naheliegende Weise eine Wahrscheinlichkeit zuweisen, die man mit einem groÿen
P
abkürzt
P (A) = pr + ps + . . . + pt .
(6.6)
Diese Festsetzung lässt sich problemlos auf unendliche Teilmengen von
wenn
Ω
Ω
erweitern,
abzählbar ist.
Besonderes einfach ist die Bestimmung der Wahrscheinlichkeiten von Ereignissen bei
Laplace-Experimenten mit der Ergebnismenge
lichkeit eines Ereignisses
P (A) =
Für eine beliebige Menge
mente von
A
Ω.
Hier ergibt sich für die Wahrschein-
A:
A
Anzahl der Elemente von
Anzahl der Elemente von
wird mit
|A|
|A|
A
=
.
Ω
|Ω|
(6.7)
die Anzahl der Elemente bezeichnet. Die Ele-
werden günstige, die Elemente von
Ω
mögliche Fälle genannt. Daher sagt
man bei Laplace-Ereignissen, dass die Wahrscheinlichkeit eines Ereignisses das Verhältnis der für
A
günstigen zu den möglichen Fällen ist
P (A) =
Anzahl der für
A
günstigen Fälle
Anzahl der möglichen Fälle
.
(6.8)
Bei einem fairen Würfel beträgt die Wahrscheinlichkeit eine ungerade Zahl zu werfen
somit 3/6, denn es gibt 3 günstige und 6 mögliche Fälle. Setzt man im Roulette auf die
ungeraden Zahlen, sind 18 Ausfälle günstig und wegen der 0 sind 37 Fälle möglich, die
Wahrscheinlichkeit des Ereignisses ist somit 18/37.
∅ den Wert 0 zu, wird durch 6.6 eine Abbildung P :
P(Ω) → R hergestellt, wobei P(Ω) die Potenzmenge von Ω bezeichnet. Diese Abbildung
Weist man der leeren Menge
erfüllt die in der folgenden Denition geforderten Eigenschaften.
71
6 Einführung in die Wahrscheinlichkeitsrechnung
Denition 6.4.
P(Ω)
Ω
Es sei
eine abzählbare Ergebnismenge eines Zufallsexperiments und
die Potenzmenge von
scheinlichkeitsmaÿ
Ω.
P : P(Ω) → R ein WahrΩ, wenn sie folgenden Axiomen
Dann heiÿt eine Abbildung
oder kurz eine
Wahrscheinlichkeit
auf
genügt:
0 ≤ P (A).
1. Nichtnegativität:
2. Normiertheit:
3. Additivität:
(Ω, P )
Das Paar
P (Ω) = 1.
P (A ∪ B) = P (A) + P (B),
falls
A ∩ B = ∅.
wird ein abzählbarer Wahrscheinlichkeitsraum genannt.
Es lässt sich umgekehrt sehr leicht zeigen, dass zu jedem abzählbaren Wahrscheinlichkeitsraum
(Ω, P ) genau eine Verteilung p gehört, sodass die Wahrscheinlichkeit eines
A über die Gleichung 6.6 erfolgt. Damit sind für abzählbare Ergebnismen-
Ereignisses
gen die beiden Denitionen 6.2 und 6.4 gleichwertig. Da Verteilungen nur die beiden
einfachen Bedingungen (6.2) und (6.3) erfüllen müssen, ist es meist einfacher Verteilungen zu bestimmen.
6.6 Rechenregeln für Ereignisse
Halten wir noch einmal fest, dass jedes Ereignis durch eine Teilmenge
menge
Ω
A
der Ergebnis-
dargestellt wird. Man sagt, das Ereignis A ist eingetreten, wenn das Ergeb-
nis des Zufallsexperiments ein Element von
A
ist. Die zugeordnete Wahrscheinlichkeit
des Eintretens des Ereignisses ist durch den Wert
P (A)
des Wahrscheinlichkeitsmaÿes
bestimmt. Aus den Axiomen der Denition 6.4 lassen sich eine Reihe nützlicher Rechenregeln herleiten. Zunächst seien noch einige Aussagen und Bezeichnungen eingeführt.
(1) Die Menge
Ω
wird als sicheres Ereignis bezeichnet, weil es immer eintritt.
(2) Die leere Menge
∅
heiÿt das unmögliche Ereignis, das niemals eintritt.
(3) Ein Ereignis, das genau dann eintritt, wenn
komplementäre Ereignis
Ereignis
Ā
ergibt genau
(4) Das Ereignis
(5) Das Ereignis
A∩B
A ⊂ Ω
nicht eintritt, heiÿt das zu
Ā ⊂ Ω. Die Vereinigung von A und dem komplementären
Ω, daher wird Ā auch durch das Symbol Ω \ A dargestellt.
tritt genau dann ein, wenn sowohl
A∪B
A
tritt genau dann ein, wenn
A
A
als auch
oder
B
B
eintreten.
(oder beide zugleich)
eintreten.
A und B heiÿen unverträglich, wenn sie nicht beide zugleich eintreten
A ∩ B = ∅.
(6) Zwei Ereignisse
können, d.h.
(7) Die Dierenz
B
72
eintritt.
A\B
der Ereignisse
A und B
tritt genau dann ein, wenn
A aber nicht
6.6 Rechenregeln für Ereignisse
Aus der Denition 6.4 lassen sich eine Reihe von Folgerungen ableiten, die ohne Beweis
im folgenden Satz zusammengestellt werden.
Satz 6.1. Für die Funktion P (A) gelten folgende Gesetze:
1. Für das unmögliche Ereignis ∅ gilt: P (∅) = 0.
2. Für das zum Ereignis A komplementäre Ereignis Ā gilt: P (Ā) = 1 − P (A).
3. Für die Vereinigung zweier beliebiger Ereignisse A und B gilt:
P (A ∪ B) = P (A) + P (B) − P (A ∩ B)
P (A ∪ B) ≤ P (A) + P (B)
P (A ∪ B) = P (A) + P (B), wenn A ∩ B = ∅
4. Für die Dierenz zwischen den beliebigen Ereignissen B und A gilt:
P (B \ A) = P (B) − P (A ∩ B)
5. Für zwei Ereignisse A und B mit der Beziehung A ⊂ B gilt:
P (A) ≤ P (B),
P (B) = P (A) + P (B \ A).
Ich werde diese Regeln am bereits vertrauten Modell des Laplace-Würfels erläutern.
Beispiel 6.1.
Ein Laplace-Würfel werde einmal geworfen, das Ergebnis wird mit
X
bezeichnet. Wir betrachten folgende vier Ereignisse
A = { 1, 3, 5 }
a)
X
ist ungerade. Dies ergibt die Menge
b)
X
ist gerade. Dies ergibt die Menge
c)
X < 3.
Dies ergibt die Menge
C = { 1, 2 }
d)
X = 4.
Dies ergibt die Menge
D = {4}
Die Menge
B
ist komplementär zu
mit
B = Ā = { 2, 4, 6 }
mit
mit
P (A) = 1/2.
mit
P (B) = 1/2.
P (C) = 1/3.
P (A) = 1/6.
A, und es gilt 1 = P (A) + P (B). Der Durchschnitt
von A und C ist die Menge E = { 1 },
F = { 1, 2, 3, 5 }. Es gilt damit
die Vereinigung der beiden Mengen ist die Menge
P (F ) = P (A ∪ C) = 2/3 = 1/2 + 1/3 − 1/6 = P (A) + P (C) − P (A ∩ C).
Der Durchschnitt der Mengen
die Menge
G = { 1, 3, 4, 5 }.
A
und
D
ist leer, die Vereinigung beider Mengen ergibt
Es gilt damit
P (G) = P (A ∪ D) = 2/3 = 1/2 + 1/6 = P (A) + P (D).
Die Menge
{ 3, 5 }.
A\C
enthält alle Elemente von
A,
die nicht in
C
liegen, also ist
Der Durchschnitt beider Mengen besteht nur aus der Menge
{1}
A\C =
und damit ist
dann
P (A \ C) = 1/3 = P (A) − P (A ∩ C) = 1/2 − 1/6.
73
6 Einführung in die Wahrscheinlichkeitsrechnung
Das folgenden Beispiel stammt von Mayer:
Beispiel 6.2.
Ein Student muss zwei Klausuren in den Fächern A und B schreiben, die
er mit den Wahrscheinlichkeiten 0,7 und 0,8 besteht. Beide Klausuren besteht er mit
einer Wahrscheinlichkeit von 0,6. Wie hoch ist die Wahrscheinlichkeit wenigstens eine
Klausur zu bestehen?
Seien die zu den Ereignissen gehörenden Mengen ebenfalls
A und B
genannt, so gilt also
P (A ∪ B) = P (A) + P (B) − P (A ∩ B) = 0, 7 + 0, 8 − 0, 6 = 0, 9
Beispiel 6.3.
In einer Urne benden sich 100 Kugeln mit den Nummern 1 bis 100. Eine
Kugel werde zufällig gezogen, deren Nummer sei
keiten der folgenden vier Ereignisse: a)
c)
X
X
X.
enthält die Zier 9 und ist durch 6 teilbar. d)
die Zier 9. e)
X
Wie hoch sind die Wahrscheinlich-
ist durch 6 teilbar. b)
X
X
enthält die Zier 9.
ist durch 6 teilbar oder enthält
ist durch 6 teilbar, enthält aber nicht die Zier 9.
Hier ist für a) zunächst die Ereignismenge
Für b) wird die Menge
B
durch 6 zu bilden.
mit allen Zahlen zwischen 1 und 100, die die Zier 9 enthalten.
A ∪ B und
Menge A \ B .
für c) wird die Ereignismenge
abschlieÿend für e) die
A für die Teilbarkeit von X
für d) die Ereignismenge
A∩B
benötigt und
A = { 6, 12, 18, . . . , 90, 96 }
B = { 9, 19, 29, . . . , 90, 91, . . . , 99 }
A ∩ B = { 90, 96 }
Die Mengen
A
und
B
bestehen aus 16 bzw. 19 Zahlen, der gemeinsame Durchschnitt
aus zwei Zahlen. Somit gilt zunächst
P (A) = 16/100 = 0, 16
P (B) = 19/100 = 0, 19
P (A ∩ B) = 2/100 = 0, 02
Damit ergeben sich weiter
P (A ∪ B) = P (A) + P (B) − P (A ∩ B) = 0, 16 + 0, 19 − 0, 02 = 0, 33
P (A \ B) = P (A) − P (A ∩ B) = 0, 16 − 0, 02 = 0, 14
6.7 Abhängige mehrstuge Zufallsexperimente
Bisher wurden nur einstuge Zufallsexperimente betrachtet wie etwa das einmalige Werfen einer Münze. Eine Folge einstuger Zufallsexperimente wird als stochastischer Prozess oder ein mehrstuges Zufallsexperiment genannt, etwa das Ziehen der Lottozahlen.
Mehrstuge Zufallsexperimente werden oft durch Baumdiagramme dargestellt. Von einem Anfangsknoten verzweigen sich die Zweige zu den Ergebnissen des ersten Experiments, wobei deren Wahrscheinlichkeiten an die Kanten geschrieben werden. Von jedem
74
6.7 Abhängige mehrstuge Zufallsexperimente
Ergebnis der ersten Stufe gehen dann die der zweiten Stufe aus, wobei eine Baumstruktur
entsteht. Betrachten wir dazu ein Beispiel.
Beispiel 6.4.
In einer Urne benden sich die vier Buchstaben ANNE, d.h. der Buchsta-
be N kommt zweimal vor. Unser hilfreicher blinder Ae zieht mit verbundenen Augen
zwei Buchstaben ohne Zurücklegen, wobei die Reihenfolge beachtet wird. Welche Kombinationen ergeben sich mit welchen Wahrscheinlichkeiten?
Start
1/4
1/4
A
1/2
E
N
1/3
2/3
1/3
2/3
1/3
E
N
A
N
A
1/3
1/3
E
N
Abbildung 6.2: Baumdiagramm zum Beispiel 6.4
In der ersten Stufe werden die Buchstaben A und E mit der Wahrscheinlichkeit von 1/4
und ein N mit einer Wahrscheinlichkeit von 1/2 gezogen. Auf ein A folgt ein E mit einer
Wahrscheinlichkeit 1/3 und ein N mit einer Wahrscheinlichkeit von 2/3, also haben die
Ergebnisse AE und AN die Wahrscheinlichkeiten
1/4 · 1/3 bzw. 1/4 · 2/3. Auf ein E folgt
ein A mit einer Wahrscheinlichkeit 1/3 und ein N mit einer Wahrscheinlichkeit von 2/3,
also haben die Ergebisse AE und AN die Wahrscheinlichkeiten
1/4 · 1/3
bzw.
1/4 · 2/3.
Auf ein N folgen alle drei Buchstaben mit einer Wahrscheinlichkeit von 1/3, also haben
die Ergebnisse NA, NE und NN jeweils die Wahrscheinlichkeiten
1/2 · 1/3.
Das wird
viel übersichtlicher durch das abgebildete Baumdiagramm. Die folgende Tabelle zeigt
die Ergebnismenge
Ω
mit den zugehörigen Wahrscheinlichkeiten, also die Verteilung.
Tabelle 6.2: Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.4
Ω
AE
AN
EA
EN
NA
NE
NN
p
1/12
1/6
1/12
1/6
1/6
1/6
1/6
Das Ereignis, dass der zweite Buchstabe ein N ist, entspricht der Menge
A = { AN, EN, N N }
mit
P (A) = 3 · 1/6 = 1/2
Die Vorgehensweise bei mehrstugen Zufallsexperimenten ist also wie folgt.
1. Die Zweige jeder Stufe werden mit den Wahrscheinlichkeiten belegt und führen zu
den Knoten, welche die Ergebnisse dieser Stufe darstellen.
2. Die Wahrscheinlickeit eines Pfades ist gleich dem Produkt der Wahrscheinlichkeiten längs des Pfades. Dies wird als
Pfadregel
bezeichnet.
75
6 Einführung in die Wahrscheinlichkeitsrechnung
3. Zur Berechnung der Wahrscheinlichkeit eines bestimmten Ereignisses werden alle
Pfade bestimmt, die zu diesem Ereignis gehören und die einzelnen Wahrscheinlichkeiten werden entsprechend der Pfadregel berechnet und zusammengezählt.
Nun sollten Sie das folgende Beispiel von Engel selbst lösen können.
Beispiel 6.5.
In einer Urne benden sich die Buchstaben des Wortes ANANAS. Es
werden zwei Buchstaben zufällig ohne Zurücklegen gezogen. Bestimmen Sie die Ergebnismenge und die Verteilung. Mit welcher Wahrscheinlichkeit ist der zweite Buchstabe
kein A?
Zunächst wird das Baumdiagramm erstellt, siehe Abbildung 6.3.
Start
1/2
1/3
A
2/5
N
2/5
A
1/6
1/5
N
3/5
S
A
S
1/5
1/5
N
S
3/5
2/5
A
N
Abbildung 6.3: Baumdiagramm von Beispiel 6.5
Daraus ergeben sich die Ergebnismenge und die Verteilung
Tabelle 6.3: Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.5
Ω
AA
AN
AS
NA
NN
NS
SA
SN
p
1/5
1/5
1/10
1/5
1/15
1/15
1/10
1/15
Das Ereignis, dass der zweite Buchstabe kein A ist, entspricht der Menge
A = { AN, AS, N N, N S, SN } mit P (A) = 1/5 + 1/10 + 1/15 + 1/15 + 1/15 = 1/2
6.8 Unabhängige mehrstuge Zufallsexperimente
Die bisher betrachteten mehrstugen Zufallsexperimente hatten in jeder Stufe Ergebnismengen, die vom Ausgang der vorherigen Stufen abhängig waren. Beim Ziehen von
Buchstaben aus den Urnen fehlen die bereits gezogenen Buchstaben. Das wird anders,
wenn die gezogenen Buchstaben wieder in die Urne zurückgelegt werden. Es werden jetzt
mehrstugen Zufallsexperimente betrachtet, bei denen jede Stufe durch einen Wahrscheinlichkeitsraum
(Ωi , Pi )
beschrieben werden kann und wo sich die einzelnen Stufen
nicht gegenseitig beeinussen.
76
6.8 Unabhängige mehrstuge Zufallsexperimente
Beispiel 6.6. Beginnen wir mit der Urne, worin die Buchstaben ANNE liegen, abe diesmal wird der gezogene Buchstabe zurückgelegt. Welche Kombinationen ergeben sich bei
zweimaligem Ziehen mit welchen Wahrscheinlichkeiten? Mit welcher Wahrscheinlichkeit
ist der zweite Buchstabe ein N?
Start
1/4
1/4
1/2
A
1/4
E
1/4
A
1/2
E
1/4
N
N
1/4
A
1/2
E
1/4
N
1/4
A
1/2
E
N
Abbildung 6.4: Baumdiagramm zum Beispiel 6.4
Durch das Zurücklegen sind alle Verzweigungen der zweiten und der ersten Stufe gleich
In der ersten Stufe werden die Buchstaben A und E mit der Wahrscheinlichkeit von
1/4 und ein N mit einer Wahrscheinlichkeit von 1/2 gezogen, und dies bleibt auch so
in der zweiten Stufe. Die Wahrscheinlichkeit eines Paars wie AE ist das Produkt der
Einzelwahrscheinlichkeiten also
die Ergebnismenge
Ω
p(AE) = p(A)p(E) = 1/16.
Die folgende Tabelle zeigt
mit den zugehörigen Wahrscheinlichkeiten, also die Verteilung.
Tabelle 6.4: Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.6
Beispiel 6.7.
Ω
AA
AE
AN
EA
EE
EN
NA
NE
NN
p
1/16
1/16
1/8
1/16
1/16
1/8
1/8
1/8
1/4
Beide Zeiger der Glücksräder der Abbildung 6.1 auf Seite 70 werden un-
abhängig voneinander in Schwung gebracht. Der Zeiger des ersten Glücksrad kann im
roten oder im dreimal so groÿen grünen Sektor stehen bleiben, während der Zeiger des
zweiten Glücksrads sogar in drei Sektoren enden kann. Die erste Stufe des Zufallsex-
Ω1 = { r, g } mit den Wahrscheinlichkeiten 1/4 und 1/2 und die
Ω2 = { R, G, B } mit den Wahrscheinlichkeiten 1/6, 1/3 und 1/2. Die
periments wird durch
zweite Stufe durch
Wahrscheinlichkeit eines Paars wie rR ist auch hier das Produkt der Einzelwahrscheinlichkeiten also
Ω
p(rR) = p(r)p(R) = 1/24.
Die folgende Tabelle zeigt die Ergebnismenge
mit den zugehörigen Wahrscheinlichkeiten, also die Verteilung.
Tabelle 6.5: Diskrete Wahrscheinlichkeitsverteilung von Beispiel 6.7
Ω
rR
rG
rB
gR
gG
gB
p
1/24
1/12
1/8
1/8
1/4
3/8
Bei unabhängigen mehrstugen Zufallsexperimenten ist ein Baumdiagramm eigentlich
überüssig. Ich zeige es trotzdem:
77
6 Einführung in die Wahrscheinlichkeitsrechnung
Start
1/6
1/4
3/4
r
g
1/3
R
1/2
G
1/6
B
1/3
R
1/2
G
B
Abbildung 6.5: Baumdiagramm zum Beispiel 6.7
Die beiden Beispiele lassen sich leicht auf beliebige mehrstuge unabhängige Zufallsexperimente verallgemeinern. Ein aus
n unabhängigen Zufallsexperimenten bestehendes
Zufallsexperiment wird durch folgenden Wahrscheinlichkeitsraum beschrieben
Ω=
n
Y
Ωi = Ω1 × Ω2 × . . . × Ωn = {(ω1 , ω2 , . . . , ωn ) : ωi ∈ Ωi , 1 ≤ i ≤ n}.
(6.9)
i=1
Die Wahrscheinlichkeitsräume dieser Art nennt man
sie aus
n
(Ωi , Pi )
Wahrscheinlichkeitsräumen
Produktwahrscheinlichkeiträume , da
durch das kartesische Produkt entstehen.
Die Wahrscheinlichkeit eines Ergebnisses ist das Produkt der einzelnen Wahrscheinlichkeiten
p(ω1 , ω2 , . . . , ωn ) = p1 (ω1 )p2 (ω2 ) · · · pn (ωn ),
wobei die
pi
die Verteilungen auf
n
das kartesische Produkt Ω1 .
Wenn die
n
Stufen jewils
ni
Ωi
sind. Falls alle
Ωi
gleich
Ω1
sind, schreibt man für
Ausfälle haben, besteht der Produktwahrscheinlichkeits-
raum aus
N=
n
Y
ni
(6.10)
i=1
Ausfällen.
Beispiel 6.8.
Vier B-Würfel der Abbildung 6.1 auf Seite 6.1 werden gleichzeitig gewor-
n = 4 gleichen Stufen mit jeweils ni = 3
(i, j, k, l) zusammenfasst. Im Gegensatz zum
fen. Hier besteht das Zufallsexperiment aus
Ergebnissen, die man als Folge der Form
Beispiel 6.7 sind alle einzelnen Zufallsexperimente gleich. Die Ergebnismenge ist somit
Ω = Ω41 ,
und besteht aus
81 = 34
mit
Ω1 = { 1, 2, 3 }
Ergebnissen. Zur Berechnung der Wahrscheinlichkeit eines
Ergebnisses wird wieder die Pfadregel benutzt. Das Ergebnis
hat die Wahrscheinlichkeit von
(1, 2, 3, 3)
beispielsweise
1/6 · 1/6 · 2/3 · 2/3 = 1/81.
Ein besonders wichtiger Spezialfall der Produkträume entsteht im Zusammenhang mit
einem sogenannten
78
Bernoulli-Experiment . Darunter versteht man ein Zufallsexperiment,
6.9 Bedingte Wahrscheinlichkeit und stochastische Unabhängigkeit
das nur zwei Ergebnisse wie Wappen oder Zahl, Erfolg oder Misserfolg oder 1 und 0 hat.
Das erste Ergebnis soll mit einer Wahrscheinlichkeit von
Wahrscheinlichkeit von
p eintreten, das andere mit einer
1 − p.
Die n-fache unabhängige Durchführung eines Bernoullin
Experiments wird durch einen Produktraum der Form Ω1 , wobei Ω1 nur zwei Elemente
n
n
hat. Der Produktraum Ω1 hat 2 Elemente.
Beispiel 6.9.
Das Werfen von drei fairen Münzen ist ein Bernoulli-Experiment, dessen
Ergebnismenge
Ω = { W, Z }3 = { W W W, W W Z, W ZW, ZW W, W ZZ, ZW Z, ZZW, ZZZ }
aus acht gleichwahrscheinlichen Ergebnisfolgen besteht. Die Wahrscheinlichkeit genau
einmal Wappen zu werfen ist 3/8, denn das zugehörige Ereignis ist
A = { W ZZ, ZW Z, ZZW } .
Beispiel 6.10. Das sechsmalige Drehen des Glücksrads mit den Ausgängen rot und grün
ist ein Bernoulli-Experiment, dessen Ergebnismenge bereits
26 = 64
Elemente umfasst.
Beispiel 6.11. Das Werfen von zwei Würfeln ist dagegen kein Bernoulli-Experiment, da
in jeder Stufe sechs und damit mehr als zwei Ausfälle vorhanden sind. Die Ergebnismenge
Ω = { (1, 1), (1, 2), . . . , (1, 6), (2, 1), (2, 2), . . . , (2, 6), . . . , (6, 6) }
hat 36 Elemente. Jedes Paar tritt bei einem fairen Würfel mit der Wahrscheinlichkeit
1/36
auf. Beim Monopoly spielt das Ereignis einen Pasch zu werfen eine gewisse Rolle.
Ein Pasch wird durch die Menge
A = { (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) }
dargestellt, die zugehörige Wahrscheinlichkeit hat den Wert
P (A) = 1/6.
6.9 Bedingte Wahrscheinlichkeit und stochastische
Unabhängigkeit
A und B eines Zufallsexperiments zusammen,
von B verändert sich die Wahrscheinlichkeit des
In vielen Fällen hängen zwei Ereignisse
d.h. beim Eintreen des Ausgangs
A, d.h. sie ist jetzt gröÿer oder kleiner geworden. Es kann aber auch sein,
dass das Ereignis B keinen Einuss auf das Ereignis A hat. Wenn eine Mannschaft zur
Halbzeit in einem Fuÿballspiel deutlich führt (Ereignis B ) ist die Wahrscheinlichkeit eines
Sieges (Ereignis A) höher einzuschätzen als bei einem unentschiedenen Halbzeitstand.
Eintreens von
Bei der Ziehung der Lottozahlen steigt die Wahrscheinlichkeit eines hohen Gewinns,
wenn die ersten drei gezogenen Zahlen stimmen.
79
6 Einführung in die Wahrscheinlichkeitsrechnung
Denition 6.5. Die Wahrscheinlichkeit für das Ereignis A unter der Bedingung, dass das
Ereignis
B
B
bedingte Wahrscheinlichkeit
eingetreten ist, heiÿt
und man schreibt
P (A|B).
P (A|B) =
Die Ereignisse
A
und
B
von
A unter der Bedingung
Es gilt
heiÿen
P (A ∩ B)
.
P (B)
(6.11)
unabhängig, wenn die folgende Bedingung gilt
P (A ∩ B) = P (A)P (B)
Beispiel 6.12.
(6.12)
Skat wird mit einem Blatt aus 32 Karten gespielt, die in die vier Farben
Karo, Herz, Pik und Kreuz aufgeteilt sind. Von jeder Farbe gibt es jeweils die Bilder
genannten Karten Sieben, Acht, Neun, Zehn, Bube, Dame, König und Ass. Es werde
eine Karte gezogen.
A
A∩B
P (A) = 1/8
und
ist das Ereignis Herz Dame. Hier
beiden Ereignisse
A
B sei das Ereignis für
P (B) = 1/4 sowie P (A ∩ B) = 1/32, denn
gilt also P (A ∩ B) = P (A)P (B), also sind die
sei das Ereignis für das Bild Dame und
die Farbe Herz. Somit sind
und
B
unabhängig.
Man sieht sofort, dass die Ereignisse
A
und
B
genau dann unabhängig sind, wenn die
Bedingung
P (A|B) = P (A).
erfüllt ist. Die Gleichung 6.11 wird oft nach
(6.13)
P (A ∩ B)
aufgelöst
P (A ∩ B) = P (B)P (A|B),
P (A ∩ B) = P (A)P (B|A)
(6.14)
(6.15)
Die erste Gleichungen wird immer dann verwendet, wenn man
P (B) und P (A|B) kennt
oder gut schätzen kann. Der Star des FC Bayern München Arjen Robben ist sehr oft
verletzt, er spielt in einer Saison mit der Wahrscheinlichkeit von 30 Prozent, dies ist
das Ereignis
B.
Wenn er eingesetzt werden kann, gewinnen die Bayern mit einer Wahr-
scheinlichkeit von 90 Prozent, dies ist die bedingte Wahrscheinlichkeit
das Ereignis
A
P (A|B),
wobei
ein Sieg der Bayern ist. Die Wahrscheinlichkeit, dass die Bayern sowohl
siegen als auch mit Robben spielen ist somit
P (A ∩ B) = P (B)P (A|B) = 0, 3 · 0, 9 = 0, 27.
Auch für das Ereignis Herz Dame kann die Beziehung (6.14) herangezogen werden.
Hier sind
B
das Ereignis für die Farbe Herz mit
P (B) = 1/4
A das Ereignis für
P (A|B) = 1/8, also
und
das Bild Dame. Da es in jeder Farbe genau eine Dame gibt, ist
P (A ∩ B) = P (B)P (A|B) = 1/4 · 1/8 = 1/32.
Beispiel 6.13. Ich wette darauf, dass die ersten zwei gezogenen Lottozahlen beide unter
30 sind.
Hier besteht die Ergebnismenge
Ω
aus den folgenden
49 · 48
Zahlenpaaren
Ω = { (i, j) : 1 ≤ i, j ≤ 49, i 6= j } = { (1, 2), (1, 3), . . . , (49, 48) }.
80
6.9 Bedingte Wahrscheinlichkeit und stochastische Unabhängigkeit
(2, 4) hat nach der Pfadregel die Wahrscheinlichkeit 1/49 ·
zuständige Ereignis A besteht aus den folgenden 29 · 28
Jedes einzelne Ergebnis, etwa
1/48.
Das für meine Wette
Zahlenpaaren
A = { (i, j) : 1 ≤ i, j ≤ 29, i 6= j } = { (1, 2), (1, 3), . . . , (29, 28) }.
Die Wahrscheinlichkeit
P (A)
lässt sich mit bedingten Wahrscheinlichkeiten bestim-
A1 und A2 die Ereignisse,
A = A1 ∩ A2 und deshalb
men. Seien
ist, so ist
dass die erste Zahl bzw. die zweite Zahl unter 30
P (A) = P (A1 ∩ A2 ) = P (A1 )P (A2 |A1 ) = 29/49 · 28/48.
Ich werde die bedingte Wahrscheinlichkeit und die stochastische Unabhängigkeit abschlieÿend am Beispiel des Laplace-Würfels erläutern.
Beispiel 6.14.
Ein Laplace-Würfel werde einmal geworfen, das Ergebnis wird mit
X
bezeichnet. Wir betrachten folgende vier Ereignisse
A = { 1, 3, 5 }
a)
X
b)
X ≤ 3.
Dies ergibt die Menge
B = { 1, 2, 3 }
mit
P (B) = 1/2.
c)
X > 3.
Dies ergibt die Menge
C = { 4, 5, 6 }
mit
P (C) = 1/2.
d)
X < 3.
Dies ergibt die Menge
D = { 1, 2 }
e)
X = 4.
Dies ergibt die Menge
E = {4}
ist ungerade. Dies ergibt die Menge
Hier ist
von
A
P (A|B) = 2/3, denn wenn B
mit
mit
mit
P (A) = 1/2.
P (D) = 1/3.
P (A) = 1/6.
erfüllt ist, sind die Werte 1 und 3 für das Eintreen
günstig. Das ergibt sich auch aus der Formel für die bedingte Wahrscheinlichkeit
P (A|B) =
P ({ 1, 3 })
P (A ∩ B)
=
= 2/3,
P (B)
P (B)
P (A|B) > P (A).
C erfüllt ist, ist 5
also gilt für die bedingte Wahrscheinlichkeit
Dagegen ist
P (A|C) = 1/3,
denn wenn
für das Eintreen von
A
günstig. Das ergibt sich auch aus der Formel für die bedingte Wahrscheinlichkeit
P (A|C) =
P ({ 5 })
P (A ∩ C)
=
= 1/3,
P (C)
P (C)
P (A|C) < P (A).
A und D sind stochastisch unabhängig voneinander, denn wegen A ∩ D =
also gilt für die bedingte Wahrscheinlichkeit
Die Mengen
{1}
gilt
1/6 = P (A ∩ D) = P (A)P (D) = 1/2 · 1/3.
P (A|D) = P (A).
E keine gemeinsamen Elemente
gar nicht eintreten, wenn E gilt.
Somit ist
Da
A
A
kann
und
haben, ist
P (A|E) = 0,
d.h. das Ereignis
81
6 Einführung in die Wahrscheinlichkeitsrechnung
6.10 Der Satz von Bayes
Bei bestimmten Zufallsexperimenten wird die Ergebnismenge in
Bi , i = 1, . . . , n
n disjunkte Teilmengen
Ω und die
zerlegt, d.h. die Mengen ergeben vereint die Ergebnismenge
paarweisen Durchschnitte der Mengen sind leer. Dann bilden aber auch für jedes Ereignis
A⊂Ω
die Mengen
A ∩ Bi
eine Zerlegung von
A.
Deshalb gilt der folgende Satz:
Satz 1. Seien B1 , B2 ,. . . , Bn disjunkte Teilmengen, die vereint die Grundmenge Ω
ergeben. Dann gelten für jedes Ereignis A
P (A) =
P (A) =
n
X
k=1
n
X
P (A ∩ Bk ),
(6.16)
P (Bk )P (A|Bk )
(6.17)
k=1
Dies ist der sogenannte
Satz von der totalen Wahrscheinlichkeit
.
Die Gleichung (6.17) folgt aus (6.16) wegen
P (Bk )P (A|Bk ) = P (A ∩ Bk ).
Der Satz wird durch die Abbildung verdeutlicht.
B1 B2 B3
...
Bk
...
Ω
P(Bk)
Bn
P(B1)
B1
A
…
P(A|B1)
P(Bn)
Bk
P(A|Bk)
Ω
…
Bn
P(A|Bn)
A
Abbildung 6.6: Der Satz von der totalen Wahrscheinlichkeit
Nun wird die umgekehrte Frage gestellt: Wie hoch ist die Wahrscheinlichkeit für das
Ereignis
Bk , wenn man weiÿ, dass A eingetreten ist? Gefragt ist also nach der bedingten
P (Bk |A). Sei P (A) > 0, dann gilt
Wahrscheinlichkeit
P (Bk |A) = P (A ∩ Bk )/P (A) = P (Bk )P (A|Bk )/P (A),
woraus der berühmte Satz von Bayes folgt.
Satz 2. Seien B1 , B2 ,. . . , Bn disjunkte Teilmengen, die vereint die Grundmenge Ω
ergeben und A ein Ereignis mit P (A) > 0. Dann ist
P (Bk )P (A|Bk )
P (Bk |A) = Pn
i=1 P (Bi )P (A|Bi )
82
(6.18)
6.10 Der Satz von Bayes
Beispiel 6.15.
Betrachten wir eine Autofabrik, die ihre Gesamtproduktion eines be-
stimmten Autotyps auf drei Werke verteilt. Das erste Werk produziert 50, das zweite
Werk 30 und das dritte Werk 20 Prozent aller Autos. Im ersten Werk sind 1, im zweiten
Werk 5 und im dritten Werk sogar 10 Prozent aller dort hergestellten Autos nicht ohne
Mängel. Wie groÿ ist die Wahrscheinlichkeit, dass ein Käufer ein defektes Autos erhält
und mit welchen Wahrscheinlichkeiten stammen defekte Autos aus den drei Werken?
A
Hier ist
und
B3
das Ereignis, dass der Käufer ein defektes Auto erwischt und mit
B1 , B2
werden die Ereignisse bezeichnet, dass das Auto aus dem ersten, zweiten oder
dritten Werk stammt, die entsprechenden Wahrscheinlichkeiten betragen
P (B2 ) = 0, 3
P (B1 ) = 0, 5,
P (B3 ) = 0, 2. Die Wahrscheinlichkeit für ein defektes Auto aus dem
P (A|B1 ) = 0, 01, entsprechend sind P (A|B2 ) = 0, 05 und P (A|B3 ) = 0, 1
und
ersten Werk ist
zu deuten. Somit gilt nach dem Satz über die totale Wahrscheinlichkeit
P (A) = P (B1 )P (A|B1 ) + P (B2 )P (A|B2 ) + P (B3 )P (A|B3 )
P (A) = 0, 5 · 0, 01 + 0, 3 · 0, 05 + 0, 2 · 0, 1 = 0, 04.
Der Käufer erhält also mit einer Wahrscheinlichkeit von 4 Prozent ein defektes Auto.
Mit einer Wahrscheinlichkeit von
0, 5 · 0, 01 = 0, 005
werden defekte Autos im ersten
Werk hergestellt. Bezieht man diese Wahrscheinlichkeit auf die Wahrscheinlichkeit aller
defekten Autos, so ergibt sich der Anteil
P (B1 |A) = 0, 005/0, 04
des ersten Werks an
den defekten Autos. Genauso geht man für die restlichen Werke vor und erhält
P (B1 |A) = P (B1 )P (A|B1 )/P (A) = (0, 5 · 0, 01)/0, 04 = 0, 005/0, 04 = 0, 125
P (B2 |A) = P (B2 )P (A|B2 )/P (A) = (0, 3 · 0, 05)/0, 04 = 0, 015/0, 04 = 0, 375
P (B3 |A) = P (B3 )P (A|B3 )/P (A) = (0, 2 · 0, 1)/0, 04 = 0, 02/0, 04 = 0, 5
Die nötigen Rechnungen kann man in einer Arbeitstabelle organisieren.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A
B
C
D
E
FG H
I
i P(Bi) P(A|Bi) P(Bi)*P(A|Bi) P(Bi|A)
1 0,5
0,01
0,005 0,125
2 0,3
0,05
0,015 0,375
3 0,2
0,10
0,020 0,500
Σ
1
0,040
1
J
K
L MN
Start
0,5
B1
0,3
0,2
B2
0,01
0,05
B3
0,10
A
Abbildung 6.7: Arbeitstabelle zum Beispiel 6.15
i, in der Spalte B die WahrscheinlichP (Bi ) für die drei Werke und in der Spalte C die bedingten Wahrscheinlichkeiten
In der Spalte A stehen die laufende Nummern
keiten
83
6 Einführung in die Wahrscheinlichkeitsrechnung
P (A|Bi ).
In der Spalte D stehen die Produkte
P (Bi )P (A|Bi )
der Werte der Spalten B
und C und in die Zelle D7 kommt die Summe dieser Produkte, also nach dem Satz von
der totalen Wahrscheinlichkeit der Wert von
P (Bi |A)
P (A).
Die bedingten Wahrscheinlichkeiten
benden sich in der Spalte E, Formel in der Zelle E4 lautet
=E4/$D$7.
Diese Formel gilt dann entsprechend für die Zeilen 5 und 6.
Der Satz von Bayes liefert Wahrscheinlichkeiten für die Ursachen eines eingetroenen Ereignisses, wenn man weiÿ, mit welcher Wahrscheinlichkeit diese Ursachen zu dem
eingetroenen Ereignis führen. In der Politik wird die Regierung eine günstige wirtschaftliche Lage, also das eingetroene Ereignis, auf die eigenen Leistungen zurückführen, die
Opposition wird andere Ursachen ausmachen. Bei der Diagnose von Krankheiten gibt es
Tests für das Vorhandensein bestimmter Krankheiten. Leider sind solche Tests auch bei
gesunden Personen zuweilen positiv. Ich vertiefe das an einem Beispiel.
Beispiel 6.16.
Eine bestimmte Krankheit trete in einer Risikogruppe mit einer Wahr-
scheinlichkeit von 2 Prozent auf. Ein Test zeige dies mit einer Wahrscheinlichkeit von 95
Prozent an, schlage aber auch bei 10 Prozent aller Gesunden Alarm. Wie hoch ist die
Wahrscheinlichkeit einer Erkrankung, wenn der Test positiv ausfällt?
B2 die Ereignisse für das Vorhandensein bzw. Nichtvorhandensein
der Krankheit und A das Ereigniss eines positiven Tests. Hier sind P (B1 ) = 0, 02 und
P (B2 ) = 0, 98 sowie P (A|B1 ) = 0, 95 und P (A|B2 ) = 0, 1 und deshalb
Hier sind
B1
und
P (A) = P (B1 )P (A|B1 ) + P (B2 )P (A|B2 ) = 0, 02 · 0, 95 + 0, 98 · 0, 1 = 0, 117
0, 95 · 0, 02
= 0, 162393162,
P (B1 |A) =
0, 117
d.h. nur rund jeder sechste positiv getestete Person ist tatsächlich auch erkrankt. Das
liegt an der geringen Verbreitung der Krankheit und an der hohen Falschalarmwahrscheinlichkeit des Tests, was zusammen dafür sorgt, dass 83 Prozent aller positiv getesteten Pesonen gesund ist.
Für die Wahrscheinlichkeit dafür, dass der Test eine Erkrankung nicht anzeigt, muss
P (B1 |Ā)
berechnet werden, denn
Ā
ist das zu
A
komplementäre Ereignis. Somit gilt
P (Ā) = 1 − P (A) = 1 − 0, 117 = 0, 883
0, 02 · 0, 05
P (B1 )(1 − P (A|B1 ))
=
= 0, 001132503
P (B1 |Ā) =
0, 883
P (Ā)
Auch dafür lege ich eine Arbeitstabelle an, wobei auch die bedingten Wahrscheinlichkeiten der Ereignisse
Bi
unter der Voraussetzung des komplementären Ereignisses Ā
A komplemetäre Tabelle mit Ac bezeich-
bestimmt werden. In der Tabelle wird die zu
net. Die Formel in der Zelle F2 lautet
=B2*(1-C2)/(1-$D$4).
Diese Formel gilt dann entsprechend für die restlichen Zeilen.
84
6.11 Aufgaben
A
i
B
C
D
P(Bi) P(A|Bi) P(Bi)*P(A|Bi)
1
2
1 0,02
3
2 0,98
4 Summen
1
0,95
0,1
E
P(Bi|A)
F
c
P(Bi|A )
0,019 0,162393 0,001133
0,098 0,837607 0,998867
0,117
1
1
Abbildung 6.8: Arbeitstabelle für das Beispiel 6.16
Die Daten dieses Beispiels sind von mir erfunden und sollen niemand von Vorsorgeuntersuchungen abhalten. Ich möchte diesen Abschnitt mit einem Beispiel beenden, das
auf Uebe zurückgeht.
6.11 Aufgaben
Aufgabe 1. Ein Zauberer behauptet aus einem gut durchgemischten Spiel mit 32 Karten
als dritte Karte die Herz Dame zu ziehen. Wie hoch ist die Wahrscheinlichkeit dafür ohne
Tricks?
Aufgabe 2.
In einer Urne benden sich die vier Buchstaben ANANAS. Mit welchen
Wahrscheinlichkeiten entsteht der Name ANNA bei viermaligem Ziehen, und zwar einmal mit und einmal ohne Zurücklegen, wobei die Reihenfolge beachtet wird.
Aufgabe 3.
(vgl. Mayer) Eine Urne enthalte 3 weiÿe und 2 schwarze Kugeln. Aus der
Urne werden nacheinander 2 Kugeln herausgenommen, einmal ohne und das andere Mal
mit zurücklegen. Zeichnen Sie die jeweiligen Baumdiagramme und bestimmen Sie die zugehörigen Wahrscheinlichkeitsverteilungen. Wie groÿ ist jeweils die Wahrscheinlichkeit,
2 weiÿe Kugeln zu ziehen?
Aufgabe 4.
In einer Schale benden sich neun gleich aussehende Pralinen, wovon vier
nach Champagner und fünf nach Eierlikör (Igitt) schmecken. Ein Gast darf drei Pralinen zufällig aussuchen. Wie sieht die Ergebnismenge und die Verteilung aus? Zeichnen
Sie die jeweiligen Baumdiagramme und bestimmen Sie die Ergebnismenge
Ω
und die
Wahrscheinlichkeitsverteilung. Wie groÿ ist die Wahrscheinlickeit, drei Bohnen mit Eierlikörgeschmack zu erwischen?
Aufgabe 5.
Beim Spiel Mensch ärgere dich nicht darf man am Anfang dreimal hin-
tereinander würfeln, mit dem Ziel eine 6 zu werfen, da dann eine Figur ins Spielfeld
gesetzt wird. Beschreiben Sie das Zufallsexperiment durch einen Produktwahrscheinlichkeitsraum und dann das Ereignis
Wahrscheinlichkeit von
A
A,
dass keine 6 erzielt wurde. Berechnen Sie die
und geben Sie an, mit welcher Wahrscheinlichkeit wenigstens
eine 6 erreicht wird.
Aufgabe 6.
Ein Student muss Klausuren in den drei Fächern A, B, C schreiben. Er
schätzt die Wahrscheinlichkeiten für das Bestehen im Fach A mit 0,9, in B mit 0,8 und in
C mit 0,4. Die Inhalte der Fächer sind sehr verschieden, sodass das Bestehen unabhängig
85
6 Einführung in die Wahrscheinlichkeitsrechnung
voneinander ist. Man bestimme die Ergebnismenge
Ω und die Wahrscheinlichkeitsvertei-
lung. Danach gebe man an, wie hoch die Wahrscheinlichkeiten dafür sind, alle, höchstens
zwei und keine Klausur zu bestehen.
Aufgabe 7.
(vgl. Mayer) Für zwei unabhängige Ereignisse
P (A|B) = 2/3
Man berechne
und
A
und
B
gelte:
P (A ∩ B) = 1/6.
P (A), P (B), P (A ∪ B), P (B|A)
sowie
P (A\B)
und
P (B\A).
Aufgabe 8. Es seien A und B zwei Ereignisse mit P (A∩B) = 0, 6 und P (A∩ B̄) = 0, 2.
P (A)
Bestimmen Sie
Aufgabe 9.
und
P (Ā)
sowie
P (B|A)
und
P (B̄|A).
Ein Zufallsexperiment besteht darin, dass man mit einem Würfel solange
würfelt, bis zum ersten Mal eine Zahl zweimal auftritt, was spätestens beim siebten Wurf
passiert. Bestimmen Sie die Ergebnismenge
Aufgabe 10.
Ω
und die Wahrscheinlichkeitsverteilung.
Es seien drei Urnen mit je drei Kugeln betrachtet, wobei die erste Urne
drei, die zweite zwei und die dritte nur noch eine schwarze Kugel enthält, die anderen
Kugeln seien jeweils weiÿ. Das zweite Glücksrad der Abbildung 6.1 von Seite 70 werde
gedreht. Wenn der Zeiger des Glücksrads im roten Bereich zum Stehen kommt, wird eine
Kugel aus der ersten Urne gezogen, im grünen Sektor aus der zweiten und sonst aus der
dritten. Man bestimme die Ergebnismenge
Ω
und das Ereignis, dass die gezogene Kugel
schwarz ist. Danach berechne man die Wahrscheinlichkeiten dafür, dass eine gezogene
schwarze Kugel aus der ersten, zweiten oder dritten Urne stammt.
Aufgabe 11.
An einem texanischen Gericht arbeiten drei Richter B1, B2 und B3; die
Auswahl der Richter erfolgt zufällig, wobei B1 die Hälfte aller Prozesse übernimmt, auf
B2 fallen 30 % und auf B3 20 % aller Verfahren. Die Wahrscheinlichkeit eines Unschuldigen in einem Mordprozess auf einen Freispruch beim ersten Richter beträgt 90 %, beim
zweiten 50 % und beim dritten lediglich 40 %.
a) Wie groÿ ist die Wahrscheinlichkeit eines Freispruchs für einen Unschuldigen? Wie
groÿ ist die Wahrscheinlichkeit für eine Verurteilung?
b) Mit welchen Wahrscheinlichkeiten stammt der Freispruch eines Unschuldigen von B1,
B2 und B3?
c) Mit welchen Wahrscheinlichkeiten stammt eine Verurteilung eines Unschuldigen von
B1, B2 und B3?
Aufgabe 12.
In 10 Urnen benden sich schwarze und weiÿe Kugeln, und zwar in der
k-ten Urne genau
k, 1 ≤ k ≤ 10
schwarze Kugeln. Wie groÿ ist die Wahrscheinlichkeit
eine schwarze Kugel zu ziehen, wenn die Urne zufällig gewählt wird? Wie groÿ ist die
Wahrscheinlichkeit, dass eine gezogene schwarze Kugel der k-ten Urne entstammt?
86
7 Diskrete Zufallsvariable
7.1 Lernziele
Wenn Sie dieses Kapitel durchgearbeitet haben, sollten Sie
- wissen, was eine diskrete Zufallsvariable ist
- wissen, was man unter der Verteilung einer Zufallsvariable versteht
- wissen, was man unter der Wahrscheinlichkeitsfunktion und Verteilungsfunktion
versteht
- Erwartungswert, Varianz und Standardabweichung für diskrete Zufallsvariable berechnen können
- wisse, was unabhängige Zufallsvariablen sind
7.2 Einführung und Denition
Die Ergebnisse von Zufallsexperimenten sind oft aber nicht immer Zahlenbereiche, aber
fast immer ist das Ergebnis mit einer Zahl verknüpft, die man als Gewinn oder Verlust
deuten kann. Bei einem Fussballspiel sind die Ergebnisse Zahlenpaare wie 4:3 oder 0:0,
also keine Zahlen, aber ein Wettbüro setzt für jeden Ausgang eine Gewinnquote fest.
Aus der Sicht der Mathematik ergibt dies eine Funktion
X : Ω → R,
wobei
Ω
die
Ergebnismenge aller denkbaren Ausgänge des Spiels ist. Ähnlich verhält es sich beim
Roulette. Wenn ein Spieler auf eine bestimmte Zahl, etwa 13 einen Chip im Wert von
100 Euro setzt, so erhält er 3.600 Euro zurück, wenn die Kugel auf das Fach dieser
Zahl ausrollt, ansonsten streicht die Bank den Chip ein. Hier ist
Ω
der Bereich der
ganzen Zahlen zwischen 0 und 36, aber für den Spieler vereinfacht sich der Ausgang des
X : Ω → R mit
(
−100, wenn ω =
6 13;
X(ω) =
3.500, wenn ω = 13
Zufallsexperiments auf die Funktion
Denition 7.1.
(Ω, P ) ein abzählbarer Wahrscheinlichkeitsraum. Dann nennt
man eine beliebige Abbildung X : Ω → R eine Zufallsvariable , d.h eine Zufallsvariable
ordnet den Ergebnissen des Ω zugrundeliegenden Zufallsexperiments Zahlen zu.
Es sei
87
7 Diskrete Zufallsvariable
Die Bezeichnung Zufallsvariable ist ziemlich unsinnig, denn eine Zufallsvariable ist
eine genau festgelegte Funktion!
Es ist üblich Zufallsvariablen mit groÿen Buchstaben zu bezeichnen, aber für die Werte
der Funktion stehen kleine Buchstaben. Im Beispiel des Roulettespielers gibt es nur die
beiden Werte
x1 = −100
und
x2 = 3.500.
Da zunächst nur abzählbare Ergebnismengen
betrachtet werden, kann eine Zufallsvariable auch nur abzählbar viele Werte annehmen.
Es wird aber noch zusätzlich verlangt, dass der Wertebereich eine diskrete Teilmenge
der reellen Zahlen ist.
Denition 7.2.
Eine Teilmenge von
R
heiÿt diskret, wenn alle Abstände zwischen je
zwei Elementen der Menge gröÿer als eine feste Zahl
ε
sind.
Eine Menge ist genau dann diskret, wenn sie endlich ist oder abzählbar unendlich
ohne Häufungspunkte. Eine diskrete Zufallsvariable hat also einen endlichen oder oder
abzählbar unendlichen Wertebereich ohne Häufungspunkte.
Zunächst werde ich nur endliche Ergebnismengen
Ω = { ω1 , ω2 , . . . , ωN } betrachten.
x1 , x2 , xn , und es wird immer
Dann hat eine Zufallsvariable nur endlich viele Werte
angenommen, dass diese Werte aufsteigend geordnet sind. Meistens ist wie bei dem Roulettebeispiel
n
klein im Verhältnis zu
N.
Die Verallgemeinerung auf unendliche diskrete
Mengen ist nicht schwer, erfordert aber für eine Einführung unnötige mathematische
Symbolik wie Indexmengen.
7.3 Die Verteilung einer diskreten Zufallsvariablen
Von Interesse sind nicht nur die Werte der Zufallsvariablen, sondern auch die Wahrscheinlichkeiten, mit denen die Zufallsvariable diese Werte abnimmt. Für einen beliebiger Wert
xi
einer Zufallsvariablen, ergibt sich die Wahrscheinlichkeit des Auftretens von
xi
durch
die Wahrscheinlichkeit des Ereignisses
Ai = {ω : X(ω) = xi }.
Für diese Menge, mathematisch gesehen das Urbild von
xi , wird die drollige Bezeichnung
X = xi
verwendet. Entsprechend wird die Wahrscheinlichkeit des Eintretens von
xi )
xi
mit
P (X =
bezeichnet. Gemeint ist damit aber
P (Ai ) = P ({ω : X(ω) = xi }).
Im Falle des Roulettespielers gibt es nur die Werte
x1 = −100
und
x2 = 3.500.
Die
Wahrscheinlichkeiten des Auftretens sind
P (X = x1 ) = P (A1 ) = P ({ω : X(ω) = x1 }) = P ({ 0, 1, . . . , 12 } ∪ { 14, 15, . . . , 36 }).
P (X = x2 ) = P (A2 ) = P ({ω : X(ω) = x2 }) = P ({ 13 }).
88
7.4 Die Wahrscheinlichkeitsfunktion einer diskreten Zufallsvariablen
Ω in zwei disjunkte Teile, deshalb
summieren sich die Wahrscheinlichkeiten P (X = x1 ) = 36/37 und P (X = x2 ) = 1/37
gerade zu 1, also ergibt sich auf der Bildmenge X(Ω) = { x1 , x2 } eine Wahrscheinlichkeitsverteilung (f1 , f2 ). Das ist bei allen diskreten Zufallvariablen der Fall und führt zu
Die Urbilder
A1
und
A2
zerlegen die Ergebnismenge
folgender Denition.
Denition 7.3.
Es seien
x1 , x2 , . . . , xn , . . .
die Werte der Zufallsvariablen
X
und
f1 , f2 , . . . , fn , . . .
die zugehörigen Wahrscheinlichkeiten, d.h.
aller Zahlenpaare
(xi , fi ),
die
Verteilung
fi = P (X = xi ).
Dann heiÿt die Gesamtheit
der Zufallsvariablen
X.
Verteilungen können also durch eine Tabelle beschrieben werden, wobei in der ersten
Zeile die Werte und darunter die Wahrscheinlichkeiten ihres Auftretens stehen, deren
Summe immer 1 ergibt. Die Verteilung der Zufallsvariablen des Roulettebeispiels ist
somit
xi
-100
3.500
fi
36/37
1/37
7.4 Die Wahrscheinlichkeitsfunktion einer diskreten
Zufallsvariablen
Das folgenden Beispiel veranschaulicht zunächst noch mal den Begri der Verteilung.
Wir werden davon später auch noch grasche Veranschaulichungen zeigen. Kurz vor der
Sache mit dem Apfel schlägt Adam seiner Eva folgendes Spiel vor: In einer Urne benden
sich zehn Kugeln mit den Buchstaben EVASANANAS. Eva darf eine Kugel ziehen und
erhält für ein V 4 Euro und muss für ein A oder E einen Euro bezahlen. Zieht sie S
oder N geschieht gar nichts. Hier wird die Ereignismenge von den Buchstaben A, E, N,
S und V gebildet. Die Wahrscheinlichkeitsverteilung und die Werte der Zufallsvariablen
X
zeigt die folgende Tabelle:
ωi
pi
X(ωi )
fi
Die Zufallsvariable
Ereignisse
X = xi
A
E
N
S
V
0,4
0,1
0,2
0,2
0,1
-1
-1
0
0
4
0,4
0,1
0,5
X nimmt nur die Werte x1 = −1, x2 = 0 und x3 = 4 an. Die drei
i = 1, 2, 3 teilen Ω in die Mengen {A, E}, {N, S} und {V } mit
mit
89
7 Diskrete Zufallsvariable
den Wahrscheinlichkeiten
f1 = 0, 5, f2 = 0, 4
und
f3 = 0, 1.
Die Verteilung von
X
ist
demnach
xi
-1
0
4
fi
0,5
0,4
0,1
Man ordnet der Verteilung einer diskreten Zufallsvariablen eine Funktion zu, die an
den Stellen
xi
den Wert
fi
hat und sonst überall den Wert 0 hat. Ich halte dies in einer
Denition fest.
Denition 7.4.
Es seien die Paare
(xi , fi ) die Verteilung einer Zufallsvariable X . Dann
heiÿt die Funktion
(
fi ,
f (x) =
0,
die
Wahrscheinlichkeitsfunktion
für
x = xi , i = 1, 2, . . . , n, . . .;
sonst
der Zufallsvariablen
X.
Der Graph der Wahrscheinlichkeitsfunktion stimmt nur an den Punkten
(xi , fi )
mit der Abszisse überein. Die Punkte
(xi , fi )
nicht
werden durch kleine Kreise oder ähnliche
Symbole gekennzeichnet. Üblich sind auch senkrechte Stäbe von der Abszisse zu den
Punkten.
i
xi
fi
xifi
xi2fi
Fi
F(x)
f(x)
0,5
0,5
0,6
1
0
0
0,9
0,4
0,4
1,6
1
0,75
0,5
0,2
-0,1
2,1
1 -1
0,5 -0,5
2
0
0,4
3
4
0,1
x
0
0,25
-2 -1 0 1 2 3 4
E(X)= -0,1
x
0
-2 -1 0 1 2 3 4 5
Var(X)= 2,09
Abbildung 7.1: Diskrete Zufallsvariable
7.5 Verteilungsfunktion
Neben der Wahrscheinlichkeitsfunktion
Funktion
F (x),
f (x)
sehen Sie den Graph einer eng verwandten
die wie in der Beschreibenden Statistik durch Kumulierung der Wahr-
scheinlichkeiten entsteht. Damit ergibt sich folgende Denition.
Denition 7.5. Die Verteilungsfunktion F : R 7→ [0, 1] einer Zufallsvariablen X gibt für
jede reelle Zahl
den Wert
x
x
die Wahrscheinlichkeit dafür an, dass die Zufallsvariable
annimmt, d.h.
F (x) = P (X ≤ x).
90
X
höchstens
7.6 Erwartungswert und Varianz
Auch hier ist mit der Abkürzung
X≤x
das Ereignis
{ω : X(ω) ≤ x}
gemeint.
Die Verteilungsfunktion einer diskreten Zufallsvariablen ergibt sich aus der zugehörigen Wahrscheinlichkeitsfunktion durch Summation aller
F (x) = Fi =
X
fi
mit
xi ≤ x:
fi .
xi ≤x
Die Verteilungsfunktion einer diskreten Zufallsvariablen ist ein Treppenfunktion, die
xi und xi+1 den konstanten Wert Fi hat und bei
Fi+1 springt. Vor dem ersten Wert x1 hat F immer den Wert 0 und nach
dem letzten Wert xn hat F immer den Wert 1. In der Abbildung 7.1 stehen die Werte xi
in der zweiten Spalte, die fi folgen in der dritten und die kumulierten Werte Fi stehen
zwischen zwei benachbarten Werten
xi+1
zum Wert
ganz rechts.
Aus der Tabelle erhält man die Verteilungsfunktion der Zufallsvariablen

0,



0, 5,
F (x) =

0, 9,



1,
für
für
für
für
X
x < −1
−1 ≤ x < 0
0≤x<4
x≥4
Denition 7.6. Da die kumulierten Wahrscheinlichkeiten Fi sehr oft verwendet werden,
bezeichne ich die Gesamtheit aller Paare
(xi , Fi )
als kumulierte Verteilung der Zufalls-
variablen.
Es ist sinnvoll, die Verteilung und die kumulierte Verteilung in einer Tabelle wie in
der Abbildung 7.1 anzuordnen.
Jede Verteilungsfunktion
F (x)
hat folgende vier charakteristischen Eigenschaften:
(1)
F (x)
ist monoton steigend
(2)
F (x)
ist in jedem Punkt zumindest rechtsseitig stetig
(3)
limx→−∞ F (x) = 0
(4)
limx→∞ F (x) = 1
7.6 Erwartungswert und Varianz
Kehren wir zurück zum Spiel von Adam und Eva und der Frage, ob Eva sich auf dieses
Spiel einlassen soll. Zunächst muss klar sein, dass bei einer einzelnen Durchführung jeder Spieler Gewinnchancen hat. Statistisch steht im Vordergrund, wie sich der Gewinn
verteilt, wenn das Spiel mehrfach durchgeführt wird. Da die fünf Buchstaben die Wahrscheinlichkeiten
n
pA = 0, 4, pE = 0, 1, pN = 0, 2, pS = 0, 2 und pV = 0, 1 haben, wird nach
npA auftreten, der Buchstabe
Partien der Buchstabe A ungefähr mit der Häugkeit
91
7 Diskrete Zufallsvariable
E entsprechend ungefähr mit der Häugkeit
npE
usw. Evas Verlust wird somit ungefähr
gleich der folgenden Summe sein
Vn = n · pA · (−1) + n · pE · (−1) + n · pN · 0 + n · pS · 0 + n · pV · 4
Vn = n[(−1) · pA + (−1) · pE + 0 · pN + 0 · pS + 4 · pV ] = −n0, 1,
d.h. im Duchschnitt verliert Eva pro Spiel auf lange Sicht 10 Cent, also dem Wert
des terms innerhalb der eckigen Klammern, obwohl natürlich kein einziges Spiel diesen
Ausgang hat.
Der langfristige Duchschnitt wird als
Erwartungswert E(X) einer Zufallsvariablen X
bezeichnet. Er wird wird somit wie folgt deniert:
Denition 7.7.
Ω = { ω1 , ω2 , . . . , ωN } eine endliche Ergebnismenge mit dem Wahrscheinlichkeitsverteilung p und X : Ω 7→ R eine Zufallsvariable. Dann wird der folgende
Ausdruck Erwartungswert von X genannt und mit E(X) bezeichnet
Sei
E(X) =
N
X
X(ωi )pi .
(7.1)
i=1
Diese Formel lässt sich leicht auf unendliche diskrete Ergebnismengen verallgemeinern.
Der Erwartungswert entspricht dem arithmetischen Mittelwert aus der Beschreibenden
Statistik und verdichtet die Information über die Verteilung zu einem Zahlenwert. Häug
werden Entscheidungen allein über den Erwartungswert getroen. Auch über die langfristigen Chancen bei Glücksspielen spielt der Erwartungswert die entscheidende Rolle.
Es muss aber betont werden, dass der Erwartungswert nur dann sinnvoll zur Beurteilung
ist, wenn das Zufallsexperiment oft genug unter gleichen Bedingungen wiederholt wird.
Der Erwartungswert im paradiesischen Spiel ist somit
E(X) = (−1) · pA + (−1) · pE + 0 · pN + 0 · pS + 4 · pV = −0, 1.
Der Erwartungswert ist linear, d.h. es gilt für zwei Zufallsvariablen
Y : Ω 7→ R
sowie zwei beliebigen Zahlen
µ
und
X : Ω 7→ R
und
λ
E(µX + λY ) = µE(X) + λE(Y ).
(7.2)
Der Erwartungswert wird über die Gleichung (7.1) deniert, aber die Berechnung erfolgt schneller über die Verteilung der Zufallsvariablen. Für die diskrete Zufallsvariablen
X
mit der Verteilung
(xi , fi )i∈J
gilt für den
E(X) =
Erwartungswert
n
X
xi f i .
(7.3)
i=1
Der Erwartungswert ist bei diskreten Verteilungen die Summe der mit den Wahrscheinlichkeiten gewichteten Werte der Zufallsvariablen. In unserem Fall vereinfacht sich die
Rechnung unter Verwendung der Verteilung wie folgt
E(X) = x1 f1 + x2 f2 + x3 f3 = (−1) · 0, 5 + 0 · 0, 4 + 4 · 0, 1 = −0, 1.
92
7.6 Erwartungswert und Varianz
Wenn man also erste einmal die Verteilung bestimmt hat, wird der Erwartungswert über
(7.3) und nicht über (7.1) berechnet. In der vierten Spalte des abgebildeten Arbeitsblatts
nden Sie die Produkte
xi f i
und darunter deren Summe, also den Erwartungswert.
Der Erwartungswert beim Roulette mit einem Einsatz von 100 Euro auf die Zahl 13
ist der Erwartungswert
E(X) = −100 · 36/37 + 3500 · 1/37 = −2, 7027027.
Wer also 1.000 mal mit dieser Strategie setzt wird mit einem Verlust von 2,702,70 Euro
zu rechnen haben.
Wegen der Deutung des Erwartungswerts
E(X)
als dem durchschnittlichen Ausgang
eines Spiels, wird ein Spiel gerecht oder fair genannt, wenn der Erwartungswert 0 ist. Ist
E(X) > 0 heiÿt das Spiel günstig und ungünstig für E(X) < 0. Casinos bieten natürlich
nur ungünstige Spiele an. Die Varianz V ar(X) einer Zufallsvariablen X stellt ein Maÿ
für die Streuung der Verteilung. Wie in der Beschreibenden Statistik wird die Varianz
bei diskreten Verteilungen durch die Summe der mit den Wahrscheinlichkeiten gewichteten quadratischen Abweichungen der Werte der Zufallsvariablen vom Erwartungswert
deniert.
Denition 7.8.
Für eine diskrete Zufallsvariable
V ar(X) =
N
X
X : Ω 7→ R
wird die
Varianz
durch
(X(ωi ) − E(X))2 pi
(7.4)
i=1
festgelegt. Für die Varianz wird oft auch durch das Symbol
aus der Varianz heiÿt
σ2
verwendet. Die Wurzel
Standardabweichung ; bitte mit einem d in der Mitte schreiben.
Die Varianz ist somit der Erwartungswert der Zufallsvariablen
(X − E(X))2 .
Man
rechnet leicht folgende nützliche Formel nach
V ar(X) =
N
X
X(ωi )2 pi − E(X)2 = E(X 2 ) − E(X)2 .
(7.5)
i=1
Diese Formel ist zum Rechnen meist einfacher als die eigentliche Denition.
Wie der Erwartungswert kann auch die Varianz einer Zufallsvariablen durch die zugehörige Verteilung berechnet werden. Sei
lung
(xj , fj )j∈J ,
X
eine diskrete Zufallsvariable mit der Vertei-
so gilt für die Varianz
n
n
X
X
2
V ar(X) =
(xi − E(X)) fi =
x2i fi − E(X)2 .
i=1
(7.6)
i=1
93
7 Diskrete Zufallsvariable
E(X) = −0, 1
Die Varianz im paradiesischen Spiel ist somit wegen
V ar(X) = (−1 + 0, 1)2 · 0, 4 + (−1 + 0, 1)2 · 0, 1 + (0 + 0, 1)2 · 0, 2
+ (0 + 0, 1)2 · 0, 2 + (4 + 0, 1)2 · 0, 1 = 2, 09,
V ar(X) = (−1)2 · 0, 4 + (−1)2 · 0, 1 + (0)2 · 0, 2 + (0)2 · 0, 2
+ (4)2 · 0, 1 − (−0, 1)2 = 2, 09,
V ar(X) = (−1 + 0, 1)2 · 0, 5 + (0 + 0, 1)2 · 0, 4 + (−4 + 0, 1)2 · 0, 1 = 2, 09,
V ar(X) = (−1)2 · 0, 5 + (0)2 · 0, 4 + (−4)2 · 0, 1 − (−0, 1)2 = 2, 09.
Ich habe die Varianz mit alle vier möglichen Formel der berechnet, am einfachsten ist die
letzte Formel. In der fünften Spalte der Abbildung 7.1 auf Seite 90 stehen die Produkte
x2i fi . Deren Summe ist aber noch nicht die Varianz, es muss davon noch E(X)2 abgezogen
werden.
Nun kehren wir zu dem Spieler zurück, der beim Roulette 100 Euro auf die 13 setzt.
E(X) = −2, 7027027, die
(3.500, 1/37). Damit ergibt sich
Der Eerwartungswert ist
(−100, 36/37)
und
Verteilung besteht aus den Paaren
V ar(X) = (−100)2 · 36/37 + (3.500)2 · 1/37 − (−2, 7027027)2 = 340.803, 5062.
X eine Zufallsvariable ist und a
Z = X + a Zufallsvariable und es gilt:
Abschlieÿend noch zwei wichtige Rechengesetze. Wenn
eine beliebige Zahl, dann sind auch
Y = aX
und
V ar(aX) = a2 V ar(X),
V ar(X + a) = V ar(X),
Beispiel 7.1.
(7.7)
(7.8)
Es sei nun ein weiterer Spieler betrachtet, der ebenfalls mit 100 Euro
spielt, aber auf die roten Zahlen setzt. Die zugehörige Zufallsvariable sei mit
Y
bezeich-
net, die Verteilung steht in der folgenden Tabelle:
yi
-100
pi
19/37
100
18/37
Für den Erwartungswert und die Varianz der Zufallsvariablen
Y
ergibt sich:
E(Y ) = −100 · 19/37 + 100 · 18/37 = −2, 702702703,
V ar(Y ) = (−100)2 · 19/37 + (100)2 · 18/37 − (−2, 7027027)2 = 9992, 695398.
Die Erwartungswerte der zu den beiden Strategien gehörenden Zufallsvariablen sind
gleich, aber die Varianzen unterscheiden sich deutlich, deshalb ist die zweite Strategie
weniger risikoreich.
94
7.7 Bernoulli-Verteilung
7.7 Bernoulli-Verteilung
Die einfachsten Zufallsvariablen beschreiben ein sogenanntes Bernoulli-Experiment. Da-
A eingetreten ist oder nicht. Die
A wird mit p bezeichnet, das zu A komplementäre
Ereignis Ā hat deshalb die Wahrscheinlichkeit q = 1 − p. Wenn A eintritt, erhält die
Zufallsvariable B den Wert 1, sonst den Wert 0. Die Verteilung von B ist somit
bei wird nur unterschieden, ob ein bestimmtes Ereignis
Wahrscheinlichkeit des Eintretens von
Tabelle 7.1: Bernoulliverteilung
bi
0
1
fi
1−p
p
Denition 7.9. Jede dermaÿen verteilte Zufallsvariable heiÿt Bernoulli-verteilt mit dem
Parameter
p,
die Verteilung selbst wird
Bernoulli-Verteilung
Erwartungswert und Varianz einer mit dem Parameter
variablen
B
p
genannt.
Bernoulli-verteilten Zufalls-
berechnen sich wie folgt
E(B) = b1 f1 + b2 f2 = 0 · (1 − p) + 1 · p = p, ,
V ar(B) = b21 f1 + b22 f2 − p2 = 02 · (1 − p) + 12 · p − p2 = p(1 − p) = pq.
Beispiel 7.2.
(7.9)
(7.10)
Eine Mutter vespricht ihrer Tochter einen Euro, wenn die Augenzahl bei
einem Wurf mit einem fairen Würfel höher als 2 ist.
Das Ereignis
A
p = 2/3. Der ErwarV ar(B) = p(1 − p) = 2/9.
sind hier die ganzen Zahlen von 3 bis 6, somit ist
tungswert des Spiels ist
E(B) = 2/3
und die Varianz ist
7.8 Unabhängige Zufallsvariable
Zwei Zufallsvariable
X
keine Rückschlüsse auf
und
Y
Y
heiÿen unabhängig, wenn man durch Kenntnisse über
ziehen kann. Seien
(xi , fi )
und
(yj , gj )
der beiden Zufallsvariablen, so sind diese unabhängig voneinander, wenn
yj ) = P (X = xi ).
X
die Verteilungen von
P (X = xi |Y =
Daraus folgt die Bedingung für Unabhängigkeit
P (X = xi
und
Y = yj ) = P (X = xi )P (Y = yj ) = fi gj .
(7.11)
Diese Bedingung führt zu folgenden Satz.
Satz 3. Für zwei unabhängige Zufallsvariablen X und Y gelten
E(XY ) = E(X)E(Y ),
V ar(X + Y ) = V ar(X) + V ar(Y ),
(7.12)
(7.13)
95
7 Diskrete Zufallsvariable
Die Formel 7.12 folgt aus
E(XY ) =
n X
m
X
n
m
X
X
xi y j f i g j = (
xi fi )(
yj gj ) = E(X)E(Y ).
i=1 j=1
i=1
j=1
Damit leiten wir nun auch Formel 7.13 her
V ar(X + Y ) = E((X + Y )2 ) − (E(X) + E(Y ))2
= E(X 2 ) + E(Y 2 ) + 2E(X)E(Y ) − E(X)2 − 2E(X)E(Y ) + E(Y )2 ,
= E(X 2 ) − E(X)2 + E(Y 2 ) − E(Y )2 = V ar(X) + V ar(Y ).
Hier wurde ausgenutzt, dass für unabhängige Zufallsvariablen E(XY ) =
2
2
und die nützliche immer gültige Beziehung V ar(X) = E(X ) − E(X) .
E(X)E(Y ) gilt
Ohne Beweis gebe ich noch eine Verschärfung der Gleichung (7.13) an.
Satz 4. Es seien X1 , X2 , . . . Xn unabhängige Zufallsvariablen. Dann gilt
V ar(X1 + X2 + · · · + Xn ) = V ar(X1 ) + V ar(X − 2) + · · · + V ar(Xn ),
(7.14)
Unabhängige Zufallsvariablen treten fast ausschlieÿlich im Zusammenhang mit unabhängigen mehrstugen Zufallsprozessen wie etwa dem mehrfachen Werfen einer Münze
oder eines Würfels auf, wobei jeder Stufe eine Zufallsvariable zugeordnet werden kann.
Beispiel 7.3.
Weil die Tochter des Beispiels 7.2 besonders lieb war, darf sie ausnahms-
weise dreimal würfeln und erhält einen Euro für jeden Wurf, dessen Augenzahl höher
als zwei ausfällt. Die Zufallsvariable ihres Gewinns sei mit
E(X)
und
X
bezeichnet. Bestimmen Sie
V ar(X).
Hier wird das Bernoulli-Experiment des Beispiels 7.2 dreimal unabhängig wiederholt, in
jeder Stufe kann der Gewinn durch eine Bernoulli-verteilte Zufallsvariable
p = 2/3 beschrieben werden und es
E(X) = 3 · 2/3 = 2 und V ar(X) = 3 · 2/9 = 2/3
Parameter
gilt
X = B1 + B1 + B3 .
Bi
mit dem
Daher sind
7.9 Zusammenfassung
(1) Eine diskrete Zufallsvariable
X
raum in die reellen Zahlen, also
(2) Für jeden Wert
xi
von
ist eine Abbildung von einem Wahrscheinlichkeits-
X : Ω = { ω1 , ω2 , . . . , ωN } → R.
X gibt es eine mit X = xi bezeichnete Teilmenge
xi besteht, also aus allen ω ∈ Ω mit X(ω) = xi .
von
Ω,
die
aus allen Urbildern von
(3) Die Verteilung besteht aus allen Paaren
(xi , fi )
mit
fi = P (X = xi ).
(4) Erwartungswert und Varianz einer Zufallsvariablen ergeben sich durch
E(X) =
V ar(X) =
n
X
i=1
n
X
i=1
96
xi f i ,
(7.15)
x2i fi − E(X)2 .
(7.16)
7.9 Zusammenfassung
(5) Es seien
X 1 , X2 ,
. . . Xn
beliebig e Zufallsvariablen. Dann gilt
E(X1 + X2 + · · · + Xn ) = E(X1 ) + E(X2 ) + · · · + E(Xn ).
(7.17)
(6) Zwei Zufallsvariablen heiÿen unabhängig, wenn der Ausgang der einen keinen Einuss auf den Ausgang der anderen hat.
(7) Es seien
X 1 , X2 ,
. . . Xn
unabhängige
Zufallsvariablen. Dann gilt
V ar(X1 + X2 + · · · + Xn ) = V ar(X1 ) + V ar(X2 ) + · · · + V ar(Xn ),
Beispiel 7.4.
(7.18)
Zum Abschluss wird nochmal das Beispiel 7.3 betrachtet. Es werden die
Verteilung bestimmt und die Wahrscheinlichkeits- sowie die Verteilungsfunktion darge-
E(X) und V ar(X) erneut berechnet.
wird mit A bezeichnet, erfolglose Würfe mit Ā. Da ein Wurf
Augenzahl gröÿer als 2 ist, sind P (A) = 2/3 und P (Ā) = 1/3.
stellt und mit Hilfe der Verteilung
Jeder erfolgreiche Wurf
erfolgreich ist, wenn die
Damit gibt es folgende in der Tabelle aufgeführten 8 Ergebnisse beim dreimaligem Würfeln:
Nr.
ωi
xi
pi
fi .
1
ĀĀĀ
0
(1/3)3
(1/3)3
2
ĀĀA
ĀAĀ
AĀĀ
1
(1/3)2 · 2/3
(1/3)2 · 2/3
(1/3)2 · 2/3
3 · (1/3)2 · 2/3
ĀAA
AĀA
AAĀ
AAA
2
1/3 · (2/3)2
1/3 · (2/3)2
1/3 · (2/3)2
(2/3)3
3 · 1/3 · (2/3)2
(2/3)3
3
4
5
6
7
8
Die Höhe
X
1
1
2
2
3
des Gewinns ist eine Zufallsvariable, deren Verteilung in der folgen-
den Abbildung zu sehen ist. Die Werte der Verteilung stehen in der dritten Spalte
der Abbildung und wurden aus der letzen Spalte der Tabelle übernommen, z.B. ist
f2 = 3 · (1/3)2 · 2/3 = 2/9 = 0, 2̄. Dies ist die Wahrscheinlichkeit für X = x2 = 1.
i xi
fi
xifi
xi2fi
Fi
1 0 0,0370 0,0000 0,0000 0,0370
2 1 0,2222 0,2222 0,2222 0,2593
0,5 f(x)
0,4
0,75
3 2 0,4444 0,8889 1,7778 0,7037 0,3
4 3 0,2963 0,8889 2,6667 1,0000 0,2
0,5
0,1
0,25
E(X) = 2,0000 4,6667
0,0
Var(X)= 0,6667
F(x)
1
x
0
1
2
0
3
x
-1
0
1
2
3
Abbildung 7.2: Diskrete Zufallsvariable
97
7 Diskrete Zufallsvariable
7.10 Aufgaben
Aufgabe 1.
(Mayer) Zwei Spieler A und B spielen folgendes Spiel: Es wird mit zwei
fairen Würfeln gewürfelt. Unterscheiden sich die Augenzahlen höchstens um 1, so bekommt A von B 6 Euro ansonsten bekommt B von A 5 Euro. Welcher Spieler ist im
Vorteil?
Aufgabe 2.
(Engel) Chuck-a-luck wird in den USA nach folgenden Regeln gespielt:
Ein Spieler darf eine Zahl zwischen 1 und 6 wählen und bezahlt einen Einsatz. Danach
werden drei faire Würfel geworfen. Der Spieler bekommt für jeden Würfel, worauf seine
Zahl erscheint, seinen Einsatz zurück, also insgesamt das 0-, 1-, 2- oder 3-fache seines
Einsatzes. Man bestimme die Verteilung und die kumulierte Verteilung und stelle die
Wahrscheinlichkeits- sowie die Verteilungsfunktion dar. Danach berechne man mit Hilfe
der Verteilung
Aufgabe 3.
E(X)
Sei
X
und
V ar(X).
Ist das Spiel gerecht oder ungünstig für den Spieler?
die Augenzahl des Würfels, der an je einer Seite eine 1 und eine 2
hat und dessen restliche vier Seiten 3 zeigen. Dieses Zufallsgerät werde ich im folgenden
B-Würfel nennen. Man bestimme die Verteilung und die kumulierte Verteilung und stelle
die Wahrscheinlichkeits- sowie die Verteilungsfunktion dar. Danach berechne man mit
Hilfe der Verteilung
Aufgabe 4.
E(X)
und
V ar(X).
S die Summe der Augenzahlen.
E(S) und V ar(S). Man überprüfe
Zwei B-Würfel werden geworfen. Es sei
Man bestimme die Verteilung und berechne damit
die Berechnungen von
E(S)
und
V ar(S)
durch Verwendung der Ergebnisse der vorigen
Aufgabe.
Aufgabe 5.
E(T )
T das Produkt der Augenzahlen.
E(T ) und V ar(T ). Auch hier kann
Zwei B-Würfel werden geworfen. Es sei
Man bestimme die Verteilung und berechne damit
nochmal anders berechnet werden.
Aufgabe 6.
Beim Spiel Monopoly werden zwei faire Würfel gleichzeitig geworfen. Die
Zufallsvariable
S
sei die Summe der Augenzahlen. Man bestimme die Verteilung und die
kumulierte Verteilung und stelle die Wahrscheinlichkeits- sowie die Verteilungsfunktion
dar. Danach berechne man mit Hilfe der Verteilung
98
E(S)
und
V ar(S).
8 Ausgewählte Lösungen
8.1 Zu Kapitel 2
1.) An einem Kochkurs nahmen neun Männer und elf Frauen teil. Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher
Art ist das beschriebene Merkmal und welche möglichen Ausprägungen gibt es? Berechnen Sie die Häugkeitstabelle und stellen dann die Daten als Säulendiagramm
dar. Warum gibt es hier keine kumulierten Häugkeiten und somit auch keine Verteilungsfunktion?
Die statistischen Einheiten sind die Teilnehmer, die zusammen die statistische Gesamtheit bilden. Das Merkmal ist das Geschlecht des Teilnehmers, die möglichen
Ausprägungen sind männlich und weiblich. Dieses Merkmal ist nominal, daher
gibt es keine Anordnung und folglich auch weder kumulierte Häugkeiten noch die
Verteilungsfunktion. Die Häugkeitstabelle und das Säulendiagramm sind abgebildet.
A
1
2
3
4
5
6
7
8
9
B
C
D
Absolute
Relative
GeschlechtHäufigkeit Häufigkeit
Männlich
9
0,45
Weiblich
11
0,55
Summen
20
1
E
F
G
H
Säulendiagramm
0,6
0,4
0,2
0
Geschlecht
Männlich
Weiblich
0,45
0,55
Abbildung 8.1: Häugkeitstabelle und Säulendiagramm.
8.2 Zu Kapitel 3
1.) Im Sportunterricht kam eine Gruppe von Mädchen beim Kugelstoÿen auf folgende
Weiten
X
3,23
in [m]
2,35
5,37
3,49
6,90
2,93
1,81
4,26
4,44
2,73.
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen
Ausprägungen gibt es?
99
8 Ausgewählte Lösungen
Die statistischen Einheiten sind die Mädchen, die zusammen die Gesamtheit bilden. Das Merkmal sind die erzielten Weiten. Dieses Merkmal ist metrisch stetig.
b) Berechnen Sie das untere Quartil, den Median, das obere Quartil, das arithmetische Mittel, die Varianz und die Standardabweichung sowie die empirische
Varianz und die empirische Standardabweichung und dann noch den Variationskoezienten des Merkmals
X.
Die Lösung nden Sie im abgebildeten Arbeitsblatt.
A
B
C
D
E
F
1 i
xi
x(i)
x(i)2
Q1
2
1 3,23 1,81
3,2761
Q2
3
2 2,35 2,35
5,5225
Q3
4
3 5,37 2,73
7,4529
xquer
σ2
5
4 3,49 2,93
8,5849
6
5 6,90 3,23 10,4329
σ
s2
7
6 2,93 3,49 12,1801
8
7 1,81 4,26 18,1476
s
9
8 4,26 4,44 19,7136
v
10
9 4,44 5,37 28,8369
11 10 2,73 6,90 47,6100
12
37,51 161,7575
G
2,73
3,36
4,44
3,751
2,105749
1,451119912
2,339721111
1,529614694
0,386862147
H
3,751
2,105749
1,451119912
2,339721111
1,529614694
Abbildung 8.2: Maÿzahlen der Aufgabe
2.) In der Tabelle 8.1 sind die Noten der Teilnehmer eines Kurses aufgeführt. Welcher
Art ist das beschriebene Merkmal und welche möglichen Ausprägungen gibt es?
Berechnen Sie die Häugkeitstabelle und zeichnen dann die Stabverteilung sowie
die empirische Verteilungsfunktion. Geben Sie abschlieÿend den Modus, das untere
Quartil, den Median und das obere Quartil sowie das 95 % Quantil an. Warum ist
es hier nicht sinnvoll Mittelwert und Varianz zu berechnen?
Tabelle 8.1: Notenverteilung der Teilnehmer
Note
sehr gut
gut
befriedigend
ausreichend
mangelhaft
6
5
5
3
1
ni
Die statistischen Einheiten sind die Teilnehmer, die zusammen die statistische Gesamtheit bilden. Das untersuchte Merkmal ist die Note des Teilnehmers, die möglichen Ausprägungen sind sehr gut, gut usw. Das Merkmal ist ordinal, folglich
sollten Mittelwert und Varianz nicht berechnet werden, was aber gerade bei Noten
fast immer doch gemacht wird. Die Häugkeitstabelle und die beiden Diagramme
sind abgebildet. Ich habe die Noten wie in der Schule üblich durch die Zahlen 1 bis
5 codiert.
Modus: Für den Modus wird der Index
ist das der Index
100
i=1
mit
ni = 6 .
i
mit dem gröÿten Wert von
Die zugehörige Ausprägung
ai
ni
gesucht, hier
ist der Modus,
8.2 Zu Kapitel 3
1
2
3
4
5
6
7
8
9
10
A
i
1
2
3
4
5
B
ai
C D
ni Ni
1
2
3
4
5
6
5
5
3
1
Modus 1
Q1 1
Q2 2
Q3 3
E
fi
6
11
16
19
20
F
Fi
0,3
0,25
0,25
0,15
0,05
G
0,3
0,55
0,8
0,95
1
x0,95 4 und 5
H
I
0,35
1,2
0,3
1
0,25
J
0,8
0,2
0,6
0,15
0,1
0,4
0,05
0,2
0
0
0 1 2 3 4 5 6
0
1
2
3
4
5
6
Abbildung 8.3: Häugkeitstabelle, Diagramme und Maÿzahlen der Verteilung.
also
a1 = sehr
gut.
Unteres Quartil: Zum ersten Mal wird für den Index
ist
a1
i = 1 Fi > 0, 25 > Fi−1 ,
also
(sehr gut) das untere Quartil.
Median: Zum ersten Mal wird für den Index
i = 2 Fi > 0, 5 > Fi−1 ,
also ist
a2
(gut)
der Median.
Oberes Quartil: Zum ersten Mal wird für den Index
a3
i = 3 Fi > 0, 75 > Fi−1 ,
also ist
(befriedigend) das obere Quartil.
Das Quantil
x0,95
i = 4 die Gleichung Fi = 0, 95
a4 (ausreichend) als auch a5 (mangelhaft).
ist nicht eindeutig, da für den Index
gilt, somit ergeben sich sowohl die Werte
Eine Mittelung zwischen a4 und a5 ist hier nicht statthaft, da das betrachtete Merkmal
ordinal ist.
3.) Ein Gastwirt zählt die Anzahl
X
der Gäste an seinen Tischen und kommt auf fol-
gende Werte:
3
6
5
8
6
4
4
4
3
6.
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
Die statistischen Einheiten sind die Tische, die zusammen die Gesamtheit bilden.
Das Merkmal sind die Anzahl der Gäste am Tisch. Dieses Merkmal ist metrisch
diskret.
b) Berechnen Sie die Häugkeitstabelle und zeichnen Sie dann die Stabverteilung
für die relativen Häugkeiten sowie die empirische Verteilungsfunktion.
c) Berechnen Sie den Modus, das untere Quartil, den Median, das obere Quartil, die
Quantile
x0,2
sowie
x0,9 ,
das arithmetische Mittel, die Varianz und die Standard-
abweichung sowie die empirische Varianz und die empirische Standardabweichung
und dann noch den Variationskoezienten des Merkmals
X.
i mit dem gröÿten Wert von ni gesucht,
ni = 3. Die zugehörigen Ausprägungen a2 = 4
Modus: Für den Modus wird der Index
hier gilt für
i=2
und
i=4
mit
101
8 Ausgewählte Lösungen
A B C D E F G
1 xi x(i)
i ai ni Ni
2 3 3
1 3 2 2
2 4 3 5
3 6 3
3 5 1 6
4 5 4
5 8 4
4 6 3 9
6 6 4
5 8 1 10
7 4 5
8 4 6
9 4 6
10 3 6
2
11 6 8
0
H
fi
I
J
K
Fi
0,2
0,3
0,1
0,3
0,1
3
0
L
M
N
O
P
fi
0,2
0,5
0,6
0,9
1
0,2
0,1
ai
2 3 4 5 6 7 8
3 3
0 0,2
3
4
0,2 0,2
4
4
0 0,3
4 5
0,5 0,5
R
S
T
U V W
3
4
5
6
8
Fi
1
0,8
0,6
0,4
0,2
0
0,3
0
Q
ai
X
0,2
0,5
0,6
0,9
1
2 3 4 5 6 7 8
5 5
0 0,2
5 6
0,6 0,6
6 6
0 0,2
8
6
8
0,9 0,9
8
1
8
0 0,1
9
1
Abbildung 8.4: Häugkeitstabelle und Diagramme
und
a4 = 6
sind Modi.
Unteres Quartil: Zum ersten Mal wird für den Index
also ist
a2 = 4
i = 2 Fi > 0, 25 > Fi−1
,
das untere Quartil.
i = 3 Fi > 0, 5 aber Fi−1 = 0, 5,
somit ist der Mittelwert von a3 und a2 der Median, also Q2 = 4, 5.
Oberes Quartil: Zum ersten Mal wird für den Index i = 4 Fi > 0, 75 > Fi−1 , also
ist a4 = 6 das obere Quartil.
Wie beim Median begründet sind x0,2 = 3, 5 und x0,9 = 7.
Median: Zum ersten Mal wird für den Index
Für die restlichen Maÿzahlen gelten
x̄ = (3 · 2 + 4 · 3 + 5 · 1 + 6 · 3 + 8 · 1)/10 = 4, 9
σ 2 = (32 · 2 + 42 · 3 + 52 · 1 + 62 · 3 + 82 · 1)/10 − 4, 92 = 2, 29
s2 = (10/9) · σ 2 = 2, 54̄
√
σ = σ 2 = 1, 51327460
√
s = s2 = 1, 59513148
v = σ/x̄ = 0, 30883155
4.) Erstellen Sie den einfachen Boxplot zu den Daten des Beispiels 2.1 auf Seite 12.
Für einen einfachen Boxplot werden neben den drei Quartilen
der kleinste Q0 und der gröÿte Q4 Wert
Q1 = 6, Q2 = 7, Q3 = 8 und Q4 = 10, das
Q1 , Q2
der Daten benötigt. Hier sind
ergibt den folgenden Boxplot:
Einfacher Boxplot: Studiendauer in Semester
4
5
6
7
8
9
10
11
Abbildung 8.5: Boxplot zu den Daten des Beispiels 2.1
102
und
Q3 noch
Q0 = 5,
8.2 Zu Kapitel 3
5.) In der folgenden Urliste ist das Lebensalter
X
von Studenten eines Kurses aufgeführt.
19, 21, 26, 20, 22, 19, 20, 19, 23, 21, 52, 22, 19, 21, 20, 23, 22, 21, 21, 20, 20
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung?
b) Welcher Art ist das beschriebene Merkmal und welche möglichen Werte gibt es?
c) Berechnen Sie die Häugkeitstabelle und zeichnen Sie dann die Stabverteilung
für die relativen Häugkeiten sowie die empirische Verteilungsfunktion.
d) Berechnen Sie den Modus, das untere Quartil, den Median, das obere Quartil, die
Quantile
x0,4
sowie
x0,9 ,
das arithmetische Mittel, die Varianz und die Standard-
abweichung sowie die empirische Varianz und die empirische Standardabweichung
und dann noch den Variationskoezienten des Merkmals
X.
e) Der Wert 52 ist ein Zahlendreher und wäre korrekt 25. Wie ändern sich die
Ergebnisse von d) dadurch?
f ) Ein anderer Auswerter dieser Daten unterdrückt den Ausreiÿer von 52 ganz, geht
also nur noch von 20 statt 21 Werten aus. Wie ändern sich dadurch die Ergebnisse
von d)?
Bis auf die beiden letzten Fragen sind alle Antworten im folgenden Arbeitsblatt
versammelt.
i
ai ni Ni
1
2
3
4
5
6
7
19
20
21
22
23
26
52
4
5
5
3
2
1
1
4
9
14
17
19
20
21
fi
Fi
0,190476
0,238095
0,238095
0,142857
0,095238
0,047619
0,047619
0,190476
0,428571
0,666667
0,809524
0,904762
0,952381
1,000000
Modus 20 und 21 xquer
2
Q1
20 σ
21
22
19
23
Q2
Q3
x0,1
x0,9
22,4285714
46,4353741
6,8143506
48,7571429
6,98263151
0,30382455
σ
s2
s
v
1
0,8
0,6
0,4
0,2
0
0,2
0,1
0
10
20
30
40
50
10
20
30
40
50
Abbildung 8.6: Häugkeitstabelle, Diagramme und Maÿzahlen.
6.) In einem Projekt zur Betriebsinformatik wurden die Studierenden unter anderem
nach dem Alter ihres Vaters gefragt. Hier ist die geordnete Stichprobe:
103
8 Ausgewählte Lösungen
44 46 49 50 50 51 51 51 51 51 52 52 53 53 53 54 55 56 57 58 60
Man erstelle beide Varianten des Boxplots.
n = 21 bereits geordnete Daten. Somit
Q2 = x11 = 52, Q3 = x16 = 54 und Q4 = x21 = 60.
Es sind
sind
Q0 = 44, Q1 = x6 = 51,
Der einfache Boxplot sieht daher
wie folgt aus
Einfacher Boxplot: Alter von Vätern
42
44
46
48
50
52
54
56
58
60
62
Abbildung 8.7: Einfacher Boxplot
Der Interquartilsabstand ist
IQR = Q3 − Q1 = 54 − 51 = 3,
das 1,5-fache davon
Q1 − 4, 5 =
46, 5, also Z0 = 49. Der obere Zaun ist die gröÿte Beobachtung unterhalb von Q3 +
4, 5 = 58, 5, also Z4 = 58. Ausreiÿer nach unten sind alle Werte unterhalb von Z0 ,
also 46 und 44. Ausreiÿer nach oben sind alle Werte oberhalb von Z4 , also nur 60.
beträgt 4,5. Der untere Zaun ist die kleinste Beobachtung oberhalb von
Der zweite Boxplot sieht daher wie folgt aus
Variante des Boxplots: Alter von Vätern
42
44
46
48
50
52
54
56
58
60
62
Abbildung 8.8: Variante des Boxplots
8.3 Zu Kapitel 4
1.) (Wikipedia, 19.2.2009) Es liegen für 32 europäische Länder als Indikator für den
Wohlstand die Zahlen der PKWs pro 1000 Einwohner vor. Die Werte werden in
Klassen eingeteilt wie folgt. In 9 Ländern kommen z.B. auf je 1.000 Einwohner mehr
Tabelle 8.2: Brumm, Brumm
[0, 200]
(200, 300]
(300, 400]
(400, 500]
(500, 700]
5
6
6
9
6
als 400 und bis zu 500 PKW. Erstellen Sie die klassierte Häugkeitstabelle, das Histogramm sowie die approximierende Verteilungsfunktion. Berechnen Sie dann näherungsweise die Quartile
104
Q1 , Q2
und
Q3
sowie den Mittelwert und die Varianz.
8.3 Zu Kapitel 4
i xi-1* xi* ni Ni
1
2
3
4
5
0
200
300
400
500
200
300
400
500
700
5
6
6
9
6
5
11
17
26
32
fi
fi*
0,15625
0,1875
0,1875
0,28125
0,1875
Fi
0,00078125
0,001875
0,001875
0,0028125
0,0009375
Modus
0,003
450,00 xquer
2
250,00 σ
Q1
Q2
Q3
0,15625
0,34375
0,53125
0,8125
1
367,19
25876,46
160,86
26711,19
163,44
383,33 σ
2
477,78 s
s
1
0,8
0,002
0,6
0,4
0,001
0,2
0
-100
100
300
500
0
-100
700
100
300
500
700
Abbildung 8.9: Lösung zur Aufgabe
2.) Die Daten seien wieder die Körpergröÿen der Abbildung 4.1, aber die Klassengrenzen
seien 1,50, 1,70, 1,80, 1,90 und 2,10. Erstellen Sie die klassierte Häugkeitstabelle,
das Histogramm sowie die approximierende Verteilungsfunktion. Berechnen Sie dann
näherungsweise die Quartile
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
L
fi*
und
Q3
M
Fi
N
F G
i xi-1*
H
xi*
I J
n i Ni
1
2
3
4
1,70
1,80
1,90
2,10
4 4 0,2
1 0,2
7 11 0,35 3,5 0,55
6 17 0,3
3 0,85
3 20 0,15 0,75
1
1,50
1,70
1,80
1,90
K
fi
Q1 , Q2
4
3
2
1
0
sowie den Mittelwert und die Varianz.
O
Modus
Q1
Q2
Q3
P
Q
1,75 xquer
2
1,71429 σ
1,78571 σ
2
1,86667 s
s
R
1,7875
0,01546875
0,12437343
0,016282895
0,127604446
1
0,8
0,6
0,4
0,2
0
1,40
1,60
1,80
2,00
Größe in [m]
2,20
1,40
1,60
1,80
2,00
Größe in [m]
2,20
Q1
1,7+((0,25-0,2)*(1,8-1,7))/(0,55-0,2)
Q2
1,7+((0,5-0,2)*(1,8-1,7))/(0,55-0,2)
Q3
1,8+((0,75-0,55)*(1,9-1,8))/(0,85-0,55)
xquer 0,2*1,6+0,35*1,75+0,3*1,85+0,15*2
σ2
0,2*1,6^2+0,35*1,75^2+0,3*1,85^2+0,15*2^2-R1^2
Abbildung 8.10: Klassierte Häugkeitstabelle und Diagramme
105
8 Ausgewählte Lösungen
8.4 Zu Kapitel 5
1.) In der Kleinstadt des Beispiels 5.1 auf Seite 52 hat der erfolgreichste der fünf Bäcker
sein Geschäft auf seine zwei Söhne verteilt, die Jahresgewinne von 60 und 90 Tausend
Euro erwirtschaften. Die Jahresgewinne der anderen Bäckereien veränderten sich
nicht. Somit sind die Jahresgewinne der nun sechs Bäcker 60, 40, 60, 90, 20 und 90
in Tausend Euro.
a) Erstellen Sie die Häugkeitstabelle und berechnen Sie die beiden Gini-Koezienten
und zeichnen Sie die Lorenzkurve.
i
1
2
3
4
5
6
xi
x(i)
60 20
40 40
60 60
90 60
20 90
90 90
360 360
fi
0,1667
0,1667
0,1667
0,1667
0,1667
0,1667
1,0000
qi
Fi
0,0556
0,1111
0,1667
0,1667
0,2500
0,2500
1,0000
0,0
0,1667
0,3333
0,5000
0,6667
0,8333
1,0000
0,0000
Qi
0,000
0,0556
0,1667
0,3333
0,5000
0,7500
1,0000
0,0000
Gi
1,0
0,8
0,0093
0,0370
0,0833
0,1389
0,2083
0,2917
0,2315
0,6
0,4
0,2
0,0
0,0 0,2 0,4 0,6 0,8 1,0
Abbildung 8.11: Häugkeitstabelle und Lorenzkurve
Der normierte Gini-Koezient ist 6/5-mal gröÿer als der Gini-Koezient, hat
also den Wert 0,2778.
b) Zeichnen Sie die Konzentrationskurve und berechnen Sie den Rosenbluth- und
den Herndahl-Index.
xi
x(i)
60 90
40 90
90 60
60 60
20 40
90 20
360 360
ci
0,250
0,250
0,167
0,167
0,111
0,056
1,000
i
0
1
2
3
4
5
6
0
Ci
0,000
0,250
0,500
0,667
0,833
0,944
1,000
0,000
KR
ci2
0,250
0,500
0,500
0,667
0,556
0,333
0,217
0,063
0,063
0,028
0,028
0,012
0,003
0,196
1,0
0,8
0,6
0,4
0,2
0,0
0
1
2
3
4
5
6
Abbildung 8.12: Konzentrationskurve und Rosenbluth- sowie Herndahl-Index
c) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
Die statistischen Einheiten sind die Bäckereien, die insgesamt die statistische
106
8.4 Zu Kapitel 5
Gesamtheit der Untersuchung bilden. Das untersuchte Merkmal ist der Jahresgewinn, die möglichen Werte sind die reellen Zahlen. Das Merkmal ist stetig
metrisch.
2.) Auf Drängen der EU-Kommission wurde der Energiemarkt in Costa Asturia neu
geordnet, das bisher gröÿte Unternehmen wurde in drei Anbieter mit je 20 Prozent
Marktanteil aufgeteilt. Das bisher zweitgröÿte Unternehmen konnte seinen Marktanteil um fünf Prozent auf Kosten des kleinsten Unternehmens steigern, sodass die nun
sechs Anbieter Marktanteile von 25, dreimal 20, 10 und 5 Prozent haben. Zeichnen
Sie die Konzentrationskurve und berechnen sie den Rosenbluth- und den HerndahlIndex.
ci
i
Ci
KR
K_H
1,0
0 0,00
0,25 1 0,25 0,250 0,063
0,8
0,20 2 0,45 0,400 0,040
0,6
0,20 3 0,65 0,600 0,040
0,4
0,20 4 0,85 0,800 0,040
0,2
0,10 5 0,95 0,500 0,010
0,05 6 1,00 0,300 0,003
1,00 0 0,00 0,213 0,195
0,0
0
1
2
3
4
5
6
Abbildung 8.13: Konzentrationskurve und Rosenbluth- sowie Herndahl-Index
3.) (Anderson et al.). In der Tabelle 8.3 ist die Zahl der Personen in Privathaushalten
in der BRD 1970 aufgeführt.
Tabelle 8.3: Gröÿe von Haushalten, BRD 1970
Haushaltsgröÿe
Zahl der Haushalte in 1000
1
2
3
4
5527
5959
4314
3351
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
Die statistischen Einheiten sind die Haushalte, die insgesamt die statistische Gesamtheit der Untersuchung bilden. Das untersuchte Merkmal ist die Anzahl von
Personen, die in dem Haushalt wohnen, die möglichen Werte sind die natürlichen
Zahlen. Das Merkmal ist diskret metrisch.
b) Erstellen Sie die Häugkeitstabelle und berechnen Sie den Gini-Koezienten und
zeichnen Sie die Lorenzkurve.
107
8 Ausgewählte Lösungen
A
B
1 xi
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
C
ni
1
2
3
4
D
fi
5527
5959
4314
3351
19151
xi*ni
0,2886
0,3112
0,2253
0,1750
1
E
F
qi
5527
11918
12942
13404
43791
G
Fi
0,1262
0,2722
0,2955
0,3061
1
H
Qi
0
0,2886
0,5998
0,8250
1,0000
0
I
J
Gi
0
0,1262
0,3984
0,6939
1,0000
0
0,036
0,163
0,246
0,296
0,258
Verteilungsfunktion
Stabdiagramm
1,20
0,35
0,30
0,25
0,20
0,15
0,10
0,05
0,00
K
L
M
fi
1,00
0,80
0,60
1
0,40
0,8
Fi
1
1
0,0000 -0,5
0,2886
1
0,0000
0,0000
2
2
0,0000
0,3112
1
2
0,2886
0,2886
3
3
0,0000
0,2253
2
3
0,5998
0,5998
4
4
0,0000
0,1750
3
4
0,8250
0,8250
Lorenzkurve
4 100,00%
5,5 100,00%
0,6
0,20
0,4
0,00
0
1
2
3
4
Haushaltsgröße
0,2
0
1
2 3 4 5
Haushaltsgröße
0
0
0,2
0,4
0,6
0,8
1
Abbildung 8.14: Häugkeitstabelle und Diagramme.
Zu sehen sind auch noch das Stabdiagramm und die empirische Verteilungsfunktion.
4.) Diese Aufgabe stammt von von der Lippe, ich habe nur andere Zahlen verwendet:
200 Angehörige eines primitiven Volksstammes, sogenannte Urmenschen, gehen
auf die Jagd nach Federvieh. Ihre Beute beträgt 1.000 Wildgänse. Durch das an sich
nur bei primitiven Völkern bekannte Gerangel um Geld, Gut und Prestige entstand
trotz Eingreifens des Häuptlings eine etwas ungleiche Verteilung der Beute. Es bekamen 78 Jäger drei, 58 fünf, 41 sechs und 23 sogar zehn Gänse. Erstellen Sie die
Lorenzkurve und berechnen Sie die beiden Gini-Koezienten.
i
1
2
3
4
ai
3
5
6
10
ni
ni*ai
78 234
58 290
41 246
23 230
200 1000
fi
0,390
0,290
0,205
0,115
1
qi
Fi
Qi
Gi
0,234
0,290
0,246
0,230
1
0
0,390
0,680
0,885
1,000
0
0
0,234
0,524
0,770
1,000
0
0,091
0,220
0,265
0,204
0,220
1
0,8
0,6
0,4
0,2
0
0 0,2 0,4 0,6 0,8 1
Abbildung 8.15: Häugkeitstabelle und Lorenzkurve
Der normierte Gini-Koezient ist 200/199-mal gröÿer als der Gini-Koezient, hat
also den Wert 0,221.
5.) (Anderson et al.) In der folgenden Tabelle steht die Verteilung der Beschäftigten auf
Arbeitsstätten im Produzierenden Gewerbe in Westdeutschland im Jahr 1970.
108
8.4 Zu Kapitel 5
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
Die statistischen Einheiten sind die Arbeitsstätten, die insgesamt die statistische
Gesamtheit der Untersuchung bilden. Das untersuchte Merkmal ist die Anzahl
der Mitarbeiter, die möglichen Werte sind die natürlichen Zahlen. Das Merkmal
ist diskret metrisch.
b) Erstellen Sie die Häugkeitstabelle und berechnen Sie die beiden Gini-Koezienten
und zeichnen Sie die Lorenzkurve.
i
xi*
x(i)* ni
si
fi
1
1
4 3493
735
2
4
9 1231
800
3
9
19 636
854
4 19
49 442 1350
5 49
99 176 1226
6 99 199
98 1353
7 199 499
62 1884
8 499 ∞
32 4658
6170 12860
0,5661
0,1995
0,1031
0,0716
0,0285
0,0159
0,0100
0,0052
qi
Fi
Qi
Gi
0,0572
0,0622
0,0664
0,1050
0,0953
0,1052
0,1465
0,3622
0
0,5661
0,7656
0,8687
0,9404
0,9689
0,9848
0,9948
1,0000
0
0,0572
0,1194
0,1858
0,2907
0,3861
0,4913
0,6378
1,0000
0,0324
0,0352
0,0315
0,0341
0,0193
0,0139
0,0113
0,8222
1
0,8
0,6
0,4
0,2
0
0
0,2
0,4
0,6
0,8
1
Abbildung 8.16: Häugkeitstabelle und Lorenzkurve
Wegen der groÿen Zahl sind die Werte beider Gini-Koezienten fast gleich.
6.) (Uebe) In einem Betrieb wurden folgende Daten über die monatlichen Einkommen
(in 100
e)
der beschäftigten Frauen erhoben:
Tabelle 8.4: Fiktive Einkommen
Einkommen
Anzahl der Frauen
(6, 12]
(12, 16]
(16, 20]
(20, 24]
(24, 30]
10
15
10
5
4
a) Was ist die statistische Einheit und was ist die statistische Gesamtheit der Untersuchung? Welcher Art ist das beschriebene Merkmal und welche möglichen Werte
gibt es?
Die statistische Einheit ist eine Mitarbeiterin, die Gesamtheit sind alle Mitarbeiterinnen des Betriebs. Das Merkmal ist metrisch und stetig, die möglichen Werte
sind alle positiven Zahlen.
b) Stellen Sie die durch die Tabelle 8.4 gegebene Einkommensverteilung als Häugkeitstabelle und als Histogramm dar und erstellen Sie dann den Graphen der
approximierenden Verteilungsfunktion.
109
8 Ausgewählte Lösungen
1
2
A
B
UG
OG
3
4
5
6
7
8
6
12
16
20
24
9
10
11
x
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
6
6
12
12
12
16
16
16
20
20
20
24
24
24
30
30
C
12
16
20
24
30
VDF
0
0,038
0,038
0
0,085
0,085
0
0,057
0,057
0
0,028
0,028
0
0,015
0,015
0
D
E
F
G
H
∆i ni
fi
^fi
nimi
qi
6 10 0,2273 0,038 90 12,89%
4 15 0,3409 0,085 210 30,09%
4 10 0,2273 0,057 180 25,79%
4 5 0,1136 0,028 110 15,76%
6 4 0,0909 0,015 108 15,47%
44
698
1
VF
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
3,00
6,00
0,00
0,00
30,00
40,00
I
J
K
Fi
Qi
Gi
0,0000
0,2273
0,5682
0,7955
0,9091
1,0000
0,0000
0,1289
0,4298
0,6877
0,8453
1,0000
M
1,00
1,00
0,75
0,05
0,50
0,04
0,03
0,25
0,02
P
Lorenzkurve
E
i
n
k
o
m
m
e
n
0,07
0,06
O
0,00 0,00
1,00 1,00
1,00
0,08
N
0,0293
0,1905
0,2540
0,1742
0,1678
0,1843
Histogramm und
Verteilungsfunktion
0,09
L
1,00
0,80
0,60
0,40
0,20
0,01
0,00
0,00
0,00
3
6
9
12 15 18 21 24 27 30
0,00
0,20
0,40
0,60
0,80
1,00
Mitarbeiter
Einkommen in 100 €
Abbildung 8.17: Häugkeitstabelle, Histogramm und Verteilungsfunktion.
c) Erstellen Sie die Lorenzkurve und berechnen Sie die beiden Gini-Koezienten.
Der normierte gini-Koezient hat den Wert
0, 1886 = 44 · 0, 1843/43.
d) Berechnen Sie für die Einkommen der Frauen näherungsweise Modus, unteres
Quartil, Median, oberes Quartil, die Quantile
x0,1
sowie
x0,9 ,
Mittelwert sowie
Varianz und empirische Varianz und Standardabweichung und empirische Standardabweichung und den Variationskoezient.
Modus: 14
Quartile und Quantile:
Q1
Q2
Q3
x0,1
x0,9
= x0,25 ≈ 12 + (0, 25 − 0, 2273) · (16 − 12)/(0, 5682 − 0, 2273) = 12, 26635377
= x0,5 ≈ 12 + (0, 5 − 0, 2273) · (16 − 12)/(0, 5682 − 0, 2273) = 15, 19976533
= x0,25 ≈ 16 + (0, 75 − 0, 5682) · (20 − 16)/(0, 7955 − 0, 56823) = 19, 1997184
≈ 6 + (0, 1 − 0, 0) · (12 − 6)/(0, 2273 − 0) = 8, 639683238
≈ 20 + (0, 9 − 0, 7955) · (24 − 20)/(0, 9091 − 0, 7955) = 23, 67957746
Mittelwert, Varianz, empirische Varianz, Standardabweichung, empirische Stan-
110
8.5 Zu Kapitel 6
dardabweichung:
x̄ ≈ (10 · 9 + 15 · 14 + 10 · 18 + 5 · 22 + 4 · 27)/44 = 15, 86363636
σ 2 ≈ (10 · (9 − 15, 8636364)2 + 15 · (14 − 15, 8636364)2 + 10 · (18 − 15, 8636364)2
+ 5 · (22 − 15, 8636364)2 + 4 · (27 − 15, 8636364)2 )/44 = 28, 48140496s2 = (n/(n − 1)) · σ 2 = (44/
√
σ = σ 2 ≈ 5, 336797257
√
s = s2 ≈ 5, 398496385
7.) Man beweise die Beziehung (5.5) auf Seite 61.
Pn
KH =
2
i=1 xi
P
2
( ni=1 xi )
nσ 2 + nx̄2
1
=
=
2
2
n x̄
n
2
σ 2
vX
+1
+1 =
x̄
n
8.5 Zu Kapitel 6
Aufgabe 1.
Ein Zauberer behauptet aus einem gut durchgemischten Spiel mit 32 Kar-
ten als dritte Karte die Herz Dame zu ziehen. Wie hoch ist die Wahrscheinlichkeit dafür
ohne Tricks?
Zunächst muss also zweimal aus 32 bzw. 31 Karten nicht die Herz Dame gezogen werden,
und dann aus 30 Karten die Herz Dame gescht werden, was mit folgender Wahrscheinlichkeit geschieht
p = 31/32 · 30/31 · 1/30 = 1/32 = 0, 03125
Aufgabe 2.
In einer Urne benden sich die vier Buchstaben ANANAS. Mit welchen
Wahrscheinlichkeiten entsteht der Name ANNA bei viermaligem Ziehen, und zwar einmal mit und einmal ohne Zurücklegen, wobei die Reihenfolge beachtet wird.
pm = 1/2 · 1/3 · 1/3 · 1/6 = 0, 009259259
po = 1/2 · 2/5 · 1/4 · 2/3 = 0, 033333333
Aufgabe 3.
mit Zurücklegen,
ohne Zurücklegen,
(vgl. Mayer) Eine Urne enthalte 3 weiÿe und 2 schwarze Kugeln. Aus der
Urne werden nacheinander 2 Kugeln herausgenommen, einmal ohne und das andere Mal
mit zurücklegen. Zeichnen Sie die jeweiligen Baumdiagramme und bestimmen Sie die zugehörigen Wahrscheinlichkeitsverteilungen. Wie groÿ ist jeweils die Wahrscheinlichkeit,
2 weiÿe Kugeln zu ziehen?
Das Baumdiagramm ohne Zurücklegen ist links, das Baumdiagramm mit Zurücklegen
rechts zu sehen. Die Wahrscheinlichkeitsverteilungen sind in der folgenden Tabelle zu
sehen.
Ω
Mit Zurücklegen
p
Ohne Zurücklegen
p
SS
SW
WS
WW
0,1
0,3
0,3
0,3
0,16
0,24
0,24
0,36
111
8 Ausgewählte Lösungen
Start
Start
2/5
3/5
S
2/5
W
1/4
3/4
S
S
1/2
W
3/5
1/2
S
W
2/5
W
3/5
S
P(WW)=3/5 * 1/2= 3/10 = 0,3
2/5
W
3/5
S
W
P(WW)=3/5 * 3/5= 9/25 = 0,36
Abbildung 8.18: Baumdiagramme
Aufgabe 4.
In einer Schale benden sich neun gleich aussehende Pralinen, wovon vier
nach Champagner und fünf nach Eierlikör (Igitt) schmecken. Ein Gast darf drei Pralinen zufällig aussuchen. Wie sieht die Ergebnismenge und die Verteilung aus? Zeichnen
Sie die jeweiligen Baumdiagramme und bestimmen Sie die Ergebnismenge
Ω
und die
Wahrscheinlichkeitsverteilung. Wie groÿ ist die Wahrscheinlickeit, drei Bohnen mit Eierlikörgeschmack zu erwischen?
Die Ergebnismenge sind alle Folgen der Form
pagner und
E
XY Z ,
wobei
X
und
wie Eierlikör stehen. Somit hat die Ergebnismenge
Y
Ω
für
C
wie Cham-
acht Elemente. Die
zugehörigen Wahrscheinlichkeiten werden über das Baumdiagramm berechnet.
5/9
4/8
E
Start
4/9
4/8
E
5/8
C
C
3/8
E
C
3/7
4/7
4/7
3/7
4/7
3/7
5/7
2/7
E
C
E
C
E
C
E
C
Abbildung 8.19: Baumdiagramm und Verteilung
Die Wahrscheinlichkeitsverteilung ist in der folgenden Tabelle zu sehen.
Ω
CCC
CCE
CEC
CEE
ECC
ECE
EEC
EEE
p
0,0476
0,1190
0,1190
0,1587
0,1190
0,1587
0,1587
0,1190
Aufgabe 5.
Beim Spiel Mensch ärgere dich nicht darf man am Anfang dreimal hin-
tereinander würfeln, mit dem Ziel eine 6 zu werfen, da dann eine Figur ins Spielfeld
gesetzt wird. Beschreiben Sie das Zufallsexperiment durch einen Produktwahrscheinlichkeitsraum und dann das Ereignis
Wahrscheinlichkeit von
eine 6 erreicht wird.
112
A
A,
dass keine 6 erzielt wurde. Berechnen Sie die
und geben Sie an, mit welcher Wahrscheinlichkeit wenigstens
8.5 Zu Kapitel 6
Ω1 = { 1, 2, 3, 4, 5, 6 }
Jedes einzelne Zufallsexperiment wird durch die Grundmenge
be-
schrieben, die Ergebnismenge ist somit
Ω = Ω31 = { (k, l, m) : 1 ≤ k, l, m ≤ 6 } .
A
Das Ereignis
A
besteht aus allen Tripeln
(k, l, m)
mit Werten zwischen 1 und 5, d.h.
tritt ein, wenn man dreimal hintereinander keine 6 würfelt. In jeder Stufe besteht
P (A) = 5/6 · 5/6 ·
5/6 = 0, 5787 und folglich fällt mindestens eine 6 mit der Wahrscheinlichkeit des zu A
komplementären Ereignisses, also P (Ā) = 1 − 0, 578703704 = 0, 421296296.
dafür die Wahrscheinlichkeit von 5/6, nach der Pfadregel ist deshalb
Aufgabe 6.
Ein Student muss Klausuren in den drei Fächern A, B, C schreiben. Er
schätzt die Wahrscheinlichkeiten für das Bestehen im Fach A mit 0,9, in B mit 0,8 und in
C mit 0,4. Die Inhalte der Fächer sind sehr verschieden, sodass das Bestehen unabhängig
voneinander ist. Man bestimme die Ergebnismenge
Ω und die Wahrscheinlichkeitsvertei-
lung. Danach gebe man an, wie hoch die Wahrscheinlichkeiten dafür sind, alle, höchstens
zwei und keine Klausur zu bestehen.
Der Student kann jede der drei Klausuren bestehen oder nicht bestehen. Das Bestehen
A, das Durchfallen mit Ā gekennzeichnet. Es sind P (A) = 0, 9
P (Ā) = 0, 1. Genauso gelten P (B) = 0, 8 und somit P (B̄) = 0, 2 sowie
P (C) = 0, 4 und somit P (C̄) = 0, 5. Die Wahrscheinlichkeitsverteilungen sind in der
im Fach A wird durch
und somit
folgenden Tabelle zu sehen.
Ω
ABC
AB C̄
AB̄C
ĀBC
AB̄ C̄
ĀB C̄
ĀB̄C
ĀB̄ C̄
p
0,288
0,432
0,072
0,032
0,108
0,048
0,008
0,012
Die Wahrscheinlichkeit von
0, 9 · 0, 2 · 0, 4.
AB̄C
berechnet sich beispielsweise durch das Produkt
Alle Klausuren werden mit der Wahrscheinlichkeit
P (ABC) = P (A) · P (B) · P (C) = 0, 9 · 0, 8 · 0, 4 = 0, 288
bestanden. Höchstens zwei Klausuren werden somit mit der Wahrscheinlichkeit
0, 288 = 0, 712
1−
bestanden. Mit der Wahrscheinlichkeit
P (ĀB̄ C̄) = P (Ā) · P (B̄) · P (Ā) = 0, 1 · 0, 2 · 0, 6 = 0, 012
fällt der Student durch alle Klausuren.
Aufgabe 7.
(vgl. Mayer) Für zwei unabhängige Ereignisse
P (A|B) = 2/3
Man berechne
Da
A
und
B
und
und
B
gelte:
P (A ∩ B) = 1/6.
P (A), P (B), P (A ∪ B), P (B|A)
unabhängig sind, gilt
A
sowie
P (A\B)
P (A) = P (A|B) = 2/3.
und
P (B\A).
Aus
1/6 = P (A ∩ B) = P (A)P (B)
113
8 Ausgewählte Lösungen
P (A) = 2/3
folgt wegen
somit
P (B) = 1/6/2/3 = 1/4.
Weiter gelten
P (A ∪ B) = P (A) + P (B) − P (A ∩ B) = 2/3 + 1/4 − 1/6 = 3/4
P (B|A) = P (B) = 1/4
P (A\B) = P (A) − P (A ∩ B) = 2/3 − 1/6 = 1/2
P (B\A) = P (B) − P (A ∩ B) = 1/4 − 1/6 = 1/12
Aufgabe 8. Es seien A und B zwei Ereignisse mit P (A∩B) = 0, 6 und P (A∩ B̄) = 0, 2.
Bestimmen Sie
P (A)
und
P (Ā)
sowie
P (B|A)
und
P (B̄|A).
P (A) = P (A ∩ B) + P (A ∩ B̄) = 0, 6 + 0, 2 = 0, 8
P (Ā) = 1 − P (A) = 1 − 0, 8 = 0, 2
P (B|A) = P (A ∩ B)/P (A) = 0, 6/0, 8 = 0, 75
P (B̄|A) = P (A ∩ B̄)/P (A) = 0, 2 · 0, 8 = 0, 25.
Aufgabe 9.
Ein Zufallsexperiment besteht darin, dass man mit einem Würfel solange
würfelt, bis zum ersten Mal eine Zahl zweimal auftritt, was spätestens beim siebten Wurf
passiert. Bestimmen Sie die Ergebnismenge
Ω
und die Wahrscheinlichkeitsverteilung.
Beim zweiten Wurf ist Schluss, wenn die gewürfelte Zahl mit der Zahl des ersten Wurfs
übereinstimmt, wofür eine Wahrscheinlichkeit von 1/6 besteht. Mit einer Wahrscheinlichkeit von 5/6 muss man ein drittes Mal würfeln. Trit man eine der beiden bereits
gewürfelten Zahlen ist Schluss, also mit einer Wahrscheinlichkeit von
5/6 · 1/3 = 5/18.
Mit einer Wahrscheinlichkeit von 2/3 muss man ein viertes Mal würfeln. Trit man eine der drei bereits gewürfelten Zahlen ist Schluss, also mit einer Wahrscheinlichkeit von
5/6·2/3·1/2 = 5/18. Mit einer Wahrscheinlichkeit von 1/2 muss man ein fünftes Mal würfeln. Trit man eine der vier bereits gewürfelten Zahlen ist Schluss, also mit einer Wahr-
5/6 · 2/3 · 1/2 · 2/3 = 5/27. Trit man eine der fünf bereits gewürfelten
Zahlen ist Schluss, also mit einer Wahrscheinlichkeit von 5/6·2/3·1/2·1/3·5/6 = 25/324.
scheinlichkeit von
Endgültig Schluss ist beim siebten Versuch, den man aber nur mit einer Wahrscheinlichkeit von
5/6 · 2/3 · 1/2 · 1/3 · 1/6 = 5/324
erreicht. Die Wahrscheinlichkeitsverteilung ist
in der folgenden Tabelle zu sehen.
Ω
2
3
4
5
6
7
p
0,166667
0,277778
0,277778
0,185185
0,077160
0,015432
Aufgabe 10.
Es seien drei Urnen mit je drei Kugeln betrachtet, wobei die erste Urne
drei, die zweite zwei und die dritte nur noch eine schwarze Kugel enthält, die anderen
Kugeln seien jeweils weiÿ. Das zweite Glücksrad der Abbildung 6.1 von Seite 70 werde
gedreht. Wenn der Zeiger des Glücksrads im roten Bereich zum Stehen kommt, wird eine
Kugel aus der ersten Urne gezogen, im grünen Sektor aus der zweiten und sonst aus der
dritten. Man bestimme die Ergebnismenge
Ω
und das Ereignis, dass die gezogene Kugel
schwarz ist. Danach berechne man die Wahrscheinlichkeiten dafür, dass eine gezogene
schwarze Kugel aus der ersten, zweiten oder dritten Urne stammt.
114
8.5 Zu Kapitel 6
Die Ergebnismenge setzt sich aus dem Ergebnis des Glücksrads und dem anschlieÿenden
Ziehen einer Kugel aus der entsprechenden Urne zusammen. Das Zufallsexperiment hat
daher folgende Verteilung
Die Menge
A,
Ω
RS
GS
GW
BS
BW
p
1/6
2/9
1/9
1/6
1/3
die das Ereignis des Ziehens einer schwarzen Kugel beschreibt, ist
A = { RS, GS, BS }
P (A) = 1/6 + 2/9 + 1/6 = 5/9.
mit
Nun werde ich die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel über den
Satz der totalen Wahrscheinlichkeit berechnen und anschlieÿend die Wahrscheinlichkeit
dafür ermitteln, dass eine gezogene schwarze Kugel der zweiten Urne entstammt. Dafür
wird folgende Excel-Tabelle eingerichtet:
A
2
i
3
1
4
2
5
3
6 Summen
B
P(Bi)
0,16666667
0,33333333
0,5
1
C
P(A|Bi)
1
0,66666667
0,33333333
D
P(Bi)*P(A|Bi)
E
P(Bi|A)
0,16666667
0,22222222
0,16666667
0,55555556
0,3
0,4
0,3
1
Abbildung 8.20: Arbeitstabelle für die Aufgabe 10
Die Ereignisse
B1 , B2
und
B3
stehen für den Zeigerstand des Glücksrads, die zugehöri-
gen Wahrscheinlichkeiten benden sich in der Spalte B. In der Spalte C sehen Sie die
P (A|Bi ). In der Zelle D6 steht die Summe der Produkte
von P (A). Die Formel in der Zelle E3 lautet
bedingten Wahrscheinlichkeiten
P (Bi )P (A|Bi ),
also der Wert
=D3/$D$6.
Diese Formel gilt dann entsprechend für die restlichen Zeilen. Eine schwarze Kugel
stammt also mit den Wahrscheinlichkeiten 0,3, 0,4 und 0,3 aus der ersten, zweiten oder
dritten Urne.
Aufgabe 11.
An einem texanischen Gericht arbeiten drei Richter B1, B2 und B3; die
Auswahl der Richter erfolgt zufällig, wobei B1 die Hälfte aller Prozesse übernimmt, auf
B2 fallen 30 % und auf B3 20 % aller Verfahren. Die Wahrscheinlichkeit eines Unschuldigen in einem Mordprozess auf einen Freispruch beim ersten Richter beträgt 90 %, beim
zweiten 50 % und beim dritten lediglich 40 %.
a) Wie groÿ ist die Wahrscheinlichkeit eines Freispruchs für einen Unschuldigen? Wie
groÿ ist die Wahrscheinlichkeit für eine Verurteilung?
115
8 Ausgewählte Lösungen
b) Mit welchen Wahrscheinlichkeiten stammt der Freispruch eines Unschuldigen von B1,
B2 und B3?
c) Mit welchen Wahrscheinlichkeiten stammt eine Verurteilung eines Unschuldigen von
B1, B2 und B3?
Die Ergebnisse kann man dem abgebildeten Arbeitsblatt entnehmen. Aus I10 folgt, dass
ein Unschuldiger mit der Wahrscheinlichkeit von 0,68 frei gesprochen und folglich mit
der Wahrscheinlichkeit von 0,32 verurteilt wird. Ein Freispruch geht mit der Wahrscheinlichkeit von 0,66176 auf den ersten Richter zurück, der auch nur rund 16 Prozent aller
Fehlurteile zu verantworten hat. Genauso werden die Leistungen der beiden anderen
Richter gedeutet.
F
G
H
I
J
K
P(Bi|A)
P(Bi|Ac)
P(Bi) P(A|Bi) P(Bi)*P(A|Bi)
6
i
7
1 0,5
0,9
0,45 0,661764706 0,15625
8
2 0,3
0,5
0,15 0,220588235 0,46875
9
3 0,2
0,4
0,08 0,117647059
0,375
10 Summen
1
0,68
1
1
Abbildung 8.21: Arbeitstabelle für den Satz von Bayes
Aufgabe 12.
In 10 Urnen benden sich schwarze und weiÿe Kugeln, und zwar in der
k-ten Urne genau
k, 1 ≤ k ≤ 10
schwarze Kugeln. Wie groÿ ist die Wahrscheinlichkeit
eine schwarze Kugel zu ziehen, wenn die Urne zufällig gewählt wird? Wie groÿ ist die
Wahrscheinlichkeit, dass eine gezogene schwarze Kugel der k-ten Urne entstammt?
Seien
Bk
die Ereignisse, dass die k-te Urne gewählt wird, und
S
das Ereignis, dass
die gezogene Kugel schwarz ist. Da die Urnen mit gleicher Wahrscheinlichkeit gewählt
werden, sind
p(Bk ) = 1/10.
Hier sind zusätzlich
p(S|Bk ) = k/10,
also nach dem Satz
von der totalen Wahrscheinlichkeit
p(S) = 1/10
10
X
k/10 = 1/100
10
X
k = 10(10 + 1)/2 · 1/100 = 55/100.
k=1
k=1
Aus dem Satz von Bayes folgen
p(Bk |S) = p(S|Bk )/p(S) = k/55.
8.6 Zu Kapitel 7
Aufgabe 1.
(Mayer) Zwei Spieler A und B spielen folgendes Spiel: Es wird mit zwei
fairen Würfeln gewürfelt. Unterscheiden sich die Augenzahlen höchstens um 1, so bekommt A von B 6 Euro ansonsten bekommt B von A 5 Euro. Welcher Spieler ist im
116
8.6 Zu Kapitel 7
Vorteil?
Es gibt beim Werfen von zwei fairen Würfeln 36 Kombinationen. Für den Spieler A
(1, 1) bis (6, 6) und die 5 Pärchen
(1, 2), (2, 1) bis (5, 6), (6, 5). Die Verteilung des Ausgangs X aus der Sicht des Spielers A
ist somit (6, 16/36), (−5, 20/36). Der Erwartungswert ist
sind davon nur 16 günstig, nämlich alle 6 Paschs von
E(X) = 6 · 16/36 − 5 · 20/36 = 1/9 = 0, 111 . . .
Das Spiel ist also auf lange Sicht für Spieler B vorteilhaft.
Aufgabe 2.
(Engel) Chuck-a-luck wird in den USA nach folgenden Regeln gespielt:
Ein Spieler darf eine Zahl zwischen 1 und 6 wählen und bezahlt einen Einsatz. Danach
werden drei faire Würfel geworfen. Der Spieler bekommt für jeden Würfel, worauf seine
Zahl erscheint, seinen Einsatz zurück, also insgesamt das 0-, 1-, 2- oder 3-fache seines
Einsatzes. Man bestimme die Verteilung und die kumulierte Verteilung und stelle die
Wahrscheinlichkeits- sowie die Verteilungsfunktion dar. Danach berechne man mit Hilfe der Verteilung
E(X) und V ar(X). Ist das Spiel gerecht oder ungünstig für den Spieler?
Das Spiel ähnelt dem Mutter-Tochter-Spiel. Jeder Würfel, auf dem die gewählte Zahl
erscheint, wird mit
P (Ā) = 5/6.
A
bezeichnet, erfolglose Würfe mit
Ā.
Hier sind
P (A) = 1/6
und
Damit gibt es folgende in der Tabelle aufgeführten 8 Ergebnisse beim
dreimaligem Würfeln:
Nr.
ωi
xi
pi
fi .
1
ĀĀĀ
-1
(5/6)3
(5/6)3 = 125/216
2
ĀĀA
ĀAĀ
AĀĀ
1
(5/6)2 · 1/6
(5/6)2 · 1/6
(5/6)2 · 1/6
3 · (5/6)2 · 1/6 = 25/72
ĀAA
AĀA
AAĀ
AAA
2
5/6 · (1/6)2
5/6 · (1/6)2
5/6 · (1/6)2
(1/6)3
3 · 5/6 · (1/6)2 = 5/72
(1/6)3 = 1/216
3
4
5
6
7
8
1
1
2
2
3
Der Erwartungswert des Spiels aus der Sicht des Spielers ist somit
E(X) = −1 · 125/216 + 1 · 25/72 + 2 · 5/72 + 3 · 1/216 = −0, 0787
Das Spiel ist also wie zu erwarten ungünstig für den Spieler. Die Höhe
X
des Gewinns
ist eine Zufallsvariable, deren Verteilung in der folgenden Abbildung zu sehen ist. Die
Werte der Verteilung stehen in der dritten Spalte der Abbildung und wurden aus der
2
letzen Spalte der Tabelle übernommen, z.B. ist f2 = 3 · (5/6) · 1/6 = 25/72. Dies ist die
Wahrscheinlichkeit für
X = x2 = 1.
117
8 Ausgewählte Lösungen
i xi
fi
xi2fi
xifi
Fi
F(x)
f(x)
0,6
1
0,5
0,75
0,4
0,3 0,5
0,2
0,25
0,1
0
0,0
x
1 -1 0,5787 -0,5787 0,5787 0,5787
2 1 0,3472 0,3472 0,3472 0,9259
3 2 0,0694 0,1389 0,2778 0,9954
4 3 0,0046 0,0139 0,0417 1,0000
E(X) = -0,0787 1,2454
-2
Var(X)= 1,2392
-1
0
1
2
x
-2 -1 0
3
1
2
3
Abbildung 8.22: Verteilung von Chuck-a-luck
Aufgabe 3.
X
Sei
die Augenzahl des Würfels, der an je einer Seite eine 1 und eine 2
hat und dessen restliche vier Seiten 3 zeigen. Dieses Zufallsgerät werde ich im folgenden
B-Würfel nennen. Man bestimme die Verteilung und die kumulierte Verteilung und stelle
die Wahrscheinlichkeits- sowie die Verteilungsfunktion dar. Danach berechne man mit
Hilfe der Verteilung
i
xi
fi
E(X)
und
xi2fi
xifi
V ar(X).
Fi
1
1
1/6
1/6
1/6
1/6
2
2
1/6
1/3
2/3
8/9
3
3
2/3
2
6
1
2,5 6,8333
1
0,6
0,75
0,5
0,4
0,2
x
0,0
0
E(X)= 2,5
Aufgabe 4.
F(x)
f(x)
1
2
0,25
x
0
3
0
1
2
3
Var(X)= 0,5833
S die Summe der Augenzahlen.
E(S) und V ar(S). Man überprüfe
Zwei B-Würfel werden geworfen. Es sei
Man bestimme die Verteilung und berechne damit
die Berechnungen von
E(S)
und
V ar(S)
durch Verwendung der Ergebnisse der vorigen
Aufgabe.
Ω
pi
si
fi
si
fi
sifi
2
si fi
(1, 1)
1/36
2
1/36
(1, 2)
1/36
3
(2, 1)
1/36
3
1/18
(1, 3)
1/9
4
2
3
4
5
1/36 1/18 1/4
2/9
0,0556 0,1667 1,0000 1,1111
(2, 2)
1/36
4
(3, 1)
1/9
4
1/4
(2, 3)
1/9
5
(3, 2)
1/9
5
2/9
(3, 3)
4/9 1
6
4/9 1
6 Summe
4/9
2,6667
5,0000
E(X)= 5,0000
0,1111 0,5000 4,0000 5,5556 16,0000 26,1667
Var(X)= 1,1667
Die Zufallsvariable
S
ist die Summe der beiden Zufallsvariablen
X1
und
X2 ,
wel-
che die Augenzahl des jeweiligen Würfels beschreiben. In der vorigen Aufgabe wur-
118
8.6 Zu Kapitel 7
V ar(Xi ) = 0, 58333 . . . ermiitelt. Da beide Zufallsvariablen
unabhängig voneinander sind, gelten E(S) = E(X1 ) + E(X2 ) = 2 · 2, 5 = 5 und
V ar(S) = V ar(X1 ) + V ar(X2 ) = 1, 166 . . .
den
E(Xi ) = 2, 5
Aufgabe 5.
und
Man bestimme die Verteilung und berechne damit
E(T )
T das Produkt der Augenzahlen.
E(T ) und V ar(T ). Auch hier kann
Zwei B-Würfel werden geworfen. Es sei
nochmal anders berechnet werden.
Ω
pi
ti
gi
(1, 1)
1/36
1
1/36
(1, 3)
1/9
3
(3, 1)
1/9
3
2/9
si
fi
tifi
1
2
3
4
1/36 1/18 2/9
1/36
0,0278 0,1111 0,6667 0,1111
6
2/9
1,3333
2
0,0278 0,2222 2,0000 0,4444
8,0000 36,0000 46,6944 Var(X)= 7,6319
ti fi
Die Zufallsvariable
(1, 2)
1/36
2
T
(2, 1)
1/36
2
1/18
(2, 2)
1/36
4
1/36
(2, 3)
1/9
6
(3, 2)
1/9
6
2/9
9 Summe
4/9 1
4,0000 6,2500
(3, 3)
4/9 1
9
4/9 1
E(X)= 6,2500
ist das Produkt der beiden Zufallsvariablen
X1
und
X2 ,
wel-
che die Augenzahl des jeweiligen Würfels beschreiben. In der vorigen Aufgabe wurden
E(Xi ) = 2, 5 bestimmt, also gilt
E(T ) = E(X1 )E(X2 ) = 6, 25.
Aufgabe 6.
wegen der Unabhängigkeit der beiden Zufallsvariablen
Beim Spiel Monopoly werden zwei faire Würfel gleichzeitig geworfen. Die
Zufallsvariable
S
sei die Summe der Augenzahlen. Man bestimme die Verteilung und die
kumulierte Verteilung und stelle die Wahrscheinlichkeits- sowie die Verteilungsfunktion
dar. Danach berechne man mit Hilfe der Verteilung
E(S)
und
V ar(S).
Das Werfen von zwei fairen Würfeln ist ein Laplace-Experiment mit folgender Ergebnismenge
Ω = { (i, j) : 1 ≤ i ≤ 6, 1 ≤ j ≤ 6 }
Für das Auftreten eines Summenwerts müssen die zugehörigen Paare gefunden werden,
etwa für die Summe 4 die drei Paare
(1, 3), (2, 2)und (2, 2),
von denen jedes mit einer
Wahrscheinlichkeit von 1/36 auftritt, also hat der Gesamtwert 4 eine Wahrscheinlichkeit
von 3/36. Auf diese Weise ergibt sich folgende Verteilung
xi
2
3
4
5
6
7
8
9
10
11
12
fi
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
119
Index
arithmetisches Mittel, 27
relative, 43
Ausprägung, 12
Häugkeitsliste, 12
Ausreiÿer, 21
Häugkeitstabelle, 13
Balkendiagramm, 14
Bernoulli-Experiment, 78
Herndahl-Index, 60
Histogramm, 44
Bernoulli-Verteilung, 95
Interquartilsabstand, 25
Bestandsmasse, 4
Intervallskala, 7
Bewegungsmasse, 4
Boxplot, 25
Klassen, 42
Klassenbreite, 42
Datenmatrix, 8
Klassenmitte, 43
Dichtefunktion
Klassenmittelwert, 43
empirische, 44
Disparität, 51
empirische Verteilungsfunktion, 15
Ereignismasse, 4
Ereignisse, 68
Ergebnismenge, 68
Erwartungswert, 92
Fragebogen, 7
geschlossene Fragen, 8
oene Fragen, 8
Gini-Koezient, 54
normiert, 56
Gleichverteilung, 69
Grundgesamtheit, 2, 4
Gruppierte Daten, 13
Häugkeit
Konzentration
absolute, 51
relative, 51
Konzentrationskurve, 59
Konzentrationsrate, 59
Kreisdiagramm, 18
Lagemaÿe, 19
Laplace-Experimente, 69
Lorenzkurve, 54
Median, 20
Mehrfachfrage, 8
Merkmal, 4
dichotom, 5
kardinal, 5
kategoriell, 5
metrisch, 5
Nominal, 5
absolute, 12
Ordinal, 5
relative, 12
polytom, 5
Häugkeitsdichte
absolute, 43
qualitatativ, 6
quantitativ, 6
121
Index
Merkmalsausprägung, 4
Wahrscheinlichkeit, 72
Merkmalsträger, 4, 5
Wahrscheinlichkeitsfunktion, 90
Mittelwert, 27
Wahrscheinlichkeitsmaÿ, 72
Modalwert, 19
Wahrscheinlichkeitstheorie, 2
Modus, 19
Wahrscheinlichkeitsverteilung
diskret, 68
Nominalskala, 7
Zufallsvariable, 87
Ordinalskala, 7
Pfadregel, 75
Produktwahrscheinlichkeitraum, 78
Quantil, 22
Quartil
oberes, 22
unteres, 22
Rosenbluth-Index, 60
Säulendiagramm, 14
Schiefemaÿe, 19
Skalenniveau, 6
Spannweite, 25
Stabdiagramme, 14
Standardabweichung, 31, 93
empirische, 31
Statistik, 1
beschreibende, 2
schlieÿende, 2
Statistische Einheit, 4
Stichprobe, 2
Stichprobenvarianz, 30
Streuungsmaÿe, 19
Treppenfunktion, 15
Urliste, 11
Varianz, 29, 93
empirische, 30
Variationskoezient, 31
Verschiebungssatz von Steiner, 29
Verteilungsfunktion
approximierende empirische, 46
Vollerhebung, 2
122