Das Budget

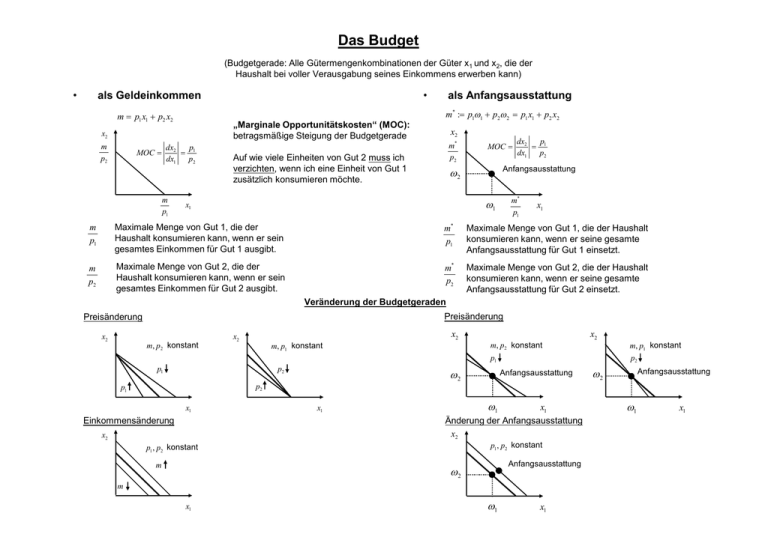
Das Budget
(Budgetgerade: Alle Gütermengenkombinationen der Güter x1 und x2, die der
Haushalt bei voller Verausgabung seines Einkommens erwerben kann)
•
als Geldeinkommen
„Marginale Opportunitätskosten“ (MOC):
betragsmäßige Steigung der Budgetgerade
x2
dx2
p
 1
dx1
p2
MOC 
m
p1
als Anfangsausstattung
m* : p11  p2 2  p1 x1  p2 x2
m  p1 x1  p2 x2
m
p2
•
x2
m*
p2
Auf wie viele Einheiten von Gut 2 muss ich
verzichten, wenn ich eine Einheit von Gut 1
zusätzlich konsumieren möchte.
MOC 
2
Anfangsausstattung
m*
p1
1
x1
dx2
p
 1
dx1
p2
x1
m
p1
Maximale Menge von Gut 1, die der
Haushalt konsumieren kann, wenn er sein
gesamtes Einkommen für Gut 1 ausgibt.
m*
p1
Maximale Menge von Gut 1, die der Haushalt
konsumieren kann, wenn er seine gesamte
Anfangsausstattung für Gut 1 einsetzt.
m
p2
Maximale Menge von Gut 2, die der
Haushalt konsumieren kann, wenn er sein
gesamtes Einkommen für Gut 2 ausgibt.
m*
p2
Maximale Menge von Gut 2, die der Haushalt
konsumieren kann, wenn er seine gesamte
Anfangsausstattung für Gut 2 einsetzt.
Veränderung der Budgetgeraden
Preisänderung
Preisänderung
x2
m, p2 konstant
x2
x2
m, p1 konstant
p1
p2
x2
m, p2 konstant
m, p1 konstant
p1
p2
2
Anfangsausstattung
2
Anfangsausstattung
p2
p1
x1
Einkommensänderung
x2
x1
1
x1
Änderung der Anfangsausstattung
x2
p1 , p2 konstant
p1 , p2 konstant
m
Anfangsausstattung
2
m
x1
1
x1
1
x1
Präferenzen
präferieren = vorziehen
f
%
Schwache Präferenz bedeutet, dass ein
Güterbündel dem anderen mindestens
gleichzusetzen ist.
"A ist mindestens so gut wie B"
f Starke Präferenz bedeutet, dass ein
Güterbündel dem anderen strikt vorgezogen
wird.
"A ist besser als B"
~ Indifferenz bedeutet, dass kein
Güterbündel dem anderen vorgezogen wird.
"A ist genau so gut wie B"
Präferenzen sind vom Budget unabhängig!
Axiom der Vollständigkeit:
Jedes Individuum kann alle Güter entsprechend der
schwachen Präferenzrelation ordnen.
Axiom der Transitivität:
Sind drei Güterbündel A, B, und C mit A f B und
%
B f C gegeben, so folgt A f C.
%
%
--> Indifferenzkurven können sich nicht schneiden
Axiom der Monotonie:
„Mehr ist besser“, Nicht-Sättigung
Axiom der Konvexität:
Extreme sind schlecht, Mischungen sind gut
--> konvexe Indifferenzkurven
Die Axiome der Vollständigkeit und der Transitivität
werden immer vorausgesetzt.
Indifferenzkurven
Gütermengenkombinationen, zwischen denen
das Individuum indifferent ist
Grenzrate der Substitution (MRS)
betragsmäßige Steigung der Indifferenzkurve
x2
x2
Güter
Ungüter
10
5
x1
x2
Sättigung
10
x2
dx2
MU 1
= MRS =
dx1
MU 2
Δ x2 = 1 = MRS
x1
Neutrales
Gut 2
6
x1
5 10
x1
x1
x2
MZB =
Δ x1 = 1
10
5
x2
konkav
bei Gütern
x2
konvex
bei Gütern
x1
x2
x1
x2
Perfekte
Substitute
x1
Perfekte
Komplemente
u( x1 , x2 ) = ax1 + bx2
x1
u ( x1 , x2 ) = min {ax1 , bx2 }
mit a, b > 0
mit a, b > 0
„Marginale Zahlungsbereitschaft“ (MZB) für Gut 1
ausgedrückt in Einheiten von Gut 2:
Wenn ich eine Einheit von Gut 1 zusätzlich konsumieren könnte,
dann wäre ich bereit auf MRS Einheiten von Gut 2 zu
verzichten, ohne mich besser oder schlechter zu stellen.
Nutzenfunktionen
Jeder Gütermengenkombination wird ein bestimmtes
Nutzenniveau zugeordnet.
Nutzenfunktionen repräsentieren Präferenzordnungen, wenn
- bei Indifferenz zwischen A und B, u ( A ) = u ( B ) gilt,
- bei schwacher Präferenz für A gegenüber B, u ( A ) ≥ u ( B ) gilt.
Ordinale Nutzentheorie
Kardinale Nutzentheorie
• Nutzen als Beschreibung einer
Präferenzordnung
• nur Rangordnung relevant
• Nutzen als Maß für die Befriedigung
• absolute Höhe relevant
--> Monotone Transformation
Das Haushaltsoptimum, das „Bestmögliche“
(Die Güterkombination, bei der der Nutzen des Haushaltes unter Einhaltung seines Budgets maximal ist, wird als das Haushaltsoptimum bezeichnet.
Formal: max u ( x1 , x2 ) unter der Nebenbedingung: p1 x1 + p2 x2 ≤ m )
x1 , x2
x2
Budgetgerade
dx2
p
= 1
dx1
p2
MOC =
Indifferenzkurven
x2
x2
dx2
MRS = MZB =
dx1
I3
I2
I3
x2*
I1
x1
I2
I1
x1
*
1
x
x1
!
MRS = MOC
• Inneres Optimum
Konvexe Indifferenzkurven: z.B.Cobb-Douglas-Nutzenfunktion:
u ( x1 , x2 ) = x1a x2 (1−a )
• differenzierbare
Indifferenzkurven
Perfekte Komplemente
Perfekte Substitute
u ( x1 , x2 ) = min {ax1 , bx2 }
u( x1, x2 ) = ax1 + bx2
I3
x2*
I2
I1
x1
x1*
m
a
p1 + p2
b
x2
MRS konstant!
MRS < MOC
*
I2
I2
I1
x2*
x1*
x1* =
m
x2* = 0
p1
x1
I1
x2* =
m
b
p2 + p1
a
x2* =
(1 − a ) m
p2
x1
x1*
x2* =
m
p2
x2
x2
I1
I2
I2
x1
x1* = 0
x2
ax1* = bx2*
x1* =
MRS konstant!
MRS > MOC
MRS nicht definiert !
x2
am
p1
Streng konkave Indifferenzkurven
x2
x2
x1* =
Vorsicht: Randlösungen
MRS konstant!
MRS = MOC
I1
I2
--> Berührpunkt kein Optimum
m = p1 x1* + p2 x2*
x1
Jedes Güterbündel auf der
Budgetgeraden ist optimal.
I1
x1
Komparative Statik
Untersuchung, wie das Haushaltsoptimum von Preisen, Geldeinkommen oder Anfangsausstattung beeinflusst wird.
G
G
Budget als Geldeinkommen (G): x1  x1  p1 , p2 , m 
Preis-Konsum-Kurve = geometrischer Ort aller
Haushaltsoptima für variierende p1 und festgelegte
Werte von p2 und m
Einkommens-Konsum-Kurve = Optimale
Konsummenge bei variierenden Einkommen
und konstantem Preisverhältnis
x2
x2
Preis-Konsum-Kurve
m
D
m
C
Einkommens-Konsum-Kurve
D
B
C
m
B
D
C
B
B
p1
0
B
x1
C
x1
C
p1
D
x1
D
p1
0
x1
B
x1
C
x1
x1
D
x1
Engelkurve
Nachfragekurve
(Preis-Mengen-Diagramm)
m
p1
B
p1
Nachfragekurve
C
m
D
m
C
m
B
Engel-Kurve
(normales Gut)
p1
D
p1
0
B
x1
C
x1
D
x1
Preiselastizität der Nachfrage
(Preiselastiziät)
Der Preis von Gut 1 steigt um 1
Prozent. Um wie viel Prozent ändert
sich die Nachfrage nach Gut 1?
 x1 , p1
dx1
x
x p
 1  1 1
dp1 p1 x1
p1
 x1 , p1  0 nicht gewöhnliche Güter
 x1 , p1  0 gewöhnliche Güter
0
x1
B
x1
Einfluss des Preises des anderen Gutes
(Kreuzpreiselastiziät)
Der Preis eines Gutes steigt um 1
Prozent. Um wie viel Prozent ändert
sich die Nachfrage eines anderen
Gutes?
 x1 , p2
dx1
x
x p
 1  1 2
dp2 p2 x1
p2
x1
0
p2
Substitute
x1
0
p2
Komplemente
C
x1
x1
D
x1
Einfluss des Einkommens
(Einkommenselastiziät)
Das Einkommen steigt um 1
Prozent. Um wie viel Prozent
ändert sich die Nachfrage nach
Gut 1?
dx
1
 x1 ,m 
x1
x m
 1
dm m x1
m
 x1 ,m  0
inferiore Güter
 x1 ,m  0
normale Güter
 x1 ,m  1
Luxusgüter
0   x1 ,m  1
notwendige Güter
s1 x1 ,m  s2 x2 ,m  1
Komparative Statik II - Teileffekte
Der Gesamteffekt (Nachfrageänderung) einer Preisänderung wird aufgespalten in den Substitutionseffekt und den Einkommenseffekt.
Eine Änderung des Preises bewirkt:
Substitutionseffekt
x2
A
Einkommenseffekt
• Relative Preisänderung bei konstanter Kaufkraft
(Realeinkommen)
• Änderung des Realeinkommen bei konstantem
(neuen) Preisverhältnis
SE1  x1H  x1 A
N
x2
EE1  x1N  x1H
A
N
H
H
GE1  SE1  EE1  x1N  x1 A
0
Substitutionseffekt
x1
Einkommenseffekt
0
x1
Als Substitutionseffekt wird die Nachfrageänderung aufgrund der
Preisänderung eines Gutes bezeichnet, die sich bei (hypothetisch)
konstant gehaltener Kaufkraft, d.h. das ursprüngliche Konsumbündel ist
leistbar, und geändertem Preisverhältnis ergibt.
Als Einkommenseffekt wird die Nachfrageänderung aufgrund der
Preisänderung eines Gutes bezeichnet, die infolge einer Änderung der
Kaufkraft eintritt, wobei der relative Preis konstant gehalten wird.
Grafisch: Drehung der alten Budgetgeraden im ursprünglichen
Optimum bis der Anstieg das neue Preisverhältnis widerspiegelt.
Ermittlung des Hilfs-Haushaltsoptimums.
Grafisch: Verschiebung der Hilfsbudgetgeraden bis zur
neuen Indifferenzkurve, d.h. ins neue Haushaltsoptimum.
Slutsky - Gleichungen
Budget als Geldeinkommen
x1G

p1

Gesamteffekt
x1S
p1

x1 A

p1

Budget als
Anfangsausstattung
x G
 1 x1B
m 


Gesamteffekt
Der Substitutionseffekt ist stets negativ.
x1 A

p1

Substitutionseffekt Einkommenseffekt
. . . bei Einkommensvariation
inferiores Gut
 x1
 0
m
x1
 x1
 x 1s

m
 p1
x1
 x1
 0
 p1
 x1
m
Gesamteffekt
normales Gut

 x 1s
 p1
Giffen-Gut
gewöhnliches Gut
. . . bei Preisvariation
Substitutionseffekt
x1S
p1

Substitutionseffekt
Nettonachfrage

 x1
 0
m
 x1
 0
 p1
x1S
p1

Gut 1 ist
normal . . .
Gut 1 ist
inferior . . .
1
 x
 x 1G
(
 m
1
1


1
x1G

1
m



KonsumEinkommenseffekt
AnfangsausstatungsEinkommenseffekt
x1G

1  x1 
m


gesamter Einkommenseffekt
Nettoangebot
0
 x1 )  0
eindeutiger Gesamteffekt
 x 1G
(
 m
x1G
x1

m


 x1 )  0
uneindeutiger Gesamteffekt

1
 x
 x 1G
(
 m
1
1


0
 x1 )  0
uneindeutiger Gesamteffekt
 x 1G
(
 m
1
 x1 )  0
eindeutiger Gesamteffekt
Arbeitsangebot & Sparen
Intertemporale Konsumentscheidung
Arbeitsangebot
Betrachtung von Einkommen und Konsum in verschiedenen Perioden
Budgetgleichung:
wF + pC = w24 + pC u
Budgetgerade:
C=
m1 +
•Gegenwartswert
Budgetgleichung:
w
( 24 − F ) + C u
p
(1 + r ) m1 + m2 = (1 + r ) c1 + c2
•Zukunftswertwert
Frage: Arbeiten oder Freizeit?
m2
c2
= c1 +
(1 + r )
(1 + r )
Frage: Mehr heute oder mehr morgen konsumieren?
Haushaltsoptimum:
Budgetgerade mit Anfangsausstattung
und positiven Zins r:
Haushaltsoptimum:
C
C
u
+ 24
!
dC
w
= MRS = MOC =
dF
p
w
p
c2
c2
(1 + r ) m 1 + m 2
Anfangsausstattung
(m 1 , m 2 )
Anfangsausstattung
( 24, C )
u
I2
C
(1 + r ) m 1 + m 2
r >0
m1 + m2
I3
!
dc2
= MRS = MOC = 1 + r
dc1
(m 1 , m 2 )
m2
m2
r =0
u
I1
24 h
0
Freizeit
F
F
Gesamteffekt
=
Substitutionseffekt
m2
+
1 + r
0
c1
m1
m1 +
m2
1 + r
Slutsky-Gleichung:
Auswirkung einer Lohnänderung auf das Arbeitsangebot
∂F s
∂w
{
m1 + m2
m1
m1
24 - F
Slutsky-Gleichung:
∂F
∂w
{
0
+
∂F
( 24 − F )
∂
m
14243
gesamter Einkommenseffekt
mit m = 24 w+ pC u
Auswirkung einer Zinsänderung auf den Konsum in Periode 1
∂c1
∂c1s
=
+
∂ (1 + r )
∂ (1 + r )
1
424
3
1
424
3
Gesamteffekt
Substitutionseffekt
( m1 − c1 ) < 0
( m1 − c1 ) > 0
∂c1
( m1 − c1 )
∂
m
14243
gesamter Einkommenseffekt
mit m =(1+ r )c1 + c2
Schuldner
Gläubiger
c1
Marktnachfrage und Erlöse
p
p
p
Horizontale Addition der
individuellen
Nachfragekurven zur
Marktnachfrage
q  p  x A  p  xB  p
0
x Ap
xB p
0
Nachfragefunktion
q p 
0
Inverse Nachfragefunktion
p
Gibt die nachgefragte Menge in
Abhängigkeit vom Preis an
p(0)
Prohibitivpreis
Gibt den Preis in Abhängigkeit
von der nachgefragten Menge an
p
q  p  a  b  p
p q  c  e  q
p ( q)
p
q
0
Erlös
q ( p)
q(0)
q
Sättigungsmenge
p
Erlös in Abhängigkeit vom Preis
r  p  q  p  p
Erlös in Abhängigkeit von der Menge
r q  p q  q
p
q
0
q
Grenzerlös
Grenzerlös bezüglich des Preises
Um wie viel verändert sich der Erlös, wenn
der Preis um eine kleine Einheit steigt.
MR p 
Grenzerlös bezüglich der Menge
Um wie viel verändert sich der Erlös,
wenn die Menge um eine kleine Einheit
steigt.
dr
dq
q p
dp
dp
MRq 
dr
dp
 pq
dq
dq
Amoroso - Robinson - Relation
Zusammenhang zwischen Grenzerlös und Preiselastizität der Nachfrage
 q, p 
dq p

dp q

dr
1
MRq 
 p 1 
  q, p
dq

dr
 q 1   q , p 
MR p 
dp
r, p
Maximum der Erlösfunktion
r
!
MR 0
p q
MR  q 
0
q


