5.3 Quantisierung freier elektromagnetischer Felder

5.3 Quantisierung freier elektromagnetischer Felder
Zur Quantisierung des elektromagnetischen Strahlungsfeldes werden für die kanonisch konjugierten
Felder Ak (r, t) und πk (r, t) Feldoperatoren Âk bzw. π̂k mit den Vertauschungsrelationen angesetzt:
h̄
π̂k (r, t), Âl (r , t) = δkl δ(r − r′ )1
i
′
und
′
π̂k (r, t), π̂l (r , t) = 0 = Âk (r, t), Âl (r , t) .
Wir schreiben die Lösungen der homogenen Wellengleichung
′
A = 0 als Linearkombination von
ebenen Wellen
2
1 XX
1
A(r, t) = √
uj (q) √ exp {iq · r} exp {−i2πνj (q)t} + k.k. .
2 j=1 q
V
Die Basisvektoren des Gitters a1 , a2 , a3 spannen die Elementarzelle bzw. das Periodizitätsgebiet
Ω = (a1 , a2 , a3 ) auf und die Vektoren La1 , La2 , La3 das Grundgebiet V = L3 Ω mit 1 ≪ L. Die
periodischen Randbedingungen für die ebenen Wellen exp iq · (r + Laj ) = exp {iq · r} erfordern die
Bedingung exp {iq · aj L} = 1, woraus sich die diskreten Ausbreitungsvektoren
m2
m3
m1
b1 +
b2 +
b3 mit ganzen Zahlen m1 , m2 , m3
q=
L
L
L
2π
ergeben. Dabei erfüllen die reziproken Gittervektoren bj =
ak × al mit zyklischen (j, k, l) die
Ω
Bedingungen aj · bk = 2πδjk .
Ferner bezeichnen uj (q) den Polarisationsvektor für zwei verchiedene Polarisationsrichtungen,
νj (q) = v|q|/2π die Frequenz der Welle mit dem Dispersionsgesetz, und k.k.” den konjugiert kom”
plexen Term. Wegen ∇ · A = 0 erfüllen die reellen Polarisationsvektoren die Bedingung q · uj (q) = 0,
so dass es nur zwei transversale, linear unabhängige Polarisationsrichtungen j = 1, 2 gibt.
Beim Übergang zu den Feldoperatoren A(r, t) −→ Â(r, t) ist die Reihenentwicklung von der Form
P
wie in Abschn. 2.3 ψ̂(x) = ν ψν (x)aν mit dem Vernichtungsoperator aν für ein Teilchen bzw. hier
P P
Â(r, t) = j q ψj (q, r)cj (q, t) mit den Vernichtungs- und Erzeugungsoperatoren cj (q, t) und c+
j (q, t)
2
1 XX
Â(r, t) = √
2 j=1 q
s
h̄
1
1
uj (q) √ exp {iq · r} cj (q, t) + uj (q) √ exp {−iq · r} c+
j (q, t) .
2πενj (q)
V
V
Die zeitabhängigen Vernichtungs- und Erzeugungsoperatoren für die Photonen
r
r
2πενj (q)
2πενj (q)
+
cj (q, t) =
exp − i2πνj (q)t
bzw. cj (q, t) =
exp i2πνj (q)t
h̄
h̄
erfüllen die Schwingungsgleichung
2
∂ 2 cj (q, t)
∂cj (q, t)
= −i2πνj (q)cj (q, t) oder
+ 2πνj (q) cj (q, t) = 0.
∂t
∂t2
ˆ (r, t) = (π1 , π2 , π3 ) ist dann
Das zu A(r, t) = (A1 , A2 , A3 ) gehörige Impulsfeld ~π
s
2 X
X
1
∂
Â
1
h̄
ˆ (r, t) = ε
= √
~π
− iε2πνj (q)uj (q) √ exp {iq · r} cj (q, t)
∂t
2πενj (q)
2 j=1 q
V
1
+ iε2πνj (q)uj (q) √ exp {−iq · r} c+
j (q, t) .
V
ˆ führen dann zu den Vertauschungsrelationen
Die Vertauschungsrelationen der Feldoperatoren  und ~π
für die Vernichtungs- und Erzeugungsoperatoren cj (q, t) und c+
j (q, t) für ein Photon der Polarisation
j, der Wellenzahl |q| und der Energie hνj (q) = vh̄|q|
+
+
′
′
′
′
′
′
cj (q, t), c+
(q,
t),
c
(q
,
t)
=
0
=
c
1
;
c
(q,
t),
c
δ
(q
,
t)
=
δ
(q
,
t)
.
j
j
jj qq
j
j′
j′
Zum Beweis sei darauf hingewiesen, dass die Operatoren cj (q, t) und c+
j (q, t) jeweils einem Photon
der beiden unabhängigen Polarisationsrichtungen j = 1, 2 zugeordnet sind, sodass u2j (q) = 1 und
1 X
′
′
′
uj ·uj = δjj zu setzen ist. Ferner gilt die Vollständigkeitsbeziehung
exp iq·(r−r ) = δ(r−r′ ).
V q
Beim Einsetzen der Feldoperatoren Â(r, t) und π̂(r, t) in den Energie-Operator
1
Ĥ =
2
Z h Z h
i
2 i 3
∂ Â 2 1
1 ˆ2
1
1
3
2
+ (∇ × Â) d r =
∇ × Â(r, t)
ε
~π (r, t) +
dr
∂t
µ
2
ε
µ
ergibt sich bei Verwendung der Vertauschungsrelationen für die Erzeugungs- und Vernichtungsoperatoren c+
j (q, t) und cj (q, t) die Form einer Summe ungekoppelter harmonischer Oszillatoren, die durch
die beiden Indizes j und q abgezählt werden,
Ĥ =
2 X
X
j=1 q
1
+
hνj (q) cj (q, t)cj (q, t) +
.
2
1
2
Jeder einzelne Oszillator hat die äquidistanten Energieeigenwerte hνj (q) nj (q) +
mit den Besetzungszahlen nj (q) = 0, 1, 2, . . . die angeben, wieviele Photonen der Energie hνj (q) = vh̄|q| und mit
dem Impuls h̄q im Grundgebiet V vorhanden sind.
Der Energie-Operator ist mit dem Feldoperator Â(r, t) und damit auch mit denen der elektrischen
Feldstärke und der magnetischen Induktion nicht vertauschbar. Die elektromagnetischen Felder und
die Anzahl der Photonen, die sich aus dem Photonenzahloperator
N̂ =
2 X
X
c+
j (q, t)cj (q, t)
j=1 q
ergeben, sind somit nicht gleichzeitig scharf meßbar.
Der Beweis für den Feldoperator Ĥ, wie er sich aus der Form der Operatoren Ȧ und ∇ × A ergibt,
wird einfach, wenn man die folgendenZ Zusammenhänge
berücksichtigt.
Z
1
1 ˆ2 3
(∇ × Â)2 d3r.
~π d r =
⊲ Die beiden Integrale sind gleich
ε
µ
1
⊲ Für die ebenen Wellen ϕq (r) = √ exp {iq · r}
V
gelten die Orthonormalitäts- und Vollständigkeitsbeziehungen
Z
X
′
3
1
ϕq (r)ϕ∗q (r′ ) = δ(r − r′ ).
exp i(q − q) · r d r = δqq′ und
hϕq |ϕq′ i =
V V
q
⊲
q2
Es gilt die Dispersionsbeziehung 2πνj (q) = v|q| bzw.
= v 2 q2 = 4π 2 νj2 (q).
εµ
⊲ Zu berücksichtigen sind nur Terme mit der gleichen Anzahl von Erzeugungsoperatoren c+
j (q, t)
⊲
und Vernichtungsoperatoren cj (q, t).
Wegen ∇ · A = 0 handelt es sich um Transversalwellen mit q · uj (q) = 0 und uj · uj ′ = δjj ′ mit
der Folge q × uj (q) · q × uj ′ (q) = q2 uj (q) · uj ′ (q) − q · uj (q) q · uj ′ (q) = δjj ′ q2 .
5.4 Elektron-Photon-Wechselwirkung
Bei der Wechselwirkung der quantisierten elektromagnetischen Wellen, also der Photonen, mit freien
oder gebundenen Atomen geht man von der Lorentz-Kraft aus, die die elektromagnetischen Felder E
und B auf die als geladene Massenpunkte idealisierten Elektronen und Atomkerne ausüben.
Im Rahmen der klassischen Mechanik bewegt sich eine Punktladung der Masse m und der Ladung
e auf einer Bahnkurve r(t), die bei gegebenen E und B durch die Lorentz-Kraft
mr̈ = e(E + ṙ × B)
bestimmt ist. Die Ladungen und Ströme, die die Felder E und B erzeugen, seien vom Ort der untersuchten Materie weit entfernt, sodass hier nur die Ladungen und Ströme der betrachteten Punktladungen eine Rolle spielen. Wir verwenden die elektrodynamischen Potenziale A und φ mit B = ∇ × A
und E = −Ȧ − ∇φ in Strahlungseichung mit φ = 0 und ∇ · A = 0, vergl. Abschn. 4.1, also
B = ∇ × A und E = −Ȧ.
Im nichtrelativistischen Fall ergibt sich dann die Bahnkurve r(t) aus der Lagrange-Funktion
L(r, ṙ) =
m 2
ṙ + eṙ · A und den Euler-Lagrange-Gleichungen
2
d ∂L ∂L
−
= 0.
dt ∂ ṙ
∂r
∂L
= mṙ + eA und die Hamilton-Funktion ist
∂ ṙ
2
m
1
m
p − eA .
H(r, p) = ṙ · p − L(r, ṙ) = mṙ2 + eṙ · A − ṙ2 − eṙ · A = ṙ2 =
2
2
2m
Geht man davon aus, dass sich die Elektronen bzw. die Atomkerne in einem effektiven Einteilchenpotenzial v(r) bewegen, das von der umgebenden Materie verursacht wird, so lautet die EinelektronenHamilton-Funktion mit der Elektronenmasse me
2
1
H=
p − eA + v(r).
2me
Der zu r kanonisch konjugierte Impuls ist p =
h̄
Beim Übergang zur Quantenmechanik ist der Impulsoperator p = ∇ einzusetzen und die Energie der
i
freien elektromagnetischen Felder nach Abschn. 4.1 hinzuzufügen. Der Energie-Operator beschreibt
dann das Elektron, die elektromagnetische Strahlung und die Wechselwirkung zwischen beiden
2
1 h̄
∇ − eA + v(r) +
H=
2me i
2
1 h̄
∇ − eA + v(r) +
=
2me i
Z
1 ε0 E2 +
2
Z
1 h
ε0 Ȧ2 +
2
1 2 3
B dr
µ0
i
1
2
(∇ × A) d3r.
µ0
Vernachlässigt man den kleinen Term mit A2 , so erhält man wegen ∇ · A = 0 für den gemischten Term
↓
1 h̄ 1 h̄ eh̄
− e (∇ · A + A · ∇) =
− e (A · ∇ + ∇· A +A · ∇) = −
A · ∇,
2me
i
2me
i
ime
wobei der Pfeil auf dem Term ∇ · A anzeigt, dass der Operator ∇ nur das A differenziert, und es folgt
Z
i
1
h̄2
eh̄
1 h
2
2
∆ + v(r) −
A·∇
ε0 Ȧ +
(∇ × A) d3r
H =−
+
2me
im
2
µ0
|
| e{z }
{z
}
{z
}
|
Kristallelektron
Elektron-Licht-WW
freies Strahlungsfeld
ein Einelektronen-Energieoperator aus drei Teilen, mit einem Teil HKE des Kristallelektrons, einem
Teil HEL der Elektron-Licht-Wechselwirkung und einem Teil HL des freien Strahlungsfeldes.
Der Übergang zu dem Vielelektronensystem und einem quantisierten Strahlungsfeld ist nun mit
dem Teilchenzahlformalismus denkbar einfach. Wir schreiben den Operator im Fock-Raum der Elektronen und Photonen
Ĥ = ĤKE + ĤEL + ĤL
mit dem Operator der Kristallelektronen und dem Teilchenzahloperator ank der Bloch-Zustände
ĤKE =
BZ
XX
n
En (k)a+
nk ank
k
1
mit ψn (k, r) = √
exp {ik · r} un (k, r),
3
N
dem Operator des freien Strahlungsfeldes mit dem Teilchenzahloperator der Photonen cj (q)
ĤL =
2 X
X
j=1 q
1
+
hνj (q) cj (q, t)cj (q, t) +
2
und dem Operator der Elektron-Photon-Wechselwirkung mit dem Operator  des Vektorpotenzials
HEL
2
eh̄ 1 X X
√
=−
ime 2 j=1 q
s
h 1
h̄
√ exp {iq · r} uj (q) · ∇cj (q, t)
2πε0 νj (q)
V
i
1
+
+ √ exp {−iq · r} uj (q) · ∇cj (q, t) .
V
Dieser Operator ist zunächst nur für die Photonen ein Teilchenzahloperator, in Bezug auf die Elektronen
aber ein Einelektronenoperator. Er lässt sich jedoch nach Abschn. 2.1 direkt in einen Fock-Operator
mit den Erzeugungs- und Vernichtungsoperatoren der Bloch-Zustände a+
nk , ank umschreiben
XX
Elekt
Ĥ
=
hnk|H Elekt |n′ k′ ia+
nk an′ k′ ,
n,k n′ ,k′
und man erhält für den Fock-Operator
ĤEL
i
X X Xh
+
+
+
′
′
′
′
=
M (n, k; n , k ; j, q)ank an′ k′ cj (q, t) + M (n, k; n , k ; j, −q)ank an′ k′ cj (q, t)
n,k n′ ,k′ j,q
mit dem Übergangsmatrixelement zwischen den Bloch-Zuständen |nki = ψn (k, r)
eh̄ 1
√
M (n, k; n , k ; j, q) = −
ime 2
′
′
s
′ ′
1
h̄
nk √ exp {iq · r} uj (q) · ∇n k .
2πε0 νj (q)
V
Hier bezeichnen also a+
nk und ank die Erzeugungs- bzw. Vernichtungsoperatoren für ein Elektron im
Bloch-Zustand ψn (k, r) mit der Energie En (k) und c+
j (q, t) bzw. cj (q, t) die Erzeugungs- und Vernichtungsoperatoren für ein Photon der Energie hνj (q) mit dem Impuls h̄q und der Dispersionsbeziehung
2πνj (q) = v|q|, wobei v die Lichtgeschwindigleit im Medium bezeichnet. Die Vektoren uj (q) mit
q · uj (q) = 0 geben die Amplituden und die Polarisation senkrecht zum Wellenvektor q an.
Zur Veranschaulichung betrachten wir einen Laserstrahl, der von einem Resonator erzeugt wird,
und der aus einzelnen diskreten Linien, den sogenannten Moden besteht. Seien n1 , n2 , . . . die Besetzungszahlen der Bloch-Zustände und l1 , l2 . . . die der Photonenzustände, so sind die Teilchenzahlzustände für den Operator
Ĥ = ĤKE + ĤEL + ĤL
durch |nli = |n1 n2 . . . l1 l2 . . .i
˙
ˆ zu
gegeben. Der Erwartungswert der elektrischen Feldstärke berechnet sich wegen Ê = −Â = − 1ε ~π
1 ˆ nli = 0,
hÊi = hnl|Ê|nli = hnl − ε ~π
ˆ nur einzelne Photonenzahloperatoren mit hnl|c (q, t)|nli = 0 = hnl|c+ (q, t)|nli
weil der Operator ~π
j
j
enthält. Jedoch ergibt sich für die Streuung bei der Messung der elektrischen Feldstärke
2 2
2
2
2
(∆Ê) = nl (Ê − hÊi1 ) nl = nl hÊ i − hÊi nl = nlhÊ inl .
Der Ausdruck ist für jede einzelne Mode proportional zu 2lν + 1 mit lν = 0, 1, 2, . . ., also von Null
verschieden, wie auch beim eindimensionalen harmonischen Oszillator.
Anwendungsbeispiel: Elektronische Interbandübergänge
Bei der Interpretation der Energiebänder En (k) der Kristalle als Einelektronenenergieniveaus muss
man verschiedene Anregungsprozesse unterscheiden.
⊲ Bei elektrischen Feldern E, die zur Beschleunigung von Elektronen führen, ändert sich der BlochZustand quasistetig von ψn (k, r) nach ψn (k′ , r).
⊲ Bei der Absorption eines Photons hinreichender Energie, wird aber ein Elektron im Zustand
ψV (k, r) aus dem Valenzband entfernt und in einen Zustand ψL (k, r) im Leitungsband angeregt,
wobei ein Loch im Valenzband zurückbleibt.
⊲ Bei der Photoemission wird andererseits ein Elektron aus einem Zustand ψV (k, r) im Valenzband
entfernt und befindet sich anschließend außerhalb des Kristalles.
Die drei Vorgänge haben unterschiedliche Endzustände und entsprechende Experimente sind bezüglich
der Energiebänder nicht unmittelbar vergleichbar.
So gibt es z.B. bei der elektrischen Leitfähigkeit auch Streuprozesse der Leitungselektronen untereinander, und bei der Absorption eines Photons entsteht ein Elektron-Loch-Paar, wobei zwischen
Elektron und Loch eine anziehende Wechselwirkung existiert, die zu den Exzitonen führt. Beides
hängt mit dem Koopmans-Theorem, vergl. Abschn. 3.2, zusammen, wonach die Energiebänder zwar
die Photoemission genähert beschreiben, für die inneren Anregungen im Festkörper aber Korrekturen
erforderlich sind.
Wir setzen voraus, dass der Operator der Wechselwirkung zwischen Elektronen und dem Licht ĤEL nur
eine kleine Störung des durch den Operator Ĥ0 = ĤKE + ĤL beschriebenen ungestörten Systems verursacht. Die elektromagnetische Welle kann dann mit der zeitabhängigen Störungsthoerie berücksichtigt
werden, und die Übergangswahrscheinlichkeit pro Zeiteinheit für einen Übergang vom Anfangszustand
|ai in einen Endzustand |ei von Ĥ0 lässt sich mit der Goldenen Regel der Quantenmechanik berechnen
Wae
2
2π ′
′
=
. . . Nnk . . . ; . . . Mjq . . . ĤEL . . . Nnk . . . ; . . . Mjq . . . δ |Ea − Eb | ,
h̄
′
′
. . . ; . . . Mjq
. . .i den
wobei Ea den Anfangszustand |ai = | . . . Nnk . . . ; . . . Mjq . . .i und |ei = | . . . Nnk
Endzustand von Ĥ0 bezeichnen, mit den Besetzungszahlen Nnk für die Bloch-Zustände und Mjq für
die Photonen. Wir gehen davon aus, dass reichlich Licht eingestrahlt wird, so dass sich das Photonenreservoir durch einen Absorptions- oder Emissionsprozess praktisch nicht verändert.
Beim Einsetzen des Elektron-Licht Wechselwirkungsoperators ĤEL betrachten wir nur den einen
Summanden mit a+
n′ k′ ank cj (q), der die Absorption eines Photons der Energie hνj (q) beschreibt, und erhalten für die Übergangswahrscheinlichkeit pro Zeiteinheit für ein Elektron vom Bloch-Zustand ψn (k, r)
in einen Zustand ψn′ (k′ , r) mit dem Übergangsmatrixelement
Wnk,n′ k′
2
h̄
2π X e2 h̄2
′ ′ 1
=
n k √ exp {iq · r} uj (q) · ∇nk 2
h̄ j,q 2me 2πε0 νj (q)
V
× δ |En′ (k ) − En (k)| − hνj (q) .
′
Setzt in man das Integral die Bloch-Funktionen |nki = ψn (k, r) ein,
I=
Z
V
1
ψn+′ (k′ , r) √ exp {iq · r} uj (q) · ∇ψn (k, r) d3r,
V
so kann man die Integration über das Grundgebiet V = L3 Ω zerlegen in eine Integration r1 über die
Elementarzelle Ω und in eine Summe über die durch einen Gittervektor R abgezählten Elementarzellen,
indem man r = R + r1 setzt und die Bloch-Bedingung
ψn (k, r) = ψn (k, r1 + R) = exp {ik · R} ψn (k, r1 )
beachtet. Dann lässt sich die Summe über die L3 Gittervektoren R in V separat ausführen
I=
V Z
X
R
∗ ′
1
exp i(k − k + q) · R ψn′ (k , r1 ) √ exp {iq · r1 } uj (q) · ∇ψn (k, r1 ) d3r1 ,
V
Ω
′
die wegen
V
1 X
′
exp
i(k
−
k
+
q)
·
R
= δk′ −k,q
L3
R
nur für k′ − k = q + G nicht verschwindet, wobei G einen reziproken Gittervektor bezeichnet.
Nun sind die Ausbreitungsvektoren der Elektronen am Rande der Brillouin-Zone etwa |k| = 2π/a,
mit der Gitterkonstanten a in der Größenordnung einiger Å, z.B. a = 5, 43 Å bei Silicium. Photonen
haben bei Energien von weniger als 10 eV viel größere Wellenlängen λ > 1 µm = 104 Å ≫ a und
Wellenvektoren |q| = 2π/λ ≪ |k| außer in einer kleinen Umgebung des Γ-Punktex bei k = 0. Deshalb
finden optische Übergänge zwischen verschiedenen Bändern in erster Näherung der Störungstheorie
nur bei k′ = k statt, was auch als k-Auswahlregel bezeichnet wird. Intrabandübergänge innerhalb
eines Energiebandes sind in dieser Näherung verboten. Betrachtet man den zweiten Term von ĤEL , so
findet man die gleiche Auswahlregel auch für Emissionsvorgänge.
Die Elementarprozesse der Absorption bzw. Emission eines Photons sind also
hνj (q)
′
EV (k)
e−
e−
EL (k )
hνj (q)
EL (k)
e−
e
−
Energiesatz
Impulssatz
EV (k) + hνj (q) = EL (k′ )
h̄k + h̄q = h̄k′ ≈ h̄k
Energiesatz
Impulssatz
EL (k) = EV (k′ ) + hνj (q)
h̄k = h̄k′ + h̄q ≈ h̄k′ ,
EV (k′ )
und es gelten die Erhaltungssätze von Energie und Impuls.
5.5 Photon-Phonon-Wechselwirkung
In einem einfachen Modell des Festkörpers geht man davon aus, dass die thermischen Gitterschwingungen die Atome aus ihren Ruhelagen auslenken. Die dadurch entstehenden Abweichungen im periodischen Elektronenpotenzial führen zu der in Festkörpern wirksamen Elektron-Phonon-Kopplung, die die
Ursache ist für die Umwandlung elektrischer Energie in Wärme nach dem Ohmschen Gesetz. Andererseits bilden sich durch die Auslenkungen auch atomare elektrische Dipole, sodass eine Dipoldichte oder
Polarisation entsteht. Diese Dipolmomente sind bei gegeneinander schwingenden Nachbaratomen, also
bei optischen Phononen, und bei polaren Halbleitern besonders groß und in einfacher Näherung proportional zu Auslenkung des Atoms aus seiner Ruhelage. Im elektrischen Feld der elektromagnetischen
Strahlung E = −Ȧ ist dann als Polarisationsarbeit die Energie
Z
E = − P(r, t) · E(r, t) d3r
aufzuwenden, die dem Energieoperator des Lichtes hinzuzufügen ist, und die Phonon-Photon-Wechselwirkung beschreibt. Dazu wird die Polaristion P durch die
Erzeugungs- und Vernichtungsoperatoren b+
l (p) bzw. bl (p) der Phononen,
mit der Energie h̄ωl (p) und dem Impuls h̄p, ausgedrückt, und die elektrische Feldstärke E durch die
Erzeugungs- und Vernichtungsoperatoren c+
j (q) bzw. cj (q) der Photonen.
In dem Ausdruck der Phonon-Photon-Wechselwirkung treten dann Terme der Art c+
j (q)bl (p) und
b+
l (p)cj (q) mit
hνj (q) = h̄ωl (p) (Energiesatz) und h̄q = h̄p (Impulssatz)
auf, die die Emission eines Photons bzw. die Absorption eines Photons beschreiben. Hierbei wird die
Energie des Photons unmittelbar in die Energie eines Phonons umgewandelt, und der Impulssatz kann
nur mit einem optischen Phonon mit p am Γ-Punkt, also bei h̄p ≈ 0 erfüllt werden.
Außerdem gibt es Terme, die Zweiphononenprozesse mit akustischen Phononen darstellen
hνj (q) = h̄ωl1 (p1 ) + h̄ωl2 (p2 ) mit h̄q = h̄p1 + h̄p2 ≈ 0,
bei denen die Impulse der beiden Phononen entgegengesetzt gleich sein müssen.
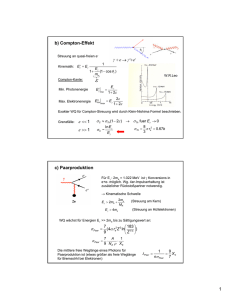
Die Absorption bzw. Emission eines Photons beschreiben dann die Diagramme:
hνj (q)
h̄ωl1 (p1 )
h̄ωl1 (p1 )
h̄ωl2 (p2 )
h̄ωl2 (p2 )
hνj (q)
b
Die optischen Eigenschaften von Halbleitern und Metallen werden hauptsächlich durch die ElektronPhoton-Phonon-Kopplung bestimmt.