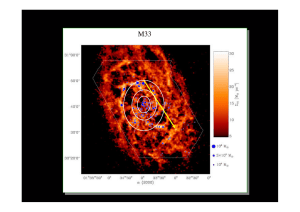
3.6 Kinematik und Massen 3.6.1 Allgemeines

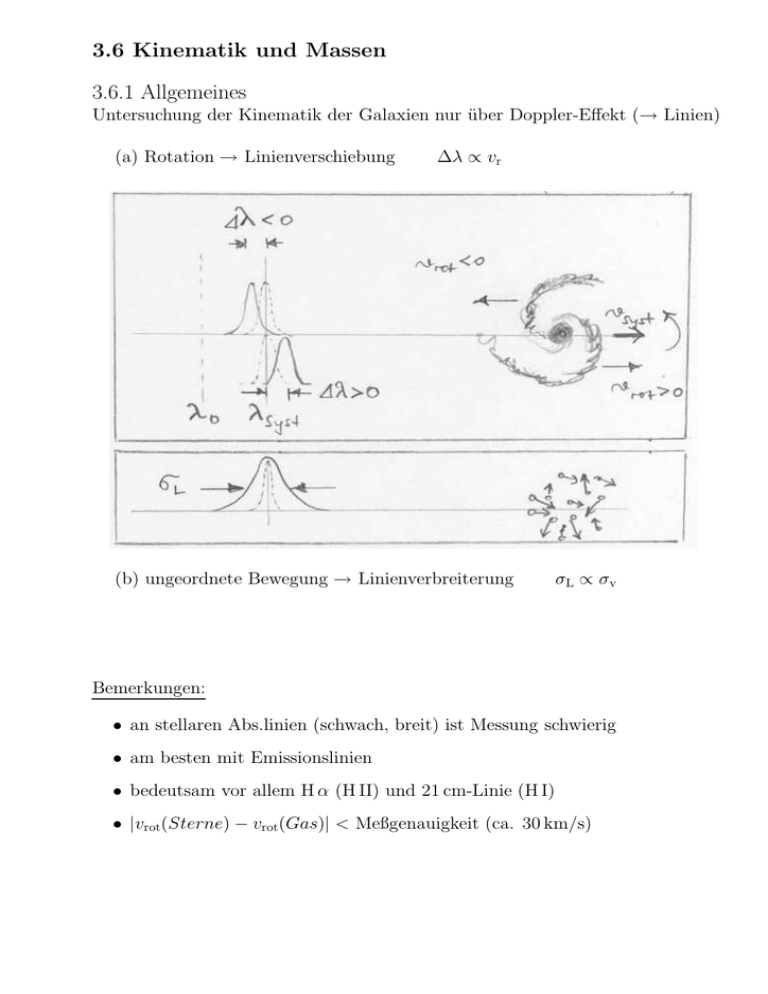
3.6 Kinematik und Massen
3.6.1 Allgemeines
Untersuchung der Kinematik der Galaxien nur über Doppler-Effekt (→ Linien)
(a) Rotation → Linienverschiebung
∆λ ∝ vr
(b) ungeordnete Bewegung → Linienverbreiterung
σL ∝ σv
Bemerkungen:
• an stellaren Abs.linien (schwach, breit) ist Messung schwierig
• am besten mit Emissionslinien
• bedeutsam vor allem H α (H II) und 21 cm-Linie (H I)
• |vrot(Sterne) − vrot(Gas)| < Meßgenauigkeit (ca. 30 km/s)
3.6.2 Messung der Rotationskurve (RK) vrot(R)
einfachste Methode (entferntere Galaxien): Langspaltspektroskopie
Bemerkung: Korrektur bzgl. Neigung zur Sichtlinie aus Achsenverhältnis a/b
3.6.3 Ergebnisse
(A) Scheiben von Spiralgalaxien
i.allg. vmax ≫ σv
⇒
v(R) (“Rotationskurve”) untersuchen
Ergebnisse:
• typische Form der RK vmax ≈ const für R ≈ Rp ...R25
• fester Hubble-Typ: vmax ∝ L1/4
Tully-Fisher-Relation
• festes L: vmax ↓ für Sa→Sc
(starke Zentrumskonzentration (Bulge) → vmax groß)
• Spiralarme → wellenförmige Strukturen in RK
Abbildung:
Beispiele für gemessene Rotationskurven von Sb-Galaxien (links) und Sc-Galaxien
(rechts); aus Rubin et al. 1980...1985)
(B) Bulges und Elliptische
keine Em.linien, nur stellare Absorption → schwierig, weil
(a) schwach,
(b) breit (50...100 km/s),
(c) keine Neigungskorrektur möglich
Ergebnisse:
• im Mittel gilt σv (E) ≈ 2 σv (Sp)
• σv ∝ L1/4
Faber-Jackson-Relation
Problem: Wenn ungeordnete Bewegungskomponente dominiert
−→ sind Bulges und E’s überhaupt Rotationsellipsoide?
Im Prinzip kann die dreidimensionale Gestalt von E’s sein:
(a) oblat
“Pfannkuchen”
(b) prolate
“Zigarre, Balken”
Modellierung:
Sternsysteme, deren Abplattung ǫ = 1 − b/a durch Rotation erfolgt
→ Vergleich von vmax /σv = f (ǫ) aus Beobachtung und Modellen
Modelle:
(a) σv isotrop; oblat
→ IO-Modell
(b) σv isotrop; prolat
→ IP-Modell
Ergebnisse:
• Bulges und kleine E’s entsprechen i. allg. IO-Modell
→ durch Rotation abgeflacht, σv isotrop
• große E’s:
disky E’s entsprechen IO-Modell
→ durch Rotation abgeflacht, σv isotrop
boxy E’s weder IO noch IP, sondern anisotrop prolate
→ Rotation zu langsam, um Abplattung zu erklären
→ Stabilität gegen Gravitationskollaps durch ungeordnete Bewegung
→ Anisotropie: σv (a) > σv (b) (bzw. triaxiale Struktur?)
3.6.4 Massen, Massenverteilung, m/L
(A) Allgemeines Vorgehen
(B) Deutung der flachen RK
(C) Ergebnisse
typische Massen und Masse-Leuchtkraft-Verhältnisse m/L:
Typ
m (1010 m⊙ )
m/L (m⊙ /L⊙)
100...1000
0.01
100
10
5
0.01
10...20
am letzten Meßpunkt der RK
E (Riesen)
E (Zwerge)
Sa
Sb
Sc
Irr
10
5
zum Vergleich Sonnenumgebung (Sternzählungen): mvis /L ≈ 1
⇒ Dunkle Materie besteht nicht aus normaler Sternpopulation.
Dunkle Materie in sphärischer oder flacher Anordnung?
→ Vergleich der RK in Halo und Scheibe (für gleiches R):
sphärisch → vrot(Halo) = vrot(Scheibe)
flach
→ vrot(Halo) ≈ (0.2...0.4)vrot(Scheibe)
(a) Kinematik entfernter Objekte im Halo des MSS:
(b) Kinematik der Ring-Galaxie AO 136 0801
In beiden Fällen sind RK von Halo und Scheibe ähnlich
→ etwa sphärischer dunkler Halo
3.6.5 Massereiche dunkle Halos (Koronae)
(A) Hinweise auf deren Existenz:
- Rotationskurven der Scheibengalaxien
- Kinematik der Außengebiete (z.B. Kugelsternhaufen) und
Satelliten des MSS
- heißes Gas in Elliptischen Galaxien
- Dynamik von Doppelgalaxien
(B) Woraus könnten dunkle Halos bestehen?
(a) mit Sicherheit nicht:
- Sterne mit m/L < 1
- kühles H I-Gas
- heißes Gas
- Staub
(b) mit Wahrscheinlichkeit nicht:
- massereiche Schwarze Löcher
- stellare Endstadien (WZ, NS, SL)
- Asteroiden, Kometen
- UFOs,...
(c) vielleicht:
- MACHOs (Massive Astrophysical Compact Halo Objects):
Sterne mit m < 0.5 m⊙
substellare Objekte (Braune Zwerge, “Jupiter”)
- WIMPs (Weakly Interacting Massive Particles)
Elementarteilchen (nichtbaryonische Materie) 1 . . . 100 GeV
(C) MACHOs als Mikro-Gravitationslinsen
Paczýnski (1986): Halo-Machos mit mM ≈ 10−7...102 m⊙ mittels GL-Effekt
mit Sternen der LMC als Hintergrund nachweisbar
Prinzip:
1. Lichtablenkung im Gravitationsfeld eines (dunklen) Vordergundobjekts
2. ...verbunden mit Lichtverstärkung der Hintergrundquelle.
3. Verstärkung ändert sich, wenn sich Linse relativ zur Quelle bewegt.
Wenn sich Quelle, Linse und Beobachter auf einer Linie befinden, führt die
Lichtablenkung zur Entstehung eines Rings (Einstein-Ring).
R0 =
s
4 G mM Ds − Dd
c2
Ds · D d
= “Einsteinradius”
.
Abschätzung der Größe des Einstein-Rings:
sei Ds (LMC) = 53 kpc und Dd = 10 kpc
q
−→ R0 = 8′′ 10−4 mM /m⊙
(”Mikro-Gravitationslinseneffekt”)
Die Verstärkung µ ist abhängig vom ”Impakt-Parameter” u (relativer projizierter
Abstand von Linse und Quelle):
√
µ(t) = (u2 + 2)/(u u2 + 4),
u = u(t) = r(t)/R0
Für u = 1 (d.h. r = R0) ergibt sich µlim = 1.34 (Schwellwert für Detektion)
Abbildung oben: Einstein-Ring eines MACHOs und 5 mögliche relative Bahnen eines Hintergrundsterns.
Rechts: die dazu gehörigen Lichtkurven. Als Schwellwert für die Detektion eines Ereignisses kann die
Verstärkung µ = 1.34 angenommen werden.
Abbildung rechts:
Lichtkurve eines Mikro-GravitationslinsenEreignisses in B (oben) bzw. in R
(Mitte). Das untere Diagramm zeigt das
Verhältnis der Verstärkungen µR /µB .
Man beachte, dass die Lichtkurven
(a) streng symmetrisch und
(b) streng achromatisch sind.
Dauer eines Ereignisses:
∆t =
R0
vtrans
Beispiel: Linse = MACHO im gal. Halo
bedecktes Objekt = Stern in der LMC
⇒
q
Dd = 10 kpc, vtrans = 200 km s−1 → ∆t = 0.2 a mM /m⊙
für mM /m⊙ = 10−7
→ ∆t = 30 min
2
für mM /m⊙ = 10
→ ∆t = 2 a
Wahrscheinlichkeit p für Verstärkung eines beliebigen Sterns in der LMC:
p =
Gesamtfläche aller Einsteinscheiben vor LMC
≈ 10−6
Gesamtfläche der LMC
bei 106 Sternen → im statist. Mittel zu jedem Zeitpunkt 1 Ereignis!
mehrere Projekte zur Bestimmung von p (seit ca. 1990):
- MACHO (0.72o LMC mit CCD)
- EROS (0.42o LMC mit CCD und 252o LMC photographisch)
- OGLE (0.252o gal. Zentrum (Bulge) mit CCD)
⇒ Ergebnisse (aktueller Stand 2004):
• Der Mikro-Gravitationslinsen-Effekt wird beobachtet,...
• ... aber MACHOs liefern nur einen kleinen Beitrag
zur Masse des dunklen Halos
maximal etwa 20% in Form von Weißen Zwergen, aber umstritten,
da dann einige Ungereimtheiten (→ kosmologische Kernsynthese).
(D) WIMPs
Was spricht für für nicht-baryonische Natur der DM?
• Mikro-Gravitationslinsen-Suche:
DM aus baryonischer Materie kann für Galaxis mit hoher Wahrscheinlichkeit ausgeschlossen werden.
• Großskalige kosmische Struktur (siehe 5.3, 5.4):
erfordert offensichtlich Existenz nicht-baryonischer Materie
• beobachtete Häufigkeiten der leichten chemischen Elemente:
Modell der primordialen Kernsynthese (siehe “Kosmologisches Standardmodell”) setzt Grenzen an Masse der baryonischen Materie
→ viel kleiner als dynamische Masse
• Teilchenphysik:
Existenz von WIMPs wird von Physik vorausgesagt (SUSY-Teilchen, insbesondere Neutralino X1o mit m ≈ 10 . . . 1000 GeV)
• Kosmologie:
WIMPs sollten im frühen Universum (idealer Teilchenbeschleuniger!) in
großen Massen erzeugt worden sein
Prinzipien der experimentellen Suche nach WIMPs:
• zwar geringe Wechselwirkung mit “normaler Materie”,
aber hohe Flussdichten: ca. 106 (m/GeV)−1 cm−2 s−1
• dennoch: erwartete Ereignisrate gering: < 1 Ereignis kg−1 d−1
• → Detektoren müssen große Massen besitzen...
• → gute Abschirmung gegen Hintergrund (kosmische Strahlung etc.)
• nutzbar: Modulation der Ereignisrate infolge Bewegung der Erde um Sonne
(→ Änderung der Richtung relativ zu galaktischem Hintergrund.)
einige DM-Experimente (nicht vollständig):
• direkte Messung: kryogene Halbleiter-Detektoren
Messung der Gitterschwingungen (Ladung und Temperatur) beim Einschlag
eines WIMPs:
– EDELWEISS II
ca. 30 kg Ge bei T = 0.01 K
in Tunnel in franz. Alpen
– Heidelberg-Moscow Ge experiment
6 kg reines 76Ge
im Gran-Sasso-Tunnel, ital. Alpen
– DAMA (particle DArk MAtter searches)
ca. 100 kg Na
im Gran-Sasso-Tunnel, ital. Alpen
Suche nach jahrezeitlichen Schwankungen
– CRESST II
(Cryogenic Rare Event Search with Superconducting Thermometers)
10 kg Kristall-Detektoren im Gran-Sasso-Tunnel, ital. Alpen
– CDMS II
Soudan mine in Minnesota, USA
• indirekte Methode: Cerenkov-Detektoren
Suche nach Neutrinos aus WIMP-Annihilation:
– HESS (High Energy Stereoscopic System, Namibia)
– AMANDA (Antartic Muon and Neutrino Detector)
Antarktis, Beobachtung Richtung Nordpol (→ durch Erde hindurch)
– ICE CUBE (geplante Erweiterung von AMANDA)
4 800 Detektoren in einigen km3 Eis