1. WH
Werbung

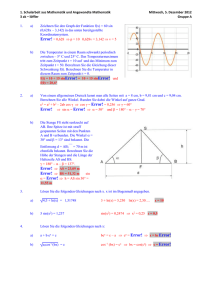
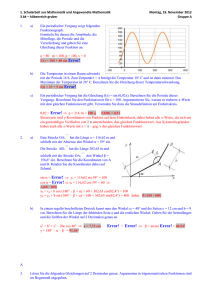
1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 bk – höbenreich-gruber 1. a) Der Wasserstand in einem Staubecken schwankt zwischen den Werten 50 m und 70 m. Der geringste Wasserstand ist nach 18 Tagen erreicht und nach weiteren 40 Tagen ist der Wasserstand maximal. Berechnen Sie die Gleichung dieses Wasserstandes W(t). W(t) = 60 + 10 sin Error! = 60 + 10 sin Error! b) Skizzieren Sie den Verlauf der Funktion f(x) = 5 + 3 sin (0,157x). Berechnen Sie dazu die Mittellage, die Amplitude, die Periode und die Verschiebung. Benutzen Sie das folgenden Koordinatensystem: m=5 a=3 v=0 2. Montag, 22. Oktober 2012 Gruppe A a) Error! = 0,157 p = 40 Auf einer Straße fahren hintereinander die Fahrzeuge A und B mit gleicher Geschwindigkeit. Ein Beobachter im Punkt C (Normalentfernung zur Straße d = 5 m misst zu einem bestimmten Zeitpunkt den Winkel = 2° und den Winkel = 8°. Berechnen Sie den Abstand t der beiden Fahrzeuge A und B. tan = Error! s = Error! = 35,58 m tan(90° – + ) = Error! t = d tan(90° – + ) – s = 5 tan 84° – 35,58 = 11,99 m 12 m b) In dem allgemeinen Dreieck (siehe Skizze) kennt man die Seiten s = 8 cm und t = 12 cm und den Winkel = 55,77°. Berechnen Sie die Länge der Seite r und die Größe der Winkel und . r2 = s2 + t2 – 2 s t cos() = 100 r = 10 cm Error! = Error! = arcsin Error!= 82,81° = 180° – – = 41,42° 3. Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in trigonometrischen Funktionen sind im Bogenmaß angegeben. a) b) 4. ln (sin2(3x) – 0,2) = –0,2294 3;e2x + 3 = 148,4 sin2(3x) – 0,2 = 0,795 sin2(3x) = 0,995 3x = 1,5 x = 0,5 e2x + 3 = 3.268.148 2x + 3 = 15 x = 6 Lösen Sie die folgenden Gleichungen nach x: a) b arcsin(cx2) = r arcsin(cx2) = Error! b) Error! = s Error! cx2 = sin Error! x2 = Error! x = 10ax = ks ax = log(ks) x = Error! 1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 bk – höbenreich-gruber 1. a) Der Wasserstand in einem Staubecken schwankt zwischen den Werten 40 m und 100 m. Der geringste Wasserstand ist nach 12 Tagen erreicht und nach weiteren 40 Tagen ist der Wasserstand maximal. Berechnen Sie die Gleichung dieses Wasserstandes W(t). W(t) = 70 + 30 sin Error! = 70 + 30 sin Error! b) Skizzieren Sie den Verlauf der Funktion f(x) = 5 + 3 sin (0,157x). Berechnen Sie dazu die Mittellage, die Amplitude, die Periode und die Verschiebung. Benutzen Sie das folgenden Koordinatensystem: m=5 a=3 v=0 2. Montag, 22. Oktober 2012 Gruppe B a) Error! = 0,157 p = 40 Auf einer Straße fahren hintereinander die Fahrzeuge A und B mit gleicher Geschwindigkeit. Ein Beobachter im Punkt C (Normalentfernung zur Straße d = 5 m misst zu einem bestimmten Zeitpunkt den Winkel = 4° und den Winkel = 10°. Berechnen Sie den Abstand t der beiden Fahrzeuge A und B. tan = Error! s = Error! = 28,36 m tan(90° – + ) = Error! t = d tan(90° – + ) – s = 5 tan 84° – 28,36 = 19,22 m b) In dem allgemeinen Dreieck (siehe Skizze) kennt man die Seiten s = 8 cm und t = 15 cm und den Winkel = 52,83°. Berechnen Sie die Länge der Seite r und die Größe der Winkel und . r2 = s2 + t2 – 2 s t cos() = 144 r = 12 cm Error! = Error! = arcsin Error!= 95,08° = 180° – – = 32,09° 3. Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in trigonometrischen Funktionen sind im Bogenmaß angegeben. a) b) 4. ln (sin2(5x) – 0,2) = –0,2294 3;e2x +5 = 148,4 sin2(5x) – 0,2 = 0,795 sin2(5x) = 0,995 5x = 1,50 x = 0,3 e2x + 3 = 3.268.148 2x + 5 = 15 x = 5 Lösen Sie die folgenden Gleichungen nach x: a) s arcsin(bx2) = k arcsin(bx2) = Error! b) Error! = r Error! bx2 = sin Error! x2 = Error! x = 10ax = kr ax = log(kr) x = Error! 1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 bk – höbenreich-gruber 1. 2. 3. a) Der Wasserstand in einem Staubecken schwankt zwischen den Werten 50 m und 70 m. Der geringste Wasserstand ist nach 18 Tagen erreicht und nach weiteren 40 Tagen ist der Wasserstand maximal. Berechnen Sie die Gleichung dieses Wasserstandes W(t). b) Skizzieren Sie den Verlauf der Funktion f(x) = 5 + 3 sin (0,157x). Berechnen Sie dazu die Mittellage, die Amplitude, die Periode und die Verschiebung. Benutzen Sie das folgenden Koordinatensystem: a) Auf einer Straße fahren hintereinander die Fahrzeuge A und B mit gleicher Geschwindigkeit. Ein Beobachter im Punkt C (Normalentfernung zur Straße d = 5 m misst zu einem bestimmten Zeitpunkt den Winkel = 2° und den Winkel = 8°. Berechnen Sie den Abstand t der beiden Fahrzeuge A und B. b) In dem allgemeinen Dreieck (siehe Skizze) kennt man die Seiten s = 8 cm und t = 12 cm und den Winkel = 55,77°. Berechnen Sie die Länge der Seite r und die Größe der Winkel und . Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in trigonometrischen Funktionen sind im Bogenmaß angegeben. a) b) 4. Montag, 22. Oktober 2012 Gruppe A ln (sin2(3x) – 0,2) = –0,2294 3;e2x + 3 = 148,4 Lösen Sie die folgenden Gleichungen nach x: a) b) b arcsin(cx2) = r Error! = s 1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 bk – höbenreich-gruber 1. 2. 3. a) Der Wasserstand in einem Staubecken schwankt zwischen den Werten 40 m und 100 m. Der geringste Wasserstand ist nach 12 Tagen erreicht und nach weiteren 40 Tagen ist der Wasserstand maximal. Berechnen Sie die Gleichung dieses Wasserstandes W(t). b) Skizzieren Sie den Verlauf der Funktion f(x) = 5 + 3 sin (0,157x). Berechnen Sie dazu die Mittellage, die Amplitude, die Periode und die Verschiebung. Benutzen Sie das folgenden Koordinatensystem: a) Auf einer Straße fahren hintereinander die Fahrzeuge A und B mit gleicher Geschwindigkeit. Ein Beobachter im Punkt C (Normalentfernung zur Straße d = 5 m misst zu einem bestimmten Zeitpunkt den Winkel = 4° und den Winkel = 10°. Berechnen Sie den Abstand t der beiden Fahrzeuge A und B. b) In dem allgemeinen Dreieck (siehe Skizze) kennt man die Seiten s = 8 cm und t = 15 cm und den Winkel = 52,83°. Berechnen Sie die Länge der Seite r und die Größe der Winkel und . Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in trigonometrischen Funktionen sind im Bogenmaß angegeben. a) b) 4. Montag, 22. Oktober 2012 Gruppe B ln (sin2(5x) – 0,2) = –0,2294 3;e2x +5 = 148,4 Lösen Sie die folgenden Gleichungen nach x: a) b) s arcsin(bx2) = k Error! = r