Grundbegriffe der Vektorrechnung

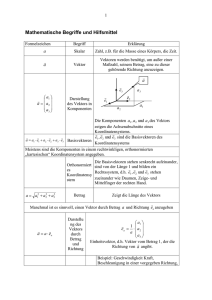
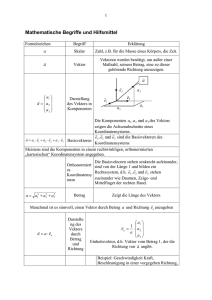
R. Brinkmann http://brinkmann-du.de
Seite 1
17.11.2010
Grundbegriffe der Vektorrechnung
Vektor und Skalar
Ein Teil der in Naturwissenschaft und Technik auftretenden Größen ist bei
festgelegter Maßeinheit durch die Angabe einer Maßzahl vollständig bestimmt.
Solche Größen sind beispielsweise:
Länge, Masse, Arbeit, Energie, Zeit, Temperatur und Potential.
Diese Größen können auf einer Skala dargestellt werden und heißen deshalb skalare
Größen oder Skalare.
Größen, die zu ihrer eindeutigen Bestimmung neben der Angabe der Maßzahl noch
die der Richtung benötigen, heißen vektorielle Größen oder Vektoren.
Die Geschwindigkeit und die Beschleunigung sind solche Größen.
Vektoren werden durch Pfeile dargestellt. Die Pfeillänge bestimmt den Betrag des
Vektors, die Richtung des Pfeils bestimmt die Richtung des Vektors.
Ein Vektor ist somit im Vergleich zu einem Skalar eine gerichtete Größe.
Unterschieden werden freie Vektoren, liniengebundene Vektoren und ortsgebundene
Vektoren.
Die wesentliche Eigenschaft eines freien Vektors ist, dass er entlang seiner
Wirkungslinie und parallel im Raum verschoben werden darf.
Vektoren von gleicher Länge und gleicher Richtung sind einander gleich.
JJJG G
JJJG G
AB = a und CD = b
G
AB = a = a
G
CD = b = b
B
a
A
Die Kraft, die an einem Körper angreift,
stellt einen liniengebundenen Vektor dar.
Dieser darf entlang seiner Wirkungslinie
beliebig verschoben werden, nicht aber
parallel dazu.
D
b
C
Wirkungslinie
F
Ein ortsgebundener Vektor, auch Ortsvektor genannt hat einen festen Angriffspunkt
und darf nicht verschoben werden.
Addition von Vektoren.
G
G
G
Einen Vektor b zu einem Vektor a addieren heißt, den Vektor b parallel zu sich
G selbst
so zu verschieben, dass sein Anfangspunkt
a fällt.
G auf den Endpunkt des Vektors
G
Die Verbindung des Anfangspunktes von a mit dem Endpunkt von b ergibt den
G
G G G
Summenvektor c.
c = a+b
Erstellt von R. Brinkmann p50_vektor_01.doc
20.03.2010 10:28
Seite 1 von 5
R. Brinkmann http://brinkmann-du.de
Seite 2
17.11.2010
Addition zweier Vektoren
b
b
c=
a+
b
b
a
a
a
a+
b
b
)
(
a
b
a
a
+
+b
c
c
c
Bei der Addition von drei Vektoren
müssen diese nicht in einer Ebene liegen.
Jeder der drei Vektoren ist eine gerichtete
Strecke im Raum.
Die drei Vektoren können ein räumliches
Gebilde aufspannen.
Es gilt das Assoziativgesetz:
G G G G G G
G G G
a+b +c = a+ b+c = a+b+c
(
b+
b+
Für die Addition zweier
Vektoren
gilt das
Kommutativgesetz.
G G G G
a+b = b+a
a+b
)
b
a
Zwei betragsgleiche Vektoren mit
entgegengesetzter Richtung heißen
Gegenvektoren. Addiert man diese, so erhält man
als Summe einen Vektor, dessen Anfangspunkt
mit seinem Zielpunkt zusammenfällt. Da der
Betrag dieses Summenvektors Null ist, heißt er
Nullvektor. Er hat keine bestimmte Richtung.
a
-a
G
G
G
a + −a = 0
( )
Subtraktion von Vektoren.
Subtraktion zweier Vektoren
-a
Die Vektorsubtraktion kann auf die
Vektoraddition zurückgeführt werden.
Ein Vektor wird subtrahiert, indem man
den Gegenvektor addiert.
c=b-a
b
a
Erstellt von R. Brinkmann p50_vektor_01.doc
20.03.2010 10:28
Seite 2 von 5
R. Brinkmann http://brinkmann-du.de
Seite 3
17.11.2010
Beispiel 1:
Vektoraddition zeichnerisch.
An einem Stromverteilermast greifen in einem Punkt 4 Kräfte an, die in einer Ebene
liegen sollen. Zeichnerisch ist der Betrag und die Richtung der Resultierenden zu
bestimmen. Zeichenmaßstab: 1 cm entspricht 100N.
Zeichnerische Lösung:
Aufgabenstellung:
F2 = 400 N
F3 = 300 N
120
F2 = 400 N
70
80
120
F1 = 380N
70
F4 = 440N
80
F3 = 300 N
42
F4 = 440N
F1 = 380 N
R = 220 N
JG JG JJG JJG JJG
R = F1 + F2 + F3 + F4
JJG
JG JG
⇒ R = 220N und ) F1 ,R = −42 0
(
)
Der Betrag der Resultierenden beträgt 220 N. Das bedeutet, an dem Verteilermast
wirkt eine Restkraft von 220 N.
JG
Die Wirkungsrichtung beträgt in Bezug auf F1 − 420 oder 3180
Bemerkung:
Gegen den Uhrzeigersinn (links herum) werden Winkel von der Bezugsgeraden
ausgehend positiv gezählt, im Uhrzeigersinn (rechts herum) hingegen negativ.
Die zeichnerische Lösung ist immer nur eine Näherungslösung. Sie ist nur so genau,
wie gezeichnet werden kann. Eine rechnerische Lösung, die in einem späteren
Kapitel behandelt wird liefert als exaktes Ergebnis:
JG
JG JG
R = 224,009N und ) F1 ,R = −41,585 0
(
)
Beispiel 2:
Gesucht ist die Entfernung des
Halbierungspunktes E der Strecke DB vom
Punkt
A, wenn B der Endpunkt des Vektors
JJJG
AB
JJJG und D der Endpunkt des
JJJG Vektors
JJJG
AD ist und die Vektoren AB und AD
vom Punkte A ausgehen.
D
E
A
Erstellt von R. Brinkmann p50_vektor_01.doc
C
20.03.2010 10:28
B
Seite 3 von 5
R. Brinkmann http://brinkmann-du.de
Seite 4
17.11.2010
Lösung:
JJJG JJJG JJJG
JJJG JJJG JJJG
AD + DB = AB ⇔ DB = AB − AD
Da E der
der Strecke DB ist, gilt:
JJJG Halbierungspunkt
JJJG JJJG
JJJG DB AB − AD
DE =
=
2
2
JJJG JJJG JJJG JJJG
JJJG
JJJG JJJG JJJG JJJG AB − AD AB + AD
=
Für AE gilt dann AE = AD + DE = AD +
2
2
1 JJJG JJJG
Für die Strecke AE gilt: AE = AB + AD
2
JJJG JJJG JJJG
Da aber AC = AB + AD ist, muss E auch Halbierungspunkt der
Strecke AC sein.
Damit ist bewiesen, dass im Parallelogramm die Diagonalen durch ihren Schnittpunkt
halbiert werden.
Kosinus- und Sinussatz als Hilfsmittel für Vektorberechnungen.
Bislang wurden Vektoren zeichnerisch addiert. Ergebnisse von zeichnerischen
Lösungen sind nicht immer genau.
Kosinussatz:
In jedem Dreieck lässt sich das Quadrat
einer Seite aus den beiden anderen
Seiten und deren eingeschlossenem
Winkel berechnen
a2 = b2 + c 2 − 2 ⋅ b ⋅ c ⋅ cos ( α )
b2 = a2 + c 2 − 2 ⋅ a ⋅ c ⋅ cos ( β )
c 2 = a2 + b2 − 2 ⋅ a ⋅ b ⋅ cos ( γ )
Sinussatz:
In jedem Dreieck ist das Verhältnis von
Seitenlänge zum Sinus des
gegenüberliegenden Winkels für alle
Seiten dasselbe:
a
b
c
=
=
sin ( α ) sin ( β ) sin ( γ )
C
γ
b
a
β
α
c
A
B
C
γ
b
a
β
α
A
c
B
Beispiel 3
JG
JJG
JJG
JJG
Zwei Kräfte F1 und F2 mit F1 = F1 = 60N und F2 = F2 = 40N
schließen miteinander einen WinkelJGvon α = 50 0 ein.
JG
JG
JJG
Wie groß ist die resultierende Kraft R ? Welchen Winkel bildet R mit F1 bzw. F2?
Erstellt von R. Brinkmann p50_vektor_01.doc
20.03.2010 10:28
Seite 4 von 5
R. Brinkmann http://brinkmann-du.de
JG JG JJG
R = F1 + F2
JG JJG
( F1 ,F2
(
Seite 5
) ist α = 50
17.11.2010
0
α2
β = 180 0 − 50 0 = 130 0
Nach dem Kosinussatz gilt:
R=
=
(
F2
F12 + F22 − 2 ⋅ F1 ⋅ F2 ⋅ cos ( β )
(
R
F2
α2
α α1
))
602 + 402 − 2 ⋅ 60 ⋅ 40 ⋅ cos 130 0 N 2
β
F1
≈ 91,024N
Nach dem Sinussatz gilt:
sin ( β )
F
R
=
⇔ sin ( α1 ) = 2 ⋅ sin ( β )
F2 sin ( α1 )
R
sin ( α1 ) =
(
)
40
⋅ sin 130 0 ≈ 0,337
91,024
⇒ α1 = arc sin ( 0,337 ) ≈ 19,672 0 ist der von R und F1 eingeschlossene Winkel.
Da α1 und α 2 sich zu α = 50 0 ergänzen, wird der zwischen F2 und R liegende Winkel
α 2 = 50 0 − α1 = 50 0 − 19,672 0 ≈ 30,328 0
Zusammenfassung:
1. Ein Vektor ist eine gerichtete, orientierte Strecke im Raum.
2. Vektoren sind gleich, wenn sie in Betrag, Richtung und Orientierung
übereinstimmen.
3. Zwei Vektoren werden addiert, indem man
den Anfangspunkt des einen Vektors an die
Spitze des anderen setzt.
G G
Der Summenvektor a + b
zeigt dann vom Anfangspunkt des ersten
Vektors zum Endpunkt des zweiten Vektors.
a+
b
b
a
4. Vektor und Gegenvektor haben den gleichen Betrag und die gleiche Richtung,
aber entgegengesetzte Orientierung.
G G G
5. Den Differenzvektor c = b − a
G
erhält man, indem man zu b
den Gegenvektor
von a addiert :
G G G
G
b − a = b + −a
( )
Erstellt von R. Brinkmann p50_vektor_01.doc
-a
c=b-a
b
a
20.03.2010 10:28
Seite 5 von 5