Höhere Mathematik I für Bau, Geo, Umwelt — Blatt 4

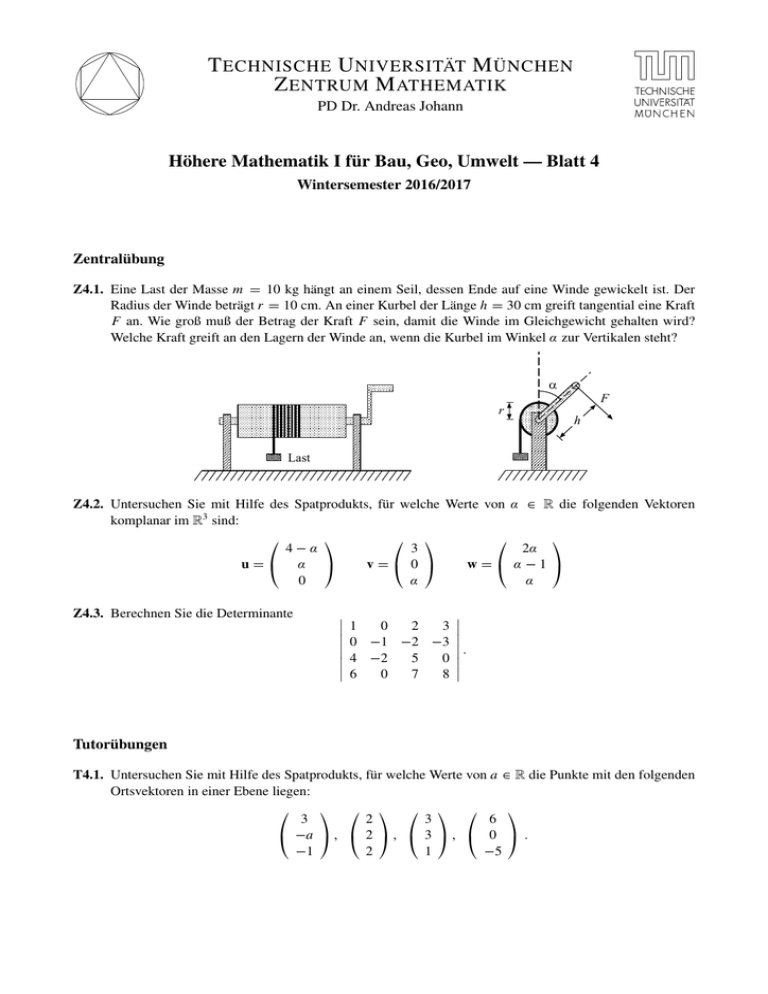
T ECHNISCHE U NIVERSITÄT M ÜNCHEN
Z ENTRUM M ATHEMATIK
PD Dr. Andreas Johann
Höhere Mathematik I für Bau, Geo, Umwelt — Blatt 4
Wintersemester 2016/2017
Zentralübung
Z4.1. Eine Last der Masse m = 10 kg hängt an einem Seil, dessen Ende auf eine Winde gewickelt ist. Der
Radius der Winde beträgt r = 10 cm. An einer Kurbel der Länge h = 30 cm greift tangential eine Kraft
F an. Wie groß muß der Betrag der Kraft F sein, damit die Winde im Gleichgewicht gehalten wird?
Welche Kraft greift an den Lagern der Winde an, wenn die Kurbel im Winkel α zur Vertikalen steht?
α
F
r
h
Last
Z4.2. Untersuchen Sie mit Hilfe des Spatprodukts, für welche Werte von α ∈ R die folgenden Vektoren
komplanar im R3 sind:






4−α
3
2α
u= α 
v= 0 
w= α−1 
0
α
α
Z4.3. Berechnen Sie die Determinante
1
0
2
3 0 −1 −2 −3 .
4 −2
5
0 6
0
7
8 Tutorübungen
T4.1. Untersuchen Sie mit Hilfe des Spatprodukts, für welche Werte von a ∈ R die Punkte mit den folgenden
Ortsvektoren in einer Ebene liegen:

     

6
3
2
3
 −a  ,  2  ,  3  ,  0  .
−5
1
2
−1
T4.2. Gegeben sei ein Dreieck im R3 , dessen Eckpunkte durch die Ortsvektoren
 
 


2
3
x +1
a =  1 , b =  1 , c =  3 
0
2
2
gegeben sind. Bestimmen Sie ein x ∈ N, sodass das Dreieck den Flächeninhalt 3 besitzt.
T4.3. Berechnen Sie die folgende Determinante:
2
0 −3 2 1 −2 −1 0 1 −2
1 1 1
1
2 1 T4.4. Wir betrachten erneut den Raum P2 ([0, 1]) der reellen Polynome mit Grad kleiner gleich 2 auf dem
Intervall [0, 1] zusammen mit dem Skalarprodukt
Z
h p, qi :=
1
p(x) · q(x)dx
für p, q ∈ P2 ([0, 1])
0
von Blatt 3 Aufgabe T3.4. Seien nun die Polynome p1 , p2 , p3 ∈ P2 ([0, 1]) gegeben als
p1 (x) = 2x 2 − 1;
p2 (x) = x;
und
3
p3 (x) = − x + 1
2
√
gegeben. Zudem sei für p ∈ P2 ([0, 1]) die vom Skalarprodukt induzierte Norm p P := h p, pi
gegeben. Berechnen Sie
(a) Jeweils paarweise von p1 , p2 und p3 das Skalarprodukt.
(b) Die Norm von p1 , p2 und p3 .
(c) Den Winkel den p1 und p3 einschließen.
(Hinweis: für diese Teilaufgabe dürfen Sie einen Taschenrechner verwenden.)
Die Tutoraufgaben werden am 11.11.2016 besprochen.