A 7e Wahrscheinlichkeitsverteilungen

Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
Wahrscheinlichkeitsverteilungen
Lernziele:
•
•
•
Wahrscheinlichkeitsfunktion und Verteilungsfunktion diskreter Verteilungen
berechnen und zeichnen können.
Dichtefunktion und Verteilungsfunktion stetiger Verteilungen berechnen und
zeichnen können
Erwartungswerte diskreter und stetiger Verteilungen berechnen können.
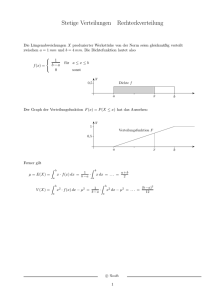
Wahrscheinlichkeitsfunktion diskreter Verteilungen
Achsenbezeichnung: 1. Achse ist die x-Achse, 2. Achse ist die Wahrscheinlichkeits -Achse
Beispiel: Würfeln mit einem fairen Würfel: Ω={1,2,3,4,5,6}
Die Zufallsgröße X sei die Augensumme, x sei der jeweilige Versuchsausgang.
Die Wahrscheinlichkeit für die Augensumme x schreiben wir als W(X=x).
Weil alle Versuchsausgänge die Wahrscheinlichkeit 1/6 haben können wir die
Wahrscheinlichkeitsfunktion leicht zeichnen (alle Werte auf der „y-Achse“, besser W-Achse
betragen 1/6):
Wahrscheinlichkeitsfunktion:
1
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
Beispiel: “ Mensch-ärgere dich nicht“
(man kann erst beginnen, wenn man einen 6er würfelt).
Definition von X:
X=k, wenn der 6er erst beim k-ten mal kommt.
1
(Wahrscheinlichkeit für 6er beim 1. mal würfeln)
6
5 1
P(X=2)= ⋅ (Wahrscheinlichkeit für 6er erst beim 2. mal würfeln)
6 6
5 5 1
P(X=3)= ⋅ ⋅ (Wahrscheinlichkeit für 6er erst beim 3. mal würfeln)
6 6 6
5
1
P(X=k)= ( ) k −1 ⋅ (Wahrscheinlichkeit für 6er erst beim k. mal würfeln)
6
6
P(X=1)=
Wahrscheinlichkeitsfunktion:
Bei stetigen Verteilungen ist die Angabe einer Wahrscheinlichkeitsfunktion sinnlos, da
das genaue Erzielen eines bestimmten Ereignisse die Wahrscheinlichkeit Null besitzt
(die Wahrscheinlichkeit, eine Zahl in [3,4] genau zu erraten (auf unendlich viele Kommastellen genau ist nicht möglich, oder besser, unendlich unwahrscheinlich).
Eine sehr übersichtliche Darstellung ist die
Verteilungsfunktion F(x) einer diskreten Verteilung
2
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
Verteilungsfunktion F(x) diskreter Verteilungen
F(x) = P(X=x1 oder X=x2 oder X=x3 ………oder X=xk),
alle Wahrscheinlichkeiten werden also summiert.
k
Gute Schreibweise: F(x)=
∑ P( X = xi )
i =1
Beispiel: Würfeln mit einem fairen Würfel: Ω={1,2,3,4,5,6}
Verteilungsfunktion:
3
7. Semester
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
Beispiel: “ Mensch-ärgere dich nicht“
F(x)= P(X≤k) =P(X=1)+P(X=2)+P(X=3)+…..+P(X=k) =
1 5 1 5 5 1
5
1
+ ⋅ + ⋅ ⋅ +…+ ( ) k −1 ⋅ =
6
6
6 6 6 6 6 6
5 k
1− ( )
1
6
⋅
6 1− 5
6
5 k
=1- ( ) (Summe einer „geometrischen Folge“ ,wird in der Schulstunde erklärt)
6
Verteilungsfunktion:
Eigenschaften von diskreten Verteilungsfunktionen:
1. P(X≤a)=F(a)
2. P(X>a)=1-F(a)
3. P(a<X≤b)=F(b)-F(a)
(woher kennen wir das schon:
Funktion an der oberen Grenze minus Funktion an der unteren Grenze?)
4
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
Dichtefunktion f(x) stetiger Verteilungen
Bei stetigen Verteilungen wird die Wahrscheinlichkeitsfunktion nun als
(Wahrscheinlichkeits-)Dichtefunktion f(x) bezeichnet. Wichtiger ist allerdings die
Verteilungsfunktion F(x) stetiger Verteilungen
Sie gibt die Wahrscheinlichkeit an, dass eine Messgröße, die durch eine Dichtefunktion f(x)
beschrieben wird, in einem Intervall [a,b] liegt.
b
Die Wahrscheinlichkeit für P(a<X≤b)=F(b)-F(a)= ∫ f ( x ) dx
a
Eigenschaften von stetigen Verteilungsfunktionen:
a
1. P(X≤a)=F(a)=
∫ f ( x)dx
−∞
∞
2. P(X≥a)=1-F(a)=
∫ f ( x)dx
a
b
3. P(a≤X≤b)=F(b)-F(a)=
∫ f ( x)dx
a
5
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
Übung:
Eine Bergbaufirma geht von folgender- empirisch ermittelter- Dichtefunktion für den monatlichen Absatz eines seltenen Erzes aus (in kg):
0,04x
f(x)= 0,4-0,04x
0
0≤x≤5
5<x≤10
Sonst
Berechnen Sie die Wahrscheinlichkeit für:
a. mehr als 5000 kg verkauft. Lösung: 0,5
b. Absatz zwischen 4000kg und 6000 kg. Lösung: 0,36
Übung:
Die Lebensdauern von Solarzellen sei verteilt nach
4
1- x 2
5
0≤x≤1,5
0
Sonst
f(x)
Berechnen Sie die Wahrscheinlichkeit für:
a. Lebensdauer >10 Jahre. Lösung:14,8%
b. Lebensdauer zwischen 3 und 8 Jahren. Lösung: 42,8%
c. Lebensdauer genau (auf die Minute genau)10 Jahre. Lösung ungefähr 0%
Hierzu ein mathematischer Witz:
„Wie alt ist dieses Dinosaurierskelett, Herr Museumswärter?“
„56 Millionen Jahre und 14 Tage“.
„Wieso und 14 Tage?“
„Nun, vor 14 Tagen habe ich hier mit der Arbeit begonnen, da war es schon 56 Millionen Jahre alt“.
6
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
Erwartungswerte E(x) diskreter und stetiger Verteilungen
In der Statistik haben wir definiert:
x ⋅ n + x ⋅ n + .........xk ⋅ nk
Mittelwert μ einer Datenmenge; μ = 1 1 2 2
,
n
der Wert x1 kommt dabei n1 mal vor usw, n1+ n2 +….+ nk=n,
eine elegante Schreibweise lautet:
k
μ=
n
∑ xi ⋅ ni
i =1
In der Wahrscheinlichkeitsrechnung definieren wir den
Erwartungswert E(X) für diskrete Verteilungen ähnlich:
k
E(x)= ∑ xi ⋅ P ( X = xi )
i =1
die relativen Häufigkeiten
ni
n
approximation die Wahrscheinlichkeiten
P( X = xi )
Beispiel: Würfeln mit einem fairen Würfel: Ω={1,2,3,4,5,6}
1
E(X)= ⋅ (1 + 2 + 3 + 4 + 5 + 6) = 3,5
6
Hat man eine sogenannte Gewinnfunktion g(X), die jedem xi einen Gewinn (oder Verlust)
zuordnet, so lautet der
Erwartungswert einer Gewinnfunktion
k
E(x)= ∑ g ( xi ) ⋅ P ( X = xi )
i =1
Übung:
Eine Versicherung versichert Maschinen, bei denen die Störungen A,B, und C mit den Wahrscheinlichkeiten 0,01 sowie 0,15 sowie 0,1 auftreten. Die zu zahlenden Schadensbeträge lauten 15000€,2000€ und 7000€. Berechnen Sie den Erwartungswert (der Gewinnfunktion).
Lösung: 1150€
Übung:
X sei die Augensumme beim Werfen 2er fairer Würfel. Berechnen Sie den Erwartungswert.
Eventuell können Sie die Berechnung durch die Zeichnung der Wahrscheinlichkeitsfunktion
abkürzen.
Lösung:7
7
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
Den Erwartungswert E(x) einer stetigen Verteilung definieren wir mit Hilfe des Integrals:
E( X ) =
+∞
∫ x ⋅ f ( x)dx
−∞
Den Erwartungswert E(G(x)) der Gewinnfunktion einer stetigen Verteilung wird definiert:
E( X ) =
+∞
∫ g ( x) ⋅ f ( x)dx
−∞
Einige Eigenschaften des Erwartungswerts einer stetigen Verteilung:
E(X+c)=E(X)+c
E(a X)=a E(X)
E(a X+c)=a E(X)+c
E(g(X)+c)=E(g(X))+c
Beispiel: “ Tierarzt“
Eine seltene (p=0,06), nicht übertragbare Schweinekrankheit wird getestet wie folgt:
Der Arzt verlangt 100€ pro Blutuntersuchung, aus Kostengründen schlägt der Bauer vor, dass
zuerst die Blutproben aller 5 Schweine eines Käfigs gemischt werden, erst wenn dieser Test
positiv ist werden alle Blutproben auch einzeln untersucht. Diskutieren Sie den Vorschlag des
Bauern.
Lösung:
X… Ergebnis der ersten Blutprobe
x1… negativ
x2… positiv
k
E(g(
E(g(X
g(X))= ∑ g ( xi ) ⋅ P ( X = xi )
i =1
100€
alle gesund
600 €
Mindestens 1 krank
g(x)
8
Mathematik: LehrerInnenteam
Arbeitsblatt 7e
7. Semester
P(X=negativ)=0,945
P(X=positiv)= 1- 0,945
E(g(X))= 100 ⋅ 0,94 + 600 ⋅ (1 − 0,945 ) ≅ 233€
Angenommen, der Bauer hat 50 Schweine und möchte Sie möglichst gleichmäßig auf Käfige
aufteilen.
Wie teilt er die Schweine am besten auf, sodass die Kosten für die Blutuntersuchungen minimal sind:
(x…Tiere pro Käfig)
Er berechnet das Minimum der
50
E(g(X))-Funktion
⋅ 0,94 x ⋅100 + ( x + 1) ⋅100 ⋅ (1 − 0,94 x ) (Begründung?)
x
mit Geogebra oder einem Computeralgebraprogramm (viel Spass sonst!) zu 4,64 er wird also
5 Schweine pro Käfig halten um die Kosten zu minimieren.
9