4_Kapitel PC0

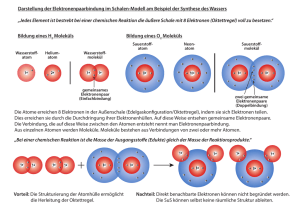
4.
Mikroskopische Betrachtungen: Dualismus Teilchen-Welle, Atomkerne, Elektronen, Atome, Moleküle
Mikroskopische Systeme sind nicht kontinuierlich also
nicht durch Formeln der klassischen Physik beschreibbar
Im 18. und 19. Jahrhundert nutzte man die Farbzerlegung
im Glasprisma für erste spektroskopische Untersuchungen
Folgende experimentelle Effekte zeigen direkt, dass die mikroskopische Welt
diskret (abgestuft, gequantelt) ist:
→
Die Frauenhoferschen Linien (1814 Frauenhofer: Dunkle Linien im
Sonnenspektrum)
Absorptionslinien im Sonnenspektrum wie sie von Frauenhofer (Optiker) 1814
gefunden wurden. Die Absorptionen stammen mehrheitlich von der Sonnenatmosphäre (auch Eisen, und andere Schweratome). Natürlich sind auch Absorptionslinien aus der Erdatmosphäre enthalten (schwächer).
→
Linienspektren von Atomen (1859 Bunsen und Kirchhoff)
He-Entladungslampe (links) und das wellenlängenaufgelöste He-AtomEmissionsspektrum (hinter dem Prisma) im sichtbaren Wellenlängen-
bereich. Es gibt weitere, nicht-sichtbare Linien im ultravioletten Bereich
(unter 440 nm).
Für das Wasserstoffatom wurden Linienserien über einen breiten Wellenlängenbereich gefunden.
Name der Serie Grundniveau Wellenlängenbereich Entdeckungsjahr
Lyman-Serie
1
ultraviolett
1906
Balmer-Serie
2
sichtbar
1885
Paschen-Serie
3
infrarot
1908
Brackett-Serie
4
infrarot
1922
Pfund-Serie
5
infrarot
1924
Emissionsspektrum des Eisens. Die hohe Liniendichte ist auf die vielen Elektronen des Eisens und seine komplexe Elektronenstruktur zurückzuführen (3 dSchale)
Schnell wurde klar, dass die Linien wie ein „bar code“ spezifisch für einzelne
Elemente sind und sich atomare und molekulare mikroskopische Eigenschaften
in den Spektren abbilden. Dies half auch bei der Entdeckung von seltenen Elementen.
Stickstoffentladungslampe und zugehöriges sichtbares Emissionsspektrum (Beachte das Spektrum ist stärker aufgespreizt gegenüber
dem He-Spektrum von oben).
Unsere Interpretation heute: Die hohe Liniendichte entsteht durch die
gleichzeitige Schwingungsanregung bei der elektronischen Anregung.
Fazit: Auch in Molekülen sind die internen Energien gequantelt (diskret).
Damals: Völlig unklar blieb, warum es scharfe Linien gibt und welche
Bedeutung sie besitzen.
Die klassische Physik lässt nicht zu, dass nur diskrete Energien möglich
sind: Alles ist kontinuierlich.
Fazit: Um Atome und Moleküle verstehen zu können müssen wir uns um
die Eigenschaften mikroskopischer Materie kümmern.
4.1 Die Wellennatur der Materie: Die Beugung mit Teilchenstrahlen
Die Beugung mit Elektronen:
Dass Teilchen Impuls und kinetische Energie besitzen ist trivial. De Broglie forderte jedoch 1924, dass Materie auch Welleneigenschaft besitzt.
Seine theoretisch gefundene Behauptung:
mit p Impuls = mv
De Broglie (1924)
Also ein bewegtes mikroskopisches Teilchen hat eine Wellenlänge. Die
Bestätigung der Wellennatur der Materie erfolgte durch Beugung von
Elektronen an Kristallgittern (Davisson und Germer, 1927).
Elektronen fallen von links oben auf einen Kristall. Wenn Elektronen Welleneigenschaft besitzen, muss es Beugung an den Atomen der Oberfläche aber auch an den Atomen der unteren Schicht geben. Jedes Atom
ist Ausgangspunkt einer Kugelwelle. Die „reflektierten Strahlen“ werden
nur bei dem Winkel sichtbar, bei welchem sich die Wellen aus beiden
Ebenen durch positive Interferenz verstärken. Dazu muss der Gangunterschied der beiden Wellen 2gsinΘ ein ganzzahliges Vielfaches von λ
sein:
2g sinΘ = n λ
"Braggsche Reflektionsbedingung"
Man kann diesen Beugungseffekt vielfältig nutzen:
⇒
⇒
⇒
Bei bekannten λ, n, Θ kann man nun die Gitterkonstante g berechnen
Mit bekanntem Θ, g, n kann man die Wellenlänge λ bestimmen
(Gittermonochromator)
Mit Teilchen bekannter Masse und Geschwindigkeit und bekanntem Θ kann man die Wellenlänge λ der Teilchen bestimmen.
Die intensivsten Reflektionen beobachtet man für n=1 und λ ≈ g .Für
typische Kristallgitterabstände führen hochenergetische 10 kV-Elektronen zu den intensivsten Streuspektren, da dann die Wellenlänge λ der
Elektronen nach de Broglie ungefähr gleich der Gitterkonstanten g (0,1 0,2 nm) ist.
Vorlesungsversuch: Elektronenbeugung an Graphit
Prinzip: Schnelle Elektronen werden an einer polykristallinen Schicht
von Graphit (senkrechter Einfall zur Schichtstruktur) gebeugt und treffen
dann auf einen Fluoreszenzschirm, wo sie Interferenzringe erzeugen.
Messmethode: Elektronen treten aus der Glühkathode C aus und werden durch ein System von Elektroden G1, G2, G4 gebündelt und durch
eine Hochspannung UA an der Elektrode G3 beschleunigt. Die Elektronen treten durch eine dünne Graphitschicht durch und interferieren dabei. Die gebeugten Elektronen treffen im Abstand 2R als System von
Ringen mit Durchmesser 2r auf einen Fluoreszenzschirm.
e--Strahl trifft senkrecht
zum Schichtaufbau.
Die hintereinander
liegenden Atome definieren
den beobachteten
„Gitterabstand“
Braggsche Reflektionsbedingung:
Broglie-Wellenlänge:
2g sinΘ=nλ mit n=1,2….de
λ=h/p=h/mv
mit UA=1/2 mv2 folgt λ =h/(2meUA)1/2.
Der Braggwinkel Θ wird aus dem Radius der Interferenzringe r bestimmt,
wobei der Beugungswinkel zur Mittelachse α = 2Θ ist (Θ aus vorangegangener Abb).
Mit sinα = r/(2R) gilt: r= 2Rsin(2Θ)
Mit der Beziehung sin2Θ=2sinΘ für kleine Θ.
ist r=2R⋅ sin2Θ=2R⋅2sinΘ für kleine Θ.
Es folgt demnach r=2R2⋅(nλ/2g)=2R(nλ/g) oder g = 2Rnλ/r
Bei bekanntem Radius des Glaskolbens R, berechnetem λ und gemessenem r wird der Abstand g der Atomebenen bestimmt.
Rechenbeispiel: UA=10,7kV daraus die de Broglie-Wellenlänge:
λ=6,626⋅10-34Js/(2⋅9,109⋅10-31kg⋅1,609⋅10-19C⋅10,7⋅103 V)1/2=11,83⋅10-12m
(für n=1): g=2Rλ/r eingesetzt: R=65⋅10-3m, 2r1=18⋅10-3m 2r2=31⋅10-3m
Ergebnis: g1=171 pm (Literatur 213 pm) g2=99pm (Literatur 123pm)
Wichtiges Experiment: Verändern der Elektronenenergie
Größere Energie - kleinere Wellenlänge - weniger „Ablenkung“
Kleinere Energie – größere Wellenlänge – mehr „Ablenkung“
Fazit: De Broglie hat Recht! λ=h/p=h/mv h war noch unklar, da man g
nicht kannte
4.2 Die mikroskopische Materie ist diskret und es gibt
verschiedene (Elementar-) Teilchen
4.2.1 Ionen und Elektronen
Durch Gasentladungen bei niedrigen Drücken werden geladene Teilchen
erzeugt.
Erklärung:
"Spontane" Ionen (z.B. aus kosmischer Strahlung) gewinnen kinetische
Energie
1
mv 2 = q ⋅ U
2
mit U als Potentialdifferenz an den Elektroden.
€
Durch Stoßprozesse entstehen lawinenartig neue Ladungsträger. Die
Entladung wird stationär, wenn jeder Ladungsträger für seinen Ersatz
sorgt. Beachte, dass die Elektroden Löcher haben. Neben der Leuchterscheinung in der Röhre beobachtet man auf dem Glas auf beiden Seiten
auch ein schwaches Leuchten. Bringt man leitfähige Farbstoffmoleküle
auf, so kann man das Leuchten verstärken. Offensichtlich gibt es geladene Teilchen, die durch die Löcher in den Elektroden fliegen.
(+) Anode → Kathodenstrahl mit negativen Ladungsträgern
(-) Kathode → Kanalstrahl mit positiven Ladungsträgern
Frage: Wie groß ist Ladung q und Masse m der Teilchen in den jeweiligen Strahlen?
Vorlesungsversuch : Spezifische Ladung des Elektrons
Prinzip: Elektronen werden in einem elektrischen Feld beschleunigt und
treten unter rechtem Winkel in ein Magnetfeld ein. Die spezifische Ladung des Elektrons kann dann aus der Beschleunigungsspannung, der
magnetischen Feldstärke und dem Radius der Elektronenbahn bestimmen.
Messmethode: Die Elektronen werden durch die Spannung U beschleunigt. Hierbei sind die potentielle Energie
und die kinetische
Energie
1
2
gleich und wir erhalten mit e ⋅ U = mv2 das Ladungs-
e
v2
(1). Die Geschwindigkeit kann
=
m 2U
wie folgt ermittelt werden: treten die Elektronen
in ein zur Bewegungs€
Masseverhältnis des Elektrons zu
richtung
senkrechtes Feld ein, so erfahren sie eine Lorentzkraft

 
F = e ⋅ v × B = e ⋅ v ⋅ B ⋅ sin(90°) = e€⋅ v ⋅ B , die senkrecht auf die Magnetfeldlinien
und die Bewegungsrichtung steht und die Elektronen auf eine Kreisbahn
€
zwingt. Auf der Kreisbahn sind Zentrifugalkraft
und die Lorentz-
e
⋅ B ⋅ r . Diese Beziehung wird in (1) eingem
e
2U
e e 2 B2 ⋅ r 2
setzt:
und umgeformt:
= 2 2 (2). Nun muss noch die
= 2
m B ⋅r
m m 2U
 4 3 2
€
I
Magnetfeldstärke bestimmt werden: B =   ⋅ µ0 ⋅ n ⋅ (3) wobei µ0 die
R
5
€
€
N
magnetische Feldkonstante ( 4π ⋅10−7 2 ), n die Wicklungszahl der HelmA
holtzspulen, I der Spulenstrom €
und R der Radius der Spulen ist.
kraft gleich und es folgt v =
Aus (3) wird die Magnetfeldstärke
berechnet und
€
dann aus (2) mit dem gemessenen Radius R bei
der Spannung U das Ladungs-Masseverhältnis
bestimmt.
Rechenbeispiel: Mit einem Spulenradius von 20
cm, einem Spulenstrom von 4.1 A und einer Windungszahl von 154 ergibt sich aus Gleichung (3)
ein Magnetfeld der Stärke 2.84.10-3 T. Eine Beschleunigungsspannung von 250 V wird benötigt um die Elektronen auf
eine Kreisbahn von 2 cm zu zwingen. Nach Gleichung (2) folgt damit ein
e/m-Verhältnis von 1.5.1011 As/kg.
4.2.2 Bestimmung des Verhältnisses von Ladung zu Masse von
Ionen (Flugzeitmassenspektrometrie: Inzwischen fliegen Proteine
und DNA-Fragmente im Massenspektrometer)
Die Spannung am Entstehungsort der Ionen sei U:
Es gilt dann:
Epot (zu Beginn) = Ekin (in feldfreier Strecke)
Also:
mit:
daraus:
m 2Ut 2
= 2

q
mit t als Flugzeit, m als Masse des Teilchens, v der Geschwindigkeit
des Teilchens im feldfreien Bereich und
€ U als Größe des Potentials am
Ionisierungsort.
⇒ Die schweren Ionen sind langsamer und kommen später als die
leichten Ionen: Ein solches Gerät heißt Flugzeit-Massenspektrometer.
Beispiel:
Wasserstoffion H+
m
Kg
 
=1,0443⋅10−8
As
 q  H+
Ampere A: 1A=1C/1s
Heutige Interpretation:
€
Die leichtesten Kanalstrahlteilchen sind die Wasserstoffionen.
Die Kathodenstrahlteilchen sind ca. 1840 mal leichter ("Elektronen").
Frage: Können wir q messen? Daraus wäre dann m bestimmbar.
4.2.3 Bestimmung der Elementarladung
Durch Zerstäuben von Öl entstehen durch Reibungselektrizität negativ
geladene Öltröpfchen. Diese fallen bei ausgeschaltetem elektrischen
Feld mit konstanter Geschwindigkeit v1 nach dem "Stokesschen Gesetz":
F(Gravitation) = meff ⋅ g = F(Luftreibung) = 6 π r η v1
Mit dieser Formel hat man nun einen Zugang zur Masse des Tröpfchens!
€
Dabei ist F(Gravitation) die Erdanziehungskraft, r der Tröpfchenradius,
η die Zähigkeit der Luft und
die vorher bekannte experimentell
gefundene Reibungskraft.
Bei der Berechnung muss man berücksichtigen, dass das Öl die Luft
verdrängt:
Die effektive Masse der Tröpfchen ist
meff = 4 π r 3 (ρÖl − ρLuft )
3
mit
als Dichte des Öls. Die Differenz ρÖl − ρLuft wird eingesetzt, um
€ die Verminderung der Fallgeschwindigkeit durch Auftrieb zu berücksich-
tigen.
€
⇒
⇒
Bestimmung des Tröpfchenradius r aus
(
)
3
meff g 4 πr ρÖl − ρLuft g
r=
=
6πηv1
6πηv1 3
€
€
r=
9 η v1
daraus ist die Masse des Tröpfchens bestimmbar.
2 ρÖl − ρLuft g
(
)
Bei eingeschaltetem elektrischem Feld E können die Tröpfchen zum
Stillstand gebracht werden:
F(Gravitation) = meff ⋅ g = F(elektrostatisch) = q ⋅ E
€
Dabei ist qE die Kraft, die das elektrische Feld der Stärke E auf Tröpfchen der Ladung q ausübt.
Die Feldstärke eines mit der Spannung U geladenen Plattenkondensators bei Plattenabstand d ist E=U/d in [V/m].
Versuche mit Tröpfchen verschiedener Größe zeigen, dass q ein negatives ganzzahliges Vielfaches einer kleinsten Ladung e ist.
e = 1,602 ⋅ 10 -19 As (auch Coulomb, C)
"Elementarladung"
-12
Mit (m/e)Elektron = 5,685 ⋅ 10 kg/As und (m/e)H+ = 1,0443 ⋅ 10-8
kg/As ergibt sich mit der Annahme gleicher Beträge der Ladung auf eund H+ ("Elementarladung")
me- = 9,109 ⋅ 10-31 kg
mH+ = 1,673 ⋅ 10-27 kg
______________________
Frage nun: Wie muss man sich ein H-Atom in seinen Dimensionen vorstellen?
Wo ist H+ (der positive Kern, hier das Proton) und wo ist das Elektron?
4.2.4 Die Dimensionen: Atome, Elektronen und Atomkerne (Rutherford 1911)
Ablenkung der α-Teilchen (dessen Masse ist 4
x
Masse des Protons
(H+)) durch Streuung an Atomkernen der Folie. Befund: Die meisten He2+
passieren ungestreut!
Rutherford schloss daraus auf kleine Kernradien (∼10-14 m im Vergleich
zu ~10-10 m Atomradius). Offenbar ist fast die gesamte Atommasse in
dem sehr kleinen (positiv geladenen) Atomkern konzentriert.
Wenn darüber hinaus die Elektronen klein gegenüber dem Gesamtatom
sind, sollte das Coulombsche Gesetz die Elektron-Kern Wechselwirkung
gut beschreiben.
Die Atome sind in der Relation der Abstände unserem Sonnensystem
ähnlich (Gravitation hat gleich Abstandsabhängigkeit wie CoulombGesetz), also essentiell leer.
Es entstehen viele Fragen: Warum kollabiert das Atom nicht? Was hält
benachbarte Atome auf Abstand? ……
Weiteres Problem:
⇒ Beschleunigte elektrische Ladungen (Elektronen auf Bahn) strahlen
aber nach der klassischen Elektrodynamik Energie ab (Zeichnung): Absturz von Elektronen in den Atomkern auf Spiralbahnen, erwartet nach
etwa 10-10 s. Das findet aber nicht statt: Also das ist eine weitere Bestätigung, dass mikroskopische Materie kompliziert zu beschreiben ist.
Offensichtlich kann die Stabilität von Atomen mit der klassischen Physik
nicht richtig beschrieben werden! Ebenso ist die diskrete Lichtemission
von Atomen nur mit bestimmten Farben klassisch nicht erklärbar.
Diesen Phänomenen kommt man näher, wenn man berücksichtigt, dass
Elementarteilchen auch Welleneigenschaften aufweisen.
3.2.2 Das Bohrsche Atommodell
Das Bohrsche Atommodell erklärt die Stabilität der Elektronenbahnen
und die Lichtemission von Atomen mit diskreten Farben an Hand der
Welleneigenschaften der Elektronen. Danach kann sich das Elektronen
stabil nur auf Kreisbahnen mit einem Umfang bewegen, in welche die
Wellenlänge des Elektrons als stehende Welle konstruktiv interferierend
„hineinpasst“.
konstruktive Interferenz
destruktive Interferenz
Modell von Bohr:
Nach Bohr läuft das Elektron mit der Masse me auf einer Kreisbahn mit
Radius r um den gemeinsamen Schwerpunkt von Elektron und Kern
der Masse mK und Ladung Z⋅e. Dies entspricht der Bewegung eines
Teilchens mit der reduzierten Masse µ = me · mK / (me + mK) um das
Zentrum des Kerns bei r = 0.
Da die Zentrifugalkraft µv2/r der stationären Umlaufbahn des Elektrons
gerade durch die Coulombkraft Fc kompensiert wird, muss gelten
1
Z ⋅ e2
µ v2
=
⋅
4 π ε0
r
r2
€
Daraus folgt für den Radius r der Kreisbahn
.
Solange die Geschwindigkeit v nicht eingeschränkt ist, ist jeder Radius r
erlaubt!
Schreibt man der Materie Wellennatur zu, gehört zu einer stationären
Bahn des Elektrons um den Kern eine stehende Welle. Der Bahnumfang
dieser Welle muss ein ganzzahliges Vielfaches der de Broglie-Wellenlänge λ = h / p = h / (µ · v) sein, damit sich die stehende Welle nicht
durch Interferenz auslöscht:
2πr=n⋅λ
(n = 1, 2, 3 .....)
Beispiel:
Danach sind für die Geschwindigkeit v des Elektrons
v =
n
h
h
=
⋅
µ⋅ λ 2π r µ
nur bestimmte Werte erlaubt: Quantelung durch ganze Zahlen n.
€ Ebenso sind dann für den Drehimpuls (Kapitel 1.7; v⊥r)

µ ⋅v ⋅ r = L = n ⋅ 
Abkürzung:  = h / 2π
und für die Radien der Elektronenbahnen
€
€
r =
€
n 2 h 2 ε0
n2
=
a0
Z
π µ Z e2
nur bestimmte Werte erlaubt.
Dabei ist a0 = ε0 h2 / (π µ e2) = 5,29177 · 10-11 m ≅ 0,5 Å der kleinste
Radius der Elektronenbahn für n = 1 im Wasserstoffatom (Z = 1): Bohrscher Radius.
Zu jeder möglichen durch n = 1, 2, 3… charakterisierten Elektronenbahn
gehört eine bestimmte Energie, welche die Summe aus potentieller und
kinetischer Energie ist.
Die potentielle Energie des Elektrons wird für r = ∞ mit Null festgesetzt.
Für r < ∞ ist die Energie wegen der Coulombanziehung des Elektrons
durch den Kern kleiner, d.h. negativ. Die potentielle Energie entspricht
der Arbeit, die frei wird, wenn sich das Elektron durch die elektrostatische Anziehungskraft von r=∞ nach r bewegt:
E
r
Ze 2  1
Ze 2 1 1
=
= ∫ F dr = ∫
dr =
(− + )
− 
c
4 πε0
2
πε
4
r
r ∞


r =∞
r =∞
r = ∞ 4 πε r
0
0
r
pot
r
Ze 2
Unbestimmtes Integral
€
Die kinetische Energie des Elektrons Ekin
E
kin
=
1 Z ⋅ e2
µ v2
=
⋅
ist wegen
4 π ε0 r 2
r
1
1
Z ⋅ e2 1
µ v2
=
⋅
⋅ =− E .
4 π ε0
2
r
2
2 pot €
€ Die Gesamtenergie ist dann
E = Ekin + E pot = −
1 Z ⋅ e2
⋅
2 4 π ε0 r
also negativ und geht für r → ∞ , das heißt n → ∞ , gegen Null. Setzen
€ wir den für r abgeleiteten Ausdruck in E ein, folgt
µ e4 ⋅ Z 2
Z2
E =−
= − Ry ⋅ 2 ,
8 ε02 h2 n2
n
€
wobei Ry die Rydbergkonstante in Energieeinheiten [J] ist und n als
Hauptquantenzahl bezeichnet wird.
Beispiel:
H-Atom Z = 1, n = 1 → E = - 2,178⋅10-18J = -13,6 eV
Die Ionisierungsenergie des Elektrons in der 1. Bahn (Bohrscher Radius)
ist also 13.6 eV. Ry=2,178⋅10-18J =13,6eV. Ry/(hc)= =1,097⋅107m-1 in
Wellenzahleneinheiten.
Wenn ein Elektron von einer weiter vom Atomkern entfernten Kreisbahn
2 (höhere Energie) auf eine näher am Kern liegende Bahn 1 herunterfällt, wird die dabei freiwerdende Energie (Energiedifferenz ΔE=E2-E1 der
Bahnen) als Licht abgestrahlt.
Bei Atomen mit mehr als einem Elektron ist die Elektronenenergie nicht
nur von der Hauptquantenzahl n = 1, 2, 3… abhängig, sondern auch von
der Nebenquantenzahl l=n-1,n-2,…0 sowie in Magnetfeldern von der
magnetischen Quantenzahl m=+l,+l-1,…-l und in elektrischen Feldern
von der Spinquantenzahl.
4.3 Die Wellennatur des Lichtes
Phänomene wie "Beugung", "Brechung", "Interferenz" und "Polarisation"
des Lichtes lassen sich durch das Wellenmodell erklären.
⇒
Zur Ausbreitung von Wellen ist nach der Erfahrung der makroskopischen Welt ein Träger notwendig (Wasserwelle, Schallwelle).
Wer ist der Träger der Lichtwelle? ("Lichtäther"?)
Ein Träger ist nicht notwendig. Vielmehr erzeugt eine sich zeitliches änderndes elektrisches Feld E ein sich zeitlich änderndes Magnetfeld H,
das wiederum ein sich zeitlich änderndes elektrisches Feld erzeugt usw.
Dieser Prozess führt zu einer Fortpflanzung der elektromagnetischen
Welle im Raum. Die harmonisch schwingenden elektrischen und magnetischen Vektoren des elektromagnetischen Lichtfeldes sind immer senkrecht zueinander orientiert und senkrecht zur Fortpflanzungsrichtung des
Lichtes.
Natürliches Licht ist unpolarisiert, das heißt E und H schwingen in allen
möglichen Orientierungen (statistische Änderungen im Laufe der Zeit),
aber senkrecht zueinander und senkrecht zur Fortpflanzungsrichtung
des Lichtes.
Bei linear polarisiertem Licht schwingen E und H jeweils in einer Ebene,
die sich zeitlich nicht ändert.
Linear polarisiertes Licht
Sich im Raum fortpflanzende elektromagnetische Felder transportieren
Energie! Stehende Wellen (s. Kapitel 1.9.9) dagegen transportieren keine Energie, sondern speichern Energie.
4.4 Die Teilchennatur des Lichtes
4.4.1 Der photoelektrische Effekt
Materialien, die mit genügend kurzwelligem UV-Licht bestrahlt werden,
emittieren Elektronen.
⇒
Elektronenemission wird nur beobachtet, wenn die Lichtfrequenz ν
über einer Schwellenfrequenz ν0 liegt (unabhängig von der Lichtintensität!)
⇒
Die kinetische Energie Ekin der ausgelösten Elektronen ist abhängig von der Lichtfrequenz ν bzw. von ν - ν0 (unabhängig von
der Lichtintensität!). Die Änderung der Lichtintensität ändert nur die
Anzahl der Photoelektronen pro Sekunde (Strom): Messung durch
Photozellen.
Wenn das Licht nur Wellennatur hätte, könnte sich die transportierte
Energie unabhängig von der Frequenz der Wellen zeitliche so lange akkumulieren, bis das Elektron abgelöst wird. Eine Grenzfrequenz, bei der
erst das Elektron abgelöst wird, könnte hierbei nicht auftreten.
Nach Einstein (1905) transportiert die elektromagnetische Welle Energie
in Portionen, den Photonen oder Lichtquanten (Teilchen). Ihre Energie E
ist proportional zur Lichtfrequenz ν: E = h ν mit h als Proportionalitätskonstante (Plancksches Wirkungsquantum). Nur wenn das Lichtquant
genügend Energie hat, um die Kräfte zu überwinden, die das Elektron an
das Metall binden, wird ein Photoelektron abgelöst (Schwellenfrequenz
υ0).
Messung des Planckschen Wirkungsquantums:
Die Überschussenergie zur Elektronenaustrittsarbeit konzentriert sich in
der kinetischen Energie der Elektronen
hν − hν0 =
€
1
m v2
2
mit
als kinetischer Energie der Elektronen,
als Schwellenenergie (Elektronenaustrittsarbeit aus Metall: Arbeitsfunktion A; Ionisierungsenergie bei Atomen und Molekülen ) und h ν −h ν 0 als Überschussenergie.
Wenn gerade keine Elektronen mehr durch€ das Bremsgitter treten, ist die
Bremsenergie gleich der kinetischen Energie
mit UBrems
1
mv 2 = h(ν − ν 0 )
2
als Spannung, bei der gerade kein Strom mehr fließt.
eUBrems =
€
UBrems =
h
(ν − ν 0 )
e
Dies ist die "Einstein Gleichung" zur experimentellen Bestimmung der
€ Konstanten h (Plancksches Wirkungsquantum).
→ h = 6,626 x 10-34 Js
(aus Steigung der lichtelektrischen Gerade
bei bekannter Elementarladung e)
→ hν0 = A beträgt einige eV (1 eV = 1,602 ⋅ 10-19 J).
Der kleine Wert der Planck Konstante bewirkt, dass die Quantisierung
der Energie in der makroskopischen Welt nicht bemerkt wird.
Beispiel:
Das Energiequant eines Pendels mit einer Oszillationsperiode von 1 s
beträgt nur 6,626 x 10-34 J
Vorlesungsversuch: Bestimmung des Planckschen Wirkungsquantums aus dem photoelektrischen Effekt
Prinzip: Licht fällt auf ein Material mit geringer Elektronenaustrittsarbeit
A (Fotokathode) und löst Elektronen ab. Diese Fotoelektronen gelangen
zur Anode und laden sie negativ auf. Die Potentialdifferenz wächst bis zu
einer Grenzspannung UG, bei der die komplette kinetische Energie ½
mv2 der Fotoelektronen benötigt wird, um UG zu überwinden.
Messmethode: Mit Hilfe von optischen Filtern werden einzelne Spektrallinien einer Hg-Lampe selektiert und jeweils mit dem Licht der selektierten Wellenlänge λ (bzw. Frequenz ν=c/λ) eine Fotokathode bestrahlt.
Dann wird mit einem Spannungsverstärker und Voltmeter die Spannung
U zwischen Kathode und Anode gemessen und der stationäre Wert
(Spannung steigt nicht weiter an) notiert.
Ergebnisbeispiel:
hν - A=½ mv2 eUG=½ mv2
Ladung eines Elektrons e = 1,609⋅10-19C
Durch die verschiedenen Oberflächen von Kathode und Anode (verschiedene Austrittsarbeiten) entsteht ein zusätzliches Kontaktpotential φ:
hν - A = eUG + eφ
UG= (hν-A)/e - φ = hν/e – A/e - φ
Aus der Steigung ΔU/Δν lässt sich h/e und bei bekannter Elementarladung (Millikan-Versuch) das Plancksche Wirkungsquantum h bestimmen.
Wertetabelle:
λ[nm]
366
405
436
564
ν/1012 [s-1]
820
740
688
549
U[V]
1,77
1,49
1,28
0,78
1V=1J/1C
1eV=1,609⋅10-19C⋅1J/1C
Steigung ΔU/Δν aus Ausgleichgeraden der Auftragung U(ν).
h=(ΔU/Δν)⋅e =(0,4V/1014s-1)⋅1,602⋅10-19C=6,41⋅10-34Js.
Literaturwert: h=6,6260755⋅10-34Js
4.4.2 Die Heisenbergsche Unschärferelation
Wir stellen uns Photonen als Sinuswelle mit der Energie hν vor.
Angenommen wir könnten die Frequenz messen indem wird die Durchgänge der Maxima während einer Messzeit Δt zählen. Wie die Abbildung
unten nahelegt hat man immer einen Messfehler von etwas weniger als
einer Schwingung. Wir nehmen der Einfachheit halber eine Schwingung
als Messfehler an.
Δt
tt
tt
Es ergibt sich bei vorgegebener Messzeit Δt eine Frequenz ν aus der
Anzahl der Schwingungen N in der Messzeit: ν = N / Δt
Die Unschärfe der Frequenz ist dann eine Schwingung in der Zeit Δt:
€
Daraus folgt mit E = hν : ΔE ⋅ Δt = h ⋅ Δν ⋅ Δt = h ⋅
In der Praxis geht es doch genauer: ΔE ⋅ Δt ≥
€
1
Δt = h
Δt
h
=
2π
Heisenbergsche Unschärferelation (für Zeit und Energie)
€
Man sieht also, dass die Größen t und E nicht unabhängig genau bestimmbar sind.
Wenn Teilchen Eigenschaften von Wellen aufweisen, die im allgemeinen
eine hohe räumliche Ausdehnung besitzen, stellt sich auch hier das gleiche Problem. Wie lässt sich ein (räumlich) lokalisiertes Teilchen durch
eine (ausgedehnte) Welle darstellen? Wie kann die Welle „lokalisiert“
werden, um ein Teilchen an einem definierten Ort zu beschreiben?
Zur Charakterisierung der Lage von Teilchen ist eine räumlich im Bereich
Δx begrenzte Welle notwendig, die man durch Überlagerung vieler Wellen geringfügig verschiedenen Frequenzen ν erhält. Durch negative Interferenz (Wellenberg trifft auf Wellental) löschen sich diese Wellen in
bestimmten Raumbereich aus, in anderen Bereichen verstärken sie sich
(Wellenberg trifft auf Wellenberg).
http://www.physik.uni-wuerzburg.de/femto-welt/pulsframe.html
Der Doppelspaltversuch in der Interpretation der Unschärferelation:
https://www.youtube.com/watch?v=wEzRdZGYNvA&feature=player_e
mbedded
→
Um x genau festzulegen (kleines Δx), muss man viele Einzelwellen in einem größeren Bereich von Wellenlängen überlagern:
dadurch wird die Unschärfe der Teilchenwellenlänge Δλ und damit
auch des Teilchenimpulses Δp groß! Das Produkt Δx⋅Δp ist dann
konstant, wie im Fall von ΔE und Δt.
Es gilt die Beziehung
Δ x ⋅ Δ p ≥  Heisenbergsche Unschärferelation
(Ort und Impuls)
€ Demnach ist eine gleichzeitige genaue Kenntnis von Ort und Impuls, so-
wie von Energie und Zeit eines Teilchens prinzipiell unmöglich. Größen
mit dieser Eigenschaft nennen wir komplementäre Größen.
Beispiel:
Die Position des Elektrons auf der Kreisbahn um den Atomkern ist völlig
unbekannt, so dass die Unschärfe des Elektronenortes Δx ungefähr
gleich dem Durchmesser der Kreisbahn 2a0 = 1Å ist.
Δ x ≈ 10−10 m
Δv ≥
€
Δ x⋅Δ p ≥ 

m
1 ⋅10−34 J ⋅ sec
≈ −30
= 10 6
−10
m Δ x 10€ kg ⋅10 m
s
mit me ≈ 1 ⋅
.
€
Nach Bohr gilt für die Geschwindigkeit v des Elektrons in n = 1 :
v=
nh
= 2.2 ⋅ 10 6 m / s
2π µ r
Die Unbestimmtheit der Geschwindigkeit beträgt also etwa 50% ihres
Betrages!
€
4.4.3
Absorptions- und Emissionsspektren von Atomen
Das Bohrsche Atommodell kann die Linienspektren vieler Atome sehr
gut beschreiben.
Linienspektrum von Wasserstoffatomen
Phänomenologisch beobachtet man getrennte Serien von Linien mit den
Wellenzahlen
˜ 
˜ 1
1
1
ν = [ m−1] = R  2 − 2 
n1,n2 >0
y n
λ
n 
1
2
Die Wellenzahl einer Spektrallinie ist also die Differenz zweier Terme
€
/ni2 (Balmer-Formel).
Lyman-Serie
Balmer-Serie
Paschen-Serie
Brackett-Serie
n1 = 1
n1 = 2
n1 = 3
n1 = 4
n2 = 2, 3, 4, 5 . . . .
n2 = 3, 4, 5, 6 . . . .
n2 = 4, 5, 6, 7 . . . .
n2 = 5, 6, 7, 8 . . . .
=1.097·107 m-1 ist die Rydbergkonstante in Wellenzahleneinheiten;
Ry = 2,178⋅10-18J = 13,6eV in Energieeinheiten.
Im Bohrschen Atommodell werden diese empirischen Terme als Energien der Elektronenkreisbahnen gedeutet. Die Energie der stabilsten
Kreisbahn mit n=1 ist nach Bohr E=-13.6eV in Übereinstimmung mit der
empirischen Rydbergformel.
Vorlesungsversuch: Emissionsspektrum von Atomen
Prinzip: Das Licht einer Hg-Leuchtstoffröhre, einer Hg-Hochdrucklampe,
einer Na- und einer Cd-Spektrallampe wird von einem Lichtleiter aufgefangen und zu dem Eintrittspalt eines Monochromators geleitet. Dort wird
mit einem optischen Gitter die Lichtintensität I nach den Wellenlängen λ
aufgespreizt und das Spektrum I(λ) mit einer linearen Anordnung optischer Dioden gemessen.
Messmethode: Messung des Emissionsspektrums einer HgLeuchtstoffröhre im Hörsaal. Messung des Emissionsspektrums verschiedenfarbiger Bereiche auf einem Laptop-Schirm. Messung des Absorptionsspektrums einer KMnO4-Lösung mit bekannter Konzentration c
in Wasser in einer Küvette bekannter Weglänge l und Berechnung des
Absorptionskoeffizienten ε nach Lambert-Beer.
Ergebnisbeispiele: Hg-Linien der Leuchtstoffröhre: 185nm, 253nm,
365nm. Breitbandiges Emissionsspektrum der Leuchtstoffbeschichtung.
Weitere Linien im sichtbaren Bereich bei 405nm, 436nm, 546nm 579nm
⇒ Plasma erscheint bläulich weiß.
Vorlesungsversuch: Bestimmung von Energieniveaus durch Elektronenstoß (Franck-Hertz Experiment)
Prinzip: Die Differenz der Energieniveaus von Atomen und Molekülen
lassen sich durch Messung der Lichtabsorption und Lichtemission, aber
auch durch Anregung der Energiezustände durch Elektronenstoß
bestimmen. Freie Elektronen variabler Energie eU regen das Valenzelektron z.B. von Quecksilberatomen elektronisch an, wenn eU genau
gleich der Energiedifferenz zwischen dem 1. angeregten Hg-Zustand
und dem Hg-Grundzustand ist.
Messmethode: Elektronen werden in einer mit Quecksilberdampf gefüllten, evakuierten Glasröhre in einem elektrischen Feld mit angelegter
Spannung U1 zwischen Emissionskathode C (Heizspannung UH) und
Anode A beschleunigt. Wenn die Energie eU dieser freien Elektronen
den Wert 4.86 eV erreicht, wird das Valenzelektron des Hg durch inelastische Stöße mit den freien Elektronen in sein 1. angeregtes Niveau gebracht. Die freien Elektronen verlieren entsprechend ihre Energie und
können das Feld zwischen Anode A und Gegenelektrode S mit Spannung U2 nicht mehr durchqueren: der Elektronenstrom I erreicht ein Minimum. Bei U1 = 2⋅4,86eV werden 2 Hg-Atome in Folge durch dasselbe
Elektron angeregt: 2. Minimum usw. Der Abstand zwischen den Minima
ist gleich der Anregungsenergie des Hg-Atoms.
Ergebnisbeispiele: ΔE = 4,86eV
ΔE = hν = hc/λ λ = h⋅c/ΔE
-34
8
-1
λ = 6,626⋅10 Js ⋅ 2,9979⋅10 ms /(4,86J/C ⋅1,602⋅10-19C) = 253 nm
Elektronisch angeregte Hg-Atome emittieren Licht bei 253nm!
⇒ Anregung muss nicht durch Photonen erfolgen.
4.5 Elementarteilchen – Der Spin
Die relativistische Quantenmechanik und Experimente zeigen, dass zur
Beschreibung des Wasserstoffatoms eine weitere Quantenzahl notwendig ist: die Spinquantenzahl des Elektrons s.
Der zur Spinquantenzahl s gehörende Freiheitsgrad der Bewegung ist
klassisch die „Eigenrotation“ des Elektrons. Der Drehimpuls für diese
Bewegung steht senkrecht auf der Rotationsebene. Seine Richtung ist
durch die „rechte Hand“-Regel gegeben.
4.5.1 Experimenteller Nachweis des Elektronenspins
Stern-Gerlach Versuch:
Ein Strahl von Ag-Atomen (ein äußeres Elektron im s-Orbital) durchläuft
ein inhomogenes magnetisches Feld. Der Silberstrahl wird in zwei Teilstrahlen aufgespalten.
Annahme: Die rotierende elektrische Ladung des äußeren Ag-Elektrons
erzeugt ein Magnetfeld, das mit dem äußeren Magnetfeld wechselwirkt.
Die Richtung dieses inneren Magnetfeldes hängt von der Rotationsrichtung ab. Dadurch findet je nach Orientierung der Elektronenrotation
und damit des inneren Magnetfeldes zum äußeren Magnetfeld Anziehung oder Abstoßung statt: Aufspaltung in 2 Teilstrahlen.
Das Experiment zeigt, daß die beiden Einstellmöglichkeiten der „Eigenrotation“ und des dadurch hervorgerufenen inneren Magnetfeldes im äußeren Magnetfeld verschiedene Energien haben (Anziehung und Abstoßung: 2 Teilstrahlen).
Übergänge zwischen Elektronenspinniveaus durch resonante Absorption
von Mikrowellenstrahlung werden in der Elektronenspinresonanz (ESR
oder englisch electron paramagnetic resonance, EPR) genutzt. Die Probe benötigt hierfür einen ungepaarten Elektronenspin um über ein magnetisches Moment zu verfügen (Radikal).
4.5.2 Der Kernspin
Wie das Elektron hat auch das Proton eine „Eigenrotation“ und bildet
somit ein kleines inneres Magnetfeld aus. Dieses kann sich in Richtung
oder Gegenrichtung zu einem äußeren Magnetfeld einstellen.
Strahlt man die geringe Energiedifferenz ΔE dieser beiden Einstellmöglichkeiten als Radiofrequenz hν ein (ΔE= hν), führt das zum „Umklappen“
des Kernspins und die Radiostrahlung wird absorbiert. Da in einem Molekül die ein Proton umgebenden Elektronen das äußere Magnetfeld geringfügig abschirmen, hat jedes Proton abhängig von seiner chemischen
Umgebung eine etwas verschiedene Absorptionsfrequenz. Aus diesem
Grund ist die kernmagnetische Resonanzspektroskopie (Nuclear Magnetic Resonance: NMR) eine hervorragende chemische Analysenmethode:
Ein 1H-NMR Spektrum gibt an, wie H-Atome an N-,C, O-Atome usw. gebunden sind.