Mechanik 4 (Erhaltungssätze)
Werbung

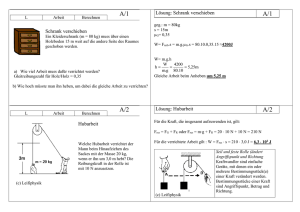
1.4 Erhaltungssätze Einer der wichtigsten Begriffe in der Physik ist der Begriff Energie. Ohne Energie wäre das Leben auf der Erde nicht möglich. Insbesondere in der modernen Gesellschaft des 21. Jahrhunderts ist der „Hunger nach Energie“ fast nicht zu stillen und die enorme Nachfrage kann nur mit schwerwiegenden Folgen für Umwelt und Klima gedeckt werden. Im folgenden Kapitel sollen der Begriff Energie näher untersucht werden und wichtige Begriffe, Sätze und Zusammenhänge rund um das Thema Energie erklärt werden. 1.4.1 Physikalische Arbeit Um einen Körper der Masse m aus dem Ruhezustand in Bewegung zu versetzen, benötigt man die Kraft F. Wirkt auf diesen Körper längs eines Weges s ein konstante Kraft F, so wird im physikalischen Sinne Arbeit verrichtet. Arbeit wird deshalb als das Produkt aus Kraft und Kraftweg definiert: Die Einheit der Arbeit ist somit das Produkt aus und und wird mit bzw. abgekürzt. Um den Begriff Arbeit etwas zu veranschaulichen, folgen nun drei Beispiele, bei denen im physikalischen Sinn Arbeit verrichtet wird. 1. Hubarbeit: Um einen Körper der Masse auf eine beliebige Höhe anzuheben, muss Hubarbeit verrichtet werden. Der Strecke aus der Formel entspricht dabei die Höhendifferenz und der Kraft entspricht die Gewichtskraft , der entgegengewirkt werden muss, um den Körper anzuheben: [07] Kran © M. Brennscheidt Für die Hubarbeit ergibt sich somit die Formel: Beispiele: Ein Kran hebt Betonklötze an Ein Mensch klettert auf einen Berg Ein Mensch geht die Treppen in einem Haus hoch Lance Armstrong fährt auf einen Alpenpass Die Hubarbeit kann in einem sog. Kraft-Weg-Diagramm graphisch veranschaulicht werden. Da sich beim Anheben eines Körpers dessen Masse nicht ändert, ist die erforderliche Kraft beim Verrichten der Hubarbeit konstant. Dies zeigt sich im Diagramm durch den waagerechten Verlauf des Funktionsgraphen: Die verrichtete Hubarbeit entspricht im Kraft-Weg-Diagramm dann der Fläche unter dem Funktionsgraphen. Die Fläche ist in diesem Fall ein Rechteck mit den Seitenlängen und und dem Flächeninhalt . 2. Beschleunigungsarbeit Beim Beschleunigen eines Körpers der Masse aus der Ruhelage auf eine Geschwindigkeit wird Beschleunigungsarbeit verrichtet. Die Strecke kann in diesem Fall mit dem Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung berechnet werden. Die beschleunigende Kraft kann durch die Grundgleichung der Mechanik bestimmt werden (2. Newtonsches Axiom). Für die Beschleunigungsarbeit ergibt sich somit: Die Beschleunigung kann wiederum durch das Geschwindigkeits-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung berechnet werden: © M. Brennscheidt Durch Einsetzen in die obige Gleichung folgt: Es ergibt sich somit die Beschleunigungsarbeit: Beispiele: Ein Flugzeug wird beim Start beschleunigt, damit es abheben kann. Ein Pfeil wird beim Bogenschießen beschleunigt. Ein Auto beschleunigt von Null auf . 3. Spannarbeit: Beim Auslenken einer Feder aus ihrer Ruhelage wird Spannarbeit verrichtet. Die Strecke entspricht der Auslenkung aus der Ruhelage, und der Kraft entspricht gemäß dem Hookeschen Gesetz die Federkraft , der beim Auslenken entgegengewirkt werden muss. © M. Brennscheidt Im Gegensatz zur Hubarbeit und zur Beschleunigungsarbeit ist bei der Spannarbeit darauf zu achten, dass die Kraft nicht konstant ist, sondern mit zunehmender Auslenkung der Feder größer wird. Zur Veranschaulichung soll deshalb zunächst das Kraft-Weg-Diagramm betrachtet werden: Es ist zu erkennen, dass die Kraft mit zunehmender Auslenkung lineare ansteigt. Die Arbeit entspricht in diesem Fall deshalb nicht mehr der Fläche eines Rechtecks, sondern der Fläche eines Dreiecks, also genau der Hälfte eines Rechtecks. Bei der Berechnung der Spannarbeit muss deshalb der Faktor berücksichtigt werden: Für die Spannarbeit ergibt sich somit die Formel: Beispiele: Federn im Auto Katapulte im Mittelalter Bungeespringen [08] Bungeesprung © M. Brennscheidt Anmerkung: Physikalische Arbeit gibt es in sämtlichen Teilbereichen der Physik. Die vier oben behandelten Arbeitsformen stammen nur aus dem Bereich der Mechanik. Auf andere Arbeitsformen, wie zum Beispiel die elektrische Arbeit, wird im weiteren Verlauf des Buches eingegangen. 1.4.2 Energie Energie ist die Fähigkeit von Körpern Arbeit zu verrichten. So muss zum Beispiel ein Mensch Energie durch Nahrung zu sich nehmen, damit er arbeiten kann. Man unterscheidet bei der Energie zwischen Energieform und Energieträger. Ein Beispiel für eine Energieform ist die chemische Energie. Diese ist in den Energieträgern Erdöl oder Kohle gespeichert. Energieform: chemische Energie Bewegungsenergie /Kinetische Energie Lageenergie/ Potentielle Energie Spannenergie Elektrische Energie Solarenergie Kernenergie Wärmeenergie Energieträger: Kohle, Erdöl, Erdgas, Nahrungsmittel Fahrendes Auto, Gewehrkugel,… Fahrradfahrer auf einem Berg, Wasser in einem Stausee Sportbogen, Armbrust, Trampolin Elektronen, Ladungsträger Licht Atomkerne Luft, Erdboden, Gegenstände Die verschiedenen Energieformen können ineinander umgewandelt werden. Bei der Umwandlung von Energie wird physikalische Arbeit verrichtet. Hierzu ein Beispiel: Ein Auto wird an einer Tankstelle mit Benzin betankt. Es besitzt dann einen großen Vorrat an chemischer Energie. Beschleunigt man nun das Auto von 0 auf 50km/h, so wird ein Teil der chemischen Energie in Bewegungsenergie bzw. kinetische Energie umgewandelt. Bei diesem Vorgang wurde Beschleunigungsarbeit verrichtet. Um den Betrag der kinetischen Energie des Autos nach dem Beschleunigen zu berechnen, reicht es, die verrichtete Arbeit zu berechnen. Das Auto hat deshalb nach dem Beschleunigen folgende kinetische Energie: Energie und Arbeit sind also betraglich gleich. Aus diesem Grund wir Energie auch häufig als gespeicherte Arbeit bezeichnet. Analog zur kinetischen Energie können nun auch die potentielle Energie, sowie die Spannenergie definiert werden: Um einem Körper potentielle Energie zuzuführen, muss zunächst Hubarbeit verrichtet werden. So erhalten zum Beispiel Steine potentielle Energie, wenn sie auf der Baustelle auf ein Gerüst transportiert werden. Es leuchtet sofort ein, dass bei diesem Vorgang Hubarbeit verrichtet werden muss. Aus diesem Grund sind auch Hubarbeit und potentielle Energie betraglich gleich. Für die potentielle Energie eine Körpers gilt somit: © M. Brennscheidt Um einem Körper Spannenergie zuzuführen, muss zunächst Spannarbeit verrichtet werden. Möchte man beispielsweise einen Sportbogen spannen, so muss man hierzu Spannarbeit verrichten. Durch das Spannen gewinnt der Bogen dann an Spannenergie, die beim Abschießen des Bogens auf den Pfeil übertragen wird. Auch hier sind die verrichtete Spannarbeit und die Spannenergie des Sportbogens betraglich gleich. Für die Spannenergie gilt somit die Formel: Zusammenfassung: Energie ist die Fähigkeit von Körpern Arbeit zu verrichten. Verschiedene Energieformen können ineinander umgewandelt werden. Beim Umwandeln von Energie wird Arbeit verrichtet. In der Mechanik, gibt es drei wesentliche Energieformen, kinetische Energie, potentielle Energie und Spannenergie: Energie ist der Zustand eines Körpers, und Arbeit der Vorgang, bei dem einem Körper Energie zugeführt wird. 1.4.3 Der Energieerhaltungssatz Der Energieerhaltungssatz ist einer der wichtigsten Sätze der Physik. Er besagt, dass bei der Umwandlung von Energie von einer Energieform in eine andere niemals Energie verloren geht oder „verbraucht“ wird. In einem abgeschlossenen System bleibt die Summe aller Energien immer gleich. Die Gesamtenergie ist konstant. Der Energieerhaltungssatz kann sehr einfach am Beispiel eines Skateboard-Fahrers in der Halfpipe veranschaulicht werden. © M. Brennscheidt In einer Halfpipe wird potentielle Energie in kinetische Energie umgewandelt und umgekehrt. Der Skater startet aus der Höhe und fährt die Halfpipe hinab. Dabei beschleunigt er und seine Geschwindigkeit nimmt zu. Es wird also Beschleunigungsarbeit verrichtet. Dabei wird seine potentielle Energie in kinetische Energie umgewandelt. Ist der Skater im waagerechten Bereich angekommen, so wird seine Geschwindigkeit maximal, da die gesamte potentielle Energie in kinetische Energie umgewandelt wurde. Fährt er die Halfpipe auf der anderen Seite wieder hoch, so wird der Vorgang umgekehrt. Es wird Hubarbeit verrichtet, wobei seine kinetische Energie zurück in potentielle Energie umgewandelt wird. Wäre dieser Vorgang reibungsfrei, so könnte der Skateboardfahrer ohne zusätzlich physikalische Arbeit aufzuwenden, unendlich lange hin und herfahren. Die Gesamtenergie bleibt also im abgeschlossenen System Halfpipe erhalten. Die Umwandlung von potentieller Energie in kinetische Energie und umgekehrt kann an einem Diagramm veranschaulicht werden: Die blaue Kurve zeigt den Verlauf der potentiellen Energie des Skateboard-Fahrers. Diese ist am linken und rechten Rand der Halfpipe maximal und nimmt in der Mitte der Halfpipe den Wert Null an. Die rote Kurve zeigt den Verlauf der kinetischen Energie. Diese ist links und rechts gleich Null, besitzt aber in der Mitte der Halfpipe ein Maximum. Summiert man potentielle und kinetische Energie auf, so ergibt sich die Gesamtenergie in Form der grünen Kurve. Diese ist während des gesamten Vorgangs konstant. Die Gesamtenergie bleibt also erhalten. Anmerkung: Nach dem Energieerhaltungssatz kann Energie niemals „verbraucht“ werden, sondern lediglich in andere Energieformen umgewandelt werden. Wenn im Alltag von Energieverbrauch die Rede ist, ist damit im physikalischen Sinne kein Verlust der Energie gemeint, sondern die Umwandlung von einer wertvollen in eine weniger wertvolle Energieform. So wird zum Beispiel in einer Ölheizung die wertvolle chemische Energie des Erdöls in weniger wertvolle Wärmeenergie der Luft umgewandelt. Weniger wertvoll bedeutet in diesem Zusammenhang, dass die Wärmeenergie außer zum Heizen für den Menschen nutzlos ist und diese „verloren“ geht, sobald ein Fenster geöffnet wird. Dennoch bleibt auch bei diesem Vorgang die Energie gemäß dem Energieerhaltungssatz erhalten. © M. Brennscheidt 1.4.4 Die physikalische Leistung Um einen Körper der Masse auf eine gewisse Höhe anzuheben, muss die Hubarbeit verrichtet werden. Bei dieser Berechnung ist es unerheblich, in welcher Zeit diese Hubarbeit verrichtet wird. Sie kann in ein paar Sekunden, aber auch in mehreren Tagen verrichtet werden. Im Alltag hingegen spielt die Zeit, in der Arbeit verrichtet wird, jedoch eine entscheidende Rolle. Fährt zum Beispiel ein Radprofi innerhalb von 60 Minuten einen Alpenpass hoch, so hat er im physikalischen Sinne mehr „geleistet“ als ein gleich schwerer Hobby-Radfahrer, der für die gleiche Höhendifferenz mehrere Stunden benötigt. Die zu verrichtende Arbeit ist jedoch für beide identisch. Die Leistungen von Radprofi und Hobby-Radfahrer können verglichen werden, indem man angibt, wer wieviel Arbeit in welcher Zeit verrichtet hat. Hieraus folgt die physikalische Definition der Leistung: Unter der physikalischen Leistung hierzu benötigten Zeit : versteht man den Quotienten aus verrichteter Arbeit Die Einheit der Leistung ist , kurz der Dampfmaschine James Watt. und der , benannt nach dem englischen Ingenieur und Entwickler Beispiele: Die Leistung einer handelsüblichen Glühlampe beträgt ca. . Das bedeutet, dass Arbeit verrichtet werden müssen, um die Glühlampe für eine Sekunde zum leuchten zu bringen. Für eine ganze Stunde (3600s) bedeutet dies schon umgangssprachlich einen „Energieverbrauch“ von . Physikalisch korrekt wird bei einer Glühlampe elektrische Energie zu 90% in Wärme und zu 10% in Licht umgewandelt. [09] Glühlampe © M. Brennscheidt [10] Porsche Carrera GT Bei Autos wurde die Leistung früher in Pferdestärken, kurz angegeben. Heutzutage wird die Leistung jedoch in Kilowatt, kurz angegeben. Ein Porsche Carrera GT hat beispielsweise eine Leistung von 450kW (612PS), wohingegen ein Opel Corsa nur eine Leistung von ca. 59kW besitzt. 1.4.5 Stoßvorgänge Im Alltag und in der Technik spielen Vorgänge eine große Rolle, bei denen Körper zusammenstoßen. Man spricht hierbei von sog. Stoßvorgängen. Um die Untersuchung solcher Stoßvorgänge zu vereinfachen, ist es sinnvoll, zunächst nur den Stoß zweier Körper zu betrachten. So kollidieren beispielsweise zwei Autos bei einem Autounfall oder zwei Billardkugeln stoßen beim Billardspielen gegeneinander. Stoßvorgänge können grundsätzlich in zwei verschiedene Kategorien aufgeteilt werden, die elastischen Stöße und die inelastischen Stöße. 1. Elastische Stöße: Bei elastischen Stößen treffen zwei Körper aufeinander und verformen sich dabei in der Regel nicht bzw. nehmen nach dem Stoß wieder ihre ursprüngliche Form an. Der Stoßvorgang selbst ist sehr kurz und beide Stoßpartner trennen sich nach dem Stoß wieder voneinander. Das bekannteste Beispiel für einen elastischen Stoß ist der Stoß zweier Billardkugeln. [11] Billard Weitere Beispiele: Ein Fußballspieler schießt einen Elfmeter Ein Tennisspieler macht einen Aufschlag Zwei Curlingsteine treffen aufeinander © M. Brennscheidt 2. Inelastische Stöße: Bei inelastischen Stößen treffen zwei Körper aufeinander und verformen sich beim Aufprall. Beide Stoßpartner trennen sich nach dem Stoß nicht, sondern bewegen sich mit einer gemeinsamen Geschwindigkeit weiter. Das bekannteste Beispiel für einen inelastischen Stoß ist ein Autounfall, bei dem sich die Autos ineinander „verkeilen“. [12] Autounfall Weitere Beispiele: Ein Geschoss trifft auf eine kugelsichere Weste Ein Torwart fängt einen Ball Verformungsenergie: Um Stoßvorgänge wie den inelastischen oder den elastischen Stoß beschreiben zu können, reicht das Wissen über den Energieerhaltungssatz nicht aus. So wird beim inelastischen Stoß häufig davon gesprochen, dass der Energieerhaltungssatz nicht gilt. Auch die Messwerte aus dem Experiment mit der Luftkissenfahrbahn deuten auf eine Verletzung des Energieerhaltungssatzes hin: Berechnet man die kinetische Energie zweier Stoßpartner vor einem inelastischen Stoß, so ist diese größer, als die kinetische Energie der der beiden Stoßpartner nach dem Stoß. Dies bedeutet jedoch nicht, dass sich ein Teil der Energie gewissermaßen „in Luft aufgelöst“ hat, sondern, dass diese Energie in andere Energieformen umgewandelt wurde. Diese bis jetzt unbekannte Energieform bezeichnet man in der Physik als Verformungsenergie . Die Verformungsenergie kann man sich leicht am Beispiel eines Autounfalls verdeutlichen. Fährt ein Auto bei einem Unfall gegen eine Betonwand, so wird das Auto innerhalb von kürzester Zeit auf die Geschwindigkeit Null abgebremst. Die gesamte kinetische Energie, die das Auto beim Fahren hatte, wird beim Unfall durch die Verformung des Autos absorbiert. © M. Brennscheidt [13] Crashtest Aus diesem Grund besitzen moderne Autos eine relativ weiche Knautschzone im Motorraum und eine sehr harte Fahrgastzelle. Die Knautschzone hat den Sinn, bei einem Unfall einen möglichst großen Teil der kinetischen Energie des Autos zu absorbieren, so dass diese nicht auf die Fahrzeuginsassen übertragen wird. In den Anfängen des Automobilbaus wurden Autokarosserien möglichst stabil konstruiert. Eine solche Bauweise stellt jedoch eine große Gefahr für die Fahrzeuginsassen dar, da eine sehr stabile Karosserie weniger Energie durch Verformung absobieren kann und somit mehr Energie auf die Fahrzeuginsassen übertragen wird. Heutzutage werden deshalb nur noch die Fahrgastzellen, also der Innenraum des Autos, möglichst stabil konstruiert, damit die Fahrzeuginsassen bei einem Unfall nicht zerquetscht werden. Im Gegensatz zum inelastischen Stoß darf beim elastischen Stoß mit dem Energieerhaltungssatz gerechnet werden, da sich die beiden Stoßpartner (z. B. Billardkugeln) beim Stoß so gut wie nicht verformen oder nach dem Stoß ihre ursprüngliche Form wieder annehmen (z.B. zwei weiche völlig elastische Gummibälle). Der Impuls: Zur Beschreibung von Stoßvorgängen ist es sinnvoll eine neue physikalische Größe einzuführen, den sog. Impuls. Ein Körper mit der Masse , der sich mit der Geschwindigkeit bewegt, hat den Impuls . Den Impuls eines Körpers kann man sich vorstellen als ein Maß für die Schwierigkeit, den Körper in den Ruhezustand zu überführen. Zum Beispiel hat ein schwerer Lastwagen, der sich mit einer bestimmten Geschwindigkeit bewegt, einen größeren Impuls, als ein leichtes Auto mit gleicher Geschwindigkeit. Man benötigt eine größere Kraft, um den Lastwagen in einer vorgegebenen Zeit zu stoppen. Bei Geschossen, wie zum Beispiel einer Gewehrkugel, ist der Impuls ein Maß für die Zerstörungskraft der Gewehrkugel. So besitzt eine Kugel mit hoher Masse und einer hohen Geschwindigkeit eine große Zerstörungskraft. © M. Brennscheidt Der Impulserhaltungssatz: Sowohl beim inelastischen, als auch beim elastischen Stoß gilt der sog. Impulserhaltungssatz: Die Summe der Impulse vor dem Stoß ist gleich der Summe der Impulse nach dem Stoß. In einem abgeschlossenen System ist der Gesamtimpuls konstant. Anmerkung: Um die Schreibarbeit zu verringern, werden bei Rechnungen mit dem Impulserhaltungssatz selten die Indizes „vorher“ und „nachher“ verwendet. Stattdessen werden die Impulse nach dem Stoß mit einem Strich ‘ gekennzeichnet und die Impulse vor dem Stoß ohne einen Strich geschrieben. In diesem Fall lautet der Impulserhaltungssatz: 1. Impulserhaltungssatz des zentralen inelastischen Stoßes: Zwei Körper mit den Massen und mit den Geschwindigkeiten und stoßen inelastisch zusammen. Nach dem Stoß bewegen sich die beiden Stoßpartner gemeinsam mit der Geschwindigkeit weiter. Es gilt der Impulserhaltungssatz: Da sich die Körper nach dem Stoß gemeinsam weiterbewegen ist . Daraus folgt: Mit dem Impulserhaltungssatz kann nun zum Beispiel die gemeinsame Geschwindigkeit der Körper nach dem Stoß berechnet werden. Es ist anzumerken, dass dies mit dem Energieerhaltungssatz aufgrund der Verformungsenergie nicht möglich ist: 2. Impulserhaltungssatz des zentralen elastischen Stoßes: Zwei Körper mit den Massen m1 und m2 mit den Geschwindigkeiten v1 und v2 stoßen elastisch zusammen. Nach dem Stoß bewegen sich die Körper getrennt voneinander mit den © M. Brennscheidt Geschwindigkeiten v1’ und v2’ weiter. Es gilt sowohl der Impulserhaltungssatz als auch der Energieerhaltungssatz: und Anmerkung: Bei sämtlichen Rechnungen mit dem Impulserhaltungssatz ist es von entscheidender Bedeutung die Fahrtrichtung der beiden Stoßpartner zu beachten. Fahren zwei Körper aufeinander zu, so sind die Vorzeichen der beiden Geschwindigkeiten unbedingt unterschiedlich zu wählen (Zwei Autos prallen frontal aufeinander). Fahren beide hingegen in die gleiche Richtung, so sind die Vorzeichen gleich (Ein schnelles Auto fährt auf einen langsamen LKW auf). © M. Brennscheidt