dt kraft f

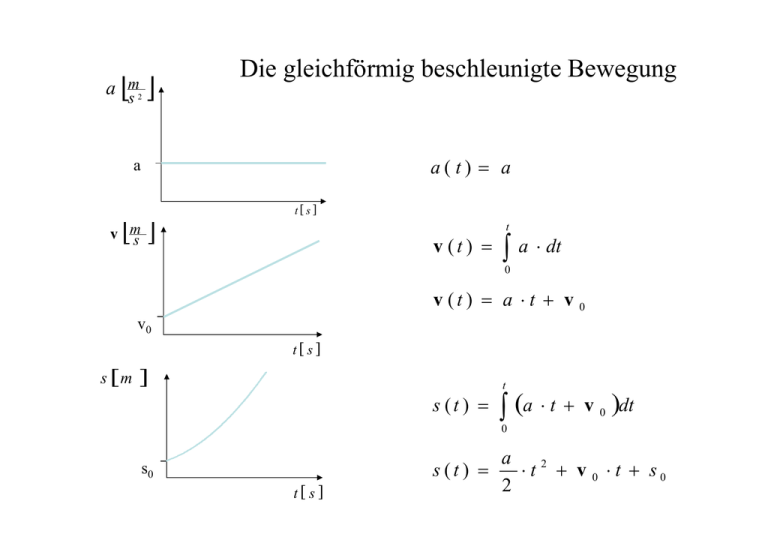
a
[ ]
m
s2
Die gleichförmig beschleunigte Bewegung
a( t) = a
a
[ ]
t[ s]
t
v ms
v (t ) =
∫ a ⋅ dt
0
v (t ) = a ⋅ t + v 0
v0
t[ s]
s [m
]
t
s (t ) =
∫ (a ⋅ t +
v 0 )dt
0
s0
t[ s]
s (t ) =
a
⋅ t 2 + v 0 ⋅ t + s0
2
Einführung in die
Experimentalphysik für Pharmazeuten
Joachim Rädler
e-mail [email protected]
Experimentelle Vorlesungsbegleitung : Christian Hundschell
Vorlesung: Montags 11.15 bis 12.45, Liebig HS
Übung : Montags 10.00 bis 11.00, Liebig HS
Klausur: am 31. Juli. 2006 von 11.15 bis 12.45
erster Montag nach Semesterende !
Web-Seite zur Vorlesung :
http://www.physik.uni-muenchen.de/kurs/PPh
Wichtige Begriffe dieser Vorlesung:
Impuls
Arbeit, Energie, kinetische Energie
Starrer Körper: Drehmoment, Drehimpuls
Erhaltungssätze:
- Impulserhaltung
- Energieerhaltung
- Drehimpulserhaltung
Die Newtonschen Grundgesetze
1. Newtonsche Axiom (Trägheitsprinzip)
Ein Körper, der sich völlig selbst überlassen ist, verharrt im Zustand der
Ruhe oder der gleichförmigen Bewegung.
2. Newtonsche Axiom (Aktionsprinzip)
Ursache für eine Bewegungsänderung ist eine Kraft. Sie ist definiert als
F = m⋅a
[N=kg·m/s2= 1 Newton]
m : „träge Masse“
3. Newtonsche Axiom (Reaktionsprinzip)
Bei zwei Körpern, die nur miteinander, aber nicht mit anderen Körpern
wechselwirken, ist die Kraft F12 auf den einen Körper entgegengesetzt
gleich der Kraft F21 auf den anderen Körper.
F12 = −F21
(actio=reactio)
Impuls
p = m⋅v
Definition des Impulses
als „Bewegungszustand“ (Newton)
Exakte Formulierung des 2. Newtonsche Axiom (Aktionsprinzip)
Ursache für eine Änderung des Bewegungszustands ist eine Kraft. Sie
ist definiert als die Ableitung des Impulses nach der Zeit
d
F= p
dt
Beweis :
r
r
F ⋅ dt = dp
für m=const.
F = m ⋅a
d
d
d
F = p = (m ⋅ v ) = m ⋅ v = m ⋅ a
dt
dt
dt
Kraftstoß=Impulsänderung
Der zentrale Stoß
v2
v1
nachher
vorher
m1 v1 + m2 v 2 = m1 v1′ + m2 v′2
Impulserhaltungssatz
In einem abgeschlossenen System (keine äußeren Kräfte)
bleibt der Gesamtimpuls konstant
∑m ⋅v
i
i
= const
Impulserhaltungssatz
m1
v1
m2
m2
m1
v2
Aus dem Wechselwirkungssatz (Actio=Reactio) folgt:
Die Kräfte auf Wagen 1 und Wagen2 sind zu jedem Zeitpunkt gleich groß aber
entgegengerichtet.
m1 ⋅ v1 = p1 = ∫ F1dt = − ∫ F2 dt = − p2 = −m2 ⋅ v 2
m1 ⋅ v1 + m2 ⋅ v 2 = 0
In einem abgeschlossenen System (keine äußeren Kräfte) bleibt der
Gesamtimpuls konstant
Die gleichförmige Rotation
y
ϕ (t) = ω ⋅t
ω: Winkelgeschwindigkeit
r ⎛ r ⋅ cos(ωt ) ⎞
⎟⎟
r = ⎜⎜
⎝ r ⋅ sin(ωt ) ⎠
v
r
y = r ⋅sin ϕ
ϕ
x = r ⋅ cosϕ
x
⎛ − ω ⋅ r ⋅ sin(ω ⋅ t ) ⎞
r
v
⎟⎟ = ω ⋅ r ⋅ e (t )
v(t ) = ⎜⎜
⎝ ω ⋅ r ⋅ cos(ω ⋅ t ) ⎠
Der Geschwindigkeitsbetrag ist konstant : v= ω⋅r
⎛ − sin ωt ⎞
r
⎟⎟
Die Richtung des Einheitsvektors „kreist“ : e(t ) = ⎜⎜
⎝ cos ωt ⎠
Die Zentripetalbeschleunigung
y
der gleichförmigen Rotationsbewegung
r
v
r ⎛ r ⋅ cos(ϕ ) ⎞
⎟⎟
r = ⎜⎜
r
ϕ
⋅
sin(
)
⎝
⎠
y = r ⋅sin ϕ
ϕ
x = r ⋅ cosϕ
v
⎛ − cos(ω ⋅ t ) ⎞
v dv
v
2
⎟⎟
a=
⇒ a (t ) = ω ⋅ r ⎜⎜
dt
⎝ − sin(ω ⋅ t ) ⎠
v
a(t) = ω 2 ⋅ r ⋅ cos 2 (ω ⋅ t) + sin2 (ω ⋅t) = ω 2 ⋅ r
Zentripetalbeschleunigung:
a = ω2 ⋅r
mit v = ω ⋅ r folgt
v2
a=
r
a
x
Scheinkräfte
Scheinkräfte sind Trägheitskräfte, welche von mitbewegten
Beobachtern in beschleunigten Bezugssystemen beobachtet
werden.
Ftr
a
Beobachter im Wagen:
-Eine Kraft zieht die Kugel
plötzlich nach hinten.
Beobachter außerhalb:
-Wagen wird beschleunigt,
daher Zugkraft auf Feder.
Scheinkräfte: die Zentrifugalkraft
Newtonsche Axiome gelten nur in ruhenden oder
gleichförmig bewegten systemen. In beschleunigten
Systemen treten Scheinkräfte auf.
Das Newtonsche Gravitationsgesetz
r
m⋅M
FG = −G
r2
G=6,673 ·10-11 Nm2/kg2
(Gravitationskonstante)
v2
m⋅M
=m
G
2
r
r
4π
T =
⋅ r3
G⋅M
2
Ansatz : FG=FP
(Gravitationskraft=Zentripetalkraft)
mit v = 2π r / T
folgt
2
Dritte Keplersche Gesetz
Die elastische Federkraft
Kräfte können über das dynamische Grundgesetz gemessen werden:
1 N ist die Kraft, die eine Masse von 1 kg mit 1 m/s2 beschleunigt.
oder auch über ihre Deformationswirkung auf einen Festkörper (Feder):
FD = − D ⋅ ( x − x0 )
Federkonstante
Federauslenkung
Hook‘sches Gesetz
F
Beispiel eines Kraftmeßgeräts: Das Kraftmikroskop
D = 10
x=
−3
N
m
F 1nN ⋅ m
=
= 10 −6 m
D 0,001N
AFM experiments with single molecules
custom-built instrument (M. Rief, H. Gaub et al., Science 275, 1295 (1997)):
Deflection
intermolecular forces
(binding interactions)
Piezopath
intramolecular forces
(polymer elasticity)
Force [pN]
600
400
200
0
-200
-400
0
100
200
300
Extension [nm]
400
Wo ist die klassische Mechanik relevant ?
mesoscale
Time Scale
Monte Carlo
10-6 S
10-8 S
molecular
dynamics
quantum
chemistry
10-12 S
domain
exp(- ∆E/kT)
F = MA
Ηψ = Εψ
10-10 M 10-8 M 10-6 M
Length Scale
10-4 M
continuum
Wie funktionieren
Molekulardynamik Simulationen ?
Poly(vinylidene fluoride)
„Trockene“ Reibung
Reibungskräfte wirken entgegen der angelegten Kraft und der
Geschwindigkeit.
FR= µ* FN
Fext
FN=m*g
Trockene Reibungskraft unabhängig von Geschwindigkeit und Auflagefäche !
Typen der Reibung:
- Haftreibung
- Gleitreibung
- Rollreibung
µH
µG
µR
Stahl/Stahl
Stahl/Stahl
(Öl)
Gummi-Asphalt
µH
µG
0,78
0,42
0,05
0,8-1,1
0,03
0,7-0,9
Gleitreibung auf atomarer Skala
- der Kleben-Rutschen Prozess (stick-slip)
Rollreibung
Eisenbahn µG=0,002
KFZ
µG=0,02
Rollreibung ist eine ständige Bergaufbewegung, weil der Untergrund
inelastisch verformt wird.
Arbeit und Energie
Mechanische Arbeit
h
F = m⋅g
Gewichtskraft
W = m⋅ g ⋅h
Hubarbeit
(gegen die Schwerkraft)
FG
x
Eine reibungsfreie waagerechte
Verschiebung verrichtet keine Arbeit
W⊥ = m ⋅ g ⋅ ∆x = 0
Zug-Arbeit am Schlitten
W = F ⋅ s ⋅ cos ϑ
Die Arbeit
Die Arbeit W (work) wird definiert als das Produkt aus dem Weg den ein
Körper zurücklegt und der Kraft, die in Richtung dieses Weges wirkt.
v v
W = F ⋅ s = F ⋅ s ⋅ cos(α )
Die Arbeit ist das
Skalarprodukt aus Kraft und Weg
v
F
v
s
α
F cos(α )
Einheit: 1 J(oule)=1 Nm=1 kgm2/s2
Bei veränderlicher Kraft summieren wir
über kleine Wegelemente
r r
v v
W = ∑ F ⋅ ∆s = ∫ F ⋅ ds
v
∆s
v
F
Die elastische Verformungsarbeit
x=0
s
F
Für die Federkraft gilt: F = − D ⋅ s
v v
D 2
WD = ∫ Fds = ∫ − D ⋅ s ⋅ ds = − s
2
Kann man Arbeit sparen?
Goldene Regel der Mechanik:
Bei reibungsfreien (idealen) Maschinen gilt: Die dem Kraftwandler
zugeführte Arbeit Wzu ist gleich der von ihm abgegebenen Arbeit Wab.
Wzu = Wab
Geleistete “Zugarbeit” :
Wzu = F×s
Erbrachte Hub-Arbeit :
Wab = FG×h
Da am Flaschenzug mit einer losen Rolle
FG= 2×F und h = s/2 gilt,
ergibt sich daraus
Wzu = Wab.
Potentielle Energie
- Energie ist die Fähigkeit, Arbeit zu verrichten.
Ein Körper, an dem mechanische Arbeit geleistet
worden ist, hat die Fähigkeit gewonnen diese Arbeit
wieder zurückzugeben. Die von ihm aufgenommene
Energie wird potentielle Energie genannt
D 2
= −WD = s
2
Feder:
E pot
Lage:
E pot = −WH = m ⋅ g ⋅ h
Konservative Kraft und potentielle Energie
F =−
dE pot
dx
Im dreidimensionalen Raum gilt :
r
⎛ dV dV dV ⎞
r
⎟⎟ = − grad V (r )
F = −⎜⎜
,
,
⎝ dx dy dz ⎠
Beschleunigungsarbeit und kinetische Energie
Herleitung für den Fall gleichförmig beschleunigter Bewegung
Der zurückgelegte Weg :
F
2
a 2 a ⎛v⎞
v2
s = ⋅t = ⋅⎜ ⎟ =
2
2 ⎝a⎠
2a
Bei der Beschleunigung
verrichtete Arbeit :
v2 m ⋅ v2
W = F ⋅s = m⋅a⋅
=
2a
2
Wkin
m 2
= v
2
Def. Kinetische Energie
Energiesatz der Mechanik
Wenn nur konservative Kräfte wirken,
also keine Reibung auftritt, dann gilt:
Die Summe aus potentieller und kinetischer Energie
eines abgeschlossenen Systems ist unveränderlich.
E pot + Ekin = E ges = konstant
Beispiel : Die schiefe Ebene
Epot+Ekin=const
m 2
m⋅ g ⋅h = v
2
h
α
v max = 2 gh
Lösung des Pendelproblems
mit Hilfe des Energiesatzes
Das Pendel
Epot+Ekin=const
Es gibt 2 ausgezeichnete Punkte
1. ϑ=ϑmax mit Ekin=0 und
E ges = E pot (ϑmax ) = mgh
2. ϑ=0
mit Epot=0 und
mv 2max
Ekin (0) =
2
1.)+2.)
v max = 2 gh
Das asymmetrische Pendel
links und rechts gilt
E ges = E pot (ϑmax ) = mgh
Die Winkel lassen sich
ableiten aus :
h = l − l ⋅ cos ϑ
≈ l − l ⋅ (1 − ϑ + ...)
2
≈ lϑ
2
Der allgemeine Energieerhaltungssatz
- In einem abgeschlossenen System ist Gesamtenergie konstant.
- Energie kann man weder vernichten noch erzeugen.
- Die Energieformen können nur ineinander umgewandelt werden.
- Dies schließt alle Formen von Energie ein. (Elektrische, mechanische,
chemische Energie, Wärmeenergie, etc.)
Perpetuum mobile
Die von nicht-konservativen Kräften verrichtete Arbeit,WNK
entspricht der Änderung der mechanischen Gesamtenergie
∆E ges = ∆E pot + ∆Ekin = Wdissipativ
Die Leistung
Die Leistung P ist definiert als die verrichtete
Arbeit pro Zeiteinheit.
dW
P=
dt
Einheit: 1 W(att)=1 J/s=1 kgm2/s3
- Ein Mensch kann ca. 100 W Dauerleistung leisten (Glühbirne).
- 1 PS entspricht 735,5 W
Der zentrale, maximal inelastische Stoß
v1
v2
v1’ =v2’=v’
nachher
vorher
m1 v1 + m2 v 2 = (m1 + m2 ) v′
Betrachte Spezialfall v2=0
Energie vor dem Stoß
Evor =
m1 2
v1
2
Impulserhaltung
Energie nach dem Stoß :
Enach =
m1 + m2 2
m1
m1 2
v′ =
v1
2
(m1 + m2 ) 2
Chemische Reaktionen :
auch reaktive Stöße müssen den Impulssatz erfüllen
A + BC ⎯⎯→ AB + C
K
r
r
r
r
p A + pBC = p AB + pC
Ekin ( A) + Ekin ( BC ) =
Ekin ( AB) + Ekin (C ) + ∆Echem
Die kinetische Energie ist nicht
erhalten, sondern hängt von der
Umwandlung „innerer Energie“ ab.
Energiebilanz
für endotherme und exotherme
Reaktionen
Der schiefe, elastische Stoß
y
ϑ1
ϑ2
x
Impulserhaltung :
mv1 = mv1′ x + mv′2 x
0 = mv1′ y + mv′2 y
Energieerhaltung :
m 2 m 2 m
m 2 m
2
2
v1 = v1′ x + v′2 x + v1′ y + v′2 y
2
2
2
2
2
Für den Spezialfall:
v2=0, m1=m2
erhält man stets
ϑ1 + ϑ2 = π 2
Elastische Proton-Proton Streuung
nach dem Stoß schließen die
Bahnen einen Winkel von 90° ein.
Kollision von zwei Billardkugeln
(im Zeitlupenverfahren gefilmt)
aus Dransfeld et al.
Drehbewegungen und der starre Körper
Punktmassen-Systeme
„Abgeschlossenes System“ :
* Keine äußeren Kräfte
* nur WW-Kräfte
* Inertialsystem
In einem abgeschlossenen System gilt :
Der Gesamtimpuls ist erhalten.
Die Gesamtenergie ist erhalten.
(einschließlich der Wärme in nicht konservativen Systemen)
Der Gesamtdrehimpuls ist erhalten.
Der starrer Körper
- bisher: Bewegung von Massepunkten. Reine
Translationsbewegungen.
- jetzt: ausgedehnte Körper. Translations- und
Rotationsbewegungen.
B
A
B
A
Wirkungslinie
Kräfte wirken entlang der
Verbindungslinie:
Gleichgewicht
Kräfte wirken nicht entlang der
Verbindungslinie:
Rotation
Neu : Es wirkt ein „Drehmoment“
Drehmoment
l : Länge des Hebels
Kraft senkrecht auf Hebel
M =l×F
[Nm]
D
F
Drehmoment= Hebelarm *Kraft
l
F
α
α
F ⋅ sin(α )
Kraft wirkt unter beliebigem Winkel
D
M = l ⋅ Fsenkr . = l ⋅ F ⋅ sin(α )
Mechanisches Gleichgewicht
l1
F1
F1 ⋅l1 = F2 ⋅l 2
l2
D
(Hebelgesetz)
F2
Ein Körper ist dann im Gleichgewicht,
wenn die Summe aller äußerer Kräfte und
die Summe aller Drehmomente Null ist.
Anwendungen des Hebelgesetzes:
Brechstange, Schere, Schubkarre,
Getriebe, Gliedmaßen, Baukran ...
„Kraft mal Kraftarm=
Last mal Lastarm“
Schwerpunkt
Def.
M = ∑ mi
rs
Gesamtmasse
m ⋅r
∑
=
∑m
i
i
Schwerpunkt
m2
m1
rs
m3
i
Der Schwerpunkt eines abgeschlossenen Systems ist unbeschleunigt.
Bei Einwirkung einer äußeren Kraft Fext beschleunigt sich der
Schwerpunkt gemäß :
2
d rS
M 2 = Fext
dt
(Schwerpunktsatz)
Aussagen über den Schwerpunkt
-Kräfte, die am Schwerpunkt angreifen, wirken auf einen
ausgedehnten Körper, wie Kräfte auf einen Massepunkt.
Schwerpunkt=„Gravitationszentrum“
∑l m ⋅ g = l
i
i
SP
M ges ⋅ g
Die Summe aller Drehmomente =
Drehmoment der ges. Masse im Schwerpunkt
Ein Körper, der am Schwerpunkt
aufgehängt wird, erfährt im
Schwerefeld kein Drehmoment.
Drei Gleichgewichtsarten
Stabiles GGW:
Jede Verrückung x erhöht die
Lage des Schwerpunktes
d 2 E pot
dx 2
>0
Kleine Auslenkung x
=> Rückstellkräfte
Frück~ - x
Labiles GGW:
Jede Verrückung erniedrigt die
Lage des Schwerpunktes
Indifferentes GGW:
Jede Verrückung läßt die Lage
des Schwerpunkts unverändert
Der Drehimpuls
v
ω
m
v
v
v
r
v
ω
v
r
: Winkelgeschwindigkeit
: Bahnvektor
m : Masse
Definition
Bahngeschwindigkeit
Drehimpuls :
v = r ×ω
L = r × mv
Der Drehimpuls hat die Einheit kg·m2/s
Erhaltung des Drehimpulses
Wir betrachten die zeitliche
Ableitung des Drehimpulses L
dL
=M
dt
d(mv)
dL
= r⋅
= r ⋅ Fa = M
dt
dt
Grundgleichung
der rotierenden Bewegung
(analog zu dp/dt=Fa)
Bei Abwesenheit eines äußeren Drehmoments
bleibt der Drehimpuls konstant.
r
r
M = 0 ⇒ L = const
(DrehimpulsErhaltungssatz)
Der Drehimpuls ist auch bei
nicht-kreisförmigen Bewegungen erhalten.
Der Drehimpuls bezieht sich immer auf einen (Dreh)-Punkt
Motivation :
Trägheitsmoment
Das Trägheitsmoment ist die „träge Masse“ der Drehbewegung
L = r × mv = mr 2 ⋅ ω = I ⋅ ω
„Drehimpuls“ = „Drehträgheit“ mal “Drehgeschwindigkeit“
M = I ⋅ dω dt
„Drehkraft“ = „Drehträgheit“ mal “Drehbeschleunigung“
Definition : Trägheitsmoment I
Einzelne Massenpunkte
I = ∑ mi ⋅ ri
i
2
Achse
Trägheitsmoment einer
kontinuierlicher Massenverteilung
I = ∑ mi ⋅ ri ⇒ ∫ r dm
2
2
i
r
Achse
dm
Rotationsenergie
Jedes einzelne Masseelement
besitzt die kinetische Energie
m 2 m 2 2
v = ω r
2
2
Gesamtenergie:
ERot
I 2
mi 2 2 1
2
2
∑ 2 ri ω = 2 ∑ mi ri ⋅ ω = 2 ω
i
i
I 2
= ω
2
Rotationsenergie
eines starren Körpers
Das Drehmoment als Vektorprodukt
v v v
M = r ×F
Eigenschaften :
v v
M ⊥r
v
v
M ⊥F
v
v v
M = r ⋅ F ⋅ sin(α )
v v
v v
r × F = −F × r
Rechte-Hand-Regel
Es trägt nur die Projektion auf die
Senkrechte bei
Das Kreuzprodukt ist antikommutativ!
Der Drehsinn: Winkelgeschwindigkeit als Vektor
v
ω
m
v
v
v
r
v
r r r
v =ω×r
ω
v
r
v
v
„Rechte-Hand-Regel“
„Korkenzieherregel“
Drehimpuls als Vektor
v
ω
v
r
v
v
v v v
v =ω×r
v r
r
v
L = r × mv = I ⋅ ω
v
ω
v
r
v
v
Was passiert, wenn ein
v Drehmoment wirkt?
∆L
v
v
v
v v
v
L
L
d
F v
= M ⇒ ∆ L = M ⋅ ∆t
M
dt
v
r
v
v
∆ L parallel M
Dynamik starrer Körper
Wurfparabel eines starren Körpers
• Schwerpunkt beschreibt Wurfparabel M aSchwerpunkt =Fa
r
r
L = Iω
• Rotation um den Schwerpunkt:
Die Bewegung eines ausgedehnten Körpers lässt sich immer
zusammensetzen aus der Translation des Schwerpunkts und die Rotation
des Körpers um den Schwerpunkt. Der freie starre Körper hat sechs
Freiheitsgrade der Bewegung.
Analogien zwischen Translations- und Rotationsbewegungen
Ort
Translation
v
r
Beschleunigung
v
v
v
a
Masse
m
Geschwindigkeit
v
v
v dp
F = m⋅a =
Kraft
dt
v
v
p = m⋅ v
Impuls
m 2
Kinetische Energie
⋅v
2
Rotation
Winkel
ϕ
v
Winkelgeschw.
ω
Winkelbeschl.
v
α
2
I
=
m
r
∑ iiv
Trägheitsmoment
v
v dL
Drehmoment M = I ⋅ α =
dt
v
v
Drehimpuls
L = I ⋅ω
I
Rotationsenergie
⋅ω 2
2
Symmetrieachsen und freie Achsen
Feste Drehachse
Freie Drehachse
Die Rotation um freie Achsen erfordert kein Drehmoment.
Jeder starre Körper besitzt (mindestens) drei freie Achsen, und diese
stehen senkrecht aufeinander.
Der kräftefreie Kreisel : Nutation
Ein Kreisel ist ein Körper, der sich um eine freie Achse dreht.
Rotiert ein Körper um eine seiner freien Achsen, sind Drehachse und
Drehimpuls parallel zueinander.
Kreisel im Schwerefeld : Präzession
von oben:
∆Φ
Das Rad läuft um die
Aufhängung mit Umlauffrequenz
L
∆L
v
M ∆Φ
v =
∆t
L
Höhere Drehimpulse stabilisieren die Drehachse
v
∆L v
=M
∆t
v v
∆ L = L ⋅ ∆Φ
Präzession des Kreisels