Technische Mechanik III - FSMB

Technische Mechanik III
Die Kinetik starrer KÄ
orper ist eine
wichtige Grundlage fÄ
ur Ingenieure.
Nach der Kinematik werden die
kinetischen
Grundgleichungen
sowie Arbeit und Energie fÄ
ur
starre KÄ
orper formuliert und
angewandt. Auf dieser Basis werden
Probleme der Maschinendynamik,
wie Auswuchten und mechanische
Schwingungen behandelt.
Teil I enthÄ
alt die Statik, Teil II die
Festigkeitslehre.
Technische
Mechanik III
Kinetik starrer Körper
Werner Hübner, Thomas Schmid
Fachbereich 05, Studiengang Verfahrenstechnik
Papier und Verpackung
c VervielfÄ
°
altigung nur mit Zustimmung des Autors
200414
Fachhochschule München
Munich University of Applied Sciences
2
3
Inhaltsverzeichnis von TM III
1 Kinematik des Massenpunktes
1.1 Bewegung in kartesischen Koordinaten . . . .
1.2 Bewegung in Zylinderkoordinaten . . . . . . .
1.3 Die ebene Kreisbewegung . . . . . . . . . . .
1.3.1 Allgemeines . . . . . . . . . . . . . . .
1.3.2 Umfangs- und Winkelgeschwindigkeit
1.3.3 Zentripetalbeschleunigung . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8
8
9
11
11
11
13
2 Kinematik des starren KÄ
orpers
2.1 Freiheitsgrade . . . . . . . . . . . . . . . . . . . . .
2.2 Der Vektor der Winkelgeschwindigkeit . . . . . . .
2.2.1 Drehung um eine feste Achse . . . . . . . .
2.2.2 Drehung um einen Fixpunkt . . . . . . . .
2.2.3 Allgemeine Bewegung eines starren KÄ
orpers
2.2.4 Addition von Winkelgeschwindigkeiten . . .
2.2.5 Zusatzbedingung . . . . . . . . . . . . . . .
2.3 Die ebene Bewegung, der Momentanpol . . . . . .
2.3.1 Allgemeines . . . . . . . . . . . . . . . . . .
2.3.2 Das rollende Rad . . . . . . . . . . . . . . .
2.4 Planetengetriebe . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
14
14
16
16
17
18
19
20
21
21
22
25
.
.
.
.
.
28
28
28
29
32
35
.
.
.
.
.
.
.
.
.
.
.
.
3 Die Grundgesetze der Kinetik
3.1 Impuls und Drall . . . . . . . . . . . . . . . . . . . .
3.1.1 Impuls . . . . . . . . . . . . . . . . . . . . . .
3.1.2 Drall oder Drehimpuls . . . . . . . . . . . . .
3.2 Das 1. kinetische Grundgesetz, der Schwerpunktsatz
3.3 Das 2. kinetische Grundgesetz, der Drallsatz . . . . .
.
.
.
.
.
.
.
.
.
.
4 Arbeit, Energie und Leistung
4.1 Arbeit . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.1 De¯nition . . . . . . . . . . . . . . . . . . .
4.1.2 Beispiel Reibung . . . . . . . . . . . . . . .
4.1.3 Beispiel Schwerkraft . . . . . . . . . . . . .
4.1.4 Beispiel Feder . . . . . . . . . . . . . . . . .
4.2 Potenzielle Energie . . . . . . . . . . . . . . . . . .
4.3 Energie und Leistung beim Massenpunkt . . . . . .
4.3.1 Das Beispiel des freien Falls . . . . . . . . .
4.3.2 Die kinetische Energie . . . . . . . . . . . .
4.3.3 Arbeitssatz und Energieerhaltungssatz . . .
4.3.4 Die Leistung . . . . . . . . . . . . . . . . .
4.4 Energie und Leistung beim starren KÄ
orper . . . . .
4.4.1 Die Arbeit beim starren KÄ
orper . . . . . . .
4.4.2 Die kinetische Energie beim starren KÄ
orper
4.4.3 Arbeits- und Energieerhaltungssatz . . . . .
4.4.4 Die Leistung . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
38
38
38
39
40
40
41
42
42
43
44
44
45
45
46
47
47
5 Kinetik der reinen Translation
5.1 Der schiefe Wurf . . . . . . .
5.2 Raketenbewegung . . . . . . .
5.3 Satellitenbewegung . . . . . .
5.4 BewegungswiderstÄ
ande . . . .
5.4.1 Gleitreibung . . . . .
5.4.2 Viskose Reibung . . .
5.4.3 Luftwiderstand . . . .
5.4.4 Der Rollwiderstand . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
48
48
49
50
52
52
53
53
54
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
5
6 Kinetik der ebenen Bewegung
6.1 Das Rad auf der schiefen Ebene . . . . . . . . . . . . . . .
6.1.1 Schwerpunktsatz und Drallsatz . . . . . . . . . . .
6.1.2 Kinematische ZusammenhÄ
ange bei reinem Rollen .
6.1.3 Geschwindigkeit, Weg und Zeit . . . . . . . . . . .
6.1.4 Rollen mit Gleiten . . . . . . . . . . . . . . . . . .
6.2 Vorgehen bei der Berechnung ebener kinetischer Probleme
6.2.1 LÄ
osung mit dem Schwerpunktsatz und Drallsatz .
6.2.2 LÄ
osung mit dem Arbeitssatz oder dem
Energieerhaltungssatz . . . . . . . . . . . . . . . .
6.3 Das Beispiel ScheibenrÄ
ader und Seile . . . . . . . . . . . .
6.3.1 LÄ
osung mit dem Schwerpunktsatz und Drallsatz .
6.3.2 LÄ
osung mit dem Energieerhaltungssatz . . . . . . .
56
56
56
56
58
59
60
60
7 MassentrÄ
agheitsmomente
7.1 Drall und TrÄ
agheitsmomente . . . . . . . . . . . .
7.2 Symmetrie und HaupttrÄ
agheitsmomente . . . . . .
7.3 Parallel verschobene Achsen, der Steinersche Satz
7.4 Zusammengesetzte KÄ
orper . . . . . . . . . . . . . .
7.5 Wichtige TrÄ
agheitsmomente . . . . . . . . . . . . .
7.6 MassentrÄ
agheitsmomente bei gedrehten Achsen . .
.
.
.
.
.
.
70
70
72
75
76
78
82
.
.
.
.
.
84
84
86
87
88
88
8 Fliehkraft und Unwucht
8.1 Die Fliehkraft . . . . .
8.2 Statische Unwucht . .
8.3 Dynamische Unwucht
Ä
8.4 Uberlagerung
. . . . .
8.5 Rotor mit Schieflage .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
62
64
64
68
9 Freie, ungedÄ
ampfte Schwingungen
9.1 Grundbegri®e am Feder-Masse-Schwinger
9.2 Freie, ungedÄ
ampfte Schwingungen . . . .
9.2.1 Mathematisches Pendel . . . . . .
9.2.2 KÄ
orperpendel . . . . . . . . . . . .
9.2.3 Drehpendel . . . . . . . . . . . . .
9.2.4 Stab . . . . . . . . . . . . . . . . .
9.2.5 Balken . . . . . . . . . . . . . . . .
9.2.6 Torsion . . . . . . . . . . . . . . .
9.2.7 Zusammengesetzte Systeme . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
90
90
93
93
94
94
96
96
97
97
10 Sonstige Schwingungen
99
10.1 Erzwungene Schwingungen . . . . . . . . . . . . . . . . . 99
10.2 Der Ein°uss der DÄ
ampfung . . . . . . . . . . . . . . . . . 102
10.3 Koppelschwingungen . . . . . . . . . . . . . . . . . . . . . 104
11 Sto¼probleme
106
11.1 Der gerade, zentrale Sto¼ . . . . . . . . . . . . . . . . . . 106
11.2 Der gerade, exzentische Sto¼ . . . . . . . . . . . . . . . . . 108
Literatur
112
6
7
Vorwort
Dieser Teil der Technische Mechanik, die Kinetik starrer KÄorper beginnt
mit der Kinematik, deren VerstÄ
andnis grundlegend fÄ
ur die Kinetik ist.
Die Herleitungen der wichtigsten Gleichungen werden mathematisch
und axiomatisch korrekt durchgefÄ
uhrt. Sie werden so geschrieben, dass
sie auch fÄ
ur die LÄ
osung echt dreidimensionaler Probleme verwendet
werden kÄ
onnen. Dadurch erscheinen sie teilweise etwas kompliziert. Die
Anschaulichkeit soll in der Lehrveranstaltung durch viele { u
Äberwiegend
Ä
ebene { Ubungsaufgaben
erreicht werden.
Leider kÄ
onnen hier die Relativkinematik und Kreisele®ekte nicht
behandelt werden.
Die fÄ
ur Papieringenieure wichtigen Teile der Rotorkinetik, besonders
die Unwucht-Thematik werden jedoch dargestellt. Ebenso wird eine
EinfÄ
uhrung in die Grundlagen der mechanischen Schwingungen gegeben.
Dieses Thema ist von zunehmender Bedeutung, da heutige Maschinen
immer schneller laufen.
Mit dem Schwerpunktsatz und dem Drallsatz lassen sich sÄ
amtliche
Probleme der Kinetik lÄ
osen. Bei Systemen mit einem Freiheitsgrad
ist auch der Arbeitssatz hilfreich. Die Prinzipien\ der Mechanik
"
(d’Alembert, Lagrange) werden hier nicht behandelt. Dazu wÄ
are
eine ausfÄ
uhrlichere Darstellung einschlie¼lich der Grundbegri®e der
Variationsrechnung erforderlich. Manche einfache\ Herleitungen sind
"
eine Beleidigung fÄ
ur einen brillianten Geist wie d’Alembert. Auch
fÄ
uhrt ein salopper Umgang mit den Prinzipien oft zu Verwirrungen,
Ä
insbesondere wenn die Zeit fÄ
ur genÄ
ugend viele Ubungsaufgaben
fehlt.
MÄ
unchen, im November 2004
Werner HÄ
ubner
8
1 KINEMATIK DES MASSENPUNKTES
1
Kinematik des Massenpunktes
1.2 Bewegung in Zylinderkoordinaten
Deshalb gelten fÄ
ur die Komponenten der Geschwindigkeit ~v und der
Beschleunigung ~a:
9
Der Massenpunkt ist eine Idealisierung: Er ist das Modell eines
KÄ
orpers, dessen Drehbewegung vernachlÄ
assigt wird. Die Lage eines
Massenpunktes ist durch seinen Ort
~r = ~r(t)
d~r
= ~r_
dt
Aus dieser folgt die Beschleunigung
(acceleration)
d~v
~a = ~a(t) =
= ~v_ = ~Är
dt
ax = v_ x = x
Ä >
=
ay = v_ y = yÄ
>
az = v_ z = zÄ ;
v=
q
vx2 + vy2 + vz2
(1.5)
a=
q
a2x + a2y + a2z
(1.6)
(1.1)
1.2
Bewegung in Zylinderkoordinaten
Zylinderkoordinaten sind mitdrehende Koordinaten. Wird die
z-Richtung au¼er Acht gelassen, hei¼en sie auch Polarkoordinaten.
(1.2)
Die Beschleunigung ist eine Geschwindigkeitsänderung und
Bild 1.1.
Massenpunkt P
damit eine rein kinematische Größe, hat also nichts mit Kräften
zu tun!
1.1
9
vx = x_ >
=
vy = y_
>
vz = z_ ;
Die BetrÄ
age sind
eindeutig gegeben. Daraus folgt die Geschwindigkeit
(velocity)
~v = ~v (t) =
9
Nach Bild 1.2 gelten fÄ
ur eine kleine
Drehung d'
d~er = 1d'~eϕ ; d~eϕ = 1d'(¡~er )
Dividiert man formal mit dt, so erhÄ
alt
man daraus die Gleichungen
Bewegung in kartesischen Koordinaten
Der Ortsvektor lautet in kartesischen Koordinaten
~r = x~ex + y~ey + z~ez
(1.3)
Kennzeichnend fÄ
ur das kartesische System ist die zeitliche Konstanz der
Achsen:
~e_ x = ~0; ~e_ y = ~0; ~e_ z = ~0
(1.4)
d~er
´ ~e_ r = '~
_ eϕ
dt
d~eϕ
´ ~e_ ϕ = ¡'~
_ er
dt
d~ez
´ ~e_ z = ~0
dt
Bild 1.2. Polarkoordinaten
(1.7)
10
1 KINEMATIK DES MASSENPUNKTES
1.3
Aus dem Ortsvektor
~r = r~er + 0 ¢ ~eϕ + z~ez
~a = (r~
_ er + r_ '~
_ eϕ ) + (r_ '~
_ eϕ + r'~
Äeϕ ¡ r '_ '~
_ er ) + zÄ~ez
r = const. ) r_ = 0; rÄ = 0 und
2
~a = (Ä
r ¡ r'_ )~er + (r '
Ä + 2r_ ')~
_ eϕ + zÄ~ez
Die Komponenten von Geschwindigkeit und Beschleunigung lauten also
>
;
(1.8)
ar = rÄ ¡ r'_ 2
aϕ = r'Ä + 2r_ '_
az = zÄ
Mit der Umfangsgeschwindigkeit
u = vϕ = r '_
Allgemeines
Die Beziehungen fÄ
ur die ebene Kreisbewegung kÄ
onnen als Sonderfall aus
den Gleichungen (1.8) bis (1.12) abgelesen werden: Hier gelten:
~v = r~
_ er + r'~
_ eϕ + z~
_ ez
9
>
=
11
Die ebene Kreisbewegung
1.3.1
erhÄ
alt man durch Di®erenzieren und unter Verwendung von (1.7)
vr = r_
vϕ = r'_
vz = z_
1.3 Die ebene Kreisbewegung
9
>
=
>
;
(1.9)
(1.10)
z(t) ´ 0
Aus (1.8) und (1.9) erhÄ
alt man die Komponenten
vr = 0
vϕ = r '_
)
ar = ¡r'_ 2
aϕ = r '
Ä
(1.13)
)
(1.14)
Bild 1.3.
Kreisbewegung
lassen sich die Beschleunigungen auch in der Form schreiben:
ar = v_ r ¡
u2
r
aϕ = r'Ä + 2vr
(1.11)
u
r
Der Term 2r_ '_ hei¼t Coriolis-Beschleunigung1 .
(1.12)
1.3.2
Umfangs- und Winkelgeschwindigkeit
Die GrÄ
o¼e u = vϕ = r '_ hei¼t Umfangsgeschwindigkeit, '_ = ! hei¼t
Winkelgeschwindigkeit. Es gilt die Beziehung
'_ ´ !;
u = !r
(1.15)
Bemerkung:
Der Massenpunkt selbst hat nur eine Geschwindigkeit, keine
Winkelgeschwindigkeit. ! bezieht sich hier auf den Fahrstrahl.
Die Einheit der Winkelgeschwindigkeit ! ist
rad/s oder 1/s wobei 1 rad =
1
Gustave G. Coriolis, 1792 - 1843
180◦
π
= 57; 3◦ .
12
1 KINEMATIK DES MASSENPUNKTES
Anschauliche Deutung (nach Bild 1.4 ):
Die Geschwindigkeit v gibt an, wieviel Meter in einer Sekunde
durchlaufen werden. Die GrÄ
o¼e ! gibt an, wieviele Winkeleinheiten
(1 rad = 57,3◦) in einer Sekunde durchlaufen werden. Technisch
interessiert meist, wie oft der Winkel 2¼ in einer Sekunde durchlaufen
wird. Diese GrÄ
o¼e hei¼t Drehzahl oder Drehfrequenz und wird mit n
bezeichnet.
1.3 Die ebene Kreisbewegung
1.3.3
13
Zentripetalbeschleunigung
Die Radialkomponente in (1.14)
u2
= ¡ar
r
hei¼t Zentripetalbeschleunigung. Diese ist
r'_ 2 = r! 2 =
² nach innen zum Mittelpunkt gerichtet,
Es gilt
2¼
! = 2¼n =
T
² quadratisch proportional zur Winkelgeschwindigkeit bzw. zur
Umfangsgeschwindigkeit.
(1.16)
Anschauliche Deutung der Zentripetalbeschleunigung:
Die Einheit von n ist ebenfalls
Ä
² Eine Beschleunigung ist stets die Anderung
der Geschwindigkeit (und
kein Ma¼ fÄ
ur die Kraft!)
s−1 = 1/s, frÄ
uher U/s.
Bild 1.4. Einheitskreis mit
Bogenmaßen
Wegen der grÄ
o¼eren Zahlen ist (leider) auch die antiquierte, fÄ
ur die
Messtechnik und fÄ
ur Berechnungen unhandliche Einheit 1/min oder
min−1 gebrÄ
auchlich:
nalt = 60n;
nalt in 1/min; n in 1/s
Eine Schwierigkeit ist, dass n und ! die gleiche Einheit (1/s) haben. Bei
Herleitungen arbeitet man am besten mit !, Zahlenwerte sollten stets
als Drehzahl n in 1/s angeben werden! Wichtige Werte sind:
n = 50 s−1 ; ! = 314 rad= s; nalt = 3000 min−1
Die GrÄ
o¼e T in (1.16) ist die Zeit fÄ
ur eine Umdrehung. Bei den
Schwingungen (Kapitel 9) gilt (1.16) mit f = n. Dort hei¼en
! Kreisfrequenz, f Frequenz und T Periodendauer.
² Bei ! = const. gilt gemÄ
a¼ Bild 1.5
j~v1 j = j~v2 j = u
~v2 = ~v1 + d~v
dv = ud'
dv
d'
u2
=u
= u'_ = r '_ 2 = r!2 =
dt
dt
r
² d~v ist nach innen gerichtet.
Bild 1.5. Zur
Zentripetalbeschleunigung
Bemerkung: In der Kinetik wird die Zentrifugalkraft eingefÄ
uhrt. Dies ist
im mitdrehenden Koordinatensystem eine nach au¼en gerichtete Kraft.
Ä
2 KINEMATIK DES STARREN KORPERS
14
2
Kinematik des starren Körpers
2.1
Freiheitsgrade
Freiheitsgrade sind die zur Beschreibung des Ortes und der Lage
Ä
erforderlichen unabhÄ
angigen Koordinaten. Tab. 2.1 gibt eine Ubersicht
u
oglichen FÄ
alle.
Äber die mÄ
rÄ
aumlich
eben
vx
vy
vz
!x
!y
!z
Allgemein
*
*
*
*
*
*
Reine Translation
*
*
*
0
0
0
Drehung um Fixpunkt
0
0
0
*
*
*
Allgemein
*
*
0
0
0
*
Reine Translation
*
*
0
0
0
0
Drehung um feste Achse
0
0
0
0
0
*
Tab. 2.1. Freiheitsgrade
Bemerkungen:
² Die allgemeine rÄaumliche Bewegung eines starren KÄ
orpers wird durch
6 Freiheitsgrade beschrieben: 3 Freiheitsgrade der Translation und
3 Freiheitsgrade der Rotation.
² Im Folgenden wird hÄ
au¯g der Sonderfall der allgemeinen ebenen
Bewegung mit vx ; vy und !z behandelt.
2.1 Freiheitsgrade
15
² Reine Translation kann auch auf einer
Kreisbahn erfolgen. So ist die Bewegung
der im Bild 2.1 dargestellten Gondeln eines
Riesenrads eine Translation; die Gondeln
drehen sich nicht!
Bild 2.1. Riesenrad
Ä
2 KINEMATIK DES STARREN KORPERS
16
2.2
Der Vektor der Winkelgeschwindigkeit
Ziel dieses Abschnittes ist, die allgemeine Bewegung eines starren
KÄ
orpers zu beschreiben. Nur bei dem Sonderfall der reinen Translation
wird die Bewegung durch die Geschwindigkeit ~v allein beschrieben. In
allen anderen FÄ
allen kommt eine Drehbewegung hinzu.
2.2.1
Drehung um eine feste Achse
2.2.2
Bei dem KÄ
orper von Bild 2.2 wird die Achse AB entfernt. Er soll nun
im Punkt C gelagert sein, und zwar so, dass Drehbewegungen in allen
Richtungen mÄ
oglich sind. Dann hei¼t C Fixpunkt. Nun ist ~
! ist nicht
mehr raumfest, sondern wechselt die Richtung. Auch hier gilt eine (2.1)
entsprechende Gleichung
(2.2)
allerdings nur momentan, d.h. fÄ
ur
einen bestimmten Zeitpunkt. Die
Veranschaulichung erfolgt nach
Bild 2.3 mit der Rechte-HandRegel
² Die Finger zeigen in Richtung
der Geschwindigkeit ~v
u = j~
! jj~s j sin ° = !s sin ° = !h
fÄ
ur u schreiben
² Der
Daumen
kennzeichnet
den
Vektor
der
Winkelgeschwindigkeit !
~
(2.1)
Bild 2.2. Drehung eines Körpers
17
Drehung um einen Fixpunkt
~v = ~
! £ ~s
Der in Bild 2.2 dargestellte KÄ
orper soll in A und B gelagert sein. In
einem Punkt C wird ein kÄ
orperfestes Koordinatensystem ~er ; ~eϕ ; ~ez
eingefÄ
uhrt. Dabei ist die z-Achse eine feste Achse. Ein beliebiger Punkt
~
P hat die Umfangsgeschwindigkeit ~u. FÄ
ur diese gilt mit ~u?~ez ; ~u?FP
nach (1.15) u = ! h. Fasst man ~
! = !~ez als einen in der Drehachse
liegenden Vektor und ~s als kÄorperfesten Vektor auf, so kann man wegen
~u = ~
! £ ~s
2.2 Der Vektor der Winkelgeschwindigkeit
Bild 2.3. Rechte-Hand-Regel
Ä
2 KINEMATIK DES STARREN KORPERS
18
2.2.3
Allgemeine Bewegung eines starren KÄ
orpers
Der Punkt C des KÄ
orpers von Bild 2.2 soll nun frei beweglich sein, so
dass fÄ
ur seine Geschwindigkeit gilt: ~vC = ~r_ C . FÄ
ur die Geschwindigkeit
eines beliebigen Punktes P des KÄ
orpers gilt dann mit
~r = ~rC + ~s
2.2 Der Vektor der Winkelgeschwindigkeit
19
Beweis, dass ~
! bei einem starren KÄ
orper u
Ä berall gleich ist:
! ∗.
Annahme, ~
! gelte nur fÄ
ur den Punkt C, beim Punkt C∗ gelte ~
Entsprechend (2.3) mÄ
usste dann ausgehend von C∗ gelten
~v = ~vC ∗ + ~
! ∗ £ ~s ∗
(2.4)
FÄ
ur den Punkt C∗ selbst gilt mit ~c = ~s ¡ ~s ∗
(siehe Bild 2.4 ) die wichtige Vektorbeziehung fÄ
ur
die allgemeine Bewegung eines starren KÄ
orpers
~vC ∗ = ~vC + !
~ £ (~s ¡ ~s ∗ )
Setzt man dies in (2.4) ein, so erhÄ
alt man
~v = ~vC + !
~ £ ~s
(2.3)
Man beachte, dass im Kreuzprodukt der vom
bewegten Bezugspunkt C ausgehende Vektor ~s =
~r ¡ ~rC und nicht der vom Ursprung 0 des ruhenden
(nicht beschleunigten) Systems ausgehende Vektor
~r steht.
! £ ~s + (~
!∗ ¡~
!) £ ~s ∗
~v = ~vC + ~
und wegen (2.3)
Bild 2.4. Allgemeine
Bewegung
(~
!∗ ¡~
! ) £ ~s ∗ = ~0
FÄ
ur beliebige ~s ∗ muss also gelten
~
!∗ = ~
!
FÄ
ur die allgemeine Bewegung des starren KÄ
orpers gelten nach (2.3)
² Die Geschwindigkeit ~v ist an jedem Punkt verschieden
² !
~ ist ein freier Vektor
² !
~ ist an allen Stellen eines starren KÄ
orpers gleich
Bild 2.5. Eine
Winkelgeschwindigkeit
2.2.4
q. e. d.
Addition von Winkelgeschwindigkeiten
Dreht sich ein starrer KÄ
orper gleichzeitig mit
Winkelgeschwindigkeiten, so kÄ
onnen diese addiert werden:
!
~ =!
~1 + ~
!2 + ¢ ¢ ¢
mehreren
(2.5)
Ä
2 KINEMATIK DES STARREN KORPERS
20
2.3 Die ebene Bewegung, der Momentanpol
Beispiel Kollermu
Ä hle:
2.3
Die Gesamtdrehung der in Bild 2.6
skizzerten KollermÄ
uhle setzt sich aus
!1 und !3 zusammen:
2.3.1
2
Bild 2.6. Kollermühle
Es gilt fÄ
ur die Geschwindigkeit des Punktes 1
!1
r
vy1 = !3 r = !1 a )
=
a
!3
Es muss also der resulierende Winkelgeschwindigkeitsvektor ~
! durch den
Punkt M gehen.
2.2.5
Die ebene Bewegung, der Momentanpol
Allgemeines
Jede ebene Bewegung kann als Drehung um
einen momentan in Ruhe be¯ndlichen Punkt, den
Momentanpol, aufgefasst werden.
3
!1
6
7
!
~ =4 0 5
!3
21
Die anschauliche Deutung erfolgt nach Bild 2.8 :
Ä
Geometrische Orter
fÄ
ur den Momentanpol M
sind die Geraden g1 und g2 die durch die
Punkte 1 bzw. 2 gehen und senkrecht auf den
Geschwindigkeitsvektoren ~v1 bzw. ~v2 stehen. Mit den
senkrechten AbstÄ
anden h1 und h2 muss gelten:
v1
v2
!z =
oder !z =
h1
h2
Zusatzbedingung
Aus (2.3) kann man bei gegebenen ~vC und !
~ die Geschwindigkeit
eines beliebigen Punktes ~v = ~v1 berechnen. Es liegt umgekehrt
nahe, bei vorgegebenen Geschwindigkeiten ~vC und ~v1 den Vektor der
Winkelgeschwindigkeit !
~ zu berechnen.
Die Geschwindigkeiten kÄ
onnen jedoch nicht
beliebig vorgegeben werden. Vielmehr muss
gelten
~s1 ¢ ~v1 = ~s1 ¢ ~vC
(2.6)
d.h.
die
Projektionen
der
beiden
Geschwindigkeiten auf die Gerade durch
die Punkte C und 1 mÄ
ussen gleich sein.
Bild 2.7.
Zusatzbedingung
Beweis fÄ
ur (2.6): Aus (2.3) folgt
~ £ ~s1 ;
~v1 ¡ ~vC = !
~s1 ¢ (~v1 ¡ ~vC ) = ~s1 ¢ (~
! £ ~s1 ) = 0 q. e. d.
Bild 2.8.
Momentanpol M
Die ebene Bewegung eines starren KÄ
orpers ist durch
die Geschwindigkeit eines Punktes und durch die
Bewegungsrichtung eines zweiten Punktes gegeben. Der
zweite Punkt kann auch der Momentanpol mit ~v = ~0 sein.
Ä
2 KINEMATIK DES STARREN KORPERS
22
2.3.2
Das rollende Rad
3
2
3
2
3
2
² Der Verlauf der Geschwindigkeit auf der Achse M2 ist durch das
Geschwindigkeitsdreieck gegeben.
~
² Ein beliebiger Punkt P bewegt sich senkrecht zu dem Vektor MP
3
vx
vS
0
sx
6
7 6
7 6
7 6
7
4 v y 5 = 4 0 5 + 4 0 5 £ 4 sy 5
0
0
0
¡!
¹
² Der Betrag der Geschwindigkeit ist vP = ! MP
Bild 2.9. Rollendes Rad
FÄ
ur den Momentanpol M ist sx = 0 und sy = ¡r. Aus vx = 0 erhÄ
alt
man
vS
0 = vS ¡ !r und daraus ! =
r
Schreibt man (2.3) ausgehend von dem
Bezugspunkt M, so gilt fÄ
ur die Punkte parallel
zur y-Achse, also auf der Geraden M2
2
3
2
3
2
3
2
3
vy = 0
FÄ
ur den Schwerpunkt S ist also vSx = vS = !r,
und fÄ
ur den Punkt 2 gilt vSx = v2 = !2r.
² Bei ! = const. ist die Beschleunigung ~aP zum Mittelpunkt S
gerichtet.
² Auch der Momentanpol M hat eine
Beschleunigung, und zwar
~aM = [0; r! 2 ; 0]
obwohl
er
momentan
Geschwindigkeit hat.
keine
² Zu jedem Zeitpunkt wird ein neuer Punkt
Momentanpol.
vx
0
0
0
6
7 6
7 6
7 6
7
4 vy 5 = 4 0 5 + 4 0 5 £ 4 y 5
0
0
¡!
0
vx = !y;
23
FÄ
ur das rollende Rad gelten nach Bild 2.10 und Bild 2.11 :
Bild 2.9 zeigt ein rollendes Rad. Auf
dieses wendet man die Gleichung (2.3)
an und zwar zunÄ
achst ausgehend vom
Schwerpunkt S
2
2.3 Die ebene Bewegung, der Momentanpol
Bild 2.10.
Geschwindigkeitsdreieck
Bild 2.11.
Geschwindigkeiten am
rollenden Rad
24
Ä
2 KINEMATIK DES STARREN KORPERS
2.4
Die Absolutbewegung des materiellen
Punktes P, der zur Zeit t = 0
Momentanpol war, folgt gemÄ
a¼ Bild 2.12
zu
x = r' ¡ r sin '
y = r
¡ r cos '
Dies ist die Parameterdarstellung fÄ
ur
die in Bild 2.13 dargestellte gewÄohnliche
Zykloide.
2.4 Planetengetriebe
25
Planetengetriebe
Planetengetriebe | auch Umlaufgetriebe genannt | sind ein
anschauliches, technisches Beispiel fÄ
ur die ebene Bewegung von starren
KÄ
orpern. Bild 2.14 zeigt eine schematische Darstellung.
Bild 2.12. Abrollbewegung
Bild 2.13. Gewöhnliche Zykloide
Bild 2.14. Planetengetriebe
FÄ
ur die Geschwindigkeiten von Punkten auf der y-Achse gilt allgemein
v = vS + ! y
FÄ
ur den Eingri®spunkt Q gilt auf dem Sonnenrad 1
vQ = !1 a
und auf dem Planentenrad b
vQ = vb ¡ !b b
FÄ
ur den Eingri®spunkt R gilt auf dem Planentenrad b
vR = vb + !b b
und auf dem Au¼enkranz 3
vR = !3 c
Ä
2 KINEMATIK DES STARREN KORPERS
26
Durch Gleichsetzen erhÄ
alt man
2.4 Planetengetriebe
27
FÄ
ur die Anwendung folgen aus (2.10) die MÄ
oglichkeiten der Tab. 2.2 .
Dabei kÄ
onnen die nicht festen RÄ
ader antreibend oder angetrieben sein.
vb ¡ !b b = !1a
vb + !b b = !3c
Sonnenrad
1
Daraus folgen fÄ
ur die Bewegung des Planetenrades:
!3 c + !1 a
2
!3 c ¡ !1 a
!b =
2b
vb =
PlanetenradtrÄ
ager
2
Au¼enkranz
3
(2.7)
fest
!3 =
a+c
!2
c
(2.8)
In Bild 2.15 sind die FÄ
alle fÄ
ur
!b > 0; !b = 0 und !b < 0
dargestellt.
Bild 2.15. Bewegung des Planetenrades
fest
Ä
UbersetzungsverhÄ
altnisse
!1 =
a+c
!2
a
Tab. 2.2. Übersetzungsverhältnisse bei einem Planetenradgetriebe
FÄ
ur den PlanetenradtrÄager 2 gilt vb = !2 r2 . Der Bahnradius r2 des
Planetenrades ist der Mittelwert aus a und c. Deshalb gilt
a+c
vb = !2
(2.9)
2
Andererseits gilt fÄ
ur vb die Gleichung (2.7). Durch Gleichsetzen von (2.7)
und (2.9) erhÄ
alt man die fÄ
ur die Berechnung der GetriebeÄ
ubersetzungen
wichtige Beziehung
!1 a ¡ !2 (a + c) + !3 c = 0
a
!3 = ¡ !1
c
fest
(2.10)
28
3 DIE GRUNDGESETZE DER KINETIK
3
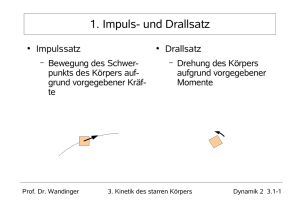
Die Grundgesetze der Kinetik
Die Kinetik beschreibt den Zusammenhang zwischen KrÄ
aften und
Bewegungen.
3.1
3.1 Impuls und Drall
FÄ
ur ein System mit konstanter Masse folgt aus (3.3)
R
R
m~r_ S = ~r_ dm oder m~vS = ~v dm
K
p
~ = m~vS
(3.5)
Impuls
Der Impuls eines Massenelements ist
d~
p = ~v dm = ~r_ dm
Impuls = Masse mal Schwerpunktgeschwindigkeit
(3.1)
Der Impuls eines KÄ
orpers folgt daraus durch Integration u
Äber den
KÄ
orper (K) zu
p
~=
(3.4)
K
Damit gilt fÄ
ur den in (3.2) de¯nierten Impuls eines KÄ
orpers oder Systems
Impuls und Drall
3.1.1
29
R
~v dm:
(3.2)
3.1.2
Drall oder Drehimpuls
Der Drall eines Massenelements dm bezÄ
uglich des Punktes 0 ist nach
Bild 3.1
K
FÄ
ur den Massenmittelpunkt (Schwerpunkt) S gilt nach TM I, Kapitel 7
m~rS =
R
~rdm
(3.3)
K
In der Technischen Mechanik werden vorwiegend Systeme mit
konstanter Masse behandelt, z.B.
² starre KÄ
orper,
² deformierbare KÄ
orper,
² beliebig abgegrenzte Mehrmassensysteme.
(Dagegen werden in der Fluidmechanik Systeme betrachtet, deren Masse
nicht konstant ist, z.B. Ausschnitte aus einer StrÄ
omung).
~ 0 = ~r £ ~v dm
dL
(3.6)
Ä
Beim Ubergang
vom Massenelement auf einen
KÄ
orper verwendet man als Bezugspunkt meist
den Schwerpunkt S:
~r = ~rS + ~s
FÄ
ur die Geschwindigkeit des Massenelements
gilt
~v = ~vS + ~
! £ ~s:
Damit erhÄ
alt man
~ 0 = [~rS £ ~v + ~s £ ~vS + ~s £ (~
dL
! £ ~s)] dm
Bild 3.1. Starrer Körper
30
3 DIE GRUNDGESETZE DER KINETIK
FÄ
ur ein System mit konstanter Masse, insbesondere fÄ
ur den starren
KÄorper, folgt daraus durch Integration der Drall bzgl. 0
R
R
R
Nach (3.4) gilt ~v dm = m~vS . Da ~s vom Schwerpunkt ausgeht, gilt
R
~sdm = 0. Mit dem Drall bezÄ
uglich S
~S =
L
Z
~s £ (~
! £ ~s)dm
(3.7)
erhÄ
alt man
~ 0 = ~rS £ m~vS + L
~S
L
(3.8)
~ S = ~0. Trotzdem existiert fÄ
FÄ
ur einen Massenpunkt ist L
ur diesen
~ 0 = ~rS £ m~vS = ~rS £ p
Sonderfall ein Drall bzgl. 0 nÄ
amlich L
~.
Setzt man in (3.7) ~
! und ~s in Matrizenform ein, so erhÄ
alt man mit
2
3
2
3
2
3
!x
x
!y z ¡ !z y
6
7
6
7
6
7
!
~ = 4 !y 5 ; ~s = 4 y 5 ; ~
! £ ~s = 4 !z x ¡ !x z 5
!z
z
!x y ¡ !y x
den Drall bzgl. des Schwerpunkts
~S =
L
Z
2
6
4
(y 2
z2) !
3
+
xy !y ¡
xz !z
x ¡
7
2
2
¡yx !x + (z + x ) !y ¡
yz !z 5dm(3.9)
¡zx !x ¡
zy !y + (y2 + x2 ) !z
FÄ
ur den Sonderfall der ebenen Bewegung gelten !x = !y = 0. FÄ
ur
KÄ
orper
die zur xy-Ebene
symmetrisch sind, wird in Kapitel 7 gezeigt,
R
R
dass zxdm = 0 und yzdm = 0 gelten. Der Drallvektor ist dann
3
0
7
~S = 6
L
4 0 5
J z !z
Darin ist
R
(3.11)
das MassentrÄagheitsmoment bzgl. der z-Achse und der Betrag des Dralls
also
LSz = Jz !z
(3.12)
Bei der ebenen Bewegung muss die z-Achse nicht fest sein, sie darf sich
parallel verschieben.
Der Drehimpuls oder Drall ist analog zum Impuls de¯niert:
Dreh-Impuls = Dreh-Masse mal Dreh-Geschwindigkeit.
oder mit den hier verwendeten Bezeichnungen
Drall = MassentrÄ
agheitsmoment mal Winkelgeschwindigkeit
Der Drall bei ebener Bewegung
2
31
Jz = (x2 + y 2 )dm
~ 0 = ~rS £ ~v dm + ~sdm £ ~vS + ~s £ (~
L
! £ ~s)dm
R
3.1 Impuls und Drall
(3.10)
Einige Beispiele fÄ
ur Jz (bezÄ
uglich S) sind in Tab. 3.1 zu ¯nden, die
ausfÄ
uhrlichere Darstellung ¯ndet sich in Kapitel 7.
Kreiszylinder, homogen
Jz = 12 mr 2
Kreisring
Jz = mr2
Stab bzgl. Schwerpunkt
Jz =
Stab bzgl. Ende
Jz̄ = 13 ml2
Kugel
Jz = 25 mr 2
1
2
12 ml
Tab. 3.1. Wichtige Massenträgheitsmomente
32
3 DIE GRUNDGESETZE DER KINETIK
3.2
Das 1. kinetische Grundgesetz, der Schwerpunktsatz
Grundlage der Kinetik sind die 3 Newton2 schen Gesetze (1687):
1. Das TrÄ
agheitsgesetz (Ä
ahnlich bei Galilei3 , 1630):
Jeder KÄ
orper bleibt im Zustand der Ruhe oder der gleichfÄ
ormig
geradlinigen Bewegung, sofern keine a
u¼eren
KrÄ
a
fte
auf
ihn
Ä
einwirken.
2. Das Bewegungsgesetz:
Ä
Die Anderung
der Bewegung(sgrÄ
o¼e) ist der einwirkenden a
Äu¼eren
Kraft proportional und erfolgt in der Richtung, in der jene Kraft
wirkt.
3. Das Gegenwirkungsgesetz (actio = reactio):
Eine Wirkung ist immer einer Gegenwirkung gleich; mit anderen
Worten, die zwischen zwei KÄ
orpern geschehenden Wirkungen sind
immer einander gleich und treten in entgegengesetzten Richtungen
auf.
FÄ
ur die Berechnung terrestrischer Probleme ist die Formulierung fÄ
ur ein
4
Massenelement von Euler (1740) vorteilhaft:
d
d
~
(d~
p) = (~v dm) = dF~ oder dm~v_ = dF
(3.13)
dt
dt
~ mÄ
Bei den Kraftanteilen dF
ussen innere und Äau¼ere unterschieden
werden
~ = dF
~ (i) + dF~ (a)
dF
(3.14)
Betrachtet man das ganze System (Integration), so heben sich die
inneren Kraftanteile auf, und man erhÄ
alt den Impulssatz
d
~ (a)
~
p=F
(3.15)
dt
2
Sir Isaak Newton, 1643 - 1727
Galileo Galilei, 1564 — 1642
4
Leonhard Euler, 1707 — 1783
3
3.2 Das 1. kinetische Grundgesetz, der Schwerpunktsatz
33
FÄ
ur ein System mit konstanter Masse p
~ = m~vS (3.5) und ~v_ S = ~aS erhÄ
alt
man
m~aS = F~ (a)
(3.16)
Dies ist das 1. kinetische Grundgesetz oder der Schwerpunktsatz. Dieser
lautet in Worten:
Der Schwerpunkt des KÄ
orpers wird so beschleunigt, als ob
sÄ
amtliche Ä
au¼ere KrÄ
afte in ihm angreifen wÄ
urden.
Dabei ist zu beachten:
² Nur Ä
au¼ere KrÄ
afte kÄ
onnen die Bewegung des Schwerpunktes
beein°ussen (Beispiele s.u.).
² Die KrÄ
afte mÄ
ussen nicht im Schwerpunkt angreifen!
² Man braucht einen KÄ
orper nicht als Massenpunkt zu betrachten.
Beispiele zum ersten Punkt:
Die Treibladung in einer Pistole erzeugt innere KrÄ
afte, der
Schwerpunkt von Kugel und GehÄ
ause bleibt zunÄ
achst erhalten.
Dies erklÄ
art den RÄ
ucksto¼.
Will eine Person aus einem Boot ans Ufer springen, so bleibt auch
hier der Schwerpunkt erhalten und die Person landet eventuell im
Wasser.
34
3 DIE GRUNDGESETZE DER KINETIK
FÄ
ur den Massenpunkt lautet das 1. kinetische Grundgesetz:
m~a = F~ oder m~v_ = F~
3.3
(3.17)
und wird in dieser Form hÄ
au¯g als das Newtonsche Grundgesetz\
"
bezeichnet.
Durch Integration des Schwerpunktsatzes (3.16) u
alt man
Äber die Zeit erhÄ
m~vS ¡ m~vS0 =
Zt
^~
~ dt∗ = F
F
(3.18)
t0
(Manche Autoren bezeichnen diese Beziehung anstelle von (3.15) als
Impulssatz.)
Ist der Kraftsto¼\ (siehe Kapitel 11) auf der rechten Seite gleich 0, so
"
erhÄ
alt man den Impulserhaltungssatz
m~vS = m~vS1 = const.
3.3 Das 2. kinetische Grundgesetz, der Drallsatz
(3.19)
35
Das 2. kinetische Grundgesetz, der Drallsatz
Der Drallsatz wird auch Drehimpuls-Satz oder Momentensatz genannt.
FÄ
ur ein Massenelement gilt analog zu (3.16) als 2. Grundgesetz
~_ 0 = dM
~0
dL
(3.20)
FÄ
ur die linke Seite gilt die De¯nition (3.6). Di®erenziert man diese, so
erhÄ
alt man wegen ~r_ = ~v
~ + dM
~τ
~r £ ~v_ dm = ~r £ dF
(3.21)
Darin ist der Schubspannungsanteil (vgl. TM II)
2
3
¿yz ¡ ¿zy
7
~τ = 6
dM
4 ¿zx ¡ ¿xz 5 dxdydz
¿xy ¡ ¿yx
(3.22)
Multipliziert man das 1. kinetische Grundgesetz fÄ
ur
~ mit ~r£, so erkennt
ein Massenelement ~v_ dm = dF
man mit (3.21), dass
~ τ = ~0
dM
Bild 3.2.
Schubspannungen
am Element
oder
¿yz = ¿zy ; ¿zx = ¿xz ; ¿xy = ¿yx
(3.23)
gilt und dies auch bei beschleunigten KÄ
orpern.
Also lautet der Drallsatz fÄ
ur ein Massenelement
_~
~0
dL0 = ~r £ dF~ = dM
~ = dF~ (a) + dF~ (i) , wobei sich die inneren KrÄ
Darin ist dF
afte bei der
Integration herausheben.
FÄ
ur den ganzen KÄ
orper und auch fÄ
ur ein ganzes System gilt
~ (a)
~_ 0 = M
L
0
(3.24)
36
3 DIE GRUNDGESETZE DER KINETIK
Geht man zum Schwerpunkt als Bezugspunkt
u
Äber, so folgt aus (3.8)
~_ 0 = ~vS £ m~vS + ~rS £ m~v_ S + L
~_ S
L
und nach Bild 3.3
~ (a) = M
~ (a) + ~rS £ F
~ (a)
M
0
S
37
Integriert man (3.27), so folgt
~S ¡ L
~ S0 =
L
(3.25)
Zt
~ (a) dt∗
M
S
(3.29)
t0
Ist die rechte Seite | der Drehsto¼ | gleich Null, so erhÄ
alt man
(3.26)
Aus (3.23), (3.25) und (3.26) erhÄ
alt man mit dem
~ (a)
Schwerpunktsatz m~v_ S = F
~_ S = M
~ (a)
L
S
3.3 Das 2. kinetische Grundgesetz, der Drallsatz
~S = L
~ S0 = const.
L
Bild 3.3. Drehmoment
bzgl. S
Dies ist der Drallerhaltungssatz. Er gilt ebenso wie fÄ
ur den
Bezugspunkt 0 auch fÄ
ur den Schwerpunkt S.
Zur Axiomatik: Bei der hier gewÄ
ahlten Darstellung ist der Drallsatz
ein vom Schwerpunktsatz unabhÄ
angiges Grundgesetz. Aus beiden folgt
(3.23), die Gleichheit der Schubspannungen. Letztere folgt in der Statik
aus dem Momentengleichgewicht.
(3.27)
Im ebenen Fall lautet der Drallsatz fÄ
ur ein kÄ
orperfestes Bezugssystem
mit (3.12) bei Jz = const.
JSz !_ z = MSz
(3.30)
(3.28)
Die Gleichung (3.23) kann in der Kinetik anstelle
Axiom (nicht zu beweisen) angenommen werden
Axiom5 ). Damit | und nur damit | kann der
1. kinetischen Grundgesetz hergeleitet werden.
manchen Darstellungen verschwiegen.
In Worten lautet der Drallsatz :
Ä
Die zeitliche Anderung
des Dralls ist gleich dem
au¼eren Moment. Drall und Moment mÄ
ussen dabei auf
Ä
denselben Punkt bezogen sein, der entweder raumfest oder
Schwerpunkt sein muss.
5
Ludwig Boltzmann, 1844 — 1906
des Drallsatzes als
(Boltzmannsches
Drallsatz aus dem
Letzteres wird in
38
4 ARBEIT, ENERGIE UND LEISTUNG
4
Arbeit, Energie und Leistung
4.1
4.1.1
4.1 Arbeit
4.1.2
39
Beispiel Reibung
Wie man aus Bild 4.1 sieht, ist die Arbeit der
au¼eren KrÄ
afte
Ä
Arbeit
De¯nition
dW (a) = F dx
Mit der saloppen Formulierung: Arbeit = Kraft mal Weg\ kommt
"
man in der Mechanik nicht weit, das Drehmoment kÄ
onnte man ebenso
beschreiben. Exakt formuliert gilt
~ ¢ d~r
dW = F
(4.1)
die Arbeit der Reibungskraft
dW = ¡Rdx
(4.4)
oder in Komponenten
dW = Fx dx + Fy dy + Fz dz
Bild 4.1. Arbeit
infolge Reibung
(4.2)
Daraus erhÄ
alt man durch Integration
W =
Z
F~ ¢ d~r
oder genauer W01 =
Die Einheit der Arbeit ist
1 Nm = 1 J
Z 1
0
F~ ¢ d~r
(4.3)
(Joule, Aussprache: [dschu:l])
Das Vorzeichen der Arbeit hÄ
angt von der Systemabgrenzung, d.h. von
der betrachteten Kraft ab. Hier wird, wie in der Thermodynamik, die
einem System zugefÄ
uhrte Arbeit positiv de¯niert.
Die Arbeit ist im allgemeinen wegabhÄ
angig. FÄ
ur die
Arbeit lÄ
angs der Wege I und II von Bild 4.2 gelten
WI =
Z 1
0
~ ¢ d~r
F
bzw. WII =
Z 1
0
~ ¢ d~r
F
Beispiel von Bild 4.2 : Arbeit eines Radfahrers auf
verschiedenen Wegen:
Weg I:
Weg II:
100 m Feldweg mit FI = 100 N,
WI = 10 000 J
150 m Stra¼e mit FII = 40 N,
WII = 6 000 J
Bild 4.2.
Abhängigkeit vom
Weg
40
4 ARBEIT, ENERGIE UND LEISTUNG
4.1.3
4.2 Potenzielle Energie
4.2
Beispiel Schwerkraft
Potenzielle Energie
FÄ
ur das Beispiel der Schwerkraft nach Bild 4.3 ist die Arbeit unabhÄ
angig
vom Weg
Da in Bild 4.3 dz nach oben zeigt, ist die Arbeit der
au¼eren Kraft
Ä
W = WI = WII
dW (a) = +F dz
dW = ¡mgdz
(4.5)
W = W01 = ¡mg
Bild 4.3. Arbeit
bei Schwerkraft
dW (a) = F dx
¸x1
x0
1
= ¡ cx2 ¡ 0
2
(4.6)
(4.8)
(4.9)
(4.10)
FÄ
ur das Beispiel der Federkraft ist die potenzielle Energie fÄ
ur die
gespannte Feder (vgl. (4.6)) Ep1 = 12 cx2 . FÄ
ur die entspannte Feder
(x = 0) gilt Ep0 = 0. Der Zusammenhang mit der Arbeit W01 ist
dW = ¡cxdx
1 2
cx
2
dz = ¡mgz1 + mgz0
wobei
dW = ¡dEp :
die Arbeit der nach links wirkenden Federkraft cx
ist
·
z0
potenzielle Energie oder auch Potenzial genannt wird. Dabei beachte
man die Vorzeichen!
Die Arbeit der die Feder spannenden Kraft F~ ist
W01 = ¡
Z z1
W01 = ¡Ep1 + Ep0
Ep = mgz
Beispiel Feder
Also erhÄ
alt man mit x1 = x und x0 = 0 aus (4.3)
(4.7)
In der Mechanik nennt man Systeme, in denen (4.7) gilt, konservativ.
Betrachtet man im Beispiel von Bild 4.3 die Arbeit der Schwerkraft, so
gilt
die Arbeit der Schwerkraft
4.1.4
41
Bild 4.4. Arbeit an
einer Feder
1
1
W01 = ¡ cx2 = ¡Ep1 + Ep0 ;
Ep1 = ¡W01 = cx2
(4.11)
2
2
In der Festigkeitslehre wird W = 12 cx2 als FormÄanderungsenergie einer
Feder bezeichnet.
42
4 ARBEIT, ENERGIE UND LEISTUNG
4.3
Energie und Leistung beim Massenpunkt
4.3.1
4.3.2
Das Beispiel des freien Falls
Es wird der freie Fall eines Massenpunktes unter Schwerkraftein°u¼ vom
Punkt 1 zum Punkt 0 betrachtet. Das Newtonsche Grundgesetz lautet
dv
m
= ¡mg
dt
Multipliziert man beide Seiten formal mit dz, so erhÄ
alt man rechts die
Arbeit dW und mit v = dz=dt
mvdv = ¡mgdz
1
mv 2
2
¸0
1
·
= ¡ mgz
1
2
2 mv0
¡
1
2
2 mv1
Ek0
¡
Ek1
¸0
1
Ep1
¡
Ep0
FÄ
ur den wichtigen Sonderfall
Bild 4.5. Freier
Fall
v1 = 0; z0 = 0; z1 = h
gelten
1
mv 2 = mgh;
2 0
Die kinetische Energie
Die kinetische Energie wird nun unabhÄ
angig vom Beispiel des vorigen
Abschnitts hergeleitet. FÄ
ur den Massenpunkt gilt nach Kapitel 3
~
m~v_ = F
Die Skalarmultiplikation mit d~r und Integration u
Äber den Weg ergibt
Z 1
0
m~v_ ¢ d~r =
Z 1
0
F~ ¢ d~r
(4.13)
Rechts steht die Arbeit W01 , links wird mit d~r = ~v dt weiter umgeformt
R
m ~v_ ¢ ~v dt
·
= mgz1 ¡ mgz0
=
43
FÄ
ur die zeitliche Ableitung von ~v 2 gilt:
d 2
(~v ) = 2~v ¢ ~v_
dt
Damit wird die linke Seite von (4.13) zu
Die Integration ergibt
·
4.3 Energie und Leistung beim Massenpunkt
und daraus v0 =
p
2gh
(4.12)
¸
1
1
1
1
m~v 2 = m~v 21 ¡ m~v 20 = Ek1 ¡ Ek0
2
2
2
0
Ek hei¼t kinetische Energie und ist fÄ
ur den Massenpunkt
1
Ek = m~v 2
2
(4.14)
44
4 ARBEIT, ENERGIE UND LEISTUNG
4.3.3
4.4
Arbeitssatz und Energieerhaltungssatz
Aus (4.13) erhÄ
alt man den Arbeitssatz.
Ek1 ¡ Ek0 =
Z 1
0
F~ ¢ d~r
4.4 Energie und Leistung beim starren KÄorper
(4.15)
X
Körper
4.4.1
oder
Ek1 + Ep1 = Ek0 + Ep0
(4.16)
(4.17)
Dies ist der Energieerhaltungssatz oder Energiesatz.
4.3.4
Einheit der Leistung: W = Watt = J/s = Nm/s
Abgeleitete Einheit 1 kW = 1000 W.
Antiquierte Einheit 1 PS = 75 kp m/s = 735,5 W
1 kW = 1,36 PS
0
¢F ¢ d~r
(4.19)
0 Körper
Die Arbeit beim starren KÄ
orper
~v = ~vS + ~
! £ ~s
(4.20)
d~r = d~rS + d~
' £ ~s
(4.21)
gilt
~ ¢ d~r = ¢F
~ ¢ d~rS + ¢F
~ ¢ (d~
¢F
' £ ~s)
Die Umstellung des Spatproduktes ergibt
~ ¢ d~r = ¢F
~ ¢ d~rS + (~s £ ¢F
~ ) ¢ d~
¢F
'
Die Leistung P ist die pro Zeiteinheit verrichtete Arbeit
dW
~ ¢ d~r = F
~ ¢ ~v
=F
dt
dt
dW =
Z1 X
und man erhÄ
alt
Die Leistung
P =
(¢Ek1 ¡ ¢Ek0 ) =
Z1
ZunÄ
achst soll der Term ¢F~ ¢ d~r auf der rechten Seite von (4.19)
umgeformt werden. Analog zu
oder
Ek + Ep = const.
Energie und Leistung beim starren Körper
Die Beziehungen des vorigen Abschnittes gelten nun statt fÄ
ur den
Massenpunkt m fÄ
ur das Massenelement ¢m. Anstelle von (4.15) kann
man schreiben
Hat die Kraft F~ ein Potenzial, wie z.B. die Schwerkraft, die Federkraft,
nicht aber die Reibungskraft, so gilt mit (4.8)
Ek1 ¡ Ek0 = Ep0 ¡ Ep1
45
(4.18)
~ S = ~s £ ¢F~
Analog zu (3.21) gilt wegen ¢Mτ = 0 die Beziehung ¢M
und man erhÄ
alt
~ ¢ d~r = ¢F
~ ¢ d~rS + ¢M
~ S ¢ d~
¢F
'
Wie bei der Herleitung von Schwerpunktsatz und Drallsatz heben sich
die inneren KrÄ
afte und die Momente aus den inneren KrÄ
aften auf. Man
erhÄ
alt nach Integration u
orper fÄ
ur die rechte Seite von (4.19)
Äber den KÄ
X
~ (a) ¢ d~rS + M
~ (a) ¢ d~
¢F~ ¢ d~r = dW = F
'
S
Körper
46
4 ARBEIT, ENERGIE UND LEISTUNG
4.4.2
Die kinetische Energie beim starren KÄ
orper
4.4.3
Auf der linken Seite von (4.19) erscheint die kinetische Energie des
Massenelements
1
¢Ek = ¢m~v 2
(4.22)
2
Hierin setzt man die kinematische Beziehung fÄ
ur den starren KÄ
orper
(4.20) ein
und erhÄ
alt
~s¢m = 0
(4.23)
FÄ
ur den Fall der ebenen Bewegung in der x; y-Ebene gilt
Damit ist auch die linke Seite von (4.19) ermittelt worden.
Ek1 ¡ Ek0 =
Z 1
0
F~ (a) ¢ d~rS +
Z 1
0
~ (a) ¢ d~
M
'
S
(4.25)
Die Leistung
Die Leistung erhÄ
alt man durch Ableitung der Arbeit nach der Zeit
~ S aus (3.7) die kinetische Energie des starren
folgt mit dem Drall L
KÄorpers zu
1
1
Ek = m~vS 2 + Jz !z2
2
2
Integriert man (4.19) u
alt man den
Äber den Weg von 0 bis 1, so erhÄ
Arbeitssatz fÄ
ur den starren KÄ
orper
4.4.4
und ~u ¢ (~
! £ ~s) = ~
! ¢ [~s £ (~
! £ ~s)]
1
1
~S
Ek = m~vS 2 + ~
!¢L
2
2
Arbeits- und Energieerhaltungssatz
Der Energiesatz lautet auch hier Ek + Ep = const. (vgl. (4.17)).
i
1h 2
¢Ek =
~vS + 2~vS ¢ (~
! £ ~s) + ~u ¢ (~
! £ ~s) ¢m
2
Wegen
Körper
47
Man beachte, dass Ek1 und Ek2 rotatorische Anteile nach (4.24)
enthalten.
! £ ~s ´ ~vS + ~u
~v = ~vS + ~
P
4.4 Energie und Leistung beim starren KÄorper
P = dW=dt
FÄ
ur den Fall der ebenen Bewegung folgt also aus (4.24) und (4.25) der
Leistungssatz
(a)
P = ~vS ¢ ~v_ S m + !z Jz !_ z = F~ (a) ¢ ~vS + MSz !z
(4.26)
Neben der wichtigen Formel (4.18) fÄ
ur die translatorische Bewegung gilt
fÄ
ur die Leistung bei reiner Rotation
(4.24)
P = M!
mit ! = 2¼n
(4.27)
48
5
5
KINETIK DER REINEN TRANSLATION
Kinetik der reinen Translation
5.2 Raketenbewegung
5.2
49
Raketenbewegung
von
Die
dies
der
Das Besondere an der Raketenbewegung ist die verÄ
anderliche Masse
m = m(t). FÄ
ur eine senkrecht aufsteigende Rakete kann man aus dem
Impulssatz die Gleichung
dv
dm
m
= ¡mg + S mit S = ¹vr = ¡vr
(5.3)
dt
dt
herleiten. Darin sind S die Schubkraft, ¹ die pro Zeiteinheit
ausstrÄ
omende Masse (Einheit kg/s) und vr die Strahlgeschwindigkeit
relativ zur Rakete.
integriert und dem jeweiligen Problem angepasst. Der Drallsatz wird
nicht verwendet.
Ohne g, bzw. fÄ
ur kurze Brennzeiten, erhÄ
alt man | ausgehend von einem
beliebigen Zustand m1 ; v1 | die Raketengrundgleichung
³
´
m1
¢v = v ¡ v1 = vr ln
und daraus ¢m = m1 1 ¡ e−∆v/vr (5.4)
m
Diese Gleichungen sind fÄ
ur ManÄ
over von Raumfahrzeugen und Satelliten
wichtig.
In der Kinetik der reinen Translation wird die Bewegung
Massenpunkten\ unter dem Ein°uss von KrÄ
aften untersucht.
"
betrachteten KÄ
orper mÄ
ussen nicht wirklich klein sein, wie
der Ausdruck Massenpunkt vermuten lÄ
asst. Vielmehr wird von
Betrachtung der Drehung abgesehen.
Zur Behandlung dieser Probleme wird der Schwerpunktsatz
~ (a)
m~Är S = F
Die folgenden, nur kurz angerissenen Abschnitte stellen interessante
Gebiete der Technischen Mechanik dar.
5.1
Der schiefe Wurf
Der schiefe Wurf ohne Luftwiderstand kann mit dem Newtonschen
Grundgesetz berechnet werden. In Koordinaten lautet dieses
mÄ
x=0
mÄ
y = ¡mg
Diese Gleichungen
Anfangsbedingungen
Bahnen. Wird der
berÄ
ucksichtigt, lauten
p
(5.1)
werden | ausgehend von verschiedenen
| integriert. Es ergeben sich parabelfÄ
ormige
in Abschnitt 5.4.3 de¯nierte Luftwiderstand
mit k = ½cW AS =(2m) die Di®erentialgleichungen
x
Ä = ¡k x_ 2 +py_ 2 x_
yÄ = ¡g ¡ ¡k x_ 2 + y_ 2 y_
Diese werden am besten numerisch integriert.
(5.2)
Im erdnahen Feld folgt die erreichbare Geschwindigkeit aus (2) durch
Integration vom Zustand t1 ; v1 ; m1 = mL + mT aus
•
¶
mT
vmax = v1 + vr ln 1 +
¡ g(t ¡ t1 )
(5.5)
mL
Um eine hohe Geschwindigkeit zu erreichen, mÄ
ussen folgende Werte
mÄ
oglichst gro¼ sein:
² das VerhÄ
altnis Treibsto®masse zu Leermasse mT =mL
² die Strahlgeschwindigkeit vr (Chemie)
² die Anfangsgeschwindigkeit v1 (Mehrstufenprinzip)
50
5
5.3
KINETIK DER REINEN TRANSLATION
Satellitenbewegung
Betrachtet wird das ZweikÄ
orperproblem Erde und Erdsatellit bzw.
klassisch Sonne und Planet. Ausgegangen wird von den 3 Keplerschen6
Gesetzen und von der Ellipsengleichung in Parameterform. FÄ
ur
Satellitenbewegungen um die Erde lassen sich daraus die folgenden
Beziehungen ableiten: FÄ
ur den Kraftfaktor in einem beliebigen
Abstand r vom Erdmittelpunkt gilt (fÄ
ur r ¸ R):
R2
r2
An der Erdober°Ä
ache sind
g(r) = g0
(5.6)
g0 = 0,00981 km/s2 und r = R ¼ 6370 km
FÄ
ur die Umlaufzeit auf einer Ellipsenbahn mit der gro¼en Halbachse a
gilt
T = 2¼
s
a3
g0 R2
(5.7)
Die Geschwindigkeit an einer beliebigen Stelle r der Bahn wird durch
die Binetsche Gleichung gegeben
•
¶
1
2
2 2
¡
(5.8)
v = g0 R
r a
FÄ
ur eine erdnahe Kreisbahn (a = r ¼ R) ergibt sich die 1. kosmische
Geschwindigkeit
v=
p
(5.9)
p
(5.10)
g0 R = 7; 9 km/s
Die 2. kosmische Geschwindigkeit, die Fluchtgeschwindigkeit, erhÄ
alt man
aus (5.8) fÄ
ur r ¼ R und a ! 1 zu
v=
6
2g0 R = 11; 2 km/s
Johannes Kepler, 1571 - 1630
5.3 Satellitenbewegung
51
52
5
5.4
KINETIK DER REINEN TRANSLATION
Bewegungswiderstände
5.4.2
FÄ
ur
reale
Ingenieurprobleme
ist
die
BewegungswiderstÄ
ande von hoher Bedeutung.
Betrachtung
der
² Aufgrund von BewegungswiderstÄ
anden geht mechanische Energie in
WÄ
armeenergie u
Äber und damit meist verloren.
² Die
BewegungswiderstÄ
ande
Geschwindigkeitsrichtung
F~W = ¡FW ~ev
5.4.1
mit ~ev =
wirken
entgegen
~v
v
der
(5.11)
Gleitreibung
Viskose Reibung
In Bild 5.2 ist ein KÄ
orper dargestellt, der
sich auf einem Fluid¯lm der SpalthÄ
ohe s
bewegt. FÄ
ur dessen Bewegungswiderstand
gilt
v
FW = ´A
(5.13)
s
Bild 5.2. Viskose Reibung
Darin sind
A FlÄ
ache
s SpalthÄ
ohe
v Geschwindigkeit
´ dynamische ZÄ
ahigkeit.
1 Pa s = 1 kg m−1 s−1
(5.12)
Die Reibungskraft R hÄ
angt nicht vom Betrag von ~v ab.
Siehe auch TM I.
53
Die Einheit von ´ ist Pascal-Sekunden
Im Fall der Gleitreibung ist der Bewegungswiderstand
FW = R = ¹N
5.4 BewegungswiderstÄande
Man beachte dass FW » v . Dieses Widerstandsgesetz gilt in Luft fÄ
ur
Geschwindigkeiten bis etwa 1 m/s.
Bild 5.1.
Gleitreibung
5.4.3
Luftwiderstand
Bereits von Newton wurde der Widerstand einer senkrecht
ur einen beliebigen
angestrÄ
omten Platte mit FW = ½Av 2 angegeben. FÄ
KÄ
orper gilt
1
FW = cW ½v 2 AS
(5.14)
2
mit
1
2
Staudruck
(Einheit: N/m2 )
2 ½v
½ Dichte
(Einheit: kg/m3 )
AS Schatten°Ä
ache
(Einheit: m2 )
cW Widerstandsbeiwert (Einheit: |)
Ein Beispiel fÄ
ur den cW -Wert: Bei einer Kugel ist cW ¼ 0; 5.
54
5
5.4.4
KINETIK DER REINEN TRANSLATION
Der Rollwiderstand
Der Rollwiderstand ist ein Sonderfall der BewegungswiderstÄ
ande. Dieser
darf nicht mit dem im nÄ
achsten Kapitel behandelten reinen Rollen
verwechselt werden, bei dem die Haftreibungskraft keinen Energieverlust
bewirkt.
Um den Widerstand eines rollenden Rades
zu deuten, nimmt man an, dass das Rad
einen kleinen Wulst vor sich herschiebt. Das
Momentengleichgewicht in Bild 5.3 lautet:
1 <¾ :
¡rFx + f Fz = 0
Mit den KrÄ
aftegleichungen
Fx = R
und Fz = N
folgt daraus
f
R= N
r
Bild 5.3. Rollwiderstand
Beispiele fÄ
ur f sind:
f ¼ 0; 5 mm
f ¼ 5 : : : 10 ¹m
bei
bei
bei
bei
StahlrÄ
adern auf Schienen
r = 500 mm wird ¹ = 0; 001
Kugellagern
r = 5 mm wird ¹ = 0; 001
Bei GummirÄ
adern gelten andere Mechanismen. Als grobe NÄ
aherung
kann man bei diesen mit
R = ¹r N
rechnen.
mit ¹r ¼ 0; 015 : : : 0; 02
5.4 BewegungswiderstÄande
55
56
6
6
Kinetik der ebenen Bewegung
6.1
6.1.1
KINETIK DER EBENEN BEWEGUNG
Das Rad auf der schiefen Ebene
Schwerpunktsatz und Drallsatz
Ein typisches Beispiel fÄ
ur die Berechnungen der Kinetik ist das Rad
auf einer schiefen Ebene. Betrachtet wird ein | wie in der Statik |
freigeschnittenes Rad, dessen Geschwindigkeit x_ nach unten und dessen
Winkelgeschwindigkeit ! = '_ rechtsdrehend angenommen wird. Wie in
der Statik werden KrÄ
afte eingetragen: die eingeprÄ
agte Gewichtskraft mg
sowie die ReaktionskrÄ
afte N und R.
Der Schwerpunktsatz in y-Richtung lautet
mÄ
y = N ¡ mg cos ®
Daraus folgt mit yÄ = 0
6.1 Das Rad auf der schiefen Ebene
57
Aus den drei Gleichungen (6.2), (6.3) und (6.4) folgen die drei
Unbekannten x
Ä; ';
Ä R. Hier ist R = RH die Haftreibungskraft, also
eine Reaktionskraft. Ihre Richtung kann deshalb willkÄ
urlich angesetzt
werden (Bild 6.1). Die Elimination von R = RH tritt bei vielen Aufgaben
ahnlich auf: (6.4) wird in (6.3) eingesetzt. Au¼erdem wird (6.3) durch r
Ä
dividiert
J
x
Ä=R
r2
Diese Beziehung wird zu (6.2) addiert
•
¶
J
x
Ä = mg sin ®
r2
Zur Kontrolle: Der Massenausdruck bei x
Ä hat stets positive Vorzeichen.
Man erhÄ
alt fÄ
ur die 3 Unbekannten
g sin ®
x
Ä=
(6.5)
1 + J=mr 2
m+
(6.1)
'Ä =
(6.6)
In x-Richtung ergibt der Schwerpunktsatz
mit vS = x_
1 g sin ®
r 1 + J=mr 2
R=
J g sin ®
mg sin ®
=
2
2
r 1 + J=mr
mr2 =J + 1
(6.7)
N = mg cos ®
mÄ
x = mg sin ® ¡ R
(6.2)
Der Drallsatz in Richtung von '_ ergibt sich
mit dem TrÄ
agheitsmoment JS = J
J'
Ä = +rR
(6.3)
Bild 6.1. Rad auf der
schiefen Ebene
Bei zylindrischen Scheiben und Walzen (aber nicht immer!) ist
J = 12 mr 2 , wodurch sich die AusdrÄ
ucke vereinfachen. Wie aus TM I,
Kapitel 12 bekannt ist, kann die Haftreibungskraft R nicht beliebig gro¼
werden
R = RH · ¹0 N = ¹0 mg cos ®
6.1.2
Reines Rollen tritt also nur auf, wenn
Kinematische ZusammenhÄ
ange bei reinem Rollen
tan ® · ¹0
Aus der kinematischen Grundgleichung fÄ
ur den starren KÄ
orper
~v = ~vS + ~
! £ ~s
folgt hier ausgehend vom Momentanpol M
v = !r
oder x_ = 'r
_
und damit x
Ä = 'r
Ä
(6.8)
(6.4)
Ã
mr 2
+1
J
!
(6.9)
58
6
6.1.3
KINETIK DER EBENEN BEWEGUNG
Geschwindigkeit, Weg und Zeit
6.1.4
Aus der Gleichung (6.5)
x
Ä=
g sin ®
= a = const.
1 + J=mr 2
folgt durch Integration mit v0 = 0; s0 = 0
1
x_ = v = at; s = at2
2
und daraus
r
2s
t=
a
sowie
p
v = 2as
(6.10)
59
Rollen mit Gleiten
Bei kleinem ¹0 oder gro¼em ® tritt Rollen mit Gleiten auf. Dabei gelten
wie oben
N = mg cos ®
mÄ
x = mg sin ® ¡ R
J 'Ä = rR
(6.11)
(6.12)
Diese Beziehung folgt einfacher aus dem Energieerhaltungssatz:
1
1
mv 2 + J!2 = mgs sin ®
(6.13)
2
2
Die kinematische Bedingung ist wie oben ! = v=r (6.4). Also gilt
•
6.1 Das Rad auf der schiefen Ebene
¶
J
m + 2 v 2 = 2mgs sin ®
r
Unter Verwendung der in (6.10) mit a abgekÄ
urzten, konstanten
Beschleunigung erhÄ
alt man v 2 = 2as. Aus (6.10) folgt, dass ein
Hohlzylinder mit J = mr 2 weniger beschleunigt wird als ein Vollzylinder
mit J = 12 mr 2 . Dies gilt unabhÄ
angig von Masse und Radius.
FÄ
ur die GrÄ
o¼en x_ und '_ gibt es hier keinen kinematischen
Zusammenhang (so wie die Gleichung (6.4) v = !r beim reinen Rollen).
Dagegen erhÄ
alt man hier eine weitere Gleichung aus dem Coulomb'schen
Gesetz fÄ
ur die Gleitreibung
R = RG = ¹N = ¹mg cos ®;
(6.14)
Dabei ist R eine eingeprÄ
agte Kraft, deren Richtung entgegen x_ ist
(Die GrÄ
o¼e RH beim reinen Rollen ist eine Reaktionskraft und kann
dort willkÄ
urlich angenommen werden). Mit (6.8) folgen aus dem
Schwerpunktsatz und dem Drallsatz
x
Ä = g(sin ® ¡ ¹ cos ®)
(6.15)
1 mr 2
'Ä = ¹g
cos ®
r
J
(6.16)
60
6
6.2
6.2.1
KINETIK DER EBENEN BEWEGUNG
Vorgehen bei der Berechnung ebener kinetischer
Probleme
6.2 Vorgehen bei der Berechnung ebener kinetischer Probleme
In vielen FÄ
allen ist yÄS = 0; dann wird durch (6.18) das
KrÄ
aftegleichgewicht in y-Richtung beschrieben.
Drallsatz bezÄ
uglich des Schwerpunktes:
LÄ
osung mit dem Schwerpunktsatz und Drallsatz
JS '
Ä=
Das Vorgehen erfolgt Ä
ahnlich wie in der Statik und wird hier fÄ
ur Systeme
mit mehreren KÄ
orpern formuliert.
1. KÄorper freischneiden:
Die zu berechnenden KÄ
orper freigeschnitten skizzieren (bei
Schwingungsaufgaben in einer ausgelenkten Lage)
2. Kinematische GrÄo¼en eintragen:
(Schwerpunktgeschwindigkeiten x_ = vS
und Winkelgeschwindigkeiten '_ = !).
Die Richtungen nach der Anschauung festlegen und dann
beibehalten.
ReaktionskrÄ
afte sind z.B.:
RH ,
SeilkrÄ
afte
Si ,
4. Bewegungsgleichungen aufstellen:
(Drei Bewegungsgleichungen fÄ
ur jeden KÄ
orper).
Schwerpunktsatz fÄ
ur die Bewegungsrichtung (z.B. x):
mÄ
xS =
P
Fxi
(6.17)
Dabei mÄ
ussen die KrÄ
afte Fxi in Richtung von x positiv angesetzt
werden. FÄ
ur die y-Richtung folgt entsprechend
mÄ
yS =
P
Fyi
MSi
(6.19)
Momente MSi im Drehsinn von '_ werden positiv angesetzt.
5. Kinematische ZusammenhÄange aufstellen:
(ZusammenhÄ
ange zwischen den unter Punkt 2 eingefÄ
uhrten,
kinematischen GrÄ
o¼en x_ und ').
_ FÄ
ur den beliebigen Bezugspunkt C
gilt
~v = ~vC + !
~ £ ~s:
Praktisches Vorgehen: Zuerst den Momentanpol M bestimmen. Mit
¹ gilt z.B.
r = MS
x_ S = 'r
_
und deshalb auch x
ÄS = 'r
Ä
(6.20)
6. Gleichungen au°Äosen:
Die Zahl der Unbekannten und die Zahl der Gleichungen mÄ
ussen
u
Äbereinstimmen.
Gewichtskraft G = mg, Gleitreibungskraft R.
Haftreibungskraft
P
Dabei auf das Vorzeichen achten; evtl. gilt auch x_ S = ¡'r.
_
3. KrÄafte eintragen:
(SÄ
amtliche eingeprÄ
agte KrÄ
afte und ReaktionskrÄ
afte.)
EingeprÄ
agte KrÄ
afte sind z.B.:
Normalkraft N ,
Federkraft cx .
61
(6.18)
Das beschriebene Vorgehen fÄ
uhrt | auch bei komplizierten Systemen
| immer zum Ziel. Weitere SÄ
atze werden nicht benÄ
otigt.
62
6
6.2.2
KINETIK DER EBENEN BEWEGUNG
LÄ
osung
mit
dem
Energieerhaltungssatz
Arbeitssatz
oder
dem
Bei Systemen mit einem 1 Freiheitsgrad kann die LÄ
osung auch mit
dem Arbeitssatz oder | wenn keine Reibung vorhanden ist | dem
Energieerhaltungssatz gewonnen werden. Dabei sind folgende Punkte
zu beachten:
² Den rotatorischen Term nicht vergessen! FÄ
ur die kinetische Energie
gilt beim starren KÄ
orper fÄ
ur die ebene Bewegung
Ek = 12 mvS2 + 12 JS ! 2
fÄ
ur die rÄ
aumliche Bewegung lautet der 2. Term
Kapitel 4 und 7).
1
!
2~
£ J¹ £ !
~ (siehe
² Die Haftreibungskraft RH leistet keine Arbeit. Deshalb kann bei
reinem Rollen der Energieerhaltungssatz verwendet werden.
Diese MÄ
oglichkeit ist besonders dann gÄ
unstig, wenn v(s) gesucht wird.
Wenn dagegen v(t) gesucht wird, ist es einfacher, Schwerpunkt- und
Drallsatz zu verwenden.
1
Dies bedeutet, dass nach Berücksichtigung der kinematischen Zusammenhänge
das System durch eine kinematische Größe beschreibbar sein muss. Bei Systemen
mit mehreren Freiheitsgraden muss man entweder mit dem Schwerpunktsatz und
dem Drallsatz arbeiten und alle Zwangskräfte eliminieren oder die Lagrangeschen
Bewegungsgleichungen 2. Art verwenden, siehe dazu [1].
6.2 Vorgehen bei der Berechnung ebener kinetischer Probleme
63
64
6.3
6
KINETIK DER EBENEN BEWEGUNG
Das Beispiel Scheibenräder und Seile
Die oben beschriebenen Vorgehensweisen
werden bei dem in Bild 6.2 dargestellten
System
mit
mehreren
Massen
angewandt. Ein Aufzug der Masse mQ
wird u
Äber zwei gleiche Seilrollen durch
die Masse mG gehoben.
6.3 Das Beispiel ScheibenrÄader und Seile
65
2. Kinematische GrÄo¼en eintragen:
x;
_ y;
_ ';
_ Ã_
3. KrÄafte eintragen:
EingeprÄ
agte KrÄ
afte sind
(mQ + mR )g; mG g
Die ReaktionskrÄ
afte
S1 ; S2 ; S3
werden je zweimal eingetragen.
Bild 6.2. Aufzug, Problemstellung
Bild 6.3. Aufzug, freigeschnitten
6.3.1
LÄ
osung mit dem Schwerpunktsatz und Drallsatz
1. KÄorper freischneiden (Bild 6.3 ):
Das rechte Rad muss nicht freigeschnitten werden, da sein
Schwerpunkt Fixpunkt ist. Wenn die Stangenkraft nicht interessiert,
kÄ
onnen die linke Masse und das Rad zusammen berechnet werden,
es braucht nicht geschnitten zu werden.
4. Bewegungsgleichungen aufstellen:
FÄ
ur die linke Masse lautet der Schwerpunktsatz
":
(mQ + mR )Ä
x = S1 + S2 ¡ (mQ + mR )g
(6.21)
FÄ
ur das linke Rad lautet der Drallsatz
<¾
:
J'
Ä = ¡rS1 + rS2
FÄ
ur das rechte Rad lautet der Drallsatz
½> : J ÃÄ = rS3 ¡ rS2
(6.22)
(6.23)
FÄ
ur die rechte Masse lautet der Schwerpunktsatz
#:
mG yÄ = ¡S3 + mG g
ur die Ruhe gilt!
Man beachte, dass S3 = mG g nur fÄ
(6.24)
66
6
KINETIK DER EBENEN BEWEGUNG
5. Kinematische ZusammenhÄange aufstellen:
Momentanpol des linken Rades ist der Punkt 1. Aus dem
Geschwindigkeitsdreieck in Bild 6.4 liest man ab
'_ =
x_
r
(6.25)
6.3 Das Beispiel ScheibenrÄader und Seile
67
Die Addition der ersten beiden und der letzten beiden Gleichungen von
(6.29) ergibt
3
(mQ + mR )Ä
x = 2S2 ¡ (mQ + mR )g
2
(mR + 2mG )Ä
x = ¡S2 + mG g
j¢2
v2 = 2x_
Die Elimination von S2 erfolgt durch Addition dieser Gleichungen, wobei
die 2. Gleichung mit 2 multipliziert wird. Man erhÄ
alt
7
(mQ + mR + 4mG )Ä
x = (2mG ¡ mQ ¡ mR )g
2
FÄ
ur das rechte Rad gilt v3 = v2 und
v2
x_
Ã_ =
=2
(6.26)
r
r
FÄ
ur die rechte Masse gilt
y_ = v4 = v2 = 2x_
x
Ä=
(6.27)
Bild 6.4. Aufzug, Kinematik
2mG ¡ mQ ¡ mR
g
mQ + 72 mR + 4mG
(6.30)
FÄ
ur die Zahlenwerte
mQ = 70 kg; mG = 65 kg; mR = 20 kg; g = 10 m= s2
6. Gleichungen au°Äosen:
ergibt sich
Mit
J=
x
Ä = 1 m= s2
1
2
2 mR r
(6.28)
und den kinematischen Bedingungen (6.25) bis (6.27) lauten die
Bewegungsgleichungen (6.21) bis (6.24)
(mQ + mR )Ä
x =
1
Ä
2 mR x
= ¡S1 + S2
mR x
Ä
=
2mG x
Ä
=
¡ S2 + S3
S3 = mG (g ¡ 2Ä
x) = 520 N (nicht S3 = mG g = 650 N)
Aus der 3. Gleichung von (6.29) folgt wegen der TrÄ
agheit des rechten
Rades
¡ (mQ + mR )g
S1 + S2
Aus der 4. Gleichung von (6.29) folgt damit
(6.29)
¡ S3 + mG g
AbzÄ
ahlen der Unbekannten. Die vier GrÄ
o¼en x
Ä; S1 ; S2 ; S3 sind aus
den vier Gleichungen (6.29) bestimmbar.
Ä = 500 N
S2 = S3 ¡ mR x
Aus der 2. Gleichung von (6.29) folgt wegen der TrÄ
agheit des linken
Rades
1
S1 = S2 ¡ mR x
Ä = 490 N
2
Die erste Gleichung von (6.29) lautet mit Zahlenwerten
90 kg x
Ä = 990 N ¡ 900 N
Also ist x
Ä = 1 N= kg = 1 m= s2 .
68
6
6.3.2
KINETIK DER EBENEN BEWEGUNG
LÄ
osung mit dem Energieerhaltungssatz
Der Energieerhaltungssatz lautet
Ek + Ep = Ek0 + Ep0 = const.
1
1 _2 1
1
(mQ + mR )x_ 2 + J '_ 2 +
J Ã + mG y_ 2
2
2
2
2
+ (mQ + mR )gx ¡ mG gy = const.
Einsetzen der kinematischen Beziehungen (6.25) bis (6.27) sowie der
Beziehung (6.28) J = 12 mR r 2
·
1
1
(mQ + mR ) + mR
2
2
¸
1
4mR + 4mG x_ 2
2
+ (mQ + mR ¡ 2mG)gx = const.
+
Di®erenzieren nach der Zeit ergibt
·
¸
1
(mQ + mR ) + mR + 2mR + 4mG xÄ
_ x + (mQ + mR ¡ 2mG )g x_ = 0:
2
FÄ
ur x_ 6= 0 folgt daraus wie oben
•
¶
7
mQ + mR + 4mG x
Ä = (2mG ¡ mQ ¡ mR )g
2
Mit dieser Methode kÄ
onnen die SeilkrÄ
afte nicht bestimmt werden.
Sind Winkelfunktionen im Spiel, so darf erst nach dem Di®erenzieren
linearisiert werden.
6.3 Das Beispiel ScheibenrÄader und Seile
69
Ä
7 MASSENTRAGHEITSMOMENTE
70
7
Massenträgheitsmomente
In (3.7) wurde der Drall fÄ
ur den Schwerpunkt de¯niert
R
~s £ (~
! £ ~s)dm
Die daraus folgende Gleichung (3.9) schreibt man als Matrizengleichung
in der Form
2
32
3
Jx
¡Jxy ¡Jxz
!x
76
7
~S = 6
L
Jy
¡Jyz 5 4 !y 5
4 ¡Jyx
¡Jzx ¡Jzy
Jz
!z
(7.1)
Die Hauptdiagonalglieder sind TrÄagheitsmomente, die Terme
mit
gemischten
Indizes
hei¼en
Deviationsmomente
oder
Zentrifugalmomente.
R
Jx = (y2 + z 2 )dm
R
Jy = (z 2 + x2 )dm
R
Jz = (x2 + y 2 )dm
(7.2)
Jyz = Jzy =
(7.3)
Jzx = Jxz =
(7.4)
Jxy = Jyx =
R
R
R
yzdm
(7.5)
zxdm
(7.6)
xydm
(7.7)
Man beachte, dass in (7.1) negative Vorzeichen und in (7.5) bis (7.7)
positive stehen. Manche Autoren de¯nieren auch umgekehrt.
Schreibt man den Drall (7.1) in der Form
~ S = J¹ ¢ ~
L
!
² Die TrÄ
agheitsmomente sind stets > 0.
² Der TrÄ
agheitstensor ist symmetrisch, d.h. es gelten Jxy = Jyx usw.
Der KÄ
orper kann dabei vÄ
ollig unsymmetrisch sein.
² Die Deviationsmomente kÄ
onnen auch negativ sein.
Drall und Trägheitsmomente
~S =
L
71
FÄ
ur die TrÄ
agheitseigenschaften eines KÄ
orpers gilt:
Bei der ebenen Bewegung in der x; y-Ebene als Symmetrieebene ist
nur das MassentrÄ
agheitsmoment Jz von Interesse. Dieses kann dabei
als skalare GrÄ
o¼e wie eine Masse behandelt werden. Viele Probleme der
Rotorkinetik lassen sich jedoch nicht als ebene Bewegung beschreiben.
7.1
7.1 Drall und TrÄagheitsmomente
(7.8)
so kennzeichnet die quadratische Matrix den TrÄagheitstensor J¹ bzgl. des
x; y; z-Systems.
Ä
7 MASSENTRAGHEITSMOMENTE
72
7.2
Symmetrie und Hauptträgheitsmomente
7.2 Symmetrie und HaupttrÄagheitsmomente
Ist au¼erdem auch !x = !y = 0, so folgt nach (7.1) der Drall wie in
(3.10) zu
2
Ist die xz-Ebene (?~ey ) Symmetrieebene,
so gibt es nach Bild 7.1 zu jedem
Massenelement dm1 vorne
3
0
7
~S = 6
L
4 0 5
Jz !z
dm1 = dm mit y1 = y
(7.10)
Ist die y; z-Ebene (?~ex ) Symmetrieebene, so sind
ein hinteres
Jzx = 0; Jxy = 0
dm2 = dm mit y2 = ¡y
(7.11)
Ist die z; x-Ebene (?~ey ) Symmetrieebene, so sind auch
Bild 7.1. Symmetrie
so dass
Jyz = 0; Jxy = 0
Jyz =
Jxy =
Z
Z
y1 zdm +
xy1 dm +
Z
Z
(7.12)
Gibt es zwei zueinander senkrechte Symmetrieebenen, so gelten
y2 zdm = 0
)
Jyz = 0
xy2 dm = 0
)
Jxy = 0
Jyz = 0; Jzx = 0; Jxy = 0
und die Matrix J hat die Hauptachsenform
2
gelten. Dann lautet die Matrix des TrÄ
agheitstensors
2
73
3
Jx
0 ¡Jxz
6
7
J =4 0
Jy
0 5
¡Jzx 0
Jz
(7.9)
3
Jx 0 0
6
7
J = 4 0 Jy 0 5
0 0 Jz
In diesem Fall hei¼en Jx ; Jy ; Jz HaupttrÄagheitsmomente
(7.13)
Ä
7 MASSENTRAGHEITSMOMENTE
74
7.3
Folgerungen fu
Är Rotoren
² FÄ
ur rotierende Maschinenteile ist in der Regel ein TrÄ
agheitstensor
der Form von (7.13) anzustreben.
² Ein besonders wichtiger Sonderfall ist
Jx = Jy
(7.14)
FÄ
ur diesen ist auch fÄ
ur alle Achsen senkrecht zur z-Achse J =
Jx , und man spricht von symmetrischen Rotoren. Dabei muss die
geometrische Form nicht symmetrisch sein. Beispiele sind senkrechte
Prismen, deren Querschnitte gleichseitige Polygone sind (Dreieck,
Quadrat, 5-Eck, 6-Eck).
² Zu vermeiden sind Rotoren, bei denen
Jx = Jy = Jz
(7.15)
gilt, also Rotoren in der Form von Kugeln, WÄ
urfeln usw. Bei diesen
werden von der unvermeidlichen Unwucht stets Eigenschwingungen
angeregt.
² Die Drehung um die mittlere Hauptachse ist instabil. Daraus folgt,
dass bei einem Rotor, der um die z-Achse rotiert, der Fall
Jx < Jz < Jy
7.3 Parallel verschobene Achsen, der Steinersche Satz
(7.16)
unbedingt vermieden werden sollte.
FÄ
ur den letzten Punkt gibt es zwei wichtige Beispiele:
Ein hochgeworfer Quader dreht stabil um die Achsen mit dem
grÄ
o¼ten und dem kleinsten TrÄ
agheitsmoment; es gelingt jedoch
nicht, ihn um die Achse mit dem mittleren stabil rotieren zu
lassen.
Ist die StiellÄ
ange einer zwei°Ä
ugeligen Luftschraube gerade so,
dass das TrÄ
agheitsmoment um die Drehachse das mittlere ist,
so gelingt keine stabile Drehung.
75
Parallel verschobene Achsen, der Steinersche Satz
Gegeben sind die TrÄ
agheits- und Deviationsmomente fÄ
ur den Punkt 0.
Dann gelten nach (7.2) bis (7.7) sinngemÄ
a¼
R
Jx̄ = R (¹
y 2 + z¹2 )dm
Jȳ = R (¹
z2 + x
¹2 )dm
Jz̄ =
(¹
x2 + y¹2)dm
R
Jȳz̄ = R y¹z¹dm
Jz̄ x̄ = R z¹x
¹dm
Jx̄ȳ =
x
¹y¹dm
FÄ
ur die Koordinatentransformation gelten
nach Bild 7.2
x
¹ = x + a
y¹ = y + b
(7.17)
z¹ = z + c
Die Koordinaten x; y; z gehen vom
Schwerpunkt aus. Deshalb gelten
R
xdm = xS m
= 0;
R
R
ydm = 0;
zdm = 0
Bild 7.2.
Parallelverschiebung
und man erhÄ
alt
Jx̄ = Jx + (b2 + c2 )m (7.18)
Jȳz̄ = Jyz + bcm
(7.21)
Jȳ = Jy + (c + a )m (7.19)
Jz̄x̄ = Jzx + cam
(7.22)
Jz̄ = Jz + (a2 + b2 )m (7.20)
Jx̄ȳ = Jxy + abm
(7.23)
2
2
Diese ZusammenhÄ
ange hei¼en Steinerscher Satz. Dabei sollte man sich
merken:
² Die MassentrÄ
agheitsmomente sind bzgl. des Schwerpunktes am
kleinsten.
² Vom Schwerpunkt ausgehend werden die TrÄ
agheitsmomente stets
grÄ
o¼er (Pluszeichen).
Falls (7.5) bis (7.7) mit umgekehrtem Vorzeichen de¯niert werden, muss
in (7.21) bis (7.23) statt des Plus- ein Minuszeichen stehen.
Ä
7 MASSENTRAGHEITSMOMENTE
76
7.4
Zusammengesetzte Körper
Eine wichtige Ingenieuraufgabe ist, TrÄ
agheitsmomente von KÄ
orpern
zu berechnen, die aus bekannten TeilkÄ
orpern zusammengesetzt sind.
Dies wird am Beispiel der Zylinder von Bild 7.3 gezeigt. Mit den
Schwerpunktkoordinaten der TeilkÄ
orper
³S1 ´ ³1 ;
³S2 ´ ³2
folgt fÄ
ur den Gesamtschwerpunkt nach TM I,
(7.20)
m1 ³1 + m2 ³2
(7.24)
m1 + m2
Wenn die Radien ri und die LÄ
angen li hei¼en,
folgt fÄ
ur den Zylinder 1 das TrÄ
agheitsmoment
bezÄ
uglich des Punktes 1 zu
³S =
Jx1,1 = m1
Ã
r12
l2
+ 1
4
12
!
Bild 7.3. Zusammengesetzte
Vollzylinder
(7.25)
Die Punkte 1 und 2 haben vom Gesamtschwerpunkt S die AbstÄ
ande
c1 = z1 = ³1 ¡ ³S
c2 = z2 = ³2 ¡ ³S
hier ist c1 < 0
(7.26)
Mit dem Steinerschen Satz gelten bzgl. des Gesamtschwerpunkts S
Jx2,S =
³
r12
³ 42
r
m1 42
Jx1,S = m1
+
+
l12
12
l22
12
+ c21
+ c22
´
´
und das gesamte TrÄ
agheitsmoment bzgl. S ist
Jx = Jx1,S + Jx2,S
(7.27)
7.4 Zusammengesetzte KÄorper
77
Ä
7 MASSENTRAGHEITSMOMENTE
78
7.5
7.5 Wichtige TrÄagheitsmomente
Wichtige Trägheitsmomente
³
m = ½¼l ra2 ¡ ri2
m = ½¼r 2 l
Jx = Jy =
1
1
Jx = Jy = mr2 + ml2
4
12
Jz =
Jz =
1 2
mr
2
79
´
´
1 ³ 2
1
m ra + ri2 + ml2
4
12
´
1 ³ 2
m ra + ri2
2
Zu beachten ist das Pluszeichen!
7.7 Hohlzylinder
7.4 Kreiszylinder
Jx = Jy =
l)h¿r
1 2
mr
2
Jz = mr 2
1
Jx = Jy = mr2
4
Jz =
m = ½2¼rA
1 2
mr
2
7.8 Dünner Kreisring
7.5 Kreisscheibe
2
Jx = Jy = Jz = mr2
5
m = ½lA
Jx = Jy =
4
m = ½ ¼r 3
3
1
ml2 ; Jz ¼ 0
12
7.9 Kugel
Bzgl. des Stabendes gelten
1
Jx̄ = Jȳ = ml2 ; Jz̄ ¼ 0
3
Tab. 7.2. Massenträgheitsmomente
7.6 Stab
Tab. 7.1. Massenträgheitsmomente
Ä
7 MASSENTRAGHEITSMOMENTE
80
7.5 Wichtige TrÄagheitsmomente
81
Herleitungen
1
m = ½ ¼r2 h
3
Zum Kreiszylinder:
(r ist hier variabel, der Au¼enradius hei¼t ra ).
Schwerpunkthöhe
R
Jz = (x2 + y 2 )dm =
1
hS = h
4
dm = ½l2¼rdr
3
3
Jx = Jy = mr 2 + mh2
20
80
Jz =
"
r4
Jz = ½l2¼
4
3
mr2
10
7.10 Gerader Kreiskegel
#ra
R 2
r dm
1
= ½l ¼ra4
2
0
1
Jz = mra2
2
Bild 7.13. Kreiszylinder
m = ½abc
Jx + Jy =
Bzgl. des Schwerpunkts S gelten
Jx =
Jy
=
Jz
=
¢
R¡ 2
R
x + y2 + 2z 2 dm = Jz + 2 z 2 dm
(7.28)
FÄ
ur rotationssymmetrische KÄ
orper gilt also stets
1
m(b2 + c2 )
12
1
m(c2 + a2 )
12
1
m(a2 + b2 )
12
R
Jx = Jy = 12 Jz + z 2 dm:
Mit
(7.29)
dm = ½¼ra2 dz
7.11 Quader
Tab. 7.3. Massenträgheitsmomente
folgt wie beim Stab
Z
2
z dm = ½¼a
2
"
z3
3
#+l/2
−l/2
= ½¼a2
1 3
1
l = ml2
12
12
Zum Hohlzylinder:
³
´
1
1
Jz = ½¼l ra4 ¡ ri4 = ½¼l(ra2 ¡ ri2 )(ra2 + ri2 )
2
2
1
Jz = m(ra2 + ri2 )
2
Ä
7 MASSENTRAGHEITSMOMENTE
82
7.6
Massenträgheitsmomente bei gedrehten Achsen
Die Darstellung der Winkelgeschwindigkeiten, des Dralls und der
TrÄ
agheitsmomente in gedrehten Koordinaten ist fÄ
ur die Rotordynamik
wichtig. Sie erfolgt im dreidimensionalen Fall am besten in der
~ gilt z.B.:
u
ur den Vektor L
Äbersichtlichen Matrizenform. FÄ
∗
L = QL d.h.
2
3
2
32
3
Entsprechend gilt fÄ
ur die dem Tensor J¹ entsprechende Matrix J
(7.30)
Die Transformationsmatrizen Q werden fÄ
ur die Drehungen um die
Koordinatenachsen dargestellt.
FÄ
ur die Drehung um die x-Achse gilt
2
3
1
0
0
6
7
Qα = 4 0 cos ® sin ® 5
0 ¡ sin ® cos ®
(7.31)
3
cos ¯ 0 ¡ sin ¯
6
7
Qβ = 4 0
1
0
5
sin ¯ 0 cos ¯
3
cos ° sin ° 0
6
7
Qγ = 4 ¡ sin ° cos ° 0 5
0
0
1
2
3
Jx cos2 ' + Jz sin2 '
0 ¡(Jx ¡ Jz ) sin ' cos '
6
7
∗
J =4
0
Jy
0
5 (7.34)
¡(Jx ¡ Jz ) sin ' cos ' 0
Jx sin2 ' + Jz cos2 '
∗
Jxz
= (Jx ¡ Jz ) sin ' cos ' ¼ (Jx ¡ Jz )'
(7.35)
det(J ¡ Ji 1) = 0 wobei 1 = diag(1; 1; 1)
(7.36)
Hat J eine beliebige Form, so folgen die HaupttrÄ
agheitsmomente
J1 ; J2 ; J3 als Eigenwerte von J aus der Beziehung
Dies ist eine kubische Gleichung, deren LÄ
osungen zwar stets reell sind
(wegen der Symmetrie des Tensors), die aber im allgemeinen nicht
analytisch sondern numerisch berechnet werden.
Die Hauptrichtungen sind durch die zu Ji gehÄ
orenden Eigenvektoren ni
von J gegeben. Sie folgen aus
i = 1::: 3
(7.37)
Dies sind fÄ
ur jedes Ji drei homogene Gleichungen. Die LÄ
osungen von
(7.37) werden so normiert, dass
jni j = 1
(7.32)
(7.38)
ni
gilt. Die drei
2
bilden dann die Transformationsmatrix Q
3
n1 n12 n13 7
6 1
6
7
Q = 6 n21 n22 n23 7
4
FÄ
ur die Drehung um die z-Achse gilt
2
Hat J die Hauptachsenform von (7.13) so erhÄ
alt man bei einer Drehung
um die negative y-Achse mit dem Winkel ' = ¡¯ (s. Bild 7.7 )
(J ¡ Ji 1)ni = 0;
FÄ
ur die Drehung um die y-Achse gilt
2
83
Diese Formel wird z.B. bei einem schief auf der Welle sitzenden Zylinder
benÄ
otigt. FÄ
ur kleine ' ergibt sich
L∗x
¢ ¢ ¢
Lx
6 ∗ 7 6
76
7
L
=
¢
¢
¢
4 y 5 4
5 4 Ly 5
¢ ¢ ¢
Lz
L∗z
J ∗ = QJQT
7.6 MassentrÄagheitsmomente bei gedrehten Achsen
n31
n32
n33
(7.39)
5
und das nach (7.30) gedrehte J ∗ erhÄ
alt die Form von (7.13)
(7.33)
∗
J =J
H
2
J
6 1
6
=6 0
4
0
0
J2
0
3
0 7
7
0 7 = diag(J1 ; J2 ; J3 )
J3
5
(7.40)
84
8 FLIEHKRAFT UND UNWUCHT
8
Fliehkraft und Unwucht
8.1
Die technisch wichtige Fliehkraft wird hier fÄ
ur einen exzentrischen Rotor
hergeleitet. (Sie ist zunÄ
achst keine eingeprÄ
agte Kraft und wird vielfach
als Scheinkraft bezeichnet).
Der in Bild 8.1 dargestellte KÄ
orper der Masse m soll um den
Lagerpunkt C mit der konstanten Winkelgeschwindigkeit '_ rotieren.
Der Punkt C kann fest oder bewegt sein. Auf den KÄ
orper wirken die
~
Gewichtskraft m~g und die Lagerkraft FC (vom Lager auf den KÄ
orper
wirkend).
F~ (a) = F~C + m~g
(8.1)
Dabei ist die Fliehkraft F~F nicht in F (a) enthalten!
Nach Bild 8.1 gilt ~rS = ~rC + e~er und deshalb mit ~e_r = '~
_ eϕ , ~e_ϕ = ¡'~
_ er
von (1.7) und '
Ä=0
(8.2)
Setzt man dies in den Schwerpunktsatz
m~rÄS = F~ (a)
(8.3)
ein, so erhÄ
alt man
~F + F~ (a)
m~rÄC = me'_ 2~er + F~ (a) = F
(8.4)
Die GrÄ
o¼e
FF = me'_ 2 = me! 2
85
Be¯ndet sich der Rotor in einem GehÄ
ause der
Masse mG , so gilt fÄ
ur dieses nach Bild 8.2
mG~rÄC = ¡F~C + mG~g
(8.6)
Die Fliehkraft
~rÄS = ~rÄC ¡ e'_ 2~er
8.1 Die Fliehkraft
(8.5)
Bild 8.1. Fliehkraft
ist die stets radial nach au¼en (~er -Richtung) wirkende Fliehkraft.
Mit (8.1) und (8.4) erhÄ
alt man fÄ
ur das
Gesamtsystem den Schwerpunktsatz in der
Form
~F + (mG + m)~g (8.7)
(mG + m)~rÄC = F
In dieser Gleichung darf die Rotormasse m
auf der linken Seite nicht vergessen werden.
Bild 8.2. Kräfte auf das
Gehäuse
Wie diese Herleitung zeigt, wirkt die Fliehkraft also im mitdrehenden
Koordinatensystem. Sie ist eine real auftretende Kraft. Deshalb ist der
Ausdruck Scheinkraft\ irrefÄ
uhrend.
"
86
8 FLIEHKRAFT UND UNWUCHT
8.2
Statische Unwucht
8.3
Unwucht ergibt umlaufende LagerkrÄ
afte und fÄ
uhrt deshalb zu unruhigem
Lauf einer Maschine. Fast jeder technisch eingesetzte Rotor wird
ausgewuchtet und zwar statisch und dynamisch.
Kennzeichen der statischen Unwucht:
87
Dynamische Unwucht
Kennzeichen der dynamischen Unwucht:
Die Massenverteilung ist nicht symmetrisch zur Drehachse,
genauer: die Drehachse ist keine HaupttrÄ
agheitsachse.
Trotzdem kann der Schwerpunkt auf der Drehachse liegen. In
Bild 8.4 wird die dynamische Unwucht durch die zwei Massen
md an dem sonst symmetrischen Rotor dargestellt. Man erhÄ
alt das
Momentengleichgewicht
Der Schwerpunkt liegt nicht auf der Drehachse, d.h.
Es gibt eine SchwerpunktexzentrizitÄ
at e.
Die statische Unwucht wird durch
A2 L = md r! 2 l
me (z.B. in g mm)
und daraus
LagerkrÄ
afte
ausgedrÄ
uckt. Sie bewirkt umlaufende
LagerkrÄ
afte
1
A1 = B1 = me ! 2
(8.8)
2
die
umlaufenden
l
(8.10)
L
Das rein dynamische Auswuchten
erfolgt nach Bild 8.4 durch die
zwei Ausgleichsmassen m2 . Diese
be¯nden sich jeweils gegenÄ
uber
von den Massen md und sind
vom gleichen Betrag wie diese.
Der Raumwinkel gegenÄ
uber der
kÄ
orperfesten x-Achse wird als °2
angenommen.
A2 = B2 = md r! 2
Bild 8.3. Statische Unwucht
Statisches Auswuchten (auch Auswiegen genannt) erfolgt durch eine
Ausgleichsmasse auf der Gegenseite des Schwerpunkts oder { wie in
Bild 8.3 { zwei Ausgleichsmassen m1 in den Ausgleichsebenen
2m1 r = me
8.3 Dynamische Unwucht
(8.9)
Der Winkel dieser Ausgleichsmassen gegenÄ
uber der kÄorperfesten x-Achse
wird fÄ
ur die weitere Darstellung als °1 angenommen.
Bild 8.4. Dynamische Unwucht
88
8.4
8 FLIEHKRAFT UND UNWUCHT
~ = A
~1 + A
~2 ;
A
(8.11)
~ = B
~1 + B
~2
B
89
Jxz = (JxH ¡ JzH )'
Überlagerung
Bei dem unausgewuchteten
Rotor von Bild 8.4 ist
In der Praxis treten
die statische und die
dynamische
Unwucht
fast
immer
gekoppelt
auf.
Auswuchtmaschinen
messen die resultierenden
LagerkrÄ
afte
Jxz = md rl
(8.12)
Bild 8.6. Rotor mit Schieflage
Bild 8.5. Überlagerung
unter den Winkeln °A und °B . Daraus werden die Ausgleichsmassen
und die zugehÄ
origen Winkel in den Ausgleichsebenen links und rechts
berechnet. Dies ist eine algebraisch komplizierte Berechnung, die in
der Auswuchtmaschine durch einen Prozessor erledigt wird. Nach dem
Auswuchten sind keine umlaufenden LagerkrÄ
afte mehr vorhanden.
8.5
8.5 Rotor mit Schieflage
FÄ
ur die symmetrischen Ausgleichsmassen mA = m2 nach Bild 8.7 lautet
das Deviationsmoment
l
l
(Jzx )A = mA (¡r) + mA r(¡ )
2
2
(Jzx )A = ¡mA rl
Die Ausgleichsmassen mA werden so
gewÄ
ahlt, dass mit Jxz aus (8.12)
Jxz + (Jzx )A = 0
Rotor mit Schieflage
In vielen FÄ
allen rÄ
uhrt die dynamische Unwucht von einer Schieflage eines
sonst symmetrischen Rotors her. BezÄ
uglich des mitdrehenden Systems,
dessen z-Achse die Drehachse ist, erhÄ
alt man nach der Theorie der
MassentrÄ
agheitsmomente (vgl. (7.61)) ein Deviationsmoment
(8.13)
ist.
Bild 8.7. Symmetrische
Ausgleichsmassen
Bei einem dynamisch ausgewuchteten Rotor fallen also Hauptachse und
Drehachse zusammen.
90
9
9
Ä
FREIE, UNGEDAMPFTE
SCHWINGUNGEN
Freie, ungedämpfte Schwingungen
9.1
Grundbegriffe am Feder-Masse-Schwinger
Betrachtet wird ein Feder-Masse-System im Schwerefeld. Die Masse wird
um z ausgelenkt.
Der Schwerpunktsatz lautet dafÄ
ur
und man erhÄ
alt die Di®erentialgleichung
mit
!0 =
r
c
m
x = C1 cos !0 t + C2 sin !0 t
(9.6)
Die Ableitungen nach der Zeit sind
x_ = !0 (¡C1 sin !0 t + C2 cos !0 t)
(9.7)
x
Ä = ¡!02 (C1 cos !0 t + C2 sin !0 t)
(9.8)
x(0) = x0 = C1
x(0)
_
= v0 = C2 !0
(9.4)
(9.9)
(9.10)
Die Periodendauer T der Schwingung
ergibt sich aus !0 T = 2¼ zu
2¼
(9.11)
T =
!0
(9.3)
Die Gewichtskraft und die statische Federkraft
(Vorspannung) sind also ohne Ein°uss auf die
Schwingung. Aus (9.3) erhÄ
alt man die normierte
Darstellung
x
Ä + !02 x = 0
Die LÄ
osung von (9.4) ist
Die unbekannten Konstanten C1 und C2 erhÄ
alt man aus den
Anfangsbedingungen bei t = 0
(9.1)
FÄ
ur z_ = zÄ = 0 erhÄ
alt man die statische
Gleichgewichtslage z = xst
mg
xst =
(9.2)
c
Mit z = xst + x erhÄ
alt man aus (9.1) fÄ
ur die
Schwingung um die Gleichgewichtslage
mÄ
x + cx = 0
91
Man sieht, dass mit x nach (9.6) und mit x
Ä nach (9.8) die Gleichung
x
Ä + !02 x = 0 erfÄ
ullt wird.
mÄ
z = ¡cz + mg
mÄ
z + cz = mg
9.1 Grundbegri®e am Feder-Masse-Schwinger
Bild 9.2. Zeitfunktion bei C2 = 0
Bild 9.1.
Feder-Masse-System
(9.5)
Die GrÄ
o¼e !0 hei¼t nach DIN 1311 Kennkreisfrequenz. FÄ
ur das
ungedÄ
ampfte System (9.4) ist !0 zugleich die Eigenkreisfrequenz.
Der Kehrwert
r
1
!0
1
c
f0 = =
=
(9.12)
T
2¼
2¼ m
hei¼t Kennfrequenz und wird in Hertz (1 Hz = 1/s) gemessen. FÄ
ur das
ungedÄ
ampfte System (9.4) ist f0 die Eigenfrequenz.
92
9
Ä
FREIE, UNGEDAMPFTE
SCHWINGUNGEN
9.2
Ermittelt man die Federstei¯gkeit aus (9.2)
g
c=m
xst
9.2.1
und setzt sie in (9.12) ein, so erhÄ
alt man
r
1
g
f0 =
(9.13)
2¼ xst
Die Masse hebt sich heraus. Die Fallbeschleunigung g wird dabei nur
zur Ermittlung von c verwendet. Die Gleichung (9.13) gilt deshalb auch,
wenn die Masse quer zu ~g schwingt.
Zahlenwerte fÄ
ur (9.13):
xst =
xst =
xst =
xst =
100 mm ) f0 = 1; 6 Hz
10 mm ) f0 =
1 mm ) f0 =
0; 1 mm ) f0 =
5 Hz
16 Hz
50 Hz
xst = 0; 01 mm ) f0 = 160 Hz
FÄ
ur AbschÄ
atzungen von Frequenzen gilt (9.13) sehr allgemein.
9.2 Freie, ungedÄampfte Schwingungen
(9.14)
93
Freie, ungedämpfte Schwingungen
Mathematisches Pendel
Aus dem Schwerpunktsatz erhÄ
alt man
mÄ
x = ¡mg sin '
Bei kleinen AusschlÄ
agen sind
x
Ä = l'Ä und sin ' ¼ '
Man erhÄ
alt die Schwingungsdi®erentialgleichung
g
'Ä + ' = 0
(9.15)
l
mit
r
g
(9.16)
!0 =
l
Bild 9.3.
Mathematisches
Pendel
94
9
9.2.2
Ä
FREIE, UNGEDAMPFTE
SCHWINGUNGEN
95
KÄ
orperpendel
Das KÄ
orperpendel wird auch physisches (nicht physikalisches) Pendel
genannt. Der Drallsatz bzgl. A ergibt
JA '
Ä = ¡mgb sin '
Bei kleinen AusschlÄ
agen gilt also
mgb
'Ä +
'=0
JA
Der Vergleich ergibt
cD = cr 2
(9.18)
Bild 9.4.
Körperpendel
Der Drallsatz lautet
(9.19)
'Ä +
cD
'=0
J
(9.20)
cD
J
(9.21)
!0 =
r
Diese Formel ist genauso wichtig wie (9.5).
Die GrÄ
o¼e cD hei¼t Drehfederkonstante und
hat die Einheit Nm.
(9.22)
Einheiten: c in N/m, cD in Nm.
Drehpendel
J'
Ä = ¡cD '
HÄ
au¯g wird die Drehfederkonstante durch
eine lineare Feder erzeugt. Dann gilt
wegen F = cr' und M = ¡rF anstelle
von (9.19)
J 'Ä = M = ¡cr 2 '
(9.17)
Schreibt man dies in der Form von (9.15)
g
'Ä + ' = 0
lr
so hei¼t
JA
lr =
mb
reduzierte PendellÄange.
9.2.3
9.2 Freie, ungedÄampfte Schwingungen
Bild 9.5. Drehpendel
Bild 9.6. Drehpendel mit linearer
Feder
96
9
9.2.4
Ä
FREIE, UNGEDAMPFTE
SCHWINGUNGEN
Stab
9.2 Freie, ungedÄampfte Schwingungen
9.2.6
97
Torsion
Solange die Stabmasse klein gegenÄ
uber der Scheibenmasse m ist, kann
das System von Bild 9.9 als Schwinger nach (9.19) behandelt werden.
Solange die Stabmasse klein gegenÄ
uber der Masse m
ist, kann das System von Bild 9.7 als Schwinger
nach (9.3) behandelt werden. Nach Kapitel II,1 der
Elastostatik gilt
EA
c=
(9.23)
l
Der Drallsatz ergibt
J 'Ä = ¡Mt
Mit dem Torsionsmoment Mt aus Kapitel
II,10 und ' = #(l) gilt
GIt
'=0
l
FÄ
ur die Eigenkreisfrequenz gilt also
(9.20) mit
J 'Ä +
Bild 9.7. Stab mit
Masse
GIt
(9.26)
l
Das FlÄ
achenmoment fÄ
ur Torsion ist bei
einen massiven Stab
¼
¼
It = Ip = 2Iy = r4 = d4
2
32
cD =
9.2.5
Balken
Solange die Balkenmasse klein gegenÄ
uber der Masse m ist, kÄ
onnen die
Balken von Bild 9.8 als Schwinger nach (9.3) behandelt werden.
Wegen c = F=w ergeben sich die
Federstei¯gkeiten aus den Tabellen der
Festigkeitslehre. In den dargestellten
Beispielen sind die Federstei¯gkeiten
3EIy
c1 = 3
(9.24)
l
c2 =
48EIy
l3
9.2.7
Bild 9.9. Drehschwinger
Zusammengesetzte Systeme
Weggleich angeordnete Federn verlÄ
angern sich bei Belastung durch
eine Zugkraft F um denselben Federweg ¢l. Wie das Beispiel rechts
in Bild 9.10 zeigt, ist der u
Äbliche Ausdruck Parallelschaltung\
"
missverstÄ
andlich.
(9.25)
Bild 9.8. Balken mit Masse
98
9
F
= F1
Ä
FREIE, UNGEDAMPFTE
SCHWINGUNGEN
99
10
+ F2
= c1 ¢l + c2 ¢l
Sonstige Schwingungen
10.1
Erzwungene Schwingungen
F = (c1 + c2 )¢l
Der Vergleich mit F = c¢l liefert
c = c1 + c2
(9.27)
Bild 9.10. Weggleiche
Federn
In kraftgleich angeordneten Federn wirkt bei Belastung dieselbe Kraft F
(Schnittprinzip). Die Federwege addieren sich.
¢l = ¢l1 + ¢l2
F
F
=
+
c1
c2
¢l =
•
¶
c < c1 ;
c < c2
(10.1)
beschrieben. Die LÄ
osung setzt sich aus 2
Anteilen zusammen. Zu der behandelten
homogenen LÄ
osung kommt die partikulÄare
hinzu, so dass insgesamt gilt
Bild 10.1. Schwinger mit
Erregerkraft
(10.2)
Fast alle praktischen Anwendungen weisen DÄ
ampfung auf. Diese
bewirkt, dass xh { also der mit !0 schwingende Anteil { stets nach
kurzer Zeit abklingt. Deshalb braucht fÄ
ur technische Anwendungen im
allgemeinen nur der Anteil xp { also der mit der Erreger-Kreisfrequenz
− schwingende { betrachtet zu werden. Die GrÄ
o¼e xp muss nur die
Di®erentialgleichung (10.1) erfÄ
ullen:
Der Vergleich mit ¢l = F=c liefert
Die daraus folgende Formel
c1 c2
c=
c1 + c2
zeigt, dass fÄ
ur c gelten
mÄ
x + cx = F0 cos −t
x = xh (C1 ; C2 ; !0 ; t) + xp (F0 ; −; t)
1
1
+
F
c1 c2
1
1
1
=
+
c
c1 c2
Die bisher verwendeten Schwingungsdi®erentialgleichungen haben rechts eine Null. Sie
werden homogen genannt, und ihre LÄ
osung mit
xh (t) bezeichnet. Das System von Bild 10.1
wird { ausgehend von der Gleichgewichtslage {
durch die Gleichung
(9.28)
Bild 9.11.
Kraftgleiche
Federn
(9.29)
mÄ
xp + cxp = F0 cos −t
(10.3)
Die Anfangsbedingungen werden durch C1 und C2 berÄ
ucksichtigt. In
(10.3) sind die folgenden 2 FÄ
alle sorgfÄ
altig zu unterscheiden:
² Schwingungen mit konstanter Kraftamplitude (Fall a, Weganregung)
² Schwingungen mit Fliehkraftanregung (Fall b)
100
10 SONSTIGE SCHWINGUNGEN
10.1 Erzwungene Schwingungen
101
a) Konstante Kraftamplitude
b) Fliehkraftanregung
Bei einer konstantem Kraftamplitude gilt in
(10.3) F0 = const. Mit dem Ansatz
Bei dem technisch wichtigen Fall der Fliehkraftanregung
(Unwucht) ist
xp = A cos −t
F0 = mu r−2
(10.4)
erhÄ
alt man aus (10.3)
³
2
und man erhÄ
alt aus (10.3) mit dem Ansatz (10.4) Ä
ahnlich
wie oben
´
¡m− + c A cos −t = F0 cos −t
Bild 10.4.
Fliehkraftanregung
mu r−2
c ¡ m−2
mu r
A=
Vb = x∞ Vb
m
A=
(10.5)
(10.8)
Die VergrÄ
o¼erungsfunktion wird hier mit
c = m!02
Die GrÄ
o¼e Va hei¼t VergrÄo¼erungsfunktion.
Mit m = c=!02 erhÄ
alt man
!2
Va = 2 0 2
!0 ¡ −
´
Daraus ergibt sich
Daraus ergibt sich
F0
A=
c ¡ m−2
F0
Va = x0 Va
c
³
¡m−2 + c A cos −t = mu r−2 cos −t
Bild 10.2. Konstante
Kraftamplitude
A=
(10.7)
Vb =
(10.6)
−2
!02 ¡ −2
Bild 10.3.
Vergrößerungsfunktion, Fall a
(10.9)
Bild 10.5.
Vergrößerungsfunktion Fall b
PhÄ
anomene:
PhÄ
anomene:
² Bei sehr kleinem − schwingt die Masse wie die Erregung.
² Bei − < !0 schwingt die Masse gleichphasig zur Erregung.
² Bei − = !0 treten sehr gro¼e Amplituden auf. Man nennt dies
Resonanz .
² Bei − > !0 schwingt die Masse gegenphasig zur Erregung.
² Bei sehr gro¼em − werden die Amplituden sehr klein.
² Bei sehr kleinem − sind die Amplituden sehr klein.
² Wie bei a) gelten:
{ Bei − < !0 schwingt die Masse gleichphasig zur Erregung.
{ Bei − = !0 tritt Resonanz auf.
{ Bei − > !0 schwingt die Masse gegenphasig zur Erregung.
² Bei sehr gro¼em − schwingt die Masse gegenphasig zur Erregung mit
der Amplitude x∞ .
102
10 SONSTIGE SCHWINGUNGEN
10.2
Der Einfluss der Dämpfung
Die Di®erentialgleichung fÄ
ur gedÄ
ampfte Schwingungssysteme lautet
F0
x
Ä + 2#!0 x_ + !02 x =
cos −t
(10.10)
m
# hei¼t DÄampfungsgrad. Die Eigenkreisfrequenz lautet
p
!d = !0 1 ¡ #2
10.2 Der Ein°uss der DÄampfung
Erzwungene
Schwingungen
haben
Amplitudenverhalten von Bild 10.7 .
103
im
Frequenzbereich
das
(10.11)
Freie Schwingungen (F0 = 0) haben im Zeitbereich das Verhalten von
Bild 10.6 .
Bild 10.7. Amplituden-Frequenz-Darstellung bei gedämpften Schwingungen mit
verschiedenen Dämpfungsgraden
links: Fall a) Weganregung, rechts: Fall b) Unwuchtanregung
Wichtige PhÄ
anomene sind:
Bild 10.6. Zeitfunktionen bei gedämpften Schwingungen mit verschiedenen
Dämpfungsgraden
links: nach Anfangsauslenkung, rechts: nach Anfangsgeschwindigkeit.
Wichtige PhÄ
anomene bei vorhandener DÄ
ampfung sind:
² Die Amplituden nehmen exponentiell mit der Zeit ab
² Die Periodendauer wird mit zunehmendem # etwas grÄ
o¼er als im
ungedÄ
ampften Fall
² Optimales Einschwingen erfolgt fÄ
ur # = 0; 7
² Im Resonanzbereich gibt es ein Maximum. FÄ
ur # · 0; 25 gilt mit
guter NÄ
aherung
1
Vmax ¼
2#
² Die Schwingung und ihre Erregung sind stets phasenverschoben.
² Im Resonanzfall − = !0 ist die Phasenverschiebung genau 90◦
² Die dargestellten Kurven gelten nur fÄ
ur sehr langsames Hoch- bzw.
Herunterfahren, den quasi-stationÄaren Fall
² Beim Hochfahren von Maschinen treten viel niedrigere Maxima auf;
beim ungebremsten (langsamen) Herunterfahren ist dagegen Vorsicht
geboten.
104
10.3
10 SONSTIGE SCHWINGUNGEN
Koppelschwingungen
Bisher wurden ausschlie¼lich Schwinger
mit einem Freiheitsgrad behandelt.
In der Praxis treten jedoch meist
Koppelschwingungen auf. Bild 10.8
zeigt ein einfaches Modell, mit dem z.B.
die Schwingungen bei einem Motorrad
behandelt werden. Dieses hat zwei
Freiheitsgrade: x(t) und '(t). WÄ
are
der Schwerpunkt in der Mitte und die
beiden Federn gleich, so wÄ
aren x(t) und
'(t) entkoppelt. Im allgemeinen Fall
treten neue, interessante PhÄ
anomene
auf, deren Behandlung jedoch den
Rahmen dieser EinfÄ
uhrung sprengt.
Bild 10.8. Einfacher
Koppelschwinger
10.3 Koppelschwingungen
105
106
11
11
STOSSPROBLEME
Stoßprobleme
11.1
11.1 Der gerade, zentrale Sto¼
107
so ergibt die Division dieser Gleichungen
v¹1 + v1 = v¹2 + v2
Der gerade, zentrale Stoß
Daraus folgt
Grundlage fÄ
ur den geraden, zentralen Sto¼ ist die Impulserhaltung
v¹1 ¡ v¹2 = ¡(v1 ¡ v2 )
(11.4)
Der allgemeine Fall
Im allgemeinen Fall wird (11.4) durch
Im folgenden werden zwei GrenzfÄ
alle und der allgemeine Fall behandelt.
Bei diesen Sto¼vorgÄ
angen gilt der Satz:
(11.1)
Beide Massen bewegen sich nach dem Sto¼ wie eine Masse.
bzw. v¹1 ¡ v¹2 = 0
(11.2)
Der ideal elastische Sto¼
Es gilt neben (11.1) der Energieerhaltungssatz
1
1
1
1
m1 v¹12 + m2 v¹22 = m1 v12 + m2 v22
2
2
2
2
Umgestellt erhÄ
alt man daraus
1
1
m1 (¹
v12 ¡ v12) = ¡ m2 (¹
v22 ¡ v22 )
2
2
Stellt man auch (11.1) um
m1 (¹
v1 ¡ v1 ) = ¡m2 (¹
v2 ¡ v2 )
0·"·1
(11.6)
Die obigen SonderfÄ
alle folgen aus (11.5) fÄ
ur
" = 0, ideal plastischer Fall,
" = 1, ideal elastischer Fall.
Beispiele fÄ
ur " bei realen Sto¼vorgÄ
angen sind:
Der ideal plastische Sto¼
v¹1 = v¹2
(11.5)
ersetzt, wobei " Sto¼faktor hei¼t mit
Bild 11.1. Stoß von zwei Kugeln
m1 v¹1 + m2 v¹2 = m1 v1 + m2 v2
v¹1 ¡ v¹2 = ¡"(v1 ¡ v2 )
(11.3)
Glas auf Glas : " ¼ 0; 94
Stahl auf Stahl: " ¼ 0; 7
Der Energieerhaltungssatz geht in die Gleichung (11.5) mit " = 1 ein
und darf nicht mehr zusÄ
atzlich verwendet werden.
Die Au°Ä
osung von (11.1) und (11.5) ergibt
v¹1 =
m1 v1 + m2 v2 + "m2 (v2 ¡ v1 )
m1 + m2
(11.7)
v¹2 =
m1 v1 + m2 v2 + "m1 (v1 ¡ v2 )
m1 + m2
(11.8)
FÄ
ur den Sonderfall ideal plastisch " = 0 gilt (11.2), das hei¼t v¹1 = v¹2 .
alt man
FÄ
ur den Sonderfall m1 = m2 und " = 1 (ideal elastisch) erhÄ
v¹1 = v2
und
v¹2 = v1
Beispiele sind die Sto¼vorgÄ
ange zwischen Billardkugeln, Stahlkugeln und
MÄ
unzen.
108
11.2
11
STOSSPROBLEME
Der gerade, exzentische Stoß
11.2 Der gerade, exzentische Sto¼
109
Die Integration u
Äber die Sto¼zeit ¢t ergibt
JA (¹
! ¡ 0) = ¡hm(¹
v ¡ v)
Ein Beispiel
Der gerade, exzentrische Sto¼ wird an dem in Bild 11.2 dargestellten
Beispiel eines KÄ
orperpendels betrachtet. Dieses hat die Masse M und
das TrÄ
agheitsmoment JA bzgl. A. Das KÄ
orperpendel ist vor dem
Sto¼ in Ruhe (! = 0). Im Abstand h vom AufhÄ
angepunkt tri®t
die Masse m mit der Geschwindigkeit v auf und bleibt nach dem
Sto¼ mit dem KÄ
orperpendel fest verbunden (ideal plastischer Sto¼).
WÄ
ahrend des Sto¼vorganges kÄ
onnen die eingeprÄ
agten KrÄ
afte, wie z.B.
die Gewichtskraft, als klein gegenÄ
uber den Sto¼krÄ
aften angenommen
werden.
(11.13)
Da sich nach dem Sto¼ das System wie ein starrer KÄ
orper bewegen soll,
gilt
v¹ = !
¹h
(11.14)
und man erhÄ
alt aus (11.13)
(JA + mh2 )¹
! = hmv
(11.15)
¹ A = LA.
Dies entspricht dem Drallerhaltungssatz bzgl. A L
LÄ
ost man (11.15) nach !
¹ auf, so ergibt sich
!
¹=
mh
v:
JA + mh2
(11.16)
Lagerkraft, Sto¼mittelpunkt, Kraftsto¼
Die Kraft auf das Lager A erhÄ
alt man aus [(11:9) ¡ h(11:11)]
(JA ¡ M bh)!_ = hFA
Bild 11.2. Körperpendel und Massenpunkt sowie die daran angreifenden Kräfte
Der Drallsatz bzgl. des raumfesten Punktes A lautet
A <¾ :
JA !_ = hF
(11.9)
Der Schwerpunktsatz fÄ
ur die kleine Masse lautet
!:
mv_ = ¡F
(11.10)
Der Schwerpunktsatz fÄ
ur das KÄ
orperpendel lautet
!:
M !b
_ = F ¡ FA
(11.11)
Aus [(11:9) + h(11:10)] folgt
JA !_ = ¡hmv_
(11.12)
(11.17)
Daraus erkennt man, dass fÄ
ur
JA
h=
(11.18)
bM
keine Sto¼kraft auf das Lager entsteht. Der Punkt im Abstand h hei¼t
Sto¼mittelpunkt. Beim Pendelschlagwerk und beim Hammer sollte der
Sto¼ im Sto¼mittelpunkt erfolgen. Der Abstand h nach (11.18) entspricht
der reduzierten PendellÄ
ange von (9.18).
Aus (11.17) erhÄ
alt man durch Integration den Kraftsto¼
Z∆t
0
FA dt = (JA ¡ Mbh)
!
¹¡0
mv
= (JA ¡ M bh)
h
JA + mh2
110
11
STOSSPROBLEME
nicht aber die Kraft FA selbst. Man erkennt
da¼ der Kraftsto¼ dem Impuls mv proportional
ist und die gleiche Dimension wie dieser besitzt:
Ns = kg m/s.
Aus dem zeitlichen Verlauf der Kraft nach
Bild 11.3
wird in der messtechnischen
Schwingungsanalyse
(Modalanalyse)
das
Spektrum des Eingangssignals berechnet. Deshalb
ist dort die genaue Messung dieser Funktion von
Bedeutung.
Bild 11.3. Kraftstoß
11.2 Der gerade, exzentische Sto¼
111
112
113
Literatur zu TM III
[1] Werner Hauger, Walter Schnell u. Dietmar Gross:
Technische Mechanik, Band 3: Kinetik
Springer, Berlin, . . . 20058
—C 19,952
[2] Istv¶
an Szab¶
o, EinfÄ
uhrung in die Technische Mechanik
Springer, Berlin . . . , 20038
—C 69,95
[3] S. Graham Kelly:
Mechanical Vibrations (Schaum's Outline Series)
McGraw-Hill, New York, . . . 1996
—C 15,50
[4] Kurt Magnus u. Hans-Heinrich MÄ
uller:
Grundlagen der Technischen Mechanik,
Teubner, Stuttgart 19906
—C 20,90
[5] Dubbel: Taschenbuch fÄ
ur den Maschinenbau
(Hrsg.: Wolfgang Beitz u. Karl-Heinz KÄ
uttner):
Springer, Berlin . . . 200121 .
Neuau°age im Herbst 2004
Dubbel interaktiv (CD-ROM) 2002 —C 29,95
[6] HÄ
utte: Die Grundlagen der Ingenieurwissenschaften.
(Hrsg.: Horst Czichos)
Springer, Berlin . . . 200432 .
—C 79,95
—C 54,95
[7] Jens Wittenburg:
Dynamics of Systems of Rigid Bodies
Teubner, Stuttgart 1977
—C 39,-
[8] Istv¶
an Szab¶
o:
Geschichte der mechanischen Prinzipien
BirkhÄ
auser, Basel . . . 19963 (Nachdruck)
—C 75,-
Siehe auch das Literaturverzeichnis von TM I.
2
Die Preise sind von 2004, lt. Auskunft der Buchhandlung Völkl