Merkhilfe - Merz Schule

Abiturprüfung Mathematik 2017
Merkhilfe
S. 1/8
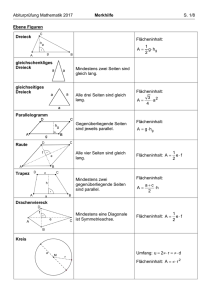
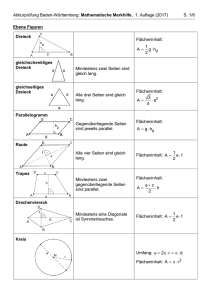
Ebene Figuren
Dreieck
Flächeninhalt:
A=
gleichschenkliges
Dreieck
a
gleichseitiges
Dreieck
Mindestens zwei Seiten sind
gleich lang.
a
a
a
1
g ⋅ hg
2
Alle drei Seiten sind gleich
lang.
Flächeninhalt:
3 2
A=
⋅a
4
a
Parallelogramm
Gegenüberliegende Seiten
sind jeweils parallel.
Flächeninhalt:
Alle vier Seiten sind gleich
lang.
Flächeninhalt: A =
Mindestens zwei
gegenüberliegende Seiten
sind parallel.
Flächeninhalt:
Mindestens eine Diagonale
ist Symmetrieachse.
Flächeninhalt: A =
A = g ⋅ hg
Raute
1
e⋅f
2
Trapez
A=
a+c
⋅h
2
Drachenviereck
1
e⋅f
2
Kreis
Umfang: u = 2π ⋅ r = π ⋅ d
Flächeninhalt: A = π ⋅ r 2
Abiturprüfung Mathematik 2017
Merkhilfe
S. 2/8
Körperberechnungen
Prisma
Volumen: V = G ⋅ h
Zylinder
Volumen: V = G ⋅ h = π ⋅ r 2 ⋅ h
Flächeninhalt der Mantelfläche: M = 2π ⋅ r ⋅ h
Quader
Volumen: V = a ⋅ b ⋅ c
Länge der Raumdiagonalen: e = a 2 + b 2 + c 2
Pyramide
Volumen: V =
1
G⋅h
3
Kegel
Volumen: V =
1
π ⋅r2 ⋅h
3
Flächeninhalt der Mantelfläche: M = π ⋅ r ⋅ s
Kugel
Volumen: V =
4
π ⋅ r3
3
Oberflächeninhalt: O = 4π ⋅ r 2
Merkhilfe
Abiturprüfung Mathematik 2017
S. 3/8
g
Elementargeometrie
h
b
Strahlensätze
a+b c +d
=
a
c
a c
= ;
b d
Falls g || h, gilt:
v
a
a+b v
=
a
u
u
c
d
Winkelsummensatz
Die Summe der Innenwinkel im Dreieck beträgt 180°.
Satz des Thales
Liegt C auf dem Halbkreis über AB,
so ist der Winkel bei C ein rechter Winkel.
Rechtwinkliges Dreieck
Satz des Pythagoras a 2 + b 2 = c 2
Trigonometrie
sin α =
a
b
a
, cos α = , tan α =
c
c
b
tan α =
sin α
, (sin α )2 + (cos α )2 = 1
cos α
Winkelfunktionen
sin
Gradmaß α
0°
Bogenmaß x
0
sin
0
cos
1
30 °
45 °
60 °
90 °
1
π
6
1
2
1
3
2
1
π
4
1
2
2
1
2
2
1
π
3
1
3
2
1
2
1
π
2
1
cos
0
Potenzen und Logarithmen
Potenzen
x0 = 1
x −a =
xa ⋅ xb = x a +b
xa
x a ⋅ y a = ( x y )a
Logarithmen
loga (b) =
ln(b)
ln(a)
xb
xa
1
xn = n x
1
xa
= x a −b
x
=  
ya  y 
(xa )b = xab
a
loga (1) = 0
log a (b x ) = x ⋅ log a (b)
 1
log a   = − log a (b )
b
Merkhilfe
Abiturprüfung Mathematik 2017
S. 4/8
Terme und Gleichungen
(a + b) ⋅ (a − b) = a 2 − b 2
(a ± b )2 = a 2 ± 2a b + b 2
Binomische Formeln
Quadratische Gleichung
2
p
p
x1;2 = − ±   − q
2
2
2
x +px+q = 0
ax +bx +c = 0
− b ± b2 − 4a c
x1;2 =
2a
x n = a (a > 0)
falls n gerade:
x1;2 = ± n a
falls n ungerade:
x =na
falls n ungerade:
x = −n−a
2
Potenzgleichungen
x n = a (a < 0)
Exponentialgleichungen
a x = b ⇔ x = loga (b) ( a, b > 0 )
Geraden in der Ebene
Punktsteigungsform
y = mx + c
y − yP
m= Q
x Q − xP
y = m ⋅ (x − xQ ) + yQ
Parallele zur y-Achse
x=u
Steigungswinkel α
m = tan α
Orthogonalität
m g ⋅ m h = −1 ⇒ g ⊥ h
Hauptform
Steigung
Ableitungen
Ableitungsregel
f(x)
f'(x)
g(x) + h(x)
g'(x) + h'(x)
Faktorregel
c⋅g(x)
c⋅g'(x)
Potenzregel
xr
r ⋅ xr −1
Produktregel
u(x)⋅v(x)
u'(x)⋅v(x) + u(x)⋅v'(x)
u(v(x))
u'(v(x))⋅v'(x)
Summenregel
Kettenregel
Spezielle Ableitungen
( x)
'
=
1
2 x
'
1
 1
  =−
x
x2
(sin x ) ' = cos x
(cos x ) ' = − sin x
(ex )' = ex
Merkhilfe
Abiturprüfung Mathematik 2017
S. 5/8
Untersuchung von Funktionen und Graphen
Symmetrie
Spiegelung
Achsensymmetrie zur y-Achse
⇔
f (−x ) = f ( x)
Punktsymmetrie zum Ursprung
⇔
f ( − x ) = − f ( x ) für alle x
an der x-Achse:
y = − f ( x)
an der y-Achse:
y = f (−x)
Verschiebung um c in x-Richtung:
y = f ( x − c)
um d in y-Richtung:
y = f (x) + d
Streckung
Monotonie
für alle x
1
in x-Richtung:
b
y = f (b ⋅ x )
mit Faktor a in y-Richtung:
y = a ⋅ f (x)
f ' ( x ) > 0 für alle x ∈ I ⇒
f streng monoton wachsend auf I
f ' ( x ) < 0 für alle x ∈ I ⇒
f streng monoton fallend auf I
mit Faktor
f ' ( x 0 ) = 0 und
Vorzeichenwechsel "+ nach –" von f ' bei x0
f ' ( x 0 ) = 0 und
f ' '(x 0 ) < 0
f ' ( x 0 ) = 0 und
Vorzeichenwechsel "– nach +" von f ' bei x0
oder
f ' ( x 0 ) = 0 und
f ' '(x 0 ) > 0
Wendepunkt
f ' ' ( x 0 ) = 0 und
Vorzeichenwechsel von f ' ' bei x0
oder
f ' ' ( x 0 ) = 0 und
f ' ' ' (x 0 ) ≠ 0
Hochpunkt
oder
Tiefpunkt
Tangente
Steigung m t = f ' (u)
Normale
Steigung mn =
−1
f '(u)
y = f '(u)(x − u) + f(u)
y=
−1
(x − u) + f(u)
f '(u)
allgemeine Sinusfunktion
f ( x) = a ⋅ sin( b ( x − c )) + d
(Amplitude
|a|, Periode
2π
)
b
Merkhilfe
Abiturprüfung Mathematik 2017
S. 6/8
Integralrechnung
x
Integralfunktion
Ia (x) = ∫ f (u) du
a
Hauptsatz
I a ' ( x ) = f ( x)
b
∫ f(x) dx = [F(x)]a = F(b) − F(a)
b
a
t
Bestandsfunktion
F(t) = F(t 0 ) + ∫ f (x) dx
t0
b
Mittelwert
Volumen eines
Rotationskörpers
1
m=
f(x) dx
b − a ∫a
b
V = π ⋅ ∫ (f (x )) dx
2
a
Stammfunktionen
Regel
Funktion
Stammfunktion
Summenregel
f(x) + g(x)
F(x) + G(x)
k⋅f(x)
k⋅F(x)
Lineare Verkettung
f (a x + b)
Spezialfälle
xr (r ≠ -1)
1
⋅ F (a x + b)
a
1
⋅ x r +1
r +1
Faktorregel
1
(x > 0)
x
ln(x)
sin x
− cos x
cos x
sin x
ex
ex
Differenzialgleichung
Funktionsterm
Wachstumsfunktionen
linear
f ' (t) = k
f (t ) = k ⋅ t + c
exponentiell
f ' (t) = k ⋅ f (t)
f ( t ) = a ⋅ ek ⋅ t
beschränkt
f ' (t ) = k ⋅ (S − f ( t ))
f ( t ) = S − a ⋅ e −k ⋅ t
Merkhilfe
Abiturprüfung Mathematik 2017
S. 7/8
Analytische Geometrie
Mittelpunkt der
Strecke AB
Orthogonalität
 a + b a + b2 a3 + b3 
M  1 1| 2
|

2
2
 2

r
| a |= a12 + a22 + a32
r
1 r
a0 = r ⋅ a
|a|
r r
a ⋅ b = a1 b1 + a2 b2 + a3 b3
r
r r
r
a ⋅ b = | a | ⋅ | b | ⋅ cos ϕ
r r
a ⋅b
r
cos ϕ = r
|a|⋅|b|
r r
r r
a ⊥ b ⇔ a⋅b = 0
Geradengleichung
r r
r
g: x = p + r ⋅ u
Betrag eines Vektors
Einheitsvektor
Skalarprodukt
Winkel zwischen
zwei Vektoren
Ebenengleichungen
Parameterform
Normalenform
r r
r
r
E: x = p + r ⋅ u + s ⋅ v
r r r
E: x − p ⋅ n = 0
Koordinatenform
E: a x1 + b x2 + c x3 = d
Schnittwinkel
Gerade – Gerade
Gerade – Ebene
Ebene – Ebene
(
)
r r
| u1 ⋅ u2 |
cos ϕ = r
r
| u1 | ⋅ | u2 |
r r
| u⋅n |
r
sin ϕ = r
|u|⋅| n|
r r
| n1 ⋅ n2 |
cos ϕ = r
r
| n1 | ⋅ | n2 |
Abstandsberechnungen
uuur
AB = (b1 − a1 )2 + (b2 − a2 )2 + (b3 − a3 )2
Punkt – Punkt
d(A;B) =
Punkt – Ebene
r r r
HNF von E: ( x − p ) ⋅ n0 = 0
(
)
r r r
d(Q;E) = q − p ⋅ n0
Windschiefe Geraden
bzw.
a x1 + b x2 + c x3 − d
bzw. d(Q;E) =
a2 + b2 + c 2
a q1 + b q2 + c q3 − d
a2 + b2 + c 2
r r
r
g: x = p + r ⋅ u ; h: x = q + s ⋅ v
r r r
r
r
r
r
d(g;h) = q − p ⋅ n0 , wobei n0 ⊥ u und n0 ⊥ v
(
)
=0
Merkhilfe
Abiturprüfung Mathematik 2017
S. 8/8
Wahrscheinlichkeit
Gegenereignis
P( A ) = 1 − P( A )
Additionssatz
P( A ∪ B) = P( A ) + P(B) − P( A ∩ B)
Spezieller Multiplikationssatz
P( A ∩ B) = P( A ) ⋅ P(B)
A,B unabhängig
Pfadregeln für Baumdiagramme
Die Wahrscheinlichkeiten längs eines Pfades werden multipliziert.
Die Wahrscheinlichkeiten der einzelnen Pfade werden addiert.
Erwartungswert einer Zufallsvariable X mit den Werten x1 , x 2 ,..., xn :
E( X) = x1 ⋅ P( X = x1) + x 2 ⋅ P( X = x 2 ) + ... + x n ⋅ P( X = x n )
Binomialverteilung:
n
Formel von Bernoulli P( X = k ) =   ⋅ pk ⋅ (1 − p)n −k
k 
E( X) = n ⋅ p
Erwartungswert
Statistische Tests
Beim Testen einer Hypothese H0 können folgende Fehler auftreten:
H0 ist wahr
H0 ist falsch
H0 wird verworfen
Fehler 1. Art
richtige Entscheidung
H0 wird nicht verworfen
richtige Entscheidung
Fehler 2. Art
Als Signifikanzniveau α bezeichnet man den Wert, den die Wahrscheinlichkeit für den
Fehler 1. Art nicht überschreiten darf.
Einseitiger Signifikanztest
Nullhypothese H0
Gegenhypothese H1
Ablehnungsbereich
linksseitiger Test
p ≥ p0
p < p0
{0;1;...; g}
rechtsseitiger Test
p ≤ p0
p > p0
{g; g + 1;.....;n}
Hinweis:
Die Merkhilfe stellt keine Formelsammlung im klassischen Sinn dar. Bezeichnungen werden nicht
erklärt und Voraussetzungen für die Gültigkeit der Formeln in der Regel nicht dargestellt.