Stochastik in der Schule SiS

Stochastik in der Schule
SiS
Zeitschrift des Vereins zur Förderung des schulischen Stochastikunterrichts
Inhaltsverzeichnis
NORBERT HENZE
Heft 1, Band 36 (2016)
Stochastische Extremwertprobleme im Fächer-Modell II:
Maxima von Wartezeiten und Sammelbilderprobleme
2
GERHARD KOCKLÄUNER
Pareto-Einkommensverteilung
10
KATRIN WÖLFEL
Der Satz von Bayes: Eine geschichtsträchtige Idee
mit vielfältigen Anwendungsmöglichkeiten
15
Stochastische Simulationen mit TinkerPlots –
ROLF BIEHLER,
DANIEL FRISCHEMEIER UND Von einfachen Zufallsexperimenten zum informellen
Hypothesentesten
SUSANNE PODWORNY
22
KYLE CAUDLE UND
ERICA DANIELS
28
Wurde die Lotterie bei den Hungerspielen manipuliert?
Berichte
PHILIPP ULLMANN
Bericht über die Herbsttagung des AK Stochastik
vom 20.–22. November 2015 in Paderborn
32
Bibliographische Rundschau
35
Vorwort der Herausgeberin
Liebe Leserin, lieber Leser,
im ersten Heft des neuen Jahres finden Sie vielfältige
Beiträge zum Lehren und Lernen von Stochastik an
Schule und Universität. Gemeinsam ist, dass sie die besondere Bedeutung von Verteilungen als grundlegendes
stochastisches Konzept zur Modellierung stochastischer
Situationen hervorheben.
Nachdem Norbert Henze zuvor Minima von Wartezeiten und Kollisionsprobleme untersucht hat (SiS Heft 3
2015), folgt nun der zweite Teil seines anlässlich der
Herbsttagung des AK Stochastik 2014 gehaltenen Vortrages zum Thema „Stochastische Extremwertprobleme
im Teilchen-Fächer-Modell“. Darin greift er Maxima
von Wartezeiten und Sammelbilderprobleme auf. Diese
stochastischen Probleme führen auf die Gumbel-Verteilung, eine Grenzverteilung für Maxima von unabhängigen und identisch verteilten Zufallsvariablen.
Gerhard Kockläuner befasst sich mit der Modellierung
der Nettoeinkommensverteilung in Deutschland mit der
Pareto-Verteilung sowie mit Darstellungen der zugehörigen Lorenzfunktion und des Gini-Koeffizienten.
Stochastik in der Schule 36 (2016) 1
Anschließend lädt Kathrin Wölfel auf eine Reise in die
Geschichte des Satzes von Bayes ein und arbeitet dabei das ursprüngliche Problem der Wahrscheinlichkeit
von Ursachen sowie den Verdienst von Pierre Simon
Laplace heraus, der diesen Satz zu seinem Durchbruch
verhalf.
Rolf Biehler, Daniel Frischemeier und Susanne Podworny untersuchen das Potential der Software TinkerPlots
für stochastische Simulationen einfacher Zufallsexperimente im schulischen Kontext. Dabei werden Stichprobenverteilungen erzeugt und zur Schätzung von Ereigniswahrscheinlichkeiten genutzt.
Das Heft schließt mit einer Übersetzung aus der Zeitschrift Teaching Statistics. Hierfür haben wir einen Artikel ausgewählt, der aufgrund seines Bezugs zu einer
aktuellen Romanverfilmung, der „Tribute von Panem“,
für Lernende motivierend sein dürfte. Kyle Caudle und
Erica Daniels führen darin die Grundidee des Randomisierungstests mittels Simulation aus.
Ich wünsche Ihnen eine anregende Lektüre.
Paderborn, Januar 2016
Katja Krüger
1
Stochastische Extremwertprobleme im Fächer-Modell II:
Maxima von Wartezeiten und Sammelbilderprobleme
N ORBERT H ENZE , K ARLSRUHE
Zusammenfassung: Im Fächermodell mit n Fächern
werden in einem Besetzungsvorgang s verschiedene
der Fächer zufällig mit je einem Teilchen besetzt.
Diese Besetzungsvorgänge werden in unabhängiger
Folge wiederholt, bis jedes Fach mindestens ein Teilchen enthält. Die zufällige Anzahl Vn,s der hierzu erforderlichen Besetzungsvorgänge ist ein Maximum
von Wartezeiten auf den ersten Treffer in BernoulliKetten. Wir geben die Verteilung von Vn,s an und
zeigen, dass sich diese Verteilung bei wachsendem
n unter gewissen Voraussetzungen einer GumbelVerteilung annähert. Letztere ist eine der klassischen
Grenzverteilungen für Maxima von unabhängigen
und identisch verteilten Zufallsvariablen.
Das sogenannte Sammelbilderproblem (Problem der
vollständigen Serie, Coupon-Collector-Problem) betrifft die in diesem Zusammenhang in natürlicher
Weise auftretende Zufallsvariable
1 Einleitung
Zu diesem Problem gibt es eine umfangreiche Literatur, siehe z.B. Althoff 2000, Boneh/Hofri 1997, Fricke 1984, Haake 2006, Jäger/Schupp 1987, Treiber
1988.
Wer hat es nicht schon einmal erlebt, das Sammelfieber, das wieder anlässlich der FußballWeltmeisterschaft 2014 in Brasilien bei Millionen
von Fans ausbrach, als es galt, ein Sammelalbum
mit 640 Plätzen zu füllen, wobei man Tüten mit
je 5 verschiedenen Sammelbildern kaufen konnte.
In der im Folgenden gewählten abstrakten Einkleidung als Fächermodell nehmen wir an, dass n von
1 bis n nummerierte Fächer vorliegen. Bei einem
Besetzungsvorgang werden dann s verschiedene der
n Fächer zufällig“ ausgewählt und jeweils mit ei”
nem Teilchen besetzt. Dieser Vorgang wird solange in unabhängiger Folge wiederholt, bis jedes Fach
mindestens ein Teilchen enthält. Dabei bedeute in
”
unabhängiger Folge“, dass Ereignisse, die sich auf
unterschiedliche Besetzungsvorgänge beziehen, stochastisch unabhängig sind.
Offenbar liegt beim WM-Sammelalbum der Fall
n = 640, s = 5 vor. Weitere konkrete Einkleidungen sind der Würfelwurf (n = 6, s = 1), wenn man
die sechs möglichen Augenzahlen als Fächer auffasst
und solange wirft, bis jede Zahl aufgetreten ist, sowie ein Lotto-Wartezeitproblem mit n = 49, s = 6.
Hier entsprechen die Fächer den möglichen Gewinnzahlen, und ein Besetzungsvorgang besteht in der
Notierung der 6 Gewinnzahlen einer Ausspielung.
Von Interesse ist dann die Anzahl der Ausspielungen, bis jede Zahl mindestens einmal Gewinnzahl
war. Eine weitere Einkleidung ist das Geburtstags”
Sammelproblem“ mit n = 365, s = 1: Wie viele Per-
2
sonen müssen zusammenkommen, damit jeder Tag
des Jahres Geburtstag mindestens einer dieser Personen ist? Dabei schließen wir wie üblich den 29. Februar als Geburtstag aus.
Vn,s := Anzahl der Besetzungsvorgänge, bis jedes
Fach besetzt ist.
Offenbar ist Vn,s ein Maximum von Wartezeiten, denn
bezeichnet für jedes j = 1, . . . , n die Zufallsvariable
W j die Anzahl der Besetzungsvorgänge, bis Fach Nr.
j mindestens ein Teilchen enthält, so gilt
Vn,s = max(W1 , . . . ,Wn ).
(1)
Hat jemand bei den Besetzungsvorgängen nur Fach
j im Auge und blendet alle anderen Fächer aus, so
beschreibt W j die Wartezeit bis zum ersten Treffer in
einer Bernoulli-Kette, wenn die Besetzung von Fach
j mit einem Teilchen als Treffer angesehen wird. Im
Fall s = 1 und gleich wahrscheinlicher Fächer ist diese Trefferwahrscheinlichkeit gleich 1/n, so dass W j
den Erwartungswert n besitzt. Der Erwartungswert
von Vn,s als Maximum aller W j ist jedoch deutlich
größer, vgl. Abschnitt 2.
In diesem Aufsatz betonen wir die strukturellen Eigenarten des Sammelbilderproblems, gehen auf die
Frage nach der Verteilung von Vn,1 auch bei ungleichen Wahrscheinlichkeiten für die einzelnen Fächer
ein und stellen einen Grenzwertsatz für die Wartezeit auf eine vollständige Serie vor. Als Grenzverteilung ergibt sich mit der Gumbel-Verteilung eine
der klassischen Grenzverteilungen für Maxima unabhängiger und identisch verteilter Zufallsvariablen.
Im Fall s = 1 schreiben wir kurz Vn anstelle von Vn,1 .
Stochastik in der Schule 36 (2016) 1, S. 2–9
2 Der Fall s = 1, gleich wahrscheinliche
Fächer
In diesem insbesondere in Zeitschriften zur Didaktik
der Mathematik ausführlich behandelten einfachsten
Fall lässt sich Vn wie folgt als Summe von unabhängigen Zufallsvariablen modellieren: Das erste Teilchen
belegt eines der n Fächer; wir haben also im Hinblick
auf eine vollständige Serie einen ersten Teilerfolg
erzielt. Sind bereits j < n verschiedene Fächer belegt, so gelte das Besetzen irgendeines der noch n − j
freien Fächer als (weiterer) Teilerfolg. Dabei tritt ein
Teilerfolg mit der von den Nummern der j bereits
besetzten Fächern unabhängigen Wahrscheinlichkeit
p j = (n − j)/n auf. Bezeichnet Y j die Anzahl der
Besetzungsvorgänge zwischen dem j-ten und dem
( j + 1)-ten Teilerfolg (einschließlich des letzteren),
so gilt
(2)
Vn = 1 +Y1 +Y2 + . . . +Yn−1 ,
wobei Y1 , . . . ,Yn−1 stochastisch unabhängig sin d. Die
Zufallsvariable Y j beschreibt die Anzahl der Versuche bis zum ersten Treffer in einer Bernoullikette mit
Trefferwahrscheinlichkeit p j = (n− j)/n. Es gilt also
k−1 j
j
, k ≥ 1.
1−
P(Y j = k) =
n
n
Wegen E(Y j ) = 1/p j = n/(n − j) folgt dann mit Darstellung (2) E(Vn ) = 1 + ∑n−1
j=1 E(Y j ), also
n−1
1
1
n
= n· 1+ + ... +
. (3)
E(Vn ) = ∑
2
n
j=0 n − j
Speziell erhält man hiermit E(V6 ) = 14, 7, E(V365 ) =
2364, 46 · · ·. Folglich müssen im Mittel 2365 Personen zusammenkommen, damit jeder Tag des Jahres
Geburtstag mindestens einer dieser Personen ist.
Für die durchschnittliche Teilchenzahl pro Fach bis
zum Erreichen einer vollständigen Serie, also die Zufallsvariable Vn /n, folgt aus (3)
1 1
1
Vn
= 1+ + + ... + .
(4)
E
n
2 3
n
Hier steht rechts die sogenannte n-te harmonische
Zahl
1
1
(5)
Hn := 1 + + . . . + .
2
n
Wegen
(6)
lim (ln n − Hn ) = γ,
Für die Varianz von Vn /n − ln n gilt mit der allgemeinen Rechenregel V(aX + b) = a2 V(X ) (s. z.B. Henze
2013, S. 163)
1
Vn
− ln n = 2 V(Vn ).
V
n
n
Darstellung (2) liefert wegen der Unabhängigkeit
von Y1 , . . . ,Yn−1 sowie V(Y j ) = (1 − p j )/p2j (vgl.
Henze 2013, S. 188)
V(Vn ) =
n−1
∑ V(Y j )
j=1
=
n−1
n2
=
1 − pj
2
j=1 p j
n−1
∑
j
∑ (n − j)2 · n
j=1
n−k
2
k=1 k
n−1
= n∑
n−1
n−1
1
1
.
−
n
∑
2
k=1 k
k=1 k
= n2 ∑
−2 = π2 /6 (s. z.B. Heuser 2004, S. 150)
Wegen ∑∞
k=1 k
und Hn /n → 0 für n → ∞ folgt
π2
Vn
− ln n =
.
lim V
n→∞
n
6
(8)
Sowohl Erwartungswert als auch Varianz von Vn /n −
ln n konvergieren also für n → ∞. Dieser Sachverhalt
lässt vermuten, dass die Zufallsvariable Vn /n− ln n in
Verteilung konvergiert. Diese Namensgebung bedeutet, dass eine Verteilungsfunktion G existiert, so dass
für jede Stetigkeitsstelle x von G die Limesbeziehung
Vn
− ln n ≤ x = G(x)
lim P
n→∞
n
besteht.
Wir werden dieser Frage in Abschnitt 4 nachgehen. Obwohl Vn nach (2) eine Summe unabhängiger Zufallsvariablen darstellt, greift hier kein Zentraler Grenzwertsatz mit einer asymptotischen Normalverteilung, weil die Summanden sehr unterschiedlich
große Beiträge zur Summe liefern.
Um diesen Sachverhalt zu verdeutlichen, nehmen wir
eine gerade Anzahl n = 2m von Fächern an und spalten die Summe in (2) in die Bestandteile
n→∞
wobei γ = 0, 57221 . . . die Euler-Mascheronische
Konstante bezeichnet (s. z.B. Heuser 1994, S. 185),
folgt mit (4)
Vn
− ln n = γ.
(7)
lim E
n→∞
n
Hn,1 := 1 +
m−1
∑ Yj,
j=1
2m−1
Hn,2 :=
∑
Yj
j=m
auf. Hier steht Hn,1 für die Anzahl der Teilchen, die
zur Besetzung der Hälfte aller Fächer benötigt wird,
3
und Hn,2 beschreibt die Anzahl der danach noch erforderlichen Teilchen, um die vollständige Serie zu
komplettieren. Es gilt
2m
2m
+ ...+
E(Hn,1 ) = 1 +
2m − 1
2m − (m − 1)
1
1
1
+
+ ... +
= 2m
2m 2m − 1
m+1
2m
2m
2m
+
+ ...+
E(Hn,2 ) =
m m−1
1
1
1
1
+
+ ... + + 1 ,
= 2m
m m−1
2
und wir erhalten die in Tabelle 1 angegebenen Werte.
n
E(Hn,1 )
E(Hn,2 )
6
3.7
11
20
13.4
58.6
100
68.8
449.9
640
443.1
4062.1
Tab. 1: Erwartungswerte der Wartezeiten auf die
erste bzw. zweite Hälfte einer vollständigen Serie
Im Verhältnis zur mittleren Wartezeit auf die erste Hälfte wächst also die mittlere Wartezeit auf die
zweite Hälfte bei zunehmender Fächeranzahl über alle Grenzen!
3 Die Verteilung von Vn,s
In diesem Abschnitt betrachten wir die allgemeinere
Situation, dass bei jedem Besetzungsvorgang gleichzeitig s verschiedene Fächer
je ein Teilchen erhalten.
Dabei nehmen wir alle ns Auswahlen dieser Fächer
als gleich wahrscheinlich an. Offenbar kann Vn,s jeden Wert a, a + 1, a + 1, . . . annehmen, wobei
n
n
a :=
= min m ∈ Z : ≤ m
(9)
s
s
gesetzt ist. Die Verteilung von Vn,s ergibt sich, wenn
man für festes k zunächst das Ereignis {Vn,s > k}
betrachtet. Wegen (1) gilt Vn,s > k genau dann,
wenn mindestens eines der Ereignisse {W j > k}, j =
1, . . . , n, eintritt. Es folgt also
P(Vn,s > k) = P
n
{W j > k} .
j=1
Es ist frappierend, dass sich etwa im Fall n = 640 die
mittleren Wartezeiten auf die erste bzw. zweite Hälfte einer vollständigen Serie grob im Verhältnis 1 zu 9
aufteilen. Hier sollte man sich jedoch vor Augen halten, dass allein die Besetzung des letzten freien Fachs
im Mittel 640 Teilchen erfordert.
Für die Wahrscheinlichkeit der Vereinigung beliebiger Ereignisse A1 , . . . , An gibt es die auch als Formel
des Ein- und Ausschließens bekannte Darstellung
Obige Tabelle zeigt, dass die Quotienten
E(Hn,2 )/E(Hn,1 ) bei wachsendem n immer größer
werden. In der Tat gilt mit n = 2m und den angegebenen Darstellungen für E(Hn,1 ) und E(Hn,2 ) sowie
der Definition (5) der n-ten harmonischen Zahl
(siehe z.B. Henze 2013, Kapitel 11). Dabei bezeichnet
Sr :=
∑ P (Ai1 ∩ . . . ∩ Air ) (11)
E(Hn,2 )
E(Hn,1 )
=
1
1
1
m + m−1 + . . . + 2 + 1
1
1
1
2m + 2m−1 + . . . + m+1
=
Hm
.
H2m − Hm
Nach (6) können wir für den vorzunehmenden
Grenzübergang n → ∞ Hn = ln n − γ + o(1) setzen,
wobei o(1) eine gegen Null konvergierende Folge ist.
Damit folgt wegen ln(2m) = ln 2 + ln m
E(Hn,2 )
ln m − γ + o(1)
=
E(Hn,1 )
ln(2m) − γ + o(1) − (ln m − γ + o(1))
ln m − γ + o(1)
=
ln 2 + o(1))
und somit
4
E(Hn,2 )
= ∞.
lim
n→∞ E(Hn,1 )
P
n
Aj
=
n
∑ (−1)r−1Sr
(10)
r=1
j=1
1≤i1 <...<ir ≤n
n
die sich über r Summanden erstreckende Summe
der Wahrscheinlichkeiten aller Durchschnitte von r
der n Ereignisse. Wichtig für spätere Überlegungen
ist noch, dass die bei Abbruch der alternierenden
Summe entstehenden Partialsummen abwechselnd
zu groß und zu klein sind. Es gelten also die durch
Induktion nach n einzusehenden, als BonferroniUngleichungen bezeichneten Abschätzungen
n
P
P
j=1
n
≤
Aj
∑ (−1)r−1Sr ,
(12)
r=1
Aj
2l+1
≥
j=1
2l
∑ (−1)r−1Sr .
(13)
r=1
Dabei ist in (12) l ≥ 0 und 2l + 1 ≤ n sowie in (13)
l ≥ 1 und 2l ≤ n vorausgesetzt.
Wir wählen jetzt die Ereignisse in (10) als
A j := {W j > k},
j = 1, . . . , n.
(14)
Um die in (11) auftretenden Schnitt-Wahrscheinlichkeiten zu bestimmen, können wir uns auf den Fall r ≤
n − s beschränken, da bei jedem Besetzungsvorgang
s verschiedene Fächer belegt werden. Wir wählen
für festes r ∈ {1, . . . , n − s} Indizes i1 , . . . , ir mit 1 ≤
i1 < . . . < ir ≤ n. Das Ereignis Ai1 ∩ . . . ∩ Air tritt
genau dann ein, wenn bei den ersten k Besetzungsvorgängen die Fächer mit den Nummern i1 , . . . , ir leer
bleiben. Die Wahrscheinlichkeit, dass dies bei einem
Besetzungsvorgang geschieht, ist
n−r
(15)
qr := ns ,
s
Rechts-Schiefe“, d.h. die Wahrscheinlichkeiten stei”
gen zunächst schnell an und fallen dann nach Erreichen des Maximums langsamer wieder ab. Diese
Rechts-Schiefe ist nicht weniger ausgeprägt, wenn
wir die Anzahl n der Fächer vergrößern. So zeigt Abbildung 2 ein Stabdiagramm der Verteilung von V49,6 .
Diese Zufallsvariable beschreibt die Anzahl der Ausspielungen im Lotto 6 aus 49, die nötig ist, damit jede
Zahl mindestens einmal als Gewinnzahl auftritt.
P(V49,6 = k)
0, 05
0, 04
denn unabhängig von den Fachnummern i1 , . . . , ir
müssen r festgelegte
Fächer leer bleiben, und günstig
Auswahlen von s der restlichen
hierfür sind alle n−r
s
n − r Fächer. Da Ereignisse, die sich auf unterschiedliche Besetzungsvorgänge beziehen, stochastisch unabhängig sind, gilt dann
0, 03
0, 02
0, 01
0
P(Ai1 ∩ . . . ∩ Air ) = P(A1 ∩ . . . ∩ Ar ) = qkr
und somit nach (10)
P(Vn,s > k) =
n−s
∑ (−1)
r−1
r=1
n k
q
r r
(16)
mit qr wie in (15). Durch Differenzbildung gemäß
P(Vn,s = k) = P(Vn,s > k −1)−P(Vn,s > k) ergibt sich
hieraus die Verteilung von Vn,s zu
P(Vn,s = k) =
n−s
∑ (−1)
r−1
r=1
n k−1
q (1 − qr ), (17)
r r
k ∈ {a, a + 1, a + 2, . . .} mit a wie in (9), vgl. Henze
2013, S. 193.
10
20
30
40
50
60
70 k
Abb. 2: Verteilung der Wartezeit beim
Sammelbilder-Problem mit n = 49, s = 6
Beide Abbildungen wurden mithilfe von Formel (17)
erstellt, wobei die Summanden rekursiv berechnet
wurden. Mit einer genauen Arithmetik (extended
precision) kann diese Formel bis zu einer Fächerzahl
von n = 120 verwendet werden, ohne dass numerische Instabilitäten auftreten (ab n = 121 ergab die
Summe aller Wahrscheinlichkeiten Werte größer als
Eins). Für größere Werte von n hilft ein in Abschnitt
4 vorgestellter Grenzwertsatz.
Der Erwartungswert von Vn,s ergibt sich mithilfe von (17) und der Darstellungformel E(Vn,s ) =
∑∞
k=a kP(Vn,s = k) sowie
∞
∑ kxk−1 =
k=a
P(V6,1 = k)
=
0, 08
0, 06
d ∞ k
d xa
x
=
∑
dx k=a
dx 1 − x
axa−1 − (a − 1)xa
,
(1 − x)2
zu
0, 04
E(Vn,s ) =
0, 02
n−s
∑ (−1)
r−1
r=1
0
0
5
10
15
20
25
30
35
40
k
Abb. 1: Verteilung der Wartezeit beim
Sammelbilder-Problem mit n = 6, s = 1
Abbildung 1 zeigt ein Stabdiagramm der Verteilung von V6,1 , also der Anzahl der Würfe, bis
jede Augenzahl eines echten Würfels aufgetreten
ist. Deutlich zu erkennen ist hier eine ausgeprägte
|x| < 1,
a−1
n qr (qr − a(qr − 1))
,
1 − qr
r
s. z.B. Henze 2013, S. 193. Hiermit erhält man etwa
E(V49,6 ) = 35, 08 . . ..
4 Ein Grenzwertsatz für Vn
Wir haben in (7) und (8) gesehen, dass Erwartungswert und Varianz der im Folgenden mit
Vn∗ :=
Vn
− ln n
n
5
bezeichneten Zufallsvariablen beim Grenzübergang
n → ∞ konvergieren. Natürlich erhebt sich sofort
die Frage, ob nicht auch die Wahrscheinlichkeiten
P(Vn∗ ≤ x), x ∈ R, gegen von x abhängende Werte G(x) streben. Wir untersuchen im Folgenden für
festes x ∈ R die komplementäre Wahrscheinlichkeit
P(Vn∗ > x) und wählen hierzu n so groß, dass x +
ln n ≥ 1 gilt. Setzen wir kn := n(x + ln n), so gilt
nach Definition von Vn∗ , wegen der Ganzzahligkeit
von Vn sowie (16)
P(Vn∗ > x) = P(Vn > n(x + ln n))
= P(Vn > kn )
=
n−1
∑ (−1)
r−1
r=1
n kn
q
r r
(18)
Nach Übergang zum komplementären Ereignis und
Einsetzen von Vn∗ = Vn /n − ln n ergibt sich also der
Grenzwertsatz
lim P (Vn ≤ n(x + ln n)) = G(x),
n→∞
Die Funktion G ist nach Emil Julius Gumbel (1891
– 1966) benannt und heißt Verteilungsfunktion der
Gumbelschen Extremwertverteilung. Abbildung 3
zeigt ein Schaubild der Dichte g(x) = G
(x) =
exp(−(x + e−x )) dieser Verteilung.
0,2
0,1
lim inf P(Vn∗ > x) ≥
n→∞
∑ (−1)r−1
r=1
2l
∑ (−1)r−1
r=1
e−xr
r!
,
∑ (−1)r−1
r=1
e−xr
r!
∞
(−e−x )r
r!
r=1
= − exp(−e−x ) − 1
= −∑
= 1 − exp(−e−x ),
und wir erhalten
lim P(Vn∗
n→∞
6
−3 −2 −1
0
1
2
3
4
5
x
Abb. 3: Dichte der Gumbelschen
Extremwertverteilung
Der Graph dieser Dichte weist die gleiche Asymmetrie auf wie die Stabdiagramme in Abb.1 und Abb. 2.
Der Erwartungswert der Extremwertverteilung von
Gumbel ist die Euler-Mascheroni-Konstante γ, und
die Varianz ist gleich π2 /6.
Bevor wir Konsequenzen von (21) aufzeigen, soll
noch der Nachweis von (20) geführt werden. Hierzu
setzen wir nr := n(n − 1) · . . . · (n − r + 1) sowie
e−xr
r!
folgen. Lassen wir jetzt l gegen Unendlich streben,
so ergibt sich
∞
g(x) = exp(−(x + e−x ))
(20)
gelten. Mit (20) würde dann für jedes feste l
n→∞
(22)
0,3
gilt. Im Hinblick auf (18) ist diese Aussage wichtig;
es besteht jedoch das Problem, dass in (18) bei wachsendem n auch die Anzahl der Summanden zunimmt.
Hier helfen die Bonferroni-Ungleichungen (12) und
(13), wonach für festes l
2l+1
∗
r−1 n
qkr n ,
P(Vn > x) ≤ ∑ (−1)
r
r=1
2l
∗
r−1 n
qkr n
P(Vn > x) ≥ ∑ (−1)
r
r=1
lim sup P(Vn∗ > x) ≤
x ∈ R.
G(x) := exp(− exp(−x)),
(19)
Wir werden sehen, dass für jedes r ≥ 1
e−xr
n kn
qr =
lim
n→∞ r
r!
2l+1
(21)
wobei
mit qr wie in (15) mit s = 1, also
n−r
.
qr =
n
x ∈ R,
εn := n(x + ln n) − n(x + ln n).
Dann gilt
n kn
q
r r
1 nr r r kn
· r ·n · 1−
r! n
n
r
1 n
r n(x+ln n) r εn
· r · nr · 1 −
· 1−
.
r! n
n
n
=
=
Hier konvergieren der zweite Faktor und (wegen
−1 ≤ εn ≤ 0) auch der letzte gegen Eins, so dass nur
> x) = 1 − exp(− exp(−x)).
r n(x+ln n)
= e−xr
lim n · 1 −
n→∞
n
r
(23)
zu zeigen ist. Der Klammerausdruck links ist gleich
exp(an ) mit
r
.
an := r ln n + n(x + ln n) ln 1 −
n
Zu zeigen bleibt also limn→∞ an = −rx. Mit der
Ungleichung lnt ≤ t − 1 ergibt sich unmittelbar
an ≤ −rx, und die durch Ersetzen von t durch
1/t in obiger Logarithmus-Ungleichung folgende
Abschätzung lnt ≥ 1 − 1/t liefert
an ≥ r ln n − n(x + ln n) ·
= −r2 ·
r
n−r
n
ln n
−
· rx.
n−r n−r
Da diese untere Schranke für an gegen −rx konvergiert, folgt an → −rx, was noch zu zeigen war.
Wahrscheinlichkeiten besitzen? Intuitiv ist zu erwarten, dass Vn dann im Mittel größer wird“. Zur Präzi”
sierung bezeichne p j die Wahrscheinlichkeit, dass
ein Teilchen in Fach Nr. j fällt. Dabei gelte p j > 0
für jedes j sowie p1 + . . . + pn = 1. Wie in (14) sei
bei festem k A j das Ereignis, dass nach k Besetzungsvorgängen Fach Nr. j noch frei ist.
Zu vorgegebenen r ∈ {1, . . . , n − 1} und i1 , . . . , ir mit
1 ≤ i1 < i2 < . . . < ir ≤ n ist die Wahrscheinlichkeit, dass bei einem Besetzungsvorgang die Fächer
mit den Nummern i1 , . . . , ir frei bleiben, durch 1 −
pi1 − . . . − pir gegeben. Wegen der Unabhängigkeit
von Ereignissen, die sich auf verschiedene Besetzungsvorgänge beziehen, gilt dann
P(Ai1 ∩ . . . ∩ Air ) = (1 − pi1 − . . . − pir )k
Die Formel des Ein- und Ausschließens (vgl. (10),
(11)) liefert unter Beachtung von P(A1 ∩ . . .∩ An ) = 0
Der Grenzwertsatz (21) besagt
−x
P (Vn ≤ n(x + ln n)) ≈ exp(−e )
(24)
für großes n. Wählt man ein p mit 0 < p < 1 und
setzt p = exp(−e−x ), so folgt ln p = −e−x und somit ln(− ln p) = −x, also x p = − ln(− ln p). Insbesondere ergibt sich x0.5 ≈ 0, 3665, x0.9 ≈ 2, 250 und
x0,95 ≈ 2, 970. Für n = 640 folgt dann aus (24)
P(V640 ≤ 4370) ≈ 0, 5,
P(V640 ≤ 5575) ≈ 0, 9,
P(V640 ≤ 6036) ≈ 0, 95.
Würde man also die Sticker beim Sammelalbum zur
Fußball-WM 2014 einzeln kaufen können, so wäre
das Album mit einer fünfprozentigen Wahrscheinlichkeit selbst nach dem Kauf von stolzen 6036 Bildern immer noch nicht komplett. Diese Aussage gilt
auch, wenn die Sticker in Tüten zu je s verschiedenen
Stickern gekauft werden, denn es gilt in Verallgemeinerung von (21) in der Situation von Abschnitt 3
sVn,s
− ln n ≤ x = exp(− exp(−x)), x ∈ R.
lim P
n→∞
n
Der Beweis hierfür verläuft ganz analog wie der Fall
s = 1; man muss nur qr in (19) durch das in (15) eingeführte qr ersetzen.
5 Der Fall s = 1, nicht gleich
wahrscheinliche Fächer
Wie verhält sich die Wartezeit Vn auf eine vollständige Serie, wenn die einzelnen Fächer unterschiedliche
P(Vn > k) =
n−1
∑ (−1)r−1
r=1
∑
(1−pi1 − . . . −pir )k ,
1≤i1 <...<ir ≤n
und die Wahrscheinlichkeiten P(Vn = k) erhält
man hieraus bekanntermaßen durch Differenzbildung P(Vn = k) = P(Vn > k − 1) − P(Vn > k).
Für den Fall n = 3 ergibt sich speziell
P(V3 ≤ k) = 1 − (1 − p1 )k − (1 − p2 )k − (1 − p3 )k
+pk1 + pk2 + pk3 , k ≥ 3.
Als Beispiel betrachten wir die Situation von drei
Fächern, und zwar einmal mit der Gleichverteilung
p1 = p2 = p3 = 1/3, zum anderen mit der Verteilung
p1 = 1/2, p2 = 1/3, p3 = 1/6. Beide Fälle können
im Unterricht mit einem echten Würfel hergestellt
werden, wenn man einmal das Werfen einer 1 oder
2, 3 oder 4 bzw. 5 oder 6 als Belegung eines von 3
Fächern ansieht. Beim zweiten Szenario entsprechen
die Augenzahlen 1,2, oder 3 Fach 1, die Augenzahlen
4 oder 5 Fach 2 und die Augenzahl 6 Fach 3.
Tabelle 2 zeigt die Wahrscheinlichkeiten P(V3 ≤
k), nach höchstens k Besetzungsvorgängen eine
vollständige Serie erzielt zu haben, für diese beiden Szenarien. Wie zu erwarten ist für jedes k die
Wahrscheinlichkeit einer vollständigen Serie nach
höchstens k Besetzungsvorgängen im Fall verschieden wahrscheinlicher Fächer kleiner als im gleich
wahrscheinlichen Fall. Man spricht dann davon, dass
die Verteilung von V3 stochastisch größer als im
Fall gleich wahrscheinlicher Fächer ist. Das Attribut
größer“ bezieht sich dabei auf die komplementären
”
Wahrscheinlichkeiten P(V3 > k).
7
k
3
4
5
6
7
8
9
10
15
20
P(V3 ≤ k)
p1 = p2 = p3 =
0, 2222
0, 4444
0, 6173
0, 7407
0, 8258
0, 8834
0, 9921
0, 9480
0, 9931
0, 9991
1
3
P(V3 ≤ k)
p1 = 12 , p2 = 31 , p3 =
0, 1667
0, 3333
0, 4707
0, 5787
0, 6629
0, 7286
0, 9328
0, 8212
0, 9328
0, 9736
1
6
Tab. 2: Bei ungleichen Fächer-Wahrscheinlichkeiten
wird die Wartezeit V3 stochastisch größer
Da für eine ganzzahlige nichtnegative Zufallsvariable Z ganz allgemein der Erwartungswert in der Form
E(Z) =
=
∞
∞
j
∑ jP(Z = j) = ∑ ∑ 1
j=1
∞ ∞
P(Z = j)
j=1 i=1
∞
∑ ∑ P(Z = j) = ∑ P(Z ≥ i)
i=1 j=i
i=1
berechnet werden kann, ist auch der Erwartungswert
E(V3 ) =
1
1
1
+ +
p1 p2 p3
1
1
1
−
−
−
+1
1− p1 1− p2 1− p3
von V3 im Fall gleich wahrscheinlicher Fächer kleiner als im anderen Szenario: Im Fall p1 = p2 = p3 =
1
1
1
1
3 gilt E(V3 ) = 5, 5, im Fall p1 = 2 , p2 = 3 , p3 = 6
ist E(V3 ) = 7, 3.
Boneh/Hofri (1997) zeigen, dass ganz allgemein Vn
stochastisch minimal wird, wenn die Fächer gleich
wahrscheinlich sind. Somit ist auch die mittlere Wartezeit auf eine vollständige Serie am kürzesten, wenn
eine Gleichverteilung über alle Fächer vorliegt.
6 Abschließende Bemerkungen
a) Im Fall gleich wahrscheinlicher Fächer lässt sich
die Verteilung von Vn in der Form
P (Vn = k) =
n!
· Sk−1,n−1
nk
mithilfe der Stirling-Zahlen 2. Art darstellen (Hofri
1995, S. 129).
b) Im Unterschied zu Zentralen Grenzwertsätzen,
die das asymptotische Verhalten von Summen von
8
Zufallsvariablen untersuchen, interessiert man sich
bei stochastischen Extremwertproblemen insbesondere für das Verhalten des Maximums Mn =
max(X1 , . . . , Xn ) von Zufallsvariablen X1 , . . . , Xn
beim Grenzübergang n → ∞. So kann man fragen,
ob es im Fall unabhängiger und identisch verteilter
X1 , . . . , Xn Folgen (an ) und (bn ) mit bn > 0 gibt, so
dass für eine Verteilungsfunktion H
Mn − an
lim P
≤ t = H(t), t ∈ R,
(25)
n→∞
bn
gilt. Dabei soll der Entartungs-Fall ausgeschlossen
sein, dass eine Zufallsvariable mit der Verteilungsfunktion H mit Wahrscheinlichkeit Eins nur einen
Wert annimmt. Klassische Sätze der stochastischen
Extremwerttheorie besagen, dass – falls überhaupt
Konstantenfolgen (an ) und (bn ) mit (25) existieren,
die Funktion H bis auf eine affine Transformation
des Arguments nur eine von drei Funktionen sein
kann (siehe z.B. Löwe 2008). Eine davon ist die
durch (22) gegebene Verteilungsfunktion der Gumbel’schen Extremwertverteilung, die beiden anderen die Fréchet-Verteilung mit der Verteilungsfunktion Φα (x) = exp(−x−α ), x > 0, für ein α > 0 und
die Weibull-Verteilung mit der Verteilungsfunktion
Ψα (x) = exp(−(−x)α ), x < 0, und Ψα (x) = 1 für
x ≥ 0.
Das Resultat (21) besagt also, dass (25) für Vn anstelle von Mn (mit an = n ln n und bn = n) gilt, wobei
H die Verteilungsfunktion der Extremwertverteilung
von Gumbel ist.
An dieser Stelle sei darauf hingewiesen, dass sich für
Minima von Wartezeiten im Fächermodell bei wachsender Fächeranzahl asymptotisch eine WeibullVerteilung ergibt (siehe den Aufsatz Stochastische
Extremwertprobleme im Fächermodell I: Minima
von Wartezeiten und Kollisionsprobleme in Heft
3/2015).
c) Wenn man in der Situation von Abschnitt 2 solange Teilchen verteilt, bis für ein κ ∈ (0, 1) nκ Fächer
besetzt sind, so werden durch die Bedingung κ < 1
die üblicherweise extrem langen Wartezeiten auf die
letzten noch nicht besetzten Fächer ausgeschlossen.
Mit den in Abschnitt 2 eingeführten Zufallsvariablen
Y1 ,Y2 , . . . ,Yn−1 ist dann die die Wartezeit bis zur Besetzung von κn Fächern verteilt wie die Summe
1 +Y1 +Y2 + . . . +Yκn−1 .
In dieser Darstellung ist der Einfluss der einzelnen
Summanden auf die Gesamtsumme so gering, dass
mithilfe des Zentralen Grenzwertsatz von LindebergFeller (s. z.B. Brokate et al. 2015, Kapitel 23)
die asymptotische Normalverteilung dieser Summe
nachgewiesen werden kann.
d) Wartet man in der in Abschnitt 4 behandelten Situation auf c vollständige Serien und bezeichnet die
(c)
Anzahl der dafür nötigen Teilchen mit Vn , so gilt
der Grenzwertsatz (Erdős/Rényi 1961)
(c)
lim P Vn ≤ n(ln n + (c − 1) ln ln n + x)
n→∞
e−x
, x ∈ R.
= exp −
(c − 1)!
In diesem Artikel wird auch ein Resultat von Newman/Shepp (1960) ergänzt: Es gilt
(c)
= n(ln n + (c − 1) ln ln n + Kc + o(1)),
E Vn
wobei Kc = γ − ln(c − 1)! und o(1) eine Nullfolge
ist. Überraschenderweise kostet also bei einer großen
Anzahl von Fächern die erste vollständige Serie grob
gesprochen n ln n und jede weitere n ln ln n Teilchen.
Danksagung: Der Autor dankt den Gutachtern für
diverse Verbesserungsvorschläge.
Anmerkung: Diesem Aufsatz liegt ein im Rahmen
der Jahrestagung 2014 des Arbeitskreises Stochastik
der Gesellschaft für Didaktik der Mathematik gehaltener Vortrag zugrunde.
Literatur
Althoff, H. (2000): Zur Berechnung der Wahrscheinlichkeit für das Vorliegen einer vollständigen Serie (Sammelbilderproblem). In: Stochastik in der
Schule 20, S. 18–20.
Boneh, A., Hofri, M. (1997): The Coupon Collector
Problem revisited – A Survey of engineering Problems and computational Methods. In: Stochastic
Models 13, S. 39–66.
Brokate, M., Henze, N., Hettlich, F., Meister, A.,
Schranz-Kirlinger, G., Sonar, T. (2015): Grundwissen Mathematikstudium: Höhere Analysis,
Numerik und Stochastik. Springer Spektrum, Heidelberg.
Erdős, P., Rényi, A. (1961): On a Classical Problem
of Probability Theory. In: MTA Mat. Kut. Int. Kőzl.
6A, S. 215–220.
Fricke, A. (1984): Das stochastische Problem der
vollständigen Serie. In: Der Mathematikunterricht
30, S. 79–85.
Haake, H. (2006): Elementare Zugänge zum Problem
der vollständigen Serie. In: Stochastik in der Schule 26, S. 28–33.
Henze, N. (2013): Stochastik für Einsteiger. 10. Auflage: Verlag Springer Spektrum. Heidelberg.
Heuser, H. (1994): Lehrbuch der Analysis Teil 1, 11.
Auflage. B.G. Teubner, Stuttgart.
Heuser, H. (2004): Lehrbuch der Analysis Teil 2, 13.
Auflage. B.G. Teubner, Stuttgart.
Hofri, M. (1995): Analysis of Algorithms. Oxford
University Press, New York.
Jäger, J., Schupp, H. (1987): Wann sind alle Kästchen
besetzt? Oder: Das Problem der vollständigen Serie am Galton-Brett. In: Didaktik der Mathematik
15, S. 37
Löwe, M. (2008): Extremwertheorie. Lecture Note.
https://wwwmath.uni-muenster.de/statistik/loewe/
Newman, D.J,. Shepp, L. (1960): The double Dixie
Cup Problem. In: American Mathematics Monthly
67, S. 58–61.
Treiber, D. (1988): Zur Wartezeit auf eine vollständige Serie. In: Didaktik der Mathematik 16, S. 235–
237.
Anschrift des Verfassers:
Prof. Dr. Norbert Henze
Institut für Stochastik
Karlsruher Institut für Technologie (KIT)
Kaiserstr. 89–93
76131 Karlsruhe
[email protected]
9
Pareto-Einkommensverteilung
GERHARD KOCKLÄUNER, KIEL
auf Haushaltsnettoeinkommen beziehenden Tabelle 1. Haushaltsnettoeinkommen ergeben sich aus
den Haushaltsbruttoeinkommen, d. h. den gesamten
Einnahmen aller Mitglieder eines Haushaltes aus
Erwerbstätigkeit, Vermögen und eventuellen Transferzahlungen, indem davon sämtliche Steuern sowie
die Pflichtbeiträge zur Sozialversicherung abgezogen
werden.
Zusammenfassung: Nachfolgend wird die Einkommensverteilung in der Bundesrepublik Deutschland
über eine Pareto-Verteilung modelliert. Die ParetoVerteilung wird in Theorie und Empirie präsentiert.
Es zeigen sich einfache Darstellungen von zugehöriger Lorenz-Funktion und davon abhängigem GiniKoeffizienten. Die Modellanpassung erweist sich als
gut, die Einkommenskonzentration kann im Vergleich
zur Vermögenskonzentration noch als moderat beschrieben werden.
1
Rundungsbedingt ergeben die in Tabelle 1 aufgeführten Dezilanteile in der Summe nicht exakt 100 %.
Die 10 % Haushalte mit den niedrigsten Einkommen
erhalten nach Tabelle 1 nur einen Anteil von 3,7 %
an der Summe aller Haushaltsnettoeinkommen, die
10 % Haushalte mit den höchsten Einkommen verfügen dagegen über 23,1 % dieser Summe.
Einleitung
Das Einkommen, speziell das Haushaltsnettoeinkommen, ist in allen Ländern ungleich verteilt, wobei sich die Einkommenskonzentration durchaus von
Land zu Land unterscheidet (vgl. z. B. UNDP 2010,
S. 186 ff). Einen kondensierten Überblick hinsichtlich des jeweiligen Ausmaßes an Konzentration bzw.
Ungleichheit liefern, theoretisch wie empirisch, die
Lorenz-Funktion und der Gini-Koeffizient.
Die vorgenommene Anteilsberechnung beruht auf
Ergebnissen der 28. Befragung (Welle) des sozioökonomischen Panels (SOEPv28, Personen in Privathaushalten), durchgeführt vom Deutschen Institut für
Wirtschaftsforschung (DIW). Das sozioökonomische
Panel ist eine jährlich erfolgende repräsentative Wiederholungsbefragung von über 12000 Privathaushalten. Das weite Themenspektrum reicht dabei von der
Demographie über Einkommen und gegebenenfalls
auch Vermögen bis hin zur Bildung. Die hier betrachteten einzelnen Haushaltsnettoeinkommen sind dabei
gemäß OECD-Vorgaben äquivalenzgewichtet, d. h.
in jedem Haushalt bekommt der erste Erwachsene
das Gewicht 1, weitere Erwachsene sowie Kinder ab
14 Jahren das Gewicht 0,5, Kinder unter 14 Jahren
das Gewicht 0,3. So ergibt sich für einen 4-PersonenHaushalt bei zwei Erwachsenen und zwei Kindern,
beide unter 14 Jahren, die Gewichtssumme 2,1. Liegt
in diesem Haushalt nun das monatliche Nettoeinkommen bei z. B. 2100 €, wird dieser Haushalt so
bewertet, als ob alle Mitglieder über ein monatliches
Nettoeinkommen von jeweils 1000 € verfügten.
Die Modellierung von Einkommensverteilungen erfolgt traditionell durch eine Pareto-Verteilung oder
eine logarithmische Normalverteilung. Eine solche
Modellierung soll nachfolgend mit bundesdeutschen
Daten für das Jahr 2010 vorgenommen werden. Nach
der Vorstellung der betreffenden Einkommensdaten
wird, weil nur durch einen einzigen Parameter gekennzeichnet, die Pareto-Verteilung mit ihren speziellen Darstellungen für die Lorenz-Funktion und den
Gini-Koeffizienten in Theorie und Empirie präsentiert. Das Ergebnis zeigt neben einem im Vergleich
zur Vermögenskonzentration noch moderaten Ausmaß an Einkommenskonzentration eine gute Modellanpassung.
2
Daten
Die Bundeszentrale für politische Bildung (bpb)
veröffentlichte am 27.9.2013 die Angaben der sich
Dezil
1
2
3
4
5
6
7
8
9
10
Anteil
3,7
5,4
6,5
7,4
8,3
9,3
10,4
11,9
14,2
23,1
Tab. 1: Dezilanteile für das Haushaltsnettoeinkommen der Bundesrepublik Deutschland im Jahr 2010
www.bpb.de/nachschlagen/zahlen-und-fakten/soziale-situation-in-deutschland/61769/einkommensverteilung
10
Stochastik in der Schule 36 (2016) 1, S. 10–14
3
Pareto-Verteilung: Theorie
Die Pareto-Verteilung ist eine Wahrscheinlichkeitsverteilung für stetige Zufallsvariablen und wird traditionell zur Modellierung von Einkommensverteilungen genutzt. Für Y als Haushaltsnettoeinkommen und
y0 als kleinstes (positives) Haushaltsnettoeinkommen
ist die Verteilungsfunktion F der Pareto-Verteilung
durch
y
F(y) = 1 – __
y0
( )
–k
für k > 2 und y ≥ y0
(1)
definiert, die Dichtefunktion f als erste Ableitung von
F damit durch
y
k __
f(y) = __
y0 y0
( )
–k–1
für k > 2 und y ≥ y0
(2)
(Mood et al. 1974, S. 118). Gleichung (1) kennzeichnet Wahrscheinlichkeiten P(Y ≤ y) für Einkommen Y
von höchstens y. Da P(y – 1 ≤ Y ≤ y) mit steigendem
y sinkt, zeigen die Verteilungsfunktion F und die
Dichtefunktion f ein für Einkommensverteilungen typisches Bild. So treten empirisch höhere Einkommen
seltener als niedrige auf, was sich nach Gleichung (2)
in einem monoton fallenden Verlauf der Dichtefunktion f widerspiegelt.
Bei k > 2 als Vorgabe für den konstanten Parameter k
existieren der Erwartungswert E(Y) und die Varianz
V(Y), liegen diese doch bei
E(Y) =
∫
∞
y0
ky0
xf(x)dx = _____ und
k–1
ky20
V(Y) = _____ – E(Y)2
k–2
(3)
(Mood et al. 1974, S. 118). Der Erwartungswert aus
Gleichung (3) ist Bestandteil der nach Lorenz (1905)
benannten Funktion L, die eine Veranschaulichung
vorhandener Einkommenskonzentration ermöglicht.
Die Funktionswerte von L sind allgemein als – mit
dem minimalen Einkommen beginnend – kumulierte
Anteile von E(Y) (vgl. Gleichung (3)) definiert. D. h.
für die Stelle F(y), dass
1
L(F(y)) = ____
E(Y)
∫
y
y0
xf(x)dx für y ≥ y0
(4)
(Lambert 2001, S. 32).
Mit f(y) aus Gleichung (2) lässt sich L(F(y)) für eine
Pareto-Verteilung konkretisieren. Speziell ergibt sich
gemäß Gleichung (3) und Gleichung (4), aber analog auch für zur Pareto-Verteilung alternative Verteilungen, L(F(y0)) = 0 und L(F(∞)) = 1. Jede LorenzFunktion L ist damit selbst eine Verteilungsfunktion.
Bei F(y) = p, F–1 als Umkehrfunktion von F und somit F–1(p) = y kann Gleichung (4) aber nach Substitution auch als
1
L(p) = ____
E(Y)
∫
p
0
F–1(q)dq
(5)
geschrieben werden.
Wird nun nach Gleichung (1)
1
–__
F–1(p) = y0(1 – p) k für 0 ≤ p ≤ 1
(6)
bestimmt und Gleichung (6) in Gleichung (5) eingesetzt, ergibt eine einfache Integralrechnung für
L(0) = 0 und L(1) = 1 die von y0 unabhängige Lorenz-Funktionsgleichung der Pareto-Verteilung
L(p) = 1 – (1 – p)
1
1–__
k
für 0 ≤ p ≤ 1.
(7)
Gleichung (7) zeigt die Lorenz-Funktion der Pareto-Verteilung als einfach strukturierte Verteilungsfunktion. Gleichung (7) zeigt auch die allgemein für
Lorenz-Funktionen gültige Ungleichung L(p) ≤ p.
D. h. eine Lorenz-Funktion kann mit ihren Funktionswerten die Werte auf einer Winkelhalbierenden
nicht überschreiten. L(p) = p für alle p findet sich im
für Einkommensverteilungen unrealistischen Fall einer Ein-Punkt-Verteilung der Variable Y. Die Ungleichung L(p) < p ergibt sich für 0 < p < 1, wenn die Variable Y wie im Falle realer Einkommensverteilungen
unterschiedliche Werte annehmen kann. Ungleichheit
stellt damit eine Voraussetzung für vorhandene Konzentration dar.
Die Funktion L aus Gleichung (7) weist zudem bei
L' bzw. L" als erster bzw. zweiter Ableitung wegen
L'(p) ≥ 0 sowie L"(p) ≥ 0 den für alle Lorenz-Funktionen vorhandenen konvexen Verlauf auf. Für die
Pareto-Verteilung gilt speziell
1 (1 – L(p))
1 – __
k
______________
für p < 1.
(8)
L'(p) =
1–p
(
)
Aus Gleichung (8) ergibt sich folgende Interpretation
des Parameters k der Pareto-Verteilung: Bei F(y) = p
ist 1 – L(p) der Anteil von E(Y), der auf den Anteil
1 – p von Einkommen größer als y entfällt. Das für
diesen Anteil zu erwartende Einkommen liegt also
(1 – L(p))
für alle p < 1 bei ________
1 – p . Nach Gleichung (8) beträgt die Steigung der Lorenz-Funktion an der Stelle
1 -fache dieses zu erwartenden
p nun gerade das 1 – __
k
Einkommens (vgl. eine ausführliche Diskussion der
(Differenzial)gleichung (8) bei Kämpke et al. 2003).
(
)
11
Mit Hilfe der Lorenz-Funktion kann nun das Ausmaß
relativer Konzentration bzw. Ungleichheit für die
Verteilung von Y, also hier speziell des Haushaltsnettoeinkommens, auch quantitativ bestimmt werden.
Der für die Konzentrations- bzw. Ungleichheitsmessung üblicherweise genutzte Gini-Koeffizient G ist
allgemein als
G=2
∫
1
0
(p – L(p))dp = 1 – 2
∫
1
0
L(p)dp
(9)
definiert (Lambert 2001, S. 33). G erfasst als geometrisches Konzentrationsmaß in einem (p, L)-Koordinatensystem das Zweifache des Flächeninhalts
zwischen L(p) = p, d. h. dem Verlauf der LorenzFunktion im Fall ohne Konzentration, und der in der
Regel vorhandene Konzentration ausweisenden Lorenz-Funktion L (vgl. Gleichung (5)).
Einsetzen von Gleichung (7) in Gleichung (9) und
wiederum einfache Integralrechnung liefern für die
Pareto-Verteilung
1 .
G = ______
2k – 1
(10)
Nach Gleichung (10) hängt die Einkommenskonzentration gemäß Pareto ausschließlich vom Verteilungsparameter k ab.
4
Pareto-Verteilung: Empirie
Ein Vergleich von Kapitel 2 mit Kapitel 3 zeigt, dass
in Tabelle 1 die für eine empirische Bestimmung des
Parameters k einer Pareto-Verteilung erforderlichen
Daten vorliegen. Insbesondere sind die dort angegebenen Dezilanteile, in kumulierter Form, als kumulierte Anteile an der Summe aller Haushaltsnettoeinkommen auch kumulierte Anteile am arithmetischen
Mittel der betrachteten Haushaltsnettoeinkommen.
Sie bilden damit das empirische Gegenstück zu den
Funktionswerten einer Lorenz-Funktion.
Konkret bietet Tabelle 1 mit (pi , Li), i = 1, …, l = 10
und pi = 0,1i sowie Li als kumulierten Dezilanteilen,
also speziell L1 = 0,037, L2 = 0,037 + 0,054 = 0,091
usw. und rundungsbedingt L10 = 1,002 die Grundlage für einen Datensatz zur regressionsanalytischen
Berechnung des Verteilungsparameters k. Ergänzt
um den Punkt (p0 = 0, L0 = 0), ist dieser Datensatz in
der Abbildung 1 dargestellt. Diese zeigt mit den Variablenbezeichnungen p und l einen für vorhandene
Konzentration bzw. Ungleichheit charakteristischen
konvexen Verlauf. Werden die einzelnen Punkte aus
Abbildung 1 linear verbunden, ergibt sich der stückweise lineare Verlauf einer empirischen LorenzFunktion. Dieser findet sich als unterer Funktionsverlauf in Abbildung 3 unten.
12
Abb. 1: Kumulierte Dezilanteile (Daten)
Im Rahmen einer Regressionsanalyse ist nun speziell
die im Parameter k nichtlineare Lorenz-Funktion L
aus Gleichung (7) mit dem beschriebenen Datensatz
zu konfrontieren. Eine nichtlineare Regression wird
dafür aber nicht benötigt. Gleichung (7) kann linearisiert werden und zeigt sich in linearisierter Form als
(
)
1 ln(1 – p).
ln(1 – L(p)) = 1 – __
k
(11)
Gleichung (11) weist ln(1 – p) als unabhängige und
ln(1 – L(p)) als abhängige Variable aus. Dem entsprechen auf der Datenebene die Wertepaare (ln(1 – pi),
ln(1 – Li)), i = 1, …, n = 9. Der Fall l = 10, also
(p10 = 1, L10 = 1,002), muss offensichtlich ausgeschlossen werden. Ergänzt um den weiteren Punkt
(ln(1 – p0), ln(1 – L0)) sind diese Wertepaare in Abbildung 2 grafisch dargestellt.
Abb. 2: Transformierte kumulierte Dezilanteile (Daten)
In Abbildung 2 stehen die Bezeichnungen ltr und ptr
für die transformierten Variablen ln(1 – L(p)) bzw.
ln(1 – p). Im Gegensatz zu Abbildung 1 bietet Abbil-
dung 2 aber nun ein Punkt-Streudiagramm, zu dessen
modellbezogener Anpassung ein linearer Ansatz für
weite Bereiche (bis auf Punkte in der Nähe des Nullpunkts) angemessen erscheint (vgl. die Anpassungsdiskussion unten).
So kann für Gleichung (11) eine homogene lineare
1 als einzigem RegresRegressionsanalyse mit 1 – __
k
sionskoeffizienten erfolgen. Um k zu bestimmen, ist
für die gegebenen Daten die Summe von Quadraten
1 ln(1 – p ) i = 1, …,
der Residuen ln(1 – Li) – 1 – __
i
k
1
__
n = 9 bezüglich 1 – zu minimieren.
k
Wird eine solche Minimierung, z. B. mit einem Standard-Softwarepaket wie Excel oder SPSS durchgeführt, ergibt sich für die beschriebenen Daten
1 = 0,613 und damit k = 2,584.
1 – __
k
Einsetzen des ermittelten k-Wertes in Gleichung
(10) führt auf G = 0,240 ≤ 0,3 und damit ein im
Vergleich zu anderen Nationen und zur Vermögenskonzentration noch moderates Ausmaß an Einkommenskonzentration (vgl. unten). Die Korrelation
zwischen gegebenen und mit dem berechneten Wert
von k gemäß Gleichung (11) modellierten Werten
der Variable ln(1 – L(p)), also zwischen ln(1 – Li)
und 0,613 ln(1 – pi) für i = 1, …, n = 9, liegt zudem
bei 0,999 und deutet auf eine hervorragende Modellanpassung hin. Entsprechend sollten auch die über
Gleichung (7) modellierten kumulierten Dezilanteile
nahe bei denjenigen aus dem Datensatz liegen. Die
folgende Abbildung 3 zeigt – jeweils mit linearer
Verbindung und ergänzt um Randwerte – den Vergleich dieser Anteile.
(
)
Abb. 3: Kumulierte Dezilanteile (Daten und Modellierung)
Wie Abbildung 3 aber verdeutlicht, liegen die modellierten kumulierten Dezilanteile (vgl. die Bezeich-
nung (p, lm) mit dem Buchstaben m zur Modellkennzeichnung) in weiten Bereichen oberhalb der sich aus
den Daten ergebenden (vgl. (p, l)). Der Eindruck einer ausgezeichneten Modellanpassung wird dadurch
relativiert. Er wird entsprechend auch durch einen
Vergleich des nach Gleichung (10) berechneten Wertes von G mit dem Wert G = 0,271 getrübt, der sich
mit den beschriebenen Daten für das empirische Gegenstück zu Gleichung (9), d. h. für
G=1–
∑
l
1
(Li + Li–1) (pi – pi–1)
(12)
ergibt (vgl. Lambert 2001, S. 27). In Gleichung (12)
ist für i – 1 = 0 (p0 = 0, L0 = 0) zu setzen, im Beispiel
daneben rundungsbedingt L10 = 1,002. Wie Gleichung (12) zeigt, ergibt sich der empirische GiniKoeffizient, indem von Eins das Zweifache des Flächeninhalts zwischen der empirischen Lorenz-Kurve
und der p-Achse subtrahiert wird (vgl. die empirische
Lorenz-Funktion in Abbildung 3).
G = 0,271 liegt nahe bei dem in UNDP (2010, S. 186)
mit von Tabelle 1 abweichenden Daten für 2010 und
Deutschland ausgewiesenen Wert von G = 0,283; vergleiche dagegen ebendort für 2010 und Großbritannien
G = 0,360 sowie für die USA im selben Jahr G = 0,408.
Wie Spannagel & Seils (2014, S. 622) dokumentieren,
hat sich das Ausmaß der Konzentration der Haushaltsnettoeinkommen in Deutschland im Zeitablauf verändert. Es ist von 1991, damals lag der Gini-Koeffizient
bei G = 0,25, bis 2004 mehr oder weniger kontinuierlich auf das Niveau von G = 0,29 angestiegen, danach
auf das hier dokumentierte Niveau gesunken. Der in
diesem Beitrag untersuchten Einkommenskonzentration steht mit G = 0,78 für das Jahr 2012 in Deutschland aber ein entschieden größeres Ausmaß an Vermögenskonzentration bei den Nettovermögen gegenüber
(vgl. Grabka & Westermeier 2014). Deutschland weist
damit im internationalen Vergleich ein ausgesprochen
hohes Maß an Vermögensungleichheit auf.
Die Abweichung zwischen den beiden hier für die
Einkommenskonzentration in Deutschland gefundenen Werten des Gini-Koeffizienten erklärt sich
nach einer Residuenanalyse wie folgt: Bei homogenen Regressionen muss die Residuensumme nicht
notwendig Null betragen. So findet sich für die Residuen ln(1 – Li) – 0,613 ln(1 – pi), i = 1, …, n = 9,
der abhängigen Variable ln(1 – L(p)) aus Gleichung
(11): Ihre Mehrheit und auch die Summe ist positiv. Für die Residuen der abhängigen Variable L(p)
aus Gleichung (7) gilt stattdessen: Wie bereits Abbildung 3 zeigt, sind die dort ersichtlichen Residuen Li – (1 – (1 – pi)0,613), i = 1, …, n = 9 mehrheitlich
und auch in der Summe negativ. Letzteres bedeutet,
13
dass die modellierten Li-Werte die nach Tabelle 1
ermittelten tatsächlichen Li-Werte in der Regel, im
Beispiel für die ersten sieben Dezile, überschreiten.
Damit fällt das über den Gini-Koeffizienten erfasste
Ausmaß an Konzentration im gemäß Pareto modellierten Fall niedriger aus als im tatsächlichen. Ein genaueres Bild über die Residuenstruktur der Variable
L(p) liefert die folgende Abbildung 4.
Lorenz-Kurven angeht, gibt Chotikapanich (2008).
Darunter findet sich dann auch der Ansatz von Singh
& Maddala (1976), der eine dreiparametrige Erweiterung des Pareto-Ansatzes darstellend, gegenüber
diesem insbesondere für die ersten Dezile bessere
Anpassungen liefern kann.
Literatur
Chotikapanich, D. (Ed.) (2008): Modeling Income Distributions and Lorenz Curves. New York: Springer.
Grabka, M. M.; Westermeier, Ch. (2014): Anhaltend hohe
Vermögensungleichheit in Deutschland. DIW-Wochenbericht Nr. 9.2014.
Kämpke, T.; Pestel, R.; Radermacher, F. J. (2003): A Computational Concept for Normative Equity. In: European
Journal of Law and Economics Vol. 15, S. 129–163.
Lambert, P. J. (2001): The Distribution and Redistribution
of Income. Manchester: Manchester University Press.
Mood, A. et. al. (1974): Introduction to the Theory of Statistics. Tokyo: McGraw-Hill.
Singh, S. K.; G. S. Maddala (1976): A Function für the
Size Distribution of Incomes. In: Econometrica Vol. 44,
S. 963–970.
Abb. 4: Residuen bezüglich L(p)
In Abbildung 4 steht die Bezeichnung resl für die
Residuenvariable bezüglich L(p). Wie Abbildung 4
zeigt, weisen die dargestellten Residuen keine zufallsbehaftete, sondern eine deutlich nichtlineare Struktur
auf. Derartige Strukturen gelten in der Regressionsanalyse als Indiz für eine Fehlspezifikation.
Soll also auch für den Gini-Koeffizienten eine bessere Modellanpassung erfolgen, sind Alternativen zur
hier vorgestellten Pareto-Einkommensverteilung zu
betrachten.
Einen Überblick bezüglich entsprechender Ansätze,
speziell was mehrparametrige Modellierungen von
14
Spannagel, D.; Seils, E. (2014): Armut in Deutschland
wächst – Reichtum auch. WSI-Verteilungsbericht 2014.
In: WSI-Mitteilungen, S. 620–627.
UNDP (2010): Bericht über die menschliche Entwicklung
2010. Berlin: Deutsche Gesellschaft für die Vereinten
Nationen.
Anschrift des Verfassers
Gerhard Kockläuner
FB Wirtschaft
FH Kiel
Sokratesplatz 2
24149 Kiel
[email protected]
Der Satz von Bayes: Eine geschichtsträchtige Idee mit vielfältigen
Anwendungsmöglichkeiten
KATRIN WÖLFEL, ERLANGEN-NÜRNBERG
Zusammenfassung: Der Satz von Bayes ist eines der
bekanntesten Theoreme der Wahrscheinlichkeitstheorie. Wird er rein formal hergeleitet, gerät die ursprüngliche Problemstellung der Wahrscheinlichkeit
von Ursachen jedoch in den Hintergrund. Bei der Anwendung des Satzes zur Lösung vielfältiger Probleme
ist dieser Grundgedanke aber von großer Bedeutung.
Im Folgenden soll deshalb die intuitive Idee hinter
dem Theorem aus historischer Perspektive erörtert
und aufgezeigt werden, wie Fragen verschiedenster
Disziplinen dadurch „bayesianisch“ gelöst werden
können.
1
tung endlich vieler Ereignisse noch verallgemeinert
werden kann):
pr(A|B)pr(B)
pr(B|A) = ___________
pr(A)
Bei dieser formalen Herleitung des Satzes gerät dessen ursprüngliche Problemstellung, die auch heute
noch für vielerlei Anwendungen des Satzes von Bedeutung ist, ebenso wie der damalige stufenweise
Beweis dieses Theorems in den Hintergrund. Stone
(2013, S. 31) findet für diese Problematik folgende
treffende Worte:
„even though Bayes’ rule follows in a few lines of algebra from the rules of probability, no amount of staring
at the rules themselves will make Bayes’ rule obvious.
Perhaps if it were more obvious, Bayes and others
would not have had such trouble in discovering it, and
we would not expend so much effort in understanding
its subtleties.“
Einleitung
Jeder, der sich heute ein wenig mit Wahrscheinlichkeitstheorie beschäftigt, stößt schnell auf den sog.
Satz von Bayes, der häufig auch als „Formel“ oder
„Regel“ von Bayes bezeichnet wird und in diesem
Sinn im Hochschulbereich auch meist rein formal
notiert und hergeleitet wird (vgl. z. B. Koop 2003,
S. 1): Unter der Annahme, dass ein Ereignis A zuerst
eintritt, würde man die Wahrscheinlichkeit des Eintretens dieses Ereignisses A und eines weiteren Ereignisses B (pr(A 艚 B)) als Produkt der Wahrscheinlichkeit, dass A eintritt (pr(A)), und der Wahrscheinlichkeit, dass B eintritt unter der Bedingung, dass A
bereits eingetreten ist (pr(B|A)), mit Hilfe der ersten
Pfadregel berechnen, d. h.
pr(A 艚 B) = pr(A)pr(B|A).
(1)
Nimmt man hingegen an, dass B vor A eintritt, würde
sich pr(A 艚 B) berechnen lassen als
pr(A 艚 B) = pr(B)pr(A|B).
(2)
Da die linken Seiten der Gleichungen (1) und (2)
übereinstimmen, muss dies auch für die rechten Seiten gelten (da die zeitliche Präzedenz der Ereignisse
A und B für die Berechnung von pr(A 艚 B) irrelevant
ist):
pr(B|A)pr(A) = pr(A|B)pr(B)
(3)
Löst man (3) nach pr(B|A) auf, ergibt sich die als
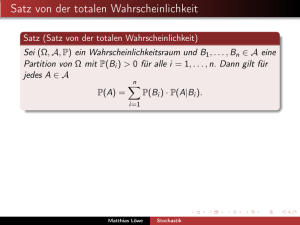
Satz von Bayes bekannte Formel (die zur BetrachStochastik in der Schule 36 (2016) 1, S. 15–21
(4)
Neben der Tatsache, dass die Geschichte der Herkunft des Satzes von Bayes für sich selbst interessant ist, da es nicht sein Namensgeber Thomas Bayes
(1701–1761) selbst war, der die Bedeutung des Satzes erkannte und ihn deshalb bekannt machte (sondern dessen Freund Richard Price und später unabhängig davon Pierre Simon Laplace), offenbart diese
Geschichte die intuitive Idee hinter dem berühmten
Satz, die bei jeder modernen Anwendung des Satzes
bewusst sein sollte.
2
Grundidee des bayesianischen
Ansatzes
Im Zentrum der bayesianischen Idee steht die Frage nach der Wahrscheinlichkeit von Ursachen (engl.
probability of causes) bzw. die der „umgekehrten
Wahrscheinlichkeit“ (engl. inverse probability):
Wenn die Folge einer unbekannten Ursache bekannt
ist, was kann dann über die Wahrscheinlichkeit verschiedener möglicher Ursachen ausgesagt werden?
Gesucht wird also die Wahrscheinlichkeit einer von
n möglichen Ursachen Ci (i 僆 {1, …, n}) bei Kenntnis der Folge E: pr(Ci|E). Diese Situation der Unsicherheit besteht bei vielen Fragestellungen verschiedenster Disziplinen: Man beobachtet ein bestimmtes
Ereignis und möchte auf dessen Ursachen schließen
können. Die bayesianische Methode zur Lösung dieses Problems besteht darin, dass man zunächst eine
15
subjektive (möglicherweise sogar willkürliche) Vermutung über die Ursache abgibt („guess“, vgl. Bayes
und Price 1763, S. 392) und diese anschließend mit
Hilfe immer neuer (objektiver) Informationen aktualisiert, wodurch man eine korrigierte Vermutung
bekommt, die stets durch neue Informationen weiter
verbessert werden kann. Die Verbindung dieser intuitiven Herangehensweise mit dem dahinter stehenden
mathematischen Konzept wird deutlich, wenn man
die Entwicklung des Theorems genauer betrachtet.
3
Ursprung des Theorems bei Thomas
Bayes (1701–1791)
Heutiger Namensgeber des Satzes ist der Engländer Thomas Bayes (1701–1761), in dessen Werk der
Satz seinen Ursprung zu haben scheint. Bayes war
Amateur-Mathematiker. Auf Grund seiner Zugehörigkeit zur presbyterianischen Kirche hatte er keinen
Zugang zu englischen Universitäten, weshalb er in
Schottland (Edinburgh) Theologie und Mathematik
studierte, bevor er ca. 1722 durch seinen ebenfalls
geistlichen Vater zum Pastor ernannt wurde und als
solcher von da an in London und später in Tunbridge
Wells wirkte. Die einzige mathematische Veröffentlichung, die Bayes zu seiner Lebenszeit tätigte,
war anonym und stammt aus dem Jahre 1736 („An
Introduction to the Doctrine of Fluxions, and a Defence of the Mathematicians Against the Objections
of the Author of the Analyst“1). Darin verteidigte er
Newtons Ideen zur Infinitesimalrechnung und widersetzte sich damit George Berkeley (der der Autor des
„Analyst“ war). Zu Beginn der 1740er Jahre erlangte
Bayes zunehmend Respekt für seine mathematischen
Arbeiten und wurde deshalb 1742 in die „Royal Society“ in London aufgenommen, die zu dieser Zeit
eine Vereinigung von Amateur-Mathematikern war
und die Bayes die Möglichkeit bot, seine Ideen mit
anderen zu diskutieren und sich mathematisch weiter
zu entwickeln.2
Auf die Frage nach der Wahrscheinlichkeit von Ursachen wurde Bayes durch ein bekanntes Werk von
Abraham de Moivre aufmerksam, der „Doctrine of
Chances“, von der drei Auflagen in der Zeit zwischen
1718 und 1756 erschienen. Dort findet sich die Idee,
dass man die Ordnung des Universums möglicherweise durch Betrachtung verschiedener Naturphänomene erschließen könne (Moivre 1756, S. 252).
So versuchte Bayes diesem Problem in den 1740er
Jahren mit einem Gedankenexperiment näher zu
kommen: Eine Kugel wird auf einen quadratischen
Tisch geworfen. Nun stellt sich die Aufgabe, zu erschließen – ohne den Kugelwurf gesehen zu haben –,
16
an welcher Stelle des Tisches die Kugel gelandet ist.
Dazu wird eine weitere Kugel auf den Tisch geworfen, deren Position in Bezug zur ersten Kugel man
beobachten kann (d. h. man weiß, ob die zweite Kugel rechts oder links bzw. über oder unter der ersten
Kugel gelandet ist). Unter der Annahme, dass eine
Kugel mit gleicher Wahrscheinlichkeit an jeder Stelle
des Tisches auftreffen kann, kann man aus der Lage
der zweiten Kugel die der ersten Kugel etwas präzisieren: Liegt die zweite Kugel links (rechts) von der
ersten Kugel, ist es wahrscheinlicher, dass die erste
Kugel in der rechten (linken) Tischhälfte liegt. Das
Werfen weiterer Kugeln ermöglicht es, die Position
der ersten Kugel stets weiter auf diese Weise einzugrenzen. Somit kann man also mit Hilfe immer neuer
Beobachtungen (Positionen der geworfenen Kugeln)
nähere Aussagen über die Vergangenheit (die Position der ersten Kugel) treffen und diesen Aussagen
sogar Wahrscheinlichkeiten zuordnen. (Bayes und
Price 1763, S. 385–388; McGrayne 2011, S. 7 f.)
Dies sei an einem fiktivem Beispiel erläutert, das
zwar nicht schultauglich ist, aber die originäre bayesianische Idee verdeutlichen soll: Man nehme an,
Bayes’ Gedankenexperiment führt nach fünf Kugelwürfen (im Anschluss an den Wurf der ursprünglichen Kugel) zu folgendem Ergebnis:
• Erster Wurf: Kugel liegt rechts und oberhalb der
ursprünglichen Kugel.
• Zweiter Wurf: Kugel liegt links und oberhalb
der ursprünglichen Kugel.
• Dritter Wurf: Kugel liegt links und unterhalb der
ursprünglichen Kugel.
• Vierter Wurf: Kugel liegt links und oberhalb der
ursprünglichen Kugel.
• Fünfter Wurf: Kugel liegt links und unterhalb
der ursprünglichen Kugel.
Die Lage der ursprünglichen Kugel ist unbekannt.
Doch bieten die fünf anschließenden Kugelwürfe
Informationen über die relative Lage der ursprünglichen Kugel. Was kann man also daraus für die Position der ursprünglichen Kugel schließen, wenn man
bayesianisch argumentiert? Dazu sei angenommen,
dass die ursprüngliche Kugel a-priori genau in der
Mitte des Tisches liegt, dass eine Kugel mit gleicher
Wahrscheinlichkeit an jeder Stelle des quadratischen
Tisches aufkommen kann und die Kugeln jeweils
tatsächlich an einem festen Platz landen, nach dem
Wurf also nicht mehr weiterrollen.
Die a-priori-Annahme, dass die ursprüngliche Kugel
genau in der Mitte des Tisches gelandet ist, kann mit
Hilfe der Informationen aus den anschließenden fünf
Kugelwürfen aktualisiert werden: Da die anschließend geworfene Kugel bei vier der fünf Würfe links
der ursprünglichen Kugel aufgekommen ist, ist es
wahrscheinlicher, dass die ursprüngliche Kugel in
der rechten Hälfte des Tisches positioniert ist.
Stellt man sich ein Raster vor, das den Tisch von
links nach rechts in sechs gleich große Abschnitte
einteilt, würde man deshalb vermuten, dass die Kugel im zweiten Abschnitt von rechts liegt. Außerdem lässt die Beobachtung, dass die Kugel dreimal
oberhalb und zweimal unterhalb der ursprünglichen
Kugel gelandet ist, darauf schließen, dass diese eher
in der unteren Tischhälfte liegt. Betrachtet man wiederum eine Rastereinteilung des Tisches (in sechs
horizontale Streifen), würde man die ursprüngliche
Kugel deshalb im dritten Abschnitt von unten einordnen. Abb. 1 veranschaulicht die Aktualisierung der
a-priori-Vermutung durch neue Informationen bei
jedem weiteren Kugelwurf. Übersetzt man Bayes’
Ideen in die heutige übliche Formulierung, so entspricht die Wahrscheinlichkeit der ursprünglichen
bzw. ersten Vermutung über eine Ursache der sog.
a-priori-Wahrscheinlichkeit (engl. prior) prprior(Ci).
Die Wahrscheinlichkeit pr(E|Ci) ermöglicht die Aktualisierung der ursprünglichen Hypothese, da sie die
Wahrscheinlichkeit einer tatsächlichen Folge E unter
der Annahme, ihr läge eine bestimmte Ursache Ci zu
Grunde, beschreibt. Im Englischen wird hierfür der
Begriff Likelihood verwendet. Die Wahrscheinlichkeit der damit überarbeiteten Vermutung pr(Ci|E)
wird heute mit a-posteriori-Wahrscheinlichkeit (engl.
posterior) bezeichnet. Daraus lässt sich die Formel
prprior(Ci) · pr(E|Ci) ~ pr(Ci|E)
(5)
folgern (~ wird dabei als „proportional zu“ gelesen;
in der englischsprachigen Literatur wird meist ⬀ hierfür verwendet). Hierbei muss betont werden, dass in
Bayes’ Arbeit niemals eine Formel wie (5) erscheint.
Stattdessen verwendete er eine geometrische Betrachtung in der damals üblichen Schreibweise nach
Newton und formulierte obige Formel nie explizit.3
Bayes war sich wohl auch der Bedeutung dieser heute berühmten Aussage nie bewusst, denn er veröffentlichte seinen Aufsatz hierzu nicht, noch erwähnte er
darin irgendeine Anwendungsmöglichkeit des Satzes.
Dass der Ursprung des Theorems heute bekannt ist,
ist Richard Price (1723–1791) zu verdanken, der als
Freund Bayes’ nach dessen Tod dessen Aufzeichnungen fand, deren Potential erkannte und sie, ergänzt
durch eigene Anmerkungen, über die Royal Society
veröffentlichte. In „An Essay Towards Solving a
Problem in the Doctrine of Chances“ verlieh Price
Bayes’ Idee zudem eine religiöse Rechtfertigung,
nämlich „to confirm the argument taken from final
causes for the existence of the Deity“ (Bayes und
Price 1763, S. 374).
4
Obwohl er heute kaum explizit mit dem Satz von
Bayes in Verbindung gebracht wird, war es der
französische Mathematiker Pierre Simon Laplace
(1749–1827), der dem Theorem zu seinem eigentlichen Durchbruch verhalf.4 Laplace, der heute als
einer der berühmtesten Wahrscheinlichkeitstheoretiker gilt, war schon in jungen Jahren professioneller
Mathematiker und wurde so bereits 1773 im Alter
von 24 Jahren in die Académie des Sciences in Paris
aufgenommen (Hahn 2005, S. 41). Als er 1774 sei-
Der Verdienst von Pierre Simon
Laplace (1749–1827)
Abb. 1: Veranschaulichung von Bayes’ Gedankenexperiment: Vermutete Lage der unbekannten (zuerst geworfenen) Kugel nach je einem weiteren Kugelwurf (am Ende nach fünf weiteren Würfen)
17
ne „Mémoire sur la Probabilité des Causes par les
Événements“ veröffentlichte, wusste er höchstwahrscheinlich nichts von der Arbeit des Engländers Thomas Bayes’ (Gillispie et al. 1997, S. 16). Er schrieb
darin das Prinzip nieder, das als „erster Versuch“ der
heutigen Regel von Bayes angesehen werden kann:
„Si un événement peut être produit par un nombre n
de causes différentes, les probabilités de l’existence de
ces causes prises de l’événement sont entre elles comme les probabilités de l’événement prises de ces causes, et la probabilité de l’existence de chacune d’elles
est égale à la probabilité de l’événement prise de cette
cause, divisée par la somme de toutes les probabilités
de l’événement prises de chacune de ces causes“ (Laplace 1774, S. 29).
Dies kann (sinngemäß) wie folgt übersetzt werden:
„Wenn ein Ereignis n verschiedene Ursachen haben
kann, verhalten sich die Wahrscheinlichkeiten der Ursachen unter der Voraussetzung des Ereignisses untereinander wie die Wahrscheinlichkeiten des Ereignisses
unter Voraussetzung dieser Ursachen, und die Wahrscheinlichkeit jeder von ihnen ist gleich der Wahrscheinlichkeit des Ereignisses unter Voraussetzung der
Ursache geteilt durch die Summe aller Wahrscheinlichkeiten des Ereignisses unter Voraussetzung jeder dieser
Ursachen“
(Suite)“ (Laplace 1783–1786, S. 300 f.). Zu dieser
Zeit hatte Laplace wohl auch bereits Bayes’ Arbeit
kennengelernt, da Bayes in einem Vorwort zur „Mémoire sur les Probabilités“ von Condorcet erwähnt
wird (Gillispie et al. 1997, S. 16, 78), und Laplace in
sein Werk offensichtlich die ursprünglichen bayesianischen Ideen integrierte (Gillispie et al. 1997, S. 72).
Möglicherweise war der Aufenthalt von Richard Price in Paris im Jahre 1781 die Ursache der Verbreitung
von Bayes’ Arbeit unter den französischen Wissenschaftlern (McGrayne 2011, S. 23). Laplace’ Beweis
des Bayes-Theorems unter Annahme gleicher Wahrscheinlichkeiten für alle möglichen Ursachen, ist wie
folgt strukturiert: Ausgehend davon, dass sich die aposteriori-Wahrscheinlichkeit pr(Ci|E) gemäß der bereits bewiesenen (grundlegenden) Überlegungen der
Wahrscheinlichkeitstheorie berechnen lässt als
pr(Ci 艚 E)
(7)
pr(Ci|E) = _________ ,
pr(E)
können Zähler und Nenner des Bruches auf der rechten Seite von Gleichung (7) spezifiziert werden. Dazu
nimmt Laplace – wie bereits erwähnt – an, dass die apriori-Wahrscheinlichkeit jeder der möglichen n Ursachen 1/n ist (Laplace 1783–1786, S. 301). Deshalb
kann pr(Ci 艚 E) durch
In heutiger mathematischer Formulierung ergibt das
genau folgende Aussage:
1 pr(E|C )
pr(Ci 艚 E) = __
n
i
pr(E|Ci)
pr(Ci|E) = ____________
n
pr(E|Cr)
r=1
und pr(E) durch
∑
(6)
Im Unterschied zur heute bekannten (allgemeineren)
Formulierung unterstellte Laplace hier (implizit) die
Annahme, dass jede der n Ursachen gleich wahrscheinlich ist (andernfalls ist (6) keine wahre Aussage). Außerdem findet sich an dieser Stelle noch kein
Beweis dieser Aussage. Bemerkenswert ist weiterhin,
dass es Laplace war, der hier als erster den Begriff der
Wahrscheinlichkeit von Ursachen (franz. probabilité
des causes) verwendete – im Aufsatz von Bayes findet man diesen Begriff nicht. In Bayes’ Arbeit wird
die Idee der Wahrscheinlichkeit von Ursachen auch
hauptsächlich durch den von Price ergänzten Anhang
deutlich (Bayes und Price 1763, S. 405 f.; Dale 1982,
S. 29), wo dieser kurze Anwendungsbeispiele des
Satzes ergänzt. Doch gerade dieser Begriff der Wahrscheinlichkeit von Ursachen war es, der in späteren
Zeiten in viel Zwiespalt mündete (vgl. Abschnitt 5).
Ein erster Beweisversuch von (6) befindet sich in der
„Mémoire sur les Probabilités“ (Laplace 1778–1781,
S. 415–417), der vollständige Beweis folgt in der
späteren „Mémoire sur les Approximations des Formules qui sont Fonctions de Très Grands Nombres
18
pr(E) =
∑
n
r=1
1
__
n pr(E|Cr)
(8)
(9)
ausgedrückt werden. Werden (8) und (9) in (7) eingesetzt, folgt unmittelbar (6). (Laplace 1783–1786,
S. 300 f.).
Nach der Französischen Revolution (1789/99), während der die (Natur-)Wissenschaften sehr große Anerkennung erlangten, publizierte Laplace 1812 sein bekanntes Werk „Théorie Analytique des Probabilités“,
das eine Zusammenfassung seiner Hauptbeiträge zur
Wahrscheinlichkeitstheorie darstellt. Auch der Satz
von Bayes in der Fassung von Laplace (1774) bzw.
Laplace (1783–1786) ist darin enthalten (Laplace
1812, S. 177), jedoch nicht der Beweis des Allgemeinfalls. Erst 1814 in seinem „Essai Philosophique
sur les Probabilités“ verallgemeinerte er ihn zu der
uns heute bekannten Form, bei der die Ursachen apriori nicht gleichwahrscheinlich sein müssen:
„si ces diverses causes considérées à priori, sont inégalement probables; il faut au lieu de la probabilité de
l’événement, résultante de chaque cause, employer le
produit de cette probabilité, par celle de la cause ellemême“ (Laplace 1814, S. 18)
Sein wiederum nur in Worten formuliertes sechstes
Prinzip lässt sich daher wie folgt übersetzen und darstellen:
„wenn diese verschiedenen a-priori betrachteten Ursachen nicht gleichwahrscheinlich sind, muss man
anstelle der Wahrscheinlichkeit des Ereignisses, die
sich bei jeder Ursache ergibt, das Produkt dieser Wahrscheinlichkeit mit der Wahrscheinlichkeit der Ursache
selbst verwenden“
pr(E|Ci)prprior(Ci)
pr(Ci|E) = ___________________
n
pr(E|Cr)prprior(Cr)
r=1
∑
(10)
Das ist das uns heute als „Satz von Bayes“ bekannte
Theorem (vgl. (4)). Im Zentrum steht die Berechnung
der a-posteriori Wahrscheinlichkeit pr(Ci|E), d. h. der
Wahrscheinlichkeit einer bestimmten Ursache Ci ,
nachdem eine tatsächlich eingetretene Folge E bekannt ist. Zu deren Berechnung benötigt man eine
erste Einschätzung der Wahrscheinlichkeit von Ci ,
die sog. a-priori-Wahrscheinlichkeit prprior(Ci), die
Wahrscheinlichkeit des Eintretens von Folge E, sollte Ci tatsächlich Ursache davon sein (pr(E|Ci)), und
die Gesamtwahrscheinlichkeit einer derartigen Folge E (pr(E)), die sich als Summe der Eintrittswahrscheinlichkeiten von E unter allen möglichen, jeweils verschiedenen Ursachen Cr (r = 1, …, n) ergibt
pr(E) =
∑
n
r=1
pr(E|Cr)prprior(Cr).
Laplace formulierte die Regel nicht nur in moderner
Form und erbrachte deren Beweis, er zeigte auch
zahlreiche Anwendungsbeispiele dafür auf, die über
die Naturwissenschaften hinaus v. a. in den Bereich
der Sozialwissenschaften (Demographie und Justizwesen) reichten. Durch Laplace wurde die eigentliche Bedeutung und Nützlichkeit des Satzes von
Bayes erschlossen. Dementsprechend wäre es wohl
auch verdient gewesen, Laplace als Namensgeber
des Satzes zu würdigen. Allerdings gab dieser öffentlich in seinem Aufsatz von 1814 zu, dass es Thomas
Bayes war, der die Grundidee dazu bereits vor ihm
hatte (Laplace 1814, S. 186). Doch selbst daran gibt
es Zweifel. So schreibt Stigler (1983) von einem
Buch mit dem Titel „Observations on Man“ von David Hartley aus dem Jahr 1749, in dem ein „erfinderischer Freund“ erwähnt wird, der die Lösung des
„inversen Problems“ gefunden habe. Stiglers Suche
dieses nicht beim Namen genannten Freundes ergibt,
dass neben Bayes auch Nicholas Saunderson dafür
in Frage kommen und damit auch der Urheber des
Satzes von Bayes sein könnte.
5
Das bayesianische Konzept
in der Kritik
In den Jahrhunderten nach Laplace wurde die bayesianische Idee zu einem Streitpunkt, an dem sich die
Geister vieler Wissenschaftler schieden.5 Das liegt
v. a. daran, dass bald zwei Ansätze unterschieden
wurden, die – obwohl von Laplace ursprünglich als
vereinbar und äquivalent beschrieben (McGrayne
2011, S. 36) – als streng gegensätzlich interpretiert
wurden: Dem bayesianischen Konzept steht das „frequentistische“ Konzept (engl. frequentist, abgeleitet
von „frequency“ (Häufigkeit)) gegenüber. Gemäß
dem frequentistischen Ansatz werden Wahrscheinlichkeiten grundsätzlich aus der Häufigkeit, mit der
ein bestimmtes Ereignis in einer großen Grundgesamtheit auftritt, abgeleitet. Eine Wahrscheinlichkeit pr(E|Ci) wird demnach bestimmt, indem eine
Stichprobe betrachtet wird und mithilfe der asymptotischen Theorie (in deren Mittelpunkt Theoreme
wie der zentrale Grenzwertsatz und das Gesetz der
großen Zahlen stehen) von der Häufigkeit des Auftretens des Ereignisses E unter der Bedingung Ci in
der Stichprobe die allgemeine Wahrscheinlichkeit
gefolgert wird. Im frequentistischen Ansatz werden
bedingte Wahrscheinlichkeiten stets auf diese Art
betrachtet, während der bayesianschen Sichtweise
der Wahrscheinlichkeiten von Ursachen pr(Ci|E) viel
Skepsis entgegen gebracht wird. Frequentisten stoßen sich v. a. an der subjektiven a-priori-Vermutung,
die Bayesianer verwenden und die der für gewöhnlich objektiven mathematischen Herangehensweise
zu widersprechen scheint. So kann man sich beispielsweise im oben beschriebenen fiktiven Beispiel
zu Bayes’ Gedankenexperiment fragen, warum man
ohne weitere Überlegung zunächst davon ausgeht,
dass die Kugel genau in der Mitte des Tisches gelandet ist. Wäre es nicht genauso gut möglich, anzunehmen, dass sie z. B. am rechten Tischrand liegt
und würde das die folgende bayesianische Argumentation nicht entscheidend beeinflussen? Bayesianer entgegnen dem, dass zum Einen a-priori-Wahrscheinlichkeiten häufig durch relative Häufigkeiten
(d. h. frequentistisch) gewählt werden können (vgl.
Schlussbeispiel). Zum Anderen bietet die Wahl einer
beliebigen a-priori-Wahrscheinlichkeit (für den Fall,
dass keinerlei begründete Vermutung möglich ist) einen Startpunkt zur Bestimmung der Wahrscheinlichkeit einer Ursache, was rein frequentistisch schlicht
unmöglich wäre. Zudem mindert eine genügend umfangreiche Aktualisierung der a-priori-Wahrscheinlichkeit – zur besseren Vorstellung sei wieder auf das
Kugelbeispiel verwiesen – mit frequentistischen Mit-
19
teln (zur Bestimmung von Wahrscheinlichkeiten der
Art pr(E|Ci)) die Gewichtung der anfänglichen Vermutung in der zu bestimmenden a-posteriori-Wahrscheinlichkeit. Hier wird der von Laplace postulierte
ergänzende Charakter der beiden so häufig als gegensätzlich beschriebenen Ansätze deutlich.
Die Ökonometrie (empirische Wirtschaftsforschung)
stellt ein typisches Beispiel für eine ganze Wissenschaftsdisziplin dar, in der die Trennung zwischen
klassischer (d. h. frequentistischer) und bayesianischer Ökonometrie sehr ausgeprägt ist. Während die
klassische Regressionsanalyse vielen geläufig ist, bedarf das bayesianische Konzept noch zunehmender
Akzeptanz. Qin (1996) gibt eine knappe Übersicht
über die Entwicklung der bayesianischen Ökonometrie, aus der hervorgeht, dass das Potenzial dieses
Konzeptes erst in den 1950ern entdeckt wurde (vgl.
z. B. Marschak 1954), in den 1960ern in erste Versuche umgesetzt wurde (vgl. z. B. Raiffa und Schlaifer
1961), bevor 1971 das erste Lehrbuch zur bayesianischen Ökonometrie von A. Zellner herausgegeben
wurde („An Introduction to Bayesian Inference in
Econometrics“). Die grundlegendste Anwendung des
Satzes von Bayes in der Ökonometrie besteht darin,
die Parameter eines Regressionsmodells zu schätzen,
doch kann die bayesianische Idee auch in komplexeren Zusammenhängen, wie z. B. der bayesianischen
Modell-Mittelung, eingesetzt werden (vgl. Wölfel
2014 für eine knappe Schilderung dieses Konzepts).
Auch hier können frequentistische und bayesianische
Ökonometrie stets als gegenseitige Ergänzung betrachtet werden (anstelle der üblichen gegenpoligen
Sichtweise).
6
Schlussbeispiel und Fazit
Um die Idee des Satzes von Bayes vor dem historischen Hintergrund schultauglich zu veranschaulichen, sei mit einer typischen Fragestellung abgeschlossen:
Von einem bestimmten Drogentest ist bekannt, dass er
im Durchschnitt bei 95 von 100 Personen, die tatsächlich Drogen konsumiert haben, ein richtiges (d. h. positives) Testergebnis liefert. Wendet man ihn hingegen
auf Personen an, die nicht unter Drogeneinfluss stehen,
zeigt er mit 99-prozentiger Wahrscheinlichkeit ein
richtiges (d. h. negatives) Testergebnis. In Deutschland
konsumiert jeder hundertste Jugendliche regelmäßig
Drogen. Wie hoch ist die Wahrscheinlichkeit, dass ein
Jugendlicher, der positiv auf Drogen getestet wurde,
tatsächlich unter Drogeneinfluss steht?
In diesem Szenario lassen sich zwei (sich gegenseitig ausschließende) Ursachen identifizieren: „der
20
Jugendliche hat Drogen genommen“ (C1) und „der
Jugendliche hat keine Drogen genommen“ (C2). Die
Folge E, die hier betrachtet wird, ist ein positives
Ergebnis des Drogentests. Um den Satz von Bayes
(Gleichung (10)) anzuwenden, müssen die a-prioriWahrscheinlichkeiten der Ursachen und die Likelihoods spezifiziert werden. Für die a-priori-Wahrscheinlichkeiten der Ursachen gilt prprior(C1) = 0,01
und prprior(C2) = 0,99; für die Likelihoods gilt
pr(E|C1) = 0,95 und pr(E|C2) = 1 – 0,99 = 0,01. Für
die gesuchte Wahrscheinlichkeit pr(C1|E) ergibt sich
deshalb gemäß (10):
pr(E|C1)prprior(C1)
pr(C1|E) = _______________________________
pr(E|C1)prprior(C1) + pr(E|C2)prprior(C2)
0,95 · 0,01
pr(C1|E) = ____________________
0,95 · 0,01 + 0,01 · 0,99 ≈ 0,4897
Das bedeutet, dass ein positiv auf Drogen getesteter
Jugendlicher nur mit einer Wahrscheinlichkeit von
ca. 49 Prozent tatsächlich unter Drogeneinfluss steht
– ein im ersten Moment wohl verblüffendes Ergebnis, wenn man von der zunächst hoch erscheinenden
Zuverlässigkeit des Drogentests (95 bzw. 99 Prozent)
ausgeht.
Das Bayes-Theorem, dessen Ursprung in der Arbeit von Thomas Bayes zu liegen scheint, dessen
moderne Form mit vielerlei Anwendungsbeispielen
jedoch auf Pierre Simon Laplace zurückgeht, löst
so eine Problemstellung, die in verschiedensten Bereichen und Disziplinen auftritt: Wie kann man von
Beobachtungen in der Realität auf deren Ursachen
schließen (wenn verschiedene Ursachen als möglich
erachtet werden)? Die Betrachtung der Wurzeln des
Theorems zeigt die intuitive Lösungsmethode dieses
„inversen Problems“: Ausgehend von einer anfänglichen a-priori-Vermutung wird diese anhand immer
neuer Beobachtungen des Eintretens bestimmter Ereignisse unter bestimmten Bedingungen aktualisiert
und so schließlich eine a-posteriori Wahrscheinlichkeit ermittelt. Diese ursprüngliche Idee bleibt bei der
rein formalen Anwendung der Formel verborgen, ermöglicht aber einen interessanten Zugang zur bayesianischen Perspektive, die eine wichtige Ergänzung
des frequentistischen Ansatzes darstellt.
Anmerkungen
1
Für genauere Erläuterungen zu dieser Veröffentlichung vgl. Dale 2003, S. 182–257.
2
Für eine genauere Analyse des Lebens von Thomas
Bayes vgl. Dale 2003, S. 37–100.
3
4
5
Bayes selbst formulierte diese Regel als „Proposition
10“ in seinem Aufsatz, vgl. Bayes und Price 1763,
S. 394; Dale 1982, S. 27. Wiederum sei für eine ausführliche Untersuchung des Aufsatzes von Bayes und
Price auf Dale 2003, S. 258–369, verwiesen.
Für eine ausführliche Dokumentation über das Leben
Laplace’, seiner Ansichten und seiner Rolle in der Gesellschaft vgl. Hahn 2005.
Für eine übersichtliche Diskussion hierzu vgl. McGrayne 2011, S. 34–58.
Literatur
Bayes, Thomas; Price, Richard (1763): An Essay Towards
Solving a Problem in the Doctrine of Chances. In: Philosophical Transaction of the Royal Society of London
(H.53), S. 370–518.
Dale, Andrew I. (1982): Bayes or Laplace? An Examination of the Origin and Early Applications of Bayes’ Theorem. In: Archive for History of Exact Sciences 27(1),
S. 23–47.
Dale, Andrew I. (2003): Most Honourable Remembrance – The Life and Work of Thomas Bayes. New York
(u. a.): Springer.
Gillispie, Charles Coulston; Fox, Robert; Grattan-Guinness, Ivor (1997): Pierre-Simon Laplace – 1749–1827
– A Life in Exact Science. Princeton, NJ: Princeton
University Press.
Hahn, Roger (2005): Pierre-Simon Laplace – 1749–1827
– A Determined Scientist. Cambridge, MA (u. a.): Harvard University Press.
Koop, Gary (2003): Bayesian Econometrics. Chichester:
Wiley.
Laplace, Pierre Simon (1774): Mémoire sur la Probabilité
des Causes par les Événements. In: Œuvres Complètes
de Laplace (1878–1912). Bd. 8. Paris: Gauthier-Villars
et Fils, S. 27–65.
Laplace, Pierre Simon (1778–1781): Mémoire sur
les Probabilités. In: Œuvres Complètes de Laplace
(1878–1912). Bd. 9. Paris: Gauthier-Villars et Fils,
S. 383–485.
Laplace, Pierre Simon (1783–1786): Mémoire sur les Approximations des Formules qui sont Fonctions de Très
Grands Nombres (Suite). In: Œuvres Complètes de La-
place (1878–1912). Bd. 10. Paris: Gauthier-Villars et
Fils, S. 296–338.
Laplace, Pierre Simon (1812): Théorie Analytique des
Probabilité. Paris: Courcier.
Laplace, Pierre Simon (1814): Essai Philosophique sur les
Probabilités. Paris: Courcier.
Marschak, Jacob (1954): Probability in the Social Sciences. Cowles Foundation Paper (H.82), S. 166–215.
McGrayne, Sharon Bertsch (2011): The Theory that Would
Not Die – How Bayes’ Rule Cracked the Enigma Code,
Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy. New Haven/
London: Yale University Press.
Moivre, Abraham de (1756): The Doctrine of Chances –
Or, a Method of Calculating the Probabilities of Events
in Play. 3. Aufl., London: A. Millar.
Qin, Duo (1996): Bayesian Econometrics: The First Twenty Years. In: Econometric Theory 12(3), S. 500–516.
Raiffa, Howard; Schlaifer, Robert (1961): Applied Statistical Decision Theory. Boston: Division of Research,
Graduate School of Business Administration, Harvard
University.
Stigler, Stephen M. (1983): Who Discovered Bayes’s
Theorem? In: The American Statistician 37(4),
S. 290–296.
Stone, James V. (2013): Bayes’ Rule: A Tutorial Introduction to Bayesian Analysis. S. l.: Sebtel Press.
Wölfel, Katrin (2014): Bayesianische Modell-Mittelung
– Eine Möglichkeit zur Modellierung von Modellunsicherheit. In: Wirtschaftswissenschaftliches Studium
43(3), S. 159–161.
Zellner, Arnold (1971): An Introduction to Bayesian Inference in Econometrics. Malabar, FL: Krieger.
Anschrift der Verfasserin
Katrin Wölfel
Institut für Wirtschaftswissenschaft
(Institute of Economics)
Friedrich-Alexander-Universität Erlangen-Nürnberg
Kochstr. 4 (17)
91054 Erlangen
[email protected]
21
Stochastische Simulationen mit TinkerPlots –
Von einfachen Zufallsexperimenten zum informellen Hypothesentesten
ROLF BIEHLER, DANIEL FRISCHEMEIER & SUSANNE PODWORNY, PADERBORN
Zusammenfassung: Die Software TinkerPlots ist
eine dynamische Datenanalyse- und Simulationssoftware, die im Mathematikunterricht für den Einsatz in
den Klassenstufen 3 bis 10 vorgesehen ist. Mit ihrer
einfach zu benutzenden Zufallsmaschine bietet sie
ein anschauliches Werkzeug zum Modellieren und Simulieren von stochastischen Zufallsexperimenten. In
diesem Artikel soll das Potential der Zufallsmaschine
exemplarisch anhand einiger Beispiele entlang der
einzelnen Klassenstufen gipfelnd in der Hinführung
zu Grundgedanken des Hypothesentestens (am Beispiel des „Hörtests“) am Ende der Jahrgangsstufe
10 vorgestellt werden.
1
Einleitung
Die Wahrscheinlichkeitsrechnung ist neben der Datenanalyse und der beurteilenden Statistik ein elementarer Teil des Stochastikunterrichts der Sekundarstufen I und II. Sie gewinnt im Laufe der Schuljahre
zunehmend an Umfang (Kaun 2006). Eine Erklärung
dafür kann sein, dass die Modellierung, das Konstruieren des Ergebnisraums sowie das Berechnen
günstiger bzw. möglicher Fälle eine hohe Herausforderung u. a. an die kombinatorischen Fähigkeiten der
Lernenden stellt. Mit Hilfe von computergestützten
Simulationen können für Schülerinnen und Schüler
interessante Aufgaben zugänglich gemacht werden,
die zu diesem Zeitpunkt (noch) nicht mit Mitteln
der Schulmathematik behandelt werden können.
Zusätzlich können verschiedene Inhalte von Stochastikunterricht (frequentistische Interpretation des
Wahrscheinlichkeitsbegriffs, Durchführen ein- und
mehrstufiger Zufallsexperimente, informelles Hypothesentesten) vertieft und somit stärker durchdrungen
werden (detaillierter nachzulesen in Biehler & Maxara 2007). Um den Hintergrund von Simulationen
verstehen und die Ergebnisse von Simulationen korrekt deuten zu können, sollte frühzeitig im Unterricht
das__empirische Gesetz der großen Zahlen sowie das
1/√ n -Gesetz (zumindest in Form von „Faustformeln“) thematisiert werden (ebenda). Im Falle eines
einfachen Bernoulli-Experiments mit der Erfolgswahrscheinlichkeit p = 0,5 (z. B. Werfen einer fairen
Münze) hat man beispielsweise die in Tab. 1 angegebenen Faustformeln für die zu erwartende relative Häufigkeit in Abhängigkeit von der Wiederholungsanzahl n mit einer Sicherheit von 95 %. Führt
man den Münzwurf beispielsweise 1000 Mal durch,
22
so liegt die relative Häufigkeit für Wappen mit einer Wahrscheinlichkeit von 95 % im Intervall [0,47;
0,53] (95 %-Prognoseintervall). Umgekehrt erhält
man für einen Versuch mit 1000 Wiederholungen, bei
dem als relative Häufigkeit 0,4 aufgetreten ist, das
95 %-Konfidenzintervall [0,37; 0,43] für die unbekannte Wahrscheinlichkeit p (vgl. Biehler, Hofmann,
Maxara und Prömmel 2011, S. 50).
Wiederholungsanzahl
n
Abweichung
von relativen
Häufigkeiten und
Wahrscheinlichkeiten
in Prozentpunkten
50
± 14 %
100
± 10 %
1000
±3%
5000
± 1,5 %
10000
±1%
Tab. 1: Faustformeln zur Genauigkeit von Simulationen: Radius des 95 %-Prognose- und des 95 %Konfidenzintervalls in Abhängigkeit von der Wiederholungszahl n
Diese Faustformeln können den Lernenden an die
Hand gegeben werden. Erstens sollen sie dazu dienen, die Genauigkeit der Simulationen einzuschätzen
und zweitens den Lernenden bewusst nahelegen, auf
eine genügend große Wiederholungsanzahl zu achten1.
Unterrichtsvorschläge zu Simulationen werden oft
mittels eines Tabellenkalkulationsprogramms (wie
Excel), GeoGebra oder CAS realisiert. Dabei überwiegt häufig die technische Komponente, da die jeweiligen Programme ein hohes Maß an Formelkenntnis erfordern. Während sich ohne Simulation das
Problem der „Verschleierung“ des mathematischen
Phänomens aufgrund der Kombinatorik stellt, kann
bei Simulationen ein anderes Problem auftreten: Verschleierung des Phänomens durch Technik, bzw. eine
zu spezifische Formel- oder Programmiersprache,
die in der jeweiligen Software notwendig ist, um das
Modell aufzustellen, die Simulation durchzuführen
und/oder die Simulation auszuwerten. Die Software
TinkerPlots (Konold & Miller 2011) mit ihrer integrierten Zufallsmaschine bietet eine Modellierung
von Zufallsexperimenten fast ohne Formeln und
Stochastik in der Schule 36 (2016) 1, S. 22–27
Programmierkenntnisse an und visualisiert darüber
hinaus den Simulationsprozess. So können Lernende
mit TinkerPlots die Simulationen selbst modellieren
und erstellen. Dabei kann die Bedienung der Software häufig sehr intuitiv erfolgen, denn TinkerPlots
stellt bei der Modellierung von Zufallsexperimenten
keine „Blackbox“ dar, wenn man einmal von der Erzeugung von Zufallszahlen absieht.
2
den Merkmalsnamen platziert wird. Die Ergebnisse
der Simulation werden automatisch in einer Tabelle
dokumentiert. Die Geschwindigkeit der Ziehungen
kann per Regler variiert werden. Besonders die Einstellung einer langsamen oder mittleren Geschwindigkeit ermöglicht es dem Lernenden, die Prozesse
bei der Ziehung nachzuvollziehen.
Die Software TinkerPlots und
ihre Zufallsmaschine
Die Software TinkerPlots wurde in den USA für den
Mathematikunterricht in den Klassen 3–10 entwickelt und bietet mit der Zufallsmaschine ein mächtiges Tool zum Simulieren von Zufallsexperimenten.
Möglichkeiten für den Einsatz in der Schule werden
in Biehler (2007) und Biehler et al. (2013) beschrieben. Einsatzmöglichkeiten der Software im Rahmen
der Lehreraus- und -fortbildung können in Frischemeier & Podworny (2014) nachgelesen werden. Die
Autoren dieses Artikels haben eine noch unveröffentlichte deutsche Version erstellt, mit der bereits
mehrere Unterrichtsversuche an Schule und Hochschule durchgeführt wurden. Eine Besonderheit gegenüber anderer Software wie z. B. Fathom (Biehler
et al. 2006) oder Tabellenkalkulationsprogrammen
wie Excel ist, dass in TinkerPlots praktisch keine
Formeln oder Programmierkenntnisse beim Durchführen einer Simulation (weder in der Modellierung,
noch in der Durchführung oder Auswertung) von Nöten sind. Ein stochastisches Modell, das mental mit
Urnen, Boxen oder Glücksrädern formuliert wurde,
kann quasi direkt in die Zufallsmaschine übertragen
werden, wodurch TinkerPlots zum expressiven Medium wird. Wir stellen die wichtigste („Simulations-“)
Komponente der Software, die oben bereits erwähnte Zufallsmaschine, kurz vor: Per Drag & Drop lässt
sich die Zufallsmaschine einfach in die Arbeitsfläche
der Software ziehen. Mit den verschiedenen Bauteilen (Box, Stapel, Kreisel, Balken, Kurve und Zähler)
lassen sich sehr viele Zufallsexperimente direkt realisieren. In der Grundeinstellung ist die Box als Urne
mit drei Kugeln gegeben (Abb. 1). Die Box repräsentiert die Ziehung aus einer Urne. Es können Kugeln
in beliebiger Anzahl hineingelegt, individuell beschriftet und die Ziehung mit oder ohne Zurücklegen
durchgeführt werden. Außerdem können Einstellungen wie die Anzahl der Wiederholungen pro Simulationsdurchlauf (Durchgänge, max. 100.000) und die
Anzahl der Ziehungen (Ziehungen pro Durchgang,
max. 100) vorgenommen werden. Die Ziehung selbst
wird in TinkerPlots visualisiert als Durcheinanderwirbeln der Kugeln bis schließlich eine oben unter
Abb. 1: Die Zufallsmaschine von TinkerPlots in der
Grundeinstellung
Schauen wir uns dieses am bekannten Beispiel des
doppelten Würfelwurfs unter der folgenden Fragestellung an: „Jemand bietet Dir ein Würfelspiel an.
Dazu sollen zwei Würfel gleichzeitig geworfen und
die Augensumme gezählt werden. Du darfst Dir vorher aussuchen, ob Du mit den Augensummen 5, 6,
7, 8 (Ereignis A) oder mit allen übrigen Augensummen (Ereignis B) gewinnen möchtest. Begründe, ob
Du eine der beiden Gewinnmöglichkeiten bevorzugen würdest.“ (Müller, 2005). Selbst wenn man mit
einfachen kombinatorischen Überlegungen zu einer
Entscheidung kommt, so gibt es im Unterricht oft
mindestens zwei Argumentationslager, eines davon
hält die beiden Würfel für nicht unterscheidbar. Eine
Simulation kann zu einer Entscheidung über konkurrierende Modelle beitragen. Wir zeigen, wie diese
Simulation in TinkerPlots zu realisieren ist. Dazu
bilden wir den doppelten Würfelwurf als Urnenziehung ab. Sechs Kugeln, beschriftet mit den Zahlen
von „1“ bis „6“, liegen in einer Box2 (siehe Abb. 2,
links) und es wird je Durchgang zweimal aus der
Box mit Zurücklegen gezogen. Insgesamt führen
wir 10000 Durchgänge aus. TinkerPlots dokumentiert automatisch die Ergebnisse für jeden Durchgang
zeilenweise in einer Tabelle (Abb. 2, mittig). Mit einem vordefinierten Befehl („Summe in ,Gesamt‘“)
ermittelt die Software zeilenweise die Zufallsgröße
23
„Augensumme“ (Abb. 2, mittig, rechte Spalte in der
Tabelle). Mithilfe eines Graphen (Abb. 2, rechts)
kann die Verteilung der Zufallsgröße „Summe“ z. B.
in Form eines Säulendiagramms dargestellt werden.
Sogenannte „Einteiler“ (grau hinterlegter Bereich in
Abb. 2, rechts) ermöglichen die freie Auswahl eines
Intervalls einer Verteilung und die Ermittlung der
Anzahlen und Anteile der Fälle in diesem Intervall,
hier eine relative Häufigkeit für das Ereignis A von
ca. 55 %. Da die Simulation sehr häufig (mehr als
1000 Durchgänge) durchgeführt wurde, können wir
anhand der relativen Häufigkeiten zu den einzelnen
Ausprägungen der Zufallsgröße „Summe“ die Wahrscheinlichkeit für das Ereignis „A“ auf 55 % und die
Wahrscheinlichkeit für das Eintreten des Ereignisses
„B“ auf 45 % schätzen. Somit ist es günstiger, auf
das Ereignis A zu setzen. Schülerinnen und Schüler
könnten sich kritisch fragen, wie genau die relative
Häufigkeit von 55 % die gesuchte Wahrscheinlichkeit schätzt. Durch mehrfaches Wiederholen von
10000 Durchgängen bekommt man ein Gefühl für
die Schwankung. Es erscheint relativ sicher, dass die
Wahrscheinlichkeit über 50 % liegt. Um die Notwendigkeit größerer Durchgangszahlen zu motivieren,
kann man auch erstmal 50 Durchgänge machen, um
zu erleben, wie unsicher die Beurteilung auf dieser
Basis ist. Hat man den Lernenden Faustregeln zur
Genauigkeit von Simulationen an die Hand gegeben,
(bei 10000 Durchgängen ist die Genauigkeit nach
den Faustformeln ± 1 Prozentpunkt (mit 95 % Sicherheit)), so kann man auch hieraus schließen, dass A
günstiger ist als B.
3
Beispiele
Wir betrachten nun zwei weiterführende Beispiele:
das Augensummenproblem beim dreifachen Würfelwurf nach de Méré aus den Anfangszeiten der Wahrscheinlichkeitsrechnung sowie den Hörtest als Einstieg in das informelle Hypothesentesten.
3.1 Dreifacher Würfelwurf: De Méré
Hat man das oben formulierte Einstiegsproblem gelöst, so kann man nun beispielsweise mit dem dreifachen Würfelwurf fortfahren. Während das Einstiegsproblem noch relativ elementar anhand der Berechnung der Wahrscheinlichkeiten für die Ereignisse „A“
und „B“ (ohne große kombinatorische Fähigkeiten)
lösbar ist, wird das beim dreifachen Würfelwurf aufgrund der sechs Mal so großen Ergebnismenge schon
erheblich schwieriger. Ein bekanntes historisches
Problem von Chevalier de Méré ist, ob beim dreifachen Würfelwurf das Auftreten der Augensumme 11
wahrscheinlicher als das Auftreten der Augensumme
12 ist, obwohl es scheinbar gleich viele Kombinationsmöglichkeiten für beide Augensummen gibt3.
Diese Frage lässt sich mit etwas Vorbereitung ab
Klasse sechs behandeln. Es können erste Vorüberlegungen zu Kombinationsmöglichkeiten von drei
Würfeln auf die entsprechenden Augensummen im
Unterricht gemeinsam thematisiert werden. Dabei
kann die Reihenfolge der einzelnen Würfelergebnisse von Schülern entweder als relevant oder als irrelevant eingeschätzt werden und somit Auslöser einer
Diskussion sein. Diese Diskussion kann, nachdem
im Unterricht das Zufallsexperiment auch händisch
durchgeführt wurde, Anlass für die Beantwortung des
Problems mithilfe einer Simulation in TinkerPlots
sein. Der Würfelwurf lässt sich wieder durch sechs
Kugeln (beschriftet mit „1“ bis „6“) in der Box (siehe
Abb. 3, links) realisieren. Es sind drei Ziehungen pro
Durchgang zur Modellierung des dreifachen Werfens
nötig und für eine möglichst hohe Genauigkeit (Abweichungen nach den Faustformeln ≤ 1 %) werden
10000 Durchgänge durchgeführt. In der Tabelle muss
nun wieder das Merkmal „Summe“ erstellt werden,
das die Ergebnisse der drei Ziehungen aufsummiert.
Dies kann einfach durch ein vordefiniertes Merkmal
geschehen, das per Klick in der Tabelle realisiert
wird.
Abb. 2: Das Zufallsexperiment „Augensumme“ in TinkerPlots
24
Abb. 3: Das Problem von de Méré – Der dreifache Würfelwurf in TinkerPlots
Die Augensumme wird für jeden Durchgang in der
entsprechenden Spalte der Tabelle automatisch dargestellt (siehe Abb. 3, mittig). Mit dem Graph-Objekt
in TinkerPlots kann die Verteilung dieses Merkmals
„Summe“ dargestellt werden (Abb. 3, rechts). Es ist
zu sehen, dass die relative Häufigkeit für die Augensumme 11 größer ist als für die Augensumme 12 und
daraufhin lässt sich schätzen, dass die Wahrscheinlichkeit für das Ereignis „Augensumme = 11“ ca.
13 % und für das Ereignis „Augensumme = 12“ ca.
11 % beträgt. Man kann auch zunächst mit kleineren Durchgangsanzahlen beginnen und beobachten,
dass keine klare Entscheidung für 11 oder 12 möglich
ist. Anschließend wird die Durchgangszahl solange
erhöht, bis man einigermaßen wiederholungsstabile
Unterschiede in den relativen Häufigkeiten erhält. Im
Unterricht könnte man als Grund für die Schwierigkeiten einer klaren Entscheidungsfindung die leicht
unterschiedlichen Anzahlen für die jeweils günstigen
Ergebnisse ausmachen und dieses Phänomen differenzierter anhand der einzelnen Kombinationsmöglichkeiten begründen.
3.2 Eine Hinführung zum informellen
Hypothesentesten: Der Hörtest
Wir wollen abschließend aufzeigen, wie man auch
die Wahrscheinlichkeitsverteilung binomialverteilter
Zufallsgrößen mithilfe von Simulationen mit TinkerPlots untersuchen kann (vgl. Biehler, Frischemeier &
Podworny 2015) – eine Hinführung zum Hypothesentesten, die durch den simulativen Zugang bereits
vor der Sekundarstufe II zugänglich gemacht werden
kann (vgl. Riemer 2009).
Ein Beispiel ist in diesem Fall der Hörtest (diese Aufgabe existiert in diversen Variationen): Ein privater
Hörfunksender hat zum „Tag des offenen Studios“
folgendes Spiel geplant. Als Studiogast bekommt man
im Tonstudio über Raumboxen 12 Musikstücke eingespielt. Jedes Musikstück wird in einer der zwei Tonqualitäten MP3-128 oder CD vorgespielt, welche es
allerdings ist, das entscheidet der Moderator. Aufgabe ist es, die Klangqualität eines jeden eingespielten
Musikstücks zu erkennen. Tom, ein Studiogast, errät
10 von 12 Tonqualitäten korrekt. Die Aufgabe für die
Lernenden ist nun zu beurteilen, ob Tom besondere
Hörfertigkeiten hat oder ob er nur geraten hat. Aufgaben dieser Art lassen sich etwa ab Klasse 8 experimentell und simulativ realisieren (Schäfer 2008). Im
Unterricht kann zu Beginn ein Experiment gestartet
werden, bei dem alle Schülerinnen und Schüler Musikqualitäten raten.4 Nach der Simulation können die
„Hörfähigkeiten“ von Tom diskutiert werden, wobei
das so genannte P-Wert Konzept (s. u.) intuitiv genutzt wird, ohne dass es zuvor ausführlich behandelt
werden müsste.
Das Zufallsexperiment kann mit TinkerPlots wie
folgt simuliert werden: Wir gehen davon aus, dass
der Studiogast rät, also keine besonderen Hörfertigkeiten besitzt. Es gibt beim Raten der Musikstücke
zwei Möglichkeiten: entweder die Person rät richtig
oder falsch. Da es insgesamt 12 Musikstücke sind,
die vorgespielt werden, läuft das Zufallsexperiment
darauf hinaus, zwölfmal zufällig zwischen „richtig“
und „falsch“ auszuwählen. In TinkerPlots lässt sich
dies beispielsweise durch eine Ziehung von zwei Kugeln aus einer Box oder aber (siehe Abb. 4, links) mit
dem Bauteil Kreisel mit zwei gleichgroßen Sektoren
(beschriftet mit „richtig“ und „falsch“) modellieren.
Um wiederum möglichst genaue Ergebnisse zu erhalten, lassen wir die Zufallsmaschine 10000 mal
laufen, das entspricht 10000 Personen, die am Ratespiel teilnehmen. Die Ergebnisse der 10000 Personen
werden automatisch in der Tabelle protokolliert, uns
interessiert nun, wie häufig jeder einzelne die „richtige“ Tonqualität geraten hat. Dafür kann wieder ein
vordefiniertes Ergebnismerkmal verwendet werden:
Tabelle → Einstellungen → Ergebnismerkmale →
‚?‘ in Gesamt zählen → „richtig“. In der neu erstellten Spalte „Anzahl_richtig“ wird nun protokolliert,
wie häufig jeweils richtig geraten wurde. Im Graphen
(Abb. 4, unten mittig) lässt sich erkennen, dass von
10000 Personen gerade einmal 195 Personen (ca.
2 %) ein ebenso gutes oder noch besseres Ergebnis
als Tom durch reines Raten erreicht haben. Diese
25
Abb. 4: Der Hörtest in TinkerPlots
„Überschreitungswahrscheinlichkeit“ nennt man in
der Statistik den P-Wert der Ergebnisse von Tom.
Wenn Tom nur geraten hätte, wäre etwas Unwahrscheinliches passiert, also sprechen die Daten dafür,
dass Tom besser ist als Raten. An das Ergebnis der
Simulation kann nun eine weiterführende Diskussion
anschließen. Mit welcher Wahrscheinlichkeit schafft
man ein gleich gutes oder noch besseres Ergebnis als
Tom? Hat dieser einfach nur glücklich geraten? Hat
er besondere Hörfähigkeiten? Das formale P-Wert
Konzept könnte später in der Oberstufe als zusätzliche Bewertungsgrundlage eingeführt werden. Bei
einem P-Wert zwischen 1 % und 5 % spricht man in
der statistischen Praxis von einer mittleren Evidenz
gegen die Hypothese des reinen Ratens.
4
Schlussbemerkung
Dieser Artikel soll exemplarisch einige Anregungen
für den Einsatz der Software TinkerPlots im Mathematikunterricht der Sekundarstufe I geben. Dabei
kann TinkerPlots sowohl als Demonstrationsmedium
des Lehrers als auch als Medium zur eigenständigen Arbeit der Schülerinnen und Schüler eingesetzt
werden. Im Rahmen einer Bachelorarbeit (Reichert
2014) haben wir eine Unterrichtsreihe zu Simulationen mit TinkerPlots für eine neunte Klasse an einer
Realschule entwickelt, durchgeführt und evaluiert.
Die Evaluation hat unter anderem gezeigt, dass inte26
ressante stochastische Fragestellungen (bis hin zum
oben beschriebenen Hörtest) mit Unterstützung der
Software TinkerPlots bereits in einer neunten Klasse einer Realschule (ohne besondere Vorkenntnisse)
thematisiert werden können, wobei aber besonders
auf eine sorgfältige Klärung des Verhältnisses von
relativen Häufigkeiten und Wahrscheinlichkeiten zu
achten ist. Auch in der Aus- und Fortbildung für angehende Grund-, Haupt-, Real- und Gesamtschullehrer an der Universität Paderborn haben wir mit dem
oben beschriebenen Konzept gute Erfahrungen gemacht. Als weitere Unterstützungsmaßnahme haben
wir einen Simulationsplan5 entwickelt, der sowohl
zur Vorbereitung einer Simulation, als auch als Strukturierungshilfe während einer Simulation verwendet
werden kann. Außerdem ist er eine hilfreiche Offline-Dokumentation für die spätere Besprechung der
Simulationen im Unterricht (Podworny 2013).
Zu den angegebenen drei Simulationen können Beispieldateien auf der Homepage der Zeitschrift „Stochastik in der Schule“ heruntergeladen werden.
Anmerkungen
1
Siehe Biehler & Prömmel
(2013) für eine stufenweise
__
Hinführung zum 1/√ n -Gesetz zur Thematisierung der
Genauigkeit von Simulationen, solange mit Mitteln
der Schulmathematik der Themenbereich Konfidenzintervalle noch nicht erschlossen ist (vgl. auch Maxara
2009, S. 21 f.).
2
Äquivalent zu dieser Simulation können auch andere Bauteile (z. B. der Kreisel mit sechs gleichgroßen
Sektoren) verwendet werden.
und Stochastik lernen – Using Tools for Learning Mathematics and Statistics. Wiesbaden: Springer Spektrum, S. 337–348.
3
Bei diesem Ansatz wird außer Acht gelassen, dass die
jeweiligen Augensummen durch eine unterschiedliche
Anzahl an Permutationen der Würfelkombinationen
erzeugt werden können.
Kaun, A. (2006): Stochastik in deutschen Lehrplänen allgemeinbildender Schulen. In: Stochastik in der Schule
26(3), S. 11–17.
4
Geeignetes Material lässt sich leicht selbst erstellen
oder findet sich z. B. unter http://www.riemer-koeln.
de (abgerufen am 04.03.2015).
5
Dieser kann unter http://fddm.uni-paderborn.de/
personen/podworny-susanne/material/ heruntergeladen werden.
Software
Konold, C. & Miller, C. (2011): TinkerPlots 2.0. Emeryville, CA: Key Curriculum Press, deutsche Adaption
(unveröffentlicht): Biehler, R.; Frischemeier, D.; Podworny, S., siehe http://lama.uni-paderborn.de/personen/
rolf-biehler/projekte/tinkerplots.html).
Literatur
Biehler, R. (2007): TINKERPLOTS: Eine Software zur
Förderung der Datenkompetenz in Primar- und früher
Sekundarstufe. Stochastik in der Schule 27(3), S. 34–42.
Biehler, R., Ben-Zvi, D., Bakker, A. & Makar, K. (2013):
Technology for Enhancing Statistical Reasoning at the
School Level. In: Clements, K.; Bishop, A.; Keitel, C.;
Kilpatrick, J. & Leung, F. (Hrsg.). Third International Handbook of Mathematics Education. New York:
Springer 2013, S. 643–689.
Biehler, R, Frischemeier, D. & Podworny, S. (2015): Informelles Hypothesentesten mit Simulationsunterstützung
in der Sekundarstufe I. Praxis der Mathematik in der
Schule 66(6), S. 21–25.
Biehler, R., Hofmann, T., Maxara, C. & Prömmel, A.
(2006): Fathom 2: Eine Einführung. Berlin [u. a.]:
Springer.
Biehler, R., Hofmann, T., Maxara, C. & Prömmel, A.
(2011): Daten und Zufall mit Fathom. Unterrichtsideen
für die SI mit Software-Einführung. Braunschweig:
Schroedel.
Biehler, R. & Maxara, C. (2007): Integration von stochastischer Simulation in den Stochastikunterricht mit Hilfe von Werkzeugsoftware. Der Mathematikunterricht
53(3), S. 46–62.
Biehler, R. & Prömmel, A. (2013). Von ersten stochastischen
Erfahrungen mit großen Zahlen bis zum
__
1/√ n -Gesetz – ein didaktisch orientiertes Stufenkonzept. Stochastik in der Schule 33(2), 14–25.
Frischemeier, D. & Podworny, S. (2014): Explorative Datenanalyse und stochastische Simulationen mit TinkerPlots – erste Einsätze in Kassel & Paderborn. In: Wassong, T.; Frischemeier, D.; Fischer, P. R.; Hochmuth,
R.; Bender, P. (Hrsg.): Mit Werkzeugen Mathematik
Maxara, C. (2009). Stochastische Simulation von Zufallsexperimenten mit Fathom – Eine theoretische Werkzeuganalyse und explorative Fallstudie. Kasseler Online-Schriften zur Didaktik der Stochastik (KaDiSto)
Bd. 7. Universität Kassel [Online: http://nbn-resolving.
org/urn:nbn:de:hebis:34-2006110215452].
Müller, J. H. (2005): Die Wahrscheinlichkeit von Augensummen – Stochastische Vorstellungen und stochastische Modellbildung. In: Praxis der Mathematik in der
Schule 47(4), S. 17–22.
Podworny, S. (2013): Mit TinkerPlots vom einfachen Simulieren zum informellen Hypothesentesten. In: Greefrath, G.; Käpnick, F. & Stein, M. (Hrsg.): Beiträge zum
Mathematikunterricht 2013, Münster: WTM Verlag,
S. 324–327.
Reichert, Simon (2014): Design, Durchführung und (beispielhafte) Auswertung einer Unterrichtsreihe zur Einführung in die computergestützte Simulation von Zufallsexperimenten mit TinkerPlots in der Sekundarstufe
I. Unveröffentlichte Bachelorarbeit. Paderborn: Universität Paderborn.
Riemer, W. (2009): Soundcheck: CD contra MP3. Ein
Hörtest als Einstieg in die Stochastik. Mathematik lehren 153, S. 21–23.
Schäfer, T. (2008). Von den Anfängen bis zum Hörtest
– Konzeption und Evaluation eines Unterrichtsexperiments zur Stochastik in Klasse 8. Unveröffentlichte
Staatsexamensarbeit. Universität Kassel.
Anschrift der Verfasser
Rolf Biehler
Institut für Mathematik
Universität Paderborn
Warburger Straße 100
33098 Paderborn
[email protected]
Daniel Frischemeier
Institut für Mathematik
Universität Paderborn
Warburger Straße 100
33098 Paderborn
[email protected]
Susanne Podworny
Universität Paderborn
Institut für Mathematik
Warburger Straße 100
33098 Paderborn
[email protected]
27
Wurde die Lotterie bei den Hungerspielen manipuliert?1
KYLE CAUDLE UND ERICA DANIELS, RAPID CITY, USA
1
Original: Did the Gamemakers Fix the Lottery
in the Hunger Games?
In: Teaching Statistics 37 (2) (2015), S. 37–40.
Übersetzung: ANNA SCHÄFER, PADERBORN
Zusammenfassung: Die Hungerspiele sind eine
jährlich stattfindende Veranstaltung in dem fiktionalen Land Panem. Jedes Jahr werden 24 Jugendliche
aus den 12 Distrikten durch eine Lotterie ausgewählt, um in der Freilichtarena zur Unterhaltung der
Bewohner des Kapitols bis auf den Tod zu kämpfen.
Mit Hilfe statistischer Analysen und Computersimulationen untersuchen wir, ob es möglich ist, dass die
Lotterie manipuliert wurde. Anhand fiktiver Daten
aus Suzanne Collins’ Buch „Die Tribute von Panem
– Tödliche Spiele“, zeigen wir wie Lernende erste
Erfahrungen mit der Durchführung eines Permutationstest sammeln können.
1
Einleitung
Panem ist ein fiktionales Land in der entfernten Zukunft, das nach dem Zusammenbruch der USA entstand. Es besteht aus 13 Gebieten, den sogenannten
Distrikten und dem Kapitol. Aufgrund der zunehmenden Ausbeutung durch das Kapitol revoltierten
die Distrikte. Der blutige Bürgerkrieg endete mit der
Zerstörung des 13. Distriktes und der erneuten Unterwerfung der anderen zwölf Distrikte. Als Strafe für
den Aufstand wurden die Hungerspiele eingeführt.
Jährlich werden seither ein Junge und ein Mädchen
zwischen 12 und 18 Jahren aus jedem Distrikt durch
eine Lotterie ausgewählt, um an den Hungerspielen
teilzunehmen. Diese Jugendlichen, genannt Tribute,
kämpfen zur Unterhaltung der Bewohner des Kapitols bis zum Tode. Ein Jugendlicher, der nicht bei der
Lotterie ausgewählt wurde, kann dabei freiwillig für
einen anderen teilnehmen. Genau das macht die Romanheldin, Katniss, die sich freiwillig als Ersatz für
ihre jüngere Schwester Prim meldet. In den reicheren
Distrikten (Distrikt 1, 2 und 4) werden Jugendliche
sogar speziell für die Spiele trainiert und nehmen
dann freiwillig teil. Diese Freiwilligen werden Karrieros genannt.
Der letzte Überlebende in der Arena gewinnt die
Hungerspiele, und als Preis bekommt sein Distrikt
im folgenden Jahr zusätzliche Lebensmittel. Die Familie des Tributs erhält Verpflegung und Schutz für
das restliche Leben des Jugendlichen. Die von Panems Polizei kontrollierte starke Beschränkung der
28
Versorgung mit Waren und Gütern führt dazu, dass die
Bewohner der meisten Distrikte mittellos und nah am
Hungern leben. Jugendliche zwischen 12 und 18 Jahren haben indessen die Möglichkeit zusätzliche Lebensmittelrationen für sich und ihre Familie zu erhalten. Dazu müssen sie ihren Namen ein weiteres Mal in
die Lotterie geben. Sie können höchstens so viele zusätzliche Rationen bekommen, wie sie Familienmitglieder haben. Dabei müssen sie für jede Ration einen
zusätzlichen Namenseintrag in die Lotterie geben.
In diesem Artikel werden die Ziehungsergebnisse
dieser Lotterie analysiert und untersucht, ob diese
manipuliert wurde. Dafür verwenden wir die Daten
der 74. Hungerspiele aus dem Roman von Suzanne
Collins (2010), die von Keller (2012) zusammengetragen wurden.
2
Die Lotterie
Die Wahrscheinlichkeit bei der Lotterie ausgewählt
zu werden hängt für jeden Jugendlichen von zwei
Faktoren ab: Seinem Alter und der Anzahl zusätzlicher Rationen, die er verlangt hat. Nach den Regeln
der Lotterie wird der Name eines Jugendlichen im
Alter von 12 Jahren einmal in die Lotterie eingetragen. Wenn sie nicht gewählt wurden, erhalten sie
im nächsten Jahr einen weiteren Eintrag, so dass sie
dann insgesamt zwei Einträge besitzen. Dieser Ablauf wiederholt sich bis zu dem Alter von 18 Jahren,
so dass dann sieben Einträge zusammen kommen.
Tabelle 1 fasst die Anzahl der Einträge zusammen,
die ein ausgewählter Jugendlicher altersbedingt nach
den Regeln der Lotterie hat.
Alter (Jahre)
Einträge
Anteil
12
1
1
___
13
2
14
3
15
4
16
5
17
6
18
7
28
2
___
28
3
___
28
4
___
28
5
___
28
6
___
28
7
___
28
Tab. 1: Lotterie-Einträge nach Alter
Stochastik in der Schule 36 (2016) 1, S. 28–32
Man kann nun die altersbezogenen Anteile der Lotterieeinträge in der dritten Spalte als Wahrscheinlichkeit auffassen, dass ein Jugendlicher in diesem Alter
entsprechend der Lotterieregeln ausgewählt wird.1
Gemäß der Romanvorlage waren unter den 24 jugendlichen Teilnehmern der Hungerspiele sieben Karrieros, die nicht durch die Lotterie ausgewählt wurden,
sondern sich freiwillig gemeldet haben. Auch die
Romanheldin Katniss nahm freiwillig als Ersatz für
ihre 12jährige Schwester Prim teil, weshalb wir bei
der Analyse der Daten Prims und nicht Katniss’ Alter
berücksichtigt haben.
Demnach kennen wir das Alter von 17 Jugendlichen,
die durch die Lotterie ausgewählt wurden. Mit Hilfe der Tabelle 1 können wir die erwarteten absoluten
Häufigkeiten ausgewählter Jugendlicher in jedem Alter ermitteln. Abb. 1 stellt beide Anzahlen gegenüber.
Abb. 1: Tatsächliche versus erwartete absolute
Häufigkeiten
Bei Betrachtung der Abb. 1 erkennt man, dass sich die
erwartete und tatsächliche Verteilung, insbesondere
für das Alter von 15 und 18 Jahren, unterscheidet. Wir
nutzen diese Daten, um Lernenden zu zeigen, wie man
einen Randomisierungstest mittels Simulation durchführt. Deren Interesse an der Verfilmung der Tribute
von Panem macht dieses zu einem besonders guten
Beispiel zur Einführung von Randomisierungstests.
3
Randomisierungstests
Sawilowsky (2005) hat bemerkt, dass Lernende
Schwierigkeiten haben, das Prinzip der Zufallsauswahl zu verstehen und dieser daher misstrauen. Wir
sind davon überzeugt, dass die Randomisierung ein
machtvolles statistisches Werkzeug ist, das im Unterricht genutzt werden sollte, um Lernenden ein intuitives Gefühl für Variabilität zu vermitteln. Diese Idee
kann einfach mit Hilfe eines Spielkartensatzes in einem handlungsorientierten Unterricht vermittelt werden, (s. dazu das ausgezeichnete Unterrichtsbeispiel
in Enders et al. 2006). Als Vorstufe des komplizier-
teren Randomisierungstests, den wir für die Analyse
der Lotterie der Hungerspiele benötigen, stellen wir
im Folgenden zunächst ein einfaches Beispiel vor um
das Testverfahren zu demonstrieren.
3.1 Ein erstes Beispiel
Wir stellen uns vor, die Hauptfigur Katniss und ihr
Freund Gale jagen Eichhörnchen. Laut der Romanvorlage unterscheiden sich beide Jugendlichen nicht
in ihren Jagdfähigkeiten. Doch an einem Tag erlegt
Katniss vier Eichhörnchen und Gale kein einziges.
Ist es dennoch richtig, dass beide die gleichen Jagdfähigkeiten haben? Wenn es keinen Unterschied in ihren Fähigkeiten gibt, hat jeder von ihnen die gleiche
Chance eines der Eichhörnchen zu erlegen. Somit
gibt es 24 = 16 Möglichkeiten, die vier Eichhörnchen
unter ihnen aufzuteilen. Von diesen 16 möglichen
Ausgängen gibt es nur eine (günstige) Möglichkeit,
in der Katniss alle vier Eichhörnchen erlegt. Somit
1
ist die Wahrscheinlichkeit dafür ___
16 (6,025 %). Es ist
also nicht sehr wahrscheinlich, dass Katniss alle Tiere erlegt, unter der Voraussetzung, dass ihre Jagdfähigkeiten gleich denen von Gale sind. Daher könnte
dies eine falsche Annahme sein.
Betrachten wir nun ein anderes Szenario, in dem es
für Katniss im Vergleich zu Gale doppelt so wahrscheinlich ist, die Eichhörnchen zu töten. Um dies zu
untersuchen, nehmen wir 3 Karten und schreiben auf
zwei davon „Katniss“ und auf eine „Gale“. Um das
Erlegen eines Eichhörnchens zu simulieren, ziehen
wir eine der drei Karten. Für die drei weiteren Eichhörnchen legen wir die erste Karte zurück und ziehen
erneut eine Karte usw. Gegenüber den Lernenden
sollte hervorgehoben werden, dass die Karte wieder
zurückgelegt werden muss, um die ursprüngliche Annahme, dass Katniss, das Eichhörnchen mit doppelter
Wahrscheinlichkeit erlegt, jedes Mal zu erfüllen. In
diesem Szenario gibt es 34 = 81 mögliche Ausgänge
und 24 = 16 Möglichkeiten, dass Katniss’ Name jedes
Mal gezogen wird, d. h. dass sie alle Eichhörnchen
16
erlegt. Die Wahrscheinlichkeit dafür wäre dann ___
81 ,
also rund 20 %. Weil diese Wahrscheinlichkeit relativ
groß ist, verwerfen wir die Annahme, dass Katniss
im Vergleich zu Gale die Eichhörnchen doppelt so
wahrscheinlich erlegt, nicht.
3.2 Die Lotterie der Hungerspiele
Bei der Lotterie der Hungerspiele interessiert uns die
Frage: Ist die Altersverteilung der (74.) Hungerspiele
mit den im Roman beschriebenen Regeln der Lotterie
vereinbar? Da es entgegen dem vorherigen Beispiel
29
nicht möglich ist, jede der möglichen Anordnungen
(d. h. Lotterieauslosungen) zu betrachten, möchten
wir einen Randomisierungstest mittels wiederholter
Stichprobenziehung durchführen – ein ausgezeichneter Weg um Lernende mittels einer einfachen Aufgabe
aktiv in den Unterrichtsprozess mit einzubeziehen.
Dazu nehmen wir 28 Karten und schreiben die Nummer 12 auf eine der Karten, die Nummer 13 auf zwei
Karten usw., so dass sie den Altersanteilen in Tabelle
1 entsprechen. Dann lassen wir die Lernenden eine
Stichprobe der Größe 17 ziehen, wobei wieder darauf
zu achten ist, dass die Stichprobe mit Zurücklegen
gezogen wird, damit die Anteile konstant bleiben.
Nach jedem Zug soll die gezogene Nummer (das Alter) notiert werden.
Nun fragen wir die Lernenden, wie viele 12en sie
gezogen haben. Mit großer Wahrscheinlichkeit wird
die Anzahl zwischen 0 und 1 liegen. Wir fragen weiter, wie viele 12-jährige sie in ihrer Stichprobe der
Größe 17 ungefähr haben sollten. Anders gesagt: Ist
1 wahrscheinlich? Was ist mit 5? Oder 10? Sie sollten überlegen, dass die erwartete absolute Häufig1
keit ___
28 · 17 ≈ 0,61 ist. Somit wäre 1 oder 2 plausibel,
aber sicher nicht 10.
Die tatsächlich beobachtete Anzahl sollte in jeder Altersgruppe dicht bei der erwarteten absoluten Häufigkeit liegen, sonst wären die Regeln der Lotterie nicht
befolgt worden. Wir fragen die Lernenden, wie sie die
Unterschiede zwischen den erwarteten und tatsächlichen Anzahlen über alle Altersgruppen messen könnten. Folgende Impulse können hilfreich sein: Können
wir einfach die Differenzen aufaddieren? Was ist,
wenn einige der Differenzen negativ sind? Die Lernenden können selbst ausprobieren und so eine sinnvolle Methode finden, um mit einem einzelnen Wert
zu messen, wie weit die tatsächlichen von der erwarteten Anzahlen in jeder Kategorie entfernt liegen.
Eine Standard-Technik um die ‚Nähe‘ zu ermitteln
ist der Chi-Quadrat-Anpassungstest. Diese Methode
nutzt auch Keller (2012). Für die Hungerspiele ist
diese Methode jedoch nicht geeignet, da alle erwarteten Anzahlen kleiner als fünf sind (Marx et al. 2006).
Doch obwohl der Chi-Quadrat-Anpassungstest nicht
durchgeführt werden kann, ist die Chi-Quadrat-Teststatistik ein gutes Maß, um die Nähe zwischen den
Stichprobenanteilen und den theoretischen ermittelten Werten zu bestimmen. Die Chi-Quadrat-Teststatistik nimmt die quadrierten Differenzen zwischen
den Stichprobenwerten und den theoretischen Werten und normalisiert diese durch Division durch den
theoretischen Wert:
30
χ2 =
∑
k
(Oi – Ei)
________
i=1
2
Ei
,
(1)
wobei Oi die tatsächliche Anzahl in der Stichprobe
mit den Kategorien i = 1, 2, …, k und Ei = n · pi die
auf der Basis der theoretischen Anteile pi erwartete
Häufigkeit in jeder Kategorie für eine Stichprobe der
Größe n.
Um den auf den Romandaten basierenden Wert der
Teststatistik zu berechnen, benötigen wir die tatsächlichen und erwarteten Anzahlen (Tabelle 2).
Alter
(Jahre)
Anteil
tatsächliche
Anzahl
erwartete
Anzahl
12
1
___
2
0,61
0
1,21
1
1,82
5
2,43
4
3,04
3
3,64
2
4,25
13
14
15
16
17
18
28
2
___
28
3
___
28
4
___
28
5
___
28
6
___
28
7
___
28
Tab. 2: Tatsächliche versus erwartete Anzahl
Neben den bereits erwähnten Annahmen (Berücksichtigung von Prims Alter statt Katniss’ Alter; Karrieros werden nicht berücksichtigt) basieren die Anzahlen in der Tabelle 2 auf der folgenden Annahme:
Die Anzahl der Kinder im Alter von 12 Jahren, die
jedes Jahr in die Lotterie aufgenommen werden, ist
in etwa gleich der Anzahl derjenigen, die die Lotterie verlassen, weil sie nun 19 Jahre alt sind. Dadurch
bleibt die Gesamtanzahl der Jugendlichen in der Lotterie von Jahr zu Jahr annähernd gleich.
Mit den Daten aus der Tabelle 2 und der Gleichung
(1) ergibt sich folgender Wert der Teststatistik:
(2 – 0,61)2 _________
(0 – 1,21)2
(2 – 4,25)2
_________
Q = _________
+
+
…
+
0,61
1,21
4,25
Q = 9,11
(2)
Nun lassen wir die Lernenden zu ihren eigenen Stichproben der Größe 17 die Teststatistik berechnen. Damit sie einen besseren Eindruck von der Variabilität
der Teststatistik ihrer Stichprobe erhalten, wird diese
Aufgabe mehrmals wiederholt. Anschließend fragen
wir, wie sich ihre Teststatistiken mit der Teststatistik zu den Roman-Daten (9,11) vergleichen lassen.
Insbesondere fragen wir, ob ihre Simulationen einen
Hinweis darauf liefern, dass die Lotterie manipuliert
wurde.
3.3 Computer Simulationen
Mit der Hilfe des Computers ziehen wir schließlich
1000 zufällige Stichproben der Größe 17 aus der
theoretischen Verteilung (Tabelle 1).2 Für jede der
1000 Stichproben berechnen wir eine StichprobenTeststatistik entsprechend der Gleichung (1). Wir
beobachten dann, wie viele der Stichproben-Teststatistiken gleich 9,11 oder größer sind. In der von uns
durchgeführten Simulation haben wir 169 solcher
Stichproben erhalten. Daraus schlussfolgern wir, dass
es unter der Voraussetzung der im Roman beschriebenen Regeln für die Lotterie eine 16,9 %ige Wahrscheinlichkeit gibt, die bei den Hungerspielen aufgetretenen tatsächlichen Anzahlen oder noch extremere
Anzahlen zu erhalten. Da diese Wahrscheinlichkeit
relativ groß ist, liefern die Daten keine Evidenz für
eine Manipulation der Lotterie.
Wir müssen aber eingestehen, dass der obige Test
nicht realistisch ist, da er die zusätzlichen Lotterieeinträge aufgrund der Extra-Rationen nicht berücksichtigt. Durch die Romanlektüre ist uns klar, dass ältere
Jugendliche mit größerer Wahrscheinlichkeit ExtraRationen fordern. Für diese Annahme gibt es mehrere
Gründe. Erstens benötigen ältere Jugendliche mehr
Lebensmittel, sobald sie ein Alter erreichen, indem
sie stark wachsen. Zweitens beginnen sie sich für ihre
Geschwister verantwortlich zu fühlen, so dass sie sich
verpflichtet fühlen, zusätzliche Rationen anzufordern.
Und zuletzt wird in dem Roman geschildert, dass viele Familien aufgrund der gefährlichen Arbeitsbedingungen ohne Vater leben, so dass (ältere) Jugendliche
wahrscheinlicher zusätzliche Rationen fordern.
Wir nehmen daher abschließend an, dass Jugendliche
zwischen 12 und 15 Jahren noch keine zusätzlichen
Rationen fordern. Im Alter von 16, 17 oder 18 Jahren
soll ein Jugendlicher einen zusätzlichen Lotterieeintrag aufgrund der Extra-Ration bekommen und dafür
ein zusätzliches Los in Kauf nehmen. Wir räumen
ein, dass diese Annahmen möglicherweise die fiktionale Situation nicht genau erfassen, aber sie sind für
uns mit Blick auf den Roman zumindest plausibel.
Tabelle 3 fasst die neuen Anzahlen der Lotterie-Einträge zusammen.
Auf der Basis dieser Anteile haben wir die erwarteten
Anzahlen neu berechnet und damit eine neue beobachtete Teststatistik bestimmt. Diese liefert den Wert
12,55. Die Durchführung eines Randomisierungstests zeigte in unserer Simulation von 1000 zufälligen
Stichproben 48mal Teststatistiken, die so groß oder
noch größer waren als die beobachtete Teststatistik.
Dies entspricht einem Anteil von 0,048. Da dieser
Wert relativ klein ist, schlussfolgern wir auf der Basis
unserer neuen Annahmen, dass wir Evidenz für eine
Manipulation der Lotterie gefunden haben.
Alter (Jahre)
12
13
14
15
16
17
18
Einträge
Anteil
1
1
___
2
2
___
3
4
6
8
10
34
34
3
___
34
4
___
34
6
___
34
8
___
34
10
___
34
Tab. 3: Lotterie-Einträge mit zusätzlichen Rationen
4
Schlussfolgerungen
Randomisierungstests sind eine ausgezeichnete Alternative zu Chi-Quadrat-Tests wenn die Voraussetzung der Mindestgröße der erwarteten Häufigkeiten
nicht erfüllt ist. Computer-Simulationen sind dabei
eine gute Möglichkeit um Lernenden zu zeigen, was
passieren würde, wenn man Experimente in einer
großen Anzahl wiederholt. Beide Ideen sind bisher
selten ein Teil von Einführungskursen zur Statistik.
Wir glauben, dass beide Ideen von Lernenden mit geringem oder keinem statistischen Hintergrundwissen
verstanden werden können. Außerdem sind wir davon überzeugt, dass eine Kombination von Statistik
und ‚Popkultur‘ Interesse erzeugen kann und die statistischen Themen damit unterhaltsamer macht. Und
daher: ‚Möge das Glück stets mit euch sein!‘3
Anmerkungen
1
Diese Deutung setzt die Annahme voraus, dass es innerhalb der Distrikte gleichviele Jugendliche in jeder
Altersklasse gibt (Anm. der Übersetzerin).
2
Ein R-Paket zur Simulation kann unter http://www.
mcs.sdsmt.edu/kcaudle/HGames_1.0.tar.gz heruntergeladen werden.
3
Im englischen Original-Roman lautet dieser Satz:
„May the odds be forever in your favor.“ Eine geeignetere Übersetzung wäre also z. B. „Mögen die Chancen
stets zu deinen Gunsten sein.“ Im deutschen Roman
und in der Verfilmung wird aber die obige Übersetzung genutzt (Anm. der Übersetzerin).
31
Literatur
Collins, S. (2010): The Hunger Games Trilogy. Scholastic
Australia.
Enders, C. K.; Stuetzle, R. und Laurenceau, J. P. (2006):
Teaching random assignment. A classroom demonstration using a deck of playing cards. In: Technology of
Psychology 34(4), S. 239–242.
Keller, B. (2012): Hunger Games survival analysis.
Brett Keller Global Health Development. http://
www.bdkeller.com/index.php/writing/hunger-gamessurvival-analysis/ (Zugriff 1.1.2016).
Marx, M. L.; Larsen, R. J. (2006): Introduction to mathematical statistics and its applications. Pearson/Prentice Hall.
Sawilowsky, S. S. (2005): Teaching random assignment:
do you believe it works? In: Journal of Modern Applied
Statistical Methods 3(1), S. 221–226.
Anschrift der Verfasser
Kyle Caudle
South Dakota School of Mines and Technology
501 East Saint Joseph Street
Rapid City, SD 57701
[email protected]
Erica Daniels
[email protected]
Bericht über die Herbsttagung des AK Stochastik
vom 20.–22. November 2015 in Paderborn
PHILIPP ULLMANN, FRANKFURT
Jedes Jahr richtet der Arbeitskreis Stochastik eine
Herbsttagung aus, die sich an interessierte Kolleginnen und Kollegen aus Schule und Hochschule richtet.
In diesem Jahr sollten Digitale Medien im Stochastikunterricht auf ihre Chancen und Möglichkeiten hin
ausgelotet werden.1
***
Den Eröffnungsvortrag Kurzes Tutorium Statistik – Kurzgeschichten zur Statistik auf YouTube am
Freitagabend hielt Mathias Bärtl von der Hochschule
Offenburg. Im Rahmen seiner Lehrtätigkeit erstellt
er kurze Lehrvideos als Begleitmaterial für seine
Grundlagenvorlesung zur Statistik. Die Videos sollen
die Praxistauglichkeit statistischer Verfahren anhand
von Problemstellungen aus dem Alltag motivieren
und dadurch das Fach attraktiver machen und zugleich Einstiege in die einzelnen Themen erleichtern.
Inzwischen hat sich eine beachtliche Zahl an Videos
angesammelt, die im YouTube-Kanal Kurzes Tutorium Statistik gesammelt und frei zugänglich sind.2
probenverteilungen und Konfidenzintervallen (s)ein
Konzept vor, den Stochastikunterricht in der Sekundarstufe II mittels Computereinsatz verständnisorientiert zu gestalten. Dieser Ansatz wird von ihm in Niedersachsen seit vielen Jahren sowohl im Unterricht als
auch in der Lehrerfortbildung erfolgreich umgesetzt
und weiterentwickelt. Insbesondere komplexe Themen wie Stichprobenverteilungen oder Prognose- und
Konfidenzintervalle werden durch die konsequente
Visualisierung begrifflich leichter fassbar.
In einem kurzweiligen Vortrag wurden zunächst
fachliche und methodisch-didaktische Überlegungen sowohl zum Gesamtkonzept als auch zum Aufbau einzelner Videos erläutert. Anschließend wurde
über die Nutzung der und Reaktionen auf die Videos
berichtet. Die anregende Diskussion wurde dann im
Weinlokal Krüger weitergeführt.
***
Der Samstagvormittag stand ganz unter dem Zeichen
der Schulpraxis. Zu Beginn stellte Reimund Vehling
unter dem Titel Stochastik in der Sek II mit GeoGebra
und dem TI-Nspire. Von Prognoseintervallen, Stich32
Abb. 1: Einige Videos aus dem YouTube-Kanal Kurzes Tutorium Statistik
Stochastik in der Schule 36 (2016) 1, S. 32–34
Konzeptes hervorheben und verweise zu den Einzelheiten gerne auf den o. g. Beitrag.
Abb. 2: Bestimmung eines Konfidenzintervalls (KI)
zu einer (vorgegebenen) empirischen Häufigkeit h
vermittels der Konfidenzellipse.
In eine ähnliche Richtung zielte dann der Vortrag
Simulations, a Revolution in the Didactics of Statistics, in dem Carel van der Giessen zunächst den
Nutzen von Simulationen im Stochastikunterricht herausarbeitete, um anschließend einige Beispiele aus
dem von ihm mitentwickelten Softwarepaket VUstat
(für: visual understanding of statistics) vorzustellen.
VUstat ist ursprünglich in den Niederlanden entwickelt worden und wird dort seit langem erfolgreich
eingesetzt. Das Paket ist inzwischen auch auf Deutsch
verfügbar und kann kostenlos heruntergeladen werden.3 Insbesondere die schrittweise kontrollierbare
Wiederholung von Zufallsexperimenten und Stichproben-Ziehungen überzeugt und erleichtert stochastisches Verständnis.
In der Mittagspause folgte ein kurzer Stadtrundgang,
bei dem Katja Krüger bekannte und weniger bekannte Sehenswürdigkeiten Paderborns (wie den Hohen
Dom mit seinem Perspektivgitter) kenntnisreich vorstellte.
Der weitere Nachmittag galt der Nachwuchsförderung. Zwei Promotionsvorhaben wurden vorgestellt
und ausführlich diskutiert. Zum einen berichtete Lea
Hausmann unter dem Titel Abschätzungen bei Lorenzkurve und Gini-Koeffizient über eine Lernumgebung, die sie im Rahmen von Schülerwochen an
der RWTH Aachen entwickelt und erprobt hat. Zum
anderen stellte Candy Walther unter dem Titel Planung und Durchführung statistischer Erhebungen im
Mathematikunterricht sein Konzept und erste Schritte einer empirischen Untersuchung vor, mit der er
dieses schulische Themenfeld mit Blick auf typische
Schülerschwierigkeiten systematisch erfassen und
strukturieren möchte.
Nach der Sitzung des AK Stochastik und der sich
anschließenden Mitgliederversammlung des Vereins
zur Förderung des Stochastikunterrichts wurde der
Abend mit einem gemeinsamen Abendessen im Ratskeller beschlossen.
***
Am Sonntagvormittag berichtete Rolf Biehler über
Stochastik kompakt – Eine Fortbildungsreihe zum
GTR-unterstützten Stochastikunterricht in der Sekundarstufe II, die im Rahmen des Deutschen Zentrums
für Lehrerfortbildung in Mathematik (DZLM) mit
und für Lehrkräfte in Nordrhein-Westfalen und Thüringen konzipiert und weiterentwickelt worden ist. In
der viertägigen Fortbildung wird Lehrkräften technisches und didaktisches Wissen zum GTR-Einsatz
vermittelt. Die behandelten Beispiele umfassen Simulationen, die Berechnung und Veranschaulichung
von Verteilungen sowie interaktive Visualisierungen
***
Den Hauptvortrag Plattformunabhängige Lernobjekte zur Statistik für Schule und Hochschule – ein Erfahrungsbericht hielt dieses Jahr Hans-Joachim Mittag, der in seiner Lehrtätigkeit an der Fernuniversität
Hagen kleine Lernobjekte zur Statistik entwickelt
hat, die in einer Web-App zusammengefasst sind und
kostenlos genutzt werden können.4
In Heft 35 (2015), Seite 6–11 ist gerade ein Aufsatz
erschienen, in dem die App ausführlich vorgestellt
wird. Daher möchte ich hier nur den Charme der
universellen Einsetzbarkeit dieses minimalistischen
Abb. 3: Web-App Statistische Methoden und statistische Daten – interaktiv
33
komplexer stochastischer Zusammenhänge (Einsdurch-Wurzel-n-Gesetz, Fehler beim Hypothesentesten, Operationscharakteristik).
Im letzten Tagungsvortrag Tools für Excel und LibreOffice zur Unterstützung elementarer Datenanalyse
mit Dotplot, Histogramm, Boxplot, Streu-/Residuendiagramm und Mehrfeldertafel stellte Thomas Wassong schließlich Tabellenblätter für LibreOffice bzw.
Excel vor, in denen einschlägige elementare Techniken der Datenanalyse, die in statistischen Programmpaketen standardmäßig vorhanden sind, nun auch in
der Tabellenkalkulation zur Verfügung stehen. Die
entsprechenden Dateien sowie eine digitale Lernumgebung, die anhand von Videos den Umgang mit den
Tools erläutert, sind im Internet frei verfügbar.5
***
Die Vorträge der diesjährigen Herbsttagung haben
deutlich gezeigt, dass digitale Medien beim Lernen
und Lehren von Stochastik wenigstens fünf mögliche Stärken aufweisen: Sie können zeitlich, räumlich
und kulturell sehr flexibel gestaltet werden (Flexibilität), bieten vielfältiges Potenzial, selbst Hand anzulegen (Interaktivität), und ermöglichen eine anschaulich-intuitive Aufbereitung von Informationen
(Visualität); dabei kann auf erweiterte Möglichkeiten
des (Be-)Rechnens zurückgegriffen werden, sei es
im Vorder- oder Hintergrund (white/black box), und
schließlich können zufällige Prozesse unmittelbar
beobachtet und erlebt werden – wieder und wieder
(Simulation). Insbesondere der letzte Punkt stützt
einen spezifischen Aspekt der Stochastik, dessen
didaktische Möglichkeiten noch lange nicht ausgeschöpft sind: Das simulationsgestützte Sammeln von
Primär- bzw. Sekundärerfahrungen mit dem Zufall.
Damit aber digitale Werkzeuge auch so genutzt werden (können), dass stochastische Begriffe und Verfahren besser verstanden und als nützlich erfahren
werden, kommt alles darauf an, Inhalte und Methoden aufeinander abzustimmen. Was das im Einzelfall
genau bedeutet und wie dies im Unterricht jeweils
erreicht werden kann, muss immer wieder neu durchdacht und zur Passung gebracht werden. Angebote,
so flexibel und interaktiv sie sein mögen, müssen zuallererst genutzt werden. Visualisierungen, so durchdacht und strukturiert sie sein mögen, müssen zuallererst gelesen und verstanden werden. Auch und gerade im digitalen Zeitalter gehört es zu den zentralen
Problemfeldern stochastikdidaktischer Forschung,
• Einstiegshürden zu senken (welche fachlichen
bzw. Werkzeugkompetenzen sind in welcher
Situation unbedingt notwendig, wünschenswert
oder gar überflüssig?),
34
• die richtige Balance zwischen Rezeption und
Konstruktion zu finden (wann ist es ratsam, vorgegebene Lernobjekte zu erkunden, wann ist es
sinnvoll, eigene Objekte zu erstellen?) und
• den Mehrwert digitaler Hilfsmittel wie etwa Videos, (Web-)Apps, GTR, CAS oder GeoGebra
im Lehr-Lern-Prozess überzeugend zu nutzen
(wann bleibt das Arbeiten mit digitalen Werkzeugen bloßes „Rumfummeln am Gerät“, unter
welchen Bedingungen kann echtes, also inhaltliches Verständnis begünstigt werden?).
Ob sich in der schulischen Praxis ein breiter Konsens zur Nutzung digitaler Medien beim Lehren und
Lernen von Stochastik etabliert und wie ein solcher
aussehen kann – das bleibt abzuwarten. Die gegenwärtige Lage bietet jedenfalls Anlass zur Hoffnung:
Sowohl eine enge Abstimmung zwischen den (nicht
immer identischen) Bedürfnissen von Schule und
Hochschule als auch der (sanfte) Transfer zwischen
Theorie und Unterrichtspraxis scheint sich bereits in
einiger Breite etabliert zu haben – und zwar in beide
Richtungen und auf Augenhöhe. Einen kleinen Beitrag dazu hat gewiss auch diese Herbsttagung geleistet.
Zum Schluss bleibt nur, all jenen Personen zu danken, die zum Gelingen dieser Tagung beigetragen haben; ebenso herzlicher Dank gilt all jenen, die schon
jetzt die kommende Herbsttagung vorbereiten, die
vom 30. September bis 2. Oktober 2016 in Rostock
stattfinden wird!
Linksammlung
1
Programm der Herbsttagung:
http://www.mathematik.uni-dortmund.de/ak-stoch/
vergangene-herbsttagungen.html#2015
2
YouTube-Kanal Kurzes Tutorium Statistik:
https://www.youtube.com/channel/
UCtBEklAtHHji2V1TsaTzZXw/videos
3
Softwarepaket VUstat: http://vustat.de
4
Web-App Statistische Methoden und statistische
Daten – interaktiv:
https://www.hamburger-fh.de/statistik-app
5
Die EDA-Tools für Excel bzw. LibreOffice finden
sich unter http://eda-el.dzlm.de
Anschrift des Verfassers
Philipp Ullmann
Universität Frankfurt
Institut für Didaktik der Mathematik
Robert-Mayer-Str. 6–8
60325 Frankfurt
[email protected]
Bibliographische Rundschau
UNTER MITARBEIT VON REIMUND VEHLING
Vorbemerkung: Die hier nachgewiesenen Veröffentlichungen sind alphabetisch nach dem Erstautor angeordnet. Ein Kurzreferat versucht, die wesentlichen
Inhalte der nachgewiesenen Zeitschriftenaufsätze
und Bücher wiederzugeben.
Rolf Biehler, Daniel Frischemeier und Susanne Podworny: Informelles Hypothesentesten mit Simulationsunterstützung in der Sekundarstufe I: In: PM,
Praxis der Mathematik, Jahrgang 57 (Dezember
2015) Heft 66, S. 21–25
Der Artikel führt anhand einer Unterrichtsreihe, die
für den Mathematikunterricht in einer achten Jahrgangsstufe konzipiert, durchgeführt und evaluiert
wurde, aus, wie man bereits in der Sekundarstufe I
Grundgedanken des Hypothesentestens am Beispiel
eines „Hörtests“ mit Softwareunterstützung vermitteln kann. Als Softwareunterstützung für die Simulation der dahinterliegenden Zufallsexperimente werden zwei Lösungsansätze vorgestellt: einer bedient
sich der Tabellenkalkulationssoftware Excel, die in
vielen Schulen zugänglich ist, der andere bedient sich
der Datenanalyse- und Simulationssoftware TinkerPlots, einer speziellen Lernsoftware für explorative
Datenanalyse und stochastische Simulationen in der
Sekundarstufe I, die es Lernenden erlaubt, ohne große Vorkenntnisse selbst Simulationen durchzuführen.
(Autorenreferat)
Volker Eisen: Stochastik in der Einführungsphase:
Vorstellungen konsolidieren und erweitern. Ein Werkstattbericht aus der Unterrichtsentwicklung „vor
Ort“: In: PM, Praxis der Mathematik, Jahrgang 57
(Dezember 2015) Heft 66, S. 34–39
Zur Diskussion steht eine Unterrichtsreihe zur Stochastik für das erste Jahr der Oberstufe, die sich u. a.
an Ideen aus dem Dialogischen Lernen nach Gallin
und Ruf orientiert. Im Fokus stehen dabei die getroffenen didaktischen Entscheidungen (konkretisiert als
Wissensmatrix und Kernideen), die Umsetzung in
Aufgaben (insbesondere zur Begriffsentwicklung)
und die Reflexion von Unterrichtsprodukten; exemplarisch verdeutlicht am Gegenstand Erwartungswert. (Autorenreferat)
Stochastik in der Schule 36 (2016) 1, S. 35–36
Anna George: Wer die höhere Zahl hat, gewinnt!
Spielerische Begegnung mit Wahrscheinlichkeiten in
Klasse 5. In: PM, Praxis der Mathematik, Jahrgang
57 (Dezember 2015) Heft 66, S. 10–14
„Wer die höhere Zahl hat, gewinnt!“ Durch das Würfeln nicht-transitiver Würfel wird ermöglicht, dass
diejenige Person, die als zweites einen geeigneten
2
Würfel wählt, mit einer Wahrscheinlichkeit von __
3 gewinnen kann, indem sie eine höhere Augenzahl würfelt. Im Artikel sollen nicht-transitive Würfel vorgestellt und die Gewinnwahrscheinlichkeiten berechnet
werden. Darüber hinaus werden nach der Sachanalyse Umsetzungsmöglichkeiten für den Unterricht aufgezeigt. Zuletzt werden Schülerlösungen für die Bestimmung der Eintrittswahrscheinlichkeiten und der
Gewinnwahrscheinlichkeiten, nicht-transitiver Würfel, dargestellt und zusammengefasst. Insbesondere
wird gezeigt, wie Schülerinnen und Schüler einer
fünften Klasse mit dem Wahrscheinlichkeitsbegriff
umgehen. (Autorenreferat)
Anselm Knebusch, Ana Alboteanu-Schirner: Ein
„Mystery“ im Statistikunterricht: In: PM, Praxis der
Mathematik, Jahrgang 57 (August 2015) Heft 64,
S. 42–44
Bei der Erforschung realer Probleme basiert Erkenntnisgewinn oft auf Selektion und Bewertung bereits
vorhandener Informationen. Durch systematische
Überlegungen werden diese in einen sinnvollen Zusammenhang gebracht. Hierbei müssen wir gerade in
der heutigen Zeit relevante Informationen aus einem
Überangebot herausfiltern. Das vorgestellte Beispiel
der Methode „Mystery“ zeigt, wie Schülerinnen und
Schüler zu einer aktiven Auseinandersetzung mit Begriffen der Statistik motiviert werden und dabei eine
systematische Auswahl von Informationen trainieren
können; dies ist die Grundlage für eine weiterführende Problemlösekompetenz. (Autorenreferat)
Heinz Laakmann; Susanne Schell: Mit Zufall durch
die Schule – Wahrscheinlichkeit. In: PM, Praxis der
Mathematik, Jahrgang 57 (Dezember 2015) Heft 66,
S. 2–9
35
Zufall und Wahrscheinlichkeit sind Themen, die
die Schülerinnen und Schüler inzwischen von der
Grundschule an begleiten. Dabei sind es vor allem
drei verschiedene Zugänge, die herangezogen werden um Wahrscheinlichkeiten zu bestimmen: subjektivistische, empirische und theoretische. Im Artikel
werden diese drei Zugänge als Modellierungen charakterisiert und Möglichkeiten zur tieferen Reflexion
der Modellannahmen diskutiert. Darauf aufbauend
wird der spiralige Erwerb dieser Modelle sowie die
Herstellung der Beziehungen zwischen ihnen über
die verschiedenen Schuljahre hinweg thematisiert.
(Autorenreferat)
Heinz Laakmann; Marcel Untiet: Das „RendevousProblem. In: PM, Praxis der Mathematik, Jahrgang
57 (Dezember 2015) Heft 66, S. 15–20
Das „Rendezvous-Problem“ kann als stochastisches
Problem im Unterricht behandelt werden, das – je
nach Modellierungsaspekt und Vorwissen der Lernenden – sowohl mit dem frequentistischen als auch
mit dem klassischen Wahrscheinlichkeitsansatz gelöst
werden kann und über die Anwendung der LaplaceRegel hinaus zur Vorstellung einer geometrischen
Wahrscheinlichkeit führt. Dabei zeigt sich der Mehrwert des Einsatzes einer Tabellenkalkulation und einer dynamischen Geometrie-Software, da Schülerinnen und Schüler aktiv am Lernprozess beteiligt sind
und selbstständig mit einfachen Simulationen oder
ggfs. vorgefertigten Programmen durch Auszählen
und Berechnen zu einer Lösung mit frequentistischen
Vorstellungen gelangen. (Autorenreferat)
Bernd Ohmann; Susanne Schnell: „Ein Mensch denkt
schon ein bisschen komplexer als ein Würfel“ – Umgang mit Vermutungen in Klasse 7: In: PM, Praxis
der Mathematik, Jahrgang 57 (Dezember 2015)
Heft 66, S. 26–30
Das Testen von Hypothesen und das „Schließen unter
Unsicherheit“ ist ein Thema, das sich in der Oberstufe
einst weder bei Lehrenden noch bei Lernenden großer Beliebtheit erfreute. Gleichwohl ist nicht nur der
klassische Hypothesentest eines der meist genutzten
Verfahren in der human- und sozialwissenschaftlichen Forschung (Leuders 2005), sondern das Aufstellen, Prüfen, Bestätigen oder ggf. Verwerfen von Vermutungen sind Tätigkeiten, die der Stochastik genuin
innewohnen (Stochastik als „ars conjectandi – Kunst
des Vermutens“ nach Jakob Bernoulli 1713). Im Arti-
36
kel wird dargestellt, wie der hypothetische Charakter
des Wahrscheinlichkeitsbegriffs sowie die Grundidee
des Hypothesentests in Klasse 7 fokussiert werden
können. (Autorenreferat)
Wolfgang Riemer; Raphaela Sonntag: Gummibärenforschung. In: PM, Praxis der Mathematik, Jahrgang
57 (Dezember 2015) Heft 66, S. 31–33
Gummibärenforschung ist witzig und spannend.
Ausgewählte Aspekte passen in eine Doppelstunde
und decken mit den Merkmalen Farbe, Gewicht und
Geschmack alle Bereiche des Statistikunterrichts von
Klasse 6 bis zum Abitur ab. Sie kann in idealer Weise
das einlösen, was Heinrich Winter 1995 in seiner ersten Grunderfahrung eingefordert hat: „Der Mathematikunterricht sollte anstreben, Erscheinungen der
Welt in einer spezifischen Art wahrzunehmen und zu
verstehen.“ (Autorenreferat)
Wolfgang Riemer; Raphaela Sonntag: Permutationen schmecken. In: PM, Praxis der Mathematik,
Jahrgang 57 (Dezember 2015) Heft 66, S. 40–41
Hör- und Geschmackstests sorgen seit Jahren für
Motivation in der beschreibenden und beurteilenden Statistik. Dabei kommen wegen der Prüfungsrelevanz meist Binomialverteilungen zum Einsatz.
Zwecks Horizonterweiterung soll hier neben dem
Binomialmodell auch ein mathematisch anspruchsvolleres Permutations-Design für einen Gummibärchen-Geschmackstest erforscht und genutzt werden.
(Autorenreferat)
Hans-Stefan Siller, Daniel Habeck, Salih Almaci,
Walter Fefler: Sportwetten und Großereignisse als
Chance. In: PM, Praxis der Mathematik, Jahrgang
57 (Dezember 2015) Heft 66, S. 42–46
„Wir wollen Deutschland einen echten Kampf bieten und werden sehen, was möglich ist. Die Gruppe
ist eine echte Herausforderung. Aber wir werden sie
annehmen. Es ist eine der schwersten Gruppen der
gesamten Auslosung.“ Dieses Zitat von Jürgen Klinsmann (vgl. RP Online, 2014) kann den Einstieg in
eine Unterrichtsreihe zur Stochastik ermöglichen.
Der Artikel zeigt einen Zugang, wie die Wahrscheinlichkeit für das Erreichen des Achtelfinales einer
WM anhand eines mathematischen Modells berechnet werden kann. (Autorenreferat)