22. Wärmestrahlung rmestrahlung rmestrahlung, Quantenmechanik

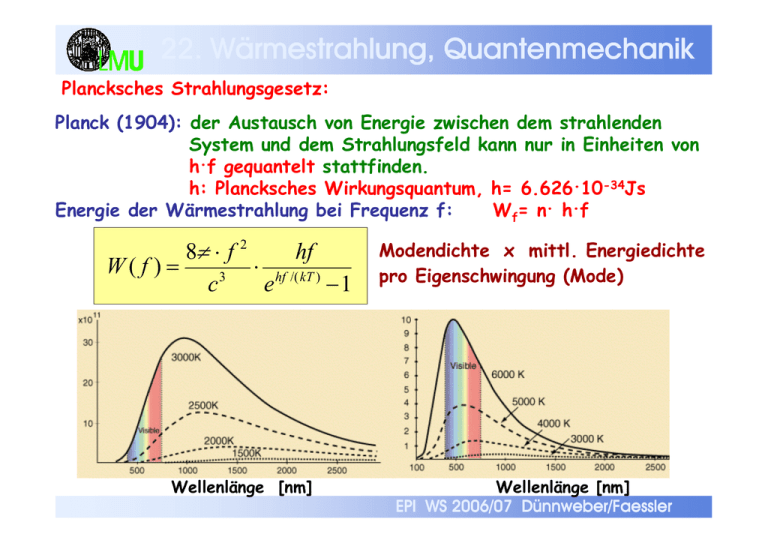
22. Wärmestrahlung,
rmestrahlung, Quantenmechanik
Plancksches Strahlungsgesetz:
Planck (1904): der Austausch von Energie zwischen dem strahlenden
System und dem Strahlungsfeld kann nur in Einheiten von
h.f gequantelt stattfinden.
h: Plancksches Wirkungsquantum, h= 6.626.10-34Js
Energie der Wärmestrahlung bei Frequenz f:
Wf= n. h.f
8π ⋅ f 2
hf
W( f ) =
⋅
c3
e hf /( kT ) − 1
Wellenlänge [nm]
Modendichte x mittl. Energiedichte
pro Eigenschwingung (Mode)
Wellenlänge [nm]
EPI WS 2006/07 Dünnweber/Faessler
22. Wärmestrahlung,
rmestrahlung, Quantenmechanik
Wiensches Verschiebungsgesetz:
Die Wellenlänge des Strahlungsmaximums verschiebt sich mit der
Temperatur gemäß dem Wienschen Verschiebungsgesetz:
λmax.T=2.9.10-3 m.K
Sonnentemperatur: ~ 5700 K
-> Wellenlänge λmax ~ 480 nm ≈ 0,5 µm *
Glühlampe (2000K): λmax = 1 µm (infrarot)
Mensch:
10 µm
*Energie h · f ≈ 3eV
für die gesamte abgestrahlte Leistung
gilt:
dW/dT ~ T4 : Stefan-Boltzmann-Gesetz
Wellenlänge [nm]
EPI WS 2006/07 Dünnweber/Faessler
„Lichtquanten“ verhalten sich wie Wellen (-> Interferenzen), aber
auch wie Teilchen:
Beispiele für Teilchencharakter:
Photoeffekt (Einstein)
Comptoneffekt:
elastische Streuung von γ an e-
Wie Stoß zweier Kugeln!
(Energien Emax bzw. E‘ unabhängig von der Lichtintensität)
EPI WS 2006/07 Dünnweber/Faessler
22. Wärmestrahlung,
rmestrahlung, Quantenmechanik
Was ist Licht: Teilchen oder Welle ?
Photoeffekt:
Ein Metall wird mit Licht einer Wellenlänge (Farbe) bestrahlt und die Energie der emittierten ‘Photoelektronen’
wird gemessen (Gegenfeldmethode: wenn gerade keine
Elektronen die Anode mehr erreichen ist eU=mv2/2)
Beobachtung: die Energie der Photonen
wird nur durch die Farbe des Lichts (λ
λ)
bestimmt, nicht durch die Intensität.
(mehr Licht -> mehr Elektronen)
Erklärung:
(Einstein 1905)
Auch das Licht
wechselwirkt in
gequantelten
Beträgen h.f
-> weitere Methode, die Naturkonstante h zu
bestimmen:
h=e.∆U/∆
∆f
∆U
∆f
EPI WS 2006/07 Dünnweber/Faessler
22. Wärmestrahlung,
rmestrahlung, Quantenmechanik
Wellen- und Photonencharakter des Lichts
Licht (elektromagnetische Wellen) verhält sich bei der Ausbreitung wie
eine Welle -> Interferenz, Beugung …
Licht wechselwirkt auf atomarem Niveau (Absorption beim Photoeffekt)
wie ein Teilchen (Photon) mit Energie hf
Wellenpaket: Lokalisierung durch Überlagerung
verschiedener Frequenzen (s. Schwebung).
∆x groß ↔ schmale Frequenzverteilung
(schmale Impulsverteilung)
∆x klein ↔ breite Impulsverteilung
Allgemein gilt die Heisenbergsche Unschärferelation:
∆p ⋅ ∆x ≥
h
= h ebenso
2π
∆E ⋅ ∆t ≥ h
Benimmt sich Materie anders als Licht?
NEIN
EPI WS 2006/07 Dünnweber/Faessler
22. Wärmestrahlung,
rmestrahlung, Quantenmechanik
Wellencharakter massiver Teilchen:
Wenn Licht Teilchencharakter besitzt, kann man dann auch bei
(Elementar-)Teilchen einen Wellencharakter finden ?
Test: Interferenzexperimente mit Elektronenstrahlen
geht sogar mit
einzelnen Elektronen
-> Wellenpaket
f
de Broglie (1924):
wie bei Licht
h
2π 

h
=
,
k
=


2π
λ 

diese Wellenlänge ist sehr klein (energieabhängig):
1 keV Elektron-> 39 pm
EPI WS 2006/07 Dünnweber/Faessler
23. Atomphysik,
Atomphysik, Röntgenstrahlung
Ebenso werden nur Lichtquanten mit der Differenzenergie ∆E
absorbiert, wenn ein Medium bestrahlt wird
(Absorptionsschattenlinien)
EPI WS 2006/07 Dünnweber/Faessler
23. Atomphysik,
Atomphysik, Röntgenstrahlung
Aufbau des Atoms:
Rutherford (1900): Streuung von α Teilchen aus radioaktivem Präparat
an einer Goldfolie (Ekin ca. 5 MeV)
-> fast gesamte Masse des Atoms ist in winzigem Kern konzentriert,
der von einer ausgedehnten Elektronenhülle umgeben ist.
Die meisten α Teilchen fliegen gerade durch die Folie durch.
EPI WS 2006/07 Dünnweber/Faessler
23. Atomphysik,
Atomphysik, Röntgenstrahlung
Bohrsches Atommodell (1913): Wasserstoffatom
-Elektronen (-) umkreisen auf geschlossenen Bahnen den Kern (+:Proton)
-Gleichgewicht aus Coulombanziehung und Zentrifugalkraft
Problem: solche Bahn ist für jeden Radius möglich
(keine diskreten Energien !) und Energie
wird abgestrahlt (> Spiralbahn)
Ausweg:
Wellenfunktion des Elektrons
stabile Bahnen nur bei bestimmten Energien und Drehimpulsen.
Für Coulombpotential: E =
−R
n2
mit n = 1,2,3,4,…
„Rydbergenergie“ R = 13,6 eV. Für n → ∞ ist E = 0, d.h.
ungebundenes Elektron.
h
L
=
n
⋅
Außerdem Drehimpuls
mit n = 0,1,2,….
2π
EPI WS 2006/07 Dünnweber/Faessler
23. Atomphysik,
Atomphysik, Röntgenstrahlung
Energieübergänge im Wasserstoffatom
1 
1
Em = R 2 − 2 
n m 
allgemein für Atom mit
einem Außenelektron und
Ladungszustand Z:
1
En = − R ⋅ Z ⋅ 2
n
2
14243
Röntgenstrahlung
für Z ≥ 10
sichtbar
n=1: Grundzustand, stabil (13.6.Z2 eV nötig, um e- zu entfernen)
n>1: angeregte Zustände, Abregung durch Aussendung von Photonen
- Atom kann nur diskrete Energien aufnehmen
-> durch Ug beschleunigtes Elektron stößt nur
elastisch in einem Gas, solange Ekin=e.Ug kleiner
als Anregungsenergie des Atoms ist.
-> sobald Ekin>E*: Anregung durch inelast. Stoß
EPI WS 2006/07 Dünnweber/Faessler
Kohärente Abregung vieler Atome (Moleküle):
LASER
Niveauschema für Atom mit metastabilem Zustand
a) externe Anregung („Pumpen“)
b) spontaner Übergang
c) stimulierte Emission
(phasengleich mit Photon c‘ von Nachbaratomen)
Laserlicht:
- kohärent (d.h. alle Wellenzüge in Phase)
- sehr geringe Divergenz
- fast monochromatisch (d.h. frequenzscharf)
EPI WS 2006/07 Dünnweber/Faessler
23. Atomphysik,
Atomphysik, Röntgenstrahlung
Franck-Hertz-Versuch:
Röhre mit Hg-Gas, das von Elektronen
aus einer Glühkathode beschossen wird
EPI WS 2006/07 Dünnweber/Faessler
23. Atomphysik,
Atomphysik, Röntgenstrahlung
Moderne Vorstellung des Atomaufbaus
Orbitale der Elektronen werden quantenmechanisch nicht durch Bahnen
beschrieben, sondern durch ‘stehende Wellen’, die durch Quantenzahlen
(n,l,m) beschrieben werden.
Wellenfuktion:
Quantenzahlen:
Haupt-QZ: n= 1,2,…
Drehimpuls-QZ: l= 0,1,..(n-1)
Magnet. QZ: m= -l,… ,+l
Spin: +/- 1/2
Das Quadrat der Wellenfunktion beschreibt die Wahrscheinlichkeit,
das Elektron zu einer Zeit t an einem Ort x anzutreffen. Das Maximum
der Wahrscheinlichkeit liegt beim s-Orbital bei der Bohrschen Bahn.
EPI WS 2006/07 Dünnweber/Faessler
23. Atomphysik,
Atomphysik, Röntgenstrahlung
Periodensystem der Elemente
Bor
Stickstoff
EPI WS 2006/07 Dünnweber/Faessler