23. Vorlesung EP
Werbung

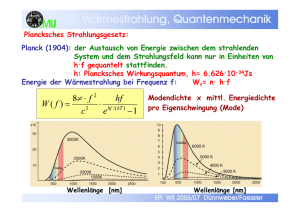
23. Vorlesung EP IV Optik 26. Beugung (Wellenoptik) V Strahlung, Atome, Kerne 27. Wärmestrahlung und Quantenmechanik Strahlung: Stoff der Optik, Wärme-, Elektrizitätslehre u. Quantenphysik Photometrie Plancksches Strahlungsgesetz Welle/Teilchen Dualismus für Strahlung und Materie Versuche: Lesliewürfel (Emissionsvermögen verschiedener Oberflächen) quadratisches Abstandsgesetz für Bestrahlungsstärke Schwarzer Strahler (Kasten mit Loch) Fotoeffekt: Entladung einer Metallplatte durch Licht Fotoeffekt: Bestimmung von h Elektronenbeugung EP WS 2009/10 Dünnweber/Faessler V.STRAHLUNG, ATOME,KERNE 27. Wärmestrahlung und Quantenmechanik Jeder Körper emittiert und absorbiert elektromagnetische Strahlung. Nicht nur Mobiltelephone, menschliche Körper, einfach alles..) Wichtig für Wärmetransport und Temperaturausgleich etc., s. Vorlesung 15, Kap.II, 15 und nächste Seite Intensität der Strahlung als Funktion der Wellenlänge und Temperatur (Sichtbares Licht nur ein Teil des Spektrums): a) kontinuierliche Strahlung: Spektrum und Intensität stark temperaturabhängig -> Wärmestrahlung b) diskrete Strahlung: Linienspektren stark von strahlender Substanz abhängig -> Atomphysik EP WS 2009/10 Dünnweber/Faessler Photometrie Photometrische Größen beschreiben den Teil der elektromagnetischen Strahlung, den das Auge wahrnimmt (sichtbares Licht). Licht transportiert Energie bzw Intensität I [Watt/m2]. (Siehe auch Vorlesung 20) Beispiel: Physikalische Intensität sei I = 1W/m2. Auge nimmt nur Bruchteil davon wahr. Dann ist gesehene Intensität= Bruchteil von 1W/m2. Man definiert photometrische Größen mit Standardkerze Candela, siehe nächste Seite EP WS 2009/10 Dünnweber/Faessler Physikalische Größe Photometrische Größe Strahlungsstärke [W/sr] Lichtstärke [ 1 Candela = 1cd = 1 lm / sr] 1 cd (SI Basiseinheit) = Lichtstärke einer Strahlungsquelle der Wellenlänge 555nm mit Strahlungsstärke 1/683 [W/sr] (sr = Steradian) Strahlungsleistung [J/s= W] Lichtstrom [ Lumen (lm] 1 W mit spektraler Verteilung V(λ) entspricht 683 lm Bestrahlungsstärke= [W/m2] Beleuchtungsstärke [ 1 Lux = 1lx= 1 lm/m2 ] (=Intensität) ----------------------------------------------------------------------------------------------------------Beipiele für Beleuchtungsstärken: Heller Sonnenschein: 10000lx; bedeckter Himmel 1000 lx; Schreibtischbeleuchtung 1000 – 4000 lx Quadratisches Abstandsgesetz (Abstand r von punktförmiger Quelle): Bestrahlungs- und Beleuchtungsstärke sind ~ (1/r)2 ! Extinktionsgesetz: Strahlungsleistung nimmt in absorbierendem Material exponentiell ab I = I0 exp(-Ex) mit materialabhängigem Extinktionskoeffizienten E EP WS 2009/10 Dünnweber/Faessler 27. Strahlung, Quantenmechanik Das Licht, das wir wahrnehmen, geht von den Oberflächen der Objekte aus Emissionsstärke (= - vermögen ) Absorptionsgrad (= - vermögen = = ausgestrahlte Strahlungsenergie E= Flächenelement ⋅ Zeit A= absorbierte Strahlungsleistung auftreffende Strahlungsleistung EP WS 2009/10 Dünnweber/Faessler 27. Strahlung, Quantenmechanik Rolle der Oberfläche für Strahlungsabsorption und -emission VERSUCH Lesliewürfel EP WS 2009/10 Dünnweber/Faessler 27. Strahlung, Quantenmechanik Kirchhoffsches Gesetz: Das Verhältnis E/A ist für alle Oberflächen gleich und hängt nur von Temperatur T und Wellenlänge ab. E/A = f (T,λ) Die Erkärung der gemessenen Funktion f(T,λ) mit den damals, um 1900 bekannten Gesetzen der Thermo- und Elektrodynamik scheiterte. Planck fand einen Weg. Der eine neue Physik, die der Quanten ankündigte. EP WS 2009/10 Dünnweber/Faessler 27. Wärmestrahlung, Quantenmechanik Schwarzkörperstrahlung Für den idealen „Schwarzen Körper“ für alle Wellenlängen λ (realisiert durch Hohlraum mit kleiner Öffnung ) ist A = 1 für alle λ , d.h. alle Energie wird absorbiert. Strahlungsgesetz: Spektrum der Wärmestrahlung, als Funktion der Wellenlänge, siehe nächste Seite. Konnte erst durch Planck 1904 quantitativ richtig erklärt werden. Seine Annahme: Energie ist quantisiert. Kleinstes Quant: E = h ·f = (h·c) / λ mit h = 6,6 · 10-34 [J·s] Der Austausch von Energie kann nur in Einheiten von (h·f) gequantelt stattfinden. EP WS 2009/10 Dünnweber/Faessler 27. Wärmestrahlung, Quantenmechanik Spektra als Funktion der Temperatur T und Wellenlänge: Die Wellenlänge des Strahlungsmaximums verschiebt sich mit der Temperatur gemäß dem Wienschen Verschiebungsgesetz: λmax.T=2.9.10-3 m.K Sonnentemperatur: ~ 5700 K -> Wellenlänge λmax ~ 480 nm ≈ 0,5 µm * Glühlampe (2000K): λmax = 1 µm (infrarot) Mensch: 10 µm *Energie h · f ≈ 3eV Für die gesamte abgestrahlte Leistung gilt (Stefan-Boltzmann-Gesetz): Wellenlänge [nm] Eschwarzer Körper = σ·T4 EP WS 2009/10 Dünnweber/Faessler „Lichtquanten“ verhalten sich wie Wellen (-> Interferenzen), aber auch wie Teilchen: Beispiele für Teilchencharakter: Versuch Photoeffekt. Erklärung siehe nächste Seite. Erklärung des Photoeffekts durch Einstein. (Dafür den Nobelpreis) Comptoneffekt: elastische Streuung von Photon γ an Elektron e- Wie Stoß zweier Kugeln! (Energien Emax bzw. E‘ unabhängig von der Lichtintensität) EP WS 2009/10 Dünnweber/Faessler 27. Wärmestrahlung, Quantenmechanik Wann Licht sich wie Teilchen verhält: Photoeffekt: Ein Metall wird mit Licht einer Wellenlänge (Farbe) bestrahlt und die Energie der emittierten ‘Photoelektronen’ wird gemessen (Gegenfeldmethode: wenn gerade keine Elektronen die Anode mehr erreichen ist eU=mv2/2) Beobachtung: die Energie der Photonen wird nur durch die Farbe des Lichts (λ λ) bestimmt, nicht durch die Intensität. (mehr Licht -> mehr Elektronen) Erklärung: (Einstein 1905) Das Licht wechselwirkt in gequantelten Beträgen h.f -> weitere Methode, die Naturkonstante h zu bestimmen: h=e.∆U/∆ ∆f ∆U ∆f EP WS 2009/10 Dünnweber/Faessler 27. Wärmestrahlung, Quantenmechanik Wann Licht sich wie eine Welle verhält Licht (elektromagnetische Wellen) verhält sich bei der Ausbreitung wie eine Welle -> Interferenz, Beugung … (Nur wenn es wechselwirkt auf atomarem Niveau (z.B. Absorption, wie oben beim Photoeffekt, verhält es sich wie ein Teilchen (Photon) mit Energie hf) Wellenpaket: Lokalisierung durch Überlagerung verschiedener Frequenzen (s. Schwebung). ∆x groß ↔ schmale Frequenzverteilung (schmale Impulsverteilung) ∆x klein ↔ breite Impulsverteilung Allgemein gilt die Heisenbergsche Unschärferelation: h ∆p ⋅ ∆x ≥ = h ebenso 2π ∆E ⋅ ∆t ≥ h Wenn sich Wellen wie Licht wie Teilchen verhalten, stellt sich Frage: Verhalten sich Teilchen wie Elektronen auch wie Wellen? EP WS 2009/10 Dünnweber/Faessler 27. Wärmestrahlung, Quantenmechanik Wellencharakter massiver Teilchen: Test: Interferenzexperimente mit Elektronenstrahlen geht sogar mit einzelnen Elektronen -> Wellenpaket f de Broglie (1924): wie bei Licht h 2π ,k= h = 2π λ diese Wellenlänge ist sehr klein (energieabhängig): 1 keV Elektron-> 39 pm EP WS 2009/10 Dünnweber/Faessler EP WS 2009/10 Dünnweber/Faessler EP WS 2009/10 Dünnweber/Faessler Zusammenfassung: EP WS 2009/10 Dünnweber/Faessler