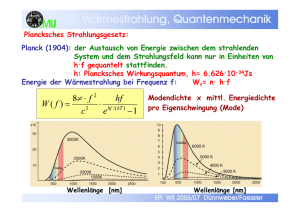
EP WS 2009/10 Dünnweber/Faessler

Für Geowissenschaftler
EP WS 2009/10 Dünnweber/Faessler
Termin Nachholklausur
Vorschlag Mittwoch 14.4.10
EP WS 2009/10 Dünnweber/Faessler
25. Vorlesung EP
V. STRAHLUNG, ATOME, KERNE
27. Wärmestrahlung und Quantenmechanik
Photometrie
Plancksches Strahlungsgesetze,
Welle/Teilchen Dualismus für Strahlung und Materie
28. Atomphysik, Röntgenstrahlung
Versuche:
Elektronenbeugung
Franck-Hertz
EP WS 2009/10 Dünnweber/Faessler
27. Wärmestrahlung, Quantenmechanik
Wellencharakter massiver Teilchen:
Test: Interferenzexperimente mit Elektronenstrahlen
Die Wellenlänge ist sehr klein (energieabhängig):
1 keV Elektron-> 39 pm = 39 •10-12 m
EP WS 2009/10 Dünnweber/Faessler
Schon vor Beobachtung der Beugung von Elektronen kam Louis de
Broglie 1924 zum Schluss, dass Teilchen auch Wellen sind mit Wellenlänge:
λ= h/p
(de Broglie- Wellenlänge)
und Frequenz f = E /h (Einsteins Relation für Photon, aber hier relativistische
Energie für Teilchen mit Masse: E= mc2 )
(Folgt aus Phase von Welle φ = ωt-kz , siehe Vorlesung 12, mit
Ausbreitungsgeschwindigkeit v = dω/dk von Wellenpaketen und spezieller Relativität)
Das Erstaunliche ist, dass sich Interferenzen, zum Beispiel beim Doppelspalt
–Experiment, auch ergeben, wenn immer garantiert nur ein Elektron auf den
Doppelspalt zufliegt.
Zusammenfassung:
Elektromagnetische Wellen und Teilchen verhalten sich wie Wellen,
bei der Ausbreitung im Raum, solange sie nicht wechselwirken.
Und wie Teilchen, wenn sie wechselwirken.
EP WS 2009/10 Dünnweber/Faessler
Neues Kapitel :
28. Atomphysik, Röntgenstrahlung
Umgekehrt werden nur Lichtquanten mit Differenzenergien ∆Ei absorbiert, wenn ein
Medium mit den entsprechenden Atomen bestrahlt wird (Absorptionsschattenlinien).
EP WS 2009/10 Dünnweber/Faessler
28. Atomphysik, Röntgenstrahlung
Aufbau des Atoms (Streuexperimente) :
Rutherford (1911): Streuung von α Teilchen aus radioaktivem Präparat
an einer Goldfolie (Ekin ca. 5 MeV)
Die meisten α Teilchen fliegen gerade durch die Folie durch.
Einige werde stark abgelenkt. Aus Winkelverteilung folgt:
-> fast gesamte Masse des Atoms ist in winzigem Kern konzentriert.
Die Elektronen umkreisen ihn zum Teil in grossem Abstand.
EP WS 2009/10 Dünnweber/Faessler
28. Atomphysik, Röntgenstrahlung
Bohrsches Atommodell (1913): Wasserstoffatom
-Elektronen (-) umkreisen auf geschlossenen Bahnen den Kern (+:Proton)
-Gleichgewicht aus Coulombanziehung und Zentrifugalkraft
Problem: solche Bahn ist für jeden Radius möglich
(keine diskreten Energien !) und Energie
wird abgestrahlt (> Spiralbahn)
Ausweg:
Stehende Welle mit de Broglie-Wellenlänge
:
λ=h/p → 2πr = nλ
Stabile Bahnen nur bei bestimmten Energien und Drehimpulsen.
Für Coulombpotential: E =
−R
mit n = 1,2,3,4,… E negativ↔gebunden
2
n
„Rydbergenergie“ R = 13,6 eV.
Für n → ∞
(Außerdem Drehimpuls pr = L=n ⋅
h
2π
ist E = 0, d.h. Elektron ungebunden.
Hier stimmt Bohrmodell nicht.)
EP WS 2009/10 Dünnweber/Faessler
28. Atomphysik, Röntgenstrahlung
Energieübergänge im Wasserstoffatom
1 
1
Em = R 2 − 2 
n m 
allgemein für Atom oder
Ion mit 1 Elektron und
Kernladung Z:
1
En = − R ⋅ Z ⋅ 2
n
2
14243
Röntgenstrahlung
für Z ≥ 10
sichtbar
n=1: Grundzustand, stabil (13.6.Z2 eV nötig, um e- zu entfernen)
n>1: angeregte Zustände, Abregung durch Aussendung von Photonen
„Serien“ waren bekannt, lange vor Bohr. Der aber nichts davon
wusste, nach seiner Aussage.
EP WS 2009/10 Dünnweber/Faessler
Laser (*1960)
Light Amplification by Stimulated Emission of Radiation
Kohärente Abregung vieler Atome (Moleküle).
Niveauschema für Atom mit metastabilem Zustand Z:
a) externe Anregung („Pumpen“) via a
b) spontaner Übergang b zum metastabilen Zustand Z
c) stimulierte Emission von Z zum Grundzustand
(phasengleich mit Photon c‘ von Nachbaratomen)
Laserlicht:
- kohärent (d.h. alle Wellenzüge in Phase)
- sehr geringe Divergenz
- fast monochromatisch (d.h. frequenzscharf)
EP WS 2009/10 Dünnweber/Faessler
28. Atomphysik, Röntgenstrahlung
Anregung von Atomen durch inelastische Elektronenstreuung
Da Atome nur diskrete Energien aufnehmen können,
erfährt ein durch eine Spannung Ug beschleunigtes
Elektron in einem Gas nur elastische Stöße,
solange seine kinetische Energie kleiner ist,
als die Anregungsenergie des Atoms!
(Diese Elektronen haben die Energie Ekin = e · Ug)
Bei den elastischen Stößen an den Atomen bleibt Ekin
fast erhalten, Stoß von leichtem mit schwerem Teilchen.)
Überschreitet Ekin aber die Anregungsenergie ∆E = (Em – En) des Atoms,
wird ein inelastischer Stoß ausgeführt, das Atom wird angeregt.
Das Elektron hat dann die Restenergie ERest = e Ug - ∆E.
Auf dieser Idee beruht das folgende historische Experiment von
Franck und Hertz, mit dem ein Beweis für diskrete AnregungsEnergien von Atomen erbracht wurde. Versuch Franck-Hertz,
s. nächste Seite
EP WS 2009/10 Dünnweber/Faessler
28. Atomphysik, Röntgenstrahlung
Franck-Hertz-Versuch 1913:
Röhre mit Hg-Gas, das von Elektronen
aus einer Glühkathode beschossen wird
EP WS 2009/10 Dünnweber/Faessler
28. Atomphysik, Röntgenstrahlung
Moderne Vorstellung des Atomaufbaus
Orbitale der Elektronen werden quantenmechanisch nicht durch klassische Bahnenbeschrieben, sondern durch ‘stehende Wellen’, die durch
Quantenzahlen (n,l,m) charakterisiert werden.
Wellenfuktion:
Quantenzahlen:
Haupt-QZ:
n = 1,2,…
Drehimpuls-QZ:
L = 0,1,..(n-1)
Drehimpulsrichtungs- QZ: Lz = -L,… ,+L
Spinrichtungs -QZ:
sz = +1/2, - 1/2
Das Quadrat der Wellenfunktion beschreibt die Wahrscheinlichkeit,
das Elektron zu einer Zeit t an einem Ort x anzutreffen. Das Maximum
der Wahrscheinlichkeit liegt beim s-Orbital bei der Bohrschen Bahn.
EP WS 2009/10 Dünnweber/Faessler
28. Atomphysik, Röntgenstrahlung
Periodensystem der Elemente
*
Bor
Stickstoff
* und m, siehe vorige Seite
EP WS 2009/10 Dünnweber/Faessler