14. elektrischer elektrischer elektrischer Strom

14. elektrischer Strom
Ladungstransport, elektrischer Strom
In Festkörpern:
Isolatoren: alle Elektronen fest am Atom
gebunden, bei Zimmertemperatur
keine freien Elektronen
-> kein Stromfluß
Metalle: Ladungsträger = Elektronen, die
nicht an best. Atome im Kristallgitter gebunden sind.
In einem elektr. Leiter sind Ladungsträger
frei beweglich
Legt man an einen solchen Leiter eine Spannung U, so geraten die
Ladungen in Bewegung, es fließt ein elektr. Strom:
Elektr. Strom: I= ∆Q/∆
∆t
[I]= Ampere; 1 A = 1 C/s
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Elektronenbewegung:
- Beschleunigung durch elektr. Felder für
kurze Zeiten (~10-14 s)
- Abbremsung durch Stöße mit Atomen
-> konstante Driftgeschwindigkeit v
(ähnlich dem Fall einer Kugel im zähen
Medium: geschwindigkeitsabh. Reibungkraft)
im Leiter: -Reibungskraft FR
- Kraft durch äußeres Feld: Fe
U
= γR ⋅ v : v ~ U
d
∆Q
∆x
I=
= A ⋅ρ⋅
= A ⋅ρ⋅ v : I ~ v
∆t
∆t
Ladung im Teilvolumen:
∆Q
∆Q
ρ=
=
⇒ ∆Q = A ⋅ ρ ⋅ ∆x
∆V A ⋅ ∆x
Fe = FR ⇒ e ⋅ E = e ⋅
Ohmsches Gesetz:
U= R.I
I~U
R: elektr. Widerstand
[R]: Ω : Ohm =V/A
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Die Driftgeschwindigkeit der Elektronen ist typisch einige mm/s. Dagegen ist
die elektrische Schalt- oder Signalgeschwindigkeit durch die Ausbreitungsgeschwindigkeit der Kraftfelder gegeben und fast gleich der Lichtgeschwindigkeit (300 000 km/s).
Analogie: Schalter
Wasserhahn
→ Leitungsdraht
→ Lampe
→ gefüllter Wasserschlauch
→ Rasensprenger
Widerstandsdraht:
R= ρ . l/A,
ρ: spezif. Widerstand
(Länge l, Querschnitt A)
- allgemein ist der Widerstand R nicht konstant, sondern hängt z.B.
von der Temperatur ab.
- Metalle: R steigt mit der Temperatur (‘Reibung’ nimmt zu)
- Halbleiter: R sinkt mit T (mehr freie Ladungsträger)
- das Ohmsche Gesetz gilt für den Fall eines konstanten Widerstands.
- für viele Materialien gilt dies bei konstanter Temperatur
EPI WS 2006/07 Dünnweber/Faessler
EPI WS 2006/07 Dünnweber/Faessler
Stromleitung in Flüssigkeiten
galvanisches Element (Batterie):
Zn Ionen gehen eher in Lösung als Cu Ionen (→ Spannungsreihe der Metalle)
Für 1 mol NaCl (≈58 gramm):
Es werden NA= 6 · 1023 Kationen/Anionen abgeschieden („Elektrolyse“)
Q = 6 · 1023 · e = 9,6 · 104 Coulomb
= „Faraday-Konstante“ = Ladung pro abgeschiedenes Mol
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Stromleitung in Flüssigkeiten
- geladene Atome-Moleküle = Ionen (pos., neg.) übernehmen
Ladungstransport anstatt der Elektronen im Festkörper
- Stromtransport = Materialtransport
transportierte Ladung: I=Q/t
- pro mol werden Q= Z.NA.e Ladungen benötigt (Z: Wertigkeit)
H2O + NaCl (Elektrolyt): Na+Cl: Z=1 (+ =Kationen > Kathode)
Zn2+ SO42- : Z=2
NA.e: Faraday-Konstante F= 96484 C/mol
Stromleitung hängt von Konzentration und Beweglichkeit der Ionen ab
ca. 104 mal geringer als in Metallen
an Elektroden: Neutralisierung der Ionen durch Elektronenaufnahme/
-abgabe und Materialablagerung oder –Lösung
(Elektrolyse)
EPI WS 2006/07 Dünnweber/Faessler
Stromleitung in Gasen
Gase sind Nichtleiter, geringe Ionendichte durch radioaktive Strahlung
und UV-Licht
→ geringer Strom bei niedriger Spannung
Gasentladung bei hoher Spannung
(Blitz in Luft bei 106 V/m)
Zwischen den Stößen gewinnt das Elektron im E-Feld genügend
Energie, um weitere Elektronen aus den Atomhüllen zu stoßen
(„Stoßionisation“, dabei auch Anregung der Atome mit nachfolgender Lichtemission).
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Stromleitung in Gasen:
Gasentladung:
Beschleunigung durch Felder,
Abbremsung durch Stöße
->konstante Driftgeschwindigkeit
→Anregen der Gasmoleküle
(Leuchterscheinungen)
→Stoßionisation (neue Ladungsträger
werden erzeugt, Lawinenverstärkung)
Anwendungen:
Leuchtstofflampen: niedriger Druck, ca. 10-2 mbar
Strahlung durch Leuchtstoffe an Röhrenwand
sichtbar machen (selbst meist UV)
Nachweis v. rad. Strahlung: Geiger-Müller Zählrohr,
Natur: Blitz
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Stromleitung im Vakuum:
- keine freien Ladungsträger
vorhanden
- Erzeugung z.B. durch Glühemission:
> freie Elektronen im Vakuum:
benötigt wird genügend Energie
zur Überwindung der Austrittsarbeit
beschleunigt durch Hochspannung
r
r
- Anwendungen: Röntgenröhre,
( F = −e ⋅ E )
Fernsehröhre
Oszilloskop,
Elektronen-Mikroskop,
Teilchenbeschleuniger
In der Atom-, Kern- und Teilchenphysik oft benutzte Einheit:
Elektronenvolt [eV]: 1 eV = 1,6 ·10-19 C·V = 1,6 ·10-19 J
Ein Elektron hat nach Durchlaufen einer Potentialdifferenz von
1 Volt die kinetische Energie 1 Elektronenvolt.
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Elektrische Stromkreise:
Widerstand
U
Widerstand R
(Leiter)
Kennlinie: Zusammenhang zwischen Strom
und Spannung
Ohmscher Widerstand (U=R.I): Gerade
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Parallel- und Serienschaltung von Widerständen:
Parallelschaltung:
Serienschaltung (Reihen-):
Der Strom I spaltet sich in die
Ströme I1 und I2 auf:
U
U
I = I1 + I2 mit I1 =
und I 2 =
R2
R1
I =U(
1 1
1
1 1
+ )⇒
= +
R1 R2
Rges R1 R2
Die Spannung U fällt nacheinander
an den Widerständen R1 und R2 ab:
U = U1 + U2
Rges = R1 + R2
→ U=Rges· I
EPI WS 2006/07 Dünnweber/Faessler
14. elektrischer Strom
Allgemein: Kirchhoffsche Gesetze
EPI WS 2006/07 Dünnweber/Faessler
r
E
Leistung
Q
Widerstandsdraht
x
U
⋅x = Q⋅U
{
Arbeit W = F ⋅ x = Q ⋅ E
U
Leistung P =
W Q
= ⋅U = I⋅U
t
t
Für Ohmschen Widerstand:
P = R · I²
→ Wärmeenergie (+ Strahlungsenergie)
Einheit von P:
Volt · Ampere = Watt
V ·A
=W
EPI WS 2006/07 Dünnweber/Faessler
15. magnetische Felder
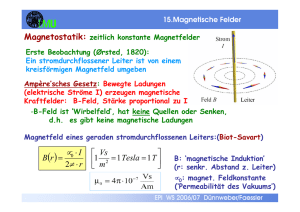
Magnetostatik: zeitlich konstante Magnetfelder
Ein stromdurchflossener Leiter ist von einem
kreisförmigen Magnetfeld umgeben
(Ørsted, 1820)
Bewegte Ladungen (elektrische Ströme)
erzeugen magnetische Kraftfelder:
B-Feld
- B-Feld ist ‘Wirbelfeld‘, hat keine Quellen oder Senken
- es gibt keine magnetische Ladung (Ampère’sches Gesetz)
In einer Spule addieren sich die Felder benachbarter Drähte vektoriell. Es ergibt sich eine im
Vergleich zum Einzeldraht höhere Feldliniendichte
im Inneren der Spule, die annähernd homogen ist.
Mit Eisenfeilspänen läßt sich das magnetische Kraftfeld sichtbar machen.
EPI WS 2006/07 Dünnweber/Faessler