13. Elektrostatik Elektrostatik

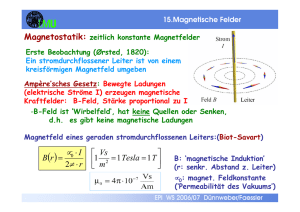
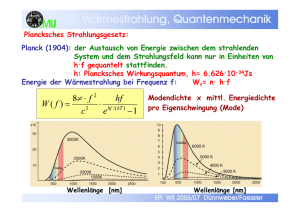
13. Elektrostatik
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
Nachweis elektrischer Ladung
Gleiche Ladungen stoßen sich ab, verteilen sich also gleichmäßig auf
leitenden Oberflächen.
Sie wandern also vom Stab auf das Elektrometer, dessen Enden sich ebenfalls
proportional zur Ladungsmenge abstoßen.
EPI WS 2006/07 Dünnweber/Faessler
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
Elektrische Ladung
•Zwei Arten (+ und -) unterscheidbar durch Kraftwirkung
•Ladung tritt in diskreten Mengen auf
•kleinste Ladungsmenge: Elementarladung e (z.B. des Elektrons)
•Die Gesamtladung eines Systems bleibt immer erhalten
Q = ± n⋅e
e = 1.6 ⋅10 −19 C
Einheit Coulomb = Amperesekunde (1 C = 1 A · s)
EPI WS 2006/07 Dünnweber/Faessler
Kräfte zwischen Ladungen – Coulomb Gesetz
r
F=
r
1 q1 ⋅ q 2 r
⋅r
2
4π ε 0 r
r
1 q1 ⋅ q 2
F=
4π ε 0 r 2
ε0 = 8,854 · 10-12 C2/(N·m2)
Elektrische Feldstärke
r
r F
E=
q2
„Dielektrizitätskonstante des Vakuums“
(d.h. Kraft pro positive Pr obeladung q 2 )
r
1
q1 r
⋅
⋅ r
4πε 0 r 2 | r |
1
q
E(r ) =
⋅ 21
4πε 0 r
r
Kraftfeld der Ladung q1: E( rr ) =
1 q1 ⋅ q 2
⋅ 2
Auf die Probeladung q2 wirkt also die Kraft
4πε 0
r
EPI WS 2006/07 Dünnweber/Faessler
F = E (r ) ⋅ q 2 =
Elektrische Felder (Feldlinien)
repräsentieren das Kraftfeld einer
Ladungsverteilung auf eine
positive Probeladung - die Liniendichte die Stärke, der Pfeil die Richtung
+
Ladungen sind Quellen
und Senken von elektrischen Feldern.
Gauß‘scher Satz:
∑
geschlossene
Oberfläche
gleiche Ladungen
verschiedene Ladungen
r
1
E ⋅ ∆A = q1
ε0
(→Coulombgesetz)
EPI WS 2006/07 Dünnweber/Faessler
Superposition von elektrischen Feldern:
Feld ist homogen
innerhalb von entgegengesetzt aufgeladenen Platten
(Plattenkondensator)
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
Potential (ϕ
ϕ):
Wenn man eine Ladung q2 im elektr. Feld vom
Ort r1 zum Ort r2 verschiebt, dann wird
Arbeit verrichtet:
r
r2
r r r
W = q 2 ⋅ r∫ E( r )d r
r1
= q2 · E · d
für homogenes
r Feld
r und
Abstand d = | r2 − r1 |
Dadurch wird potentielle Energie ∆ Epot gespeichert.
Definiert man das Potential φ= Epot / q2, so gilt
∆Epot = q2 · (φ2 - φ1)
Man definiert die Spannung U21=φ2 – φ1 = ∆Epot/q2
Die elektrische Spannung ist immer zwischen
2 Punkten definiert!
Wegen Energieerhaltung gilt:
W = q 2 ⋅ E ⋅ d = q 2 ⋅ (ϕ 2 − ϕ1 ) = q 2 ⋅ U 21
→
U21 = E · d
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
Einheit f. Spannung u. Potential: 1 Volt = 1
Joule
Coulomb
→1J=1V·C=1V·A·s
Bsp.: Elektrisches Potential eines Ortes 2 relativ zu einem (willkürlich
gewählten) Bezugspunkt 1:
ϕ(2)= 240 V, ϕ(1) = 0 V (geerdet): U21= ϕ(2) – ϕ(1) = 240 V
Merke: das Potential ist höher, wo sich mehr positive Ladung befindet
Kondensator:
2 parallele Platten, an denen eine
elektrische Spannung U anliegt.
Man findet:
E0 =
U 1 Q
= ⋅
d ε0 A
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
Kapazität C:
(zur Aufnahme von Ladungen)
C=
Q
U
Kapazität eines Plattenkondensators:
(Vakuum zwischen den Platten)
 As

1
=
1
Farad
=
1
F
 V

A
C = ε0
d
Vergrößerung der Kapazität: Medium (Isolator) zwischen die Platten
einfügen: Dielektrikum: ε0 (Vakuum) -> ε (Medium) = ε0 . εrel > ε0
Die Moleküle des Mediums mit einem elektr. Dipolmoment werden im
elektrischen Feld des Kondensators ausgerichtet (‘polarisiert‘):
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
Dielektrikum zwischen den Platten:
bei gleicher Ladungsdichte auf Platten wird das E-Feld geschwächt
(durch Polarisation des Dielektrikums).
Bei gleicher anliegender Spannung bekommt man höhere Ladungsdichte
auf den Platten, die Kapazität wächst mit εr :
Elektr. Feld:
Kapazität:
Q0
E=
A ⋅ ε 0ε r
Q
A
C = = ε 0ε r
U
d
ε0εr = ε = Dielektrizitätskonstante
mit εr > 1, meist nahe 1, für Wasser εr = 70 (für Vakuum εr = 1)
EPI WS 2006/07 Dünnweber/Faessler
r
Leiter im E
- Feld
r
E
steht immer senkrecht auf Leiteroberfläche, die Ladung sammelt
sich immer an der Oberfläche.
Faraday-Käfig: Abschirmung äußerer Felder durch ein Metallgehäuse.
Faraday-Becher:
Die Ladungen wandern zur MetallbecherOberfläche. Die Ladung kann portionsweise
bis zu sehr großen Ladungsmengen transportiert werden (→s. Bandgenerator)
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
(1) nach Trennung im elektr. Feld
sind die Kugeln geladen.
(1)
(2) jede Kugel hat im elektr. Feld
gleichviel positive wie negative
Ladungen.
nach der Trennung im Feld bleiben die
Kugeln ungeladen.
Influenz ist verantwortlich für die
Abschirmwirkung metallischer Objekte
gegenüber elektrischen Feldern:
(2)
-> Faradayscher Käfig
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
Influenz:
Der Vorgang der Aufladung von Metalloberflächen im äußeren
elektrischen Feld wird als Influenz bezeichnet.
Die Oberflächenladungen nennt man Influenzladungen.
Wenn man leitende Kugeln in ein elektrisches Feld bringt,
verschieben sich die in ihnen frei beweglichen Ladungen
(im Gegensatz zur Polarisation von nichtleitenden Dielektrika)
EPI WS 2006/07 Dünnweber/Faessler
13. Elektrostatik
EPI WS 2006/07 Dünnweber/Faessler