Vektorrechnung im 3-dimensionalen Raum - Math
Werbung

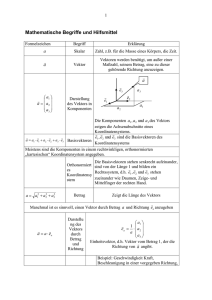
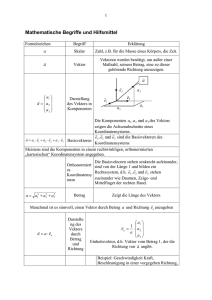
Vektorrechnung im 3-dimensionalen Raum 20 Vorkurs, Mathematik Grundbegriffe Komponentendarstellung: x r = x ex y ey z ez = y z z Betrag: ∣ r ∣ = r = r ex x 0 = ey y x y 2 y z 2 0 0 0 Normierung: er = 21 2 Nullvektor: z ez x r ∣ r ∣ Vorkurs, Mathematik Aufgaben 1-3 Aufgabe 1: Folgende Vektoren sind gegeben: 4 a = 2 , −1 b = 2 4 , 0 −2 c = 1 2 Führen Sie folgende Vektoradditionen rechnerisch durch: Aufgabe 2: a. a b, e. a − b c , f. c. b c , d. a b c − a b − c b = b1 3 b3 Untersuchen Sie , ob die drei Punkte A, B und C auf einer Geraden liegen: A 0, 1, − 1 , 22-1 a c , Bestimmen Sie die fehlenden Koordinaten so, dass die Vektoren kollinear sind 2 a = 1 , 5 Aufgabe 3: b. B −2, 1, − 2 , C 6, 1, 2 Vorkurs, Mathematik Lösungen 1-3 Lösung 1: a. 22-1 6 6 , −1 b. 2 3 , 1 c. 0 5 , 2 d. 4 7 , 1 e. 0 −1 , 1 f. 0 1 −1 Lösung 2: a = b , Lösung 3: 1 3 Die drei Punkte A, B und C liegen auf einer Geraden. Bedingung: b1 = 6 , b 3 = 15 AB = ⋅ AC , =− Vorkurs, Mathematik Skalarprodukt a ⋅ b = ∣a∣⋅∣b∣⋅cos = a b ⋅cos 0° 180° bx a ⋅ b = a x , a y , a z ⋅ b y = a x b x a y b y a z b z bz Der von diesen Vektoren eingeschlossene Winkel cos = a ⋅ b = | a | ⋅| b | ⋅b a = arccos | a | ⋅ | b | a ⋅ b = 0 ⇔ a ax bx a y b y az bz 2 x 2 2 2 2 a ⊥ b ° 23 2 a⋅a = ∣ a ∣⋅∣ a ∣⋅ cos 0 = ∣ a ∣ = a ∣ a∣= a = 2 a y a z ⋅ b x b y b z a ⋅a = a 2 x 2 2 ⇒ 2 a y az Vorkurs, Mathematik Skalarprodukt / Augaben 1-2 Aufgabe 1: a) c) Berechnen Sie das Skalarprodukt folgender Vektoren 2 a = −3 , 5 a = Aufgabe 2: −3 4 2 1 2 , 0 5 b = 3 4 1 −1 b) d) a = a = 2 1 , 1 b = 0 1 −1 1 2 , 0 5 1 2 b = 6 −1 Bestimmen Sie die fehlenden Kordinaten so, dass das Skalarprodukt den Wert k hat a) b) 24-1 b = a = a = 0 a2 , 3 b = b1 1 , −5 2 4 , a3 b = 2 1 , 2 k = −10 k=2 Vorkurs, Mathematik Skalarprodukt, Betrag / Augaben 3-6 Aufgabe 3: Berechnen Sie den Betrag des Vektors v = 1, 2, 5, 3, 4, − 3, 0 Aufgabe 4: Zeigen Sie, dass die drei Vektoren ein rechtwinkliges Dreieck bilden 1 a = 4 , −2 Aufgabe 5: c = −1 6 1 4 b = −5 , −2 c = 2 1 , 1 d = 0 1 −1 Bestimmen Sie den Parameter so, dass der Vektor a die Länge 3 hat a) 24-2 −2 2 , 3 Berechnen Sie die Beträge folgender Vektoren und geben Sie jeweils die Einheitsvektoren an 2 a = −3 , 5 Aufgabe 6: b = a = 2 , 1 b) a = AB , A = , 0, 1 , B = 1, 2, 2 Vorkurs, Mathematik Skalarprodukt, Betrag / Lösungen Lösung 1: a ) −8 , Lösung 2: a) 0 ⋅5 b 1 a 2 − 15 = −10, b) 4 4 2 a 3 = 2, b) 0, c ) 6, d) 0 a 2 = 5, b1 ∈ ℝ a 3 = −3 Lösung 3: | v | = 1 2 5 3 4 −3 0 = 64 = 8 Lösung 4: c = a b , 2 2 2 2 2 2 2 a ⊥ b Lösung 5: | a | = 38 , | b | = 45 = 3 5 , 2 1 ea = −3 , 38 5 4 1 eb = −5 , 45 −2 | c | = 6 , | d | = 2 0 1 ed = 1 2 −1 2 = 4, 1, 2 = ±2 1 ec = 6 2 1 , 1 Lösung 6: 24-3 a) | a | = 2 5 = 3 , b) | a | = 1− 2 1 = 3 , 2 2 2 5 = 9 , 2 1− = 4 , 1 = 3, 2 = −1 Vorkurs, Mathematik Richtungswinkel eines Vektors Ein Vektor ist eindeutig durch Betrag und Richtung festgelegt. Die Richtung bestimmen wir z.B. durch die Winkel, die der Vektor mit den drei Basisvektoren bildet. z az a cos = ay y a ⋅ ex ax ax = = | a | ⋅ | ex | | a |⋅1 | a| − ist der Winkel, den der Vektor ax mit der x-Achse bildet. x Richtungskosinusse: ax cos = , | a | cos = ay , | a| cos = az | a| Die Richtungswinkel sind nicht unabhängig voneinander, sondern über die Beziehung der Richtungskosinusse cos 2 cos 2 cos 2 = 1 miteinander verknüpft. 25 Vorkurs, Mathematik Richtungswinkel eines Vektors: Aufgaben 7-9 Aufgabe 7: Berechnen Sie den Winkel, der von den Vektoren a und b eingeschlossen wird. Wie groß ist der Winkel, den der Vektor a mit der x-Achse bildet? 2 a ) a = −3 , 5 Aufgabe 8: 4 b = −5 , −2 b ) a = 2 1 , 1 b = 0 1 −1 Berechnen Sie die Länge, den Einheitsvektor und die mit den Basisvektoren gebildeten Winkel des Vektors v = 2 ex − ey − 2 ez Aufgabe 9: Bestimmen Sie die Richtungswinkel der folgenden Vektoren v1 = 26-1 5 1 , 4 −3 v2 = 5 , −8 11 v3 = −2 10 Vorkurs, Mathematik Richtungswinkel eines Vektors: Lösung 7 Lösung 7: 2 a ) a = −3 , 5 ⋅ b a = | a | ⋅ | b | cos = cos = cos = b ) a = a cos = 2 x a 2y a 2z ⋅ b 2x b 2y b 2zy a ⋅ ex a = x = | a | ⋅ | ex | | a| 2 1 , 1 0 b = 1 , −1 = 90 | b | = 45 = 3 5 ax b x a y b y az bz 13 ≃ 0.314 , 38 ⋅ 45 cos = 0 , 26-2 4 b = −5 , | a | = 38 , −2 = 71.68 2 ≃ 0.324 , 38 | a | = 6 , ° = 71.07° | b | = 2 ° 2 ≃ 0.816 , 6 = 35.26° Vorkurs, Mathematik Richtungswinkel eines Vektors: Lösungen 8, 9 Lösung 8: 2 v = 2 ex − ey − 2 ez = −1 −2 ev = | v | = 2 2 12 22 = 3 v 2 1 2 = ex − ey − ez | v | 3 3 3 cos = vx 2 = , | v | 3 ° = 48.11 , cos = ° = 109.28 , vy 1 =− , | v | 3 = 131.49 cos = vz 2 =− | v | 3 ° Lösung 9: v1 : = 39,51° , = 81,12° , v2 : = 107,64 , ° = 59,66 , ° = 97,66 , v3 : 26-3 = 42,83 , = 51,89° ° = 143,91 ° ° = 48,19 ° Vorkurs, Mathematik Projektion eines Vektors auf einen zweiten Vektor b a ba ∣ ba ∣ = ∣ b ∣⋅ cos = ∣ b ∣⋅ a ⋅ b a ⋅ b = ∣ a∣ ∣ a ∣⋅∣ b∣ a a ⋅ b a b a = ∣ b a ∣ ea = ∣ b a ∣ = = ∣ a ∣ ∣ a ∣ ∣ a ∣ Durch Projektion des Vektors b auf den Vektor ba = a ⋅ b ∣ a ∣2 a ⋅ b ∣ a ∣2 a entsteht der Vektor a Es wird als Komponente des Vektors b in Richtung des Vektors 27 a abezeichnet. Vorkurs, Mathematik Projektion eines Vektors auf einen zweiten Vektor: Aufgabe 10 Bestimmen Sie die Projektion des Vektors b auf den Vektor a a ) a = 3 0 , 4 4 b = −1 , 7 ba = 28-1 2 b ) a = −2 1 a ⋅ b ∣ a ∣2 , b = 10 4 −2 a Vorkurs, Mathematik Projektion eines Vektors auf einen zweiten Vektor: Lösung 10 Lösung 10 a): 4 a ⋅ b = 3, 0, 4⋅ −1 = 12 28 = 40 7 ∣ a ∣2 = 32 02 4 2 = 25 ba = a ⋅ b 40 3 a = 0 25 ∣ a ∣2 4 8 = 5 3 0 4 = 4.8 0 6.4 Lösung 10 b): 10 a ⋅ b = 2, − 2, 1 4 −2 = 10 ∣ a ∣2 = 22 −22 12 = 9 ba = 28-2 2 a ⋅ b 10 a = −2 9 ∣ a ∣2 1 20 9 = − 20 9 10 9 Vorkurs, Mathematik