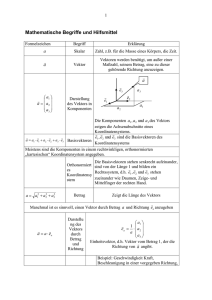
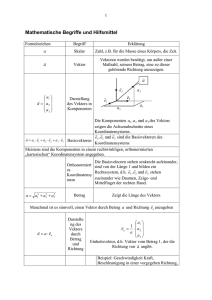
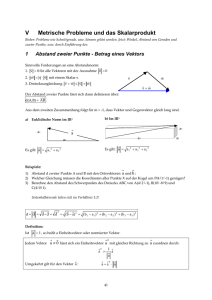
p = ( x,y ) = ( cos(α), sin(α))

David Rival
3.2 und 3.2.1:
Räumliches Sehen und
Koordinaten und Vektoren
Quelle: „Spieleprogrammierung mit DirectX und C++“,
U. Kaiser und P. Lensing, Galileo Computing (2007)
3.1 Räumliches sehen
• Mit 2 Augen werden 2 leicht unterschiedliche 2
Dimensionale Bilder erfasst . Aus den Differenzen der
beiden Einzelbilder wird die fehlende Tiefeninformation
zurück gewonnen und 3D.
• Verdeckung
• Perspektive, Tiefe aus dem Verlauf der Kanten
• Beleuchtung- Schattenwurf
• Flächenschatten und Schlagschatten
• Glanzpunkte ( besonders bei gekrümmten Formen in
Verbindung mit Flächenschatten)
• Bewegung ( die Szene, der Blick des Betrachters)
3.2.1 Koordinaten und Vektoren
(S.139)
Gebundener Vektor als ein Pfeil vom
Kreuzungspunkt der beiden Achsen zum
Punkt
Die Länge des Vektors (S.140)
Die Länge (Betrag) des Vektors
Multiplikation des Vektors v mit
einem Faktor c (Skalar)
Veränderung der Länge durch
Veränderung des Faktors
Addition von 2 Vektoren (S.141)
Addition von Vektor v1 = ( a1, b1 ) und v2 = ( a2, b2 )
v1 + v2 = (a1, b1) + (a2, b2) = ( a1 + a2, b1 + b2 )
Beide Pfeile laufen zusammen zum Ergebnisvektor:
Polarkoordinatendarstellung (S.141)
Beschreibung des Vektors durch seine Länge ‚r‘ und den Winkel ‚α‘
Berechnung der Vektoren durch die Einheitsvektoren e1 = ( 1,0) und e2 = (0,1)
e1 und e2 stehen senkrecht aufeinander und haben die Länge 1
Durch Addition, Multiplikation und Skalar kann jeder Vektor der Ebene berechnet werden
Winkelmessung (S.142)
Messung im Bogenmaß mit Radius = 1
Umfang 2 ‫ת‬
Jedem Winkel lässt sich ein Bogenmaß zwischen
0 und 2 ‫ ת‬zuordnen
Zusammenhang zwischen Winkel ‘ α ‚
und den Achsenabschnitten
Sinus und Cosinus beschreiben die Achsenabschnitte
(S.143/1)
Die Sinus- und die CosinusFunktionen beschreiben die
Achsenabschnitte eines im
Abstand 1 um den
Koordinatenursprung
umlaufenden Punktes P in
Abhängigkeit vom Winkel α, den
die Linie vom Ursprung bis zu
diesem Punkt mit der x-Achse
bildet.
p = ( x,y ) = ( cos(α), sin(α))
Radius mit beliebiger Größe (S.143/2)
Ändern des Radius auf
eine beliebige Größe r
v = r * ( cos(α), sin(α))
Sinus und Cosinus
Funktionen geben die x
und y Koordinaten eines
Vektors, wenn die
Polarkoordinaten bekannt
sind.
Berechnung der Länge (S.144)
Wenn α und r gesucht sind
(Polarkoordinaten)
Berechnung der Länge mit der Formel
des Pythagoras.
Berechnung des Quotienten x / y
Wird als Tangens des Winels α
bezeichnet.
Berechnung von α (S.145/1)
Wenn x > 0 , dann liegt der
gesuchte Bereich um den
Ursprung , zwischen – ‫ת‬/2
und ‫ת‬/2.
Berechnung von α (S.145/2)
Der Bereich zwischen – ‫ת‬/2 und
‫ת‬/2 läst sich durch die
Umkehrfunktion des Tangens,
Arcustangens berechnen.
Die Funktion wird ermittelt durch
Spiegeln des mittleren Asts der
Tangensfunktion an der geraden
y = x.
Für positive Werte von x
Berechnung von α (S.146/1)
Wenn x < 0, wird der „gegenüber“
liegende Punkt mit den
Achsenabschnitten –x und –y betrachtet.
Falls x = 0, entscheidet y,
Projektion eines Vektors auf einen
anderen. (S.146)
2 Vektoren a und b in ihrer Polarkoordinatendarstellung
Zwischen Vektoren b und a
ist der Winkel α – β
Skalarprodukt (S.147)
Zwischen Vektoren b und a
ist der Winkel α – β
Die Länge l der Projektion
des Vektors a auf den Vektor
b wird wie folgt berechnet:
l = ║a║ * cos ( α – β )
Das Skalarprodukt:
║a║ * ║b║ * cos ( α – β ) = <a,b>
Die Projektion a auf b durch:
<a,b> / ║b║² * b
Einfacher: <a,b> = a1 * b1 + a2 * b2
Durch Multiplikation mit b /
║b║ erhalten wir einen
Vektor der parallel zu b ist
und die Länge hat.
Das Ergebnis wird mit ║b║
erweitert:
(S.148/1)
Projektion des Vektors a auf b
Wenn 2 V. senkrecht stehen, dann hat die
Projektion die Länge = 0 ( <a,b> mit Länge=0)
Da die Proj. Eines V. auf sich selbst seiner
Länge entspricht.
Zerlegung eines Vektors bezüglich
anderer Vektoren mit dem
Skalarprodukt.
Zerlegung eines Vektors (S.148/2)
Zerlegung des Vektors w (1,2) bezüglich der
Vektoren v1 (-1,2) und v2 (2,1)
Die Probe: