Addition, Subtraktion, Komponentendarstellung

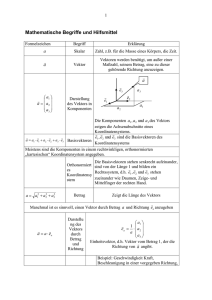
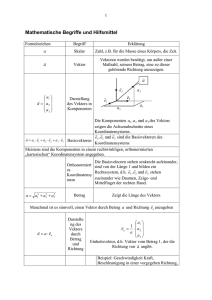
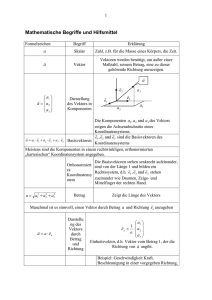
Vektoralgebra
Skalar und Skalarfeld
Skalar: Physikalische Größe, die allein durch Angabe eines reellen Zahlenwertes und einer Maßeinheit
vollständig charakterisiert ist.
Beispiele: Temperatur, Luftdruck, Wellenlänge
 Betrachtet man einen Skalar (z.B. Luftdruck) nicht an einer festen Stelle, sondern im dreidimensionalen Raum als Funktion des Ortes, so spricht man von einem Skalarfeld (Skalarfeld des Luftdrucks).
 Flächen dieses dreidimensionalen Feldes, auf denen der Skalar eine konstante Größe besitzt, werden
als Äquipotenzialflächen bezeichnet.
Im zweidimensionalen Schnitt durch das Skalarfeld (z.B. Luftdruckverteilung in der Wetterkarte) tauchen der Schnitt durch eine Äquipotenzialfläche als Äquipotenziallinie (Isobare) auf.
Vektor und Vektorfeld
Vektor: Vektoren sind gerichtete Größen. Sie werden vollständig charakterisiert durch Angabe eines
Zahlenwertes, einer Maßeinheit und einer Richtung.
Beispiele: Weg, Geschwindigkeit, Kraft, Feldstärke im elektrischen Feld
 Als geometrische Veranschaulichung eines Vektors wird üblicherweise ein Pfeil benutzt, der in die
Richtung des Vektors zeigt und dessen Länge den Betrag des Vektors repräsentiert.
Dieser Pfeil lässt sich in verschiedenen Koordinatensystemen darstellen, wobei die Wahl des Koordinatensystems der Geometrie des behandelten physikalischen Problems entsprechen sollte
– das kann spätere Rechnungen sehr vereinfachen.

Bewegungen im Raum (Länge, Breite, Höhe)  in kartesischen Koordinaten:




r  xi  y  j  z k
Dr. Hempel – Mathematische Grundlagen , Vektoralgebra1
-1-

elektrisches Feld um stromdurchflossenen Leiter  zylindrischen Geometrie
 Zylinderkoordinaten:  , , z
x    cos 
  x2  y 2
  arctan
y    sin 
y
x
zz
zz

Das Gravitationsfeld der Erde wird wegen seiner Kugelsymmetrie sinnvoll in
 Kugelkoordinaten zu behandeln sein: r , ,
x  r  sin   cos 
y  r  sin   sin 
z  r  cos 
r  x2  y2  z 2
  arctan
  arccos




y
x
z
x  y2  z2
2
Die bisherigen Betrachtungen beziehen sich auf die vektoriellen Eigenschaften in einem Punkt des
Raumes.
Kann man aber jedem Punkt des Raumes einen Vektor zuordnen (z.B. Vektor der Gravitationskraft
im Schwerefeld der Erde, Strömungsgeschwindigkeit über das Volumen eines Rohres), so spricht
man von einem Vektorfeld.
Im Ortsraum nennt man Linien (Ortskurven), die in den betreffenden Ortspunkten die gleiche Richtung haben wie die Vektoren in den Raumpunkten, Feldlinien oder Stromlinien.
Für eine physikalische Größe mit Vektorcharakter gilt für jeden
regulären Raumpunkt immer nur ein Vektor – Ausnahmen bilden
die Quellen und Senken, welche irreguläre Punkte darstellen.
Dr. Hempel – Mathematische Grundlagen , Vektoralgebra1
-2-
Vektordefinitionen
Betrag eines Vektors:
ist die absolute Länge des Vektorpfeils ohne Berücksichtigung der Richtung.
 der Betrag ist skalar und stets positiv.
 es gilt

a  a  a x2  a y2  a z2 .
Komponenten eines Vektors:
Ein Vektor im dreidimensionalen Raum lässt sich immer als Kombination dreier nicht komplanarer Vektoren (nicht in einer Ebene liegende) darstellen:




r  a  a0  b  b0  c  c0
  

Man nennt die skalaren Größen a, b und c Komponenten des Vektors r in den Richtungen a0 , b0 , c0 .

Komponenten sind Skalare!
  
Führt man in kartesischen Koordinaten die Einheitsvektoren i , j , k ein, so gilt:




r  rx  i  ry  j  rz  k
 Die Komponenten eines Vektors sind als die Beträge
der Projektionen des Vektors auf die durch die
  
Einheitsvektoren i , j , k vorgegebenen Richtungen
der Koordinatenachsen.
 Projektionen eines Vektors sind also wiederum Vektoren, Komponenten sind Skalare!
Einheitsvektoren und Richtungskosinusfunktionen
Die Einheitsvektoren in der Richtungen der kartesischen Koordinaten werden mit
  
i , j, k
bezeichnet;
ihr Betrag ist jeweils genau gleich 1.

i  i 2  1;

j 

j 2  1; k  k 2  1


Der Einheitsvektor r0 der Vektors r (in beliebiger Richtung) genügt der Bedingung:


r
r0   
r

r
rx2  ry2  rz2


r
r2
;
Dr. Hempel – Mathematische Grundlagen , Vektoralgebra1
r0 2  1
-3-

Betrachtet man einen beliebig gelegenen Einheitsvektor r0 , so spannt dieser mit den Achsen x, y und
z jeweils die Winkel  ,  und  auf.
Diese Winkel stehen mit den Komponenten des Vektors sowie seinem Betrag in Zusammenhang:
cos 
rx
rx

;
r
rx2  ry2  rz2
cos  
ry
cos  
rz
rz

2
r
rx  ry2  rz2
r

ry
rx2  ry2  rz2
;

Somit lässt sich der Vektor r0 darstellen als:




r0  cos  i  cos   j  cos   k
Die verwendeten Winkelfunktionen werden Richtungskosinusfunktionen des Vektors genannt.
Vektorvergleich




Zwei Vektoren sind zueinander parallel, wenn sie die gleiche Richtung haben.
Zwei Vektoren sind zueinander antiparallel, wenn sie die entgegengesetzte Richtung haben.
Zwei Vektoren sind gleich, wenn sie in Richtung und Betrag übereinstimmen.
Zwei Vektoren sind entgegengesetzt gleich, wenn sie den gleichen Betrag aber die entgegengesetzte
Richtung haben.
Dr. Hempel – Mathematische Grundlagen , Vektoralgebra1
-4-