Entwurf für den Inhalt

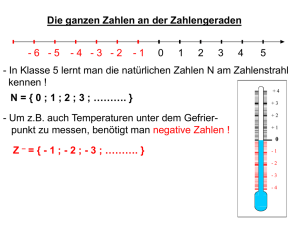
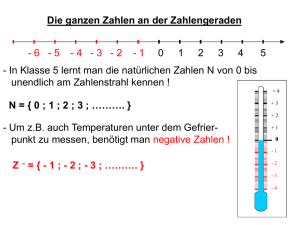
Klassische Probleme der konstruktiven Geometrie
In unserem Projekt geht es um klassische Probleme der Geometrie, welche sich schon die
alten Griechen stellten. Wir nahmen als Beispiel die Würfelverdoppelung, die
Winkeldreiteilung und die Quadratur des Greises. Wir beschäftigten uns mit den Problemen,
die bei der Konstruktion aufkommen und bewiesen auch, warum es nicht gelingt diese
Figuren zu konstruieren. Danach suchten wir noch nach Hilfsmitteln, mit denen man diese
„klassischen Probleme“ doch noch lösen kann, die aber nicht mehr zur Geometrie zählen.
Das Projekt verbindet sowohl praktische, als auch theoretische Mathematik.
I. Welche Zahlen lassen sich konstruieren?
Es geht also um die Geometrie, doch auch hier gibt es Unterschiede. Für uns ist die
Euklidische Geometrie wichtig. Euklidische Geometrie bedeutet grob, man konstruiert nur mit
Zirkel und Lineal aus gegebenen Punkten neue Punkte.
Folgende Regeln müssen berücksichtigt werden, wenn man mit der Euklidischen Geometrie
arbeiten möchte:
-
Rechenoperationen dürfen nur auf bereits konstruierte oder vorgegebene Stücke
angewandt werden
Das Lineal darf nur zum ziehen von Geraden benutzt werden(nicht zum Messen oder
zum Ziehen von Parallelen)
Bei Einsatz des Zirkels muss ein Mittelpunkt des Kreises vorhanden sein und die
Zirkeleinstellung darf während eines Zeichenschritts nicht verändert werden
Die Konstruktionsschritte müssen endlich sein
Die Einheit 1 ist bekannt
Berücksichtigt man dies, lassen sich folgende Grundoperationen anwenden:
1) Zeichnen einer Geraden durch zwei Punkte
Punkt B
Punkt A
2) Zeichnen eines Kreises um einen Mittelpunkt und durch einen davon verschiedenen Punkt
Punkt P
Mittelpunkt M
3)Ermittlung des Schnittpunktes zweier gegebener Geraden
Schnittpunkt S
4)Bestimmung der gemeinsamen Punkte eines Kreises und einer Geraden
Schnittpunkt A
Schnittpunkt B
5)Bestimmung der gemeinsamen Punkte zweier Kreise
Schnittpunkt A
Schnittpunkt B
Welche Rechenschritte kann man so konstruieren?
1)Addieren
2)Subtrahieren:
3)Multiplizieren:
4)Dividieren
5)(mehrfaches) Quadratwurzelziehen
Wie groß ist dann die Menge der Zahlen, die man mit Zirkel und Lineal
konstruieren kann?
Mit Hilfe der oben genannten Rechenschritte kann man folgende Zahlen darstellen:
1) alle Rationalen Zahlen
2) Zahlen, die sich durch rationale Rechenschritte (plus, minus, mal, geteilt) aus
vorgegebenen Zahlen ergeben
Anmerkung: man spricht in den obigen Fällen von Zahlen, die rational dargestellt sind
3) Quadratwurzelausdrücke
Aber ist dies schon alles?
Dazu schauen wir uns nochmals die möglichen Grundoperationen an:
-
-
-
den Schnittpunkt zweier Geraden der Form f(x)= mx + c erhält man durch ein lineares
Gleichungssystem. Um dieses zu lösen, benötigt man nur die Rechenschritte plus,
minus, mal, geteilt; also lassen sich die Schnittpunkte rational darstellen
Hat man die Gleichung einer Geraden und die allgemeine Kreisgleichung eines
Kreises so löst man beide Gleichungen geschickt durch Einsetzen und vereinfacht
dann durch Ausmultiplizieren. Dadurch kommt man auf eine lineares
Gleichungssystem der Form x² + px + q = 0, das man wiederum mit der
Mitternachtsformel lösen kann, wobei man wiederum nur rationale Rechenschritte und
das Quadratwurzelziehen benötigt
Bei den Schnittpunkten zweier Kreise verhält es sich ähnlich wie bei dem Schneiden
eines Kreises mit einer Gerade
So kommen wir zum
Hauptsatz über konstruierbare Zahlen:
Mit Zirkel und Lineal konstruierbar sind genau die Punkte, deren Koordinaten sich allein
durch rationale Verknüpfungen und durch ziehen von Quadratwurzeln aus den
Koordinaten der gegebenen Punkte ausdrücken lassen
II. Körper und Körpererweiterungen
Wir schweifen kurz von der Geometrie ab, um uns ein wenig theoretische Mathematik
anzueignen, die später noch wichtig ist:
Es gibt wie wir wissen unterschiedliche Zahlenmengen: Natürliche Zahlen N, ganze zahlen Z,
rationale Zahlen Q und reelle Zahlen R (und noch die komplexen Zahlen C). Will man alle
rationalen Rechenregeln uneingeschränkt benutzen, so geht dies erst in der Menge der
rationalen Zahlen (siehe Name). Man sagt auch: rationale Zahlen sind in Hinblick auf
Addition und Multiplikation abgeschlossen
Anmerkung: Subtrahiere kann man als Addition mit der Gegenzahl, dividieren als
Multiplikation mit der Kehrzahl beschreiben. Doch hierzu ist die Definition von Gegenzahl
und Kehrzahl notwendig:
-
Definition Gegenzahl: Addiert man zu einer Zahl ihre Gegenzahl, so ist das Ergebnis
ein neutrales Element (hier:0). Bsp.: (5) + (-5) = 0
Definition Kehrzahl: Multipliziert man eine Zahl (außer 0) mit ihrer Kehrzahl, so ist
das Ergebnis ein neutrales Element (hier:1). Bsp.: 5 * 1/5 = 1
Will man uneingeschränkt Wurzeln ziehen, so ist dies erst in der Menge der reellen Zahlen
möglich.
Aber wann genau ist eine Menge abgeschlossen?
Definition: Eine Zahlenmenge M ist dann abgeschlossen, wenn das Ergebnis der
Verknüpfung (z.B.: + , * ) zweier Elemente aus M wieder in der Menge M liegt.
Körper
Wir führen nun einen neuen Begriff ein, den des „ kommutativen Körpers“
Definition:
eine Menge in der man die Verknüpfungen „+“ und „*“ benutz ist ein kommutativer Körper
wenn…
- die Menge abgeschlossen ist
- es gilt das Kommutativgesetz für die Addition ( a + b = b + a)
- es gilt das Kommutativgesetz für die Multiplikation ( a * b = b * a)
- es gilt das Assoziativgesetz für die Addition ( [ a + b] + c = a + [b + c] )
- es gilt das Assoziativgesetz für die Multiplikation ( a * [b * c] = [a * b] * c = 0 )
- es gibt genau ein neutrales Element(n), sodass gilt a + n = a (Bsp.: 7 + 0 = 7)
- es gibt genau ein neutrales Element(n’) sodass gilt a * n’ = a (Bsp. 7 * 1 = 7)
- zu jedem Element existiert eine Gegenzahl, sodass eine Addition beider Zahlen das
neutrale Element ergibt ( [a] + [-a] = 0 )
- zu jedem Element (außer n) existiert eine Kehrzahl, sodass eine Multiplikation beider
zahlen das Neutrale Element ergibt ( a * 1/a = 1)
- es gilt das Distributivgesetz ( a * [b + c] = a * b + a * c )
Anmerkung: Der kleinste Körper mit unendlich vielen Zahlen ist die Menge der rationalen
Zahlen.
Reduzible und irreduzible Polynome
Definition Polynom:
Man nennt einen Term der Form ax^n + bx^n-1 + … + yx + z Polynom n-ten Grades über
einer Zahlenmenge M (z.B. den rationalen Zahlen). a, b, …, x, y sind in der Menge M.
Bsp.: Das Polynom 3x² - 15x +18 ist ein Polynom 2-ten Grades über den ganzen Zahlen.
Dieses Polynom kann man jetzt in zwei weitere Polynome niedrigeren Grades über Z
zerlegen:
3x² - 15x +18 = 3 * (x-2) * (x-3)
Nach der Zerlegung sind die Koeffizienten wieder in der Menge Z. Mathematiker sagen: Das
Polynom ist über Z reduzibel. Währe es nicht über der Menge Z zerlegbar, würde man sagen
es ist irreduzibel.
Beispiel für ein irreduzibles Polynom über Z : x² - 2
da die Lösung der Gleichung x² - 2 = 0 auf die Wurzel von 2 führen würde und diese Zahl
nicht in der Menge der ganzen Zahlen ist.
Anmerkung: Das oben genannte Polynom wäre aber über den reellen Zahlen reduzibel, da die
Wurzel von 2 durchaus eine reelle Zahl ist.
Körpererweiterung
Wir wissen ja, dass wir alle Rationalen Zahlen konstruieren können (die ja einen Körper
bilden). Zusätzlich können wir aber noch Quadratwurzelausdrücke konstruieren. Dies währe
normalerweise erst im Körper der reellen Zahlen möglich, von dem wir jedoch sehr viele
Zahlen (z.B. Kubikwurzeln, die Kreiszahl, usw.) nicht konstruieren können. Es währe also gut
einen Körper zu finden, in dem alle Zahlen vorhanden sind, die sich mit der Euklidischen
Geometrie konstruieren lassen, nicht mehr und nicht weniger.
Man muss also nur Quadratwurzelausdrücke in den Körper der rationalen Zahlen aufnehmen.
Nimmt man nur die Wurzel von 2 in die Menge der rationalen Zahlen auf, so kann man alle
Zahlen, die sich so darstellen lassen in der Form a + b √2 mit a, b € Q darstellen. Diese
Zahlen bilden auch einen Körper. Man spricht auch von einem Erweiterungskörper über Q,
der zu den rationalen Zahlen noch die Wurzel von Zwei aufnimmt. Man schreibt Q(√2 )
[sprich: Q adjungiert √2 ].
Dieser Körper hat über Q den Grad zwei, da man mit ihm ein Polynom zweiten Grades lösen
kann, welches sich nur durch Einführung der Wurzel von Zwei lösen lässt.
Man schreibt: [ Q (√2) : Q ] = 2
Unser Ziel ist es jedoch eine Körpererweiterung aufzustellen, die alle
Quadratwurzelausdrücke enthält (also auch die 8. Wurzel von 2). Hierzu reicht eine einfache
Körpererweiterung nicht; man muss die Erweiterung noch mehrfach erweitern. Dies nennt
man dann Körperturm
[Körperturm wird noch eingefügt]
Dies ist sehr wichtig zum Thema Konstruierbarkeit:
In diesem Körperturm vom Grad 2^n sind nun alle Zahlen, die man mit Zirkel und Lineal
konstruieren kann. Das heißt auch, dass man die Nullstellen eines über Q irreduziblen
Polynoms vom Grad 2^n konstruieren kann, denn die Nullstelle, denn die Nullstellen
eines solchen Polynoms haben immer Quadratwurzelausdrücke als Lösung.
Andererseits können wir die Nullstellen eines irreduziblen Polynoms, das nicht vom
Grad 2^n ist, nicht konstruieren, denn in der Lösung sind immer Kubikwurzeln enthalten.
Dies ist eine sehr wichtige Erkenntnis, denn nun können wir beweisen, dass sich eine
Sache nicht konstruieren läst, indem wir eine Gleichung finden, welche die Zahl
beschreibt und ein irreduzibles Polynom ist, welches nicht vom Grad 2