Universität Osnabrück Quaternionen

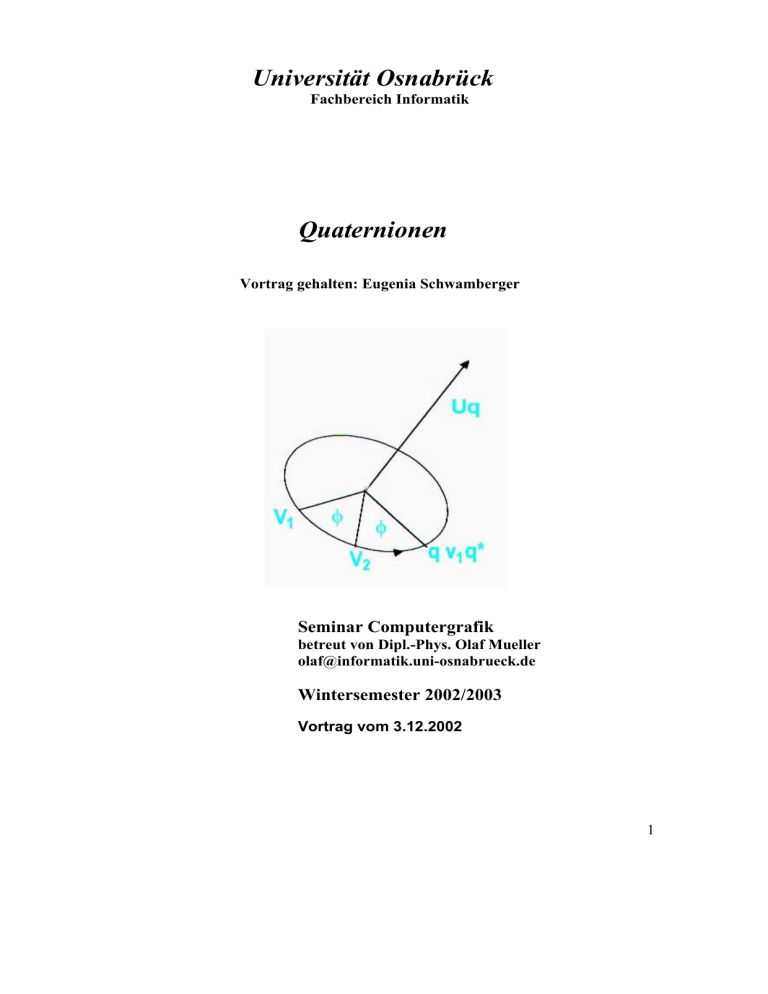
Universität Osnabrück
Fachbereich Informatik
Quaternionen
Vortrag gehalten: Eugenia Schwamberger
Seminar Computergrafik
betreut von Dipl.-Phys. Olaf Mueller
[email protected]
Wintersemester 2002/2003
Vortrag vom 3.12.2002
1
Inhalt
I.
Komplexe Zahlen.............................................3
II.
Quaternionen....................................................3
III. Transformation mit Quaternionen.....................6
IV. Matrix Conversion............................................7
V. Sphärische lineare Interpolation......................11
VI. Vorteile und Nachteile....................................12
VII. Anhang A........................................................13
VIII. Anhang B........................................................13
IX. Literatur..........................................................14
2
I. Komplexe Zahlen
Neben dem Körper der reellen Zahlen spielt noch der Körper
der komplexen Zahlen eine wichtige Rolle. Mit der Hilfe
komplexen Zahlen lassen sich sehr viele Zusammenhänge
einfacher und übersichtlicher gestalten.
Definition
Es sei C = R*R – das kartesische Produkt. An der Stelle des
geordneten Tupels (x, y) schreiben wir
x + iy ∈ C für x, y ∈ R.
Auf dieser so definierten Menge der komplexen Zahlen
definieren wir
eine Addition und eine Multiplikation durch
(x + iy) + (u + iv) = (x + u) + i(y + v)
(x + iy) * (u + iv) = (xu – yv) + i(xv + yu).
Ist z = x + iy ∈ C mit x, y ∈ R so heißt x der Realteil von z: x = Rez und y der Imaginärteil von z:
Imz.
(C, +, *) ist ein kommutativer Körper mit 1 = 1 + i0 als Einselement der Multiplikation
Für z = x + iy ∈ C definieren wir den Betrag |z| und die konjugiert komplexe Zahl z durch
|z| =
x ² + y ² , z = x – iy.
II. Quaternionen
Quaternionen wurden schon im Jahr 1843 von W. R. Hamilton als Erweiterung von Komplexen
Zahlen beschrieben, aber erst 1995 wurden sie von Shoemake im Feld der Computergrafik
eingeführt.
In manchen Bereichen sind Quaternionen besser als Euler Winkel bzw. Matrizen, vor allem, wenn
es zu Rotation und Orientierung kommt.
Ein Quaternion hat 4 Komponenten, deshalb wählen wir seine Darstellung in Form eines Vektors.
Wir beginnen mit dem mathematischen Hintergrund von Quaternionen.
Mathematischer Hintergrund
Definition. Die folgenden Definitionen sind äquivalent:
q = ( qv, qw )
= (qx, qy, qz, qw)
= i ⋅ qx + j ⋅ qy + k ⋅ qz + qw
mit qx, qy, qz, qw ∈R und i ⋅ i = -1; j ⋅ j = -1; k ⋅ k = -1; i ⋅ j = - j ⋅ i = k; k ⋅ i = -i ⋅ k = j;
j ⋅ k = - k ⋅ j = i.
3
*
i
j
k
i
-1
k
j
-k
-1
i
k
j
-i
-1
-j
Tabelle 1
Hamilton suchte 15 Jahre lang nach einer geeigneten Multiplikation in der vierten Dimension.
Auf einem Spaziergang kam ihm dann die geniale Idee, einfach auf das Kommutativgesetz zu
verzichten.
Er ritzte sofort diese Formeln in einen Stein auf der Brougham Bridge.
Den Vektor qv = (qx, qy, qz) nennt man den imaginären Teil und qw den reellen Teil des
Quaternions q
Vektoren und Skalare können in der Form: v = (v, 0) und s = (0, s) geschrieben werden.
Für den imaginären Teil können wir Vektoroperationen wie Addition, Skalierung, Produkt,
Kreuzprodukt und mehr benutzen.
Wie aus der Verknüpfungstabelle ersichtlich wird, ist die Multiplikation nicht kommutativ
Die Quaternionen bilden also einen Schiefkörper. (Siehe: Anhang A)
Wir betrachten die Multiplikation von zwei Quaternionen q und r:
q r = (i qx + j qy + k qz + qw )x(i rx + j ry + k rz + rw) =
i (qyrz – qzry + qxrw – qwrx)
+ j (-qxrz + qzrx + qyrw + qwry)
+ k (qxry – qyrx + qzrw – qwrz)
+ qwrw - qxrx - qyry – qzrz =
(qvxrv + rwqv + qwrv, qwrw – qvrv)
(i)
(Definitionen von Skalar- und Vektorprodukt im Anhang B).
Weiter definieren wir für Quaternionen: die Addition, konjugierte Quaternion, der Norm und die
Identität.
Die Addition:
q + r = (q , q ) + (r , r ) =(q + r , q + r )
v
w
v
w
v
v
w
w
Konjugierter Quaternion:
q* = (qv, qw)* = ( - qv, qw)
Die Norm: N(q)
N(q) = q q* = q* q = qv qv + qw² = qx² + qy² + qz² + qw²
Die Norm von q ist manchmal notiert als ||q||² = Ν(q).
Die Identität:
I = (0, 1)
4
Eine Folge von den obigen Gleichungen ist die multiplikative Inverse, bezeichnet mit q-1.
Behauptung: Die zu einem Quaternion q multiplikative Inverse ist:
q-1 = q*/N(q)
Beweis: Für die Inverse gilt die Gleichung q-1 * q = q * q-1
Wir leiten diese Formel von der Definition der Normen her.
q-1 · q = q · q-1 = 1 gilt für Inverse
N(q) = q · q* ⇔
1 = (q · q* ) / N(q) =>
q-1 = q*/N(q)
In dieser Formel braucht man ein Skalarprodukt, das wir schon in Formel (i) betrachten haben
s * q = (o, s) * (gv , qw) = (s * gv , s * qw) und
q * s = (gv , qw) * (0, s) = (gv * s , qw * s) = (s * gv , s * qw), dies bedeutet,
dass das Skalarprodukt kommutativ ist:
s * q = q * s = (s * gv , s * qw).
Die folgenden Regeln stammen aus der Definition:
Regeln für Konjugierte Quaternionen:
(q*)* = q
(q + r)* = q* + r*
(q r)* = r* q*
Regeln für die Norm:
N(q*) = N(q)
N(q r) = N(q) N(r)
Gesetzte für Multiplikation:
Distributivgesetze
p (s q + t r) = s p q + t p r
wobei p, q, r Quaternionen sind, und s, t - Skalaren
(s p + t q) r = s p r + t q r
Assoziativität
p (q r) = (p q) r
Quaternionen mit N(q) = 1 heißen Einheitsquaternionen.
Deshalb schreiben wir Quaternion q weiter als q = (sinφ * uq, cosφ) für solch einen
dreidimensionalen Vektor uq,
für den gilt N(uq) = 1, weil
N(q) = n(uq sinφ, cosφ) = sin² φ (uq uq) + cos² φ = sin² φ + cos² φ = 1
Die Menge aller Einheitsquaternionen bildet eine Einheitssphäre im vierdimensionalen Raum.
5
III. Transformation mit Quaternionen
Zuerst setzen wir vier Koordinaten von einem Vektor p= (px, py, pz, pw)T in die Komponenten von
einem Quaternion qp ein und nehmen an, dass wir einen Einheitsquaternion q haben mit:
(ii)
q = (sinφ * uq, cosφ).
Sei P ein Punkt im dreidimensionalen Raum, dargestellt durch einen Quaternion p = (qx, qy, qz, qw),
außerdem sei q ein Quaternion, der ungleich Null ist. Dann gilt:
Das Produkt q p q-1 führt p = ( qv, qw ) nach p´ = ( qv´, qw ) über, wobei N(v) = N(v´) ist. Die Länge
des Vektors hat sich nicht geändert.
Jede Vielfache(!= 0) von q gibt dasselbe Ergebnis. Die Potenz eines Quaternions q ist qt und
bedeutet geometrisch eine t-fache Drehung wie q.
Wenn N(q) = 1 ist, dann ist q = (sinφ * uq, cosφ) eine Rotation um eine Achse uq mit dem Winkel
2φ,
oder mit anderen Worten:
Das Produkt q p q-1 rotiert p (und auch der Punkt P) um die Achse uq mit dem Winkel 2φ.
Beispiel:
Der Punkt P(0, 2, 6) soll um 60° bzgl. der z-Achse rotiert werden.
p = 0i + 2j + 6k,
q = (uqsinφ, cosφ), uq= (0, 0, -1), φ = 30° =>
q = (- 0.5k + cos30°) = (√3/2 – 0.5k) =
q* = (√3 / 2 + 0.5k)
Berechne q p q*
q p q* = (√3/2-0.5k)(2j + 6k)( √3/2 + 0.5k) =
(i + √3j + 3 √3k + 0.5 · 6)( √3/2 + 0.5k) =
(√3i + j +6k)
Wenn man das Ergebnis in die Vektorschreibweise überführt, erhält man
P‘ = (1.73 1 6)T
Vergleiche mit den Berechnungen aus der CG - Vorlesung:
http://www-lehre.inf.uos.de/~cg/2002/Aufgaben/Blatt7/blatt/node1.html
6
IV. Matrix Conversion (Konvertierung)
Da manche Systeme Matrixmultiplikation in Hardware implementiert haben, betrachten wir die
Konvertierung eines Quaternions in eine Matrix und umgekehrt.
Es kann bewiesen werden, dass ein Quaternion q in eine Matrix Mq folgendermaßen konvertiert
werden kann:
Mq =
1-s(qy² +qz²)
s(qxqy + qwqz)
s(qxqz - qwqy)
0
s(qxqy - qwqz)
1-s(qx² +qz²)
s(qyqz + qwqx)
0
s(qxqz + qwqy) 0
s(qyqz – qwqx) 0
1-s(qx² +qy²)
0
0
1
Hier ist der Skalar s= 2/N(q).
Für Einheitsquaternionen ist diese Matrix einfacher:
Mq =
1-2(qy² +qz²)
2(qxqy + qwqz)
2(qxqz - qwqy)
0
2(qxqy - qwqz)
1-2(qx² +qz²)
2(qyqz + qwqx)
0
2(qxqz + qwqy)
2(qyqz – qwqx)
1-2(qx² +qy²)
0
0
0
0
1
Wie bekommt man diese Matrix?
Es sei gegeben Vektor p = (px, py, pz, 0) = ipx + jpy + kpz + 0
und Einheitsquaternion q = (uqsinφ, cosφ) = (qx, qy, qz, qw) = uxsinφ + uysinφ + uz sinφ + cosφ.
Dann ist q-1 = - uxsinφ - uysinφ - uz sinφ + cosφ (laut Definition).
Wir berechnen das Produkt q p q-1
Es sei nun:
a = cosφ = qw,
b = uxsinφ = qx,
(iii)
c = uysinφ = qy,
d = uz sinφ = qz;
Dann gilt q p q-1 = (ib + jc + kd + a) (ipx + jpy + kpz + 0) (- ib - jc - kd + a)
Nachdem wir ausmultipliziert, reelle und imaginäre Faktoren gruppiert, die imaginären Produkte
bestimmt und sortiert haben, bekommen wir folgendes:
7
q p q-1 = (ib + jc + kd + a) (ipx + jpy + kpz + 0) (- ib - jc - kd + a) =
((b² – c² – d² + a²) px + 2(bc – ad ) py + 2(ac + bd)pz ) i
+ (2(ad + bc) px + (- b² + c² – d² + a²) py +2(cd - ab)pz ) j
+ (2(bd - ac) px + 2(ab + cd)py + (- b² - c² + d² + a²) px )k
Dies lässt sich dann auch in Matrixform schreiben:
M=
b² – c² – d² + a²
2(bc – ad )
2(ac + bd)
px
2(ad + bc)
- b² + c² – d² + a²
2(cd - ab)
py
2(bd - ac)
2(ab + cd)
- b² - c² + d² + a²
pz
Nach dem Einsetzen von a = qw, b = qx, c = qy, d = qz und aufgrund von qx² + qy² + qz² + qw² = 1
ist die Matrix M = Mq.
Wir wollen zeigen, dass diese Matrix tatsächlich eine Rotationsmatrix ist.
Die Strategie dabei ist, die einzelnen Elemente der Matrix M durch Einsetzen der Werte für a, b, c
und d auszurechnen (die Formeln (iii)) und das Ergebnis dann mit einer bekanten Rotationsmatrix zu
vergleichen.
Erinnern wir uns an die wichtigen Sinus- und Kosinusbeziehungen:
(1) sin (2α) = 2sinα cosα
(2) cos (2α) = cos²α - sin²α
(3) sin²α + cos²α = 1
(4) 2 sin²α = 1 – cos(2α)
Außerdem soll (ux, uy, uz ) laut der Annahme ein Einheitsvektor sein, d.h.
(5) ux² + uy² + uz² = 1
Also,
b² – c² – d² + a² = ux² sin²φ - uy² sin²φ - uz² sin²φ + cos²φ
= sin²φ( ux² - uy² - uz²) + cos²φ
(nach 5)
= sin²φ( 2ux² - 1) + cos²φ
= cos²φ - sin²φ + 2 ux² sin²φ
(nach 2 und 4) = cos(2φ) + (1 - cos(2φ)) ux²
analog gilt es für die anderen Diagonalelemente:
- b² + c² – d² + a² = cos(2φ) + (1 - cos(2φ)) uy²
8
- b² – c² + d² + a² = cos(2φ) + (1 - cos(2φ)) uz²
Für das mittlere Element der oberen Zeile von M ergibt sich:
2(bc – ad ) = 2(ux sinφ uy sinφ - cosφ uz sinφ)
= 2 sin²φ ux uy - 2 sinφ cosφ uz
= (1 – cos(2φ)) ux uy - sin(2φ) uz
analog für die übrigen Elemente ist:
2(ac + bd) = (1 – cos(2φ)) ux uz + sin(2φ) uy
2(ad + bc) = (1 – cos(2φ)) ux uy + sin(2φ) uz
2(cd - ab) = (1 – cos(2φ)) uy uz - sin(2φ) ux
2(bd - ac) = (1 – cos(2φ)) ux uz - sin(2φ) uy
2(ab + cd) = (1 – cos(2φ)) uy uz + sin(2φ) ux
Wir definieren zusätzlich folgende Abkürzungen:
r = cos(2φ)
s = sin(2φ)
t = 1-cos(2φ)
Damit erhalten wir für M insgesamt:
M=
r + t ux²
t ux uy - s uz
t ux uz + s uy
t ux uy + s uz
r + t uy²
t uy uz - s ux
t ux uz - s uy
t uy uz + s ux
r + t uz²
Und dies ist genau die Matrix, die man aus dem im Skript angegebenen Produkt für Rotationen um
den Vektor (ux, uy, uz ) und den Winkel 2φ bekommt.
Die Rückwärtsumrechnung ist komplizierter.
Schlüssel dieses Prozesses sind folgende Differenzen:
m21q - m12q = 4qwqx
m02q - m20q = 4qwqy
m10q - m01q = 4qwqz
(*) (wobei mij sind Elemente von Matrix M)
d.h. wenn qw bekannt ist, können wir qx, qy, qz berechnen.
Der „trace“ einer Matrix M - tr(M) ist die Summe der Diagonalelemente der Matrix M,
also
tr(Mq) = 4- 2s(qx² +qy² +qz²) =
4 *(1- (qx² +qy² +qz²) / (qx² +qy² + qz² + qw²)) = 4qw² / (qx² +qy² + qz² + qw²) = 4qw² / N(q)
Dieses Resultat liefert die folgende Umrechnung die Komponenten für Quaternionen:
9
qw = 0.5 √tr (Mq)
qx = (m21q - m12q) / 4qw
qy = (m02q - m20q) / 4qw
qz = (m10q - m01q) / 4qw
(**)
Diese Art der Berechnung macht keinen Sinn, wenn der Skalaranteil qw = 0 wird (bei φ = 90°).
Wir gehen dann nach von der Ken Shoemake vorgeschlagenen Sonderfallbehandlung vor.
Wir berechnen alle Komponenten des Quaternions auf folgende Weise:
qw² = 0.25 tr (Mq) = 0.25(1 + m11 + m22 + m33)
TRUE
qw = √ qw²
qx = (m21q - m12q) / 4qw
qy = (m02q - m20q) / 4qw
qz = (m10q - m01q) / 4qw
qw² > ε ? (the machine precision)
FALSE
qw = 0
qx² = - 0.5 (m22 + m33)
TRUE
qx² > ε ?
qx = √qx²
qy = m01q / 2qx
qz = m02q / 2qx
FALSE
qx = 0
qy² = 0.5 (1 - m33)
TRUE
qy² > ε ?
qy = √ qy²
qz = m12q / 2qy
FALSE
y=0
z=1
Es sind also nicht mehr als eine Quadratwurzel, drei Divisionen und wenig Additionen für eine
Konvertierung notwendig.
10
V. Sphärische lineare Interpolation
Wir befassen uns weiter mit der Interpolation im Quaternionenraum.
Es sei gegeben: Einheitsquaternionen q und r und ein Parameter t∈ [0, 1].
Die gesamte Gruppe von Rotationen einer Oberfläche kann der vierdimensionalen EinheitsHypersphäre im Quaternionenraum zugeordnet werden.
Eine einfache lineare Interpolation zwischen den beiden Quaternionen führt zu einer Bewegung, die
in der Mitte beschleunigt, da wir uns nicht entlang der Oberfläche, sondern quer durch die
Hypersphäre bewegen. Um eine gleichmäßige Rotation zu erreichen müssen wir eine Sphärische
Lineare Interpolation (SLERP) anwenden, bei der wir uns an einem Bogen entlang bewegen, der den
zwei Quaternionen durchläuft.
Abb.1
Eine zweidimensionale
Analogie zeigt den
Unterschied zwischen
einer einfachen linearen
Interpolation und einer
SLERP.
Abb. 2
Die SLERP - Funktion berechnet für t ∈ [0, 1] die kürzeste
Verbindung (Großkreis) auf der vierdimensionalen
Einheitssphäre zwischen q und r.
Abb. 2: Eine dreidimensionale Analogie der Verwendung
von SLERP zur Interpolation zwischen zwei Quaternionen q
und r.
11
Eine Formel für die SLERP von q zu r mit dem Parameter t kann man auf zwei verschiedenen Arten
betrachten.
Die algebraische Form dieser Operation ist die äußere Komposition zweier Quaternionen q und r
und einem Parameter t geschrieben als:
s (q, r, t) = q (rq-1)t,
welche für die vierdimensionale Geometrie dazu kommt:
s (q, r, t) = SLERP (q, r, t) = q ⋅ sin(ϕ(1 –t)) / sinϕ + r ⋅ sin(ϕt) / sinϕ, wobei q ⋅ r = cosϕ ist.
(Diese Formel wurde von Glenn Davis vorgeschlagen.)
Die erste Formel ist für Untersuchungen und Analyse brauchbar, wobei die zweite mehr für die
praktische Anwendungen geeignet ist.
SLERP ist z. B. nützlich für die Animation von Objekten, aber nicht nützlich für die Interpolation
von Kameraorientierungen, wenn sich der „up“ – Vektor der Kamera ändert.
VI. Nachteile und Vorteile
Nachteile
• Mit Quaternionen kann man nur Rotationen berechnen. Aus diesem Grund verwendet man
am besten Matrizen und Quaternionen, was dann wieder die Umrechnungen erfordert, die
wiederum Rechnerzeit kosten.
• Nicht geeignet für Interpolation von Kameraorientierungen, wenn sich der „up“ – Vektor der
Kamera ändert.
Vorteile
• Die Rotation erfolg direkt um die gewünschte Drehachse. Bei dem Matrizenverfahren
braucht man sieben Transformationen durchzuführen.
• Es kann mit dem Verfahren wie SLERP zwischen zwei Orientierungen interpoliert werden.
• Die Verkettung zweier Transformationen a und b mit Quaternionen ist effizienter. Beim
Matrizenverfahren berechnet man das Matrixprodukt Ra ⋅ Rb. Dies ist für zwei 3 x 3 Matrizen
3x3x3 = 21 Multiplikationen und 3x3x2 = 18 Additionen notwendig. Für die Rotationen mit
Quaternionen muss qa ⋅ (qb ⋅ p ⋅ qb-1 ) ⋅ qa-1 = (qa ⋅ qb )⋅ p ⋅ (qa ⋅ qb) berechnet werden. Das
Quaternionenprodukt qa ⋅ qb kostet 4x4 = 16 Multiplikationen und 4x3 = 12 Additionen. Für
die Berechnung qa ⋅ qb müssen nur drei Vorzeichenbits invertiert werden.
12
VII. Anhang A
Körper
•
•
•
•
•
•
Sei (K, +, *) eine Menge mit zwei Verknüpfungen. K ist ein Körper, wenn
Assoziativgesetz der Multiplikation und der Addition gilt
Kommutativgesetz der Multiplikation und der Addition gilt
Nullelement und Einselement existieren
Inverse der Addition existiert
Inverse der Multiplikation existiert
Schiefkörper
•
Die Multiplikation ist nicht kommutativ
VIII. Anhang B
Vektorprodukt
•
•
•
•
|v×u| = |v|·|u| · sin(v, u)
v×u ist orthogonal zu v und u
Bilden ein Rechtsystem in der Reihenfolge:
v, u, v×u.
Skalarprodukt
•
u · v = |v|·|u| · cos(v, u)
13
IX. Literatur
• Tomas Möller, Erik Haines: Real – Time Rendering. 1999 by AK Peters.
• Alan Watt: 3D – Computergrafik. 2002 by Pearson Studium.
• B.L. van der Waerden: Hamiltons Entdeckung der Quaternionen.(erweiterte Fassung
eines Vortrags gehalten im Hamburg von der Joachim – Jungius – Gesellschaft der
Wissenschaften am 26. Juni 1973)
• Peter Meyer-Nieberg: Analysis I. Vorlesung SS2001
• Thomas Kirste: FB Informatik, TU Darmstadt Ergänzung zum Skript GDV – I
• Ken Shoemake: Animating Rotation with Quaternion Curves. SIGGRAPH, Volume 19,
Number 3, 1985 San Francisco July 22-26
14