Aufgabenstellungen zu Kapitel 3. Lernen und
Werbung
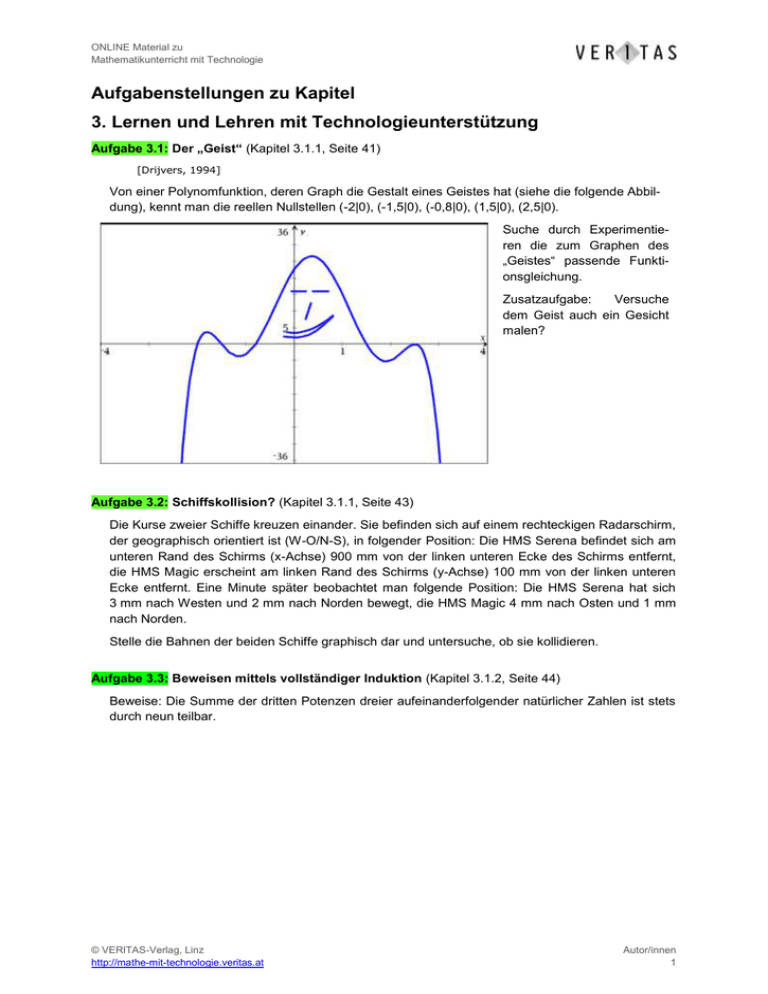
ONLINE Material zu Mathematikunterricht mit Technologie Aufgabenstellungen zu Kapitel 3. Lernen und Lehren mit Technologieunterstützung Aufgabe 3.1: Der „Geist“ (Kapitel 3.1.1, Seite 41) [Drijvers, 1994] Von einer Polynomfunktion, deren Graph die Gestalt eines Geistes hat (siehe die folgende Abbildung), kennt man die reellen Nullstellen (-2|0), (-1,5|0), (-0,8|0), (1,5|0), (2,5|0). Suche durch Experimentieren die zum Graphen des „Geistes“ passende Funktionsgleichung. Zusatzaufgabe: Versuche dem Geist auch ein Gesicht malen? Aufgabe 3.2: Schiffskollision? (Kapitel 3.1.1, Seite 43) Die Kurse zweier Schiffe kreuzen einander. Sie befinden sich auf einem rechteckigen Radarschirm, der geographisch orientiert ist (W-O/N-S), in folgender Position: Die HMS Serena befindet sich am unteren Rand des Schirms (x-Achse) 900 mm von der linken unteren Ecke des Schirms entfernt, die HMS Magic erscheint am linken Rand des Schirms (y-Achse) 100 mm von der linken unteren Ecke entfernt. Eine Minute später beobachtet man folgende Position: Die HMS Serena hat sich 3 mm nach Westen und 2 mm nach Norden bewegt, die HMS Magic 4 mm nach Osten und 1 mm nach Norden. Stelle die Bahnen der beiden Schiffe graphisch dar und untersuche, ob sie kollidieren. Aufgabe 3.3: Beweisen mittels vollständiger Induktion (Kapitel 3.1.2, Seite 44) Beweise: Die Summe der dritten Potenzen dreier aufeinanderfolgender natürlicher Zahlen ist stets durch neun teilbar. © VERITAS-Verlag, Linz http://mathe-mit-technologie.veritas.at Autor/innen 1 ONLINE Material zu Mathematikunterricht mit Technologie Aufgabe 3.4: Kostenfunktion - Polynomfunktion als Approximationsfunktion zu Datenmengen (Kapitel 3.3.3, Seite 46) Vom Kostenverlauf eines Betriebes kennt man folgende Daten: Stückzahl x in ME 0 2 3 5 8 10 12 15 18 Kosten k(x) in GE 1 000 1 600 1 770 2 000 2 100 3 000 4 070 7 000 12 090 Die Anzahl der produzierten Stück x wird in Mengeneinheiten (ME) angegeben, die Kosten k in Geldeinheiten (GE). a) Zeichne den Punktgraphen der Funktion k in einem geeigneten Koordinatensystem. Suche ein geeignetes mathematisches Modell „kost“ für die Gesamtkostenfunktion, zeichne den zugehörigen Graphen und interpretiere den Verlauf der Kostenfunktion unter Verwendung der Begriffe der Wirtschaftsmathematik („degressiv – progressiv“, „Grenzkosten“, „Fixkosten“). b) Ermittle die Stückkostenfunktion „skost“ (Kosten pro Stück). Bei welcher Stückzahl werden die Stückkosten minimal (Betriebsoptimum)? c) Zeichne in einem Koordinatensystem den Graphen der Kostenfunktion und der Stückkostenfunktion. Zeichne an der Stelle des Betriebsoptimums die Tangente an den Graphen der Kostenfunktion „kost“. Was fällt auf? d) Beweise: Es sei K eine beliebige Kostenfunktion, dann geht die Tangente an den Graphen der Kostenfunktion K an der Stelle des Betriebsoptimums stets durch den Koordinatenursprung. Aufgabe 3.5: Graphen von Sinusfunktionen (Kapitel 3.2, Seite 49) Gegeben ist die Funktion f : f(x) a sin(b x c) mit a, b, c Untersuche die Abhängigkeit der Lage der Graphen von den Parametern a, b, c und gib eine physikalische Deutung für harmonische Schwingungen an. Aufgabe 3.6: Herleiten der Berührbedingung für die Ellipse (Kapitel 3.2, Seite 51) Von einer Ellipse in erster Hauptlage kennt man die Längen der Halbachsen a und b, von einer Geraden kennt man die Steigung k und den Abschnitt auf der y-Achse d. Suche eine Beziehung zwischen a, b, k und d, so dass die Gerade Tangente an die Ellipse ist („Berührbedingung“). Aufgabe 3.7: Anteil der Linkshänder – Testen von Hypothesen (Kapitel 3.2, Seite 52) Statistiken geben den Anteil der Linkshänder mit etwa 15% an, wobei behauptet wird, dass bei Befragungen der Anteil geringer ausfallen kann als bei gezielten Tests. Um das zu überprüfen wird eine statistische Erhebung durchgeführt. Dabei werden durch einen Test unter 1 000 Personen 125 Linkshänder festgestellt. Kann man mit einer Irrtumswahrscheinlichkeit von 5% schließen, dass die Behauptung zutrifft? Versuche eine Antwort mit Hilfe der Binomial- bzw. Normalverteilung. Aufgabe 3.8: Von der Binomial- zur Normalverteilung (Kapitel 3.2, Seite 54) Werkzeug: GeoGebra: „3.8 Binomial_Normalveteilung GGB“ Verändere im gegebenen GeoGebra-Applet die Parameter n und p mit Hilfe von Schiebereglern und beschreibe die Beziehung zwischen den Histogrammen und der Gauß’schen Glockenkurve. Aufgabe 3.9 „Sekantensteigung/Tangentensteigung“ (Kapitel 3.3.1, Seite 55) © VERITAS-Verlag, Linz http://mathe-mit-technologie.veritas.at Autor/innen 2 ONLINE Material zu Mathematikunterricht mit Technologie Werkzeug: GeoGebra: „3.9_1 Differenzenquotient GGB“ und „3.9_2 Differentialquotient GGB“ Durch zwei Punkte A und B auf dem Graphen der Funktion f wird eine Sekante gelegt. Wie verändert sich die Steigung der Sekante, wenn der Punkt B gegen den Punkt A wandert? Im Lernpfad „Einführung in die Differentialrechnung“ [Hohenwarter, Jauk, Reichenberger, 2011] werden zwei scheinbar gleiche, aber didaktisch sehr verschiedene GeoGebra-Applets eingesetzt (siehe oben). Aufgabe 3.10: „Mittlere Geschwindigkeit/Momentangeschwindigkeit“ (Kapitel 3.3.1, Seite 57) Ein Körper wird mit einer Anfangsgeschwindigkeit von 20 m/s lotrecht nach oben geworfen. Die Höhe h wird in Abhängigkeit von der Zeit t durch die Funktionsgleichung h(t) 20 t 5 t2 beschrieben. Wie groß ist die Geschwindigkeit nach 3 Sekunden? Versuche einen Näherungswert für die Momentangeschwindigkeit v in einer Tabelle für t 0 zu finden. s t t s t Die mittlere Geschwindigkeit v(t) im Intervall t ist gegeben durch v(t) . t Aufgabe 3.11: Tangentensteigung und Ableitungsfunktion (Kapitel 3.3.1, Seite 57) Werkzeug: GeoGebra: „3.11_1 Tangentensteigung GGB“ und „3.11_2 Tangentensteigung GGB“ a) Beschreibe mit Hilfe eines GeoGebra–Applets aus dem Lernpfad „Einführung in die Differentialrechnung“ [Hohenwarter, Jauk, Reichenberger, 2011] die Abhängigkeit der Tangentensteigung vom Kurvenverlauf (Applet 3.11_1) b) Zeichne mit Hilfe eines weiteren interaktiven Applets dieses Lenpfades (Applet 3.11_2) die Werte der Tangentensteigungen (die 1. Ableitung) in Abhängigkeit vom x-Wert des jeweiligen Kurvenpunktes. Aufgabe 3.12: Differentialquotient von Potenzfunktionen (Kapitel 3.3.1, Seite 58) Gegeben sind vier Potenzfunktionen f1, f2, f3, f4. Berechne ihre Differenzenquotienten y fi (x h) fi (x) , vereinfache die Terme und suche Grenzwerte für h 0 . x h f1(x) x 3 f2 (x) x 7 f3 (x) 1 x f4 (x) x Aufgabe 3.13: Stetigkeit und Differenzierbarkeit (Kapitel 3.3.1, Seite 60) Gegeben ist die Funktion g mit g(x) x 2 4 . Untersuche die Funktion g an der Stelle x = -2 bezüglich Stetigkeit und Differenzierbarkeit. © VERITAS-Verlag, Linz http://mathe-mit-technologie.veritas.at Autor/innen 3 ONLINE Material zu Mathematikunterricht mit Technologie Aufgabe 3.14: Gleisarbeiten am Zentralbahnhof (Kapitel 3.3.1, Seite 61) Am Wiener Zentralbahnhof wird ein neuer Bahnsteig benötigt. Dieser soll so angelegt werden, dass das zugehörige Gleis parallel zu den Gleisen der anderen Bahnsteige im Abstand von 5 Metern verläuft. Für das Verbindungsgleis steht eine Länge von 50 m zur Verfügung. Entwickle eine Funktion, deren Graph diesen Übergang beschreibt und zwar so, dass die Züge möglichst „ruckfrei“ diese Stelle passieren können. Aufgabe 3.15: Unter- und Obersummen (Kapitel 3.3.2, Seite 64) Werkzeug: GeoGebra: „3.15 Unter- Obersummen GGB.ggb“ x2 1 . Suche Näherungswerte für den Flächeninhalt zwi2 schen dem Graphen von f und der x-Achse im Intervall [0, 4]. Gegeben ist die Funktion f mit f(x) Definiere einen Schieberegler n mit n 0,40 . Ermittle die Unter- und Obersumme mit Hilfe der GeoGebra-Funktionen „Untersumme[f,a,b,n]“ und „Obersumme[f,a,b,n]“. Bilde auch die Differenz von Obersumme und Untersumme und untersuche die Veränderungen für wachsendes n im Graphik- und im Algebrafenster. Aufgabe 3.17: Visualisierung von Flächeninhaltsfunktionen (Kapitel 3.3.2, Seite 67) Werkzeug: GeoGebra: „3.17 Flaecheninhaltsfktion GGB.ggb“ Gegeben ist die Funktion f mit f(x) = x2. Ermittle mit dem GeoGebra-Applet [Hohenwarter, Jauk, Lindner, Gassner, 2011] die Spur der Flächeninhaltsfunktion A mit fester unterer Grenze a = -3 und variabler oberer Grenze b. Wird bei fester unterer Grenze a die variable Grenze b nach rechts gezogen, so sieht man nicht nur die gefragte Fläche, sondern auch die Spur der Flächeninhaltsfunktion A. Aufgabe 3.18: Grenzwerte von Produktsummen (Kapitel 3.3.2, Seite 68) Gegeben ist die Funktion f mit f(x) = x2. b Berechne das bestimmte Integral f(x)dx mit Hilfe der Definition des Integrals als Grenzwert von a Produktsummen und verwende die Funktionswerte am rechten Rand der Rechteckstreifen. © VERITAS-Verlag, Linz http://mathe-mit-technologie.veritas.at Autor/innen 4 ONLINE Material zu Mathematikunterricht mit Technologie Aufgabe 3.19: Füllung eines Wassertanks (Kapitel 3.3.2, Seite 68) [Savard, G., Pineau, K.,2008] Um 13 Uhr enthält ein Regenwassertank 500 l Wasser. Regenwasser füllt den Tank mit einer Zuflussrate q mit q(t) 2500 t (1 2.t)2 . Die Zuflussrate q wird in Liter pro Stunde (l/h) gemessen, die Zeit- messung beginnt um 13 Uhr. a) Der Flächeninhalt zwischen dem Graphen q(t) und der x-Achse zwischen t=1 und t=3 hat den Wert 410. Was bedeutet dieser Wert bezüglich des Kontextes „Wassertank“? b) Wie groß ist das Wasservolumen im Tank um 15 Uhr? Erläutere deine Überlegungen. c) Der Tank fasst maximal 1250 Liter. Um wieviel Uhr etwa wird er überfließen? Erläutere deine Überlegungen. d) Wie kann man mit Hilfe der Integralrechnung die durchschnittliche Zuflussrate zwischen 13 Uhr und 15 Uhr ermitteln? Interpretiere den Wert graphisch im Bezug zum Graphen von q(t). e) Ermittle eine Formel für das Wasservolumen im Tank in Abhängigkeit von der Zeit und stelle diese Funktion für 10 Stunden graphisch dar. Die Messung beginnt um 13 Uhr. Erläutere deine Überlegungen. © VERITAS-Verlag, Linz http://mathe-mit-technologie.veritas.at Autor/innen 5











