Vorlesung Diffusion - Institut für Werkstoffwissenschaft

Vorlesung: Grundlagen der Werkstoffwissenschaft
6. Diffusion
Warum sich Werkstoffingenieure für
Diffusion interessieren :
Der Werkstoffingenieur muss die Kinetik der im Werkstoff
ablaufenden Vorgänge bei der Herstellung, Bearbeitung sowie beim
Einsatz beschreiben, um sie vorausberechnen zu können.
Beispiele:
 Homogenisieren
 Altern
 Sintern
 Phasenbildung
 Ausscheidungen
 Nitrieren
Wer interessiert sich wofür ?
 Werkstoffingenieure, Metallurgen, Chemiker  Phänomen
 Physiko-Chemiker, Thermodynamiker
 Triebkräfte
 Physiker
 Atomistik,
Elementarprozess
Geschichtliche Reihenfolge
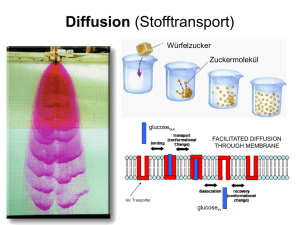
Versuch: Blaue Kupfersulfatlösung wird mit Wasser überschichtet
 Scharfe Grenzen, nach einigen Tagern dringt blaue Farbe nach oben
= Diffusion (Jedes flüssige System, das aus mischbaren Komponeneten besteht
strebt bei V und T=konst. nach Ausgleich der Konzentration)
Diffusionsausgleich jedoch nicht die einzige treibende Kraft: Brown‘sche Molekularbew.
= Selbstdiffusion (unregelmäßige Wärmebewegung)
Gut vorstellbar für Gase + Flüssigkeiten, fester Zustand jedoch starr und formgebunden
Röntgen, Laue  Feinstruktur bestätigen regelmäßig angeordnete Elementarbausteine
Erforschung der Platzwechselvorgänge in Fk jedoch erst relativ spät spät, da
„corpora non agunt nisi fluida“
(Körper sind unveränderlich außer Flüssigkeiten)
das Denken beherrschte, obwohl das Einsatzhärten schon seit Jahrhunderten bekannt war.
Erste Zweifel 1846 von Gay-Lussac
1820 beobachtet Faraday die Legierungsbildung zw. festen Metallen
 zunehmend Literatur gegen Ende des 19. Jh. über Diffusion und Reaktionsvorgänge
1896 Roberts-Austen: Diffusion von Au in Pb, sogar Bestimmung des Dk
1909 Institut von TAMMANN in Göttingen: Sich berührende Metalle können schon
unterhalb von TS unter Mk-Bildung ineinander vordringen.
Ab 1920 werden eine Reihe von Dk gemessen und veröffentlicht.
1921 Dk für C in Fe wird bestimmt.
Zur Historie der Diffusion in Metallen
W.C. Roberts - Austen G. v. Hevesy u. A. Obrutsheva
Phil. Trans Roy. Soc. A187,
Nature 115, 674 (1925)
404 (1896)
1921 erste Bestimmung der technisch wichtigen
Diffusionskonstante von Kohlenstoff in Eisen
Runge, I.: Z. anorg. Chem. 115, 293 (1921)
 sehr hoch, erreicht bei 1000°C 1/7 der Diffusionsgeschwindigkeit der Ionen in einer wässrigen Lösung bei RT
Tammann, G., u. K. Schönert: Z. anorg. Chem. 122, 27, 1922 ,
weil im System Fe-C der Kohlenstoff auf Zwischengitterplätzen
sitzt und in den Lücken zwischen den Fe-Atomen diffundieren
kann.
Diffusion
Fremddiffusion
Selbstdiffusion
Metalle
Legierungen
D AB CB 
A
kfz krz
Amorphe
Legierungen
höhere
verdünnte
Legierungen Legierungen
normale annormale
Diffusion Diffusion
Diffusion von
Interstitiellen
• Oktaederplätze
• Tetraederplätze
• Einsteinmodell
• Dk für C, N, O
Beispiel
N in Fe-Cr
• Meßmethoden
• Diffusion von
H in Fe
Chemische
Diffusion
Leerstellenmechanismus
Ultraschnell
e Diffusion
Fünffrequenzmodell
Modelle zur
Bestimmung von
Q
Selbstdiffusion
Thermisch aktivierte Bewegung von A-Atomen im reinen Element
A bzw. in einer homogenen, das Element A enthaltenden Phase AB
Fremddiffusion
Thermisch aktivierte Bewegung von Fremdatomen B in einer
Matrix A (oder einer das Element B nicht enthaltenden Legierung
ACD...) ohne gegenseitige Beeinflussung der B-Atome untereinander (praktisch unendliche Verdünnung).
Chemische Diffusion
Transport von Atomen, gekoppelt mit Transportkräften
1. Fick‘sches Gesetz
Diffusionsstrom J
2.Fick‘sche Gesetz
Diffusionsgleichung
(Einsetzen des 1. FG
in dieKontinuitätsgleichung)
Triebkräfte :
 chemisches Potential
 elektrische Felder =Elektrotransport (Elektromigration)
 Temperaturgradient = Thermotransport (Energieübertragung durch unordnete „Stöße“ zwischen atomaren Gebilden)
 elastische Spannungsfelder (elast. Verzerrungsfelder v. Versetzungen)
Snoek-Effekt
Interstitielle ( C, N, O )
führen in krz - Metallen
zu lokalen tetragonalen
Verzerrungen in {100} Richtung. Bei einachsiger Belastung wird die
statistische Besetzung
der drei Richtungen
aufgehoben, es erfolgt
eine Umverteilung auf
günstig orientierte Plätze
Elektromigration
Materialtransport durch hohe elektrische Stromdichten
in miniaturisierten Leiterbahnen
E.Arzt:Phys.Bl.52(1996)Nr.3
Poren und Hügel entstehen an Divergenzen des Masseflusses,
verursacht durch Korngrenzen. Auf der Katodenseite (rechts)
eines Segmentes mit Längskorngrenzen werden Atome durch
den Elektronenwind „weggeblasen“, sodass eine Pore entsteht
Auf der Anodenseite (links) entwickelt sich in der Stauzone ein
Hügel.
Volumendiffusion - Kurzschlussdiffusion
 Korngrenzendiffusion
 Versetzungsdiffusion
 Oberflächendiffusion
Effektive Diffusion = Überlagerung der relativen Anteile von
Volumen und Kurzschlussdiffusion
Elektromigrationsschädigung an Al-Leiterbahn (1,8µm, Stromd. 1,4 MA/cm², 227°C)
Elektromigration
Hügelbildung an einer Goldbahn
Diffusion, die an Transportkräfte gekoppelt ist 
Der thermisch makroskopisch statistischen
Bewegung ist eine Driftbewegung in Richtung der an den Atomen angreifenden
Kraft überlagert.
c
J  D
x

v c
Diffusionsterm + Driftterm
Verschiebungsgeschwindigkeit eines <v>
eines Metallstreifens der Länge l (Pore Hügel) durch Elektrotransport
I.Blech: J.Appl.Phys.,47,1203-1208(1976)
v  
e
Z*

Elementarladung
eff. Ladungszahl
mech. Kenngröße
D

(eZ *  j  
)
kt
l


j
spez. Widerstand
Atomvolumen
Stromdichte
Platzwechselmechanismen
Leerstellenmechanismus
Intersticialcy
Substitutionsmechanismus
Zwischengittermechanismus
Interstitielle Diffusion
Direkter
Platzwechsel
Ringtausch
Fremddiffusion in Metallen
Diffusion von Interstitiellen








H, N, O zweiatomige Gase
Bindungskräfte < metallische Bindungskräfte
Gasatome < Metallatome
können keine echten Gitterplätze besetzen
Einbau auf Zwischengitterplätze
Kohlenstoff auch interstitiell
hohe Beweglichkeit der Zwischengitteratome
verändern stark die Werkstoffeigenschaften
Diffusion von Substitutionellen
(Fünffrequenzenmodell)
Ultraschnelle Diffusion
Zwischengitterplätze
2 verschiedene Zwischengitterplätze:  Fremdatom in oktaetrischer Umgebung eingebaut
 Fremdatom in tetraetrischer Umgebung eingebaut
krz-Gitter (bcc)
mit Tetraederlücke
kfz-Gitter (fcc)
mit Oktaederlücke
kfz-Gitter (fcc)
mit Tetraederlücke
hex-Gitter (hcp)
mit Oktaederlücke
Anordnung der Atome in der oxydischen Keramik Strontiumtitanat
MPI für Metallforschung Science Bd. 302, S. 846
Platzwechselmechanismen
Leerstellenmechanismus
Intersticialcy
Substitutionsmechanismus
Zwischengittermechanismus
Interstitielle Diffusion
Direkter
Platzwechsel
Ringtausch
Ultraschnelle Diffusion
In Metallen mit relativ großen
Gitterabmessungen (zB. Blei)
diffundieren einige Fremdatome 103 bis 104 mal schneller
als Selbstdiffusion 
„ultraschnelle Diffusion“,
wenn der Atomradius des
Fremdatoms<0,8 Radius des
Matrixatoms, sinkt die Aktivierungsenergie auf etwa die
Hälfte des Wertes der Selbstdiffusion
(kombinierte Zwischengitter-Leerstellendiffus.)
Periodensystem
mit schnelldiffundierenden Partnern
 zugehörige Matrixmetalle
Ir Pt Au
Hg
Diffusionsmechanismen
Selbstdiffusion
über Zwischengitterplätze
Fremddiffusion
Chemische Diffusion
über
Leerstellen
Übergangszustand
nach ZENER
1
2
...zur Leerstellenkonzentration
Aus thermodynamischer Sicht ist die
Anwesenheit von Leerstellen zu fordern,
da sie die Freie Enthalpie des Metalls
gegenüber dem Idealkristall erniedrigt.
Diese Erniedrigung ist durch die Erhöhung der Entropie bedingt.
G = n.GB - T.SC
Leerstellenkonzentration
G
Gibbs‘sche Freie
Enthalpie
Gleichgewichtsbedingung
 G
0
n
Federkonstante K aus dem Hooke'schen Gesetz:
 =E. 
F/A = E . x / l
F = K . x
F = E . A .  x / l = K .  x (pot. E. d. ged. Körpers)
makroskopische Federkonstante : K = E . A / l
Federkonstante eines Atoms
: Reduzier. des Prüfk. auf einen Atomabstand
 Diffusion durch n = Zahl der Atome pro Flächeninhalt
(beinhaltet Quadrat der Gitterkonstanten)
l
= Netzebenenabstand
K = E / (l . n)  E . a0
Als Beispiel betrachten wir Kupfer:
E = 12,98 . 1010 N/m2
l = 2,556 . 10-10 m
n = 2,16 . 1019 Atome/m2
m = 10,55 . 10-26 kg
K= 23,5 N/m
 = 2,4 . 1012 s-1
Arrheniusdarstellung des Diffusionskoeffizienten
D
Q 1
ln
 
D0
R T
 Q 
D  D 0  exp  

 RT 
1 dn
C
Das 1. Fick ' sche Gesetz
 j  D
A dt
x
entspricht dem Ohm' schen Gesetz
j
c(x)
x
Das 2. Fick‘sche Gesetz
Die Konzentrationsänderung
im Inneren eines Gebietes ist
gleich der Differgenz des über
die Oberfläche dieses Gebietes abfließenden Diffusionsstromes.
C

t
div j
C
C
 div j  0 1.Fick' scheGesetz
j D
t
x
 C 1  C 2  C 3
div C 


x 1 x 2 x 3
C
C 
C 
C 
grad C    C 
e1 
e2 
e 3
r
x 1
x 2
x 3
  Hamiltonoperator
  LaplacescherOperator
² C
² C
² C
div grad C 


x1²
x 2²
x 3²
²
²
²



in kartesisch enKoordina ten
x ²
 y ² z ²
C
² C
² C 
 ² C
C

D




 div ( D grad C ) Für D = konstant:
t
y ²
z ² 
t
 x ²
oder eindimensional:
DIFFUSIONSGLEICHUNG
C
² C
 D
t
x ²
partielle ( C=f(x,t)
lineare Dgl. 2. Ordnung
vom parabolischen Typ
Differentialgleichungen
gewöhnliche Dgl.
y=f(x)
partielle Dgl.
y=f(x1, x2..... x3)
Literatur:
G. Heber: „Mathematische Hilfsmittel
der Physik II“ 1967, Wissenschaftliche
Taschenbücher Vieweg&Sohn, Braunschweig
einfachster Fall: 2 unabhängige Variable und ihre Ableitungen
über Koeffizientendeterminante Unterteilung in 3 Typen:
elliptischer Typ
hyperbolischer Typ
U U
 2 0
2
x
y
2
2
zweidimensionale Potenzialgleichung (Elektrostatik, Magnetostatik)
parabolischer Typ
2.Ordnung
linear
 2U 1  2U
 2 2 0
2
x c t
 U 
 U 
 2   
 0
 x 
 t 
Gleichung einer schwingenden Saite oder eindimensionale Wellengleich.
Dgl. für alle eindimensionalen
Ausgleichvorgänge z.B. Wärmeleitung, Diffusion
partielle lineare Dgl. 2. Ordnung
vom parabolischem Typ
2
1
1
Die Fehlerfunktion  = erf (x)
1,2
1
erf (x)
0,8
0,6
0,4
0,2
0
0
0,5
1
x
1,5
2
TRACER-Methode zur Bestimmung der Volumenselbstdiffusion
h
h  0,2  Dt
Schichtenteilung
ln C
Lösung von
C
 2C
D 2
t
x
C
C(x)

1
4 Dt
Dünnschichtlösung
x2
1
1
D
4t (d ln C / dx 2 )
x
2
C0  h
 x 
C ( x, t ) 
exp 
 Dt
 4 Dt 
x2
ln C  
4t  D
C
C
D 2
t
x
2
Elektronenstrahlmikroanalyse
c( x, t )  F  exp { x 2 / 4Dt}
Härte-Tiefe-Kurve
 2C
1
4x2


0
2
2
x
2 Dt 4 Dt 
Lichtmikroskopie
x  2 Dt
Gasnitrierte Eisen-Chrom-Legierung
mit 4,5Ma.-%Cr , T = 590°C
Quadrat der Stickstoffeindringtiefe in µm
Das Quadrat der Stickstoffeindringtiefe als Funktion der Nitrierdauer
Nitrierzeit in h
Selbstdiffusion
Chemische
Diffusion
Fremddiffusion
DCh- chemischer Dk
DA - partielle Dk
DB - partielle Dk
C
DA* - Selbst - Dk
DB* - Selbst - Dk
DAB- Fremd - Dk
DBA- Fremd - Dk
m - Thermodyn.
Faktor
s - Leerstellenflussfaktor
A
Zusammenhang zwischien den Diffusionskoeffizienten in einem
binären System
B
DCh
x
DB*
DA
DAB
DB
A
DA*
D
0
B
0,5
1
NB
N B  DA  N A  DB  DCh  ( N B  DA  N A  DB )  m  s
*
*
Grube-Hall-Methode zur Bestimmung des konzentrationsunabhängigen chemischen Diffusionskoeffizienten
Aus der 2. Fick‘schen Gleichung
C
C2
 D
t
 x2
Ergibt sich mit den folgenden Anfangsund Randbedingungen
t = 0: x<0: C(x) = C0 x>0: C(x) = 0
t > 0: x: (C/ x)=0
als Lösung für
- < x < +  :

 x 
C ( x , t )  C o 1  erf 

2 
 2 Dt  

C  C  C min
C o C max 
C min
D
x ²
3 ,28479  t
Ni-Cu 1050°C / 3h
100
Ni, Cu in Ma.-%
75
50
25
Cu
Ni
0
0
50
100
150
Randabstand in µm
200
250
300
Matano-Auswertung für konzentrationsabhängigen Diffusionskoeffizenten
1  dx 
D


2 t  dC 
C'
C  C'
 x dC
0
Den Broeder-Auswertung für konzentrationsabhängige Diffusionskoeffizienten
D
1
1

 [ A ( 1  yC )  yC ( E  D ) ]
dc
2t
dx
Mo-Drähte
Messing
l
Kupfer
Plattierungsebene
A
t=0
jA
jB
B
Marker-Drähte
Kirkendallverschiebung l
ursprüngliche Lage der Plattierungsebene
Diffusionszone
A
t>t0
B
Konzentration
cA
Matano-Ebene
t>t0
Theorie von Darken
(Interpretation des Kirkendall-Effektes)
In biären Systemen existieren 2 unterschiedliche partielle (Fremd-) Diffusionskoeffizienten DA und DB. Mit den Molenbrüchen
C
A

NA
CA  CB
und
C
B

NB
CA  CB
Zusammenhang zwischen den sog. „partiellen“ (engl. Intrisic) Diffusionskoeffizienten DA und DB der beiden Atomarten A und B und den experimentell
zugänglichen Größen: Chemischer Diffusionskoeffizient und
Markergeschwindigkeit v = l/2t
Darken‘schen
Gleichungen
 N A l
  ( D A  DB )

x
2t
~
D  D A N B  DB N A
Eine Markierungswanderung ist also nur möglich, wenn ein Konzentrationsgefälle vorliegt und die beiden partiellen Diffusionskoeffizienten DA DB sind. Z.B.
wandern im System Co-Ni die Markierungen nicht, da Dco DNi ist
Experimentelle Befunde ausgewählter Diffusionspaare
Diffundierendes
Element
Matrixmetall
D0
[.10-4m2s-1]
Q
[kJ/mol]
Mangan
-Eisen
0,35
282,6
Nickel
-Eisen
0,5
276,3
Nickel
Kupfer
2,3
243
Kupfer
Nickel
0,65
258
Kupfer
Aluminium
2,0
141,9
Aluminium
Kupfer
0,045
166
Zink
Kupfer
0,033
159,1
Interstitielle Fremddiffusion von Kohlenstoff, Stickstoff
und Sauerstoff in Eisen
Interstitielle Fremddiffusion von Kohlenstoff,
Stickstoff und Sauerstoff in Eisen
Diff.
Element
- Fe
T-Bereich
(K)
- Fe
D0
(10 -6 m 2 s -1 )
Q
( kJ / Mol )
D0
(10 -6 m 2 s -1)
Q
( kJ / Mol )
C
235 - 350
700 - 1100
1670 - 1800
0,167
6,3
1,3
78,1
91,0
81,4
74
159
N
225 - 325
700 - 1000
1670 - 1800
0,126
0,78
0,78
73,4
79,1
79,1
91
168,5
O
950 - 1150
1670 - 1800
10
111,1
575
168,5
Mehrphasendiffusion / Reaktive Diffusion
Beispiele: Schweißen, Löten, Schmelztauchen, Beschichten, Oxidwachstum
 Platzwechselvorgänge streben
Gleichgewichtseinstellungen an.
 Gleichgewichtsverhältnisse
liefert das Zustandsdiagramm
 Zusammenhang zwischen
Diffusionsverhalten zweier Metalle u. Gg-Diagramm
a) lückenloser Mischkristall
b) eutektisches System mit
Mischungslücke
c) mit zusätzlicher intermetallischer Phase
 Konzentrationsstufen: Bei der Reaktion zweier Metalle A u. B treten nur thermodynamisch
mögliche Phasen mit bestimmten Konzentrationsgrenzen auf.
 Die im Zustandsdiagramm dazwischenliegenden heterogenen Mischungen können nicht
gebildet werden.
 Die Höhe der Konzentrationsstufe im C-x-Diagramm entspricht der jeweiligen Breite des
Zweiphasengebietes im Zustandsdiagramm.
 Das Wachstum der einzelnen Phasen erfolgt nach einem parabolischen Zeitgesetz
 Der Diffusionskoeffizient bestimmt, welche Phase am schnellsten wächst.
Literatur
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
Ja. E. Geguzin: Lebender Kristall; Deutscher Verlag für Grundstoffindustrie,
Leipzig, 1984
Th. Heumann: Diffusion in Metallen; Springer-Verlag, Berlin, Heidelberg,
New York, 1992
Landolt-Börnstein: Neue Serie, III. Band 26: Herausgeber H. Mehrer,
Diffusion in festen Metallen und Legierungen, Springer-Verlag Berlin,
Heidelberg, New York, 1990
J. Philibert: atom movements; diffusion and mass transport in solids,
les editions de physique 1991
A. R. Allnatt; A. B. Lidiard: Atomic Transport in Solids,
Cambridge University Press 1993
A. L. Laskar; J. L. Bocquet; G. Brebec and C. Monty: Diffusion in
Materials; Kluwer Academic Publishers, Dordr./Boston/London, 1990
G. R. Purdy (Editor): Fundamentals and Applications of Ternary
Diffusion; Pergamon Press, New York, 1990
J. Kaur and W. Gust: Fundamentals of Grain and Interphase
Boundary Diffusion; Ziegler Press, Stuttgart, 1988
Literatur (Fortsetzung)
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
J. Kaur; W. Gust; L. Kozma: Handbook of Grain and Interphase
Boundary; Diffusion Data; Ziegler Press, Stuttgart, 1989
A. Guinier und R. Jullien: Die physikalischen Eigenschaften
von Festkörpern; Carl Hanser Verlag, München, (1992) S. 19 - 22
H. Kuzmany: Festkörperspektroskopie; Kap. 16 Neutronenstreuung,
Springer-Verlag, Berlin, 1990, S. 295 ff.
A. M. Brown, M. F. Asby: Acta Metall. 28 (1980) 1085 ff.
U. Köhler; C. Herzig: Phil. Mag. A 58 (1988) 769
M Lübbehausen; H. Mehrer: Acta Met. 38 (1990) 283 ff.
D. Bergner: DIMETA - 82: Diffusion in Metals and Alloys,
Trans. Tech. Publ. (1983)
D. Bergner: Metallurgie i Odelwenictwo 13 (1987) 523 – 532
E. Arzt; O. Kraft; U.E. Möckl: Phys. Bl. 52 (1996) Nr. 3
B. Buchmayr: Werkstoff- und Produktionstechnik mit Mathcad
Springer-Verlag, Berlin, Heidelberg, New York, 2002
D. Heger, D. Bergner: HTM 46 (1991) 6 S.311-338