10.02.2012

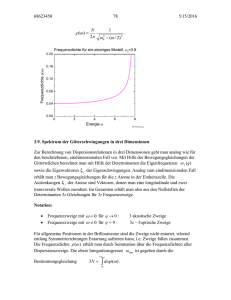
Mechanisch-thermische
Materialeigenschaften
VL # 24
Vladimir Dyakonov
[email protected]
Experimental Physics VI,
Julius-Maximilians-University of Würzburg
und
Bayerisches Zentrum für Angewandte Energieforschung e.V. (ZAE Bayern)
10 Februar 2012
Zusammenfassung II
Gitterschwingungen-Wärmeleitung
2
- Valenzelektronen sind über ganzen Kristall verschmiert (Leitungselektronen)
- Bindungsenergie resultiert hauptsächlich aus der Reduktion der kinetischen Energie der Leitungselektr.
Elastische Eigenschaften von Festkörpern
• Wasserstoffbrückenbindung
- Ionische/kovalente
Bindung vondas
H-Atom
mit zwei
Partnern
Wir behandeln
Gitter
alselektronegativen
ein Kontinuum,
dessen elastische
ROSS
+
- Bindung nur
mit 2 Partnern, da wir
H -Ion
sehr
klein,Elastizitätsmodul
kleine Bindungsenergie wegen
geringer Zahl
der
Eigenschaften
mit
dem
beschreiben
Bindungspartner
R. G
150
UND
A
• Verhalten von Festkörpern unter Wirkung von äußerer Kraft
Beschränkung auf elastischen Bereich
(Hookescher Bereich)
Spannung (stress)
4.3
Elastizitätsmodul
sym. Tensor
4. Stufe
Dehnung (strain)
Der Elastizitätstensor
sym. Tensor
2. Stufe
sym. Tensor
2. Stufe
• Spannung:
 Normalspannung:
Wir haben bereits in Abschnitt 4.1 diskutiert, d
sym. Tensor
2. Stufe
nearer Zusammenhang besteht, solange
wir uns
formationen befinden. In diesem Fall sind die D
Spannungkomponenten und umgekehrt und es
 Schub(Tangential-)spannung:
C-Tensor mit 81 Komponenten
sij =
Â
kl
Cijkl ekl .
3
Gitterschwingungen
• Nun betrachten wir die diskrete Struktur des Kristallgitters, d.h. die
Bewegung der Gitteratome um ihre Ruhelage unter den
wirkenden Kräfte
• Allgemeiner Ansatz: die so genannten harmonische und
adiabatische Näherungen
Adiabatische Näherung
4
Gitterschwingungen
Harmonische Näherung
5
Dynamik des Kristallgitters
Relevanz der Gitterschwingungen
•
•
thermische Ausdehnung
•
•
•
spezifische Wärme (Energie-Inhalt der Schwingungen)
Wärmeleitfähigkeit (Ausbreitung der thermischen
Auslenkungswellen)
Schallausbreitung, Wellen
optisches Verhalten im IR-Bereich
6
Dynamik des Kristallgitters
Massenpunkte & elastische Federn
7
Dynamik des Kristallgitters
Dispersionskurve: 1 atomiges Gitter
8
Dynamik des Kristallgitters
Phononenfrequenzen:
Dynamik des Kristallgitters
1D-Zustandsdichte: Frequenz-Raum
Dynamik des Kristallgitters
2D -Zustandsdichte
Resonanz
(Antwortfunktion
für
:
(
)
htleitende
Materialien
P(
(( ))E(
Ladungsoszillatoren
im FK:
00 Suszeptibilität
P( ) )==
E( ))
allg:
( )
- für
«
:
(
)
const.
Suszeptibilität
des
Materials
)
0 Trägheit
(- )für
) == 11 ++ (( ):) ( )
Dynamik
des
Kristallgitters
(
eines
Oszillators
: (i)
( )Gitteratome
>0
D(
))++ P(
)) 00 (( )) E(
D( ) )== 00E(
E(
P(
E( )) - für
mAtom
Phasensprung
Ladungsoszillatoren
im
FK:
P(
)
=
(
)
E(
)
- für > : ( ) 0
0
mit
Eigenfrequenz
:
dielektrische
Optische Eigenschaften
dielektrischeFunktion
Funktion
mEl.
( Resonanz
)10
= 41 ·+ m( )
- für
: (ii)
( m
) Valenzelektronen
D( Gitteratome
) = 0 E( ) + P( m
) Atom
) At.
(i)
El. Federpendel:
At.
0 ( ) E(
- für
: ( )
0 Trägheit
- -für
für «« : : (( )) const.
const.
sdichte
Ladungsoszillatoren
im FK:
dielektrische
Funktion
(ii)
Valenzelektronen
mEl.für FK gilt:
(Fern)-Infrarot
const im IR =
- -für
: : (( )) >> 00
für
Phasensprung
Phasensprung
-2 ·
mAt. 104 · mEl.
für >>(i): : Gitteratome
(( )) 00
: - -für
14 El
-1
mAtom
At. 310
s
·
10
(
)
+
(
)
(
)
=
1
+
Resonanz
At
ät - -für
(für)
( )) « Resonanz
: : - (für
: ( ) const.
½½El
Federpendel:
=
(k
/
m)
sichtba
Federpendel:
(k(0)
/ m)
(ii)
Valenzelektronen
mEl. im IR = = El
(Fern)-Infrarot
für
FK
gilt:
const
für
:
(
)
0
Trägheit
für
:
(
)
0
Trägheit
ators
- für
: ( )>0
( · )1014 s-1
Phasensprung
10
mFK:
FK:
3
für
>
:
(
)
0
quenz für
:
) const
+ im10
(IR
) (0)
( mFK
) =gilt:
1104+
4 · mEl(
-2
At
=
-2
·
mAt.
10 · mEl.
10 · ElElElim (F)-IR:
At.- für
El.
At. Resonanz
:
(
)
At.
tom
om
Federpendel: = (k / m)½
sichtbar,
)
1 + (Fern)-Infrarot
n mmEl. ( ) -=für
(Fern)-Infrarot
2/
2 sichtbar,UV
UV
El((: )) ( + )
At0( Trägheit
(0)
(
)
=
(
)
+
(Ne
µ)
·
(
El.
0
T
15 ··· 1016 s-1
14 s-1
10
atoren im FK:
15 ··· 1016 s-1
3
·
10
14
-1
10
3 · 10 s
(
)
(0) -2 ( ) „ heißt
nst
im
IR
=
(0)
» T
4
“
El
nst
im
IR
=
(0)
m
10
·
m
10
·
im
(F)-IR:
El
E
me mAtom
At.
El.
At. ( )
El
( ) ) im (F)-IR:
2/
2)-1 sichtbar, UV
2 At
(
µ)
·
(
T
At
ektronen ( m)El.= ( ) + (Ne
(Fern)-Infrarot
0
T
2
2
-1
2
( ) (0)
= ( ) + (Ne / 0µ) · ( T - )
T
15
16 -1
const
(0)
)
im((IR
)
2)-1
2 0µ) · ( T
2 -1
2
0µ) · ( T - At )
t » T
» T
( ) +
)
( )
=
10 ··· 10
14 s-1
3
·
10
( )
„
heißt
»
El
“
„ (0)
» T
T El( )
“ heißt
F-IR
El
T
T
F-IR
M-IR
F-IR (0) M-IR
N-IR
N-IR
s
F-IR
M-IR
MN-IR
200
200
VIS
VIS
El(
)
12
: : ( ( ) ) 0 Trägheit
( ) = 1 + Resonanz
El( ) +
für
für
:
mAt.
des
( Dynamik
)
0 Trägheit
( )
Federpendel:
At
Kristallgitters
4 · m ( )
-2 ·
10Optische
10
El.Eigenschaften
At.
El
= (k / m)½
(0)
( )
-2 ·
mAt. 104 · mEl.
10
El
sichtbar, UV
im (F)-IR:
(Fern)-InfrarotAt.
2/
2)-1UV
2
sichtbar,
mEl.
( ) =(Fern)-Infrarot
( )3+· 10
(Ne
14 s
-1 0µ) · ( T 1015 ··· 1016 s-1 T
15 ··· 1016 s-1
14 s-1
10
3
·
10
R = El(0)
„ “ heißt » T
F-IR
m IR = El(0)
M
)
(0)(0)
( () )
(T2 -T2 - 2)-12)-1
T
T
( )
El
(
)
El
TT
F-IR
F-IR
200 200
M-IR
M-IR
N-IR
N-IR VISVIS
Dielektrische Funktion ε(ω) entscheidend für
Ausbreitung von EM Wellen im FK!
13
Dynamik des Kristallgitters
Dielektrische Funktion
Thermische Eigenschaften des Kristallgitters
Folgende Eigenschaften von Isolatoren wurden diskutiert:
spezifische Wärme
thermische Ausdehnung
Wärmeleitfähigkeit
Notwendig sind grundlegende Beziehungen der Thermodynamik und
der statistischen Physik
Thermische Eigenschaften des Kristallgitters
Spezifische Wärme
CV hängt direkt mit der inneren Energie des Festkörpers zusammen!
Thermische Eigenschaften des Kristallgitters
Spezifische Wärme: quantenmechanisch
- Wie groß ist die mittlere Besetzungszahl < n > für die Frequenz w ?
<n>
Dynamik des2 Kristallgitters
Massenpunkte
½
+
>
<n Federn
& elastische
>
1
<n
0
0
1
kBT / hω
2
3
Abbildung 6.3: Die Bose-Einstein-Verteilungsfunktion. Bei hohen Temperaturen nimmt die Besetzungszahl in etwa proportional zur Temperatur zu. Die Funktion (hni + 12 ) nähert sich für hohe Temperaturen dem klassischen Grenzfall (gestrichelt) an.
Dreidimensionales Gitter mit mehratomiger Basis: Wir hatten bei unserer obigen Diskussion eine einatomige Basis angenommen. Liegt eine mehratomige Basis mit r Atomen vor, so
haben wir statt 3N jetzt 3rN Schwingungsmoden vorliegen. Wir müssen dann die Schwingungsfrequenzen wqr sowohl mit den erlaubten q-Vektoren als auch den möglichen Polarisationen r durchnummerieren. In Analogie zu (6.1.26) können wir die mittlere Besetzungszahl
von Phononen des Typs q, r bei der Temperatur T zu
hnqr i =
1
e
h̄wqr
kB T
(6.1.28)
1
angeben. Für die mittlere Energie finden wir damit
hU i = U eq +
1
 2 h̄wqr
q,r
|
{z
}
Nullpunktsschwingungen
+
Â
q,r
h̄wqr
h̄wqr
kB T
| e {z
.
1}
(6.1.29)
thermischeAnregungen
Wir sehen, dass sich dieser Ausdruck deutlich vom klassischen Dulong-Petit Resultat unterscheidet. Er enthält erstens die Nullpunktschwingungen und der Beitrag der thermisch angeregte Gitterschwingungen nimmt zu tiefen Temperaturen hin stark ab, da die mittlere Beset-
18
Thermische Eigenschaften des Kristallgitters
Bose-Einstein Verteilungsfunktion:
bei höheren Temperaturen
: klassisches Verhalten
der Vorlesungsstunde
vom 09.12.2010
Thermische Zusammenfassung
Eigenschaften
des Kristallgitters
• Wärmekapazität des Kristallgitters
Vergleich Debye-Einstein Zustandsdichten
- klassische Berechnung von U  Gleichverteilungssatz, ½ kBT pro Freiheitsgrad
Dulong-Petit
- quantenmechanische Betrachtung  Ausfrieren der Phononen bei T-Erniedrigung
Nullpunktsschwingungen
Einstein-Modell:
Debye-Modell:
 = vs q  D()  ²
Besetzun
thermisch angeregteGitterschwingungen Bose-Einstein
Thermische Eigenschaften des Kristallgitters
Einstein-Näherung:
• Bei tieferen Temperaturen spielen die akustischen Phononen die
dominierende Rolle und deren Zustandsdichte kann s nicht mit DeltaFunktion beschrieben werden
• Die Einstein-Näherung ist immer dann gut, wenn die optischen Phononen
dominieren, die wegen ihrer flachen Dispersion gut mit dieser
Zustandsdichte beschrieben werden können.
Thermische Eigenschaften des Kristallgitters
Debye-Näherung:
Bei der Debye-Näherung werden folgende Annahmen gemacht:
• Alle Phononenzweige werden durch 3 Zweige mit linearer Dispersion
angenähert:
7.1.6 Debye-Modell
k = vs
Näherung für
(k):
= vs · k
/ k = vs
Schallgeschwindigkeit
windigkeit
Debye-Näherung geeignet für:
- akustische Phononen
- tiefe Temperaturen, d.h. nur niederenergetische
Schwingungsmoden angeregt (kBT « opt)
k
Zustandsdichte D( )
V / (2
(6
2)
2 v 3)
s
=V
2/
(2
N/
= ( N/ k)( k/ )
= ( / k)- · D(k) = vs- k2 V / (2
#2 Schwingungen
bis Frequenz
3
vs )
:
D( ´)d ´ =V
3/
(6
2)
=V
2/
(
2 v 3)
s
Problem: In Probe mit N El.-Zellen dürfen nur N unabh. Schwingungen e
Lösung: Einführung einer Maximalfrequenz
Debye
3
D =
vs3· 6
2N
/V
Thermische Eigenschaften des Kristallgitters
Debye-Temperatur: Zusammenfassung
• Die Debye-Temperatur spielt eine wichtige Rolle in der
Festkörperphysik. Die Größe der Debye-Temperatur ist ein Maß für die
Größe der in einem Material vorkommenden Phononenfrequenzen.
• Die Debye-Temperatur gibt auch den Grenzbereich zwischen einer
klassischen und einer quantenmechanischen Beschreibung der
thermischen Eigenschaften des Kristallgitters an.
Thermische Eigenschaften des Kristallgitters
Debye-Näherung:
Thermische Eigenschaften des Kristallgitters
anharmonische Effekte:
• Gleichgewichtseigenschaften:
‣
thermische Ausdehnung
‣
Druck- und Temperaturabhängigkeit der elastischen
Konstanten
• Transporteigenschaften:
‣
Wärmeleitfähigkeit
Thermische Eigenschaften des Kristallgitters
harmonisches Pot.
versus
anharmonisches
Abschnitt
5.1
F ESTKÖRPERPHYSIK
Uel (eV)
0.01
∆R = R – R0
harmonische
Näherung
0.00
R0
-0.01
1.0
1.2
1.4
1.6
1.8
R/σ
Abbildung 5.1: Zur adiabatischen und harmonischen Näherung. Gezeigt ist die Potenzialkurve für
U zeigt auf Grund des starken
abstoßenden Potenzials für kleine
Abstände eine beträchtliche
ten Grundzustand bleiben. Daraus folgt eine beträchtliche Vereinfachung der Beschreibung,
weil die Bewegungen der Elektronen
und der Kerne entkoppelt werden.6
Asymmetrie
eine Van der Waals Wechselwirkung
anh von zwei Atomen (durchgezogene Linie) und die harmonische
Näherung (gestrichelte Linie).
Bei Auslenkung aus seiner Ruhelage R0 erfährt ein Kern eine rücktreibende Kraft, die in
atomaren Einheiten in harmonischer Näherung durch die klassische Bewegungsgleichung
M
R0 ) beschrieben wird. Daher skalieren die Frequenzen w der Kernbewegung mit
m R̈ µ ( R
dem Massenverhältnis wie
• Anharmonische Effekte:
Thermische Eigenschaften des Kristallgitters
- Superpositionsprinzip gilt nicht mehr
- 3-Phononen-Prozesse
Thermische Ausdehnung
nach Rudolf Peierls:
G = 0  Normalprozess
G ≠ 0  Umklappprozess
• Thermische Ausdehnung:
Ursache: Anharmonizität des Gitterpotenzials
mittlere Auslenkung
der Gitteratome:
thermische
Ausdehnung:
• Wärmeleitfähigkeit:
T-Gradient [K/m]
Wärmestrom [W/m²]
• Transporttheorie:
Wärme fließt von
heiß nach kalt
Wärmeleitfähigkeit [W/m K]
N.B. In harmonischer Näherung <u>=0, d.h. die Gleichgewichtsposition
≠ 0  Nichtgleichgewichtseffekt
der Atome bleibt gleich und wir haben keine thermische
Ausdehnung
Thermische Eigenschaften des Kristallgitters
Thermische Ausdehnung
Die normierte Steigung der L(T)-Abhängigkeit nennt man thermische
Ausdehnung:
Der Volumenausdehnungskoeffizient ist gegeben durch
Typische experimentelle Werte für αL liegen bei 10-5K-1 bei RT
Wärmeleitfähigkeit keine Gleichgewichtsgröß
Thermische Eigenschaften des Kristallgitters
raturgradienten getrieben und der Wärmetran
Wärmeleitfähigkeit
• In Festkörpern wird Wärme sowohl durch Phononen als auch durch Elektronen
6.4.1 Definition der Wärmeleitfähigkei
transportiert.
• In Metallen überwiegt üblicherweise der Beitrag der Elektronen.
•
Wir definieren die Wärmeleitfähigkeit k eine
Sind Isolatoren schlechte Wärmeleiter? Nein!
schen treibendem Temperaturgradient rT un
• Bei tiefen Temperaturen ist die thermische Leitfähigkeit von einigen kristallinen
Isolatoren (z.B. Al2O3, SiO2) größer als diejenige von Cu.
Jh =
k rT .
Dabei sorgt das Minuszeichen dafür, dass die
sche Wärme und führen die mittlere freie Weglänge ` = vt
Definitionsgleichung
(6.4.1) folgenden
für die Wär
Thermische Eigenschaften
desAusdruck
Kristallgitters
Boltzmann-Transporttheorie
k =
1
cV v ` .
3
Wärme
der Phononen und
deren der Phononen und der
• Spezifische
Wir sehen,
dass
die
spezifische
Wärme
Gruppengeschwindigkeit spielen eine entscheidende
entscheidende
Rolle für die Wärmeleitfähigkeit spielt. Pho
Rolle für die Wärmeleitfähigkeit
optische
Phononen
deshalb
wenig zum Wärmetransp
nahe amtragen
Zonenrand
oder optische
• Phononen
Phononen
wenig freie
zum Wärmetransport
aber auch
die tragen
mittlere
Weglänge bei
der Phononen. Diese
Rolle spielt
mittlere
freie Weglänge
• Eine wichtige
Phononen
bestimmt,
diediewir
weiter
unten noch im Detail dis
der Phononen.
• Diese wird durch die Streuprozesse der Phononen
bestimmt
Kinetische Gastheorie
Wir können das Ergebnis (6.4.9) auch sehr einfach aus der
sche Wärme und führen die mittlere freie Weglänge ` = vt
Definitionsgleichung
(6.4.1) folgenden
für die Wär
Thermische Eigenschaften
desAusdruck
Kristallgitters
Temperaturabhängigkeit der Wärmeleitfähigkeit
k =
1
cV v ` .
3
1. Temperaturabhängigkeit
der spezifischen
Wärme
V
Wir sehen,
dass die spezifische
Wärme
dercPhononen
und der
entscheidende
Rolle für der
diemittleren
Wärmeleitfähigkeit
spielt. Pho
2. Temperaturabhängigkeit
freien Weglänge l
optische Phononen tragen deshalb wenig zum Wärmetransp
Streuprozesse
aber auch die mittlere freie Weglänge der Phononen. Diese
In Nichtmetallen
sind die
Streuprozesse
Phononen:
Phononen
bestimmt,
diewichtigsten
wir weiter
unten für
noch
im Detail dis
• Phonon-Phonon-Streuung
• Streuung an Defekten, Oberflächen etc.
Kinetische
Gastheorie
Wir können das Ergebnis (6.4.9) auch sehr einfach aus der
Thermische Eigenschaften des Kristallgitters
Abschnitt 6.4
F ESTKÖRPERPHYSIK
Temperaturabhängigkeit
der Wärmeleitfähigkeit
253
Abbildung 6.15: Wärmeleitfähigkeit von Silizium. Links: hochreines Si (nach C.J. Glassbrenner, G. A.
Slack, Phys. Rev. 134, 1058 (1964)). Rechts: Hochreines natürliches Silizium (nach M. G. Holland, Phys.
4
Rev. 132, 2461 10
(1963);
W.S. Capinski, Appl. Phys. Lett. 71, 2109 (1997)) sowie isotopenreines (99.7%)
 T³
28 Si (nach W.S. Capinski, Appl.
Phys. Lett. 71, 21094 (1997)).
10
 (W / m K)
 (W / m K)
3
und dann µ eQD3/T ansteigt und dann unterhalb
10 einer von der Probengröße und Probenreinheit
10
abhängigen Temperatur
sättigt.
2
10 erhalten, müssen wir noch die TemperaturUm die Temperaturabhängigkeit von k zu
abhängigkeit von cV berücksichtigen.
Wir haben in Abschnitt 6.1 gesehen, dass cV für T
 1/T
1
2
10
Q D in etwa konstant
ist
und
für
T
⌧
Q
proportional zu T 3 verläuft. Für den mittleD
10
ren Temperaturbereich erhalten
wir, anhängig vom verwendeten
Modell, unterschiedliche TSi
28Si
0
natSi
Abhängigkeiten für cV . Die Details sind hier10allerdings
nicht
so wichtig, da die exponentielle
Rechnung dominiert.
für 28Si
T-Abhängigkeit der mittleren freien Weglänge das Verhalten
Insgesamt erwarten
Rechnung für natSi
1
-1
wir folgende Temperaturabhängigkeit
der Wärmeleitfähigkeit:
10
10
1
10
2
10
T (K)
3
10
-2
10
-1
10
0
10
T / D
8
D
< T Phys. Rev. 134, 1058 (1964)). Rechts: Hochreines natürliches Silizium
Slack,
(nach M. G. Holland, Phys.
n
Q
/T
Rev.
132,
2461
(1963);
W.S.
Capinski,
Appl.
Phys.
Lett.
71,
2109
(1997))
sowie
isotopenreines
(99.7%)
D
k µ 28 SiT(nacheW.S. Capinski,
. (6.4.20)
mitAppl.
n Phys.
' 0Lett. 371, 2109
für(1997)).
T ⌧ QD
(Ph-Ph-Streuung)
>
: 3
T
für T n Q D
(Ph-Defekt-Streuung)
Abbildung
6.15: Wärmeleitfähigkeit von Silizium.
Links:
Glassbrenner, G. A.
>1
für
Thochreines
Q Si (nach C.J.(Ph-Ph-Streuung)
und dann µ eQD /T ansteigt und dann unterhalb einer von der Probengröße und Probenreinheit
abhängigen Temperatur sättigt.