12-2 Mechanische Schwingung

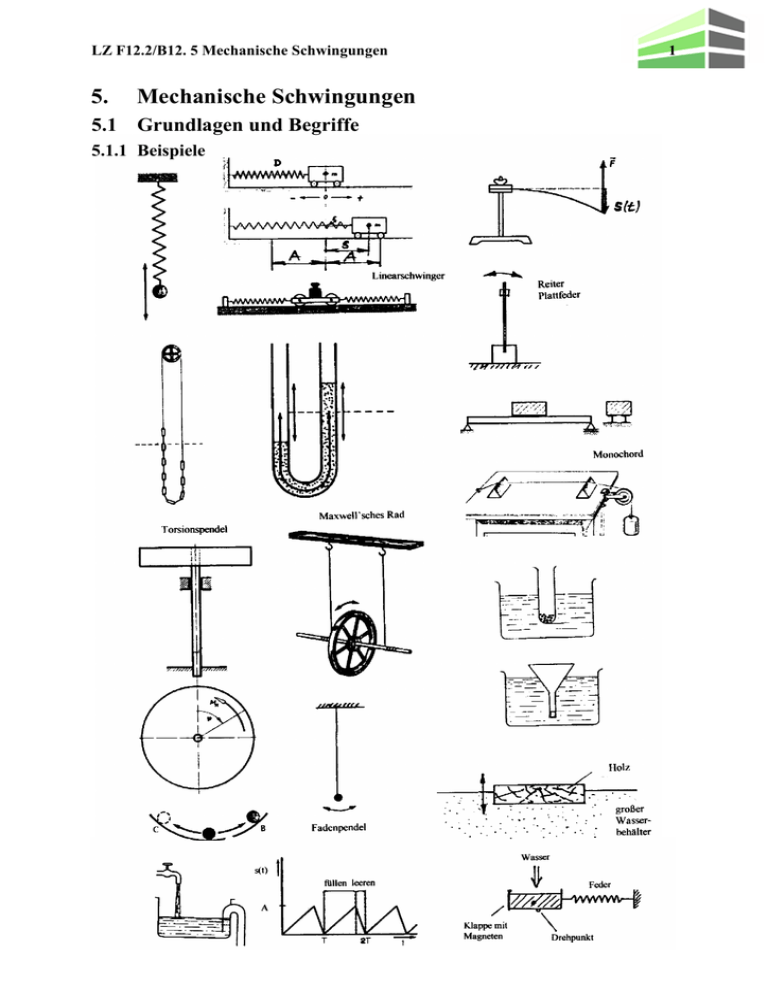
LZ F12.2/B12. 5 Mechanische Schwingungen
5.
Mechanische Schwingungen
5.1 Grundlagen und Begriffe
5.1.1 Beispiele
1
LZ F12.2/B12. 5 Mechanische Schwingungen
2
5.1.2 Begriffe
Mechanische Schwingung ist eine periodische Hin- und Herbewegung eines mechanischen
Körpers um seine Ruhelage
Periodendauer, Schwingungsdauer T ist die Zeit für eine vollständige Hin- und
Herbewegung. [T] = 1s
1
Frequenz f ist die Anzahl der Schwingungen pro Sekunde [ f ]  1  1 s 1  1Hz
s
f 
1
1
;T 
T
f
Ruhelage (RL) (Nulllage, Gleichgewichtslage) ist die Lage des Schwerpunktes des Körpers,
wenn dieser im Ruhezustand ist.
Umkehrpunkt (UP) ist der Punkt, an der der Körper seine Bewegungsrichtung ändert.
Amplitude ŷ ist die größte Entfernung (maximale Auslenkung) des Pendelkörpers von der
Ruhelage.
[ ŷ ] = 1m
(in der Formelsammlung mit A bezeichnet)
Elongation y ist die momentane Entfernung (Auslenkung) von der Ruhelage, auch y = y(t)
(in der Formelsammlung mit s = s(t) bezeichnet)
LZ F12.2/B12. 5 Mechanische Schwingungen
3
5.1.3 Reihen- und Parallelschaltung von Federn
5.1.3.1 Parallelschaltung
D1 und D2 sind die jeweiligen Federkonstanten
1)
Dehnung der Federn ∆x = ∆x1 = ∆x2
2)
F = D · ∆x
3)
F = F1 + F2
2) in 3)
D · ∆x = D1 · ∆x1 + D2 · ∆x2
mit 1)
D = D1 + D2
D = D1 + D2 + . . . + Dn ; nIN
5.1.3.2 Reihenschaltung
1)
Dehnung der Federn ∆x = ∆x1 + ∆x2
2)
x 
3)
F = F1 = F2
2) in 1)
mit 3)
F
D
F F1 F2


D D1 D2
1
1
1


D D1 D2
1
1
1
1


 ... 
D D1 D2
Dn
Für die Reihenschaltung zweier Federn gilt: D 
Übung:
; n  IN
D1  D2
D1  D2
Zwei waagrecht angeordnete Federn sind links und rechts an einer Wand
befestigt. Zwischen den beiden Federn ist eine schwingende Masse angeordnet.
Wirkt diese Schaltung als Reihen- oder Parallelschaltung?
LZ F12.2/B12. 5 Mechanische Schwingungen
4
5.2 Die harmonische Schwingung
5.2.1 Definition
Definition: Jede Schwingung, die wie eine parallele senkrechte Projektion einer Kreisbewegung abläuft, heißt harmonisch1.
Folgender Versuch soll dies verdeutlichen: Wir betrachten den Schatten eines kleinen Stiftes
der von einem parallelem Lichtbündel seitlich bestrahlt wird. Der Stift umläuft mit konstanter
Winkelgeschwindigkeit eine Kreisbahn. Gleichzeitig betrachten wir den Schatten einer
kleinen Kugel die an einer Feder vertikal auf und ab pendelt. Der Radius der Kreisbahn und
die Amplitude des Federpendels sind gleich.
Ergebnis:
Die Schwingung eines Federpendels verläuft synchron2 mit der Schattenprojektion einer geeigneten Kreisbewegung (Umlaufdauer gleich groß wie Schwingungsdauer; Start aus gleicher Position y(t)).
Beachte:
Bei der Beschreibung der harmonischen Schwingung und der Kreisbewegung
treten die gleichen Größen in verschiedener Bedeutung auf.
Formeln:
Größe
M
r
T
f


1
2
f 
1
;
T
1
T
  2   f  2   ;
Kreisbewegung
Mittelpunkt
Radius
Umlaufdauer
Drehfrequenz (n)
Drehwinkel
Winkelgeschwindigkeit
Größe
RL
ŷ
T
f


Harmonie (gr.) ... Einklang, ausgewogenes Verhältnis, Wohlklang
synchron (gr.) ... gleichzeitig, zeitgleich, gleichlaufend
   t
harm. Schwingung
Ruhelage
Amplitude
Schwingungsdauer
Frequenz
Phase
Kreisfrequenz
LZ F12.2/B12. 5 Mechanische Schwingungen
5
5.2.2 Bewegungsgleichungen
5.2.2.1 Das Zeit – Weg – Gesetz
y = y(t)
Der Ort des Massenmittelpunktes in der Ebene des Kreises beschreibt der Ortsvektor:
r  cos   r  cos t   yˆ  cos t   x(t ) 
 
r  r (t )  




 r  sin    r  sin t   yˆ  sin t   y (t )
Anfangsbedingung zum Zeitpunkt

 yˆ 

t  t0  0s ;  ( 0s)  0  0 ; r (0s )   
0
y  y(t )  yˆ  sint  bzw. s  s(t )  A  sint 
Achtung: Bei allen Aufgaben muss der Phasenwinkel     t im Bogenmaß eingesetzt
werden!!!
Umrechnung für beliebige Winkel:
 Bogen  Grad 
Umrechnung für beliebige Zeit/Winkel-Beziehungen:

1800
t  Bogen Grad


T
2 
3600
Nachfolgend werden Winkelangaben immer im Bogenmaß angegeben. Daher wird in Zukunft
keine Indexangabe mehr gemacht!
   t 
2 
 t  2   f  t
T
LZ F12.2/B12. 5 Mechanische Schwingungen
5.2.2.2 Das Zeit – Geschwindigkeits – Gesetz
v  v(t )  y(t )  y (t ) 
6
v = v(t)
dy(t )
 yˆ    cos  t 
dt
Amplitude der Geschwindigkeit:
vmax  vˆ  yˆ  
Die Geschwindigkeit führt ebenfalls eine harmonische Schwingung durch. Ihre Phase eilt

allerdings um den Winkel
der Elongation y(t) voraus.
2
5.2.2.3 Das Zeit – Beschleunigung – Gesetz
a  a(t )  v(t )  y(t ) 
a = a(t)
dv(t )
  yˆ   2  sin   t 
dt
Amplitude der Geschwindigkeit:
ˆ  2
amax  aˆ   y
Die Beschleunigung führt auch wieder eine harmonische Schwingung durch. Ihre Phase ist
gegenüber der Elongation y(t) um den Winkel  verschoben.
Die größte Beschleunigung ist in den Umkehrpunkten. Der Vektor der Beschleunigung ist
immer zur Ruhelage hin gerichtet, d.h. immer entgegen der Elongation.
LZ F12.2/B12. 5 Mechanische Schwingungen
7
5.2.2.4 Allgemeine Bewegungsgleichungen
I)
y(t )  yˆ  sint  0 
II)
v(t )  yˆ    cost  0 
III)
a(t )   yˆ   2  sint  0 
Der Winkel 0 wird definiert als die Schwingungsphase zum Zeitpunkt t = 0s.
Ist der Phasenwinkel 0  0, so ergeben sich Graphen „verschobener“ Sinuskurven.
1
 yˆ und die Bewegung erfolgt nach unten. Die
2
Amplitude beträgt y  2,0cm und die Periodendauer T  6,0s .
Übung: Zum Zeitpunkt t = 0s sei y (0s) 
Ermitteln Sie 0. Stellen Sie mit eingesetzten Werten die drei Bewegungsgleichungen
auf. Zeichnen Sie in ein Koordinatensystem alle drei Graphen ein. Wählen Sie
geeignete Maßstäbe!
5.2.2.5 Zeigerdiagramme
Zwischen der Elongation, der Geschwindigkeit und der Beschleunigung besteht eine „feste“
Winkelbeziehung. Die Zeiger (Amplituden) der drei Größen sind quasi „verschweißt“.
Die Zeigerlänge ist der jeweilige Maximalwert. Diese Zeiger drehen sich mit  = konstant
gegen den Uhrzeigersinn.
Sonderfall: Zur Zeit t = 0s erfolgt der Durchgang durch die Ruhelage nach oben, d.h. 0 = 0.
Der Schatten eines parallelen Lichtbündels in Richtung von x liefert die jeweiligen
Momentanwerte auf einer Projektionswand die parallel zur y-Achse liegt.
LZ F12.2/B12. 5 Mechanische Schwingungen
8
Übungen:
a) Anfangsbedingung: Startpunkt bei 0 = 150° umrechnen in Bogenmaß 0 = .............
Zeichnen Sie das Zeigerdiagramm!
y
x
b) Anfangsbedingung: Startpunkt beim Durchgang durch die Ruhelage nach unten.
Geben Sie 0 = ........... an! Zeichnen Sie das Zeigerdiagramm!
y
x
c) Anfangsbedingung: Startpunkt der Bewegung im oberen Umkehrpunkt (o. UP).
Geben Sie 0 = ........... an! Zeichnen Sie das Zeigerdiagramm!
y
x
LZ F12.2/B12. 5 Mechanische Schwingungen
5.3
9
Berechnung der Schwingungsdauer der harmonischen Schwingung
5.3.1 Allgemeine Betrachtung
Bei jeder Schwingung tritt eine zur

Ruhelage gerichtete Kraft F auf.

Diese „Rückstellkraft F “ ist zur
Elongation
y(t)
entgegengesetzt
gerichtet.
5.3.2 Lineares Kraftgesetz
Um einem Körper mit der Masse m eine Beschleunigung a(t)
zu erteilen, ist eine Kraft F(t) erforderlich.
Für die Kraft gilt: F(t) = m · a(t) und mit Hilfe der
Bewegungsgleichungen folgt:
y
y(t )  yˆ  sint  0 
v(t )  yˆ    sint  0 
a(t )   yˆ   2  sint  0 
F(t)
y(t)
(entgegengesetzt gerichtet)
v(t) a(t)
 m  y    sin t  0 
F(t) = ................................................
ˆ
2
 m   2  y(t )
= ....................................
 k  y(t )
= ....................................
Ergebnis:
Bei einer harmonischen Schwingung ist die Rückstellkraft F(t)
............................. und .............................. gerichtet zur Elongation y(t).
Die Proportionalitätskonstante D:
Das lineare Kraftgesetz lautet:
D = .......................
F(t) = ........................
Eine harmonischen Schwingung liegt nur dann vor, wenn das lineare Kraftgesetz gilt!
5.3.3 Frequenz und Schwingungsdauer einer harmonischen Schwingung
Aus der Richtgröße D = .................. = ............................ folgt
für die Schwingungsdauer T:
T=
und für die Eigenfrequenz f:
f =
Die Schwingungsdauer hängt nicht von der .......................................... ab!
Mechanische Schwingungen werden durch die Trägheit der schwingenden Masse m und
durch die Richtgröße D gekennzeichnet.
LZ F12.2/B12. 5 Mechanische Schwingungen
10
5.3.4 Beispiele von harmonischen Schwingungen
5.3.4.1 Federpendel (Massependel)
Die Federmasse wird gegenüber der schwingenden Masse m des Körpers vernachlässigt.
unbelastete Feder
Gleichgewichtslage
Schwingungszustände des Federpendels
grundlegende Betrachtung:
Eine Feder wird durch die Gewichtskraft Fg = m·g bis zu Gleichgewichtslage um l0 gedehnt.
In der Gleichgewichtslage gilt: Fg = Fe (elastische Federkraft mit Fe = DF·l – Hook’sches
Gesetz).
F
m g
Fg = m·g = DF·l0
 Federkonstante DF  G 
l0
l0
Betrachtung der zeitabhängigen rücktreibenden Kraftwirkung F(t):
für die Kraft gilt:
F  Fg  Fe  DF  l0  DF  l  DF  l0  l    DF (l  l0 )
mit
(l  l0 )  y(t )

F  F (t )   DF  y(t )
für die Richtgröße D gilt: D  DF 


es gilt das lineare Kraftgesetz
die Schwingung ist harmonisch
m g
und mit D  m   2
l0

Schwingungsdauer
T=

Frequenz
f =
LZ F12.2/B12. 5 Mechanische Schwingungen
11
5.3.4.2 Schwingende Flüssigkeit im U-Rohr
Reibung wird vernachlässigt. Die rücktreibende Kraft wird von der überstehenden
Flüssigkeitssäule verursacht!
grundlegende Betrachtung:
Die Masse mG der gesamten Flüssigkeit wird
durch die Masse m(t) der „überstehenden“
Flüssigkeitssäule in Bewegung versetzt. Diese
Masse verursacht die rücktreibende Kraft F(t)
(Gewichtskraft)
F(t) = - FG(t) = - m(t) · g
Gewichtskraft
m(t) = F · V(t)
V(t) = A · h(t)
-
F - Dichte der Flüssigkeit
A - Querschnitt des Rohres
Betrachtung der zeitabhängigen rücktreibenden Kraftwirkung F(t):
F(t) = - FG(t)
mit FG(t) = m(t) · g
= - g · m(t)
mit m(t) = F · V(t)
= - g · F · V(t)
mit V(t) = A · h(t)
= - g · F · A · h(t)
mit h(t) = 2 · y(t)
= - g · F · A · 2 · y(t)
g · F · A · 2 = konstant
= - D · y(t)
mit D = 2 · g · F · A

es gilt das lineare Kraftgesetz

die Schwingung ist harmonisch
für die Richtgröße D gilt:
D = 2 · g · F · A und mit D  m   2

Schwingungsdauer
T=

Frequenz
f =
LZ F12.2/B12. 5 Mechanische Schwingungen
12
5.3.4.3 Das Fadenpendel (mathematisches Pendel)
Die Reibung und Fadenmasse sind vernachlässigbar.
grundlegende Betrachtung:
Durch eine Komponente der Gewichtskraft FG wird
der Pendelkörper der Masse m beschleunigt.
Komponenten der Gewichtskraft:
F1
- Spannkraft des Fadens
F(t) - Rückstellkraft - liegt tangential zum Bogen
und wirkt entgegen der Elongation y(t)



- Winkel im Bogenmaß:  Bogen 
y (t )
l
 y (t ) 
F (t )  m  g  sin

 l 
F(t) ist nicht proportional zu y(t), d.h. allgemein ergibt sich keine harmonische Schwingung!
Deshalb ist es erforderlich, eine Näherungsbetrachtung
vorzunehmen. Ist der Winkel  klein ( ≤19° für zwei
Ziffern;  ≤7° für drei Ziffern Genauigkeit), so gilt:
für kleine Winkel :
Grad
Bogen
1
5
7
19
0,017453...
0,087266...
0,122173...
0,3316...
Bogen ≈ sin  ≈ tan 
und damit:
 y (t )  y (t )
sin

l
 l 
Betrachtung der zeitabhängigen rücktreibenden
Kraftwirkung F(t):
m g
y(t )
m g
 y(t ) 
F (t )  m  g  sin

 y (t )   D  y(t ) mit D 
  m  g 
l
l
l
 l 

es gilt das lineare Kraftgesetz

die Schwingung ist harmonisch
für die Richtgröße D gilt:
D
m g
und mit D  m   2
l

Schwingungsdauer
T=

Frequenz
f =
gilt nur für kleine Winkel
sin
0,017452...
0,087155...
0,121869...
0,3255...
LZ F12.2/B12. 5 Mechanische Schwingungen
5.3.4.4
13
Der schwingende Schwimmkörper
Reibung wird vernachlässigt.
Gleichgewichtslage

FA

Fg
ausgelenkter Zustand
A
 y(t )

FA
hK hT 0

Fg
A

FR
hT hT 0
hK
– Höhe des Körpers
hT0
– Eintauchtiefe in der Gleichgewichtslage
hT
– momentane Eintauchtiefe
A = AFl = AK
grundlegende Betrachtung:
Ein Körper taucht durch die Gewichtskraft Fg = m·g bis zu Gleichgewichtslage in eine Flüssigkeit
ein. In der Gleichgewichtslage gilt: Fg = FA (Auftriebskraft mit FA = ρFl·VFl·g ).
Fg = FA = ρFl·A· hT0·g
Betrachtung der zeitabhängigen rücktreibenden Kraftwirkung FR(t):
für die Kraft gilt:
FR (t )  Fg  FA (t )
  Fl  A  hT 0  g   Fl VFl (t )  g
  Fl  A  hT 0  g   Fl  A  hT (t )  g
  Fl  A  g  (hT 0  hT (t ))
   Fl  A  g  y (t )
  D  y (t )
mit D = ρFl·A·g = konstant
LZ F12.2/B12. 5 Mechanische Schwingungen
5.4
14
Periodische Energieumwandlung
5.4.1 Ungedämpfte harmonische Schwingung
z.B.: Federpendel: Anfangsbedingung: t 0  0s ; Start aus der R.L. nach oben; 0  0
kinetische Energie:
Ekin (t ) 
m 2
 v (t ) ; mit v(t )  yˆ    cost  
2
Ekin(t) = ...............................................
mit  2  m  D 
potentielle Energie (Spannenergie):
E pot (t ) 
D 2
 y (t ) ; mit y(t )  yˆ  sint  
2
D 2
 yˆ  sin 2 t 
Epot(t) = ...............................................
2
E pot,max 
D 2
 yˆ
2
Ekin(t) = ................................................
D
Ekin , max   yˆ 2 .
2
Ekin(t) = ................................................
Epot(t) = ...............................................
Berechnung der momentanen Gesamtenergie E(t):
E(t) = Ekin(t) + Epot(t) ;
E(t) = .....................................................................................;
Ausklammern!
E(t) = .....................................................................................;
mit sin 2 t   cos 2 t   1
D
=
zeitunabhängig!
E (t )   yˆ 2 
2
d.h., bei einer ungedämpften harmonischen Schwingung findet ständig eine Umwandlung von
.................................................................................................................................................................
Die Gesamtenergie bleibt dabei ............................................ (Energieerhaltungssatz)
Periodische Energieumwandlung „Sinusquadrat-Kurven“
LZ F12.2/B12. 5 Mechanische Schwingungen
15
5.4.2 Gedämpfte harmonische Schwingung
Die Erfahrung zeigt, dass bei jeder Schwingung die Amplitude mit der Zeit abnimmt. Diese
Abnahme der Amplitude und damit der Energieabnahme der Schwingung heißt Dämpfung.
Die Ursache der Dämpfung ist eine Energieabgabe an die Umgebung infolge der Reibung.
Die ungedämpfte harmonische Schwingung ist eine Idealisierung. Um in der Praxis ungedämpfte
harmonische Schwingungen zu erhalten, muss laufend in geeigneten Zeitpunkten der Energieverlust
durch Energiezufuhr ausgeglichen werden. (z.B. mit Hilfe der Ankerhemmung einer Pendeluhr Energie aus der Feder bzw. aus der Lageenergie der Gewichte).
Beispiel: Feder - Masse - System mit Flüssigkeitsreibung
Die Schwingungsdauer T bleibt auch bei
einer gedämpften harmonischen Schwingung
konstant.
In der Praxis kann die Dämpfung durchaus
erwünscht sein. Z.B. schwingende Türen Zeiger von Zeigerinstrumenten, usw.
Aperiodischer3 Grenzfall:
Um die Einstelldauer bei schwingungsfähigen Systemen möglichst klein zu
halten, dämpft man das System so stark,
dass die Schwingung sehr schnell
abklingt bzw. keine Schwingung durch
sehr starke Dämpfung zustande kommt.
- „kriechen“ in die Ruhelage!
3
aperiodisch (gr.) ... nicht periodisch
LZ F12.2/B12. 5 Mechanische Schwingungen
5.5
16
Freie und erzwungene Schwingung
5.5.1 Freie Schwingung - Definition
Unter einer freien Schwingung (Eigenschwingung) versteht man ein schwingungsfähiges System
(z.B. Federpendel), dass einmal "angestoßen" wird und danach sich selbst überlassen wird.
Schwingungsdauer der Eigenschwingung: T0 = ............ s
1
Frequenz der Eigenschwingung:
f0 = ............
s
5.5.2 Erzwungene Schwingung
Die gegenseitige Beeinflussung zweier schwingungsfähiger Systeme nennt man Kopplung.
Durch die Kopplung wird Energie von dem ersten System auf das zweite System übertragen und
umgekehrt. Durch die Kopplung wird das zweite System vom ersten System zum Mitschwingen
angeregt.
erstes System .... „Erreger“ - zweites System ... „Mitschwinger“ oder Resonator
Gummiband als
Kopplung
Stimmgabeln - Kopplung durch elast. Luft
Technische Bedeutung:
o
o
o
o
o
Kritische Drehzahl von Maschinen;
Schwingung bei Autofedern (Abhilfe Stoßdämpfer);
Vibrieren von Autoteilen;
Zungenfrequenzmesser;
usw.
LZ F12.2/B12. 5 Mechanische Schwingungen
17
5.5.3 Resonanz4
Die Frequenz f des Erregers (System 1) ist veränderlich. Die Frequenz f0 des Mitschwingers
(Resonator, System 2) ist dessen Eigenfrequenz und nicht veränderlich.
Versuch: Kopplung durch elastische Feder, Dämpfung des Resonators z.B. durch Wasser,
Wirbelstromdämpfung, etc.
Erreger – Exzenter
Anzeige der Amplitude yˆ e  yˆ1 über die Lage von
Körper 1
Mitschwinger – Resonator
Kopplung über Feder
Anzeige der Amplitude yˆ r  yˆ 2 über die Lage von
Körper 2
Betrachtungen:
a) f  f0 ; f0 ... Eigenfrequenz des Resonators
Amplitude
y 1  y 2 ;   0 ... synchrone Schwingungen
b) f = f0 ; Resonanzfall , maximale Amplitude y 2

Amplitude
y 2   y 1 ;   ... Resonanz; kurz vor Erreichen der
2
Frequenz f = f0 kommen beide Systeme „außer Tritt“
c) f  f0 ;
y 2 
d) f  f0 ; y 2 
y 1 ; Resonatoramplitude abnehmend;  
Im Resonanzfall ist der Mitschwinger
(Resonator) in der Lage, aus dem
Energievorrat des Erregers ein Maximum
an Schwingungsenergie zu entnehmen.
resonare (lat.) ... mittönen
2
y 1 ;    ; Amplitude des Mitschwingers geht gegen Null
Phasenverschiebung  in Abhängigkeit
vom Verhältnis Erregerfrequenz zu
Resonatorfrequenz.
4

LZ F12.2/B12. 5 Mechanische Schwingungen
18
qualitative Untersuchung der Abhängigkeit der
Resonatoramplitude von der Erregerfrequenz
y e ... Amplitude des Erregers
y r ... Amplitude des Resonators
Die Zunahme der Amplitude des Resonators für
den Fall f = f 0 nennt man Resonanz.
a ... kleine Dämpfung bis
d ... große Dämpfung
Das Maximum von y r ist umso ausgeprägter, je
kleiner die Dämpfung des Resonators ist.
Wäre theoretisch die Dämpfung Null, so würde y r gegen Unendlich gehen (mathematisch eine
Polstelle).
Vermeidung von Resonanz:
o keine Erregung (keine Kopplung)
o f  f 0 ... kritische Drehzahl vermeiden
o f = f 0 ... nur kurze Zeit, z.B. während des Anlaufes von Generatoren, Turbinen, etc.
o Dämpfung des Resonators
In der Praxis können kleine periodische Kräfte unter Umständen zur Resonanzkatastrophe führen.
o
o
o
o
Sessellist – Windböen
Brückeneinsturz (Wind, Soldaten,...)
Gebäudeeinsturz durch vibrierende Maschinen
zerspringen von Gläsern und Scheiben, ...
Versuch mit Modellauto - vibrierende Autoteile - Resonanz
Film über den Brückeneinsturz - Takomabrücke (USA)
LZ F12.2/B12. 5 Mechanische Schwingungen
19
5.6 Aufgaben und Übungen
1.0
1.1
1.2
1.3
2.0
2.1
2.2
3.0
3.1
3.2
4.0
4.1
4.2
4.3
5.0
5.1
5.2
6.0
6.1
6.2
6.3
7.0
In einem U-Rohr vom Querschnitt A wird Quecksilber der Masse m und der Dichte 
gebracht und durch Verschieben der Flüssigkeitssäule zum Schwingen gebracht.
Zeigen Sie, dass die rücktreibende Kraft zur Elongation y(t) direkt proportional ist und
drücken Sie D und T durch , A, m und g aus!
Berechnen Sie D und T für  = 13,6 g·cm-3, A = 1,0 cm2, m = 408 g, g = 10 m·s-2!
Wie viel Wasser (in g) muss man anstelle von Quecksilber in die Röhre füllen, um dieselbe
Schwingungsdauer zu erhalten?
(0,77s;28Nm-1;30g)
Ein Maschinenteil der Masse m = 25 kg vollführt eine harmonische Schwingung mit der
Frequenz f = 4,0Hz und der Amplitude ymax = 20cm.
Berechnen Sie D und die Kraft F, die die Masse in der Umkehrlage erfährt.
Setzen Sie den Ausschlag als Funktion der Zeit an und berechne die Momentangeschwindigkeit. Wie groß ist die Geschwindigkeit beim Durchgang durch die Ruhelage?
(1,6·104Nm-1; 3,2kN;5,0m·s-1)
An einer hochkant eingespannten langen, dünnen Stahlblattfeder ist eine Masse von
m = 50 g befestigt. Diese Masse wird um y = 12,1 cm ausgelenkt und dann losgelassen. Sie
führt dann angenähert eine lineare harmonische Schwingung aus (D = 0,80 N·m-1).
Berechnen Sie die Frequenz f des Systems, sowie die Periodendauer T.
Stellen Sie die Auslenkung y(t) und die Geschwindigkeit v(t) als Funktionen der Zeit dar!
(1,6s; 0,64Hz; v(t) =48cm·s-1·cos(4,0s-1·t + 0,5))
An einem Faden hängt eine Wachskugel der Masse m1. Aus einem Luftgewehr wird eine
Bleikugel der Masse m2 in die Wachskugel geschossen und bleibt darin stecken. Durch den
unelastischen Stoß beginnt das Pendel zu schwingen.
Drücken Sie die Geschwindigkeit v0 des Pendels beim Durchgang durch die Nulllage
durch y , g und die Pendellänge l aus!
Wie kann man aus der Amplitude und der Pendellänge die Geschwindigkeit der
Gewehrkugel bestimmen?
Wie vereinfacht sich der Ausdruck für die Berechnung der Geschwindigkeit, wenn
m2  m1
ist?
Einer linear und harmonisch schwingenden Masse m wird in der Ruhelage eine
Geschwindigkeit von 1,0m·s-1 erteilt, wodurch sie eine Amplitude von 10 cm erhält.
Berechnen Sie T und die Elongation y(4,0s).
Nach welcher Zeit bewegt sich die Masse ein zweites Mal durch einen Punkt der
Elongation 8,0cm?
(93ms; 0,22s)
In einem größeren (warum?) Gefäß mit Wasser schwimmt ein Reagenzglas (Masse m,
Querschnitt A). Es ist durch Bleischrot so beschwert, dass es bis zur Mitte eintaucht.
Wie hängt die rücktreibende Kraft von einer vertikalen Verschiebung y(t) des Glases ab?
Berechnen Sie die Periodendauer T und die Richtgröße D der Schwingung.
Anstelle des Reagenzglases wird ein beschwerter Trichter eingetaucht. Schwingt dieser
auch harmonisch?
Was ist über die Energie in den Umkehrpunkten und der Ruhelage eines schwingenden
Körpers zu sagen? Leite daraus vˆ  yˆ   her!
LZ F12.2/B12. 5 Mechanische Schwingungen
8.0
8.1
8.2
20
Eine auf einer horizontalen Stahlplatte hüpfende Stahlkugel führt eine periodische
Bewegung aus, wenn sämtliche Verluste an nicht mechanischer Energie vernachlässigt
werden.
Berechnen Sie die Periodendauer T, Frequenz f und die Maximalgeschwindigkeit vmax für
eine Steighöhe von h = 20 cm.
Zeichnen Sie das Zeit-Weg-Diagramm.
(2,0 m·s-1; 0,40s; 2,5Hz)
9.0
Eine Schraubenfeder wird durch m1 = 200g um 11,2 cm gedehnt.
9.1
Berechnen Sie die Federkonstante D!
9.2.0 Man hängt nun die Masse m2 = 250g an die Feder und lenkt diese um 10 cm nach unten
aus und lässt sie zur Zeit t = 0s los.
9.2.1 Berechnen Sie T und  und geben Sie die Auslenkung y, Geschwindigkeit v und
Beschleunigung a als Funktion von t an!
9.2.2 Zeichnen Sie von den Funktionen den Graphen und das Zeigerdiagramm.
9.2.3 Zu welchen Zeitpunkten beträgt die Elongation 6,5cm?
9.2.4 Berechnen Sie Ekin und Epot in Abhängigkeit von t und berechnen Sie diese Energien zum
Zeitpunkt t = 0,100s!
(D = 17,5Nm-1; T = 1,21s;  = 5,19s-1; aˆ  2,69m  s 2 ;
vˆ  51,9m  s 1 ; t1 = -0,44s + k·1,21s; t2 = -0,77s + k·1,21s; Ekin = 0,0022J; Epot = 0,066J)
10.0
10.1
10.2
11.0
11.1
12.0
12.1
12.2
13.0
13.1
13.2
13.3
13.4
13.5
13.6
13.7
Ein quaderförmiger Körper (Dichte  K  0,70 g  cm 3 ) mit der Höhe h = 10,0 cm
schwimmt in einer Flüssigkeit mit der Dichte  F  0,80 g  cm 3 . Er wird nun waagrecht in
die Flüssigkeit hineingedrückt.
Untersuchen Sie, ob der Körper harmonische Schwingungen ausführt.
Berechnen Sie die Schwingungsdauer dieser Schwingungen.
(0,59s)
An einer Schraubenfeder mit D = 16,0Nm-1 hängt die Masse m = 250g. Wird diese um
6,0cm ausgelenkt und losgelassen, so hat sie zum Zeitpunkt t = 0,10s die Geschwindigkeit
v(0,10s) = -45,23cm·s-1 und befindet sich über der Ruhelage.
Stellen Sie die 3 Bewegungsgleichungen auf.
( = 8,0s-1;0 = 2,0)
Bei einem Kettenkarussell haben die Fahrgäste die konstante Umlaufzeit T = 9,5s und den
Abstand r = 6,0m von der Drehachse. Ein entfernter Beobachter steht in der Höhe der
Rotationsebene. Für ihn führt jeder Fahrgast eine lineare harmonische Schwingung aus.
Geben Sie die Amplitude, die Schwingungsdauer und die Kreisfrequenz der linearen
Schwingung an!
Zeichnen Sie das Zeit-Ort-Diagramm für diejenigen Fahrgäste, deren Elongation zur Zeit
Null gerade Null sind, für die ersten 15s!
(6,0m; 9,5s; 0,66s-1)
Ein Körper der Masse m = 50g schwingt sinusförmig. In 10s vollendet er 8 Schwingungen.
Die Zeitrechnung möge beginnen, wenn er die Nulllage in Richtung der positiven y-Achse
passiert. Der Abstand der Umkehrpunkte beträgt 18cm.
An welcher Stelle befindet sich der Körper nach 8,0s?
Wie groß sind Geschwindigkeit und Beschleunigung nach 8,0s? Geben Sie auch die
Richtung dieser vektoriellen Größen bezüglich der y-Achse an!
Berechnen Sie die Maxima der Beträge von Geschwindigkeit und Beschleunigung!
Wann besitzt der Körper maximale Geschwindigkeits- bzw. Beschleunigungsbeträge?
Wie groß ist die Rückstellkraft nach 8,0s?
Zu welchen Zeitpunkten ist der Betrag der Rückstellkraft maximal?
Berechnen Sie den Betrag der maximalen Rückstellkraft!
(5,3cm; -0,37 m. s1 ; -1,3 m. s2 ; 45 cm. s1 ; 2,3 m. s2 ; k .0,5. T , k  N0 ;
2
(2k  1).0,25. T , k  N0 ; -6,7. 10 N ; (2k  1).0,25. T , k  N0 ; 0,11N)
LZ F12.2/B12. 5 Mechanische Schwingungen
21
14.0
14.1
14.2
14.3
Für welche Elongation erreicht ein harmonisch schwingender Körper
maximalen bzw. minimalen Geschwindigkeitsbetrag,
maximalen bzw. minimalen Beschleunigungsbetrag?
Berechnen Sie die Beträge der in 14.1 und 14.2 genannten Größen, falls die Schwingungsdauer des Systems 1,2s beträgt! (5,2. y . s1 ; 0 m. s2 ; 27. y. s2 ; 0. m. s2 )
15.0
An einer Schraubenfeder hängt ein Körper der Masse 120g. Diese ist so groß, dass man ihr
gegenüber die Masse der Feder vernachlässigen kann. Hängt man zusätzlich 45g an die
Feder, so. wird sie um weitere 8,5cm gedehnt.
Wie groß ist die Schwingungsdauer des Systems, wenn die Zusatzmasse von 45g entfernt
wird und der Körper dann wieder harmonisch schwingt?
(0,96s)
15.1
16.0
16.1
16.2
16.3
16.4
16.5
16.6
17.0
17.1
17.2
17.3
18.1
An einer Schraubenfeder hängt ein Körper der Masse 4,0kg; ihr gegenüber kann die Masse
der Feder vernachlässigt werden. Durch die Auslenkung in Richtung der Achse der Feder
wird das System zu harmonischen Schwingungen von 2,0s Schwingungsdauer angeregt.
Wie hängt die Schwingungsdauer von der Größe der Auslenkung ab?
Mit welcher maximalen Kraft muss die Auslenkung erfolgen, damit die Amplitude der
Schwingung 30cm beträgt?
Welchen Betrag haben Geschwindigkeit und Beschleunigung beim Durchgang durch die
Ruhelage?
Wie groß ist die potentielle Energie der Elastizität, die bei der in 16.2 genannten
Auslenkung des Systems gesteckt wird?
Wie groß sind potentielle und kinetische Energie beim Durchgang durch die Ruhelage?
Wie groß sind die potentielle und kinetische Energie bei einer Elongation von 10cm? Wie
groß ist die Summe aus potentieller und kinetischer Energie bei dieser Elongation?
(12N; 0,94 m. s1 ; 0 m. s2 ; 1,8J; 0J; 1,8J; 0,20J; 1,6J; 1,8J)
Vorhanden sind zwei Federn mit je den Federkonstanten D0 . Aus den Federn kann eine
Reihenschaltung I und eine Parallelschaltung II gebildet werden.
Drücken Sie die Federkonstanten der Systeme I und II durch D0 aus! Begründung!
Welche Schwingungsdauer hat I und welche II im Vergleich mit der Schwingungsdauer
T0 einer Feder alleine!
Welche Energie steckt in I und welche in II im Vergleich mit der Energie E0 einer Feder
alleine, wenn jeweils um die gleiche Strecke ausgelenkt wird?
Zeigen sie, dass die abgebildete Kette (siehe Seite 5.-1) harmonische Schwingungen
ausführt und leiten Sie eine Forme1 zur Berechnung der Frequenz ab! Die Masse des
Rades und der Schnur wird vernachlässigt!
1
2. g
.
m... Kettenmasse, l... Kettenlänge f 
2. 
l
LZ F12.2/B12. 5 Mechanische Schwingungen
(AP 85 NT: l = 56cm; v(t) = 47 cm·s-1·sin(3π·s-1·t); größer)
(AP 96: T = 0,49s; s(t) = 4,0 cm·cos(2π/0,49s·t); t1 = 0,19s)
22
Arbeitszeit ca. 35 Minuten; 20 Punkte
LZ F12.2/B12. 5 Mechanische Schwingungen
Arbeitszeit ca. 45 Minuten; Punkte 3/3/6/4/3/3/4 = 26 gesamt
23
LZ F12.2/B12. 5 Mechanische Schwingungen
Arbeitszeit ca. 60 Minuten; Punkte 35 gesamt
24
LZ F12.2/B12. 5 Mechanische Schwingungen
25
LZ F12.2/B12. 5 Mechanische Schwingungen
26
LZ F12.2/B12. 5 Mechanische Schwingungen
AP BOS 88/I
AP BOS 92/I
27
LZ F12.2/B12. 5 Mechanische Schwingungen
28
LZ F12.2/B12. 5 Mechanische Schwingungen
29
LZ F12.2/B12. 5 Mechanische Schwingungen
30
LZ F12.2/B12. 5 Mechanische Schwingungen
31
LZ F12.2/B12. 5 Mechanische Schwingungen
32
LZ F12.2/B12. 5 Mechanische Schwingungen
33
LZ F12.2/B12. 5 Mechanische Schwingungen
34
LZ F12.2/B12. 5 Mechanische Schwingungen
**************************
Ende Kapitel 5
35
**************************2015-12-15
LZ F12.2/B12. 5 Mechanische Schwingungen
36
Schwimmende Körper in Flüssigkeit
Allgemein gilt:
Fg = m·g = ρK·V·g = ρK·A·hk·g = ρFl·A·hT0·g
FA = ρFl·V·g = ρFl ·A·hT·g
y(t) = hT0 - hT(t)
In Gleichgewichtslage gilt:
hK
 hT (t )
FA
 y (t )
Fg
hT 0
 
FA FR

Fg
FA  FG
Nachweis des Linearen Kraftgesetzes:
FR (t )  FA (t )  FG   Fl  A  g  hT (t )   Fl  A  g  hT 0   Fl  A  g  hT (t )   Fl  A  g  y(t )   D  y(t )
mit D   Fl  A  g
T  2 
f 
m
 K  VK
 K  A  hK
 2 
 2 
D
 Fl  A  g
 Fl  A  g
 Fl  g
1

2
 K  hK
 2 
 K  hK
 Fl  g
LZ F12.2/B12. 5 Mechanische Schwingungen
37
5.3.4.4 Experimentelle Überprüfung der theoretisch ermittelten Formel
Federpendel
kg; l0 =
a) Bestimmung der Federkonstanten D: m =
m; D =
N
m
b) Veränderung der Amplitude y : Ergebnis: ....................................................................
c) Veränderung der Masse:
m
kg
1,00
N
= konst. ; y =
m
0,500 0,200
= konstant
Folgerung:
T
s
T2
s2
T2
= .............................
m
T 2 = ............ ;
T
s2
T2
in
kg
m
T2
................. ;
........................
T2
Linearisierung des Graphen
Die Bedeutung der Steigung des
Graphen:
......................................................
m
d) Veränderung der Federkonstanten: m = 0,50kg = konstant; y =
= konstant
N
N
D1 
, 2 Federn in Reihe; D2 
, 1 Feder
m
m
D
Folgerung: T 2 . D = .............................
N . m1
T
T 2 = ............ ...; T 2
;
s
T2
s2
T2.D
T
s2 . N . m  1
T2
Linearisierung des Graphen T 2
Die Bedeutung der Steigung des
Graphen:
LZ F12.2/B12. 5 Mechanische Schwingungen
38
1
D
......................................................
................. 
e) Zusammenfassung: T 2
T2 =
;
T
=
f) Theoretischer Wert von
T  2. .
m
D
;
;
k  ....................
.............= ....................... ; Einheit
g) Fehlerrechnung: absoluter Fehler ...
k .100%
relativer Fehler ...
k=
T2
k
k th 


T2
kth
[kth ] 
k  kth  k  ..................
= .................. %
5.3.4.4.2. Fadenpendel
a) Einfluß der Masse bei l = .............. ; m = konstant; Stahlkugel - Holzkugel

Ergebnis: ..........................................................................................
b) Veränderung der Amplitude y bei l = ............. ; m = konstant: 
Ergebnis: ..........................................................................................
c) Veränderung der Länge: m = ..........kg = konstant; y =
l
m
T
s
T2
s2
0,815
0,196
0,098
Folgerung:
T 2 = ............ ;
T
T2
s2
in
m
l
T2
= .............................
l
m = konstant
T2
........................
................. ;
LZ F12.2/B12. 5 Mechanische Schwingungen
39
T2
Linearisierung des Graphen
Die Bedeutung der Steigung des
Graphen:
......................................................
l
d) Zusammenfassung: T 2
T
= .........................;
.................
k=
f) Theoretischer Wert von
;
 T 2 = ...............;
k  ....................
k
l
=
g
k th 
= ....................... ;
g) Fehlerrechnung: absoluter Fehler ...
k  kth  k  ..................
T  2. .

k .100%
relativer Fehler ...
kth
= .................. %