4 Punkte - Ruhr-Universität Bochum

Prof. Dr. Holger Dette
Dr. Melanie Birke
Musterlösung Statistik I
Sommersemester 2009
Blatt 10
Aufgabe 1:
(4 Punkte)
Ein Statistiker hat sich bei einer Versicherung um eine Stelle beworben. Der Personalchef der Versicherung
plant, ihm als Einstellungstest n = 8 Multiple-Choice Aufgaben zum Thema Statistik vorzulegen. Jede
Frage enthält 4 Antwortmöglichkeiten von der jeweils nur eine richtig ist.
(a) Vom Standpunkt der Firma wäre es ein schwerwiegender Fehler, eine unfähige Person (=
ˆ Statistiker rät nur) einzustellen während es weniger gravierend ist, eine fähige Person (=
ˆ Statistiker hat
Kenntnisse) abzulehnen. Man stelle die Hypothesen geeignet auf.
(b) Der Personalchef legt fest, dass der Statistiker eingestellt werden soll, wenn er mindestens 6 Paare
richtig identifiziert. Man bestimme die Wahrscheinlichkeit für den Fehler erster Art.
(c) Man konstruiere einen nichtrandomisierten Test zum Niveau α = 5%. Der Statistiker hat 4 Fragen
richtig beantwortet. Wird er nach der hier konstruierten Entscheidungsregel eingestellt?
(d) Man konstruiere einen randomisierten Test zum Niveau α = 5%. Wird der Statistiker nach dieser
Entscheidungsregel bei 4 richtigen Antworten eingestellt?
(e) Der Statistiker geht davon aus, eine Frage mit einer Wahrscheinlichkeit von 85% richtig zu beantworten. Wie groß ist für den Test aus (c) die Wahrscheinlichkeit für den Fehler zweiter Art?
Lösung: (a) Es handelt sich um einen Binomialtest mit Erfolgswahrscheinlichkeit p. p = 14 entspricht
hierbei dem Raten ohne Kenntnisse. Da der schwerwiegendere Fehler für die Firma ist, dass man sich
für eine unfähige Person entscheidet und der Fehler 1. Art kontrolliert werden kann, sind die geeigneten
Hypothesen
1
(Statistiker rät nur, ist also unfähig)
4
1
H1 : p > (Statistiker hat Kenntnisse).
4
P8
1
(b) Der beschriebene Test ist mit X =
i=1 Xi ∼ Bin 8, 4 ϕ(X) = I {X ≥ 6} = I{X > 5}. Die
Wahrscheinlichkeit für den Fehler erster Art ergibt
H0
P0.25 (ϕ(X) = 1)
=
:
p=
P0.25 (X > 5) = P0.25 (X = 6) + P0.25 (X = 7) + P0.25 (X = 8) = 0.0042.
(c) Der Test ist wieder von der Art ϕk (X) = I{X > k} und wir wählen k so, dass es ein Test zum Niveau
0.05 wird. Der Test aus (a) wäre einer aber wir wollen so nah wie möglich an 0.05 herankommen und
probieren daher verschiedene k < 5 aus:
P0.25 (ϕ4 (X) = 1) = P0.25 (X > 4) = P0.25 (X = 5) + P0.25 (X = 6) + P0.25 (X = 7) + P0.25 (X = 8)
= 0.0273 < 0.05
P0.25 (ϕ3 (X) = 1) = P0.25 (X > 3) = P0.25 (X = 0) + P0.25 (X = 1) + P0.25 (X = 2) + P0.25 (X = 3)
= 0.1138 > 0.05.
Daher ist ϕ4 (X) = I{X > 4} ein nichtrandomisierter Test zum Niveau 0.05. Nach dieser Entscheidungsregel wird der Statistiker nicht eingestellt.
(d) Ein randomisierter Test ist von der Form ϕk,γ (X) = I{X > k} + γI{X = k}. Hierfür wählen wir k
und γ so, dass das Niveau genau 0.05 ergibt. Da die Grenze von 0.05 im nichtrandomisierten Test in (c)
genau zwischen k = 3 und k = 4 liegt, wählen wir hier k = 4 und bestimmen γ aus
P0.25 (ϕ4,γ ) = P0.25 (X = 5) + P0.25 (X = 6) + P0.25 (X = 7) + P0.25 (X = 8) + γP0.25 (X = 4)
= 0.0273 + γ0.0865 = 0.05.
Auflösen nach γ ergibt γ = 0.2624. Das bedeutet, dass der Statistiker bei 4 beantworteten Fragen mit
einer Wahrscheinlichkeit von 0.2624 eingestellt wird.
(e) Es gilt nun H1 mit p = 0.85. Die Wahrscheinlichkeit für den Fehler 2. Art ist dann
P0.85 (ϕ4 (X) = 0) = P0.85 (X ≤ 4) = 1 − P0.85 (X > 4) = 0.0214.
(4 Punkte)
Aufgabe 2:
1. Die Zufallsvariable X beschreibe die Brenndauer einer Glühbirne in Jahren und sei Exp( θ1 )–verteilt
mit unbekanntem Parameter θ > 0. Um herauszufinden ob die Glühbirnen im Schnitt länger oder
kürzer als ein Jahr brennen, bevor sie ersetzt werden müssen, wird der Test Φ(X) := I{X ≥ 2} mit
den Hypothesen H : θ ≤ 1 gegen A : θ > 1 durchgeführt.
(a) Man bestimme das Niveau und die Gütefunktion für dieses Testproblem.
(b) Wie groß ist die Wahrscheinlichkeit, dass nach dem Test angenommen wird, dass die Glühbirnen kürzer als ein Jahr brennen, wenn ihre tatsächliche Brenndauer im Mittel 0.25 Jahre
beträgt?
2. Es sei X exponentialverteilt mit Parameter λ > 0 und ϕc (X)
Hypothesen H0 : λ = λ0 gegen H1 : λ = λ1 mit λ0 6= λ1 .
von c die Wahrscheinlichkeiten für den Fehler 1. und 2. Art und
Eλ0 [ϕc (X)] + 1 − Eλ1 [ϕc (X)] minimiert. Was kann man über die
für den Fehler 1. bzw. 2. Art sagen?
= I{X > c} ein Test für die
Man berechne in Abhängigkeit
bestimme ein c das die Summe
Größe der Wahrscheinlichkeiten
Lösung: 1. (a) Die Gütefunktion ist
2
βϕ (θ) = Eθ [ϕ(X)] = Pθ (ϕ(X) = 1) = Pθ (X ≥ 2) = exp −
θ
und für das Niveau erhalten wir daher
α
=
sup βϕ (θ) = exp(−2) = 0.1353.
θ≤1
(b) Ist 0.25 die wahre Brenndauer, so gilt X ∼ Exp(4). Dann ist
2
= 1 − exp(−8) = 0.0003
P0.25 (ϕ(X) = 0) = 1 − exp −
0.25
2. Es ist
PH0 (ϕ(X) = 1)
= PH0 (X > c) = exp(−λ0 c)
PH1 (ϕ(X) = 0)
= PH1 (X ≤ c) = 1 − exp(−λ1 c) ≥ 1 − exp(−λ0 c).
Die Summe ist
Eλ0 [ϕc (X)] + 1 − Eλ1 [ϕc (X)]
=
exp(−λ0 c) + 1 − exp(−λ1 c)
und wegen
∂
(Eλ0 [ϕc (X)] + 1 − Eλ1 [ϕc (X)])
∂c
=
−λ0 exp(−λ0 c) + λ1 exp(−λ1 c) = 0
⇔
c=
λ1
1
log
λ1 − λ0
λ0
ist dieses c im Fall λ1 < λ0 das Minimum der Summe. Die Wahrscheinlichkeit für den Fehler erster Art
λ0 /(λ0 −λ1 )
λ1 /(λ0 −λ1 )
ist λλ10
und die Wahrscheinlichkeit für den Fehler 2. Art 1 − λλ01
. Im Fall λ0 < λ1
ist das oben bestimmte c jedoch ein lokales Maximum und das globale Mininum wird am Rand, also bei
c = 0 bzw. für c → ∞ angenommen. Beides ist keine geeignete Wahl für einen Test, denn für c = 0
ist die Wahrscheinlichkeit für den Fehler 1. Art 1 und die für den Fehler 2. Art 0, für c → ∞ gilt dies
gerade andersherum abgesehen davon, dass c → ∞ keine praktische Relevanz hat. Wir können also nicht
simultan Fehler erster und zweiter Art minimieren!
Aufgabe 3:
(4 Punkte)
Sei Φ := {ϕ | ϕ : X → [0, 1]} die Menge aller Tests auf X für die einfache Hypothese H0 : θ = θ0 gegen
die einfache Alternative H1 : θ = θ1 . βϕ bezeichne die Gütefunktion des Tests ϕ ∈ Φ.
(a) Man zeige, dass die Menge R = {(βϕ (θ0 ), 1 − βϕ (θ1 )) | ϕ ∈ Φ} konvex und punktsymmetrisch zu
( 12 , 21 ) ist.
(b) Seien nun X ∼ Exp(θ), θ0 = 1 und θ1 = 2. Man zeichne R. (Hinweis: Neyman-Pearson Lemma)
Lösung: (a) Zuerst zeigen wir die Konvexität. Dazu seinen (βϕ1 (θ0 ), 1−βϕ1 (θ1 ))T , (βϕ2 (θ0 ), 1−βϕ2 (θ1 ))T ∈
R und wir bemerken, dass wenn ϕ1 und ϕ2 Tests sind, auch tϕ1 + (1 − t)ϕ2 für t ∈ [0, 1] ein Test ist.
Nun betrachten wir für t ∈ [0, 1]
t(βϕ1 (θ0 ), 1 − βϕ1 (θ1 ))T + (1 − t)(βϕ2 (θ0 ), 1 − βϕ2 (θ1 ))T
= (tEθ0 [ϕ1 (X)] + (1 − t)Eθ0 [ϕ2 (X)], t(1 − Eθ1 [ϕ1 (X)]) + (1 − t)(1 − Eθ1 [ϕ2 (X)])))
= (Eθ0 [tϕ1 (X) + (1 − t)ϕ2 (X)], 1 − Etθ1 [ϕ1 (X) + (1 − t)ϕ2 (X)])))
T
= βtϕ1 +(1−t)ϕ2 (θ0 ), 1 − βtϕ1 +(1−t)ϕ2 (θ1 ) ∈ R.
T
T
Damit ist R konvex. Wir müssen noch zeigen, dass für alle (u, v)T ∈ R folgt (1 − u, 1 − v)T ∈ R. Als
erstes bemerken wir, dass wenn ϕ ∈ Φ auch 1 − ϕ ∈ Φ ist. Ist ϕ also ein Test, so auch 1 − ϕ (nur für die
umgedrehten Hypothesen). Dann gilt
(1 − βϕ (θ0 ), 1 − (1 − βϕ (θ1 )))T
=
(1 − Eθ0 [ϕ(X)], 1 − (1 − Eθ1 [ϕ(X)]))T
=
=
(Eθ0 [1 − ϕ(X)], 1 − Eθ1 [1 − ϕ(X)])T
(β1−ϕ (θ0 ), 1 − β1−ϕ (θ1 ))T ∈ R.
Somit ist R punktsymmetrisch zu 21 , 21 .
(b) Wegen dem Neyman-Pearson Lemma reicht es, für die Grenzen von R Neyman-Pearson-Tests zu
betrachten. Diese sind hier von der Form
θ1 exp(−θ1 X)
θ1
ϕ(X) = I
exp((θ0 − θ1 )X) > c
>c =I
θ0 exp(−θ0 X)
θ0
= I {2 exp(−X) > c}
Damit berechnen wir
βϕ (θ0 ) =
P1 (2 exp(−X) > c) = P1 (X < − log(c/2)) = 1 − exp(−(− log(c/2))) = 1 −
1 − βϕ (θ1 ) =
c
2
1 − P2 (2 exp(−X) > c) = 1 − P2 (X < − log(c/2)) = 1 − (1 − exp(−2(− log(c/2)))) =
c 2
2
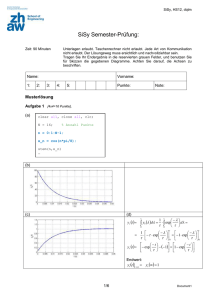
0.6
0.4
0.0
0.2
Fehler 2. Art
0.8
1.0
mit 0 < c < 2. Die Punkte {(1 − c/2, (c/2)2 )T |0 < c < 2} sind also in R und da R nach Teil (a)
punktsymmetrisch zu (1/2, 1/2)T ist, sind auch {(c/2, 1 − (c/2)2 )T |0 < c < 2} in R. Daher ergibt sich
dieses Bild.
0.0
0.2
0.4
0.6
0.8
1.0
Fehler 1. Art
Aufgabe 4:
(4 Punkte)
1. Es sei T eine suffiziente Statistik für θ ∈ IR und getestet werden sollen die Hypothesen H0 : θ = θ0
gegen H1 : θ = θ1 , θ0 6= θ1 . Man zeige, dass der Neyman-Pearson Test dann eine Funktion von T
ist.
2. Es seien X1 , . . . , Xn unabhängig identisch Exp(λ)-verteilt mit λ > 0. Man bestimme einen NeymanPearson Test ϕc für die Hypothesen H0 : λ = λ0 gegen H1 : λ = λ1 , λ0 < λ1 . Weiter finde man
einen äquivalenten Test ϕ, der nur von der für λ suffizienten Statistik abhängt und bestimme c so,
dass ϕ das Niveau α hat.
Lösung: 1. Ist T suffizient für θ, dann gilt fθ (x) = h(x)gθ (T (x)). Dann lässt sich der Neyman-Pearson
Test schreiben als
gθ1
fθ1 (X)
>c =I
(T (X)) > c .
ϕc (X) = I {fθ1 (X) > cfθ0 (X)} = I
fθ0 (X)
gθ0
Pn
2. Die suffiziente
Statistik für λ ist wegen fλ (x1 , . . . , xn ) = (λ)n exp(−λ i=1 xi )I(0,∞)n (x1 , . . . , xn )
Pn
T (X) = i=1 Xi und der Neyman-Pearson-Test ist mit 1. gegeben durch
(
)
n
X
λ1
ϕc (X) = I
Xi ) > c .
exp(−(λ1 − λ0 )
λ0
i=1
Diesen kann man nun weiter vereinfachen zu
ϕ̃c̃ (X) = I {T (X) < c̃}
1
log λλ01 c . Um einen Test zum Niveau α zu bekommen beachten wir, dass
wobei wir c̃ erhalten als λ1 −λ
0
T (X) ∼ Gamma(n, λ) und es bezeichne Fn,λ die Verteilungsfunktion von T (X). Dann sind
ϕ̃(X)
bzw.
−1
= I{T (X) < Fn,λ
(α)}
ϕ(X)
= I{
n
X
λ1
λ1
−1
Xi ) >
exp(−(λ1 − λ0 )
exp(−(λ1 − λ0 )Fn,λ
(α))}
λ0
λ
0
i=1
Tests zum Niveau α. In der Praxis würde man immer ϕ̃ bevorzugen, da er einfacher auszurechnen ist!
T (X) heißt Teststatistik!