Skript 5 - WWZ - Universität Basel

Mathematischer Vorbereitungskurs für
Ökonomen
Dr. Thomas Zehrt
Wirtschaftswissenschaftliches Zentrum
Universität Basel
Elementare Geometrie
Inhalt:
1. Die Strahlensätze
2. Winkel
3. Rechtwinklige Dreiecke
4. Kreise
5. Trigonometrische Funktionen
2
2.1
Die Strahlensätze
Der Ausgangspunkt ist der folgende: Es seien vier Geraden g1 , g2 und h1 , h2 mit den Eigenschaften
• g1 k g2 (die Geraden sind parallel)
• h1 und h2 schneiden sich in einem Punkt A
gegeben.
h1
C1
B1
A
B2
C2
h2
g2
g1
Satz 2.1 (Die Strahlensätze)
1.
AB1
AB2
=
AC1
AC2
=
B1 C1
B2 C2
2.
AB1
AC1
=
AB2
AC2
=
B1 B2
C1 C2
3.
B1 B2
AB2
=
C1 C2
AC2
4.
B1 B2
AB1
=
C1 C2
AC1
3
2.2. WINKEL
2.2
Winkel
Winkel werden insbesondere in Grad und Bogenmass angegeben, allerdings werden wir Winkel
meist im Bogenmass angeben, da diese Darstellung keine physikalische Masseinheit trägt. Die Umrechnung von beiden (Mass)Einheiten ineinander geschieht über eine Proportionalitätsgleichung.
Dabei muss man sich eigentlich nur die folgende Regel einprägen:
Grad
Bogenmass
360◦
=
2π
Beispiele: Wir wollen einige gegebene Winkel in die jeweils andere Einheit umrechnen.
1. 220◦ = x? (Bogenmass)
x
220◦
=
⇐⇒
◦
360
2π
x
=
2π ·
2. 7.21 (Bogenmass) = x? (Grad)
x
7.21
=
⇐⇒ x =
◦
360
2π
220◦
≈ 3.84
360◦
360◦ ·
7.21
≈ 413.1◦
2π
Geometrische Deutung Die Bogenlänge x eines Winkels α (in Grad gemessen) ist die Länge des
zugehörigen Segmentes auf dem Einheitskreis.
x
α
1
4
2.3
Rechtwinklige Dreiecke
Die beiden am rechten Winkel anliegenden Seiten a und b heissen Katheten, die dem rechten Winkel
gegenüberliegende Seite heisst Hypotenuse.
A
c
b
B
C
a
Satz 2.2 (Satz des Pythagoras) In einem rechtwinkligen Dreieck ist das Quadrat der Hypotenuse gleich der Summe der Kathetenquadrate:
c2
a2 + b2
=
Anwendung:
Wir wollen den Abstand von zwei Punkten A und B in der x − y−Ebene berechnen oder besser
noch, wir wollen eine allgemeine Formel finden, die uns den Abstand von zwei Punkten als Funktion
der Koordinaten dieser beiden Punkte ausgibt. Die Koordinaten von A seien (xA , yA ), die von B
seinen (xB , yB ).
A
yA
?
B
yB
xB
xA
Dazu definieren wir uns zunächst einen Hilfspunkt C in der x − y−Ebene mit den Koordinaten
(xA , yB ). Wir erhalten damit ein rechtwinkliges Dreieck mit den Eckpunkten A, B, C.
A
yA
?
b
B
yB
C
a
xB
xA
5
2.3. RECHTWINKLIGE DREIECKE
In diesem rechtwinkligen Dreieck gilt der Satz des Pythagoras ?2 = a2 + b2 und die beiden Seitenlängen a und b lassen sich leicht durch die Koordinaten der Punkte A und B ausdrücken:
CB = a = |xA − xB | = |xB − xA |
CA = b = |yA − yB | = |yB − yA |.
Insgesamt ergibt sich damit für den gesuchten Abstand:
Abstand zwischen A und B
= AB
p
a2 + b2
=
p
=
(xB − xA )2 + (yB − yA )2
Beispiel: Wir wollen den Abstand der beiden Punkte A und B mit den Koordinaten (2, 7) und
(−1, 3) berechnen. Es gilt
p
(x − xA )2 + (yB − yA )2
Abstand zwischen A und B =
p B
(−1 − 2)2 + (3 − 7)2
=
p
(−3)2 + (−4)2
=
√
9 + 16
=
√
25
=
= 5
6
2.4
Kreise
Mit Hilfe der bewiesenen Abstandsformel können wir nun Kreise im R2 beschreiben. Im allgemeinen
ist ein Kreis mit Mittelpunkt M = (xM , yM ) die Menge aller Punkte, die von diesem Mittelpunkt
einen festen Abstand r > 0, den sogenannten Radius, haben. Ein Punkt P mit den Koordinaten
(x, y) liegt also auf diesem Kreis, falls folgendes gilt:
Abstand zwischen P und M = r =
p
(x − xM )2 + (y − yM )2 .
Diese Gleichung lässt sich auch umschreiben. Eine Fallunterscheidung ist hier beim Wurzelziehen
nicht nötig, da man verlangt, dass r > 0 ist.
⇐⇒
⇐⇒
r
=
r2
=
1
=
p
(x − xM )2 + (y − yM )2
(x − xM )2 + (y − yM )2
x − xM
r
2
+
y − yM
r
2
Beispiel:
1. Wir wollen entscheiden, ob die beiden Punkte
√ A = (2, 7) und B = (−1, 3) auf dem Kreis mit
Mittelpunkt M = (1, −1) und Radius r = 20 liegen. Dazu bestimmen wir die Abstände, die
beide Punkte vom Mittelpunkt haben.
p
(x − xM )2 + (y − yM )2
Abstand zwischen A und M =
p
=
(2 − 1)2 + (7 − (−1))2
p
12 + 82
=
√
√
65 6= 20
=
Abstand zwischen B und M
=
=
=
=
p
(x − xM )2 + (y − yM )2
p
22 + 42
p
√
(−1 − 1)2 + (3 − (−1))2
20
Der Punkt A liegt also, im Gegensatz zu B, nicht auf dem Kreis.
7
2.4. KREISE
2. In der obigen ,,Normalform” ist der Gleichung direkt anzusehen, dass sie einen Kreis beschreibt. Das ändert sich allerdings sofort, wenn wir die Quadrate ausrechnen.
Die Gleichung (x√
− 1)2 + (y − 2)2 = 1 beschreibt einen Kreis mit dem Mittelpunkt (1, 2) und
dem Radius r = 1 = 1. Rechnet man die beiden Quadrate mittels binomischer Formel aus,
erhält man:
(x − 1)2 + (y − 2)2
=
1
⇐⇒
x2 − 2x + 1 + y 2 − 4y + 4
=
1
⇐⇒
x2 + y 2 − 2x − 4y + 4
=
0
Dieser letzten Gleichung kann man nicht mehr direkt ansehen, dass sie einen Kreis beschreibt!?
3. Gegeben ist die Gleichung x2 + y 2 − 10x + 6y + 32 = 0, die einen Kreis beschreibt.
!! Achtung !!
Nicht jede Gleichung dieser Gestalt beschreibt einen Kreis!!
!! Achtung !!
Wir wollen den Mittelpunkt und den Radius dieses Kreises bestimmen. Dazu ergänzen wir
quadratisch in x und y.
x2 + y 2 − 10x + 6y + 32
=
0
⇐⇒
x2 − 10x + 25 − 25 + y 2 + 6y + 9 − 9 + 32
=
0
⇐⇒
(x − 5)2 + (y + 3)2 − 34 + 32
=
0
⇐⇒
(x − 5)2 + (y + 3)2
=
2
⇐⇒
=
1
x−5
√
2
2
+
y+3
√
2
2
Der Kreis hat also den Mittelpunkt (5, −3) und den Radius
√
2.
8
2.5
Ausblick
Wir hatten gesehen, dass sich ein Kreis stets durch eine Gleichung der Form
Ax2 + By 2 + Cx + Dy + E
=
0
mit A, B, C, D, E ∈ R (wobei durchaus eine oder mehrere dieser Konstanten Null sein dürfen)
beschreiben lässt, aber dass nicht jede Gleichung dieses Typs einen Kreis beschreibt. Durch einfache
Umformungen (insbesondere durch die quadratische Ergänzung) kann man diese Gleichung aber
stets in eine sogenannte ,,Normalform“ bringen. Dieser Normalform kann man dann leicht ansehen,
um welchen Typ einer Kurve es sich handelt. Wir wollen das hier nur an wenigen Beispielen erläutern.
• A, B = 0 und (C, D) 6= (0, 0): Beschreibt stets eine Gerade!
Cx + Dy + E = 0
• Die Gleichung 25x2 + 9y 2 − 50x + 72y − 56 = 0 beschreibt eine Ellipse. Durch doppelte
quadratische Ergänzung (wie bei Kreisen) erhält man die folgende Kette von Umformungen:
0 = 25x2 − 50x + 9y 2 + 72y − 56
= 25x2 − 50x + 25 − 25 + 9y 2 + 72y + 144 − 144 − 56
= (5x − 5)2 + (3y + 12)2 − 225
225 = 25(x − 1)2 + 9(y + 4)2
(x − 1)2 (y + 4)2
+
9
25
y+4 2
x−1 2
+
1 =
3
5
1 =
Das ist fast eine Kreisgleichung, nur die beiden Zahlen im Nenner sind verschieden.
9
2.5. AUSBLICK
Die Bedeutung der vier Parameter (u, v, a, b) in einer Gleichung der Gestalt
1 =
x−u
a
2
+
y−v
b
2
veranschaulicht die folgende Skizze.
y
b
v
u
a
x
10
2.6
Trigonometrische Funktionen
Die Funktionen sin und cos lassen sich am rechtwinkligen Dreieck definieren. Dazu sei x ein nichtrechter Winkel dieses Dreiecks im Bogenmass.
A
c
b
x
B
C
a
Dann gilt:
sin(x)
=
Gegenkathete
Hypotenuse
=
b
c
cos(x)
=
Ankathete
Hypotenuse
=
a
c
Bemerkung:
Beide Funktionen sind über zwei Seitenlängen eines (rechtwinkligen, aber zunächst belibiegen) Dreiecks definiert. Es ist somit zunächst nicht klar, dass sin(x) wirklich nur von der Grösse des Winkels
abhängt. Das sieht man aber schnell ein, wenn man sich an den Strahlensatz erinnert. Dazu legen
wir zwei rechtwinklige Dreiecke mit dem selben Winkel x so übereinander, dass sich dieser Winkel
überdeckt. Man erhält dann die folgende Anordnung.
A
A
c
c
b
x
B
b
C
a
a
C
Naürlich stimmen in den beiden Dreiecken keine der Seitenlängen überein. Es gilt sicher z.B. a 6= a′
und b 6= b′ , aber die Verhältnisse aus den entsprechenden Seiten sind gleich!
sin(x) =
cos(x) =
b
b′
= ′
c
c
a
a′
= ′
c
c
Der Tangens und der Kotangens sind durch die Winkelfunktionen sin und cos definiert.
11
2.6. TRIGONOMETRISCHE FUNKTIONEN
tan(x)
=
sin(x)
cos(x)
cot(x)
=
cos(x)
sin(x)
Alle Winkelfunktionen können am Einheitskreis direkt abgelesen werden. Die folgende Skizze zeigt
das für den Sinus, den Kosinus und den Tangens.
y
P
0
cos(x)
P’
tan(x)
x
sin(x)
r=1
Q
Q’
x
Tangensträger
Wir wollen uns noch kurz überlegen, dass die Strecke QQ′ tatsächlich der tan(x) ist, d.h. wir müssen
beweisen, dass tan(x) = QQ′ ist. Dazu müssen wir uns drei Dinge überlegen und beide Aussagen
zusammenfassen:
• Nach Definition gilt tan(x) =
• Nach dem Strahlensatz gilt
sin(x)
cos(x)
QQ′
sin(x)
=
cos(x)
0Q′
• Der Punkt Q′ liegt auf dem Einheitskreis, die Strecke 0Q′ hat also die Länge 1.
Alles klar?
12
Satz 2.3 (Sehr einfache Eigenschaften der Winkelfunktionen)
sin(x)
∈
[−1, 1]
cos(x)
∈
[−1, 1]
sin(x + 2π)
=
sin(x)
cos(x + 2π)
=
cos(x)
sin2 (x) + cos2 (x)
=
1
Satz des Pythagoras
sin(−x)
=
− sin(x)
sin ist ungerade
cos(−x)
=
cos(x)
cos ist gerade
Zwei weitere wichtige Eigenschaften der Winkelfunktionen, die eine Beziehung zwischen dem Sinus
und dem Kosinus herstellen, lassen sich durch die folgenden Überlegungen herleiten:
Wir wählen ein rechtwinkliges Dreieck mit der Seitenlänge (Seite, dem rechten Winkel gegenüber)
AB = 1. Ist der Winkel x gegeben, so muss der zweite nichtrechte Winkel die Grösse π2 − x haben,
da die Winkelsumme in jedem Dreieck stets π ist.
A
π −x
2
b
x
B
C
a
Indem man nun für beide nichtrechten Winkel die zugehörigen Winkelfunktionen am Dreieck abträgt, erhält man sofort die beiden Identitäten:
π
π
b = sin(x) = cos
−x
und
a = cos(x) = sin
−x
2
2
Satz 2.4 (Eigenschaften der Winkelfunktionen)
π
sin x +
2
π
cos x +
2
=
cos(x)
=
− sin(x)
sin(π − x)
=
sin(x)
cos(π − x)
=
− cos(x)
13
2.7. AUFGABEN
2.7
Aufgaben
1. Der Schatten eines 1.20 m hohen vertikalen Stabes ist 1.40 m lang. Wie hoch ist ein Baum,
dessen Schatten zur selben Zeit 11.20 m lang ist?
2. Rechnen Sie die angegebenen Winkel jeweils in Grad bzw. Bogenmass um: 32 π, − 23 π, 10, 43◦
und −411◦ .
3. Bestimmen Sie den Umfang des Dreiecks mit den Eckpunkten
(a) (−2, −2), (3, −2) und (4, 3)
(b) (−1, −2), (2, −3) und (3, 4)
4. Bestimmen Sie die Mittelpunkte und Radien der folgenden Kreise.
3
=0
2
a)
x2 + y 2 − x + 3y −
b)
x2 + y 2 + 4x − 4y = 0
5. Bestimmen Sie alle Lösungen der folgenden Gleichung:
π
=
sin 3x +
6
1
.
2
6. Berechnen Sie den Schnittpunkt der Geraden y = x + 1 mit dem Kreis (x − 1)2 + y 2 = 4.
7. Ein Technischer Zeichner möchte 3 Punkte mit den Koordinaten (0, 3), (0, −2) und (2, 0) durch
einen Kreisbogen miteinander verbinden. Wie lautet die Gleichung des Kreises?
14
2.8
Zusatzaufgaben
1. Eine 30 m von einem Baum entfernt stehende Person mit der Augenhöhe von 1.70 m visiert
die Spitze des Baumes unter einem Winkel von 20◦ zur Horizontalen an. Wie hoch ist der
Baum?
2. Bestimmen Sie die Mittelpunkte und Radien der folgenden Kreise.
a)
x2 + y 2 − 4x + 2y − 4 = 0
b)
x2 + y 2 + 16x = 0
3. Bestimmen Sie alle Lösungen der folgenden Gleichung:
sin (2x) + sin(x) = 0.
4. Leiten Sie aus der Relation 2. aus Satz 2.1 die Relation 3. ab.
5. Leiten Sie aus der Relation 2. aus Satz 2.1 die Relation 4. ab.
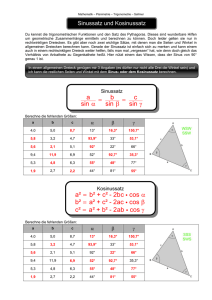
6. Beweisen Sie, dass in einem beliebigen Dreieck mit den Ecken A, B und C der Sinussatz gilt:
sin(α)
sin(β)
=
a
b
sin(γ)
.
c
=
A
α
c
b
γ
β
B
a
C
2.9. LÖSUNGEN
2.9
Lösungen
2.9.1
Lösungen der Aufgaben
1. 9.60m
2
3π
= 120◦ , − 23 π = −270◦ , 10 = 572.95◦ , 43◦ = 0.75 und −411◦ = −7.17
√
√
√
3. a) 25 + 26 + 61 ≈ 17.909
√
√
√
b) 10 + 50 + 52 ≈ 17.444
2.
4. a) Mittelpunkt (1/2, −3/2) , Radius 2
√
b) Mittelpunkt (−2, 2) , Radius 8
2π
2π
5. L = k · 2π
:
k
∈
Z
∪
+
k
·
:
k
∈
Z
3
9
3
6. (1, 2) und (−1, 0)
7. (x + 0.5)2 + (y − 0.5)2 = 2.552
15
16
2.9.2
Lösungen der Zusatzaufgaben
1. 6.99 m
2. a) Mittelpunkt (2, −1) , Radius 3
b) Mittelpunkt (−8, 0) , Radius 8
3. L = k · 2π
3 : k ∈ Z ∪ {(2k + 1) · π : k ∈ Z}
4. Mit Relation 2. aus Satz 2.1 gilt zunächst
AB2
AC2
=
B1 B2
.
C1 C2
Nach Multiplikation dieser Gleichung mit C1 C2 und Division durch AB2 folgt daraus aber
sofort die Behauptung.
5. Wie in Aufgabe 4.
6. Wir betrachten eine Höhe (z.B. zur Seite c), die das Ausgangsdreieck in zwei rechtwinlige
Dreiecke zerlegt. In dem einen Dreieck gilt
sin(α) =
h
b
sin(β) =
h
.
a
und in dem anderen Dreieck gilt
Beide Gleichungen zusammen (nach h auflösen) ergeben dann den ersten Teil des Sinussatzes:
b · sin(α) = h = a · sin(β)
sin(α)
sin(β)
=
a
b
oder
A
α
c
b
h
γ
β
B
a
C
Inhaltsverzeichnis
2.1
Die Strahlensätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2.2
Winkel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2.3
Rechtwinklige Dreiecke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.4
Kreise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.5
Ausblick . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.6
Trigonometrische Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.7
Aufgaben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
2.8
Zusatzaufgaben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.9
Lösungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
2.9.1
Lösungen der Aufgaben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
2.9.2
Lösungen der Zusatzaufgaben . . . . . . . . . . . . . . . . . . . . . . . . . . .
16