Zweitore - ate.uni

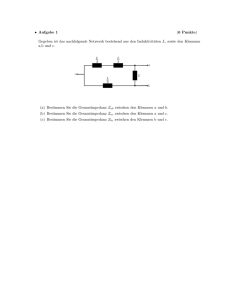
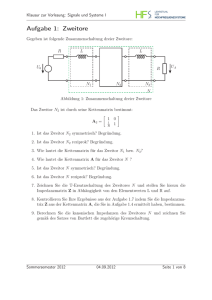
Grundlagen der Elektrotechnik
Praktikum Teil 1
Versuch B1/4
„Zweitore“
Allgemeine und Theoretische Elektrotechnik (ATE)
Elektrotechnik und Informationstechnik
Fakultät für Ingenieurwissenschaften
Universität Duisburg-Essen
Duisburg, Juli 2013
Versuch B1/4 - Zweitore
Inhaltsverzeichnis
1 Grundlagen
1.1 Einleitung . . . . . . . . . . . . . . . . . . .
1.2 Das lineare passive Zweitor . . . . . . . . .
1.3 Die Zweitorgleichungen . . . . . . . . . . . .
1.4 Die Zweitorgleichungen in Leitwertform . .
1.5 Die Zweitorgleichungen in Widerstandsform
1.6 Die Zweitorgleichungen in Kettenform . . .
.
.
.
.
.
.
1
1
1
2
3
4
5
2 Zusammenschaltung von Zweitoren
2.1 Parallelschaltung zweier Zweitore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Reihenschaltung zweier Zweitore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Kettenschaltung zweier Zweitore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
6
7
9
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Versuchsdurchführung
10
4 Hilfsblatt
12
5 Messprotokoll
12
ii
Versuch B1/4 - Zweitore
1 Grundlagen
1.1 Einleitung
Ein elektrisches Netzwerk, das von aussen durch vier Anschlüsse zugänglich ist, wird Zweitor genannt.
• Sind in einem Zweitor keine Quellen vorhanden, so heißt es passives Zweitor.
• Ein Zweitor, das Quellen enthält, wird als aktives Zweitor bezeichnet.
• Besteht ein Zweitor ausschließlich aus linearen Elementen (z.B. aus Widerständen, Spulen, Kondensatoren, Übertragern), so wird es lineares Zweitor genannt.
1.2 Das lineare passive Zweitor
Bei einem linearen passiven Zweitor stehen die vier Klemmen im Inneren durch beliebige Anordnungen von linearen passiven Elementen (z.B. Widerständen, Kapazitäten, Induktivitäten, Leitungen,
magnetischen Kopplungen) in Verbindung.
Abbildung 1. Zweitor mit Umgebung.
Ist ein Zweitor nach Bild 1 mit einem umgebenden Netzwerk verbunden, ergibt sich bei Anwendung
der Kirchhoffschen Knotengleichung
bı 1 + bı 1′ + bı 2 + bı 2′
= 0.
Eine weitergehende Aussage ist in diesem Fall nicht möglich.
Abbildung 2. Mit Eintoren beschaltetes Zweitor.
1
(1)
Versuch B1/4 - Zweitore
Lässt sich das das Zweitor umgebende Netzwerk in zwei Eintore nach Bild 2 auftrennen, so gilt
und
= − bı 1′
bı 1
(2)
= − bı 2′ .
bı 2
Die vier Anschlüsse des Zweitors sind jetzt paarweise zusammengefasst worden, wobei ein Klemmenpaar durch die Gleichheit der Ströme in den Anschlüssen gekennzeichnet ist. Ist Gleichung 2 erfüllt,
so spricht man von einem Zweitor im engeren Sinne.
Abbildung 3. Zweitorbezugspfeilsystem.
Im Folgenden sollen die Bezugspfeilrichtungen der Spannungen und Ströme nach Bild 3 festgelegt
sein.
1.3 Die Zweitorgleichungen
b 1 sowie bı 2 und u
b 2 lassen sich mit Hilfe bekannter
Die Beziehungen zwischen den Größen bı 1 und u
Methoden der Netzwerkanalyse herleiten.
Hier wird die Maschenstromanalyse angewandt. Dazu wird ein vollständiger Baum so gelegt, dass die
von außen zugänglichen Zweige 1 und 2 Verbindungszweige sind. Das Gleichungssystem der Maschenströme lautet dann














~bı = 







 · 


 · 
↔
b
Z ~bı = ~u
bı 1
bı 2
bı a
bı b
bı c
,







~u
b =






,
·
b1
u
b2
u
0
0
0
·
·
·







,






(3)
wobei die Ströme bı a , bı b , bı c usw. als zweitorinterne Hilfsgrößen zu verstehen sind.
Mit Hilfe der Cramerschen Regel ergibt sich
bı 1
bı 2
↔
= +
= −
D11
D
D12
D
b1 −
u
b1 +
u
D21
D
D22
D
b 2,
u
(4)
b 2,
u
↔
wenn D die Systemdeterminante von Z ist und Dik die zu z ik gehörige Unterdeterminante von Z .
↔
Mit Hilfe der Rechenregeln für Determinanten folgt aus der Symmetrie von Z , dass
Dik = Dki .
2
(5)
Versuch B1/4 - Zweitore
1.4 Die Zweitorgleichungen in Leitwertform
b 1 und u
b 2 bei einem linearen
Die Beziehungen zwischen den Strömen bı 1 und bı 2 und den Spannungen u
passiven Zweitor haben also die allgemeine Form:
bı 1
bı 2
oder in Matrizenschreibweise:
=
=
b 1 + y 12 u
b 2,
y 11 u
b 1 + y 22 u
b2
y 21 u
(6)
b.
Y ~u
(7)
↔
~bı =
Die Matrizenelemente haben die Dimension von Leitwerten. Deshalb werden die Gleichungen 6 bzw.
7 die Zweitorgleichungen in Leitwertform genannt.
↔
Die auftretende Matrix Y heißt Admittanzmatrix, ihre Elemente Y-Parameter. Es sei an dieser Stelle
bemerkt, dass nicht jedes lineare passive Zweitor eine Admittanzmatrix besitzt.
Die Berechnung der Admittanzmatrix (wie auch der anderen Zweitormatrizen) erfolgt in der Praxis
zweckmäßig mittels Leerlauf- bzw. Kurzschlussexperimenten. Die entsprechenden Formeln entnehme
man dem beiliegenden Hilfsblatt.
Aus Gleichung 5 folgt, dass die Admittanzmatrix symmetrisch ist, d.h.
y 12 = y 21 .
(8)
Daraus folgt zusammen mit den Zweitorgleichungen in Leitwertform (Hilfsblatt)
bı 1 b 2b
u
u 1 =0
=
bı 2 .
b 1b
u
u 2 =0
(9)
Diese Beziehung beinhaltet den Umkehrsatz für lineare passive Zweitore:
b 1 ruft in den kurzgeschlossenen Klemmen
Eine an den Klemmen 11’ angelegt Spannung u
b 2 an den Klemmen 22’
22’ den gleichen Strom hervor, wie ihn die gleiche Spannung u
angelegt in den kurzgeschlossenen Klemmen 11’ verursacht.
Folgende physikalische Interpretationen der Elemente der Admittanzmatrix sind naheliegend:
• y 12 wird Kopplungsleitwert des Zweitors genannt.
• Werden die Klemmen 22’ kurzgeschlossen, so ist der Eingangsleitwert an den Anschlüssen 11’
gleich y 11 .
• y 22 ist der Leitwert zwischen den Klemmen 22’ bei Kurzschluss an den Klemmen 11’.
Jedes lineare passive Zweitor, das eine Admittanzmatrix besitzt, lässt sich durch ein Ersatzschaltbild
nach Bild 4 (π-Schaltung) beschreiben.
Diese Ersatzschaltung beschreibt das Verhalten des Zweitors nur an den Klemmenpaaren
11’ und 22’ und nicht das Verhalten zwischen den Anschlüssen 12 und 1’2’.
Es ist
y 11
y 22
y 12
y 21
=
=
=
=
Y
Y
+Y
2+ Y
−Y 0
− Y 0.
Y
Y
Y
=
=
=
y 11 + y 21
,
y 22 + y 21 und
− y 21 .
1
0
0
,
,
und
(10)
bzw.
1
2
0
3
(11)
Versuch B1/4 - Zweitore
Abbildung 4. π-Ersatzschaltbild.
1.5 Die Zweitorgleichungen in Widerstandsform
Neben der Leitwertform ist für Zweitorgleichungen noch die Widerstandsform
b1 =
u
z 11 bı 1 + z 12 bı 2 ,
b2 =
u
oder in Matrizenschreibweise
z 21 bı 1 + z 22 bı 2
~u
b
gebräuchlich.
(12)
↔
=
Z ~bı
(13)
Es ist
z 11 =
z 21 =
y 22
y 11 y 22 − y 12 y 21
− y 12
y 11 y 22 − y 12 y 21
,
,
− y 12
sowie
y 11 y 22 − y 12 y 21
y 11
.
y 11 y 22 − y 12 y 21
z 12 =
z 22 =
(14)
Die Gleichungen 12 bzw. 13 werden die Zweitorgleichungen in Widerstandsform genannt. Die Elemente
↔
↔
von Z heißen Z-Parameter, Z selbst ist die Impedanzmatrix. Es sei hier bemerkt, dass nicht jedes
lineare passive Zweitor eine Impedanzmatrix besitzt.
Aus den Gleichungen 8 und 14 folgt
z 12 =
z 21
(15)
(16)
oder (Hilfsblatt)
b 2 u
bı 1 bı 2 =0
=
b 1 u
.
bı 2 bı 1 =0
Diese Beziehung enthält wieder den Umkehrsatz für lineare passive Zweitore:
Die Ausgangsspannung an einem offenen Klemmenpaar ändert sich bei gegebenem Eingangsstrom nicht, wenn Eingang und Ausgang des Zweitors vertauscht werden.
Interpretationen der Z-Parameter:
• Die Größe z 12 heißt Kopplungswiderstand des Zweitores.
• Der Eingangswiderstand des Zweitors an den Anschlüssen 11’ bei leerlaufenden Klemmen 22’ ist
z 11 .
4
Versuch B1/4 - Zweitore
• Fließt in die Klemmen 11’ kein Strom, so ist der Widerstand zwischen den Anschlüssen 22’ gleich
z 22 .
Aus den Zweitorgleichungen in Widerstandsform 12 bzw. 13 lässt sich ein Ersatzschaltbild nach Bild 5
(T-Schaltung) herleiten.
Auch diese Ersatzschaltung beschreibt nur das Verhalten des Zweitors an den Klemmenpaaren 11’ und
22’.
Es ist:
z 11 =
Z 1 + Z 0,
z 22 =
Z2+ Z0
z 12 =
Z0
Z1 =
z 11 − z 12 ,
Z2 =
z 22 − z 12
Z0 =
z 12 .
und
(17)
oder
und
(18)
Abbildung 5. T-Ersatzschaltbild.
1.6 Die Zweitorgleichungen in Kettenform
Durch Auflösen der Zweitorgleichungen nach je zwei der vier Spannungen und Ströme ergeben sich
insgesamt sechs Formen der Zweitorgleichungen. Eine oft verwendete Form ist die Kettenform. Hierbei
b 2 , bı 2 ) ausgedrückt:
b 1 , bı 1 ) durch die Ausgangsgrößen ( u
werden die Eingangsgrößen ( u
oder in Matrizenschreibweise:
↔
b1 =
u
bi 1
=
b1
u
bı 1
b 2 + a 12 (− bı 2 ),
a 11 u
b 2 + a 22 (− bı 2 )
a 21 u
!
!
b2
u
A
.
− bı 2
↔
=
(19)
(20)
Die Matrix A heißt Kettenmatrix, ihre Elemente Ketten- oder einfach A-Parameter. Die vier AParameter haben verschiedene Dimensionen.
Aus dem Umkehrsatz folgt
det
↔
A
= 1.
(21)
Es reichen also stets drei Z-, Y- oder A-Parameter zur Beschreibung eines linearen passiven Zweitores
aus, der vierte liegt jeweils durch den Umkehrsatz fest.
Die Kettenparameter der T -Schaltung in Bild 5 und der π-Schaltung in Bild 4 entnimmt man dem
beiliegenden Hilfsblatt.
5
Versuch B1/4 - Zweitore
2 Zusammenschaltung von Zweitoren
2.1 Parallelschaltung zweier Zweitore
Die Parallelschaltung zweier Zweitore nach Bild 6 bildet ein neues Zweitor mit den Klemmenpaaren
11’ und 22’ .
Abbildung 6. Parallelschaltung von Zweitoren.
Das elektrische Verhalten des Gesamtzweitores kann nur dann aus den Zweitorgleichungen der Einzelzweitore abgeleitet werden, wenn Gleichung 2 erfüllt ist. Das heißt, es muss gelten:
und
bı 11 = − bı 11′
bı 12 = − bı 12′
,
,
bı 21 = − bı 21′
bı 21 = − bı 22′ .
(22)
(23)
Abbildung 7. Modifizierte Zweitor-Parallelschaltung.
In der Schaltung in Bild 6 wird das im Allgemeinen nicht der Fall sein, weil zwischen den Klemmen 1’
b 1′ 2′ besteht, die bei den beiden Einzelzweitoren vor dem Zusammenschalten
und 2’ eine Spannung u
verschieden sein wird. Eine Parallelschaltung nach Bild 6 führt dann zu einem Ausgleichsstrom, der
sich zu den in den Zweitoren eintretenden Strömen addiert bzw. von diesen subtrahiert. Damit ist die
6
Versuch B1/4 - Zweitore
Voraussetzung für die Gültigkeit der Zweitorgleichungen der Einzelzweitore nicht mehr erfüllt. Durch
Zuschalten eines idealen Übertragers nach Bild 7 kann die Gleichheit der Ströme in den Klemmenpaaren der Einzelzweitore erzwungen werden.
Ebenso behalten die Zweitorgleichungen ihre Gültigkeit bei einer Parallelschaltung zweier Zweitore,
bei denen je zwei Klemmen direkt miteinander verbunden sind (Bild 8).
Abbildung 8. Zweitor-Parallelschaltung mit Dreipolen.
Die Zusammenschaltung liefert unmittelbar die Bedingung für die Teilspannungen- und -ströme und
ihre Beziehung zu den Spannungen und Strömen des Gesamtzweitores. Es gilt:
bı 1 = bı 11 + bı 21
und
b1 = u
b 21
b 11 = u
u
bı 2 = bı 12 + bı 22
,
b2 = u
b 22 .
b 12 = u
u
,
(24)
(25)
Damit folgt sofort aus den Zweitorgleichungen in Leitwertform:
bı 1
bı 2
b 1 + ( y 112 + y 212 ) u
b 2,
= ( y 111 + y 211 ) u
=
( y 121
+
oder in Matrizenschreibweise:
b1
y 221 ) u
↔1
mit
+
( y 122
↔2
+
b2
y 222 ) u
Y
=
↔1
(27)
↔
~bı = ( Y + Y ) ~u
b
b = Y~
u
↔
(26)
↔2
Y +Y .
(28)
(29)
2.2 Reihenschaltung zweier Zweitore
Werden zwei Zweitore nach Bild 9 in Reihe geschaltet, so ist auch hier im allgemeinen die Voraussetzung für die Gültigkeit der Zweitorgleichungen der Einzelzweitore, die Gleichheit der Ströme in einem
Klemmenpaar, nicht erfüllt.
Auch hier kann die Gleichheit der Ströme in einem Klemmenpaar durch einen idealen Übertrager nach
Bild 10 erzwungen werden.
7
Versuch B1/4 - Zweitore
Ebenso sind die Zweitorgleichungen der Einzelzweitore bei der Schaltung nach Bild 11 gültig.
Die Beziehung zwischen den Teilströmen- und -spannungen und dem Gesamtstrom und der Gesamtspannung lauten hier
bı 1 = bı 11 = − bı 21 , bı 2 = bı 12 = − bı 22
(30)
bzw.
b1 = u
b 21
b 11 − u
u
,
b2 = u
b 22 .
b 12 − u
u
(31)
Daraus ergibt sich zusammen mit den Zweitorgleichungen in Widerstandsform:
b1 =
u
b2 =
u
z 111 bı 11 + z 112 bı 12 − ( z 211 bı 21 + z 212 bı 22 ),
z 121 bı 11
+
z 122 bı 12
−
( z 221 bı 21
+
z 222 bı 22 )
Abbildung 9. Reihenschaltung zweier Zweitore.
Abbildung 10. Zweitor-Reihenschaltung mit Übertrager.
8
(32)
(33)
Versuch B1/4 - Zweitore
Abbildung 11. Zweitor-Reihenschaltung mit Dreipolen.
bzw.
b 1 = ( z 111 + z 211 ) bı 1 + ( z 112 + z 212 ) bı 2 ,
u
b2 =
u
( z 121
z 221 ) bı 1
+
oder im Matrizenschreibweise:
~u
b
mit
↔1
+
( z 122
↔2
+
(34)
z 222 ) bı 2
(35)
↔
= ( Z + Z )~bı = Z ~bı
↔
Z
=
↔1
(36)
↔2
Z +Z .
(37)
Gleichung 37 ergibt sich auch für die Schaltung in Bild 10.
2.3 Kettenschaltung zweier Zweitore
Sind zwei Zweitore nach Bild 12 in Kette geschaltet, so sind die Zweitorgleichungen für die Einzelzweitore gültig.
Abbildung 12. Kettenschaltung zweier Zweitore.
Es gilt:
b 11
u
bı 11
!
↔1
= A
b 12
u
− bı 12
!
,
9
b 21
u
bı 21
!
↔2
= A
!
b 22
u
.
− bı 22
(38)
Versuch B1/4 - Zweitore
Aus Bild 12 folgt sofort:
Außerdem gilt:
b1 =
u
bı 1 =
b 11 ,
u
bı 11 ,
Daraus ergibt sich
b 21
b 12 = u
u
mit
b1
u
bı 1
!
b2 =
u
bı 2 =
b2
u
bı 2
A A
↔
A
=
(39)
− bı 12 = bı 21 .
und
↔1 ↔2
=
b 22 und
u
bı 22
.
!
↔
= A
(40)
b2
u
bı 2
!
↔1↔2
A A .
(41)
(42)
3 Versuchsdurchführung
In der Versuchsdurchführung geht es darum, verschiedene Zweitorparameter von Widerstandsnetzwerken messtechnisch zu ermitteln.
Dazu stehen folgende Geräte zur Verfügung:
• ELVIS Power Supply + als Gleichspannungsquelle (10V einstellen).
• ELVIS DMM als Amperemeter (Anschlüsse Current_Lo u. Current_Hi)
für Stromstärkemessungen bı 1 und bı 2 .
• ELVIS-Anschlussadapter.
• Zur Spannungsmessung die LabVIEW Applikation DC_Voltmeter.vi (Messkanal ACH0)
und bei zwei zeitgleichen Spannungsmessungen zusätzlich DC_Voltmeter_ACH1Kanal.vi (Messkanal ACH1).
• Zwei Zweitore, namentlich einfache Widerstandsnetzwerke.
10
Versuch B1/4 - Zweitore
Versuchsablauf
ACHTUNG: Vor dem Aufbau der Schaltung das ELVIS Prototypingboard ausschalten.
Schalter: Prototyping Board Power „OFF“
Erst nach Abnahme der Schaltung durch den Versuchsbetreuer das Board einschalten.
Schalter: Prototyping Board Power „ON“
1
2
3
4
5
Bestimmung der Zweitorparameter
Von den zwei gegebenen Zweitoren sind
die Widerstandsparameter, Leitwertparameter und Kettenparameter durch Leerlauf- und
Kurzschlussmessungen zu ermitteln.
Ersatzschaltbilder
Aus den Widerstandsparametern ist die TErsatzschaltung des einen, aus den Leitwertparametern die π-Ersatzschaltung des anderen Zweitors zu bestimmen.
Umrechnung der Zweitorparameter
Aus den Elementen der Ersatzschaltungen
sind die Kettenparameter der Zweitore zu berechnen. Die Ergebnisse sollen mit den Messwerten nach 3.1 verglichen werden.
Berechnung von Gesamtparametern
Die Zweitorparameter der Parallel-, Reihenund Kettenschaltung der zwei Zweitore sind
aus den jeweils günstigen Parametern der
Einzelzweitore zu berechnen.
Messung von Gesamtparametern
Die im letzten Punkt berechneten Parameter sind durch Leerlauf und Kurzschlussmessung an der jeweiligen Zusammenschaltung
der Einzelzweitore zu ermitteln. Die gemessenen Parameter sind mit den errechneten zu
vergleichen.
• Die Messwerte und die berechneten Parameter sind jeweils sinnvoll in die beiliegenden Universalprotokolle einzutragen.
• Als Grundlage der erforderlichen Rechnungen dient das beiliegende Hilfsblatt.
11
Versuch B1/4 - Zweitore
4 Hilfsblatt
Hilfsblatt
Versuch: B1/4-Zweitore
Ersatzschaltungen
Z0+ Z1
Z0
↔
T-ESB:
Z =
↔
A =
Y
Y =
π-ESB:
↔
A =
!
Z 1 + Z 2 + ( Z 1 Z 2 )/ Z 0
1 + Z 2/ Z 0
1 + Z 1/ Z 0
1/ Z 0
↔
Z0
Z0+ Z2
+Y
−Y 0
0
1
−Y 0
Y 0+ Y
1 + Y 2/ Y 0
Y 1 + Y 2 + ( Y 1 Y 2 )/ Y
0
2
!
!
1/ Y 0
1 + Y 1/ Y
!
0
Matrizenberechnung aus Messdaten
Admittanzmatrix
Impedanzmatrix
Kettenmatrix
bı 1
bı 2
b1
u
b2
u
b1
u
bı 1
!
!
!
=
y 11
y 21
y 12
y 22
!
=
z 11
z 21
z 12
z 22
!
=
a 11
a 21
a 12
a 22
!
b1
u
b2
u
bı 1
bı 2
b2
u
− bı 2
!
!
!
↔
Y =
↔
Z =
↔
A =
bı 1 / u
b 1| b
u 2 =0
bı 2 / u
b 1| b
u 2 =0
bı 1 / u
b 2| b
u 1 =0
bı 2 / u
b 2| b
u 1 =0
b 1 / bı 1 |bı 2 =0
u
b 2 / bı 1 |bı 2 =0
u
b 1 / bı 2 |bı 1 =0
u
b 2 / bı 2 |bı 1 =0
u
↔
A → Z
1
Z =
a 21
↔
a 11
1
1
a 22
!
↔
↔
A → Y
1
Y =
a 12
↔
5 Messprotokoll
12
a 22
−1
!
b 1 / bı 2 | b
b 1/ u
b 2 |bı 2 =0 − u
u
u 2 =0
b 2 |bı 2 =0 − bı 1 / bı 2 | b
bı 1 / u
u 2 =0
Einfache Umrechnungen
↔
!
−1
a 11
!
!
Versuch B1/4 - Zweitore
Messprotokoll
Versuch:
B1/4-Zweitore Datum:
Gruppen:
und
Zweitor:
Messdaten
ub 1 = 0 V
0
ub 1 [V]
b
ı 1 [mA]
ub 2 [V]
b
ı 2 [mA]
b
ı1
= 0 mA
ub 2 = 0 V
10
0
10
10
b
ı2
= 0 mA
10
0
0
Parameter aus den Messdaten
↔


Y =
↔
↔
, Z =




A =



Vergleichsparameter aus der Rechnung


=

Ersatzschaltbildelemente
T-ESB:
Z0 =
π-ESB:
Y
0
=
Z1 =
Y
1
Es sind nur die Felder auszufüllen, die jeweils benötigt werden.
13
=
Z2 =
Y
2
=
Versuch B1/4 - Zweitore
Messprotokoll
Versuch:
B1/4-Zweitore Datum:
Gruppen:
und
Zweitor:
Messdaten
ub 1 = 0 V
0
ub 1 [V]
b
ı 1 [mA]
ub 2 [V]
b
ı 2 [mA]
b
ı1
= 0 mA
ub 2 = 0 V
10
0
10
10
b
ı2
= 0 mA
10
0
0
Parameter aus den Messdaten
↔


Y =
↔
↔
, Z =




A =



Vergleichsparameter aus der Rechnung


=

Ersatzschaltbildelemente
T-ESB:
Z0 =
π-ESB:
Y
0
=
Z1 =
Y
1
Es sind nur die Felder auszufüllen, die jeweils benötigt werden.
14
=
Z2 =
Y
2
=
Versuch B1/4 - Zweitore
Messprotokoll
Versuch:
B1/4-Zweitore Datum:
Gruppen:
und
Zweitor:
Messdaten
ub 1 = 0 V
0
ub 1 [V]
b
ı 1 [mA]
ub 2 [V]
b
ı 2 [mA]
b
ı1
= 0 mA
ub 2 = 0 V
10
0
10
10
b
ı2
= 0 mA
10
0
0
Parameter aus den Messdaten
↔


Y =
↔
↔
, Z =




A =



Vergleichsparameter aus der Rechnung


=

Ersatzschaltbildelemente
T-ESB:
Z0 =
π-ESB:
Y
0
=
Z1 =
Y
1
Es sind nur die Felder auszufüllen, die jeweils benötigt werden.
15
=
Z2 =
Y
2
=
Versuch B1/4 - Zweitore
Messprotokoll
Versuch:
B1/4-Zweitore Datum:
Gruppen:
und
Zweitor:
Messdaten
ub 1 = 0 V
0
ub 1 [V]
b
ı 1 [mA]
ub 2 [V]
b
ı 2 [mA]
b
ı1
= 0 mA
ub 2 = 0 V
10
0
10
10
b
ı2
= 0 mA
10
0
0
Parameter aus den Messdaten
↔


Y =
↔
↔
, Z =




A =



Vergleichsparameter aus der Rechnung


=

Ersatzschaltbildelemente
T-ESB:
Z0 =
π-ESB:
Y
0
=
Z1 =
Y
1
Es sind nur die Felder auszufüllen, die jeweils benötigt werden.
16
=
Z2 =
Y
2
=
Versuch B1/4 - Zweitore
Messprotokoll
Versuch:
B1/4-Zweitore Datum:
Gruppen:
und
Zweitor:
Messdaten
ub 1 = 0 V
0
ub 1 [V]
b
ı 1 [mA]
ub 2 [V]
b
ı 2 [mA]
b
ı1
= 0 mA
ub 2 = 0 V
10
0
10
10
b
ı2
= 0 mA
10
0
0
Parameter aus den Messdaten
↔


Y =
↔
↔
, Z =




A =



Vergleichsparameter aus der Rechnung


=

Ersatzschaltbildelemente
T-ESB:
Z0 =
π-ESB:
Y
0
=
Z1 =
Y
1
Es sind nur die Felder auszufüllen, die jeweils benötigt werden.
17
=
Z2 =
Y
2
=