Kapitel 9 Verteilungsmodelle
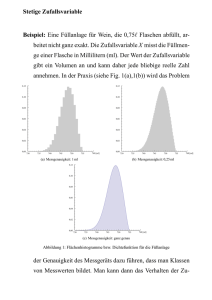
Werbung

Kapitel 9
Verteilungsmodelle
Es gibt eine Reihe von Verteilungsmodellen für univariate diskrete und stetige
Zufallsvariablen, die sich in der Praxis bewährt haben. Wir wollen uns von
diesen einige anschauen.
9.1
Diskrete Verteilungsmodelle
Es gibt eine Reihe von von Zugängen zu Verteilungsmodellen für diskrete
Zufallsvariablen. Man kann die Wahrscheinlichkeitsfunktion einer diskreten
Zufallsvariablen dadurch gewinnen, dass man den Träger TX vorgibt und
für jedes x ∈ TX die Wahrscheinlichkeit P (X = x) festlegt. Dabei müssen
natürlich die Gleichungen 5.2 und 5.1 auf Seite 147 erfüllt sein. Eine andere Möglichkeit besteht darin, auf einem geeigneten Wahrscheinlichkeitsraum
eine Zufallsvariable zu definieren. Schauen wir uns zunächst ein Beispiel für
die erste Möglichkeit an.
9.1.1
Die Gleichverteilung
Definition 9.1
Die Zufallsvariable X heißt gleichverteilt, wenn gilt
P (X = x) =
für x = 1, . . . , N .
199
1
N
(9.1)
KAPITEL 9. VERTEILUNGSMODELLE
200
Für den Erwartungswert und die Varianz der diskreten Gleichverteilung gilt
E(X) =
N +1
2
(9.2)
und
V ar(X) =
N2 − 1
12
.
(9.3)
Schauen wir uns zuerst den Erwartungswert an:
E(X) =
N
x
x=1
N
1
1 N (N + 1)
1 N +1
x=
=
=
N
N x=1
N
2
2
Für die Varianz bestimmen wir zunächst
N
N
1
1 N (N + 1)(2N + 1)
1 2
x
x =
E(X ) =
=
N
N x=1
N
6
x=1
2
=
2
(N + 1)(2N + 1)
.
6
Hierbei haben wir benutzt, das gilt
N
x=1
x2 =
N (N + 1)(2N + 1)
.
6
Die Varianz ist dann
V ar(X) = E(X 2 ) − E(X)2 =
=
(N + 1)(2N + 1) (N + 1)2
−
6
4
(N + 1)(N − 1)
N2 − 1
N +1
[4N + 2 − 3N − 3] =
=
.
12
12
12
Beispiel 76
Die Gleichverteilung ist ein sinnvolles Modell für die Augenzahl beim einmaligen Wurf eines fairen Würfels. Hier gilt
P (X = x) =
1
6
9.1. DISKRETE VERTEILUNGSMODELLE
201
für x = 1, 2, . . . , 6. Es gilt E(X) = 3.5 und V ar(X) = 35/12.
Abbildung 9.1 zeigt die Wahrscheinlichkeitsfunktion.
Abbildung 9.1: Wahrscheinlichkeitsfunktion der Gleichverteilung
0.20
c(0, 1/6)
0.15
0.10
0.05
0.00
0
2
4
6
8
c(1, 1)
9.1.2
Vom Bernoulliprozess abgeleitete Verteilungen
Einer Reihe von Verteilungen liegt der sogenannte Bernoulliprozess zu
Grunde.
Der Bernoulliprozess
Bei einem Zufallsvorgang sei ein Ereignis A mit P (A) = p von Interesse.
Man spricht auch von einem Bernoullivorgang und nennt das Ereignis A
oft auch Erfolg. Einen Bernoulliprozess erhält man nun dadurch, dass
man einen Bernoullivorgang mehrmals beobachtet, wobei folgende Annahmen getroffen werden:
• Die einzelnen Bernoullivorgänge sind voneinander unabhängig.
• Die Erfolgswahrscheinlichkeit p bleibt konstant.
Beispiel 77
Im Beispiel 58 auf Seite 152 haben wir ein Teilchen betrachtet, dass sich
zufällig auf den ganzen Zahlen bewegt, wobei es im Nullpunkt startet. Jeder
Schritt des Teilchens ist ein Bernoulliexperiment. Es gibt nur 2 Möglichkeiten.
Das Teilchen geht entweder nach links, was wir mit A, oder es geht nach
rechts, was wir mit Ā bezeichnen. Da das Teilchen sich zufällig entscheidet,
KAPITEL 9. VERTEILUNGSMODELLE
202
gilt P (A) = p = 0.5. Wenn wir unterstellen, dass die Entscheidung des
Teilchens bei einem Schritt unabhängig von den anderen Schritten getroffen
wird, und die Erfolgswahrscheinlichkeit p konstant bleibt, beobachten wir bei
n Schritten einen Bernoulliprozess der Länge n.
Beim Bernoulliprozess sind für uns zwei Zufallsvariablen von Interesse:
• Anzahl der Erfolge bei n Durchführungen.
• Anzahl der Misserfolge vor dem ersten Erfolg
Schauen wir uns die Verteilungen dieser Zufallsvariablen im Detail an.
Die Binomialverteilung
Definition 9.2
Die Zufallsvariable X heißt binomialverteilt mit den Parametern n und p,
wenn ihre Wahrscheinlichkeitsfunktion gegeben ist durch:
n x
P (X = x) =
p (1 − p)n−x
x
(9.4)
für x = 0, 1, . . . , n.
Die Binomialverteilung erhält man, wenn man bei einem Bernoulliprozess der
Länge n die Erfolge zählt. Dies kann man sich folgendermaßen klarmachen:
Sei X die Anzahl der Erfolge bei einem Bernoulliprozess der Länge n. Die Zufallsvariable X kann die Werte 0, 1, 2, . . . , n annehmen. Nimmt X den Wert x
an, so wurden x Erfolge A und n − x Mißerfolge Ā beobachtet. Aufgrund der
Unabhängigkeit der einzelnen Durchführungen beträgt die Wahrscheinlichkeit einer Folge aus x Erfolgen A und n−x Mißerfolgen Ā gleich px (1−p)n−x .
Eine Folge, die x-mal ein A und n − x-mal ein Ā enthält, ist eindeutig durch
die Positionen der A festgelegt. Wir haben im Beispiel 44 auf Seite 126 gesehen, dass es
n
n!
=
x!(n − x)!
x
Möglichkeiten gibt, die Positionen der A zu wählen. Also gilt
n x
P (X = x) =
p (1 − p)n−x für x = 0, 1, . . . , n.
x
9.1. DISKRETE VERTEILUNGSMODELLE
203
Für eine binomialverteilte Zufallsvariable X gilt
E(X) = np
und
V ar(X) = np(1 − p)
.
Beispiel 77 (fortgesetzt)
Sei X die Anzahl der Schritte nach links. Die Zufallsvariable X ist binomialverteilt mit den Parametern n = 3 und p = 0.5. Es gilt für x = 0, 1, 2, 3:
3
3
x
3−x
=
0.53
P (X = x) =
0.5 (1 − 0.5)
x
x
Tabelle 9.1 zeigt die Wahrscheinlichkeitsfunktion.
Tabelle 9.1: Wahrscheinlichkeitsfunktion der Binomialverteilung mit n = 3
und p = 0.5
x
0
1
2
3
P (X = x)
0.125
0.375
0.375
0.125
Außerdem gilt E(X) = 1.5 und V ar(X) = 0.75.
Abbildung 9.2 zeigt die Wahrscheinlichkeitsfunktion der Binomialverteilung
für n = 10 und p = 0.1, p = 0.2, p = 0.5 und p = 0.8.
Wir sehen, dass die Wahrscheinlichkeitsfunktion der Binomialverteilung für
p = 0.5 symmetrisch ist. Für p < 0.5 ist sie rechtsschief und für p > 0.5
linksschief.
KAPITEL 9. VERTEILUNGSMODELLE
204
Abbildung 9.2: Wahrscheinlichkeitsfunktion der Binomialverteilung für n =
10 und p = 0.1, p = 0.2, p = 0.5 und p = 0.8
Binomialverteilung mit n=10,p=0.1
Binomialverteilung mit n=10,p=0.2
0.30
0.25
0.3
0.20
0.2
0.15
0.10
0.1
0.05
0.0
0.00
0
1
2
3
4
5
6
7
8
9
10
0
Binomialverteilung mit n=10,p=0.5
1
2
3
4
5
6
7
8
9
10
Binomialverteilung mit n=10,p=0.8
0.30
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0.00
0.00
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
Die Binomialverteilung mit n = 1 heißt Bernoulliverteilung. Die Wahrscheinlichkeitsfunktion der Bernoulliverteilung ist gegeben durch:
P (X = x) = px (1 − p)1−x
für x = 0, 1.
Es gilt also
P (X = 0) = 1 − p
und
P (X = 1) = p.
Eine bernoulliverteilte Zufallsvariable X zählt, wie oft A bei einem Bernoullivorgang eingetreten ist. Für eine bernoulliverteilte Zufallsvariable X gilt
E(X) = p und V ar(X) = p(1 − p). Schauen wir uns erst den Erwartungswert an:
E(X) = 0 · (1 − p) + 1 · p = p .
Für die Varianz bestimmen wir
E(X 2 ) = 0 · (1 − p) + 1 · p = p
9.1. DISKRETE VERTEILUNGSMODELLE
205
und erhalten
V ar(X) = E(X 2 ) − E(X)2 = p − p2 = p(1 − p) .
Die geometrische Verteilung
Eine bernoulliverteilte Zufallsvariable zählt die Anzahl der Erfolge bei einem
Bernoulliprozess der Länge n. Schauen wir uns die Wahrscheinlichkeitsfunktion der Misserfolge vor dem ersten Erfolg an.
Definition 9.3
Die Zufallsvariable X heißt geometrisch verteilt mit Parameter p, wenn ihre
Wahrscheinlichkeitsfunktion gegeben ist durch
P (X = x) = p (1 − p)x
für x = 0, 1, . . .
(9.5)
Die geometrische Verteilung erhält man, wenn man bei einem Bernoulliprozess die Anzahl der Misserfolge vor dem ersten Erfolg zählt. Dies kann man
sich folgendermaßen klarmachen:
Sei X die Anzahl der Misserfolge vor dem ersten Erfolg bei einem Bernoulliprozess. Die Zufallsvariable X kann die Werte 0, 1, 2, . . . annehmen. Nimmt X
den Wert x an, so wurden x Mißerfolge Ā und genau ein Erfolg A beobachtet,
wobei das A das letzte Symbol in der Folge ist. Wir erhalten also
Ā
. . . Ā A
Ā
x−mal
Da die einzelnen Durchführungen unabhängig sind, beträgt die Wahrscheinlichkeit dieser Folge
(1 − p)(1 − p) · · · (1 − p) p = (1 − p)x p.
x−mal
Ist X geometrisch verteilt mit Prameter p, so gilt
E(X) =
1−p
p
V ar(X) =
1−p
p2
und
.
KAPITEL 9. VERTEILUNGSMODELLE
206
Beispiel 77 (fortgesetzt)
Wir warten so lange, bis das Teilchen zum ersten Mal nach links geht, und
zählen die Anzahl X der Schritte nach rechts vor dem ersten Schritt nach
links. Die Zufallsvariable X ist geometrisch verteilt mit p = 0.5. Es gilt
P (X = x) = 0.5x+1
für x = 0, 1, 2, .... .
Außerdem gilt E(X) = 1 und V ar(X) = 2.
Oft betrachtet man anstatt der Anzahl X der Misserfolge die Anzahl Y der
Versuche bis zum ersten Erfolg, wobei man den Erfolg mitzählt. Offensichtlich
gilt
Y = X + 1.
Die Wahrscheinlichkeitsfunktion von Y ist:
P (Y = y) = p (1 − p)y−1
für y = 1, . . .
.
(9.6)
Ausßerdem gilt
E(Y ) =
1
p
und
V ar(Y ) =
9.1.3
1−p
p2
.
Die hypergeometrische Verteilung
Wir haben die Binomialverteilung aus dem Bernoulliprozess hergeleitet. Man
kann sie aber auch aus einem einfachen Urnenmodell gewinnen. Hierzu betrachten wir eine Urne, die N Kugeln enthält, von denen M weiß und die
restlichen N −M schwarz sind. Der Anteil p der weißen Kugeln ist also M/N .
Zieht man n Kugeln mit Zurücklegen, so ist die Anzahl X der weißen Kugeln
mit den Parametern n und p binomialverteilt. Zieht man ohne Zurücklegen
aus der Urne, so besitzt die Anzahl X der weißen Kugeln eine hypergeometrische Verteilung. Die Wahrscheinlichkeit P (X = x) erhalten wir in diesem
Fall folgendermaßen:
Insgesamt gibt es Nn Möglichkeiten, von den N Kugeln n ohne Zurücklegen
Möglichkeiten, von den M weißen Kugeln x Kugeln
auszuwählen. Es gibt M
x
9.1. DISKRETE VERTEILUNGSMODELLE
207
−M Möglichkeiten, von den N − M schwarzen
auszuwählen, und es gibt Nn−x
Kugeln n − x Kugeln auszuwählen. Somit gilt
P (X = x) =
M
x
N −M
n−x
N
n
für max{0, n − (N − M )} ≤ x ≤ min{n, N }.
Definition 9.4
Die Zufallsvariable X heißt hypergeometrisch verteilt mit den Parametern
N , M und n, wenn ihre Wahrscheinlichkeitsfunktion gegeben ist durch
M
N −M
x
n−x
P (X = x) =
(9.7)
N
n
für max{0, n − (N − M )} ≤ x ≤ min{n, N }.
Es gilt
E(X) = n
M
N
und
V ar(X) = n
M N −M N −n
N
N
N −1
.
Setzen wir p = M/N , so gilt
E(X) = n p
und
N −n
.
N −1
Der Erwartungswert der Binomialverteilung und der hypergeometrischen Ve−n
kleiner als 1. Somit ist für
teilung sind also identisch. Für n > 1 ist N
N −1
n > 1 die Varianz der hypergeometrischen Verteilung kleiner als die Varianz
der Binomialverteilung.
V ar(X) = n p(1 − p)
KAPITEL 9. VERTEILUNGSMODELLE
208
Beispiel 78
Eine Urne enthält 10 Kugeln, von denen 4 weiß sind. Es werden zuerst 3
Kugeln mit Zurücklegen und dann 3 Kugeln ohne Zurücklegen gezogen. Sei
X die Anzahl der weißen Kugeln beim Ziehen mit Zurücklegen und Y die
Anzahl der weißen Kugeln beim Ziehen ohne Zurücklegen. Es gilt
3
P (X = x) =
0.4x 0.63−x
x
und
4
6
y
3−y
P (Y = y) =
.
10
3
Tabelle 9.2 zeigt die Wahrscheinlichkeitsverteilungen der Zufallsvariablen X
und Y .
Tabelle 9.2: Wahrscheinlichkeitsverteilung der hypergeometrischen und der
Binomialverteilung
Wert
0
1
2
3
Binomial- Hypergeometrische
verteilung
Verteilung
0.216
0.432
0.288
0.064
0.167
0.500
0.300
0.033
Wir sehen an der Tabelle, warum bei der Binomialverteilung die Varianz
größer ist als bei der hypergeometrischen Verteilung. Die extremen Werte 0
und 3 sind bei der Binomialverteilung wahrscheinlicher als bei der hypergeometrischen Verteilung.
Was passiert mit der Wahrscheinlichkeitsfunktion der hypergeometrischen
konstant bleibt?
Verteilung, wenn N beliebig groß wird, wobei aber p = M
N
9.1. DISKRETE VERTEILUNGSMODELLE
209
Es gilt:
P (X = x) =
M
x
N −M
(M )x (N − M )n−x n!
n−x
=
N
x! (n − x)! (N )n
n
n (M )x (N − M )n−x
=
x
(N )n
M −x+1N −M
N −M −n+x+1
n M
···
···
=
N −x+1 N −x
N −n+1
x N
Also gilt
lim P (X = x)
N →∞
M −x+1N −M
N −M −n+x+1
n M M −1
···
···
= lim
N →∞ x N N − 1
N −x+1 N −x
N −n+1
M
− N1
− x−1
1− M
− n−x−1
1− M
n M M
N
N
N
N
N
N
= lim
·
·
·
·
·
·
x
x−1
n−1
N →∞ x
N 1 − N1
1
−
1− N
1− N
N
p−
n
p
= lim
N →∞ x
1−
1
N
1
N
···
p−
1−
x−1
N
x−1
N
1 − p − n−x−1
1−p
N
·
·
·
1 − Nx
1 − n−1
N
n x
=
p (1 − p)n−x
x
Für große Werte von N können wir also die hypergeometrische Verteilung
durch die Binomialverteilung approximieren.
Außerdem bestätigt die Aussage die intuitive Annahme, dass es keinen Unterschied macht, ob man aus einer sehr großen Grundgesamtheit mit oder
ohne Zurücklegen zieht.
KAPITEL 9. VERTEILUNGSMODELLE
210
9.1.4
Die Poissonverteilung
Schauen wir uns an, was mit der Wahrscheinlichkeitsfunktion der Binomialverteilung geschieht, wenn wir n beliebig groß werden lassen. Auch hier
müssen wir beim Grenzübergang eine Restriktion berücksichtigen, da sonst
die Wahrscheinlichkeit gegen Null geht. Wir fordern, dass λ = np konstant
bleibt. Mit
λ
p= .
n
gilt also
n x
lim P (X = x) = lim
p (1 − p)n−x
n→∞
n→∞ x
=
" λ #x "
λ #n−x
n!
1−
n→∞ x!(n − x)! n
n
lim
"
"
λ #n
λ #−x
λx
(n)x
=
lim 1 −
lim 1 −
lim
x! n→∞ nx n→∞
n n→∞
n
=
λx −λ
e
x!
da gilt
n−x+1
(n)x
n n−1
···
=1
= lim
x
n→∞ n
n→∞ n
n
n
"
λ #n
lim 1 −
= e−λ
n→∞
n
"
λ #−x
lim 1 −
= 1
n→∞
n
lim
Definition 9.5
Die Zufallsvariable X heißt poissonverteilt mit dem Parameter λ, wenn ihre
Wahrscheinlichkeitsfunktion gegeben ist durch:
λx −λ
P (X = x) =
e
x!
für x = 0, 1, . . ..
(9.8)
9.1. DISKRETE VERTEILUNGSMODELLE
211
Die Poissonverteilung wird auch die Verteilung der seltenen Ereignisse genannt, da p = nλ mit wachsenem n immer kleiner wird.
Ist X poissonverteilt mit Parameter λ, so gilt
E(X) = λ
und
V ar(X) = λ
.
Abbildung 9.3 zeigt die Wahrscheinlichkeitsfunktion der Poissonverteilung
für λ = 1, λ = 2, λ = 5 und λ = 10.
Abbildung 9.3: Wahrscheinlichkeitsfunktion Poissonverteilung für λ = 1, λ =
2, λ = 5 und λ = 10
Poissonverteilung lambda=1
Poissonverteilung lambda=2
0.35
0.25
0.30
0.20
0.25
0.15
0.20
0.15
0.10
0.10
0.05
0.05
0.00
0.00
0
1
2
3
4
5
0
Poissonverteilung lambda=5
1
2
3
4
5
6
7
8
9
10
Poissonverteilung lambda=10
0.12
0.15
0.10
0.08
0.10
0.06
0.04
0.05
0.02
0.00
0.00
0
2
4
6
8
10
12
14
0
2
4
6
8
10
13
16
19
Wir sehen, dass die Wahrscheinlichkeitsfunktion der Poissonverteilung mit
wachsendem λ immer symmetrischer wird.
KAPITEL 9. VERTEILUNGSMODELLE
212
Beispiel 79
Wir haben im Beispiel 55 auf Seite 148 die Anzahl der Tore betrachtet,
die in der Saison 2001/2002 in der Fußballbundesliga je Spiel geschossen
wurden. Dabei wurden nur Spiele betrachtet, in denen höchstens 5 Tore
fielen. Es wurden aber auch mehr Tore geschossen. Tabelle 9.3 zeigt die
Häufigkeitsverteilung der Anzahl Tore in allen 306 Spielen.
Tabelle 9.3: Häufigkeitstabelle der Anzahl der Tore in einem Bundesligaspiel
in der Saison 2001/2002
x
0
1
2
3
4
5
6
7
n(X = x)
h(X = x)
23
0.075
35
0.114
74
0.242
69
0.225
56
0.183
23
0.075
19
0.062
7
0.023
Der Mittelwert der Anzahl Tore beträgt 2.9. Tabelle 9.4 zeigt die Wahrscheinlichkeitsverteilung der Poissonverteilung mit λ = 2.9.
Tabelle 9.4: Wahrscheinlichkeitsverteilung der Poissonverteilung mit Parameter λ = 2.9
x
0
P (X = x) 0.055
1
2
3
4
5
6
7
0.160
0.231
0.224
0.162
0.094
0.045
0.019
Wir sehen, dass die Wahrscheinlichkeiten und relativen Häufigkeiten gut
übereinstimmen. Dies besteht auch die Abbildung 9.4, in der beiden Verteilungen gegenübergestellt sind.
Wir werden später lernen, warum es sinnvoll ist, für λ den Mittelwert der
Beobachtungen zu wählen.
9.1. DISKRETE VERTEILUNGSMODELLE
213
Abbildung 9.4: Stabdiagramm der Anzahl der Tore mit Wahrscheinlichkeitsfunktion der Poissonverteilung mit Parameter λ = 2.9
Empirie
Modell
0.20
0.15
0.10
0.05
0.00
0
1
2
3
4
5
6
7
Warum die Poissonverteilung ein sinnvolles Modell für die Anzahl der in
einem Spiel geschossenen Tore ist, zeigen die folgenden Überlegungen.
Die Poissonverteilung spielt eine zentrale Rolle bei Ankunftsprozessen. Hier
soll die Anzahl X(a, t) der Ankünfte im Intervall (a, a + t] modelliert werden.
Dabei geht man von folgenden Annahmen aus:
1. X(a, t) und X(a∗ , t∗ ) sind unabhängig, wenn (a, a + t] und (a∗ , a∗ + t∗ ]
disjunkt sind.
2. X(a, h) hängt von h aber nicht von a ab.
3.
P (X(a, h) = 1) ≈ λh .
4.
P (X(a, h) > 1) ≈ 0 .
Annahme 1 besagt, dass die Häufigkeit des Auftretens von A in einem Intervall unabhängig ist von der Häufigkeit des Auftretens von A in einem dazu
disjunkten Intervall.
Annahme 2 besagt, dass die Häufigkeit des Auftretens von A in einem Intervall der Länge h nur von der Länge, aber nicht von der Lage des Intervalls
abhängt.
214
KAPITEL 9. VERTEILUNGSMODELLE
Annahme 3 besagt, dass die Wahrscheinlichkeit, dass A in einem sehr kleinen Intervall der Länge h genau einmal eintritt, proportional zur Länge des
Intervalls ist.
Annahme 4 besagt, dass die Wahrscheinlichkeit, dass A in einem sehr kleinen
Intervall der Länge h mehr als einmal eintritt, vernachlässigt werden kann.
Schauen wir uns dafür ein Beispiel an:
Beispiel 80
Der Verkehrsstrom einer Fernstraße wird an einem festen Beobachtungspunkt
protokolliert, wobei jeweils festgehalten wird, wann ein Fahrzeug den Beobachtungspunkt passiert.
Annahme 1 besagt, dass der Verkehrsstrom völlig regellos ist. Ereignisse in
nichtüberlappenden Intervallen sind unabhängig.
Annahme 2 besagt, dass der Verkehrsstrom von konstanter Intensität ist.
Die Wahrscheinlichkeit, dass in einem Zeitintervall der Länge h k Fahrzeuge
eintreffen, hängt von der Länge des Intervalls, nicht jedoch von seiner Lage
ab.
Annahme 4 besagt, dass das Auftreten geschlossener Fahrzeuggruppen vernachlässigt werden kann.
Unter den Annahmen 1 bis 4 ist X(a, t) poissonverteilt mit dem Parameter
λt. Es gilt also
(λt)x −λt
e
P (X(a, t) = x) =
x!
für x = 0, 1, . . . .
Dies sieht man folgendermaßen:
Wir teilen das Intervall (a, a + t] in n gleichgroße Intervalle der Länge h = nt .
Aufgrund von Annahme 4 kann A in jedem dieser Intervalle nur einmal oder
keinmal eintreten. In jedem dieser Intervalle beträgt die Wahrscheinlichkeit,
A genau einmal zu beobachten,
p = λh =
λt
n
Da die Intervalle disjunkt sind, ist das Eintreten von A in den einzelnen
Intervallen unabhängig. Außerdem ist jedes Intervall gleich lang, so dass p
konstant ist.
Es liegt also ein Bernoulliprozess der Länge n mit Erfolgswahrscheinlichkeit
vor. Somit gilt
p = λt
n
x n−x
n
λt
λt
P (X(a, t) = x) =
1−
x
n
n
9.2. STETIGE VERTEILUNGSMODELLE
215
Lassen wir n über alle Grenzen wachsen, so erhalten wir
(λt)x −λt
e
P (X(a, t) = x) =
x!
9.2
für x = 0, 1, . . . .
Stetige Verteilungsmodelle
Man erhält für eine stetige Zufallsvariable ein Modell, indem man eine Funktion fX (x)vorgibt, die die Gleichungen (5.9)und (5.10) auf Seite (154) erfüllen.
9.2.1
Die Gleichverteilung
Definition 9.6
Die Zufallsvariable X heißt gleichverteilt auf dem Intervall [a, b], wenn ihre
Dichtefunktion gegeben ist durch:
1
fX (x) = b − a
0
für a ≤ x ≤ b
(9.9)
sonst
Im Beispiel 59 auf Seite 155 haben wir die Gleichverteilung auf [0, 10] näher
betrachtet. Die Dichtefunktion ist in Abbildung 5.3 auf Seite 155 zu finden.
Die Verteilungsfunktion FX (x) ist gegeben durch:
0
−a
FX (x) = xb −
a
1
für x < a
für a ≤ x ≤ b
für x > b
Die Verteilungsfunktion der Gleichverteilung auf [0, 10] ist in Abbildung 5.4
auf Seite 156 zu finden.
Aus der Verteilungsfunktion können wir problemlos die Quantile bestimmen.
Es gilt
xp = a + p(b − a) .
(9.10)
Wir erhalten Gleichung (9.10), indem wir folgende Gleichung nach xp auflösen:
xp − a
= p.
b−a
KAPITEL 9. VERTEILUNGSMODELLE
216
Außerdem gilt
E(X) =
a+b
2
(9.11)
(a − b)2
12
(9.12)
und
V ar(X) =
Dies sieht man folgendermaßen:
b
E(X) =
a
=
1
1
x
dx =
b−a
b−a
b
a
1
x dx =
b−a
x2
2
b
a
1 (b + a) (b − a)
a+b
1 b 2 − a2
=
=
b−a
2
b−a
2
2
Für die Varianz bestimmen wir zunächst E(X 2 ). Es gilt
E(X 2 ) =
b
a
=
1
1
x2
dx =
b−a
b−a
b
a
x2 dx =
1 x 3 b
b−a 3 a
b 3 − a3
(b − a)(a2 + ab + b2 )
a2 + ab + b2
=
=
3(b − a)
3(b − a)
3
Also gilt
V ar(X) = E(X 2 ) − E(X)2 =
a2 + ab + b2 (a + b)2
−
3
4
=
a2 − 2ab + b2
4a2 + 4ab + 4b2 − 3a2 − 6ab − 3b2
=
12
12
=
(a − b)2
12
Eine zentrale Rolle spielt die Gleichverteilung auf [0, 1]. Bei dieser gilt a = 0
und b = 1.
9.2. STETIGE VERTEILUNGSMODELLE
9.2.2
217
Die Normalverteilung
Das wichtigste Verteilungsmodell ist die Normalverteilung, die von Gauss
vorgeschlagen wurde.
Definition 9.7
Die Zufallsvariable X heißt normalverteilt mit den Parametern µ und σ 2 ,
wenn ihre Dichtefunktion für x ∈ IR gegeben ist durch:
(x−µ)2
1
f (x) = √ e− 2σ2
σ 2π
(9.13)
Abbildung 9.5 zeigt die Dichtefunktion der Normalverteilung mit µ = 0 und
σ = 1, die Standardnormalverteilung heißt.
Abbildung 9.5: Dichtefunktion der Standardnormalverteilung
0.4
f(x)
0.3
0.2
0.1
0.0
−4
−2
0
2
4
x
Für eine mit den Parametern µ und σ 2 normalverteilte Zufallsvariable X gilt
E(X) = µ
und
V ar(X) = σ 2
KAPITEL 9. VERTEILUNGSMODELLE
218
Der Parameter µ beschreibt also die Lage und der Parameter σ 2 die Streuung
der Verteilung.
Abbildung 9.6 zeigt die Dichtefunktionen von zwei Normalverteilungen mit
unterschiedlichem Erwartungswert und identischen Varianzen.
Abbildung 9.6: Dichtefunktionen der Normalverteilung µ = 5 und µ = 6 und
gleichem σ 2 = 1
0.5
0.4
dnorm(x, 5)
0.3
0.2
0.1
0.0
2
4
6
8
10
x
Wir sehen, dass die Gestalten der Dichtefunktionen identisch sind und die
Dichtefunktion mit dem größeren Erwartungswert nach rechts verschoben ist.
Abbildung 9.7 zeigt die Dichtefunktionen von zwei Normalverteilungen mit
identischem Erwartungswert und unterschiedlichen Varianzen.
Abbildung 9.7: Dichtefunktionen der Normalverteilung σ 2 = 1 und σ 2 = 4
und gleichem µ = 5
0.5
0.4
dnorm(x, 6, 1)
0.3
0.2
0.1
0.0
0
2
4
6
8
10
12
x
Wir sehen, dass die Dichtefunktion mit der kleineren Varianz viel flacher ist.
9.2. STETIGE VERTEILUNGSMODELLE
219
Beispiel 81
In Tabelle 2.10 auf Seite 63 ist die Verteilung der Körpergröße von männlichen Studienanfängern zu finden. In Abbildung 9.8 ist neben dem Histogramm noch die Dichtefunktion der Normalverteilung mit den Parametern
µ = 183.1 und σ 2 = 48.7 eingezeichnet. Wir sehen, dass die Normalverteilung
ein geeignetes Modell für die Körpergröße ist.
Abbildung 9.8: Histogramm der Körpergröße von männlichen Studienanfängern mit Dichtefunktion der Normalverteilung mit den Parametern µ = 183.1
und σ 2 = 48.7
0.07
0.06
0.05
Density
0.04
0.03
0.02
0.01
0.00
160
170
180
190
200
Groesse
Die Verteilungsfunktion FX (x) kann nicht in expliziter Form angegeben werden. Um Wahrscheinlichkeiten zu bestimmen, benötigt man also Tabellen. Es
muss aber nicht jede Normalverteilung tabelliert werden, sondern es reicht
aus, Tabellen der Standardnormalverteilung zu besitzen.
Ist nämlich X normalverteilt mit den Parametern µ und σ 2 , so ist
Z=
X −µ
σ
standardnormalverteilt. Wir wollen diese Beziehung nicht beweisen, sondern
ihre Konsequenzen aufzeigen. Dabei bezeichnen wir die Dichtefunktion einer
standardnormalverteilten Zufallsvariablen Z mit φ(z) und dieVerteilungsfunktion mit Φ(z). Es gilt also
1
2
φ(z) = √ e−0.5 z
2π
(9.14)
KAPITEL 9. VERTEILUNGSMODELLE
220
und
z
Φ(z) =
−∞
1
2
√ e−0.5 u du
2π
(9.15)
Wir suchen für eine mit den Parametern µ und σ 2 normalverteilte Zufallsvariable folgende Wahrscheinlichkeit:
P (X ≤ x) = FX (x)
Es gilt
FX (x) = Φ
x−µ
σ
(9.16)
Dies sieht man folgendermaßen:
FX (x) = P (X ≤ x) = P (X − µ ≤ x − µ) = P
x−µ
x−µ
=Φ
= P Z≤
σ
σ
X −µ
x−µ
≤
σ
σ
Man muss die Verteilungsfunktion der Standardnormalverteilung nur für positive oder negative Werte von z tabellieren. Es gilt nämlich
Φ(z) = 1 − Φ(−z)
.
(9.17)
Beispiel 82
Die Fahrzeit X eines Studenten zur Universität ist normalverteilt mit Erwartungswert 40 und Varianz 4. Wie groß ist die Wahrscheinlichkeit, dass er
höchstens 36 Minuten braucht?
Gesucht ist P (X ≤ 36). Es gilt
36 − 40
= Φ(−2) .
P (X ≤ 36) = FX (36) = Φ
2
Tabelle C.1 auf Seite 434 entnehmen wir Φ(2) = 0.977. Also gilt
P (X ≤ 36) = Φ(−2) = 1 − Φ(2) = 1 − 0.977 = 0.023 .
9.2. STETIGE VERTEILUNGSMODELLE
221
Mit Hilfe von Gleichung (6.23) auf Seite 172 können wir das p-Quantil xp
einer mit den Parametern µ und σ 2 normalverteilten Zufallsvariablen aus
dem p-Quantil zp der Standardnormalverteilung folgendermaßen bestimmen:
xp = µ + zp σ
Man muss die Quantile der Standardnormalverteilung nur für Werte von p
tabellieren, die kleiner als 0.5 oder größer als 0.5 sind, da gilt
zp = −z1−p
(9.18)
Beispiel 82 (fortgesetzt)
Welche Fahrzeit wird an 20 Prozent der Tage nicht überschritten? Gesucht ist
x0.2 . Es gilt z0.2 = −z0.8 . Tabelle C.3 auf Seite 437 entnehmen wir z0.8 = 0.842.
Also gilt z0.2 = −0.842. Somit erhalten wir
x0.20 = 40 + z0.20 · 2 = 40 − 0.842 · 2 = 38.316 .
Bei der Tschebyscheff-Ungleichung haben wir Intervalle der Form
[µ − k σ, µ + k σ]
(9.19)
betrachtet. Man nennt das Intervall in Gleichung (9.19) auch das k-fache zentrale Schwankungsintervall. Die Wahrscheinlichkeit für das k-fache zentrale
Schwankungsintervall bei Normalverteilung ist
P (µ − k σ ≤ X ≤ µ + k σ) = Φ(k) − Φ(−k)
.
In der Tabelle 9.5 sind die Wahrscheinlichkeiten
P (µ − k σ ≤ X ≤ µ + k σ)
bei Normalverteilung den unteren Schranken gegenübergestellt, die sich aus
der Tschebyscheff-Ungleichung ergeben.
KAPITEL 9. VERTEILUNGSMODELLE
222
Tabelle 9.5: Wahrscheinlichkeiten des k-fachen zentralen Schwankungsintervalls bei Normalverteilung und Tschebyscheff
9.2.3
k
N (µ, σ 2 )
Tschebyscheff
1
2
3
0.683
0.954
0.997
0
0.750
0.889
Die Exponentialverteilung
Kommen wir noch einmal zum Poisson-Prozess zurück. Bei einem PoissonProzess im Intervall (0, t] ist die absolute Häufigkeit des Ereignisses A poissonverteilt mit Parameter λt.
Es gilt also
(λt)x −λt
e
für x = 0, 1, . . . .
P (X = x) =
x!
Wir wollen nun einen Poisson-Prozess so lange beobachten, bis A zum ersten
Mal eintritt. Gesucht ist Dichtefunktion fT (t) und die Verteilungsfunktion
FX (x) der Wartezeit T bis zum ersten Eintreten von A. Für t < 0 gilt
FT (t) = 0.
Für t ≥ 0 gilt:
FT (t) = P (T ≤ t) = 1 − P (T > t) = 1 − P (X = 0) = 1 − e−λt
Somit gilt:
FT (t) =
1 − e−λt für t > 0
0
sonst
Da die erste Ableitung der Verteilungsfunktion gleich der Dichtefunktion ist,
erhalten wir folgende
Definition 9.8
Die Zufallsvariable X heißt exponentialverteilt mit Parameter λ, wenn ihre
Dichtefunktion gegeben ist durch:
λ e−λx
fX (x) =
0
für x > 0
sonst
(9.20)
9.2. STETIGE VERTEILUNGSMODELLE
223
Abbildung 5.5 auf Seite 157 zeigt die Dichtefunktion der Exponentialverteilung mit λ = 1. Die Exponentialverteilung ist eine rechtsschiefe Verteilung.
Es gilt
E(X) =
1
λ
und
V ar(X) =
1
λ2
Für das p-Quantil der Exponentialverteilung gilt
xp = −
1
ln (1 − p)
λ
.
(9.21)
Wir erhalten Gleichung (9.21) folgendermaßen:
1 − e−λxp = p ⇔ e−λxp = 1 − p ⇔ −λxp = ln (1 − p) ⇔ xp = −
1
ln (1 − p)
λ
Beispiel 83
Bayer und Jankovic beobachteten im Rahmen eines BI-Projektes 30 Minuten eine Tankstelle und bestimmten die Zeiten zwischen den Ankünften von
Kunden. Tabelle 9.6 zeigt die Häufigkeitstabelle.
Tabelle 9.6: Häufigkeitstabelle der Zwischenankunftszeiten an einer Tankstelle
Zeit
von
von
von
von
von
absolute
Häufigkeit
0 bis unter 45
45 bis unter 90
90 bis unter 135
135 bis unter 180
180 bis unter 225
19
8
2
2
1
Abbildung 9.9 zeigt das Histogramm mit der Dichtefunktion der Exponentialveretilung mit Parameter λ = 0.019. Wir sehen, dass die Anpassung gut
ist.
KAPITEL 9. VERTEILUNGSMODELLE
224
Abbildung 9.9: Histogramm der Wartezeit mit der Dichtefunktion der Exponentialveretilung mit Parameter λ = 0.019
0.015
0.010
0.005
0.000
0
50
100
150
200
250
Zeit
9.2.4
Prüfverteilungen
In der schließenden Statistik verwendet man immer wieder eine Reihe von
Verteilungen, die eine Beziehung zur Normalverteilung haben. Schauen wir
uns diese an.
Die Chi-Quadrat-Verteilung
Wir wissen, dass Z = (X − µ)/σ standardnormalverteilt ist, wenn X mit den
Parametern µ und σ 2 normalverteilt ist. Die Zufallsvariable Z 2 ist in diesem
Fall chiquadratverteilt mit k = 1 Freiheitsgraden. Man nennt den Parameter
der Chi-Quadrat-Verteilung also Freiheitsgrade.
Oft betrachtet man k unabhängige standardnormalverteilte Zufallsvariablen
Z1 , . . . , Zk . In diesem Fall ist
k
Zi2
i=1
chiquadratverteilt mit k Freiheitsgraden.
Abbildung 9.10 zeigt die Dichtefunktion der Chi-Quadrat-Verteilung mit k =
3, k = 4, k = 5 und k = 10 Freiheitsgraden.
9.2. STETIGE VERTEILUNGSMODELLE
225
Abbildung 9.10: Dichtefunktion der Chi-Quadrat-Verteilung mit k = 3, k =
4, k = 5 und k = 10 Freiheitsgraden
0.25
k=3
k=4
k=5
k=10
0.20
f(x)
0.15
0.10
0.05
0.00
0
5
10
15
20
25
x
Wir sehen, dass die Dichtefunktion der Chi-Quadrat-Verteilung mit wachsender Zahl von Freiheitsgraden immer symmetrischer wird.
Die t-Verteilung
Die Zufallsvariable Z sei standardnormalverteilt und die Zufallsvariable V
chiquadratverteilt mit k Freiheitsgraden. Sind Z und V unabhängig, so ist
die Zufallsvariable
Z
T =
V /k
t-verteilt mit k Freiheitsgraden. Abbildung 9.11 zeigt die Dichtefunktion der
t-Verteilung mit k = 1, k = 3 k = 10 Freiheitsgraden. Außerdem ist noch die
Dichtefunktion der Standardnormalverteilung eingezeichnet.
Abbildung 9.11: Dichtefunktion der t-Verteillung mit k = 1, k = 3 und
k = 10 Freiheitsgraden
0.4
N(0,1)
k=1
k=3
k=10
f(x)
0.3
0.2
0.1
0.0
−6
−4
−2
0
x
2
4
6
KAPITEL 9. VERTEILUNGSMODELLE
226
Wir sehen, dass die Dichtefunktion der t-Verteilung mit wachsender Zahl
von Freiheitsgraden der Dichtefunktion der Standardnormalverteilung immer ähnlicher wird. Die t-Verteilung mit kleiner Anzahl von Freiheitsgraden
streut mehr als die Standardnormalverteilung. Dies erkennt man auch an der
Varianz der t-Verteilung. Für k ≥ 3 gilt
V ar(T ) =
n
n−2
Die Varianz von T konvergiert gegen die Varianz der Standardnormalverteilung.
Die F -Verteilung
Bei einer Vielzahl von statistischen Verfahren werden zwei Varianzen verglichen. In diesem Fall kommt die F -Verteilung ins Spiel. Ausgangspunkt sind
hier die unabhängigen Zufallsvariablen V und W , wobei V chiquadratverteilt
mit m und W chiquadratverteilt mit n Freiheitsgraden ist. In diesem Fall ist
die Zufallsvariable
V /m
F =
W/n
F -verteilt mit m und n Freiheitsgraden.
Abbildung 9.12 zeigt die Dichtefunktion der t-Verteilung mit m = 5, n = 5,
m = 5, n = 10, m = 5, n = 50 und m = 50, n = 50 Freiheitsgraden.
Abbildung 9.12: Dichtefunktion der F -Verteillung mit m = 5, n = 5, m =
5, n = 10, m = 5, n = 50 und m = 50, n = 50 Freiheitsgraden
1.4
F(5,5)
F(5,10)
F(5,50)
F(50,50)
1.2
1.0
f(x)
0.8
0.6
0.4
0.2
0.0
1
2
3
x
4
5