zweiten

1
Lernmodul 4, Kapitel 1.4–2.5
Konstruktion
Die wichtigsten Konstruktionselemente bei der Konstruktion mit Zirkel und Lineal
sind:
1. Mittelsenkrechte zwischen zwei Punkten auf einer Geraden
2. Lot fällen: einen Punkt senkrecht auf eine Gerade projezieren
3. Winkel halbieren
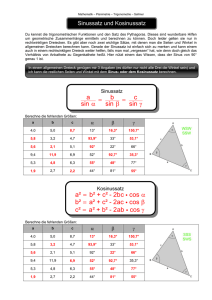
Strahlensätze
1. Strahlensatz: Werden zwei Strahlen mit einem gemeinsamen Anfangspunkt
Z von zwei Parallelen geschnitten, so verhalten sich die Abschnitte auf dem einen
Strahl wie die entsprechenden Abschnitte auf dem anderen Strahl:
ZC
ZA
=
ZD
ZB
.
Mit dem 1. Strahlensatz kann man auch folgende Beziehungen beweisen:
AC
ZA
=
BD AC
BD
,
=
.
ZB ZC
ZD
D.h. alle drei Gleichungen können für den 1. Strahlensatz verwendet werden.
2. Strahlensatz: Werden zwei Strahlen mit einem gemeinsamen Anfangspunkt Z
von zwei Parallelen geschnitten, so verhalten sich die Abschnitte auf den Parallelen
wie die entspechenden Abschnitte auf jedem der beiden Strahlen:
CD
AB
=
ZC
ZA
,
CD
AB
=
ZD
ZB
.
2
Mit den beiden Strahlensätzen sind Verhältnisse beliebiger Abschnitte möglich, d.h.
man kann z.B. folgende Beziehungen beweisen:
CD
ZC
=
AB C D
AB
,
=
.
ZA Z D
ZB
Kongruenzsätze
1. Kongruenzsatz: Dreiecke sind kongruent, wenn sie in den drei Seiten übereinstimmen (SSS).
2. Kongruenzsatz: Dreiecke sind kongruent, wenn sie in zwei Seiten und dem
eingeschlossenen Winkel übereinstimmen (SWS).
3. Kongruenzsatz: Dreiecke sind kongruent, wenn sie in einer Seite und zwei
Winkeln übereinstimmen (WSW, SWW, WWS).
4. Kongruenzsatz: Dreiecke sind kongruent, wenn sie in zwei Seiten und dem
Gegenwinkel der größeren der beiden Seiten übereinstimmen (SsW). Anders formuliert: wenn der Winkel an der kleineren der beiden Seiten liegt.
Schwerpunkt
Der Schwerpunkt einer Strecke ist logischerweise der Mittelpunkt der Strecke. Betrachten wir ein Dreieck, so können wir es jeweils parallel zu jeder Seite in dünne
Streifen zerlegen, von denen wir je den Schwerpunkt annähernd bestimmen können. Dieser ist nämlich annähernd der Mittelpunkt jedes Streifens, da er wiederum
annähernd als Strecke betrachtet werden kann. Diese Mittelpunkte liegen offenbar
jeweils auf der Seitenhalbierenden. Nun erkennen wir, dass sich die Seitenhalbierenden in einem Punkt schneiden, der der Schwerpunkt des Dreiecks sein muss.
3
Inkreismittelpunkt
Die Winkelhalbierenden eines Dreiecks treffen sich im Inkreismittelpunkt.
Um einzusehen, dass die Winkelhalbierenden zum Inkreismittelpunkt führen, betrachten wir folgendes Bild:
Hier sehen wir, dass zwei von einer Ecke des Dreiecks ausgehenden Seiten zwei
Tangenten an den Inkreis bilden. Damit gibt es je eine Linie vom Mittelpunkt
aus zu je einem Berührpunkt der jeweiligen Tangente, die jeweils senkrecht zur
Tangente ist. Da die Ecke des Dreiecks mit dem Mittelpunkt des Inkreises und je
einem Berührpunkt jeweils ein rechtwinkliges Dreieck bildet und bei den beiden
Dreiecken sowohl die Seiten d und r gleich sind, als auch der rechte Winkel jeweils
gegenüber der längsten Seite, nämlich der Hypotenuse, liegt, sind die beiden Dreiecke nach dem 4. Kongruenzsatz eindeutig bestimmt und kongruent. Also haben
sie auch den Winkel α gemeinsam und somit muss die Winkelhalbierende des Winkels zwischen den Seiten des Dreiecks durch den Mittelpunkt des Inkreises gehen.
Die Winkelhalbierende sollte nicht mit der Seitenhalbierenden verwechselt werden. Den Unterschied kann man hier sehen:
Insbesondere ist der Unterschied gut sichtbar, wenn sich die Längen der beiden
Seiten stark unterscheiden. Übrigens sind die Winkelhalbierende und die Seitenhalbierende identisch, wenn die beiden Seiten gleich lang sind.
4
Umkreismittelpunkt
Der Umkeismittelpunkt eines Dreiecks ist der Schnittpunkt der Mittelsenkrechten.
Dies kann man einsehen, wenn man überlegt, dass zwei Ecken des Dreiecks mit
dem Mittelpunkt des Umkreises ein gleichschenkliges Dreieck bilden. Da die Winkelhalbierende an der Spitze des gleichschenkligen Dreiecks gleich der Seitenhalbierenden ist (nach der Bemerkung oben) und die Seitenhalbierende senkrecht
auf der Seite steht, ist sie auch gleich der Mittelsenkrechten. Nun können die
Mittelsenkrechten auf den Seiten des Dreiecks gebildet werden, die ja durch den
Mittelpunkt des Umkreises gehen müssen und sich damit im Umkreismittelpunkt
schneiden.
Fläche und Umfang von ebenen Figuren
Für die Fläche der ebenen Figuren gilt:
Quadrat: A = a2 , Rechteck: A = a · b, Parallelogramm: A = a · h,
Dreieck: A = 21 · a · h = a·h
, Trapez: A = 12 · (a + c) · h = a+c
· h,
2
2
1
2
2
Kreis: A = π · r = 4 · π · d .
Für den Umfang der ebenen Figuren gilt:
Quadrat: U = 4 · a, Rechteck und Parallelogramm: U = 2 · (a + b),
Dreieck: U = a + b + c, Trapez: U = a + b + c + d, Kreis: U = 2 · π · r = π · d.
5
Der Satz des Pythagoras und der Satz des Thales
Ein rechtwinkliges Dreieck ist ein Dreieck, in dem ein Winkel 90◦ beträgt, in dem
also ein rechter Winkel existiert. Die beiden Seiten, die an dem rechten Winkel
liegen, heißen Katheten, die gegenüber liegende heißt Hypotenuse.
Satz des Pythagoras: In einem rechtwinkligen Dreieck ist die Summe der Quadrate der beiden Katheten gleich dem Quadrat der Hypothenuse:
a2 + b2 = c 2 .
Satz des Thales: Konstruiert man ein Dreieck aus den Endpunkten des Durchmessers eines Halbkreises und einem Punkt auf dem Halbkreis, der von den anderen
beiden verschieden ist, so erhält man stets ein rechtwinkliges Dreieck.
In der Zeichnung oben ist der Thaleskreis samt Mittelpunkt abgebildet.
Bemerkung: Um den Flächeninhalt eines rechtwinkligen Dreiecks zu berechnen,
muss keine Höhe ermittelt werden, denn die Höhe auf einer der Seiten des Dreiecks ist das Lot des übrigen Punktes des Dreiecks auf der Seite, steht also senkrecht
auf der Seite. Die beiden Katheten des rechtwinkligen Dreiecks stehen aufgrund
der Konstruktion senkrecht aufeinander und stellen jeweils zugleich das Lot einer
Ecke des Dreiecks auf der gegenüber liegenden Seite dar. Somit kann eine der
Katheten als Grundseite und die andere als Höhe des Dreiecks verwendet werden.
Der Kathetensatz
In jedem rechtwinkligen Dreieck ist das Quadrat über der Kathete inhaltsgleich
dem Rechteck, gebildet aus der Hypotenuse und dem der Kathete anliegenden
Hypotenusenabschnitt:
a2 = c · q, b2 = c · p.
6
Der Höhensatz
In jedem rechtwinkligen Dreieck ist das Quadrat über der Höhe inhaltsgleich dem
Rechteck, gebildet aus den Hypotenusenabschnitten:
h2 = p · q.
Zu den Anwendungen des Katheten- oder Höhensatzes gehören die Quadratur eines Rechtecks und umgekehrt Konstruktion eines Rechtecks aus einem Quadrat.
Winkelsätze am Kreis
Der Zentriwinkel ist doppelt so groß wie der Peripheriewinkel über dem gleichen
Bogen.
7
Peripheriewinkel über dem gleichen Bogen sind gleich groß.
Anmerkung: Für den Fall, dass der Bogen ein Halbkreis ist, d.h. der Zentriwinkel
µ = 180◦ , ist der Peripheriewinkel über dem Halbkreis 90◦ . Also ist das Dreieck,
gebildet aus Durchmesser und den beiden Schenkeln des Peripheriewinkels, rechtwinklig (⇒ Satz des Thales).
Winkelsumme eines n-Ecks
Die Summe der Innenwinkel eines (nichtausgearteten) n-Ecks (d.h. ohne sich
schneidenden Seiten) beträgt (n − 2) · 180◦ .
Sehnen- und Tangentenviereck
Ein Viereck, das einen Umkreis hat, heißt Sehnenviereck.
Ein Viereck, das einen Inkreis hat, heißt Tangentenviereck.
In jedem Sehnenviereck beträgt die Summe von zwei gegenüber liegenden Winkeln 180◦ .
In jedem Tangentenviereck sind die Summen der Gegenseiten gleich.
Kreissektor
Die Fläche eines Kreissektors mit Winkel α wird berechnet durch:
A = πr 2 ·
α
360◦
.
Die Länge L eines Kreisbogens eines Kreissektors mit Winkel α wird berechnet
durch:
α
L = 2πr ·
.
360◦
8
Trigonometrische Funktionen
Trigonometrische Funktionen sind Verhältnisse je zweier Seiten in einem rechtwinkligen Dreieck zu einander und zu einem der beiden Winkeln (den rechten
Winkel ausgenommen). Somit haben sie also immer einen Winkel als Argument:
sin α, cos α, tan α.
Sie heißen Sinus, Kosinus und Tangens.
Hierbei bekommen die Seiten Namen. Wir haben bereits Namen für die Seiten in
einem rechtwinkligen Dreieck, nämlich Hypotenuse (liegt gegenüber dem rechten
Winkel) und Katheten (liegen beide an dem rechten Winkel). Da die trigonometrischen Funktionen sich immer auf einen bestimmten Winkel beziehen, können
die Katheten hier unterschieden werden, nämlich Gegenkathete (die gegenüber
dem Winkel liegt) und Ankathete (die an dem Winkel liegt). Genauer sind diese
Funktionen so definiert:
sin α =
Gegenkathete
=
a
,
Hypotenuse
c
Ankathete
b
= ,
cos α =
Hypotenuse
c
Gegenkathete a
sin α
tan α =
= =
.
Ankathete
b cos α
Die Graphen zu den Funktionen:
Wie man unschwer erkennen kann, unterscheiden sich Sinus und Kosinus nur
durch eine Verschiebung um 90◦ . Deshalb kann man direkt die Formeln
sin α = cos(α − 90◦ ), cos α = sin(α + 90◦ )
9
folgern. Wegen der Punkt-Symmetrie von sin α und der Achsen-Symmetrie von
cos α gilt auch
sin α = sin(180◦ − α), cos α = − cos(180◦ − α).
Dies ist nicht schwer einzusehen, wenn man sich die Graphen genau anschaut.
Betrachten wir nun den Einheitskreis, d.h. Kreis mit Radius 1 um den Nullpunkt. Jeder Punkt auf dem Einheitskreis kann mit trigonometrischen Funktionen beschrieben werden, und zwar hat der Punkt P(x 0 | y0 ) die Koordinaten
y
x0
= x 0 = cos α, 10 = y0 = sin α. Mit Pythagoras folgt dann
1
sin2 α + cos2 α = 1.
Diese Gleichung ist auch als Trigonometrischer Pythagoras bekannt.
Sinussatz
In einem beliebigen (nichtausgearteten) Dreieck verhalten sich die Dreiecksseiten
wie die Sinuswerte ihrer gegenüber liegenden Winkel:
a
b
=
sin α a sin α b sin β
, =
, =
.
sin β c
sin γ c
sin γ
Oder, das Verhältnis einer Seite zum Sinus ihres gegenüber liegenden Winkels ist
konstant, d.h.:
a
b
c
=
=
.
sin α sin β
sin γ
Man beachte, dass bei der Anwendung des Sinussatzes die Symmetrie-Eigenschaft
des Sinus berücksichtigt werden muss, d.h. zu einem Ergebnis α muss auch 180◦ −
α untersucht werden. Denn es gilt ja sin α = sin(180◦ −α). Die Taschenrechner z.B.
berechnen immer den kleinsten nichtnegativen Winkel, der zu einem Sinuswert
gehört.
10
Kosinussatz
In einem beliebigen (nichtausgearteten) Dreieck ist das Quadrat über einer Seite
gleich der Summe der Quadrate über den anderen beiden Seiten, vermindert um
das doppelte Produkt dieser beiden Seiten und des Kosinus des von ihnen eingeschlossenen Winkels:
a2 = b2 + c 2 − 2bc cos α,
b2 = a2 + c 2 − 2ac cos β,
c 2 = a2 + b2 − 2ab cos γ.
Also ist der Kosinussatz eine Verallgemeinerung des Satzes des Pythagoras.
Bogenmaß
Das Bogenmaß (auch bekannt als Radiant) ist ein anderes Maß für einen Winkel.
Dabei wird ein Winkel mit der Länge des Bogens des Einheitskreises gemessen. Da
der Umfang des Einheitskreises 2π beträgt, entspricht 360◦ also 2π im Bogenmaß.
Man kann selbstverständlich auch umrechnen. Sei α in Grad und ϕ der gleiche
Winkel in Bogenmaß:
α=ϕ·
180◦
π
⇔ ϕ =α·
π
180◦
.
Additionstheoreme
Es gilt:
sin(α + β) = sin α cos β + sin β cos α,
cos(α + β) = cos α cos β − sin α sin β,
tan α + tan β
tan(α + β) =
.
1 − tan α tan β
Beweis eines Winkelsatzes am Kreis
Der Zentriwinkel ist doppelt so groß wie der Peripheriewinkel über dem gleichen
Bogen.
Beweis.
Da Peripheriewinkel über dem gleichen Bogen gleich groß sind, können wir die
Problemsituation auf die folgende reduzieren:
11
µ
ϕ
Zu zeigen ist also µ = 2ϕ. Bequemlichkeithalber setzen wir ϕ 0 = 2 , µ0 = 2 . Also
brauchen wir nur µ0 = 2ϕ 0 zu beweisen. Nehmen wir nun an, es gilt µ0 = 2ϕ 0 . Aus
der Zeichnung oben folgt:
tan µ0 =
x
y
, tan ϕ 0 =
x
r+y
, cos µ0 =
y
r
.
Diese drei Gleichungen stellen eine Beziehung zwischen ϕ und µ her. Eine Kombination der Gleichungen darf also nicht im Widerspruch enden, wenn der Satz
gilt und wir die Gleichheit µ0 = 2ϕ 0 verwenden. Durch geschickte Kombinationen
erhalten wir:
tan µ0 =
(r + y) tan ϕ 0
y
⇔ tan µ0 =
⇔ sin µ = (1 + cos µ ) tan ϕ
0
0
⇔
cos ϕ 0
sin ϕ 0
=
0
⇔
(r + r cos µ0 ) tan ϕ 0
r cos µ0
sin µ0
1 + cos µ0
1 + cos2 ϕ 0 − sin2 ϕ 0
2 sin ϕ 0 cos ϕ 0
=
=
sin ϕ 0
cos ϕ 0
=
⇔
2 cos2 ϕ 0
2 sin ϕ 0 cos ϕ 0
(1 + cos µ0 ) tan ϕ 0
cos µ0
1 + cos µ0
sin µ0
=
cos ϕ 0
sin ϕ 0
=
cos ϕ 0
sin ϕ 0
.
... was die Annahme µ = 2ϕ beweist. Wir haben in der letzten Zeile die Additionstheoreme von Sinus und Kosinus und µ0 = ϕ 0 + ϕ 0 verwendet. Zudem haben
wir den trigonometrischen Pythagoras 1 = sin2 ϕ 0 + cos2 ϕ 0 gebraucht.
12
Übungen
Aufgabe 1
a) Konstruieren Sie ein Dreieck mit a = 5cm, b = 2cm und c = 4cm.
b) Konstruieren Sie ein Dreieck mit a = 7cm, α = 40◦ und γ = 55◦ .
c) Konstruieren Sie ein Dreieck mit b = 4cm, c = 3cm und α = 65◦ .
d) Konstruieren Sie ein Dreieck mit a = 6.5cm, c = 3.5cm und α = 70◦ .
Aufgabe 2
Konstruieren Sie den Schwerpunkt zum Dreieck aus 1a), den Inkreis zum Dreieck
aus 1c) und Umkreis zum Dreieck aus 1d).
Aufgabe 3
Berechnen Sie die Fläche einer sechseckigen Grundfläche mit den gegebenen Maßen in Meter. Geben Sie das Ergebnis in Ar an (1Ar = 100m2 ).
Aufgabe 4
Konstruieren Sie ein rechtwinkliges Dreieck mit c = 7cm und b = 4cm und berechnen Sie die Fläche.
Aufgabe 5
Konstruieren Sie aus einem Quadrat mit 4cm × 4cm ein flächengleiches Rechteck
mit a = 3cm einmal mit dem Kathetensatz und einmal mit dem Höhensatz.
(Konstruieren Sie aus einem Rechteck mit a = 5cm und b = 3cm ein flächengleiches Quadrat.)
Aufgabe 6
Konstruieren Sie die beiden Tangenten an einen Kreis mit Radius r = 5cm durch
einen Punkt außerhalb des Kreises, der etwa 7cm von der Kreislinie entfernt ist.
Dabei sei der Mittelpunkt des Kreises nicht gegeben.
13
Aufgabe 7
Wie groß ist die Summe der Innenwinkel eines regelmäßigen Neunecks.
Aufgabe 8
Ein Viereck habe einen Umkreis von 12cm Durchmesser. Was ergibt die Summe
α + γ zweier Winkel im Viereck?
Aufgabe 9
Ein Viereck habe einen Inkreis mit Radius r = 4cm. Was ergibt die Summe a − b +
c − d der Seiten des Vierecks?
Aufgabe 10
Berechnen Sie die restlichen Teile der Dreiecke aus Aufgabe 1. Benutzen Sie dabei
sowohl den Sinussatz als auch den Kosinussatz. Nicht jede Situation kann man mit
beiden Sätzen lösen.
14
Lösungen
Aufgabe 3
p
.
.
x = 2 2502 − 2002 = 300m, y = 505.59m, h = 178.01m, A =
y·h
2
300·200
2
+
500·75
2
+
= 93750m = 937.5Ar.
Zu h: Eine der schnellsten Methoden h auszurechnen, ist zuerst mit dem Kosinussatz α auszurechnen und dann mit Sinus von α schließlich h zu ermitteln (h ist ja
Gegenkathete):
2502 − 3752 − y 2 .
.
= 28.34◦ , h = 375 · sin α = 178.01.
α = arccos
−2 · 375 · y
2
Aufgabe 4
Konstruiert wird das Dreieck mit dem Satz des Thales: Zuerst zeichnet man eine
Gerade, trägt zwei Punkte im Abstand von 7cm ein, konstruiert den Mittelpunkt
zwischen den beiden Punkten und schlägt einen Halbkreis um den Mittelpunkt.
Dann schlägt man um den linken Punkt einen Teilkreis mit Radius 4cm, so dass
man einen Schnittpunkt mit dem Halbkreis erhält. Jetzt verbindet man die zwei
äußeren Punkte des Durchmessers je mit dem Schnittpunkt und ist somit fertig.
Um die Fläche zu berechnen, braucht man eine Höhe auf einer der drei Seiten. Am
besten eignen sich die Seiten a und b, da sie auf einander senkrecht stehen und
somit gleichzeitig auch Höhe der jeweils anderen Seite darstellen. Also:
a=
Aufgabe 5
p
.
.
c 2 − b2 = 5.74cm, A = 22.98cm2 .
15
Aufgabe 6
Aufgabe 7
(n − 2) · 180◦ = 7 · 180◦ = 1260◦ .
Aufgabe 8
Da α und γ einander gegenüber liegen, ist die Antwort 180◦ .
Aufgabe 9
Da hier die Summe zweier gegenüber liegenden Seiten von der Summe der anderen beiden gegenüber liegenden Seiten abgezogen werden, ergibt sich 0cm.
Aufgabe 10
1a) Man berechne einen Winkel mit dem Kosinussatz und die restlichen mit dem
Sinussatz, da er einfacher zu handhaben ist, bzw. durch Winkelsumme:
2
a − b2 − c 2 .
b sin α .
.
◦
α = arccos
= 108.21 , β = arcsin
= 22.33◦ , γ = 130.54◦ .
−2bc
a
1b)
β = 85◦ , b =
a sin β .
a sin γ .
= 10.85cm, c =
= 8.92cm.
sin α
sin α
1c)
a=
p
.
b + c − 2bc cos α = 3.85cm, β = arcsin
2
2
1d)
γ = arcsin

c sin α
a
‹
b sin α
a
.
.
= 70.14◦ , γ = 44.86◦ .
a sin β .
.
.
= 30.4◦ , β = 79.6◦ , b =
= 6.8cm.
sin α
16
Lernmodul 4, K. 2.6–3.5 + Lernmodul 5, K. 1.1–1.3
Winkel zwischen Gerade und Ebene
Wir wissen bereits wie Winkel zwischen zwei Geraden gemessen werden. Wie
misst man aber einen Winkel zwischen Gerade g und Ebene E? Nun, eine Ebene
besteht aus unendlich vielen Geraden. Offensichtlich sind für uns nur die interessant, die durch den Schnittpunkt P von g mit E verlaufen. Von diesen hat eine
Gerade eine besondere Eigenschaft: sie ist die senkrechte Projektion g 0 von g auf
E (wenn g nicht senkrecht zu E ist; im Fall g senkrecht zu E können wir eine
beliebige Gerade in der Ebene durch P betrachten — jede ist zu g senkrecht). Unter einem Winkel zwischen einer Geraden g und einer Ebene E verstehen wir den
Winkel zwischen g und g 0 .
Winkel zwischen zwei Ebenen
Zwei Ebenen E1 und E2 schneiden sich in einer Gerade g. Offenbar interessieren
uns die Geraden in beiden Ebenen, die durch den gleichen Punkt P auf g verlaufen
und jeweils zu g senkrecht sind. Diese beiden Geraden g1 und g2 von E1 und E2
sind eindeutig bestimmt. Unter einem Winkel zwischen zwei Ebenen E1 und E2
verstehen wir den Winkel zwischen g1 und g2 .
Volumen und Oberfläche von Prismen
Als prismatische Körper bezeichnet man Körper, deren Querschnitt konstant ist,
also gleich bleibt. Sie werden unterteilt in gerade und schiefe Prismen. In beiden
Fällen berechnet sich Oberfläche und Volumen wie folgt, wobei G die Grundfläche,
M die Mantelfläche und h die Höhe des Prismas bezeichnet:
O = 2G + M , V = G · h.
Verschiedene Körper
Quader: Das Volumen eines Quaders berechnet sich ähnlich wie die Fläche eines
Rechtecks, also
V = a · b · c.
Die Oberfläche ist die Summe aller Flächen, die den Quader begrenzen, also
O = 2 · a · b + 2 · a · c + 2 · b · c = 2 · (a · b + a · c + b · c).
17
Würfel: Ein Würfel ist ein spezieller Quader, bei dem alle Seiten gleich lang sind.
Also:
V = a3 , O = 6 · a2 .
Prisma: Ein Prisma, oder auch Säule genannt, besteht im Kern aus einer Fläche,
die eine beliebige vieleckige ebene Figur sein kann. Diese Grundläche G begrenzt
das Prisma von zwei gegenüber liegenden Seiten, welche parallel zu einander sind.
Jeder Querschnitt parallel zur Grundfläche ist wieder die Grundfläche.
Beispiele: Dreiecksprisma, Sechsecksprisma, Trapez-Prisma.
Das Volumen berechnet sich immer gleich:
V = G · t.
Hierbei ist G die Grundfläche und t die Tiefe oder die Höhe des Prismas.
Beispiel Trapez-Prisma:
G=
a+c
2
· h, V = G · t ⇒ V =
a+c
2
· h · t.
Die Oberfläche besteht aus zwei Grundflächen und der Mantelfläche, die mit dem
Umfang U der Grundfläche zusammenhängt:
O = 2 · G + M, G =
a+c
2
· h, M = U · t, U = a + b + c + d
⇒ O = (a + c) · h + (a + b + c + d) · t.
Zylinder: Ein Zylinder ist einem Prisma sehr ähnlich. Die Grundfläche begrenzt
den Körper von zwei gegenüber liegenden Seiten und jeder Querschnitt parallel zu
der Grundfläche ist die Grundfläche. Beim Zylinder ist die Grundfläche aber ein
Kreis. Volumen und Oberfläche berechnen sich wie beim Prisma:
V = G · t, O = 2 · G + M , G = π · r 2 , M = U · t, U = 2 · π · r
⇒ V = π · r 2 · t, O = 2 · π · r 2 + 2 · π · r · t = 2πr(r + t).
Pyramide: Eine Pyramide ist ein spitzer Körper mit einer beliebigen vieleckigen
ebenen Figur als Grundfläche. Der bekannteste Typ ist die quadratische Pyramide.
Eine Pyramide hat eine Grundfläche G, eine Höhe h und eine Seitenlänge s.
Betrachten wir die quadratische Pyramide mit Seitenlänge a der Grundfläche:
V=
1
3
· G · h, G = a2 ⇒ V =
1
· a2 · h,
3
v
a 2
t
p
1
2
2
O = G + M, G = a , M = 4 · · a · h +
= a · 4 · h2 + a2
2
2
p
⇒ O = a2 + a · 4 · h2 + a2 .
Tetraeder: Ein Tetraeder ist einer Dreieckspyramide sehr ähnlich, besteht aber
grundsätzlich aus vier gleichseitigen Dreiecken und gehört zu den Platonischen
18
Körpern. Er ist also eine spezielle Dreieckspyramide. Da für die Fläche eines gleichseitigen Dreiecks gilt
p
3 2
a ,
G=
4
und die Höhe des Tetraeders
Oberfäche:
1
p a
2 3
V=
beträgt, ergibt sich für das Volumen und die
1
a3 , O =
p 2
3a .
24
Kegel: Ein Kegel ist einer Pyramide ähnlich. Er hat eine kreisförmige Grundfläche.
Ansonsten wird er wie eine Pyramide behandelt:
V=
1
3
· G · h, G = π · r 2 ⇒ V =
1
3
· π · r 2 · h,
O = G + M , G = π · r 2 , M = π · r · s ⇒ O = π · r 2 + π · r · s = πr(r + s).
Kegelstumpf: Ein Kegelstumpf ist ein Kegel, bei dem die Spitze abgeschnitten ist.
Man verwendet hier das Wissen über den Kegel und leitet Formeln für den Kegelstumpf her.
Zuerst konstruieren wir zu dem Kegelstumpf den ganzen Kegel. Dazu setzen wir
die Radien mit den Höhen ins Verhältnis und erhalten die Höhe h1 des zu konstruierenden Kegels. Nach dem zweiten Strahlensatz gilt:
h1 − h
h1
=
r2
r1
⇔
h1 − h r1 = h1 r2 ⇔ h1 r1 − hr1 = h1 r2
⇔ h1 r1 − h1 r2 = hr1 ⇔ h1 r1 − r2 = hr1 ⇔ h1 =
hr1
r1 − r2
.
Definieren wir nun die Höhe der fehlenden Kegelspitze h2 = h1 − h. Somit gilt für
das Volumen:
V=
1
3
· π · r12 · h1 −
h2 =
hr1
1
3
· π · r22 · h2 =
−h=
1
3
· π · r12 · h1 − r22 · h2 , h1 = r1
hr1 − h r1 − r2
=
h r1 − r1 + r2
= r2
h
r1 − r2
,
h
.
r1 − r2
r1 − r2
r1 − r2
r1 − r2
1
h
h
1
h
⇒ V = · π · r12 · r1
− r22 · r2
= ·π·
· r13 − r23 .
3
r1 − r2
r1 − r2
3
r1 − r2
Nach der Umformung
V=
1
3
·π·h·
r13 − r23
r1 − r2
kann nun die Polynomdivision angewendet werden und aus dem Bruch rechts wird
r12 + r22 + r1 r2 :
1
V = · π · h · r12 + r1 r2 + r22 .
3
19
Für die Oberfläche müssen wir zuerst die Seitenlängen s1 des konstruierten Kegels
und s2 der Kegelspitze berechnen:
v
Ç
v
2
2
u 2
2 2
u
2 2
q
u
r
r
−
r
+ h2
r
r
−
r
+
h
r
h
r
1
1
2
1
2
1
1
t 2
1
t
2
2
,
s1 = r1 + h1 = r1 +
=
2 =
2
r1 − r2
r1 − r2
r1 − r2
wieder mit einem Strahlensatz (diesmal mit dem ersten) erhält man
r1
s1
s2
=
h1
h2
⇔ s1 h2 = h1 s2 ⇔ s2 =
also
s2 =
r2
Ç
r1 − r2
s1 h2
h1
2
r1 − r2
( r1 −r2 )
2
+h2
r1 −r2
=
+ h2
r
r2 r
h
1 −r2
r1 r
h
1 −r2
,
.
Wir erhalten also
O = G + M + A, G = π · r12 , M = π · r1 · s1 − π · r2 · s2 , A = π · r22
⇒ O = π · r12 + π · r1 · s1 − π · r2 · s2 + π · r22 = π · r12 + r1 · s1 − r2 · s2 + r22 ,
und somit

O = π ·  r12 + r1 ·

= π ·  r12 +
r12
r1
Ç
r1 − r2
2
+h
2
r1 − r2
−
r22
= π · r12 + r1 + r2
Ç
r1 − r2
2
r1 − r2
r
r1 − r2
2
− r2 ·
+h
2
r2
Ç
r1 − r2
2
+h
2
r1 − r2

+ r22 

+ r22 
+ h2 + r22 .
Der letzte Schritt war mit der dritten Binomischen Formel möglich.
Kugel: Kommen wir nun zum schwierigsten der bisher behandelten Körper. Hier
muss man einige Tricks anwenden, um das Volumen und die Oberfläche herzuleiten. Zuerst das Volumen:
20
Stellen wir uns vor, die obere Halbkugel wäre mit 4, 9, 19, 39, usw. Zylindern
gefüllt (wie in der Zeichnung). Je kleiner man die Höhe der Zylinder wählt, desto
mehr Zylinder passen in die Halbkugel und desto näher kommt man dem Volumen
der Halbkugel. Wir teilen die Höhe in n gleiche Teile (in der Zeichnung n = 5). Wir
können dann folgende Formel für die Zylinder in der Halbkugel aufstellen (wobei
Gi die Grundfläche und hi die Höhe jedes i-ten Zylinders darstellt):
G
G
G
}|1
{ h1
z
}|2
{ h2
}|n
{ hn
z
 ‹2 z}|{
 ‹2 z}|{
 ‹2 z}|{
n
1
1
1
2
1
Vn
= π r2 −
r
r + π r2 −
r
r + . . . + π r2 −
r
r
2
n
n
n
n
n
n
 ‹2  ‹2 1
1
n
2
2
=π r
r −
r
+ ... + r −
r
n
n
n
1
n2 2
12 2
2
2
= πr
r − 2 r + ... + r − 2 r
n
n
n

2
2
‹
1
1 2
1
n
1
3
2
2
3
= πr
n − 2 1 + 2 + ... + n
.
1 − 2 + ... + 1 − 2
= πr
n
n
n
n
n
z
Für die Summe 12 + 22 + . . . + n2 gibt es eine Formel:
n
X
k=0
k2 = 12 + 22 + . . . + n2 =
n(n + 1)(2n + 1)
6
.
Somit erhalten wir:

‹
1
Vn
1
1 2
1 n(n + 1)(2n + 1)
2
2
3
3
= πr
= πr
n − 2 1 + 2 + ... + n
n− 2 ·
2
n
n
n
n
6
3
2
2
3
2
2n + n + 2n + n
2n + 3n + n
1
1
3
n−
=
πr
n
−
= πr 3
n
6n2
n
6n2
2n3 3n2
n
2n3 3n2
n
1
3
3
n − 2 − 2 − 2 = πr 1 − 3 − 3 − 3
= πr
n
6n
6n
6n
6n
6n
6n

‹

‹
2
3
1
1
1
1
= πr 3 1 − −
− 2 = πr 3 1 − −
− 2 .
6 6n 6n
3 2n 6n
Das ist also die Formel für das Volumen der Zylinder in der oberen Halbkugel. Es
sind n Zylinder, wobei wir n beliebig erhöhen können, um immer näher an das
Volumen der Halbkugel zu kommen. Wir lassen also n gegen Unendlich laufen.
Dafür gibt es in der Mathematik einen Begriff: der Limes. Der Limes ist der Grenzwert, dem sich eine Folge von Zahlen nähert, wenn die Folge gegen Unendlich
läuft. Also ergibt sich:

‹

‹
V
1
1
1
1
2 2
3
3
= lim πr 1 − −
− 2 = πr 1 −
= πr 3 · = πr 3 .
2 n→∞
3 2n 6n
3
3 3
Hierbei sind die Terme, die n im Nenner enthalten, weggefallen, da sie für n → ∞
gegen 0 laufen. Da es nur eine Halbkugel war, erhalten wir für das Volumen der
21
Kugel:
4
V = πr 3 .
3
Für die Oberfläche stellen wir uns vor, die Kugel wäre mit quadratischen Pyramiden, je mit Höhe r, gefüllt (wie in der Zeichnung oben). Dann füllen die Pyramiden
einerseits das Volumen der Kugel, andererseits pflastern die Grundflächen der Pyramiden die gesamte Oberfläche. Mit der Formel für die quadratische Pyramide
erhalten wir also:
1
1
1
1
Vn = G1 r + G2 r + . . . + Gn r = r G1 + G2 + . . . + Gn .
3
3
3
3
Bei Betrachtung des Limes ergibt sich:
1
r G1 + G2 + . . . + Gn = r · O
n→∞ 3
3
V = lim Vn = lim
n→∞
⇔ V=
1
1
r ·O ⇔ O =
3
Also gilt für die Oberfläche der Kugel:
3
r
V=
3 4 3
· πr = 4πr 2 .
r 3
O = 4πr 2 .
Rotationskörper
Rotationskörper sind Körper, die durch Drehung einer Fläche um eine Drehachse
entstehen. Hierzu gehören z.B. Reifen (Torus) und Hohlkörper eines Zylinders.
Der letztere entsteht durch Drehung eines Rechtecks um eine Drehachse, wobei
eine Seite des Rechtecks parallel zur Drehachse ist.
1. Guldinsche Regel: Die Mantelfläche M eines Rotationskörpers ist das Produkt
aus der Länge l der erzeugenden Linie m und dem Weg 2πrS des Schwerpunktes
S der erzeugenden Linie bei einer Umdrehung um die Drehachse:
M = 2πrS l.
2. Guldinsche Regel: Das Volumen eines Rotationskörpers ist das Produkt aus
dem Flächeninhalt A der erzeugenden Fläche und dem Weg 2πrS des Schwerpunktes S der erzeugenden Fläche bei einer Umdrehung um die Drehachse:
V = 2πrS A.
22
Vektor
Ein Vektor ist ein mathematisches Hilfsmittel in Gebieten, in denen Zahlen Situationen nicht exakt genug beschreiben. Z.B. stellen die reellen Zahlen einen 1dimensionalen Raum dar. In der Physik hat z.B. Kraft die Eigenschaft, dass sie eine
Richtung im Raum hat, d.h. 3-dimensional ist. Um Situationen wie diese zu beschreiben, verwendet man Vektoren.
Ein Vektor wird definiert durch eine bestimmte Anzahl von Koordinaten, die Dimension des Vektors genannt wird. Jede Koordinate wird üblicherweise mit reellen
Zahlen beschrieben. Darstellen kann man einen Vektor im gewöhnlichen Koordinatensystem als ein Pfeil. Ein Vektor hat eine bestimmte Länge, einen Winkel zu
einer der Koordinatenachsen, eine Richtung (also eine Orientierung) und einen Anfangspunkt. Desweiteren verstehen wir unter einem Vektor die Menge aller Pfeile,
die gleiche Richtung, gleiche Länge und gleiche Orientierung haben. Einen beliebigen Pfeil aus dieser Menge nennt man einen Repräsentanten des Vektors. Der
Standard-Repräsentant ist der mit dem Anfangspunkt im Ursprung. Es gibt zwei
grundsätzliche Schreibweisen von Vektoren, nämlich Spaltenvektoren und Zeilenvektoren. Meistens verstehen wir unter einem Vektor einen Spaltenvektor.
Addition und Subtraktion von Vektoren
Geometrisch: Zwei Vektoren werden addiert, indem der Anfangspunkt des zweiten Vektors an die Spitze des ersten Vektors gehängt wird. Der Summenvektor
zeigt vom Anfangspunkt des ersten Vektors zur Spitze des zweiten.
Zwei Vektoren werden subtrahiert, indem die Spitze des zweiten Vektors an die
Spitze des ersten Vektors gehängt wird. Der Differenzvektor zeigt vom Anfangspunkt des ersten Vektors zum Anfangspunkt des zweiten.
Rechnerisch: Zwei Vektoren u
~ und ~
v werden komponentenweise addiert oder subtrahiert:
 ‹
 ‹

‹
ux
vx
u x ± vx
u
~=
, ~
v=
. Dann ist w
~ =u
~±~
v=
.
uy
vy
u y ± vy
Skalarmultiplikation
Geometrisch: Ein Vektor u
~ wird mit einer reellen Zahl c multipliziert, indem der
Vektor c mal aneinander gehängt wird.
23
Rechnerisch: Ein Vektor wird mit einer reellen Zahl multipliziert, indem jede Komponente mit der Zahl multipliziert wird:
 ‹

‹
ux
c · ux
u
~=
, c ∈ R. Dann ist w
~ = c·u
~=u
~·c =
.
uy
c · uy
Ist c = 0 oder c = −1, so haben die sich ergebenden Vektoren Bezeichnungen. Bei
c = 0 ergibt sich der Nullvektor, bei c = −1 der zu u
~ inverse Vektor.
Die Vektoren c · u
~ für c ∈ R haben alle etwas gemeinsam: sie sind parallel zu
einander. Man nennt solche Vektoren kollinear.
Betrag eines Vektors
Die Länge eines Vektors ~
v heißt Betrag des Vektors und wird mit |~
v | bezeichnet.
Da die Koordinatenachsen zu einander senkrecht sind, berechnet sich der Betrag
eines Vektors mit Pythagoras:
|~
v| =
Ç
vx2 + v 2y .
Winkel eines Vektors mit den Achsen
Man kann den Winkel, den ein Vektor mit einer Achse einschließt, mit den trigonometrischen Funktionen berechnen. Mit der x-Achse schließt der Vektor ~
v folgenden
Winkel α ein:
vy
vy
vx
sin α =
, cos α =
, tan α = .
|~
v|
|~
v|
vx
Multiplikation von Vektoren
Es gibt zwei Arten der Multiplikation zwischen Vektoren: Skalarprodukt und Vektorprodukt (auch bekannt als Kreuzprodukt).
Das Skalarprodukt ist eine reelle Zahl s (wird auch Skalar genannt), die das Ergebnis eines Produkts von zwei Vektoren u
~ und ~
v ist (also Vektor mal Vektor gleich
Zahl):
 ‹  ‹
u
v
u
~·~
v=~
v·u
~ = x · x = u x vx + u y v y = s.
uy
vy
24
Das Skalarprodukt hat eine besondere Eigenschaft. Sind die Vektoren u
~ und ~
v
senkrecht auf einander, so ist das Skalarprodukt stets 0. Sind sie kollinear, so gilt:
|~
u·~
v | = |~
u| · |~
v |.
Man beachte, dass links das Vektorprodukt gebildet wird und rechts zwei reelle
Zahlen mit einander multipliziert werden.
Das Vektorprodukt ist ein Vektor, der das Ergebnis einer Multiplikation von zwei
Vektoren u
~ und ~
v ist (also Vektor mal Vektor gleich Vektor):
    

u y vz − uz v y
ux
vx
u
~×~
v = u y × v y = uz vx − u x vz  .
u x v y − u y vx
uz
vz
Hier wurden nicht ohne Absicht 3-dimensionale Vektoren genommen, denn im
2-dimensionalen macht das Vektorprodukt wenig Sinn. Der Ergebnisvektor beim
Vektorprodukt zweier Vektoren hat nämlich die Eigenschaft, dass er auf beiden
Vektoren senkrecht steht. Im 2-dimensionalen würde der Ergebnisvektor also in
die dritte nicht existente Dimension zeigen. Man kann aber vereinbaren, dass das
Ergebnis in Form einer Zahl geschrieben wird, die die Länge des Ergebnis-Vektors
darstellt (da die anderen beiden Koordinaten 0 sind). In vielen Fällen ist gerade
der Betrag des Ergebnisvektors interessant. Man kann aber auch 2-dimensionale
Vektoren in den 3-dimensionalen Raum verlagern, indem man die dritte Koordinate einfach 0 setzt und kann dann problemlos das Vektorprodukt bilden.
Sind die Vektoren u
~ und ~
v kollinear, so ist das Vektorprodukt der Nullvektor. Die
Orientierung des Ergebnisvektors ergibt sich aus der Rechte-Hand-Regel: Ist u
~ der
Daumen und ~
v der Zeigefinger, so ist der Mittelfinger der Ergebnisvektor u
~×~
v.
Ein wichtiger Unterschied zwischen dem Skalarprodukt und dem Vektorprodukt
ist, dass das Skalarprodukt kommutativ ist, d.h. das Ergebnis ändert sich nicht,
wenn man die Faktoren vertauscht. Das Vektorprodukt ist nicht kommutativ, d.h.
da kommt es auf die Reihenfolge der Vektoren an.
Winkelberechnung mit dem Skalarprodukt und dem Vektorprodukt
Wie wir vorher gesehen haben, hat das Skalarprodukt etwas mit dem Winkel zwischen den beteiligten Vektoren zu tun. Es gilt:
u
~·~
v = |~
u| · |~
v | · cos α.
Auf diese Weise lässt sich der Winkel zwischen den beiden Vektoren berechnen:


u x vx + u y v y
.
α = arccos  q
q
u2x + u2y · vx2 + v 2y
25
Auch das Vektorprodukt hängt mit dem Winkel α zwischen den beteiligten Vektoren zusammen:
|~
u×~
v | = |~
u| · |~
v | · sin α.
Auch hier kann man den Winkel berechnen:
|~
u×~
v|
α = arcsin
.
|~
u| · |~
v|
Einheitsvektor
Ein Vektor heißt Einheitsvektor, wenn sein Betrag 1 ist. Zu einem beliebigen Vektor
~
v können wir den Einheitsvektor bilden, indem wir ihn mit dem Kehrwert seiner
Länge, d.h. mit |~1v | multiplizieren, also:
~e ~v =
1
|~
v|
~
v.
2 × 2-Matrix
Unter einer Matrix wird in der Mathematik ein System von m·n Elementen verstanden, die in einem rechteckigen Schema von m Zeilen und n Spalten angeordnet
sind. Die Elemente der Matrix werden z.B. durch reelle Zahlen beschrieben. Eine
2 × 2-Matrix ist also
‹

a11 a12
.
A=
a21 a22
Die Zahlen a11 , a12 , a21 , a22 nennt man die Elemente der Matrix. Die Spalten werden auch Spaltenvektoren, die Zeilen auch Zeilenvektoren der Matrix genannt.
Addition und Subtraktion von Matrizen
Zwei Matrizen werden elementweise addiert oder subtrahiert:

‹ 
‹ 
‹
a11 a12
b11 b12
a11 + b11 a12 + b12
A+ B = B + A =
+
=
.
a21 a22
b21 b22
a21 + b21 a22 + b22
Skalarmultiplikation
Die Multiplikation einer Matrix A mit einer Zahl c geschieht elementweise:

‹ 
‹
a11 a12
c · a11 c · a12
c · A = A· c = c ·
=
.
a21 a22
c · a21 c · a22
26
Multiplikation einer Matrix mit einem Vektor
Eine 2×2-Matrix A wird mit einem Vektor ~
v multipliziert, indem das Skalarprodukt
zwischen den Zeilen der Matrix und dem Vektor ~
v gebildet wird und so ein neuer
Vektor erzeugt wird (also Matrix mal Vektor gleich Vektor):

‹  ‹ a11 vx + a12 v y
vx
a11 a12
A· ~
v=
·
=
.
vy
a21 a22
a21 vx + a22 v y
Übrigens ist es hier wichtig, auf die Reihenfolge zu achten: man kann nicht einen
Vektor mit einer Matrix multiplizieren, es sei denn, es ist ein Zeilenvektor. Zudem
muss die Dimension des Vektors der Zahl n der Spalten der Matrix entsprechen.
Eine Interpretation der Matrix in der Mathematik ist „lineare Abbildung“. Durch
Matrizen werden z.B. Punkte im Raum (dargestellt durch Vektoren) auf andere
Punkte im Raum abgebildet.
Drehmatrizen
Matrizen, die eine Drehung im Raum zur Wirkung haben, sind Matrizen der Form

‹
cos α − sin α
A=
.
sin α cos α
Für ein α dreht die Matrix A einen Punkt (also den zugehörigen Ortsvektor) im (2dimensionalen) Raum um Winkel α gegen den Uhrzeigersinn um den Ursprung,
indem die Matrix mit dem Vektor multipliziert wird.
27
Übungen
Aufgabe 1
Berechnen Sie die Winkel α und β, wenn a = 27.5cm, b = 24cm und c = 25.2cm.
Aufgabe 2
Berechnen Sie den Winkel zwischen zwei Seiten eines Tetraeders mit a = 7cm.
Aufgabe 3
Berechnen Sie den Winkel α und die Länge des Riemens. r1 = 20cm, r2 = 12cm,
d = 60cm.
Aufgabe 4
Auf einem Kreis mit Durchmesser d = 17cm sollen 7 Bohrungen in gleichmäßigem
Abstand gemacht werden. Berechnen Sie den minimalen (sm ) und maximalen (s M )
Abstand zwischen zwei Löchern.
28
Aufgabe 5
Gegeben ist ein Kreis mit Durchmesser d = 27cm mit einer Sehne von s = 15cm
Länge. Berechnen Sie die beiden zugehörigen Bogenlängen l1 und l2 .
Aufgabe 6
Sechs 1m lange Rohre werden gebunden transportiert. Die äußeren haben einen
Radius R = 20cm, das innere r = 14cm. Berechnen Sie das Volumen der Luftspalten.
Aufgabe 7
Berechnen Sie die Mantelfläche eines Kegelstumpfes mit r1 = 12cm, r2 = 5cm und
h = 8cm mit einer Guldinschen Regel.
Aufgabe 8
Berechnen Sie das Volumen eines Kreisringkörpers mit r1 = 19cm, r2 = 13cm und
h = 15cm mit einer Guldinschen Regel.
Aufgabe 9
Berechnen Sie den Schwerpunkt eines Halbkreises mit Radius r = 23cm.
29
Aufgabe 10
Angenommen, es wird ein Ball unter einem Winkel α zum Boden mit einer Anfangsgeschwindigkeit ~
v mit |~
v | = 54km/h geworfen. Der Boden sei eben und der
Luftwiderstand sei zu vernachlässigen. Unter welchem Winkel α fliegt der Ball am
weitesten?
Durch die Erdbeschleunigung (g ≈ 9.81m/s) haben wir ein Geschwindigkeit-ZeitGesetz v = g t in y-Richtung und ein Weg-Zeit-Gesetz s = v t in x-Richtung.
30
Lösungen
Aufgabe 1
.
.
.
a0 = 37.3cm, b0 = 36.5cm, c 0 = 34.8cm, d = 62.73, α = 56.26◦ , β = 32.76◦ .
Aufgabe 2
h=
p
3
a
2
.
.
= 6.06cm, α = 70.53◦ .
Aufgabe 3
Mit dem 2. Strahlensatz und den trigonometrischen Funktionen berechnet man
.
.
d1 = 37.5cm, d2 = 22.5cm, α = 64.46◦ . Mit der Winkelsumme erhält man β =
.
.
115.54◦ und damit
b2 = 51.20cm. Schließlich erhält man mit
p b1 = 85.33cm,
.
Pythagoras l = d 2 − (r1 + r2 )2 = 50.75cm. Die Länge des Riemens ist also L =
.
b1 + b2 + 2 · l = 238.04cm.
Aufgabe 4
.
.
sm = 7.38cm, s M = 16.57cm.
31
Aufgabe 5
.
.
l1 = 15.9cm, l2 = 68.92cm.
Aufgabe 6
.
.
.
.
α = 72◦ , β = 54◦ , Aα = 123.15cm2 , Aβ = 188.5cm2 , hα = 27.5cm, V = 24884cm3 .
Aufgabe 7
M = 2πrS l, rS = 8.5cm, l =
p
.
.
82 + (12 − 5)2 = 10.63cm, M = 567.72cm2 .
Aufgabe 8
.
V = 2πrS A, rS = 16cm, A = 6cm · 15cm = 90cm2 , V = 9047.79cm3 .
Aufgabe 9
.
Man berechne zuerst das Volumen einer Kugel mit r = 23cm (V = 50965.01cm3 )
als Rotationskörper eines Halbkreises (A = 12 πr 2 ) und stelle die zweite Guldinsche
Regel nach rS um:
4
3
πr 3 = 2πrS A ⇔ rS =
4πr 3
3 · 2π 12 πr 2
=
4
3π
.
r = 9.76cm.
32
Aufgabe 10
Da ~
v ein Vektor ist, der mit der x-Achse einen Winkel α einschließt, können wir
ihn in seine Komponenten zerlegen: vx = |~
v | cos α, v y = |~
v | sin α. Alternativ kann
man den Vektor ~
v mit α = 0 definieren und mit der Drehmatrix Mα drehen:

‹
 ‹
cos α − sin α
|~
v|
Mα =
, ~
v=
,
sin α cos α
0

‹  ‹ 
‹  ‹  ‹
v
v
cos α − sin α
|~
v|
|~
v | cos α
Mα · ~
v=
·
=
= x = xα .
vy
v yα
sin α cos α
0
|~
v | sin α
Als nächstes können wir die Flugdauer t 0 berechnen, indem wir die Gleichung
v
v y = g t y betrachten. D.h. nach der Zeit t y = gy wird die maximale Höhe erreicht.
Also gilt
2v y
2|~
v | sin α
t 0 = 2t y =
=
.
g
g
Die Wurfweite ergibt sich dann mit
s0 = vx t 0 = |~
v | cos α
2|~
v | sin α
g
=
2|~
v |2 sin α cos α
g
.
Die maximale Wurfweite führt also zu der Frage, wo die Funktion
s0 (α) =
2|~
v |2 sin α cos α
g
(in Abhängigkeit von α) ihr Maximum hat. Also bilden wir zuerst die ersten beiden
Ableitungen, um die notwendige und die hinreichende Bedingungen zu überprüfen. Für die notwendige Bedingung müssen die Nullstellen der ersten Ableitung
berechnet werden. Da wir in dieser Funktion ein Produkt trigonometrischer Funktionen haben, kann es umständlich oder unangenehm werden, wenn wir nicht die
Funktion vereinfachen. Man kann erkennen dass dieses Produkt Teil eines Additionstheorems (sin(α + β) = sin α cos β + sin β cos α) ist: sin(2α) = 2 sin α cos α.
Wir erhalten:
s0 (α) =
|~
v |2
sin(2α),
g
2|~
v |2
s00 (α) =
cos(2α),
g
4|~
v |2
00
s0 (α) = −
sin(2α).
g
33
Die relevante Nullstelle von s00 (α) liegt bei
2|~
v |2
g
cos(2α) = 0 ⇔ cos(2α) = 0 ⇔ α =
1
2
arccos(0) = 45◦ .
Da s000 (45◦ ) < 0, haben wir ein Maximum. Die maximale Wurfweite wird also unter
dem Winkel α = 45◦ erreicht — unabhängig von der Abwurfgeschwindigkeit.