10. Hauptsätze der W tze der W tze der Wärmelehre

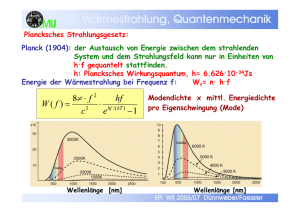
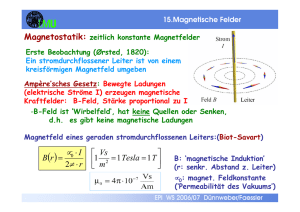
10. Hauptsä
Hauptsätze der Wä
Wärmelehre
Thermodynamik:
zunächst: Klassische Mechanik punktförmiger Teilchen, starrer und
deformierbarer Körper
aber: Bewegungsgleichungen für N=1023 Teilchen mit 6N Variablen
(Orte und Geschwindigkeiten) sind unmöglich alle behandelbar.
Ausweg: Beschreibung mit Meßgrößen (”Zustandsgrößen”) wie T,p,V,n
Die Thermodynamik beschreibt die Zusammenhänge dieser Zustandsgrößen (Mittelwerte) sowie deren Meßvorschriften.
Die Statistische Mechanik liefert den Zusammenhang zur
mikroskopischen Beschreibung.
Beispiel für ein thermodynamisches System: ideales Gas (Edelgas)
Zustandsgrößen: Volumen, Druck, Temperatur, Stoffmenge
Zustandsgleichung:
p.V = n.R.T
EPI WS 2006/07 Dünnweber/Faessler
10. Hauptsä
Hauptsätze der Wä
Wärmelehre
Zustandsgröße „Innere Energie“ U:
Die im Inneren eines abgeschlossenen Systems gespeicherte
gesamte Energie (kinetische + potentielle + Wärme + elektrische
Energie) nennt man Innere Energie. („Innere“ heißt, daß die kin.
und pot. Energie des Schwerpunkts nicht mitzählen).
Beispiel: Bei idealem Gas gibt es nur die kinetische Energie der
Moleküle: U = Q = n · cV · T = n · i/2 · R · T
(mit n = Molzahl, cV = spezifische molare Wärmekapazität, i = Zahl
der Bewegungsfreiheitsgrade, z.B. i = 3 für einatomiges Gas)
Erster Hauptsatz der Thermodynamik:
Die Innere Energie eines abgeschlossenen Systems ist erhalten.
(Verallgemeinerung der Energieerhaltung von makroskopischen
auf mikroskopische Systeme)
EPI WS 2006/07 Dünnweber/Faessler
Der Versuch „Wärmeäquivalent“ demonstriert den 1. Hauptsatz.
Er zeigt, daß sich mechanische Energie vollständig in Wärmeenergie umwandeln läßt.
Die Kupfertrommel erwärmt sich durch Reibung des lose gewickelten Drahtes und leitet die Wärme in
den Wasserbehälter, dessen Temperatur sich um ∆T erwärmt. Das Drehmoment des Motors ist so einr
r
gestellt, daß die Reibungskraft (und damit die Zugkraft des Drahtes)
, d.h. der
FR = −FG
Körper mit Masse m schwebt.
mit Weg s = Zahl der Umdrehungen x Trommelumfang
Mechanische Arbeit W = FR · s = m · g · s
Die Zunahme an Wärmeenergie (= innere Energie des Wasserbehälter) ist:
∆U=W→
∆T =
m ⋅g ⋅s
(c Wasser ⋅ M Wasser + c Trommel ⋅ M Trommel )
wie durch Messung von ∆T bestätigt wird.
EPI WS 2006/07 Dünnweber/Faessler
Andere Formulierung:
Die Summe der einem System von außen zugeführten Wärme ∆Q
und der an ihm verrichteten Arbeit ∆W ist gleich der Zunahme der
inneren Energie:
∆U = ∆Q + ∆W
Andere Formulierung:
Ein perpetuum mobile 1. Art ist unmöglich.
(Es gibt keine periodisch arbeitende Maschine, die mehr Arbeit
leistet als sie Energie aus ihrer Umgebung verbraucht.)
EPI WS 2006/07 Dünnweber/Faessler
Beispiel für den 1. Hauptsatz:
Wenn kein Wärmeaustausch mit Umgebung
(∆Q = 0):
∆U = ∆W
An einem Gasvolumen ist ∆ W = - p∆V
Beachte: bei Kompression (∆V < 0) ist die von außen geleistete
Arbeit positiv.
Daher das Minuszeichen in der Formel.
EPI WS 2006/07 Dünnweber/Faessler
10. Hauptsä
Hauptsätze der Wä
Wärmelehre
Umkehrbarkeit thermodyn. Prozesse (“Reversibilität“) ?
riesiges Energiereservoir im Wasser
Geht aber in der Realität nicht:
Warum ?
EPI WS 2006/07 Dünnweber/Faessler
10. Hauptsä
Hauptsätze der Wä
Wärmelehre
Reversibilität ?
Reversible Prozesse laufen immer über GleichgewichtsZustände und sind daher sehr langsam (bzw. idealisiert).
EPI WS 2006/07 Dünnweber/Faessler
4. Wird der Kolben langsam auf die Ausgangsposition zurückgeschoben, so wird am
System Arbeit geleistet (∆W = p ·∆V) und das System kehrt in seinen Ausgangszustand zurück.
EPI WS 2006/07 Dünnweber/Faessler
10. Hauptsä
Hauptsätze der Wä
Wärmelehre
Irreversibilität: warum verteilt sich ein Gas gleichmäßig auf ein
gegebenes Volumen ?
kurzer Exkurs in statistische Mechanik:
N=4:
P=1/16
P=4/16
… weil dieser Zustand am
wahrscheinlichsten ist !
P=6/16
Allgemein 2N solcher Mikro-Zustände
(hier: 16)
EPI WS 2006/07 Dünnweber/Faessler
Wahrscheinlichkeit für Rückkehr in oberen Zustand: P = 1/2N = 2-N
bereits bei N=100 ist 2-N ~ 10-30 ~ 0
Definiere: Entropie
∆S = k . ln(P)
[J/K]
-> eine 2N fach größere Wahrscheinlichkeit des unteren Zustands
bedeutet,daß dieser eine um ∆S = kN.ln(2) höhere Entropie besitzt.
Die Entropie ist ein Maß für die Unordnung und umso größer, je
größer die ‘Unordnung‘ ist.
(Thermodynamische Definition (alternativ): ∆S = ∆Qrev / T,
siehe Carnotscher Kreisprozeß)
2. Hauptsatz : ein abgeschlossenes System geht nie in
deutlich unwahrscheinlichere Zustände über.
Andere Formulierung:
Es gibt kein perpetuum mobile 2. Art (d.h. keine Maschine, die Arbeit
leistet, indem sie nichts weiter tut, als einen Körper abzukühlen).
EPI WS 2006/07 Dünnweber/Faessler
Kreisprozesse (Wärmekraftmaschinen)
In zyklischem Prozeß soll aus Wärme
mechanische Energie gewonnen werden.
(umgekehrt einfacher: Reibung)
Idealisiert (revers. Zustandsänderungen):
Carnot-Prozeß
Expansion:
1->2:
T1
Kompression:
2->3:
T2
T1
3->4:
T2
T1
4->1:
T2
T1
T2
EPI WS 2006/07 Dünnweber/Faessler
T1= const: ∆T=0
(∆U=∆
(∆ ∆Q-p∆
∆V)
(da ∆U=CV.∆T=0)
T1
T2
Isotherme Expansion
Fläche unter
1
= ∫ (R ⋅ T1 ) dV Kurve = Arbeit
V
V1
V2
für 1 mol (n=1)
EPI WS 2006/07 Dünnweber/Faessler
∆Q=0
T1
T2
adiabatische
Abkühlung
EPI WS 2006/07 Dünnweber/Faessler
T2= const: ∆T=0
(da ∆U=CV.∆T=0)
T1
T2
(V4<V3: ∆W>0)
Isotherme
Kompression
EPI WS 2006/07 Dünnweber/Faessler
∆Q=0
2
T1
T2
41
adiabatische
Erwärmung
EPI WS 2006/07 Dünnweber/Faessler
<0 !
abgegebene
mech. Arbeit
EPI WS 2006/07 Dünnweber/Faessler
Wirkungsgrad
RT1ln
η=
η=
− ∆WZyklus
von Maschine geleistete Arbeit
=
vom warmen Re servoir abgegebene Wärmeenergie
∆Q12
V2
V
+ RT2ln 4
V1
V3
V
RT1ln 2
V1
Für die beiden adiabatischen Zustandsänderungen (s.9, ausführlich im Lehrbuch von Trautwein et al.)
gilt:
V3 V2
V
V
=
→ ln 4 = −ln 2
V4 V1
V3
V1
η=
, oben eingesetzt :
T1 − T2
T1
Bei allen realen, irreversiblen Kreisprozessen sind die Wirkungsgrade geringer. Der (idealisierte)
Carnot-Prozeß erhält die Entropie. Mit der thermodynamischen Definition der Entropie (S=Qreversible/T)
ergibt die Entropieerhaltung direkt das obige Resultat (s. EP2).
Realisierbare gute Wirkungsgrade liegen bei 30%.
EPI WS 2006/07 Dünnweber/Faessler
Zweiter Hauptsatz : (nach Carnot-Kelvin oder Clausius)
Keine zyklisch arbeitende Maschine kann mechanische
Arbeit nur durch Abkühlung eines Wärmereservoirs
erzeugen.
Ein Teil der Wärme muß an ein zweites, kälteres
Reservoir abgegeben werden.
Alle Zustandsänderungen in einem abgeschlossenen
System bewirken eine Zunahme der Entropie:
∆S > 0 : irreversible Prozesse
∆S = 0 : reversible Prozesse (in der Realität selten)
EPI WS 2006/07 Dünnweber/Faessler
11. Wärmetransport und Stoffmischung
Ein Temperaturausgleich zwischen Körpern oder Bereichen eines
Körpers kann durch verschiedene Prozesse zustandekommen.
Strahlung: Kein direkter Kontakt, wichtig bei hohen Temperaturen
Wärmeleitung: Kein Transport von Materie, aber Leitung durch Materie
(vor allem Metalle, Festkörper)
Wärmeströmung (Konvektion): Wärmetransport mit fließender
Materie (dominant bei schlechten Wärmeleitern)
Ohne Wärmequellen führen diese Prozesse
zu vollständigem Temperaturausgleich (→ Tm)
Eine gute Isolation muss alle Wege ausschließen: Thermoskanne
(versilbert, doppelwandig, evakuiert)
EPI WS 2006/07 Dünnweber/Faessler
a) Wärmetransport durch Wärmestrahlung, d.h. durch elektromagnetische Wellen (sichtbares oder infrarotes Licht)
- dieser Transport erfolgt auch durch Vakuum (Sonne → Erde)
Die abgestrahlte Leistung P ist stark temperaturabhängig:
P = const · T4
(Stefan-Boltzmannsches Gesetz)
Außerdem verschiebt sich das Maximum
des Farbspektrums mit Wachsen der
Temperatur von rot nach blau
(exakte Beschreibung durch das
Plancksche Strahlungsgesetz).
Wärmestrahlungsleistung der Erde:
40x1012 W
EPI WS 2006/07 Dünnweber/Faessler
Wärmestrahlung
Die Wärmebildkamera basiert auf der starken Temperaturabhängigkeit der abgestrahlten Leistung (P ~ T4), die sie in Falschfarben darstellt → empfindliche Diagnostik in Medizin und Technik.
Verminderte Durchblutung beim Rauchen
Wärmeverlust
sichtbar
Falschfarbendarstellung
rot=hell, blau=dunkel
EPI WS 2006/07 Dünnweber/Faessler
Kosmische Hintergrundstrahlung
Ursprung: heißes Universum im Jahr t ≈ 400000 nach Urknall,
Temperatur 3000K
Durch Expansion des Weltalls wurde die Wellenlänge größer →
heutige 2.7K Strahlung
Ihre Anisotropie (siehe nächste Seite) gibt Auskunft über die Dichteverteilung der
Materie im Jahr 400000 → (Physik-Nobelpreis 2006)
EPI WS 2006/07 Dünnweber/Faessler
EPI WS 2006/07 Dünnweber/Faessler