Montag 31.10.2016

Mathematik für Physiker I, WS 2016/2017
Montag 31.10
$Id: reell.tex,v 1.39 2016/10/31 09:50:04 hk Exp $
§1
Die reellen Zahlen
1.2
Aussagen und Mengen
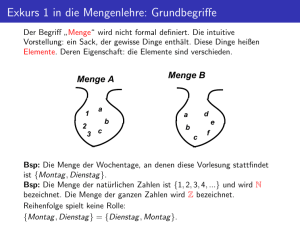
In der letzten Sitzung haben wir die verschiedenen Konstruktionsmethoden für Mengen
kennen gelernt. Insbesondere hatten wir die Mengenbildung durch Auswahl eingeführt,
hier sind eine Grundmenge M sowie eine Aussage A(x) über Elemente x von M gegeben
und mit diesen Daten konnte man dann die Menge
{x ∈ M |A(x)}
aller Elemente von M die die Eigenschaft A erfüllen bilden. Diese Form der Mengenbildung ist nur bei Vorhandensein einer explizit oder implizit vorgegebenen Obermenge M
möglich aus der Elemente ausgewählt werden, freie Mengenbildung {x|A(x)} wird nicht
zugelassen. Das übliche Beispiel weshalb diese problematisch wäre ist die sogenannte
Russelsche Antinomie. Bei dieser versucht man die Menge
R := {M |M ist eine Menge mit M ∈
/ M}
zu bilden, und die Existenz einer solchen Menge“ stellt sich als widersprüchlich heraus.
”
Das Problem entsteht bei der Frage ob R ∈ R gilt? Nehmen wir einmal an das R ∈ R
ist. Dann ist nach Definition von R auch R ∈
/ R, es kann also nicht R ∈ R sein. Damit
muss R ∈
/ R gelten, aber dann ist R eine Menge die sich nicht selbst als Element
enthält, d.h. wir haben doch R ∈ R. Eine Konstruktion wie das obige R führt also
auf Widersprüche, so etwas soll in der Mathematik aber nicht auftreten und um die
Russelsche Antinomie zu beseitigen verbietet man schlichtweg die freie Mengenbildung
und besteht auf vorgegebenen Obermengen aus denen ausgewählt wird.
Wir wollen ein letztes Beispiel einer Menge vorstellen, diese ist sogar wichtig genug
ein eigenes Symbol zu erhalten.
Definition 1.1 (Die leere Menge)
Die leere Menge ist die Menge die keine Elemente hat, geschrieben als ∅.
Natürlich ist die leere Menge für sich genommen keine interessante Menge, ihre Wichtigkeit besteht darin das sie sehr häufig vorkommt. Wir haben die leere Menge hier
sogar als eine sogenannte Definition“ eingeführt und wollen diesen Begriff jetzt ein
”
wenig besprechen.
Dass wir die Definition der leeren Menge offiziell als eine Definition bezeichnet und
numeriert haben, die Cantorsche Definition einer Menge aber nicht, ist kein Versehen
sondern gewollt. Letztere ist nämlich keine Definition im mathematischen Sinne. Im
3-1
Mathematik für Physiker I, WS 2016/2017
Montag 31.10
normalen Sprachgebrauch gibt es verschiedene Sorten von Definitionen, und die einfachste Art einer Definition ist die Verabredung einer Abkürzung. Dass beispielsweise
LS17“ für Leibniz Straße 17“ stehen soll ist eine rein willkürliche Abkürzung. Will
”
”
man dagegen definieren was ein Planet ist, so gibt es ja nach intendierten Verwendungszweck verschiedene Definitionen, wie man etwa an der Diskussion um den Status
des Pluto sehen kann. Eine Definition von Planeten beschreibt real vorhandene Objekte und dient nur dazu die gerade relevanten Aspekte dieses Objekts zu benennen. In
der Mathematik kommen solche Definitionen nicht vor, schon da die Mathematik nicht
von realen Objekten handelt, statt dessen sind alle Definitionen Verabredungen von
Abkürzungen. Der Begriff der leeren Menge ist nicht strikt nötig, anstelle von M = ∅“
”
könnte man genauso gut Die Menge M besitze keine Elemente“ sagen. Bevor das
”
Wort leere Menge“ definiert wurde gab es keine leere Menge, Planeten dagegen gibt
”
es völlig egal ob man eine Definition von Planet hat oder nicht.
Mathematische Definitionen führen also immer einen neuen Begriff in Termen bereits vorhandener Begriffe ein. Die Cantorsche Mengendefinition ist nicht von dieser
Art, da sie ihrerseits auf weitere noch nicht definierte Begriffe, wie Objekte unse”
rer Anschauung“, Zusammenfassung“ und so weiter, verweist. So etwas ist leider auch
”
nötig, mit mathematischen Definitionen alleine kommt man nicht aus. Wenn jeder neue
Begriff nur in Termen bereits vorhandener Begriffe eingeführt werden kann, so braucht
man irgendetwas mit dem alles anfangen kann. Hierfür verwendet man sogenannte
Grundbegriffe“, diese denken wir uns als vorgegeben und nicht weiter hinterfragbar.
”
Für diese Grundbegriffe gibt man dann üblicherweise eine Beschreibung an, die erklären soll was man sich unter dem Grundbegriff vorzustellen hat. Der Mengenbegriff
ist solch ein Grundbegriff und die Cantorsche Mengendefinition ist seine Erklärung.
Welche Begriffe als Grundbegriffe verwendet werden und welche definiert werden,
ist letzten Endes eine rein willkürliche Entscheidung. Es ist beispielsweise möglich den
Begriff einer Funktion als Grundbegriff zu verwenden, und Mengen dann in Termen
von Funktionen zu definieren. Es hat sich aber ein üblicher Satz“ an Grundbegriffen
”
durchgesetzt, zu denen unter anderem die Mengen gehören. Man kann mit erstaunlich
wenigen Grundbegriffen auskommen, es reichen der Mengenbegriff und ausreichend
viele logische und mathematische Begriffe um eine axiomatische Mengenlehre in Gang
zu bringen. Auf der Basis dieser Begriffe können dann kompliziertere Objekte wie
die reellen Zahlen definiert werden und ihre Axiome bewiesen werden. Als Startpunkt
im ersten Semester ist dies allerdings nicht geeignet, da man einfach zu weit unten
anfangen müsste, nicht einmal Dinge wie 2 + 2 = 4“ wären bekannt, schlimmer noch
”
es wäre noch nicht einmal definiert was 2“, 4“ und +“ überhaupt sein sollen. Daher
”
”
”
starten wir mit einem viel größeren Satz an Grundbegriffen, zu denen unter anderem
die reellen Zahlen gehören.
Da eine mathematische Definition letztlich nur eine Abkürzung ist, beschreibt sie
das definierte Objekt vollständig, die Definition und die sich aus ihr ergebenden Folgerungen sind alles was über die definierten Objekte zu sagen ist. Dies unterscheidet
mathematische Definitionen von Definitionen in anderen Gebieten, wo die definierten
Objekte letztlich reale Gegenstände sind und durchaus weitere über eine Definition
3-2
Mathematik für Physiker I, WS 2016/2017
Montag 31.10
hinausgehende Eigenschaften haben können. Insbesondere sind Fragen nach dem Status nicht definierter Konzepte keine mathematische Fragen, sondern bestenfalls Fragen
über Mathematik. Ein übliches Beispiel für die Verwirrungen die bei Fehlinterpretationen des Definitionsbegriffs entstehen ist die Frage“ was denn 0/0 ist. Wir haben den
”
Bruch a/b := ab−1 nur definiert wenn a, b ∈ R und b 6= 0 sind, dem Symbol 0/0 ist
damit keine Bedeutung zugewiesen und die Frage nach seinem Wert ist sinnlos.
In diesem Skript werden die meisten Definitionen explizit als solche ausgewiesen und
numeriert. Gelegentlich werden wir aber auch Ausnahmen zulassen, einige besonders
einfache Definitionen die eher Synonyme oder Notation sind werden einfach im laufenden Text aufgeführt, so hatten wir zum Beispiel in der ersten Sitzung die Definitionen
der Subtraktion und der Division behandelt.
Wir wollen auch noch eine Anmerkung zur Vergabe des Namens ∅“ machen.
”
Während die Physik sehr großzügig mit fest vergebenen Namen ist, beispielsweise ist v
fest für die Geschwindigkeit reserviert, gibt es in der Mathematik nur sehr wenige reservierte Namen, selbst ein Symbol wie π steht nicht immer für die Kreiszahl, sondern
kann je nach Kontext auch was ganz anderes bedeuten. Einer dieser vergebenen Namen
ist das Symbol ∅ für die leere Menge, ein anderer ist N für die Menge der natürlichen
Zahlen. Dass soll an Kommentaren zu dieser Definition erst einmal reichen, und wir
kommen zu einer weiteren wichtigen Definition.
Definition 1.2 (Teilmengen einer Menge)
Eine Menge M heißt Teilmenge einer Menge N , wenn jedes Element von M auch ein
Element von N ist. In diesem Fall schreiben wir M ⊆ N .
Ist eine Menge M keine Teilmenge einer Menge N , so wird dies mit dem Symbol
M 6⊆ N notiert. Die Schreibweise M ⊆ N für die Teilmengenbeziehung wird leider
nicht einheitlich von allen Autoren verwendet, oftmals finden Sie auch M ⊂ N anstelle
von M ⊆ N . Einige Beispiele von Teilmengen sind:
1. Es ist
{1, 2} ⊆ {1, 2, 3}
denn die beiden Elemente 1 und 2 der linken Menge sind auch Elemente der
rechten Menge.
2. Es ist auch
{1, 2, 3} ⊆ {1, 2, 3}.
Allgemein ist jede Menge eine Teilmenge von sich selbst. Will man dies nicht
haben, so spricht man von einer echten Teilmenge, d.h. eine Menge M ist eine
echte Teilmenge der Menge N wenn M ⊆ N und M 6= N ist, und wir schreiben
M ( N für M ist eine echte Teilmenge von N“. Oftmals wird anstelle von
”
M ( N aber auch die alternative Schreibweise M ⊂ N verwendet, was etwas
unglücklich ist da dies von anderen wieder als die normale Teilmengenbeziehung
interpretiert wird. Die beiden Symbole ⊆“ und (“ sind unmißverständlich,
”
”
während ⊂“ je nach Autor Teilmenge“ oder echte Teilmenge“ bedeuten kann.
”
”
”
Das ist verwirrend, aber es ist leider so.
3-3
Mathematik für Physiker I, WS 2016/2017
Montag 31.10
3. Dagegen ist
{1, {2}} 6⊆ {1, 2, 3},
denn die einelementige Menge {2} ist zwar ein Element der linken aber kein
Element der rechten Menge.
4. Das letzte Beispiel ist jetzt etwas verwirrend, wir behaupten das
∅ ⊆ {1, 2, 3}
gilt. Erinnern wir uns an die Teilmengendefinition, so bedeutet ∅ ⊆ {1, 2, 3}
das jedes Element der leeren Menge auch ein Element von {1, 2, 3} ist, und so
merkwürdig es einem auch vorkommt, dies ist wahr. Es gibt ja kein Element der
leeren Menge für das das falsch sein könnte. Mit derselben Begründung ist auch
∅⊆M
für überhaupt jede Menge M . Insbesondere ∅ ⊆ ∅.
Dieser Teilmengenbegriff wird häufig beim Nachweis der Gleichheit zweier Mengen
verwendet, es gilt für je zwei Mengen M und N
(F12) Genau dann ist M = N wenn M ⊆ N und N ⊆ M gelten.
In der Tat, dass M und N gleich sind bedeutet das diese beiden Mengen dieselben
Elemente haben, das also aus x ∈ M auch x ∈ N folgt und umgekehrt x ∈ N auch
x ∈ M impliziert. Letzteres sind aber gerade die beiden Inklusionen M ⊆ N und
N ⊆ M . Diese Beobachtung wird meist verwendet um die Gleichheit zweier Mengen
zu beweisen, um M = N einzusehen, zeigt man zum einen die Inklusion M ⊆ N und
zum anderen die Inklusion N ⊆ M .
Mit Mengen kann man rechnen, es gibt eine Vielzahl von Operationen die aus zwei
gegebenen Mengen eine neue Menge machen. Die drei wichtigsten dieser Rechenoperationen wollen wir nun einführen:
Definition 1.3: Seien M, N zwei Mengen.
1. Die Vereinigung von M und N , geschrieben als M ∪N , ist die Menge all derjenigen
Objekte die Element von M oder von N sind.
2. Der Durchschnitt von M und N , geschrieben als M ∩ N , ist die Menge all derjenigen Objekte die Element von M und von N sind.
3. Die Differenzmenge von M und N , geschrieben als M \N , ist die Menge aller
Elemente von M , die nicht zugleich Element von N sind. Alternativ nennen wir
dies auch das Komplement von N in M oder das relative Komplement von N in
M.
3-4
Mathematik für Physiker I, WS 2016/2017
Vereinigung
M ∪N
Alle x in M oder N
Durchschnitt
M ∩N
Alle x in M und N
Komplement
M \N
Alle x in M nicht in N
Montag 31.10
Anstelle der Schreibweise M \N für die Differenzmenge wird von einigen Autoren auch
das Symbol M − N verwendet. Da wir diese Begriffe nicht sofort brauchen, werden
Beispiele hierzu in den Übungsaufgaben behandelt. Wir wollen an dieser Stelle nur
noch einige Rechenregeln für die obigen Operationen einführen.
Lemma 1.1 (Grundeigenschaften der Mengenoperationen)
Seien A, B, C drei Mengen.
(a) Es gelten die beiden Distributivgesetze
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) und A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
(b) Es gelten die beiden deMorganschen Regeln
A\(B ∪ C) = (A\B) ∩ (A\C) und A\(B ∩ C) = (A\B) ∪ (A\C).
Beweis: (a) Wir beginnen mit dem Nachweis der ersten Formel. Nach (F12) müssen
wir einsehen das die beiden Inklusionen A ∩ (B ∪ C) ⊆ (A ∩ B) ∪ (A ∩ C) und (A ∩ B) ∪
(A ∩ C) ⊆ A ∩ (B ∪ C), beziehungsweise A ∩ (B ∪ C) ⊇ (A ∩ B) ∪ (A ∩ C), bestehen,
und diese werden wir beide nachweisen.
”⊆” Sei x ∈ A ∩ (B ∪ C). Dann ist x ∈ A und x ∈ B ∪ C, und es treten zwei
mögliche Fälle auf. Im ersten Fall ist x ∈ B und dann haben wir x ∈ A ∩ B, also auch
x ∈ (A ∩ B) ∪ (A ∩ C). Im zweiten Fall ist dagegen x ∈ C und wir haben x ∈ A ∩ C, also
wieder x ∈ (A ∩ B) ∪ (A ∩ C). Damit haben wir in beiden Fällen x ∈ (A ∩ B) ∪ (A ∩ C)
und die behauptete Inklusion ist bewiesen.
”⊇” Sei nun umgekehrt x ∈ (A ∩ B) ∪ (A ∩ C). Dann treten wieder zwei Fälle auf.
Im ersten Fall ist x ∈ A ∩ B, also wegen x ∈ B auch x ∈ B ∪ C und mit x ∈ A folgt
x ∈ A ∩ (B ∪ C). Im zweiten Fall haben wir dagegen x ∈ A ∩ C, also wegen x ∈ C auch
x ∈ B ∪ C und mit x ∈ A folgt erneut x ∈ A ∩ (B ∪ C). Damit haben wir in beiden
Fällen x ∈ A ∩ (B ∪ C) gezeigt und auch diese Inklusion ist bewiesen.
Zum Beweis der zweiten Formel reicht es nach (F12) wieder die beiden Inklusionen
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) und (A ∪ B) ∩ (A ∪ C) ⊆ A ∪ (B ∩ C) einzusehen.
”⊆” Sei x ∈ A ∪ (B ∩ C). Dann haben wir wieder zwei mögliche Fälle. Im ersten Fall
ist x ∈ A und dann sind auch x ∈ A ∪ B und x ∈ A ∪ C, also x ∈ (A ∪ B) ∩ (A ∪ C)
wie gewünscht. Im zweiten Fall ist x ∈ B ∩ C also x ∈ B und x ∈ C und damit ist
3-5
Mathematik für Physiker I, WS 2016/2017
Montag 31.10
wieder x ∈ A ∪ B und x ∈ A ∪ C also x ∈ (A ∪ B) ∩ (A ∪ C). Damit haben wir in
beiden Fällen x ∈ (A ∪ B) ∩ (A ∪ C) und die Inklusion ist bewiesen.
”⊇” Sei nun umgekehrt x ∈ (A∪B)∩(A∪C). Ist dann x ∈ A so ist auch x ∈ A∪(B ∩C)
und wir sind bereits fertig. Andernfalls ist x ∈
/ A. Wegen x ∈ A ∪ B ist dann x ∈ B
und wegen x ∈ A ∪ C ebenso x ∈ C, es gilt also x ∈ B ∩ C und wir haben wieder
x ∈ A ∪ (B ∩ C). Damit haben wir in beiden Fällen x ∈ A ∪ (B ∩ C) und die Inklusion
ist bewiesen.
(b) Wir beginnen mit der ersten Regel und zeigen wie in (a) beide Inklusionen A\(B ∪
C) ⊆ (A\B) ∩ (A\C) und (A\B) ∪ (A\C) ⊆ A\(B ∪ C).
”⊆” Sei also x ∈ A\(B ∪ C), d.h. x ∈ A und x ∈
/ B ∪ C. Wegen x ∈
/ B ∪ C sind
dann x ∈
/ B und x ∈
/ C, also ist x ∈ A\B sowie x ∈ A\C und es gilt folglich x ∈
(A\B) ∩ (A\C).
”⊇” Jetzt sei umgekehrt x ∈ (A\B) ∩ (A\C). Dann ist x ∈ A\B und x ∈ A\C also
x ∈ A und x ∈
/ B, x ∈
/ C, d.h. x ∈
/ B ∪ C und somit x ∈ A\(B ∪ C). Dies zeigt
(A\B) ∩ (A\C) ⊆ A\(B ∪ C).
Erneut nach (F12) ist damit die erste deMorgansche Regel bewiesen. Schließlich
kommen wir zur zweiten Regel und erneut werden wir A\(B ∩ C) ⊆ (A\B) ∪ (A\C)
und (A\B) ∪ (A\C) ⊆ A\(B ∩ C) zeigen.
”⊆” Sei x ∈ A\(B ∩ C) also x ∈ A aber x ∈
/ B ∩ C. Letzteres bedeutet x ∈
/ B oder
x∈
/ C also haben wir x ∈ A\B oder x ∈ A\C und folglich x ∈ (A\B) ∪ (A\C). Dies
zeigt A\(B ∩ C) ⊆ (A\B) ∪ (A\C).
”⊇” Schließlich sei x ∈ (A\B) ∪ (A\C). Dann treten zwei verschiedene Fälle auf.
Im ersten Fall ist x ∈ A\B, also x ∈ A und x ∈
/ B und insbesondere x ∈
/ B ∩ C,
d.h. x ∈ A\(B ∩ C). Andernfalls ist x ∈ A\C und x ∈ A\(B ∩ C) folgt analog mit
vertauschten Rollen von B und C. Damit haben wir auch (A\B) ∪ (A\C) ⊆ A\(B ∩ C)
gezeigt.
Eine letzte Anwendung von (F12) liefert auch die zweite deMorgansche Regel.
Der Beweis läßt sich durchaus ökonomischer und etwas kürzer gestalten, hier geht
es uns um die Demonstration der auf (F12) beruhenden Standardtechnik“ zum Be”
weis von Mengengleichheiten die daher stur immer wieder verwendet wurde. Da dies
die erste Aussage ist die wir hervorheben und als Lemma bezeichnen, wollen wir an
dieser Stelle noch kurz auf die hier verwendete Terminologie eingehen. Die Aussagen
der Mathematik werden als sogenannte Sätze“ formuliert und in einem aufgeschriebe”
nen Text werden sie dann oftmals numeriert und in irgendeiner Form hervorgehoben
dargestellt. Dabei ist der Name Satz“ hier ein Oberbegriff, je nach Bedeutung der Aus”
sage werden verschiedene Namen verwendet. In der Literatur finden Sie die folgenden
Bezeichnungen:
Satz Aussage mit einer mitteilenswerten, eigenständigen Bedeutung.
Hauptsatz Ein besonders wichtiger Satz.
Theorem Je nach Autor entweder ein Synonym für Satz“ oder für Hauptsatz“.
”
”
3-6
Mathematik für Physiker I, WS 2016/2017
Montag 31.10
Lemma Wie ein Satz aber mit Bedeutung hauptsächlich innerhalb der Theorie.
Proposition Je nach Autor entweder ein Synonym für Satz“ oder für Lemma“.
”
”
Hilfssatz Ein sehr spezifisches Lemma das nur für den Beweis einer oder sehr weniger
anderer Aussagen gedacht ist.
Korollar Eine unmittelbare Folgerung aus einem Satz oder Lemma, oftmals ein besonders hervorgehobener Spezialfall.
Wir werden die Namen Satz“, Lemma“ und Korollar“ verwenden. Einfache Aus”
”
”
sagen werden oftmals nicht extra als Satz formuliert sondern nur im laufenden Text
erwähnt und später ohne weiteren Verweis verwendet, dies trifft beispielsweise auf all
unsere Feststellungen (F1) und so weiter zu. Besonders selbstverständliche Aussagen
werden sogar nirgends festgehalten, beispielsweise werden wir so etwas wie A ∪ B =
B ∪ A für Mengen A, B verwenden auch ohne es irgendwo explizit zu benennen.
Wir führen jetzt eine weitere Schreibweise für mathematische Aussagen ein. Diese
haben sehr oft die Form Für alle Elemente x eine gegebenen Menge M gilt eine
”
Aussage A(x)“, eine sogenannte Allaussage, oder Es gibt ein Element x der Menge M
”
für das A(x) gilt“, eine sogenannte Existenzaussage. Man schreibt
∀(x ∈ M ) : A(x) für Für alle x ∈ M gilt A(x)“.
”
Das Symbol ∀“ ist ein sogenannter Allquantor. Entsprechend schreibt sich eine Exi”
stenzaussage als
∃(x ∈ M ) : A(x) für Es existiert ein x ∈ M mit A(x)“,
”
und hier nennt man ∃“ einen Existenzquantor. Beispielsweise übersetzt sich die Aus”
sage Für jede reelle Zahl x existiert eine natürliche Zahl n, die echt größer als x ist“
”
als Formel in
∀(x ∈ R)∃(n ∈ N) : n > x.
Ein solcher Ausdruck mit mehreren Quantoren ist dabei immer von links nach rechts
zu lesen, ein Ändern der Quantorenreihenfolge ändert auch die Bedeutung der Aussage.
Beispielsweise bedeutet
∃(n ∈ N)∀(x ∈ R) : n > x,
dass es eine natürliche Zahl n gibt, die echt größer als überhaupt alle reellen Zahlen ist,
was natürlich falsch ist. Quantoren desselben Typs kann man vertauschen, und daher
werden sie meist in zusammengefasster Form notiert, man schreibt beispielsweise
∀(x, y ∈ R) : y > x > 0 ⇒ y 2 > x2 für ∀(x ∈ R)∀(y ∈ R) : y > x > 0 ⇒ y 2 > x2 .
Wir haben jetzt Allaussagen ∀(x ∈ M ) : A(x) und Existenzaussagen ∃(x ∈ M ) : A(x)
eingeführt. Diese scheinen sich zwar formal recht ähnlich zu sein, inhaltlich unterscheiden sie sich jedoch grundlegend voneinander. Um eine Allaussage ∀(x ∈ M ) : A(x) zu
3-7
Mathematik für Physiker I, WS 2016/2017
Montag 31.10
beweisen, muss man sich ein beliebiges Element x ∈ M der zugrundeliegenden Menge
M vorgeben und für jedes solche die Aussage A(x) beweisen. Es reicht nicht dies für
einzelne x ∈ M zu tun. Als ein Beispiel nehmen wir einmal
M = N\{0, 1} = {2, 3, 4, . . .} und
A(n) = ggT(n5 − 5, (n + 1)5 − 5) = 1
letzteres für jedes n ∈ N. Probieren wir etwa n = 2 so sind n5 −5 = 27 und (n+1)5 −5 =
238 und wir haben ggT(n5 − 5, (n + 1)5 − 5) = 1. Verwenden wir dann einen Computer,
so kann man leicht etwa alle Werte 2 ≤ n ≤ 1000000 durchprobieren und die beiden
Zahlen n5 − 5 und (n + 1)5 − 5 stellen sich immer als teilerfremd heraus. Als ein Beweis
der Aussage ∀(n ∈ M ) : A(n) reicht das aber nicht aus, selbst eine so große Zahl von
Beispielen hat keine Beweiskraft. Andererseits reicht ein einzelnes Gegenbeispiel aus
die Allaussage zu widerlegen, und nehmen wir etwa
n = 1435390, so ist ggT(n5 − 5, (n + 1)5 − 5) = 1968751 > 1.
Ganz anders sieht dies bei einer Existenzaussage aus. Um eine Aussage ∃(x ∈ M ) : A(x)
zu beweisen, muss man nur ein einziges x ∈ M finden für welches die Aussage A(x) gilt.
Idealerweise geschieht dies durch möglichst direkte Angabe solch eines x, aber dies ist
nicht zwingend verlangt, es gibt Beispiele bei denen man die Existenz eines x einsehen
kann, ohne die geringste Idee zu haben wie man ein solches x konkret beschaffen kann.
Von Bedeutung sind oftmals auch die Verneinungen von All- und Existenzaussagen.
Überlegen wir uns zunächst wann eine Allaussage ∀(x ∈ M ) : A(x) falsch ist. Wie im
obigen Beispiel reicht hierfür ein einzelnes x ∈ M aus so, dass A(x) falsch ist. In
anderen Worten ist die Verneinung einer Allaussage eine Existenzaussage, nämlich
¬∀(x ∈ M ) : A(x) = ∃(x ∈ M ) : ¬A(x).
Entsprechend ist eine Existenzaussage ∃(x ∈ M ) : A(x) falsch, wenn wir eben kein
Element x von M finden können für das A(x) wahr ist, d.h. wenn die Verneinung
¬A(x) für jedes Element x von M wahr ist. Die Verneinung einer Existenzaussage wird
damit eine Allaussage
¬∃(x ∈ M ) : A(x) = ∀(x ∈ M ) : ¬A(x).
Bei Verneinung drehen sich also All- und Existenzquantoren um, d.h. Allquantoren
werden zu Existenzquantoren und Existenzquantoren werden zu Allquantoren. Sind
beispielsweise M, N zwei Mengen und A(x, y) eine Aussage über Elemente x ∈ M und
y ∈ N , so wird
¬∀(x ∈ M )∃(y ∈ N ) : A(x, y) = ∃(x ∈ M ) : ¬∃(y ∈ N ) : A(x, y)
= ∃(x ∈ M )∀(y ∈ N ) : ¬A(x, y).
Entsprechend kann man in allen solchen Fällen vorgehen, zum Verneinen werden alle
Quantoren umgedreht und die innere Aussage verneint.
3-8
Mathematik für Physiker I, WS 2016/2017
1.3
Montag 31.10
Die Anordnung der reellen Zahlen
Nachdem wir im vorigen Abschnitt alle zunächst für uns relevanten Grundlagen behandelt haben, wollen wir nun unsere im ersten Abschnitt begonnene Diskussion der reellen
Zahlen fortsetzen. Wir haben bereits die neun arithmetischen Axiome kennengelernt
die das Verhalten der Grundrechenarten kontrollieren. Jetzt kommen wir zur nächsten
Gruppe von Axiomen für die reellen Zahlen, diese beschäftigen sich nicht mehr nur mit
Addition und Multiplikation sondern auch mit der Kleiner-Gleich Beziehung zwischen
reellen Zahlen. Neben der Addition und der Multiplikation sei auf den reellen Zahlen
noch eine Anordnung gegeben, d.h. für je zwei reelle Zahlen x, y ist festgelegt ob x ≤ y
gilt oder nicht. Diese Anordnung ist für uns ein Grundbegriff, der die folgenden Axiome
erfüllen soll:
Die Ordnungsaxiome:
(R) Das Reflexivitätsgesetz: Für jedes x ∈ R ist x ≤ x.
(T) Das Transitivitätsgesetz: Für alle x, y, z ∈ R gilt
x ≤ y ∧ y ≤ z =⇒ x ≤ z.
(A) Die Antisymmetrie: Für alle x, y ∈ R gilt
x ≤ y ∧ y ≤ x =⇒ x = y.
(L) Die Ordnung ist total oder linear, d.h. für alle x, y ∈ R ist stets x ≤ y oder y ≤ x.
Erst einmal wollen wir eine kleine Anmerkung zu den vier Anordnungsaxiomen machen.
Das Reflexivitätsgesetz (R) gilt nicht automatisch nur weil wir von der Kleiner-Gleich
”
Relation“ sprechen, dies ist nur ein Name, dass tatsächlich Gleichheit auch KleinerGleich impliziert muss explizit festgehalten werden, auch wenn die Namensgebung andernfalls natürlich recht unglücklich wäre. Allerdings ist (R) tatsächlich redundant und
könnte weggelassen werden, denn die Linearität (L) ergibt insbesondere x ≤ x oder
x ≤ x, also x ≤ x, für jedes x ∈ R. Trotzdem wollen wir (R) mit als Axiom aufführen,
dies kommt da oftmals auch Anordnungen“ betrachtet werden die nur (R), (T) und
”
(A) erfüllen und aus (T) und (A) läßt sich (R) nicht herleiten.
3-9