Integrationsregeln

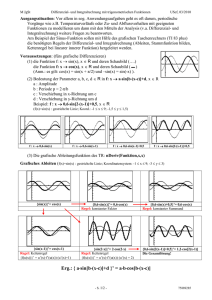
Integrationsregeln
Wir beginnen mit den einfachsten Integrationsregeln.
Bemerkung 1 (Faktorregel der Integration)
Besitzt eine Funktion f : a, b  IR eine Stammfunktion auf a, b , so besitzt
für jede reelle Zahl c  0 auch die Funktion cf eine Stammfunktion und es
gilt:
 c  f x dx  c   f x dx
Wenden wir die aus der Differentialrechung bekannte Faktorregel auf die rechte Seite an, so
erhalten wir


d
d
c   f x  dx  c 
dx
dx
 f x dx   c  f x ,
weshalb die rechte Seite eine Stammfunktion von cf ist.
Bemerkung 2 (Summenregel der Integration)
Besitzen zwei Funktionen f , g : a, b  IR eine Stammfunktion auf a, b , so
besitzt auch ihre Summe f  g eine Stammfunktion und es gilt:
 f x   gx dx   f x dx   gx dx
Mit der aus der Differentialrechnung bekannten Summenregel differenzieren wir die rechte
Seite und erhalten
d
dx
 f x   gx dx   dxd  f x dx  dxd  gx dx   f x   gx  ,
weshalb die rechte Seite eine Stammfunktion von f  g ist.
Die nächste Regel stellt einen Spezialfall der etwas später auftauchenden Substitutionsregel
dar und wird nur deshalb aufgeführt, weil häufiger Kompositionen von Funktionen betrachtet
werden, wo die innere Funktion eine Gerade ist.
1
Bemerkung 3 (lineare Substitution)
Besitzt eine Funktion f : a, b  IR eine Stammfunktion auf a, b mit
dFx   f x dx , so besitzt die Funktion x  f m  x  n  ( m  0 und n reelle
Zahlen) eine Stammfunktion und es gilt:
 f m  x  n dx  m  Fm  x  n   C
1
Wenden wir die aus der Differentialrechung bekannte Kettenregel auf die rechte Seite an,
so erhalten wir
Kettenregel
d 1
1
 Faktorregel 1 d







F
m

x

n


F
m

x

n

 f m  x  n   m  f m  x  n  ,


dx  m
m dx
m

weshalb die rechte Seite eine Stammfunktion von x  f m  x  n  ist.
Beispiel 1
(Stammfunktion eines Polynoms n-ten Grades)
Jedes Polynom n-ten Grades besitzt eine Stammfunktion. Es ist
n
n
ak
 x k 1  C.
k 1 k  1
k
  a k  x dx  
k 0
Die Aussage des Beispiels folgt sofort mit den beiden voran gehenden Bemerkungen.
Beispiel 2
(Stammfunktion einer speziellen gebrochenrationalen Funktion)
Gegeben sei für die reellen Zahlen a, b, c und d die gebrochenrationale Funktion
ax b
f :x 
cx  d
Ihre Stammfunktion lautet
ax b
a
 c  x  d dx  c  x 
bc  ad
 1 
 log 
  C.
2
c
cx  d
Durch äquivalente Umformungen erhalten wir für den Integranden
a  x  b a bc  ad
1
 

2
cx  d c
cx  d
c
und somit unter Verwendung der drei Bemerkungen die Behauptung; denn nach der Tafel der
Grundintegrale wissen wir, daß die Stammfunktion von x  1x die Logarithmusfunktion ist.
2
Zur häufig gebrauchten Bemerkung 3 noch einige Beispiele.
Beispiel 3
(Anwendung der speziellen Substitutionsregel)
Unter Verwendung der speziellen Substitutionsregel erhält man etwa folgende
Stammfunktionen:
a) Für a , b  IR mit a  b ist
1
xb
1
 x  a x  b dx  a  b  log x  a
C
b) Für A, B, C  IR mit B 2  A  D  0 ist
1
1
Ax  B  B 2  A  D
 A  x 2  2B  x  D dx  2 B 2  A  D  log Ax  B  B 2  A  D  C
c) Für a  0 ist
1
1
 sin a  x dx  2  x  4a  sin 2m  x   C
2
und
1
1
2
 cos a  x dx  2  x  4a  sin 2m  x   C .
Der Integrand der ersten Stammfunktion wird wie folgt äquivalent umgeformt:
1
x  a x  b 

1
ab
1 x  a  x  b 




a  b x  a x  b  a  b x  a x  b 

1  1
1 


a  b  x  b  x  a 
Dann folgt aber mit den voran gehenden Bemerkungen die Behauptung.
Der Integrand der zweiten Stammfunktion läßt sich wegen B 2  A  D  0 ebenfalls äquivalent umformen; denn das Nennerpolynom besitzt die beiden Nullstellen
a
 B  B2  A  D
A
b
und
und läßt sich daher umformen zu
1
1

,
A  x  2B  x  D Ax  a x  b 
2
weshalb mit a) die Behauptung folgt.
3
 B  B2  A  D
A
Für die letzte Behauptung des Beispiels verwenden wir das Additionstheorem der Kosinusfunktion und erhalten
cos2a  x   cosa  x   cosa  x   sin a  x   sin a  x   cos 2 a  x   sin 2 a  x  
 1  2 sin 2 a  x 
und damit
sin 2 a  x  
1  cos2a  x 
.
2
Integration der rechten Seite mit den Bemerkungen dieses Blattes belegt die Richtigkeit der
Aussage unter c).
Ebenso erhalten wir die zweite Stammfunktion unter c) mittels
cos2a  x   cosa  x   cosa  x   sin a  x   sin a  x   cos 2 a  x   sin 2 a  x  
 2 cos 2 a  x   1
bzw.
cos 2 a  x  
1  cos2a  x 
.
2
Wir kommen jetzt zu zwei wichtigen Integrationsregeln, die in engem Zusammenhang zur
Produkt- und Kettenregel aus der Differentialrechnung stehen.
Bemerkung 4 (partielle Integration)
Seien f , g : a, b  IR zwei differenzierbare Funktionen. Genau dann besitzt
f   g eine Stammfunktion, wenn f  g  eine Stammfunktion besitzt. Im Falle
der Existenz gilt:
 f x   gx dx  f x   gx    f x   g x 
Nach Differentiation der rechte Seite unter Verwendung von Summen- und Produktregel erhalten wir




d
d
f x   gx   d  f x   gx  
f x   gx    f x   g x  
dx
dx
dx

 f x   gx   f x   g x   f x   g x   f x   gx ,
weshalb die rechte Seite die Stammfunktion von f   g ist.
In den nachfolgenden Beispielen ermitteln wir die Stammfunktionen mittels partieller Integration, die natürlich nur dann zum Ziel führt, wenn die rechte Seite bequem berechnet werden
kann.
4
Beispiel 4
(partielle Integration)
Mit partieller Integration erhält man die folgenden Stammfunktionen:
a)  x  ln x  dx 
x2
x2
 ln x  
C
2
4
b)  ln x  dx  x  ln x   x  C
c)  x  e x dx  e x  x  1  C
d)  x  cosx  dx  x  sin x   cosx   C
Die Berechnung der Stammfunktionen mittels partieller Integration ist sehr einfach. Wir berechnen daher bloß die erste Stammfunktion und setzen f x   x und gx   ln x  . Dann gilt
für die rechte Seite:
x2
x2 1
x2
1
 ln x   
 dx 
 ln x     x dx 
2
2 x
2
2
2
2
x
x

 ln x  
C
2
4
f x   gx    f x   g x  
Bestimmte Stammfunktionen lassen sich durch wiederholte Anwendung der partiellen Integration berechnen. Eine Verallgemeinerung von Bemerkung 4 ist besonders dann nützlich,
wenn einer der Faktoren ein Polynom ist, während der andere etwa die Exponentialfunktion
oder die Sinus- bzw. Kosinusfunktion ist.
Bemerkung 5 (verallgemeinerte partielle Integration)
Seien f , g : a, b  IR zwei (n+1)-mal stetig differenzierbare Funktionen.
Dann gilt:
n
 n 1
k 
n  k 
 f x   g x dx    1  f x   g x    1
n 1
k
k 0
  f n 1 x   gx  dx
Wir differenzieren zunächst die Summe auf der rechten Seite und unterdrücken dabei die Variable x. Es ist zunächst

n
n
k
k
k 
n k  
k 
 n  k 1



1

f

g

 f k 1  g n  k  

   1  f  g
k 0
 k 0


n

n
   1 f k   g n  k 1    1 f k 1  g n  k 
k
k 0
k 0
5
k
Isolieren wir nun den ersten Summanden der ersten Summe sowie den letzten der zweiten
Summe und führen zudem noch eine Indextransformation durch, so erhalten wir
n
n
   1 f k   g n  k 1    1 f k 1  g n  k  
k
k 0
n 1
k 0

 f  g n 1    1
k 0
 f g
n 1
k
k 1

  1  f k 1  g n k    1  f n 1  g 
k
n
  1  f n 1  g
n
Differenzieren wir schließlich noch das unbestimmte Integral auf der rechten Seite, so ergibt
die rechte Seite nach Differentiation f  g n 1 . Damit ist die Behauptung gezeigt.
Beispiel 5
(verallgemeinerte partielle Integration)
Mit der verallgemeinerten partiellen Integration erhält man für jede natürliche
Zahl n  IN 0 folgende Stammfunktion:
n 1
n  1
n 1
x
x
  k!  x n 1k  C
 1k  
x

e
dx

e



k 0
 k 
Für f x   x n 1 ist f k  x   n  1    n  1  k   x n 1k die k-te Ableitung ( 0  k  n  1 ).
Der Rest folgt dann sofort mit Bemerkung 5.
Für n = 0 erhält man beispielsweise die Stammfunktion e x  x  1  C wie in Beispiel 4.
Anmerkung: Die Stammfunktionen
x
n
 cos( x ) dx und
x
n
 cos( x ) dx beispielsweise wer-
den auf die gleiche Weise berechnet.
Bemerkung 6 (Substitutionsregel)
Seien f , g : a, b  IR zwei differenzierbare Funktionen. Dann gilt:
 f gx   g x dx  f gx   C
Leiten wir die rechte Seite nach der Kettenregel ab, so erhalte wir sofort die Aussage der Bemerkung.
Diese Integrationsregel ist sehr nützlich und wir werden dazu einige Beispiel rechnen. Dabei
werden wir stets bemüht sein, den Integranden in der Weise äquivalent umzuformen, daß sein
Aussehen der Form
f gx   gx 
entspricht – also die Ableitung der inneren Funktion wieder als Faktor auftritt. Während der
Berechnung der Stammfunktion f ersetzen (substituieren) wir die innere Funktion g(x) durch
die Variable u.
6
Beispiel 6
(Substitutionsregel)
Mit der Substitutionsregel erhält man die folgenden Stammfunktionen:
a)  x  1  x 2 dx  
b)  x  e x dx 
2
1
3
1  x 
2 3
C
1 x2
e  C
2
c) 
ln x 
1
dx   ln 2 x   C
x
2
d) 
ln x 
1 1 1
dx   ln     C
2
x x x
x
e) 
tan x 
1
dx   tan 2 x   C
2
2
cos x 
Es ist mit gx   x 2 als innerer Funktion und f u   1  u als äußerer Funktion
1
1
1
2
2
 x  1  x dx   2    2x  1  x dx   2   gx   1  gx  dx   2   1  u du 
3
1
1
1 1
1
1  u 3  C 
    1  u  2 du    3  1  u  2  C  
2
2 2
3

3
1

1  x 2   C.
3
Es ist mit gx   x 2 als innerer Funktion und f u   e u als äußerer Funktion
1
1
1
1 u
1 x2
x2
x2
g x 
u
 x  e dx  2   2x  e dx  2   gx   e dx  2   e du  2  e  C  2  e  C .
Es ist mit gx   ln x  als innerer Funktion und f u   u als äußerer Funktion
ln x 
1
1 2
ln 2 x 







dx

ln
x

dx

g
x

g
x
dx

u
du

u

C

C.
 x



x
2
2
Es ist mit gx  
1
x
als innerer Funktion und f u   ln u  als äußerer Funktion
Beispiel 4
ln x 
1  1 









dx

ln


dx

ln
g
x

g
x
dx

ln
u
du





 x2
  x   x2 


.
1 1 1
 u  ln u   u  C   ln     C
x x x
Es ist mit gx   tan x  als innerer Funktion und f u   u als äußerer Funktion
tan x 
1
1 2
 cos 2 x  dx   tan x   cos 2 x  dx   gx   gx dx   u du  2 u  C 
1
 tan 2 x   C .
2
7
Anmerkung: Das Riemann-Stieltjes-Integral wird die Substitutionsregel aus einer anderen
Perspektive beleuchten und das Verständnis noch vertiefen.
Mit der linearen Substitution hatten wir bereits einen Spezialfall der Substitutionsregel kennen
gelernt. Wir wollen diesem noch zwei weitere Spezialfälle hinzufügen, da sie hin und wieder
bei der Berechnung von Stammfunktionen nützlich sein können.
Bemerkung 6 (Spezialfälle der Substitutionsregel)
Für eine differenzierbare Funktion g : a, b  IR gilt:
g x 
 gx  dx  ln gx   C
sowie
n
 g x   gx dx 
g n 1 x 
 C ( n  IN )
n 1
Im ersten Falle haben wir als äußere Funktion f u   u1 und im zweiten Falle f u   u n . Deren Stammfunktionen kennen aber wir bereits aus der Tabelle der Grundintegrale, womit die
Aussage der Bemerkung gezeigt ist.
8